Assessment of the Effective Variants Leading to Higher Efficiency for the Geothermal Doublet, Using Numerical Analysis?Case Study from Poland (Szczecin Trough)
Abstract
:1. Introduction
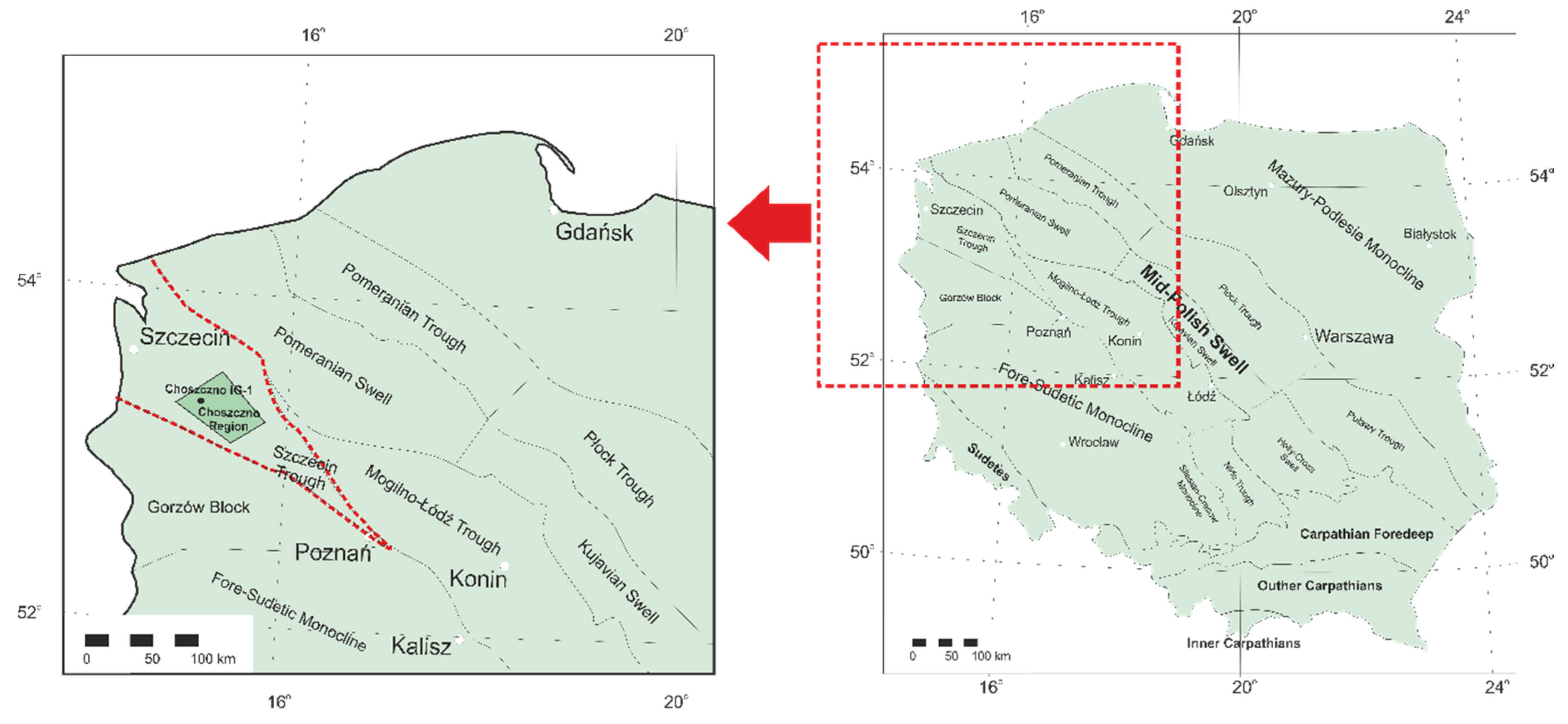
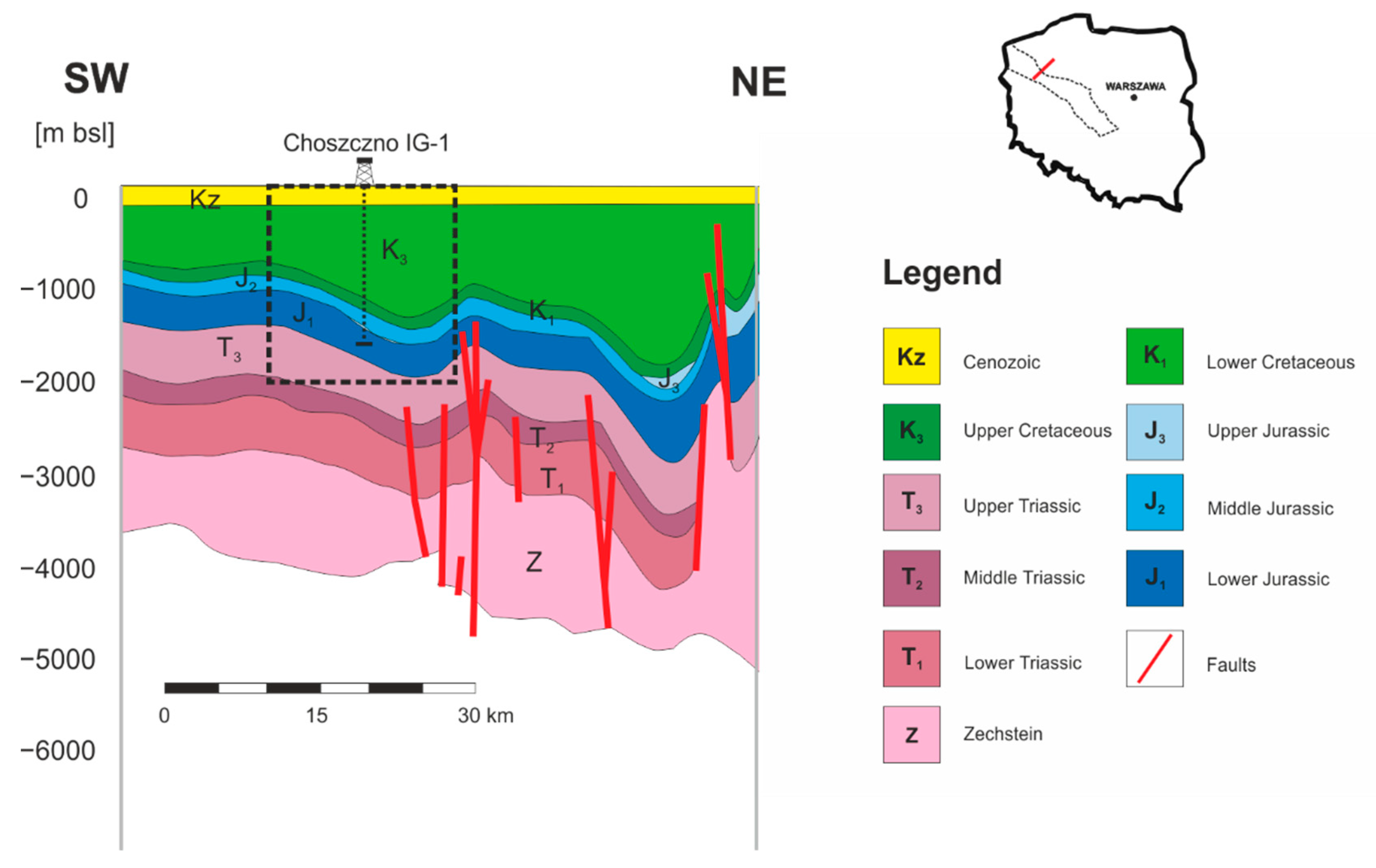
2. Geological Background
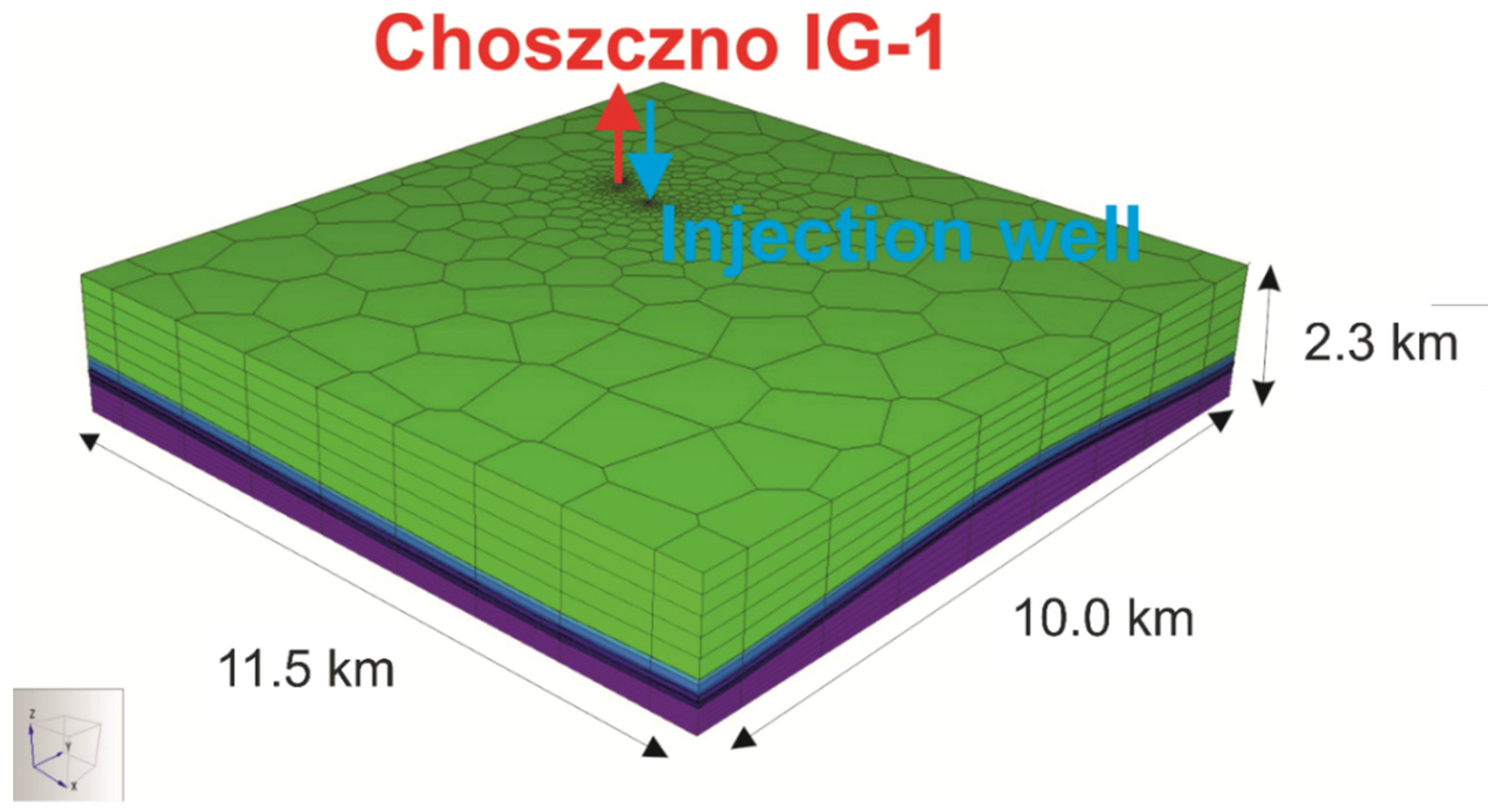
3. Numerical Methodology and Mathematical Model
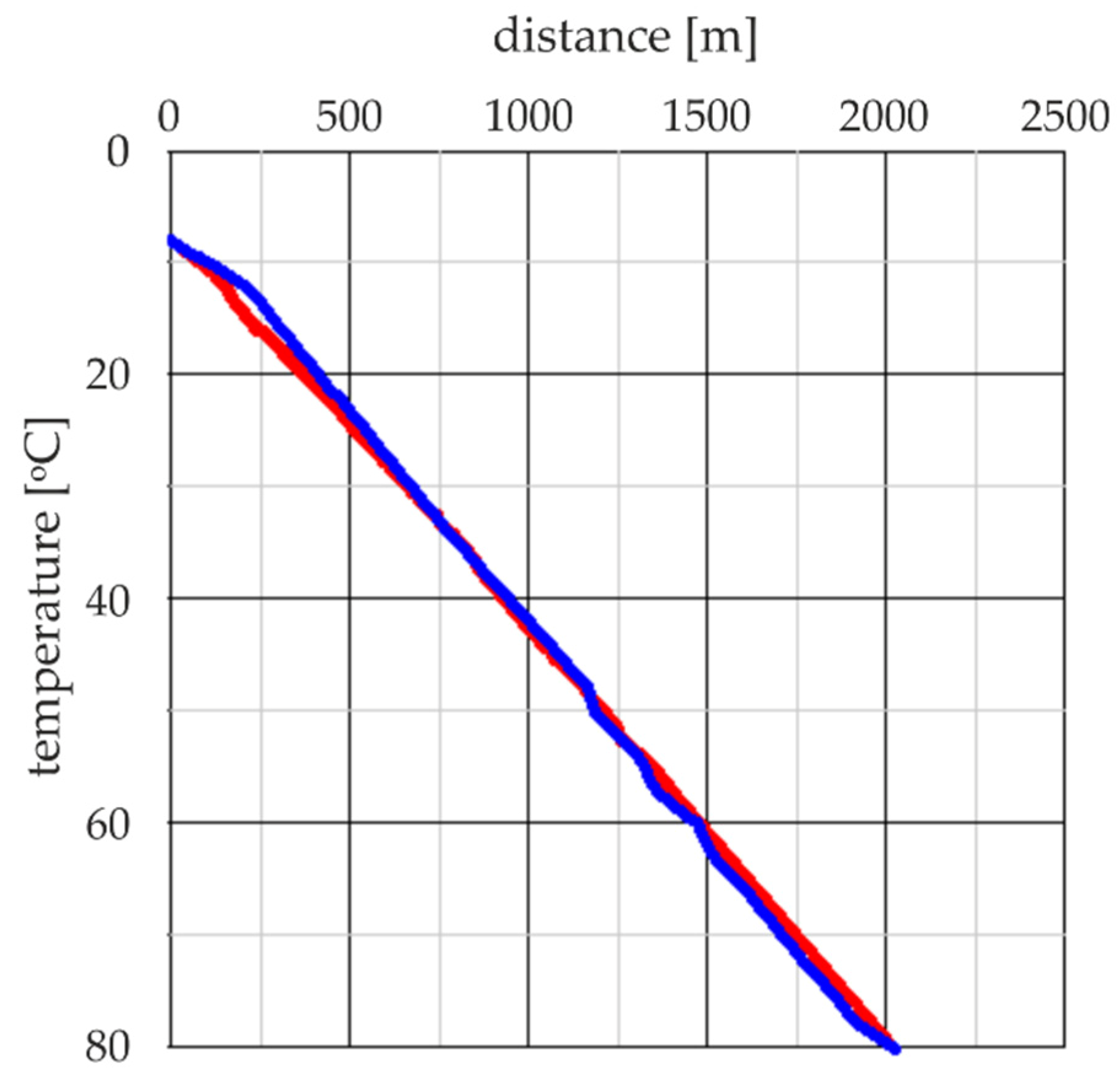
4. Results of Numerical Simulation
5. Thermal Power Estimations
- —thermal power of geothermal doublet (W),
- —brine outflow (m3/s),
- —brine specific heat (J/(kg K),
- —brine density (kg/m3),
- —brine temperature (°C),
- —assumed reference temperature (°C).
- —thermal energy (J),
- —thermal power of geothermal doublet (W),
- —time (s).
- —annual average thermal power of geothermal doublet (W),
- —energy received during time period (J),
- —analysed time period (s).
- —average amount of energy produced annually (J),
- —energy received during time period (50 years) (J),
- —number of years.
6. Discussion
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Kaczmarczyk, M.; Sowiżdżał, A.; Tomaszewska, B. Energetic and environmental aspects of individual heat generation for sustainable development at a local scale—A case study from Poland. Energies 2020, 13, 454. [Google Scholar] [CrossRef] [Green Version]
- Sowiżdżał, A.; Chmielowska, A.; Tomaszewska, B.; Operacz, A.; Chowaniec, J. Could geothermal water and Energy use improve living conditions? Environmental effects from Poland. Arch. Environ. Prot. 2019, 45, 109–118. [Google Scholar]
- Fridleifsson, I.B. Geothermal energy for the benefit of the people. Renew. Sustain. Energy Rev. 2001, 5, 299–312. [Google Scholar] [CrossRef] [Green Version]
- Badur, J.; Hyrzyński, R.; Lemański, M.; Ziółkowski, P.; Bykuć, S. On the production of electricity in Poland using a geothermal binary power plant—A thermodynamic overview—Part I. In ECOS 2019, Proceedings of the 32nd International Conference on Efficiency, Cost, Optimization, Simulation and Environmental Impact of Energy Systems, Wroclaw, Poland, 23–28 June 2019; Code, 157382; Stanek, W., Gładysz, P., Werle, S., Adamczyk, W., Eds.; Silesian University of Technology: Wroclaw, Poland, 2019; pp. 1621–1632. [Google Scholar]
- Lund, J.W. Direct utilization of geothermal energy. Energies 2010, 3, 1443–1471. [Google Scholar] [CrossRef]
- Górecki, W.; Sowiżdżał, A.; Hajto, M.; Wachowicz-Pyzik, A. Atlases of geothermal waters and energy resources in Poland. Environ. Earth Sci. 2015, 74, 7487–7495. [Google Scholar] [CrossRef] [Green Version]
- Pająk, L.; Tomaszewska, B.; Bujakowski, W.; Bielec, B.; Dendys, M. Review of the low-enthalpy lower cretaceous geothermal energy resources in Poland as an environmentally friendly source of heat for urban district heating systems. Energies 2020, 13, 1302. [Google Scholar] [CrossRef] [Green Version]
- Sowiżdżał, A. Geothermal energy resources in Poland—Overview of the current state of knowledge. Renew. Sustain. Energy Rev. 2018, 82, 4020–4027. [Google Scholar] [CrossRef]
- Barbier, E. Geothermal energy technology and current status. Renew. Sustain. Energy Rev. 2002, 6, 3–65. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’haeseleer, W. Comparison of thermodynamic cycles for power production from low-temperature geothermal heat source. Energy Convers. Manag. 2013, 66, 220–233. [Google Scholar] [CrossRef] [Green Version]
- Desideri, U.; Bidini, G. Study of possible optimization criteria for geothermal power plants. Energy Convers. Manag. 1997, 38, 168–191. [Google Scholar] [CrossRef]
- Tomasini-Montenegro, C.; Santoyo-Castelazo, E.; Gujba, H.; Romero, R.J.; Santoyo, E. Life cycle assessment of geothermal power generation technologies: An updated review. Appl. Therm. Eng. 2017, 114, 1119–1136. [Google Scholar] [CrossRef]
- DiPippo, R. Geothermal power plants: Evolution and performance assessments. Geothermics 2015, 53, 291–307. [Google Scholar] [CrossRef]
- Miecznik, M.; Sowiżdżał, A.; Tomaszewska, B.; Pająk, L. Modelling geothermal conditions in part of the Szczecin Trough—The Chociwel area. Geologos 2015, 21, 187–196. [Google Scholar] [CrossRef] [Green Version]
- Lous, M.; Larroque, F.; Dupuy, A.; Moignard, A. Thermal performance of a deep borehole heat exchanger: Insights from a synthetic coupled heat and flow model. Geothermics 2015, 57, 157–172. [Google Scholar] [CrossRef]
- Naldi, C.; Zanchini, E. Full-time-scale fluid-to-ground thermal response of a borefield with uniform fluid temperature. Energies 2019, 12, 3750. [Google Scholar] [CrossRef] [Green Version]
- Bujakowski, W.; Barbacki, A.; Miecznik, M.; Pajak, L.; Skrzypczak, R.; Sowizdzał, A. Modelling geothermal and operating parameters of EGS installations in the lower triassic sedimentary formations of the central Poland area. Renew. Energy 2015, 80, 441–453. [Google Scholar] [CrossRef]
- Miecznik, M. Problematyka modelowania numerycznego 3D złóż geotermalnych. Technika Poszukiwań Geologicznych Geotermia Zrównoważony Rozwój 2010, 1–2, 61–73. [Google Scholar]
- Chowaniec, J. Studium hydrogeologii zachodniej części Karpat polskich. Biuletyn Państwowego Instytutu Geologicznego 2009, 58, 762–773. [Google Scholar]
- Sowiżdżał, A. Perspektywy wykorzystania zasobów wód termalnych jury dolnej z regionu niecki szczecińskiej (północno-zachodnia Polska) w ciepłownictwie, balneologii i rekreacji. Przegląd Geologiczny 2010, 58, 613–621. [Google Scholar]
- Sowiżdżał, A. Potencjał Geotermalny Niecki Szczecińskiej; GEOS: Krakow, Poland, 2012; p. 119. [Google Scholar]
- Liao, K.; Zhang, S.; Ma, X.; Zou, Y. Numerical investigation of fracture compressibility and uncertainty on water-loss and production performance in tight oil reservoirs. Energies 2019, 12, 1189. [Google Scholar] [CrossRef] [Green Version]
- Liu, D.; Xiang, Y. A Semi-analytical method for three-dimensional heat transfer in multi-fracture enhanced geothermal systems. Energies 2019, 12, 1211. [Google Scholar] [CrossRef] [Green Version]
- Hyrzyński, R.; Ziółkowski, P.; Gotzman, S.; Kraszewski, B.; Badur, J. Thermodynamic analysis of the compressed air energy storage system coupled with the underground thermal energy storage. Res. Dev. Power Eng. Web Conf. E3s Web Conf. 2019, 137, 01023. [Google Scholar] [CrossRef]
- Sławiński, D. Un-stationary thermal analysis of the vertical ground heat exchanger within unsaturated soils. Renew. Energy 2020, 151, 805–815. [Google Scholar]
- Zhang, R.; Li, J.; Liu, G.; Yang, H.; Jiang, H. Analysis of coupled wellbore temperature and pressure calculation model and influence factors under multi-pressure system in deep-water drilling. Energies 2019, 12, 3533. [Google Scholar] [CrossRef] [Green Version]
- Lei, X.; Zheng, X.; Duan, C.; Ye, J.; Liu, K. Three-dimensional numerical simulation of geothermal field of buried pipe group coupled with heat and permeable groundwater. Energies 2019, 12, 3698. [Google Scholar] [CrossRef] [Green Version]
- Madejski, P.; Krakowska, P.; Habrat, M.; Puskarczyk, E.; Jędrychowski, M. Comprehensive approach for porous materials analysis using a dedicated preprocessing tool for mass and heat transfer modeling. J. Therm. Sci. 2018, 27, 479–486. [Google Scholar] [CrossRef]
- Vafai, K.; Tien, C.L. Boundary and inertial effects on flow and heat transfer in porous media. Int. J. Heat Mass. Transf. 1981, 24, 195–203. [Google Scholar] [CrossRef]
- Hooman, K. Heat and fluid flow in a rectangular microchannel filled with a porous medium. Int. J. Heat Mass Transf. 2008, 51, 5804–5810. [Google Scholar] [CrossRef]
- Ziółkowski, P. Porous structures in aspects of transpirating cooling of oxycombustion chamber walls. AIP Conf. Proc. 2019, 2077, 020065. [Google Scholar] [CrossRef]
- Moghaddam, R.N.; Jamiolahmady, M. Slip flow in porous media. Fuel 2016, 173, 298–310. [Google Scholar] [CrossRef]
- Ziółkowski, P.; Badur, J. On Navier slip and Reynolds transpiration numbers. Arch. Mech. 2018, 70, 269–300. [Google Scholar]
- Vignoles, G.L.; Charrier, P.; Preux, C.; Dubroca, B. Rarefied pure gas transport in non-isothermal porous media: Effective transport properties from homogenization of the kinetic equation. Transp. Porous Media 2008, 73, 211–232. [Google Scholar] [CrossRef] [Green Version]
- Tomaszewska, B.; Pająk, L. Dynamics of clogging processes in injection wells used to pump highly mineralized thermal waters into the sandstone structures lying under the Polish Lowlands. Arch. Environ. 2012, 38, 105–117. [Google Scholar] [CrossRef] [Green Version]
- Górecki, W.; Szczepański, A.; Hajto, M.; Papiernik, B.; Kuźniak, T.; Haładus, A.; Kania, J.; Kępińska, B.; Sowiżdżał, A.; Kotyza, J. (Eds.) Atlas Zasobów Geotermalnych Formacji Mezozoicznej na Niżu Polskim; Publisher Department of Fossil Fuels, AGH University of Science and Technology: Krakow, Poland, 2006. [Google Scholar]
- Olszewska, A.; Miśkiewicz, A.; Zakrzeska-Kołtuniewicz, G.; Lankof, L.; Pająk, L. Multi-barrier system against migration of radionuclides from radioactive waste repository. Nukleonika 2015, 60, 557–563. [Google Scholar] [CrossRef] [Green Version]
- Dąbrowski, S.; Kapuściński, J.; Nowicki, K.; Przybyłek, J.; Szczepański, A. Metodyka Modelowania Matematycznego w Badaniach i Obliczeniach Hydrogeologicznych—Poradnik Metodyczny; Bogucki Wyd. Naukowe, Poznań: Krakow, Poland, 2011; p. 362. [Google Scholar]
- Ziółkowski, P.; Badur, J. A theoretical, numerical and experimental verification of the Reynolds thermal transpiration law. Int. J. Numer. Methods Heat Fluid Flow 2018, 28, 64–80. [Google Scholar] [CrossRef]
- Madejski, P.; Krakowska, P. Research on fluid flow and permeability in low porous rock sample using laboratory and computational techniques. Energies 2019, 12, 4684. [Google Scholar]
- Dendys, M.; Tomaszewska, B.; Pająk, L. Modelowanie numeryczne jako narzędzie wspomagające badania systemow geotermalnych. In Modelowanie Matematyczne w Hydrogeologii; Krawiec, A., Jamorowska, I., Eds.; Wyd. Naukowe Uniwersytetu Mikołaja Kopernika: Krakow, Poland, 2014; pp. 199–206. [Google Scholar]
- Dendys, M.; Tomaszewska, B.; Pająk, L. Numerical modelling in research on geothermal systems. Bull. Geogr. Phisical Geogr. Ser. 2015, 9, 39–44. [Google Scholar] [CrossRef] [Green Version]
- Zdechlik, R.; Tomaszewska, B.; Dendys, M.; Pająk, L. Przegląd oprogramowania do numerycznego modelowania procesów środowiskowych w systemach geotermalnych. Przegląd Geologiczny 2015, 63, 1150–1154. [Google Scholar]
- Han, G.; Chen, Y.; Liu, X. Investigation of analysis methods for pulse decay tests considering gas adsorption. Energies 2019, 12, 2562. [Google Scholar] [CrossRef] [Green Version]
- Krakowska, P.; Puskarczyk, E.; Jędrychowski, M.; Habrat, M.; Madejski, P.; Dohnalik, M. Innovative characterization of tight sandstones from Paleozoic basins in Poland using X-ray computed tomography supported by nuclear magnetic resonance and mercury porosimetry. J. Pet. Sci. Eng. 2018, 166, 389–405. [Google Scholar] [CrossRef]
- Cao, N.; Lei, G.; Dong, P.; Li, H.; Wu, Z.; Li, Y. Stress-dependent permeability of fractures in tight reservoirs. Energies 2019, 12, 117. [Google Scholar] [CrossRef] [Green Version]
- Puskarczyk, E.; Krakowska, P.; Jędrychowski, M.; Habrat, M.; Madejski, P. A novel approach to the quantitative interpretation of petrophysical parameters using nano-CT: Example of Paleozoic carbonates. Acta Geophys. 2018, 66, 1453–1461. [Google Scholar] [CrossRef] [Green Version]
- Ma, X.; Li, X.; Zhang, S.; Zhang, Y.; Hao, X.; Liu, J. Impact of local efects on the evolution of unconventional rock permeability. Energies 2019, 12, 478. [Google Scholar] [CrossRef] [Green Version]
- Pruess, K. The TOUGH codes—A family of simulation tools for multiphase flow and transport processes in permeable media. Vadose Zone J. 2004, 3, 738–746. [Google Scholar]
- Pruess, K.; Finsterle, S.; Moridis, G.; Oldenburg, C.; Wu, Y.-S. General-purpose reservoir simulators: The TOUGH2 family. GRC Bull. 1997, 26, 53–57. [Google Scholar]
- Wachowicz-Pyzik, A.; Sowiżdżał, A.; Pająk, L. Prediction of capacity of geothermal doublet located in the vicinity of Kalisz using the numerical modelling. E3s Web Conf. 2018, 49. [Google Scholar] [CrossRef] [Green Version]
- Pruess, K.; García, J.; Kovscek, T.; Oldenburg, C.; Rutqvist, J.; Steefel, C.; Xu, T. Code Intercomparison builds confidence in numerical simulation models for geologic disposal of CO2. Energy 2004, 29, 14311–14444. [Google Scholar] [CrossRef]
- Finsterle, S.; Commer, M.; Edmiston, J.; Jung, Y.; Kowalsky, M.B.; Pau, G.S.H.; Wainwright, H.; Zhang, Y. iTOUGH2: A simulation-optimization framework for analyzing multiphysics subsurface systems. Comput. Geosci. 2017, 108, 8–20. [Google Scholar] [CrossRef] [Green Version]
- Narkiewicz, M.; Dadlez, R. Geological regional subdivision of Poland: General guidelines and proposed schemes ofsub-Cenozoic and sub-Permian units. Przegląd Geologiczny 2008, 56, 391–397. [Google Scholar]
- Central Geological Database. Available online: http://baza.pgi.gov.pl/ (accessed on 5 June 2019).
- Jaskowiak-Schoeneichowa, M. Profile Głębokich Otworów Wiertniczych Instytutu Geologicznego Choszczno IG-1; Wydawnictwa geologiczne: Warsaw, Poland, 1978; p. 130. [Google Scholar]
- Żelaźniewicz, A.; Aleksandrowski, P.; Buła, Z.; Karnkowski, P.H.; Konon, A.; Oszczypko, N.; Ślączka, A.; Żaba, J.; Żytko, K. Regionalizacja Tektoniczna Polski; Komitet Nauk Geologicznych PAN: Warsaw, Poland, 2011. [Google Scholar]
- Szewczyk, J.; Hajto, M. Strumień cieplny a temperatury wgłębne na obszarze Niżu Polskiego. In Atlas Zasobów Geotermalnych Formacji Mezozoicznej na Niżu Polskim; Górecki, W., Ed.; Wydawnictwo Ministerstwa Środowiska, NFOŚiGW, AGH, PIG: Krakow, Poland, 2006; p. 143146. [Google Scholar]
- Sowiżdżał, A. Analiza Geologiczna i Ocena Zasobów Wód i Energii Geotermalnej Formacji Mezozoicznej Niecki Szczecińskiej; AGH University of Science and Technology Publishers: Krakow, Poland, 2009; p. 146. [Google Scholar]
- Wojtowicz, J. Wyniki badań geofizyki wiertniczej. In Profile Głębokich Otworów Wiertniczych Instytutu Geologicznego Choszczno IG-1; Jaskowiak-Schoeneichowa, M., Ed.; Wydawnictwa geologiczne: Warsaw, Poland, 1978; pp. 110–113. [Google Scholar]
- Dąbrowski, A. Wyniki badań własności skał. In Profile Głębokich Otworów Wiertniczych Instytutu Geologicznego Choszczno IG-1; Jaskowiak-Schoeneichowa, M., Ed.; Wydawnictwa geologiczne: Warsaw, Poland, 1978; pp. 106–109. [Google Scholar]
- Badur, J. Rozwój Pojęcia Energii, Development of Energy Concept; IMP PAN Publishers: Gdansk, Poland, 2009; pp. 11–167. (In Polish) [Google Scholar]
- Kowalczyk, S.; Karcz, M.; Badur, J. Analysis of thermodynamic and material properties assumptions for three-dimensional SOFC modelling. Arch. Thermodyn. 2006, 27, 21–38. [Google Scholar]
- Badur, J.; Ziółkowski, P.; Kornet, S.; Kowalczyk, T.; Banaś, K.; Bryk, M.; Ziółkowski, P.J.; Stajnke, M. Enhanced energy conversion as a result of fluid-solid interaction in micro- and nanoscale. J. Theor. Appl. Mech. 2018, 56, 329–332. [Google Scholar] [CrossRef] [Green Version]
- Pruess, K.; Narasimhan, T.N. A Practical method for modeling fluid and heat flow in fractured porous media. Soc. Pet. Eng. J. 1985, 25, 14–26. [Google Scholar] [CrossRef] [Green Version]
- Pruess, K. TOUGH User’s Guide; Report LBL-20700; Lawrence Berkeley Laboratory: Berkeley, CA, USA, 1987.
- Pruess, K. TOUGH2—A General-Purpose Numerical Simulator for Multiphase Fluid and Heart Flow; Report LBNL-29400; Lawrence Berkeley Laboratory: Berkeley, CA, USA, 1991.
- Pruess, K.; Simmons, A.; Wu, Y.S.; Moridis, G. TOUGH2 Software Qualification; Report LBL-38383; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1996.
- Wu, Y.S.; Ahlers, C.F.; Fraser, P.; Simmons, A.; Pruess, K. Software Qualification of Selected TOUGH2 Modules; Research Report, Earth Sciences Division, LBL-39490, UC-800; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1996.
- Baca, R.G.; Seth, M.S. Benchmark Testing of Thermohydrologic Computer Codes; Report CNWRA 960–03; Center for Nuclear Waste Regulatory Analyses: San Antonia, TX, USA, 1996.
- Wu, Y.S.; Haukwa, C.; Mukhopadyay, S. TOUGH2 V1.4 and T2R3D V1.4: Verification and Validation; Report and User’s Manual, Rev 00; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1999.
- O’Sullivan, M.J.; Pruess, K.; Lippmann, M.J. State of the art of geothermal reservoir simulation. Geothermics 2001, 30, 395–429. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide, V2.0; Report LBNL-43134; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1999.
- Finsterle, S.; Kowalsky, M.B.; Pruess, K. TOUGH: Model use, calibration and validation. Trans. ASABE 2012, 55, 1275–1290. [Google Scholar] [CrossRef]
- Plasencia, M.; Pedersen, A.; Arnaldsson, A.; Berthet, J.C.; Jónsson, H. Geothermal model calibration using a global minimization algorithm based on finding saddle points and minima of the objective function. Comput. Geosci. 2014, 65, 110–117. [Google Scholar] [CrossRef]
- White, M.D.; Podgorney, R.; Kelkar, S.M.; McClure, M.W.; Danko, G.; Ghassemi, A.; Fu, P.; Bahrami, D.; Barbier, C.; Cheng, Q.; et al. Benchmark Problems of the Geothermal Technologies Office Code Comparison Study; PNNL-26016; Pacific Northwest National Laboratory: Richland, WA, USA, 2016.
- Rutqvist, J. An overview of TOUGH-based geomechanics models. Comput. Geosci. 2017, 108, 56–63. [Google Scholar] [CrossRef] [Green Version]
- Vasini, E.M.; Battistelli, A.; Berry, P.; Bonduá, S.; Bortolotti, V.; Cormio, C.; Geloni, C.; Pan, L. Interpretation of production tests in geothermal wells with T2Well-EWASG. Geothermics 2018, 73, 158–167. [Google Scholar] [CrossRef] [Green Version]
- Moridis, G.J.; Freeman, C.M. The RealGas and RealGasH2O options of the TOUGH+ code for the simulation of coupled fluid and heat flow in tight/shale gas systems. Comput. Geosci. 2014, 65, 56–71. [Google Scholar] [CrossRef] [Green Version]
- Doughty, C. Generating one-column grids with fractal flow dimension. Comput. Geosci. 2017, 108, 33–41. [Google Scholar] [CrossRef] [Green Version]
- Bonduá, S.; Battistelli, A.; Berry, P.; Bortolotti, V.; Consonni, A.; Cormio, C.; Geloni, C.; Vasini, E.M. 3D Voronoi grid dedicated software for modeling gas migration in deep layered sedimentary formations with TOUGH2-TMGAS. Comput. Geosci. 2017, 108, 50–55. [Google Scholar] [CrossRef]
- Sentis, M.L.; Gable, C.W. Coupling LaGrit unstructured mesh generation and model setup with TOUGH2 flow and transport: A case study. Comput. Geosci. 2017, 108, 42–49. [Google Scholar] [CrossRef]
- Lukawski, M.Z.; Silverman, R.L.; Tester, J.W. Uncertainty analysis of geothermal well drilling and completion costs. Geothermics 2016, 64, 382–391. [Google Scholar] [CrossRef] [Green Version]
- Asai, P.; Panja, P.; McLennan, J.; Moore, J. Performance evaluation of enhanced geothermal system (EGS): Surrogate models, sensitivity study and ranking key parameters. Renew. Energy 2018, 122, 184–195. [Google Scholar] [CrossRef]
- Chen, M.; Tompson, A.F.B.; Mellors, R.J.; Ramirez, A.L.; Dyer, K.M.; Yang, X.; Wagoner, J.L. An efficient Bayesian inversion of a geothermal prospect using a multivariate adaptive regression spline method. Appl. Energy 2014, 136, 619–627. [Google Scholar] [CrossRef] [Green Version]
- Olasolo, P.; Juárez, M.C.; Olasolo, J.; Morales, M.P.; Valdani, D. Economic analysis of enhanced geothermal systems (EGS). A review of software packages for estimating and simulating costs. Appl. Eng. 2016, 104, 647–658. [Google Scholar] [CrossRef]
- Gan, Q.; Elsworth, D. Production optimization in fractured geothermal reservoirs by coupled discrete fracture network modelling. Geothermics 2016, 62, 131–142. [Google Scholar] [CrossRef] [Green Version]
- Ekneligoda, T.C.; Min, K.B. Determination of optimum parameters of doublet system in a horizontally fractured geothermal reservoir. Renew. Energy 2014, 65, 152–160. [Google Scholar] [CrossRef]
- Mengying, L.; Noam, L. Comparative analysis of power plant options for enhanced geothermal systems (EGS). Energies 2014, 7, 8427–8445. [Google Scholar]
- Golub, M.; Kurevija, T.; Koščak-Kolin, S. Thermodynamic cycle optimization in the geothermal energy production. Rudarsko Geolosko Naftni Zbornik 2004, 16, 81–84. [Google Scholar]
- Chen, M.; Tompson, A.F.B.; Mellors, R.J.; Abdalla, O. An efficient optimization of well placement and control for a geothermal prospect under geological uncertainty. Appl. Energy 2015, 137, 352–363. [Google Scholar] [CrossRef] [Green Version]
- Zeng, Y.; Tang, L.; Wu, N.; Cao, Y. Analysis of influencing factors of production performance of enhanced geothermal system: A case study at Yangbajing geothermal field. Energy 2017, 127, 218–235. [Google Scholar] [CrossRef]
- Aliyu, M.D.; Chen, H.P. Optimum control parameters and long-term productivity of geothermal reservoirs using coupled thermo-hydraulic process modelling. Renew. Energy 2017, 112, 151–165. [Google Scholar] [CrossRef]
- Bayer, P.; Rybach, L.; Blum, P.; Brauchler, R. Review of life cycle environmental effects of geothermal power generation. Renew. Sustain. Energy Rev. 2013, 26, 446–463. [Google Scholar] [CrossRef]
- Willems, C.J.L.; Nick, H.M. Towards optimisation of geothermal heat recovery: An example from the West Netherlands Basin. Appl. Energy 2019, 247, 582–593. [Google Scholar] [CrossRef]
- Raos, S.; Ilak, P.; Rajšl, I.; Bilić, T.; Trullenque, G. Multiple-criteria decision-making for assessing the enhanced geothermal systems. Energies 2019, 12, 1597. [Google Scholar] [CrossRef] [Green Version]
- Luiso, P.; Paoletti, V.; Nappi, R.; La Manna, M.; Cella, F.; Gaudiosi, G.; Fedi, M.; Iorio, M. A multidisciplinary approach to characterize the geometry of active faults: The example of Mt. Massico, Southern Italy. Geophys. J. Int. 2018, 213, 1673–1681. [Google Scholar] [CrossRef]
- Wachowicz-Pyzik, A.; Sowiżdżał, A.; Pająk, L. The influence of variability of calculation grids on the results of numerical modeling of geothermal doublets—An example from the Choszczno area, north-western Poland. J. Phys. Conf. Ser. 2016, 745. [Google Scholar] [CrossRef]
- Sharqawy, M.H.; Lienhard, V.J.H.; Zubari, S.M. Thermophisical properties of seawater: A review of exisiting correlations and data. Desalin. Water Treat. 2010, 16, 354–380. [Google Scholar] [CrossRef]
- Feidt, M. Thermodynamique et Optimization Énergétique das Systems et Procédés; Technique et Documentation: Paris, France, 1987. (In French) [Google Scholar]
- Hatsopoulos, G.N.; Keenan, J.H. Principles of General Thermodynamics; Wiley: New York, NY, USA, 1965. [Google Scholar]
- Bejan, A. Entropy Generation Through Heat and Fluid Flow; Wiley: New York, NY, USA, 1982. [Google Scholar]
- Iorio, M.; Carotenuto, A.; Corniello, A.; Di Fraia, S.; Massarotti, N.; Mauro, A.; Somma, R.; Vanoli, L. Low enthalpy geothermal systems in structural controlled areas: A sustainability analysis of geothermal resource for heating plant (the Mondragone case in Southern Appennines, Italy). Energies 2020, 13, 1237. [Google Scholar] [CrossRef] [Green Version]
- Kiryukhin, A.V.; Vorozheikina, L.A.; Voronin, P.O.; Kiryukhin, P.A. Thermal and permeability structure and recharge conditions of the low temperature Paratunsky geothermal reservoirs in Kamchatka, Russia. Geothermics 2017, 70, 47–61. [Google Scholar] [CrossRef]
- Agemar, T.; Weber, J.; Schulz, R. Deep geothermal energy production in Germany. Energies 2014, 7, 4397–4416. [Google Scholar] [CrossRef]
- Dussel, M.; Lüschen, E.; Thomas, R.; Agemar, T.; Fritzer, T.; Sieblitz, S.; Huber, B.; Birner, J.; Schulz, R. Forecast for thermal water use from upper Jurassic carbonates in the Munich region (south German Molasse Basin). Geothermics 2016, 60, 13–30. [Google Scholar] [CrossRef]
- Agemar, T.; Weber, J.; Moeck, I. Assessment and public reporting of geothermal resources in Germany: Review and outlook. Energies 2018, 11, 332. [Google Scholar] [CrossRef] [Green Version]
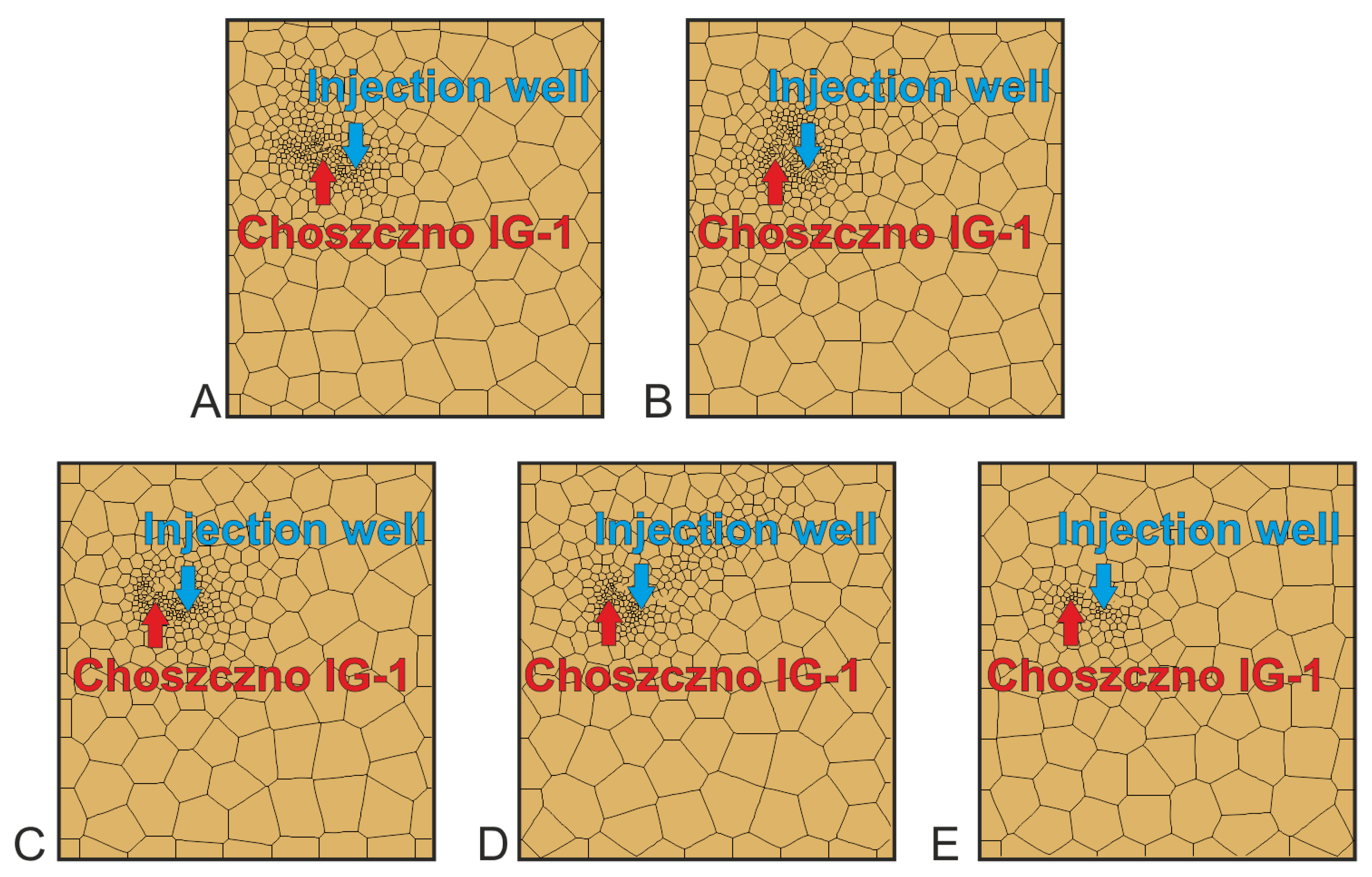
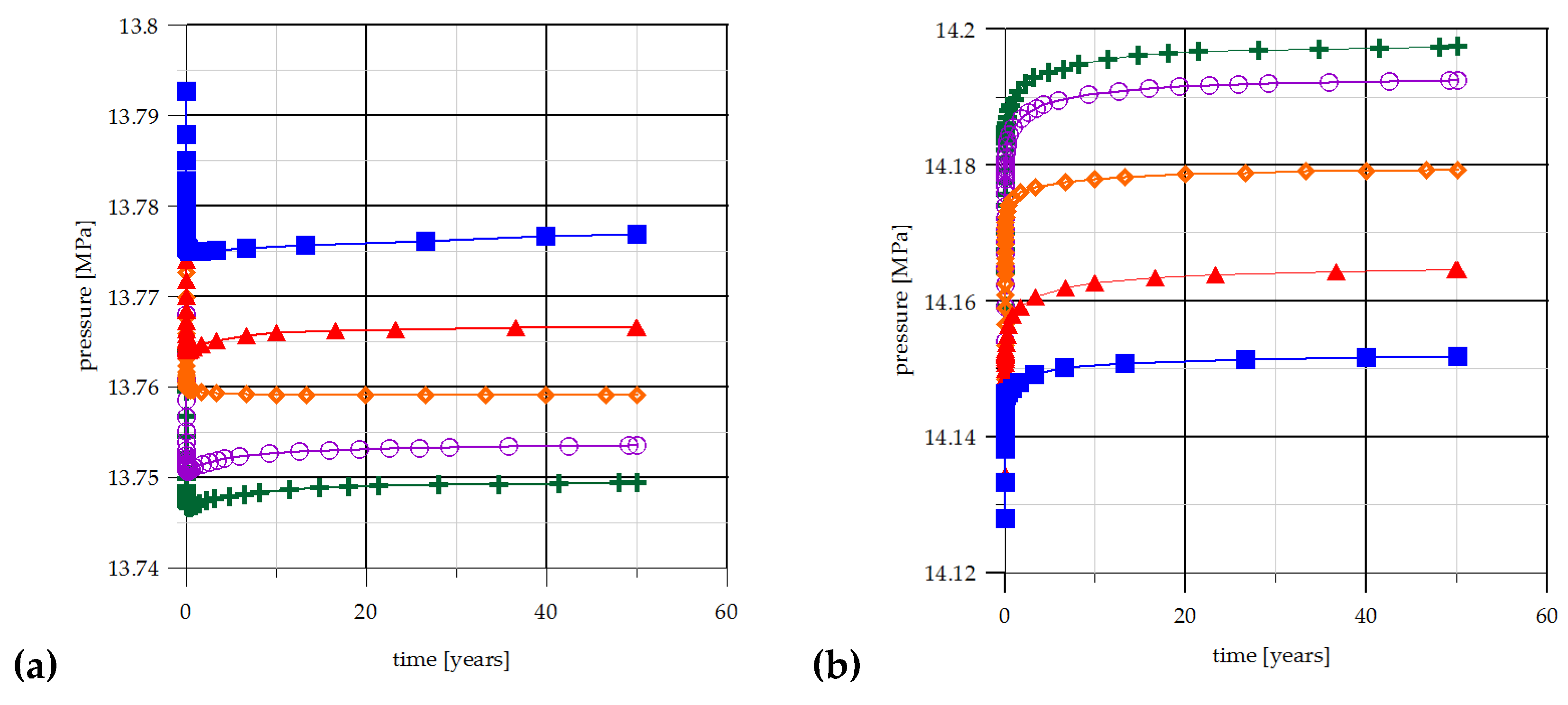
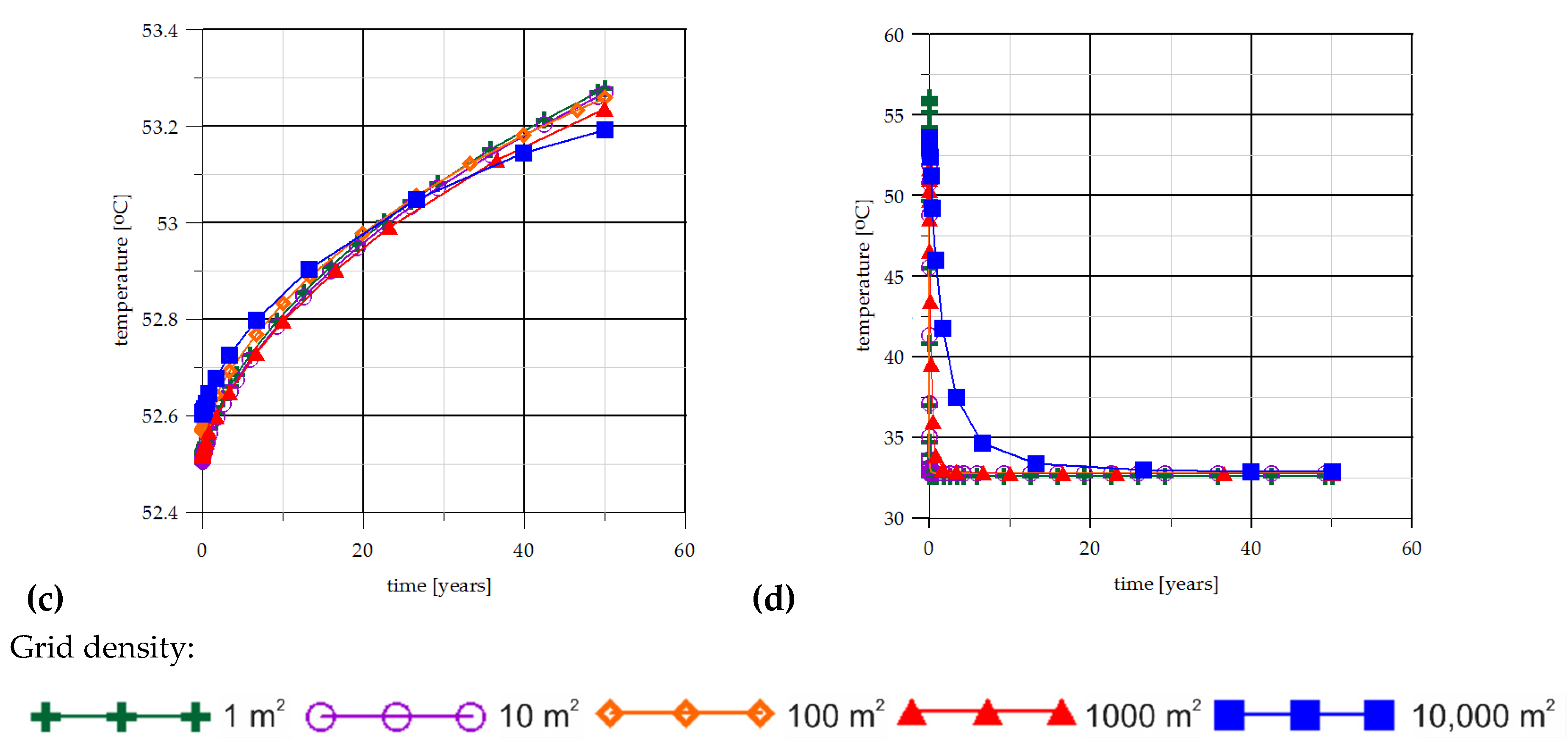

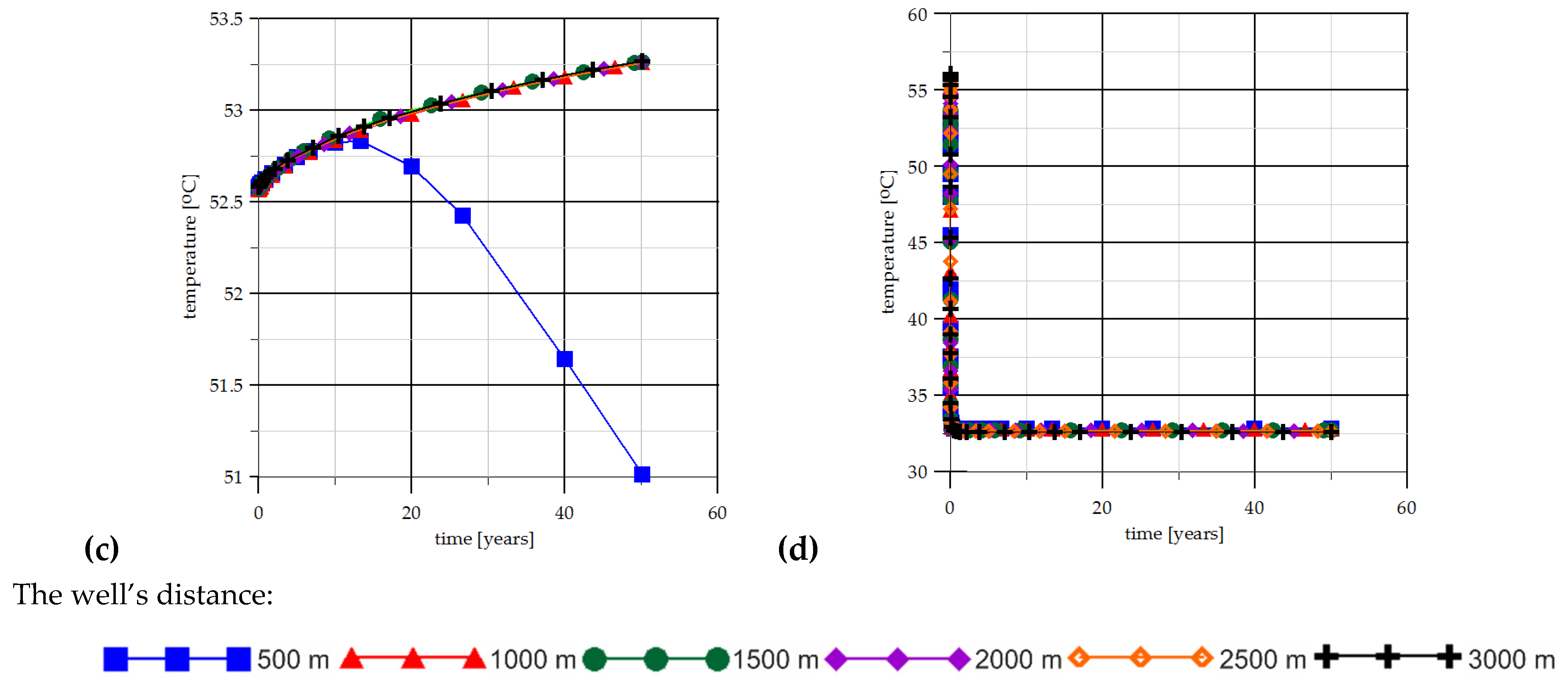


| No. | Geological Formations | Density (g/m3) | Porosity (%) | Permeability (mD) in X,Y,Z Direction | Thermal Conductivity (W/mK) | Specific Heat (J/kgK) |
|---|---|---|---|---|---|---|
| 1 | Cenozoic, Cretaceous and Upper and Middle Jurassic | 2220 | 10 | 1;1; 0.1 | 2.1 | 850 |
| 2 | Upper Toarcian | 2300 | 11 | 850; 850; 85 | 2.5 | 850 |
| 3 | Lower Toarcian | 2410 | 11.8 | 240; 240; 24 | 2.5 | 850 |
| 4 | Upper Pliensbachian | 1990 | 20.5 | 1137.5; 1137.5; 113.7 | 2.4 | 850 |
| 5 | Lower Pliensbachian | 2190 | 7.5 | 120; 120; 12 | 2.4 | 850 |
| 6 | Upper Sinemurian | 2070 | 21.5 | 1712.5; 1712.5; 171 | 3.0 | 900 |
| 7 | Lower Sinemurian | 1980 | 21.8 | 1170; 1170; 117 | 3.0 | 900 |
| 8 | Triassic | 2220 | 10 | 1;1; 0.1 | 3.0 | 900 |
| Grid Density (m2) | Results | Wells’ Distance (km) (Grid Density 100 m2) | Results | ||
|---|---|---|---|---|---|
| (TJ/yr) | (KW) | (TJ/yr) | (kW) | ||
| 1 | 5858.7 | 3713 | 0.5 | 5702.1 | 3614 |
| 10 | 5856.6 | 3711 | 1 | 5860.1 | 3714 |
| 100 | 5860.1 | 3714 | 1.5 | 5863.5 | 3716 |
| 1000 | 5853.6 | 3710 | 2 | 5861.3 | 3715 |
| 10,000 | 5858.1 | 3713 | 2.5 | 5861.1 | 3715 |
| 3 | 5863.0 | 3716 | |||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wachowicz-Pyzik, A.; Sowiżdżał, A.; Pająk, L.; Ziółkowski, P.; Badur, J. Assessment of the Effective Variants Leading to Higher Efficiency for the Geothermal Doublet, Using Numerical Analysis?Case Study from Poland (Szczecin Trough). Energies 2020, 13, 2174. https://doi.org/10.3390/en13092174
Wachowicz-Pyzik A, Sowiżdżał A, Pająk L, Ziółkowski P, Badur J. Assessment of the Effective Variants Leading to Higher Efficiency for the Geothermal Doublet, Using Numerical Analysis?Case Study from Poland (Szczecin Trough). Energies. 2020; 13(9):2174. https://doi.org/10.3390/en13092174
Chicago/Turabian StyleWachowicz-Pyzik, Anna, Anna Sowiżdżał, Leszek Pająk, Paweł Ziółkowski, and Janusz Badur. 2020. "Assessment of the Effective Variants Leading to Higher Efficiency for the Geothermal Doublet, Using Numerical Analysis?Case Study from Poland (Szczecin Trough)" Energies 13, no. 9: 2174. https://doi.org/10.3390/en13092174
APA StyleWachowicz-Pyzik, A., Sowiżdżał, A., Pająk, L., Ziółkowski, P., & Badur, J. (2020). Assessment of the Effective Variants Leading to Higher Efficiency for the Geothermal Doublet, Using Numerical Analysis?Case Study from Poland (Szczecin Trough). Energies, 13(9), 2174. https://doi.org/10.3390/en13092174







