Experimental and Computational Study of Thermal Processes in Red Clays Exposed to High Temperatures
Abstract
:1. Introduction
2. Materials and Methods
2.1. Description of Clays Selected for Investigations
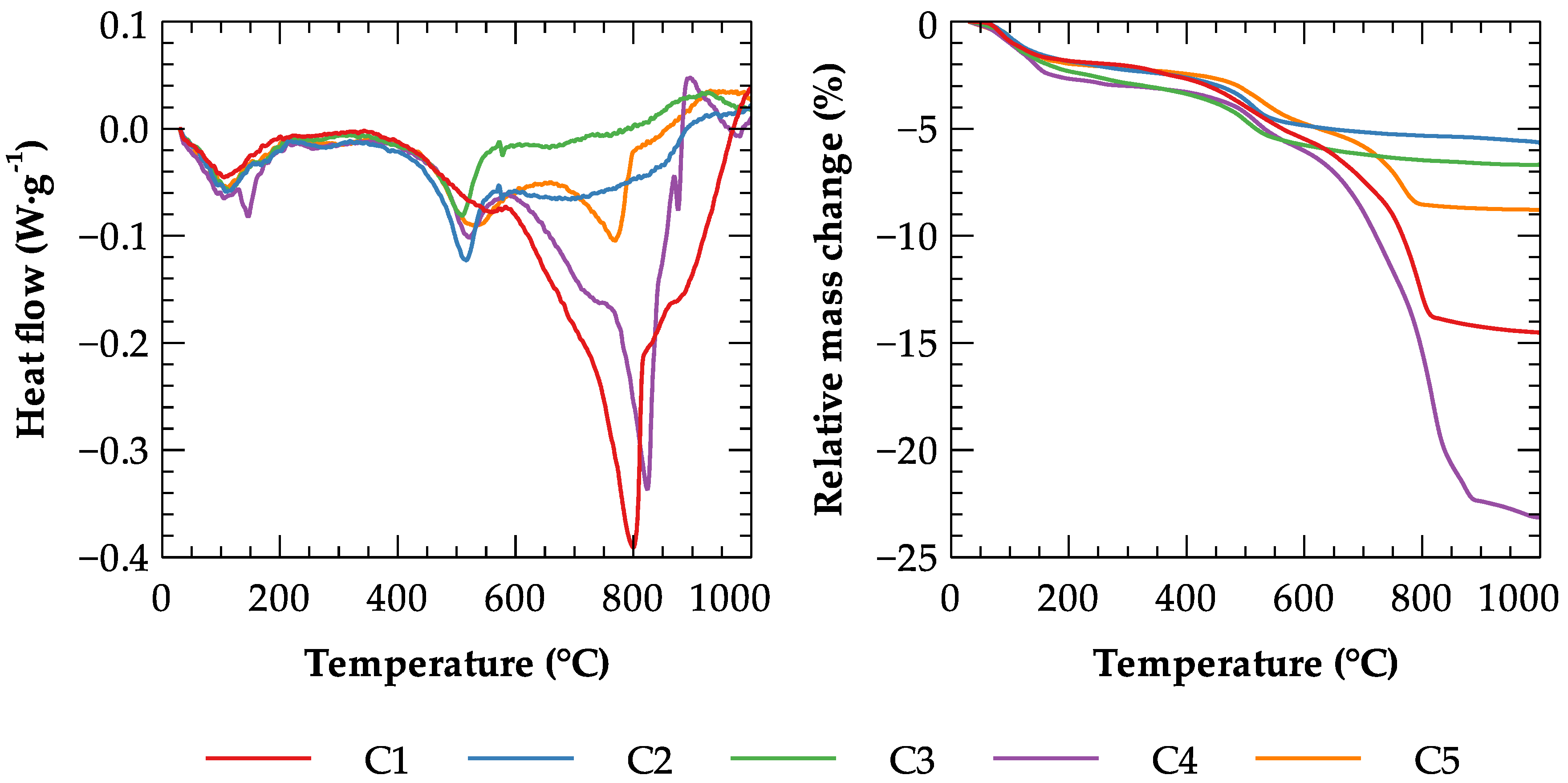
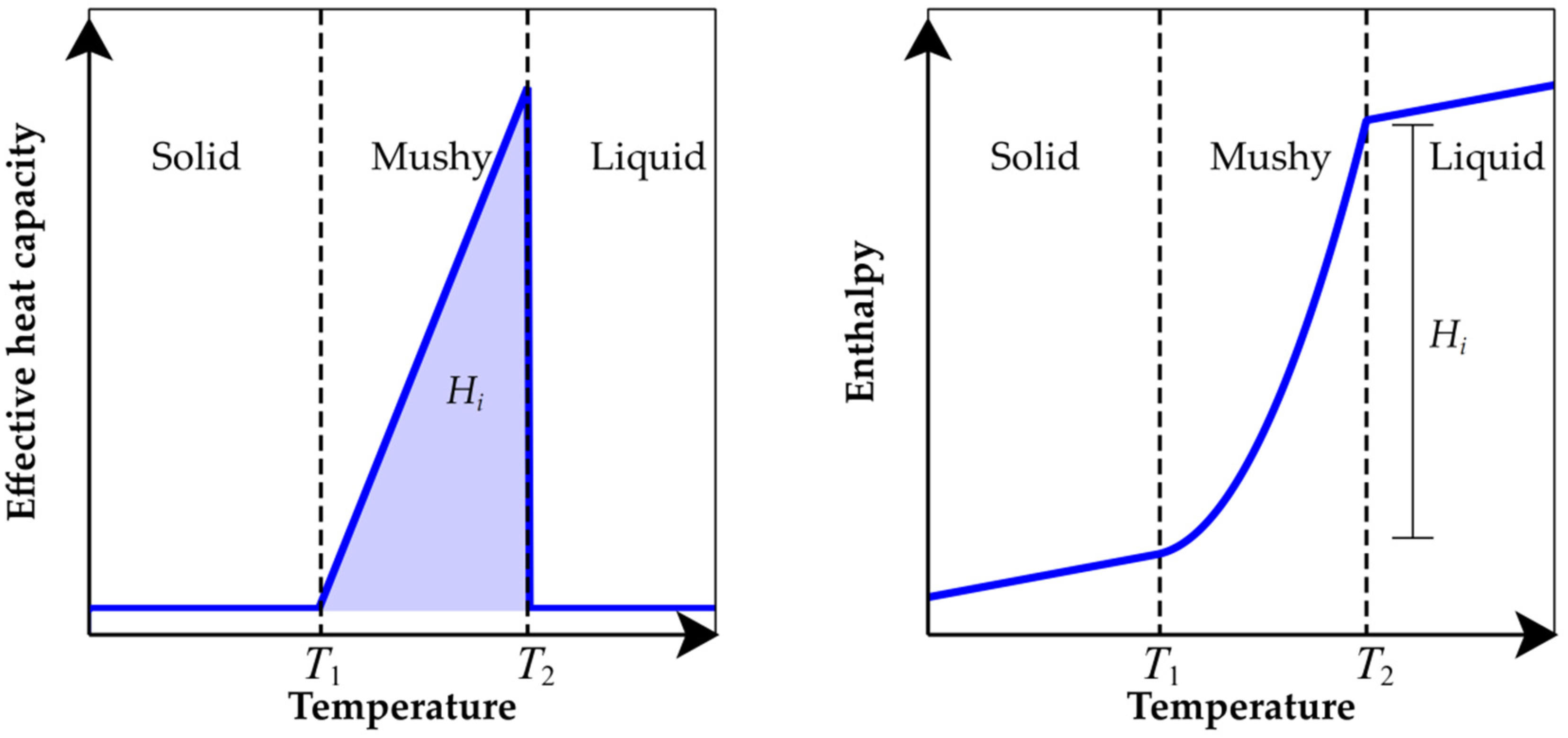
2.2. Determination of Effective Parameters Describing the High Temperature Performance
2.3. Numerical Analysis of Energy Demands during Firing
3. Results and Discussion
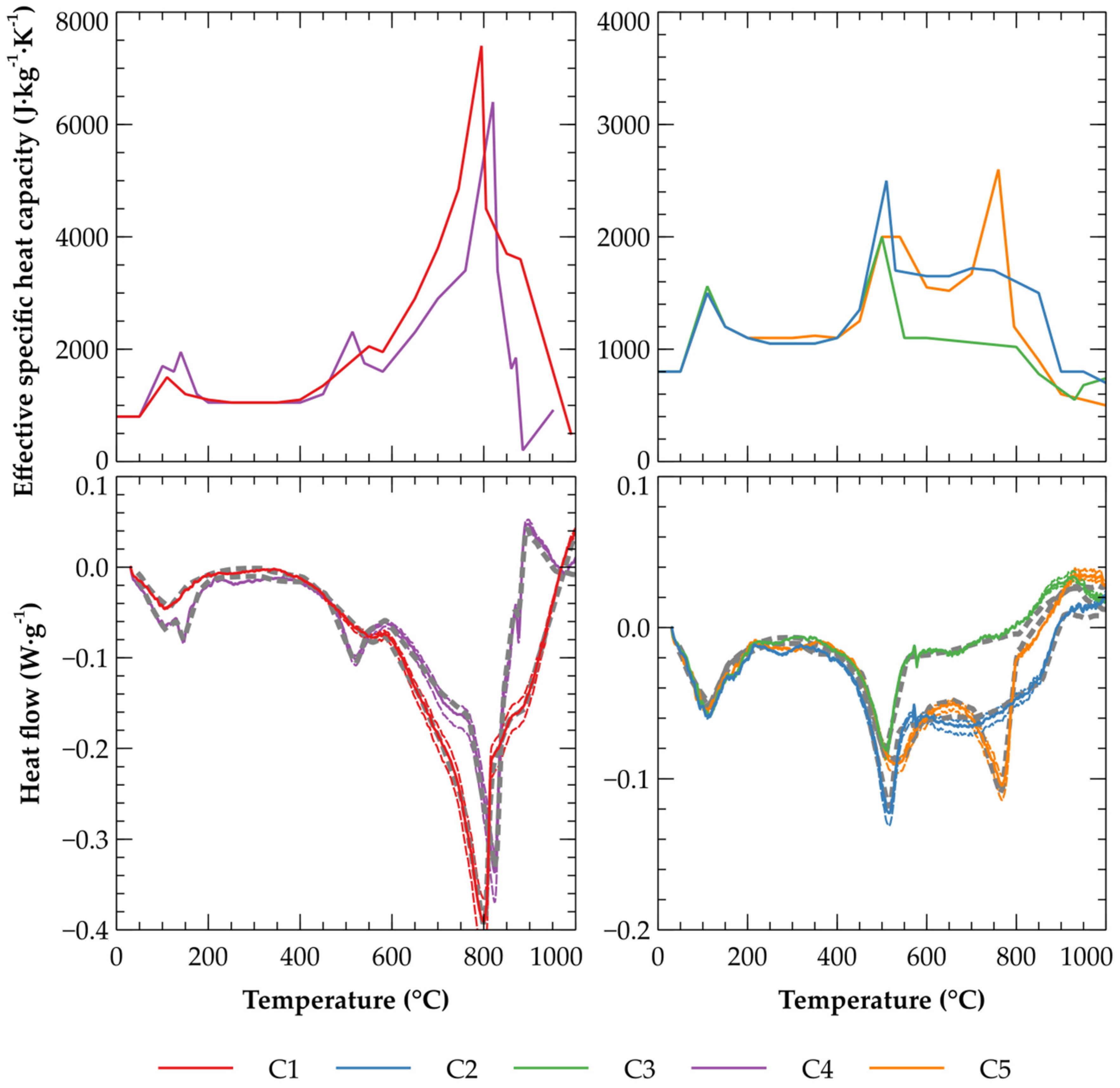
3.1. Effective Specific Heat Capacity of Clays
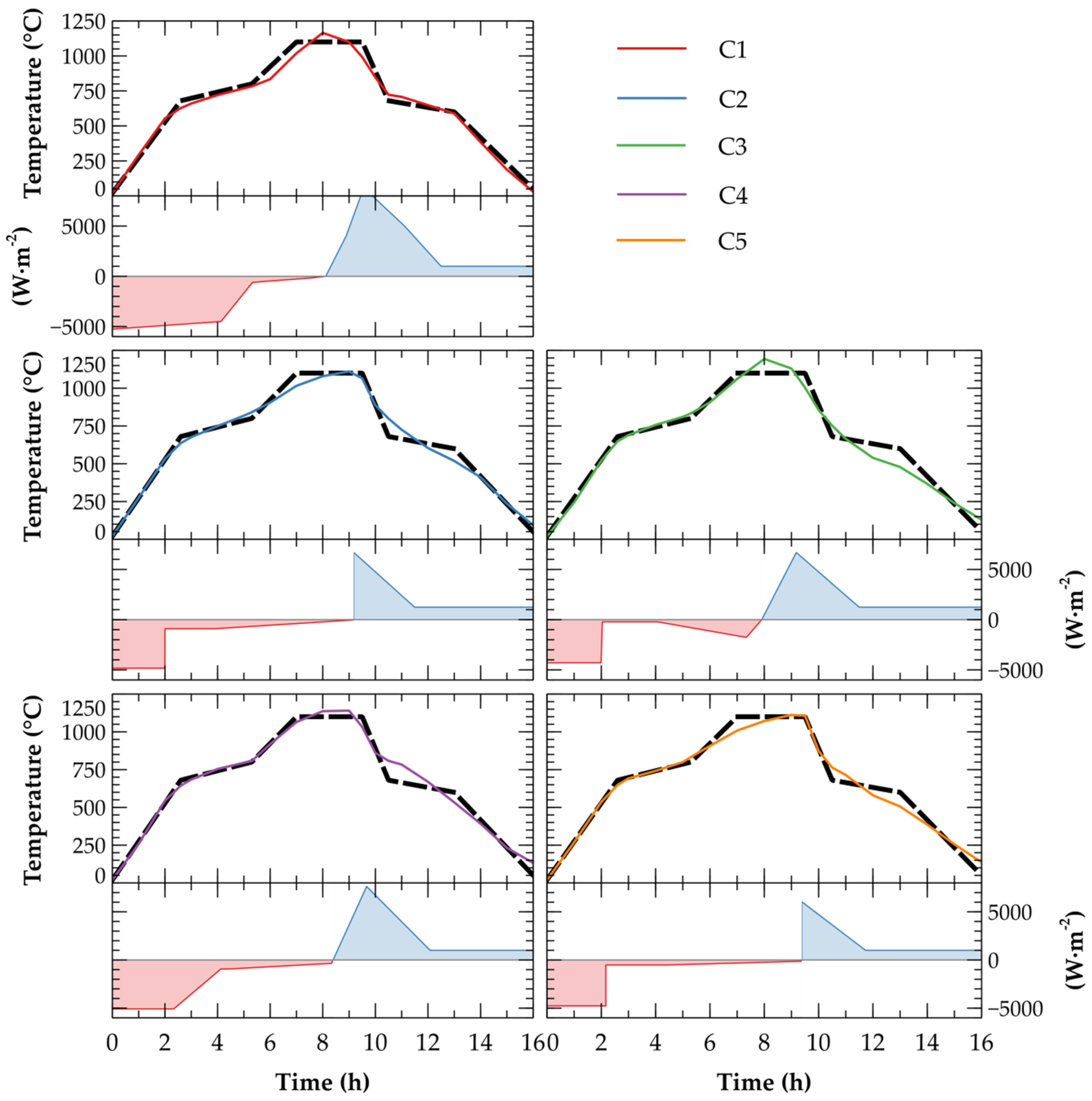
3.2. Energy Demands for Clays Firing
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Torgal, F.P.; Jalali, S. Masonry Units. In Eco-Efficient Construction and Building Materials; Springer: London, UK, 2011; pp. 131–142. [Google Scholar]
- Munoz Velasco, P.; Morales Ortiz, M.P.; Mendivil Giro, M.A.; Munoz Velasco, L. Fired clay bricks manufactured by adding wastes as sustainable construction material—A review. Constr. Build. Mater. 2014, 63, 97–107. [Google Scholar] [CrossRef]
- Rashid, K.; Haq, E.U.; Kamran, M.S.; Munir, N.; Shahid, A.; Hanif, I. Experimental and finite element analysis on thermal conductivity of burnt clay bricks reinforced with fibers. Constr. Build. Mater. 2019, 221, 190–199. [Google Scholar] [CrossRef]
- Zhang, L. Production of bricks from waste materials—A review. Constr. Build. Mater. 2013, 47, 643–655. [Google Scholar] [CrossRef]
- Ul Rehman, M.; Ahmad, M.; Rashid, K. Influence of fluxing oxides from waste on the production and physico-mechanical properties of fired clay brick: A review. J. Build. Eng. 2020, 27, 17. [Google Scholar] [CrossRef]
- Murmu, A.L.; Patel, A. Towards sustainable bricks production: An overview. Constr. Build. Mater. 2018, 165, 112–125. [Google Scholar] [CrossRef]
- Oti, J.E.; Kinuthia, J.M.; Bai, J. Engineering properties of unfired clay masonry bricks. Eng. Geol. 2009, 107, 130–139. [Google Scholar] [CrossRef]
- El-Mahllawy, M.S.; Kandeel, A.M.; Abdel Latif, M.L.; El Nagar, A.M. The Feasibility of Using Marble Cutting Waste in a Sustainable Building Clay Industry. Recycling 2018, 3, 39. [Google Scholar]
- Galán-Marín, C.; Martínez-Rocamora, A.; Solís-Guzmán, J.; Rivera-Gómez, C. Natural Stabilized Earth Panels versus Conventional Façade Systems. Economic and Environmental Impact Assessment. Sustainability 2018, 10, 1020. [Google Scholar] [CrossRef] [Green Version]
- Rempel, A.R.; Rempel, A.W. Intrinsic Evaporative Cooling by Hygroscopic Earth Materials. Geosciences 2016, 6, 38. [Google Scholar] [CrossRef] [Green Version]
- Mobili, S.; Galán-Marín, C.; Rivera-Gómez, C. A New Affordable Masonry System Based on Unfired Clay Sandwich Panel. Proceedings 2018, 2, 1378. [Google Scholar] [CrossRef] [Green Version]
- Nagaraj, H.B.; Sravan, M.V.; Arun, T.G.; Jagadish, K.S. Role of lime with cement in long-term strength of Compressed Stabilized Earth Blocks. Int. J. Sustain. Built Environ. 2014, 3, 54–61. [Google Scholar] [CrossRef] [Green Version]
- Solgi, E.; Husseini, S.M.M.; Ahmadi, A.; Gitinavard, H. A hybrid hierarchical soft computing approach for the technology selection problem in brick industry considering environmental competencies: A case study. J. Environ. Manag. 2019, 248, 109219. [Google Scholar] [CrossRef] [PubMed]
- Pisello, A.L.; Fabiani, C.; Makaremi, N.; Castaldo, V.L.; Cavalaglio, G.; Nicolini, A.; Barbanera, M.; Cotana, F. Sustainable New Brick and Thermo-Acoustic Insulation Panel from Mineralization of Stranded Driftwood Residues. Energies 2016, 9, 20. [Google Scholar] [CrossRef] [Green Version]
- Refaey, H.A.; Abdel-Aziz, A.A.; Salem, M.R.; Abdelrahman, H.E.; Al-Dosoky, M.W. Thermal performance augmentation in the cooling zone of brick tunnel kilnwith two types of guide vanes. Int. J. Therm. Sci. 2018, 130, 264–277. [Google Scholar] [CrossRef]
- Tehzeeb, A.H.; Bhuiyan, M.; Jayasuriya, N. Evaluation of brick Kiln performances using computational fluid dynamics (CFD). Energy Environ. Eng. J. 2012, 1, 86–93. [Google Scholar]
- Dugwell, D.R.; Oakley, D.E. A model of heat transfer in tunnel kilns used for firing refractories. Int. J. Heat Mass Transf. 1988, 31, 2381–2390. [Google Scholar] [CrossRef]
- Gomez, R.S.; Porto, T.R.N.; Magalhaes, H.L.F.; Moreira, G.; Andre, A.; Melo, R.B.F.; Lima, A.G.B. Natural Gas Intermittent Kiln for the Ceramic Industry: A Transient Thermal Analysis. Energies 2019, 12, 29. [Google Scholar] [CrossRef] [Green Version]
- Riedel, R. Optimization of tunnel kilns by utilization of convection. Brick Tile Ind. Int. 1989, 42, 373–379. [Google Scholar]
- Soussi, N.; Kriaa, W.; Mhiri, H.; Bournot, P. Reduction of the energy consumption of a tunnel kiln by optimization of the recovered air mass flow from the cooling zone to the firing zone. Appl. Therm. Eng. 2017, 124, 1382–1391. [Google Scholar] [CrossRef]
- Mancuhan, E.; Kucukada, K. Optimization of fuel and air use in a tunnel kiln to produce coal admixed bricks. Appl. Therm. Eng. 2006, 26, 1556–1563. [Google Scholar] [CrossRef]
- Kaya, S.; Mancuhan, E.; Kucukada, K. Modeling and optimization of the firing zone of a tunnel kiln to predict the optimal feed locations and mass fluxes of the fuel and secondary air. Appl. Energy 2009, 86, 325–332. [Google Scholar] [CrossRef]
- Bruno, A.W.; Gallipoli, D.; Perlot, C.; Mendes, J. Optimization of bricks production by earth hypercompaction prior to firing. J. Clean. Prod. 2019, 214, 475–482. [Google Scholar] [CrossRef]
- Mancuhan, E.; Kucukada, K.; Alpman, E. Mathematical modeling and simulation of the preheating zone of a tunnel kiln. J. Therm. Sci. Technol. 2011, 31, 79–89. [Google Scholar]
- Koci, V.; Madera, J.; Trnik, A.; Cerny, R. Heat transport and storage processes in differential scanning calorimeter: Computational analysis and model validation. Int. J. Heat Mass Transf. 2019, 136, 355–364. [Google Scholar] [CrossRef]
- Hasan, A.; McCormack, S.J.; Huang, M.J.; Norton, B. Characterization of phase change materials for thermal control of photovoltaics using Differential Scanning Calorimetry and Temperature History Method. Energy Convers. Manag. 2014, 81, 322–329. [Google Scholar] [CrossRef]
- Tyagi, V.V.; Buddhi, D. Thermal cycle testing of calcium chloride hexahydrate as a possible PCM for latent heat storage. Sol. Energy Mater. Sol. Cells 2008, 92, 891–899. [Google Scholar] [CrossRef]
- Sari, A.; Karaipekli, A. Preparation and thermal properties of capric acid/palmitic acid eutectic mixture as a phase change energy storage material. Mater. Lett. 2008, 62, 903–906. [Google Scholar] [CrossRef]
- Krabbenhoft, K.; Damkilde, L.; Nazem, M. An implicit mixed enthalpy-temperature method for phase-change problems. Heat Mass Transf. 2007, 43, 233–241. [Google Scholar] [CrossRef]
- Lakatos, Á.; Trník, A. Thermal Diffusion in Fibrous Aerogel Blankets. Energies 2020, 13, 823. [Google Scholar] [CrossRef] [Green Version]
- Garcia Ten, J.; Orts, M.J.; Saburit, A.; Silva, G. Thermal conductivity of traditional ceramics. Part I: Influence of bulk density and firing temperature. Ceram. Int. 2010, 36, 1951–1959. [Google Scholar] [CrossRef]
- Garcia-Ten, J.; Orts, M.J.; Saburit, A.; Silva, G. Thermal conductivity of traditional ceramics Part II: Influence of mineralogical composition. Ceram. Int. 2010, 36, 2017–2024. [Google Scholar] [CrossRef]
- Ferrer, S.; Mezquita, A.; Gomez-Tena, M.P.; Machi, C.; Monfort, E. Estimation of the heat of reaction in traditional ceramic compositions. Appl. Clay Sci. 2015, 108, 28–39. [Google Scholar] [CrossRef] [Green Version]
- Koci, J.; Zumar, J.; Pavlik, Z.; Cerny, R. Application of genetic algorithm for determination of water vapor diffusion parameters of building materials. J. Build. Phys. 2012, 35, 238–250. [Google Scholar] [CrossRef]
- Park, H.S.; Kwon, B.; Shin, Y.; Kim, Y.; Hong, T.; Choi, S.W. Cost and CO2 Emission Optimization of Steel Reinforced Concrete Columns in High-Rise Buildings. Energies 2013, 6, 5609–5624. [Google Scholar] [CrossRef]
- Suleiman, A.R.; Nehdi, M.L. Modeling Self-Healing of Concrete Using Hybrid Genetic Algorithm-Artificial Neural Network. Materials 2017, 10, 135. [Google Scholar] [CrossRef]
- Shvarzman, A.; Kovler, K.; Grader, G.S.; Shter, G.E. The effect of dehydroxylation/amorphization degree on pozzolanic activity of kaolinite. Cem. Concr. Res. 2003, 33, 405–416. [Google Scholar] [CrossRef]
- Gualtieri, A.F.; Ferrari, S. Kinetics of illite dehydroxylation. Phys. Chem. Miner. 2006, 33, 490–501. [Google Scholar] [CrossRef]
- Dolino, G. The α-inc-β transitions of quartz: A century of research on displacive phase transitions. Phase Transit. Multinatl. J. 1990, 21, 59–72. [Google Scholar] [CrossRef]
- Karunadasa, K.S.P.; Manoratne, C.H.; Pitawala, H.M.T.G.A.; Rajapakse, R.M.G. Thermal decomposition of calcium carbonate (calcite polymorph) as examined by in-situ high-temperature X-ray powder diffraction. J. Phys. Chem. Solids 2019, 134, 21–28. [Google Scholar] [CrossRef]
- Choudary, R.B.; Burri, A.; Priya, K.V.P. Fabrication and testing of clay cups. Mater. Today Proc. 2020. [Google Scholar] [CrossRef]






| Label | Deposit | GPS Coordinates | Volume of the Reserves | Mining Per Year |
|---|---|---|---|---|
| C1 | Hevlín Czech Republic | 48.7665139 N, 16.3916417 E | 4,600,000 m3 | 280,000 m3 |
| C2 | Popovice Czech Republic | 49.1647756 N, 14.5619031 E | 900,000 m3 | 70,000 m3 |
| C3 | Pelejovice Czech Republic | 49.1474286 N, 14.5970508 E | not known | 20,000 m3 |
| C4 | Libochovice Czech Republic | 50.4107231 N, 14.0273617 E | 2,100,000 m3 | 80,000 m3 |
| C5 | Kryry, Czech Republic | 50.1611986 N, 13.4253217 E | 800,000 m3 | 80,000 m3 |
| Compound | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|
| SiO2 | 41.9 | 58.5 | 58.4 | 37.5 | 50.6 |
| Al2O3 | 22.3 | 27.4 | 26.2 | 19.9 | 27.8 |
| CaO | 11.1 | 0.7 | 1.0 | 23.9 | 2.9 |
| MgO | 3.4 | 2.1 | 2.3 | 2.3 | 3.5 |
| Fe2O3 | 8.0 | 5.4 | 5.7 | 4.2 | 6.5 |
| Na2O | 0.0 | 0.0 | 0.2 | 0.0 | 0.0 |
| K2O | 4.1 | 2.2 | 2.5 | 2.5 | 4.1 |
| SO3 | 2.8 | 0.1 | 0.2 | 1.9 | 0.5 |
| TiO2 | 0.9 | 0.9 | 0.9 | 0.7 | 0.8 |
| Total (organic) carbon | 2.7 (1.2) | 0.2 (0.2) | 0.2 (0.2) | 4.4 (0.7) | 1.1 (0.2) |
| Bound water | 2.8 | 2.6 | 2.4 | 2.7 | 2.3 |
| Mineral | Chemical Formula | C1 | C2 | C3 | C4 | C5 |
|---|---|---|---|---|---|---|
| Kaolinite | Al2Si2O5(OH)4 | 1 | 22 | 20 | 14 | 2 |
| Illite-smectite | K0.65Al2.0[Al0.65Si3.35O10](OH)2 | 23 | 6 | 10 | 16 | 22 |
| Chlorite | (Mg,Fe)3(Si,Al)4O10(OH)2·(Mg,Fe)3(OH)6 | 2 | 0 | 0 | 0 | 0 |
| Quartz | SiO2 | 51 | 50 | 48 | 25 | 37 |
| Calcite + Dolomite | CaCO3 + MgCO3 | 18 | 0 | 0 | 35 | 6 |
| Feldspars | KAlSi3O8 − NaAlSi3O8 − CaAl2Si2O8 | 5 | 22 | 22 | 10 | 30 |
| Hematite | Fe2O3 | 0 | 0 | 0 | 0 | 3 |
| Clay minerals (1st + 2nd + 3rd row) | 26 | 28 | 30 | 30 | 24 |
| Label | Maximal Difference (W·g−1) | RMSE (W·g−1) |
|---|---|---|
| C1 | 0.031714 | 0.004875 |
| C2 | 0.011508 | 0.004439 |
| C3 | 0.011764 | 0.004462 |
| C4 | 0.031568 | 0.006356 |
| C5 | 0.011252 | 0.004479 |
| Segment | C1 | C2 | C3 | C4 | C5 | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| t (h) | q (W·m−2) | t (h) | q (W·m−2) | t (h) | q (W·m−2) | t (h) | q (W·m−2) | t (h) | q (W·m−2) | |
| 1 | 0.00 | −5285 | 0.00 | −4832 | 0.00 | −4292 | 0.00 | −5079 | 0.00 | −4767 |
| 2 | 4.13 | −4500 | 2.00 | −4832 | 1.99 | −4292 | 2.33 | −5079 | 2.17 | −4767 |
| 3 | 5.33 | −600 | 2.00 | −901 | 2.04 | −217 | 4.13 | −932 | 2.17 | −523 |
| 4 | 7.61 | −150 | 3.89 | −901 | 4.07 | −217 | 4.44 | −932 | 4.33 | −523 |
| 5 | 8.11 | 0 | 9.18 | −31 | 7.34 | −1766 | 8.33 | −351 | 9.38 | −134 |
| 6 | 8.89 | 4000 | 9.18 | 6690 | 9.18 | 3980 | 9.67 | 7636 | 9.38 | 6039 |
| 7 | 9.44 | 8000 | 11.49 | 1246 | 11.47 | 1000 | 12.08 | 1000 | 11.73 | 1000 |
| 8 | 9.89 | 8000 | 16.00 | 1246 | 16.00 | 1000 | 16.00 | 1000 | 16.00 | 1000 |
| 9 | 11.11 | 5000 | − | − | − | − | − | − | − | − |
| 10 | 12.50 | 1000 | − | − | − | − | − | − | − | − |
| 11 | 16.00 | 1000 | − | − | − | − | − | − | − | − |
| Label | RMSE (°C) | Energy Demands (MJ·m−2) |
|---|---|---|
| C1 | 46.98 | 173.42 |
| C2 | 44.49 | 103.06 |
| C3 | 54.86 | 88.58 |
| C4 | 51.57 | 141.28 |
| C5 | 44.82 | 92.33 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kočí, V.; Scheinherrová, L.; Maděra, J.; Keppert, M.; Suchorab, Z.; Łagód, G.; Černý, R. Experimental and Computational Study of Thermal Processes in Red Clays Exposed to High Temperatures. Energies 2020, 13, 2211. https://doi.org/10.3390/en13092211
Kočí V, Scheinherrová L, Maděra J, Keppert M, Suchorab Z, Łagód G, Černý R. Experimental and Computational Study of Thermal Processes in Red Clays Exposed to High Temperatures. Energies. 2020; 13(9):2211. https://doi.org/10.3390/en13092211
Chicago/Turabian StyleKočí, Václav, Lenka Scheinherrová, Jiří Maděra, Martin Keppert, Zbigniew Suchorab, Grzegorz Łagód, and Robert Černý. 2020. "Experimental and Computational Study of Thermal Processes in Red Clays Exposed to High Temperatures" Energies 13, no. 9: 2211. https://doi.org/10.3390/en13092211
APA StyleKočí, V., Scheinherrová, L., Maděra, J., Keppert, M., Suchorab, Z., Łagód, G., & Černý, R. (2020). Experimental and Computational Study of Thermal Processes in Red Clays Exposed to High Temperatures. Energies, 13(9), 2211. https://doi.org/10.3390/en13092211











