A Novel Servovalve Pilot Stage Actuated by a Piezo-Electric Ring Bender (Part II): Design Model and Full Simulation
Abstract
:1. Introduction
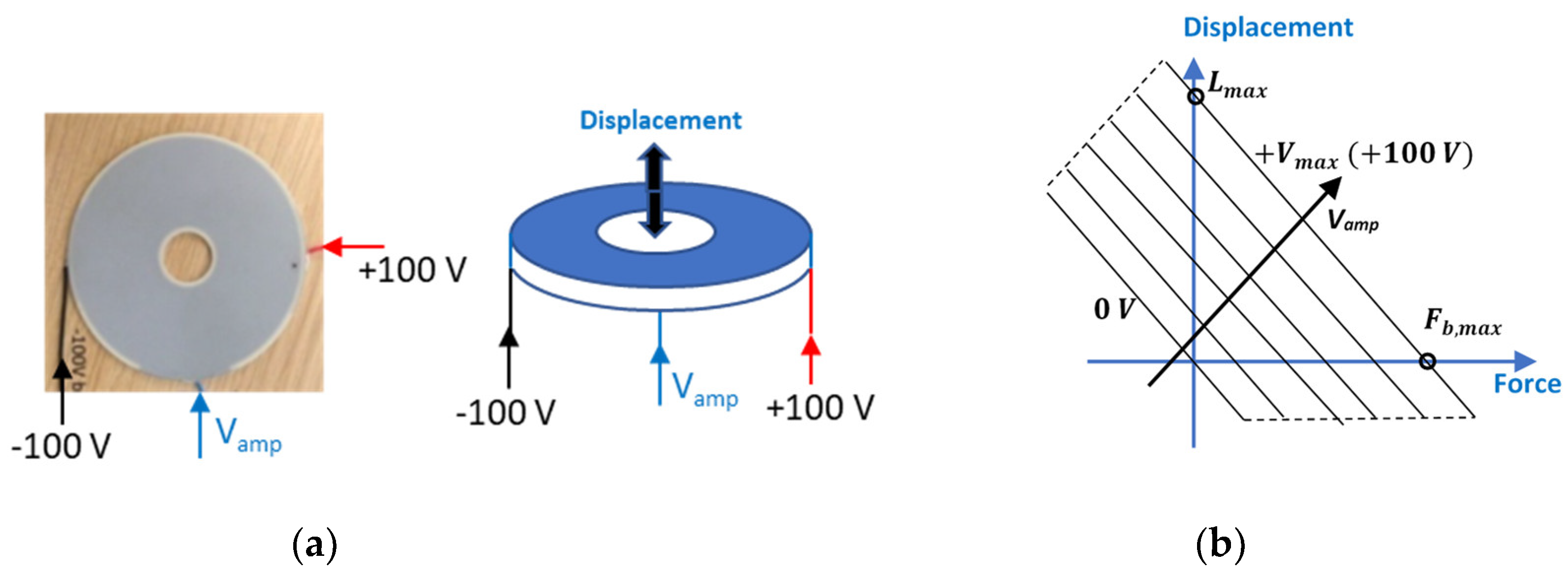
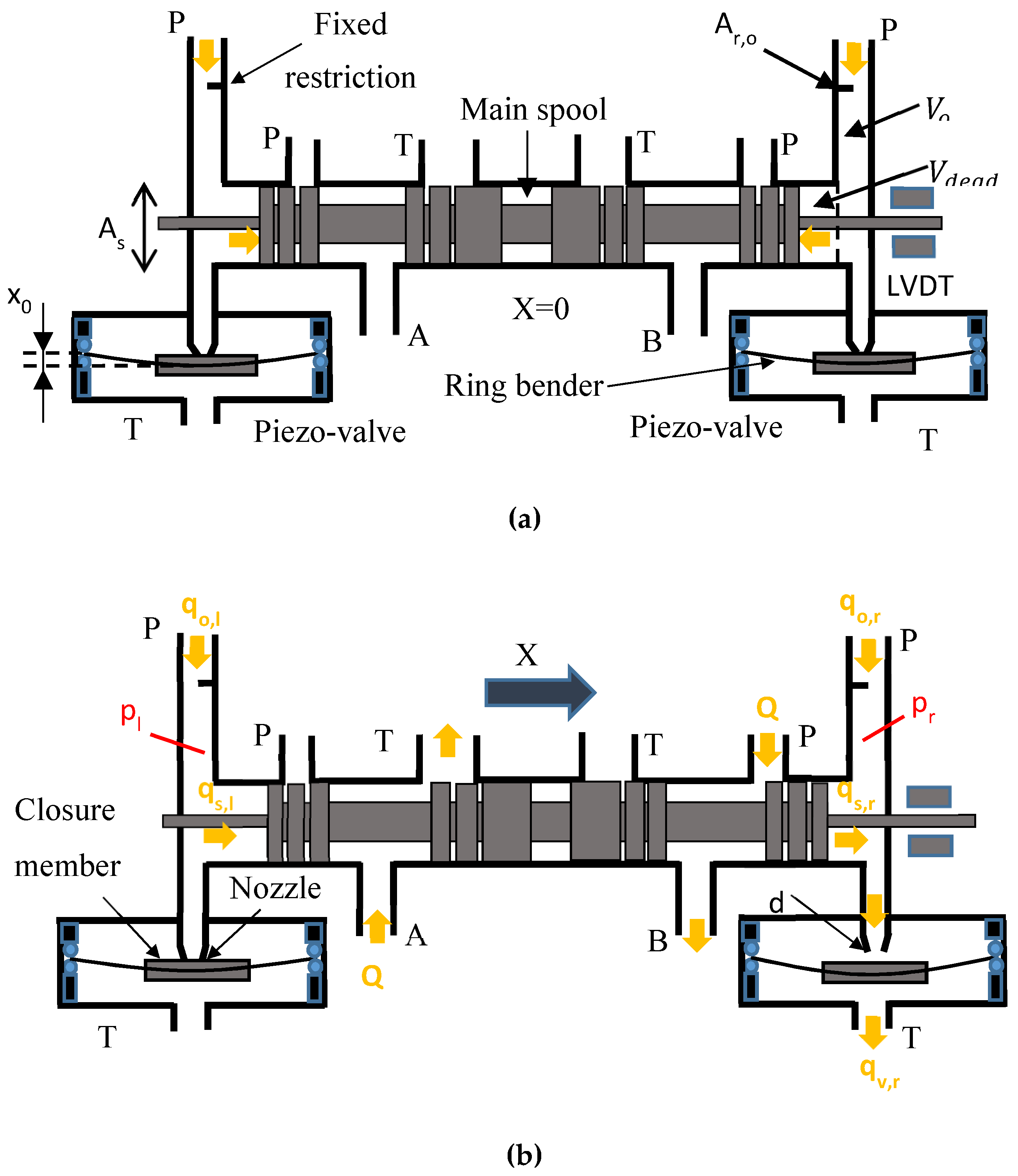
2. Novel Servovalve Architecture
3. Full Numerical Model
3.1. Main Stage Model
3.2. Pilot Stage Model
4. Simplified Numerical Model
5. Results
5.1. Choice of the Values of the Design Parameters
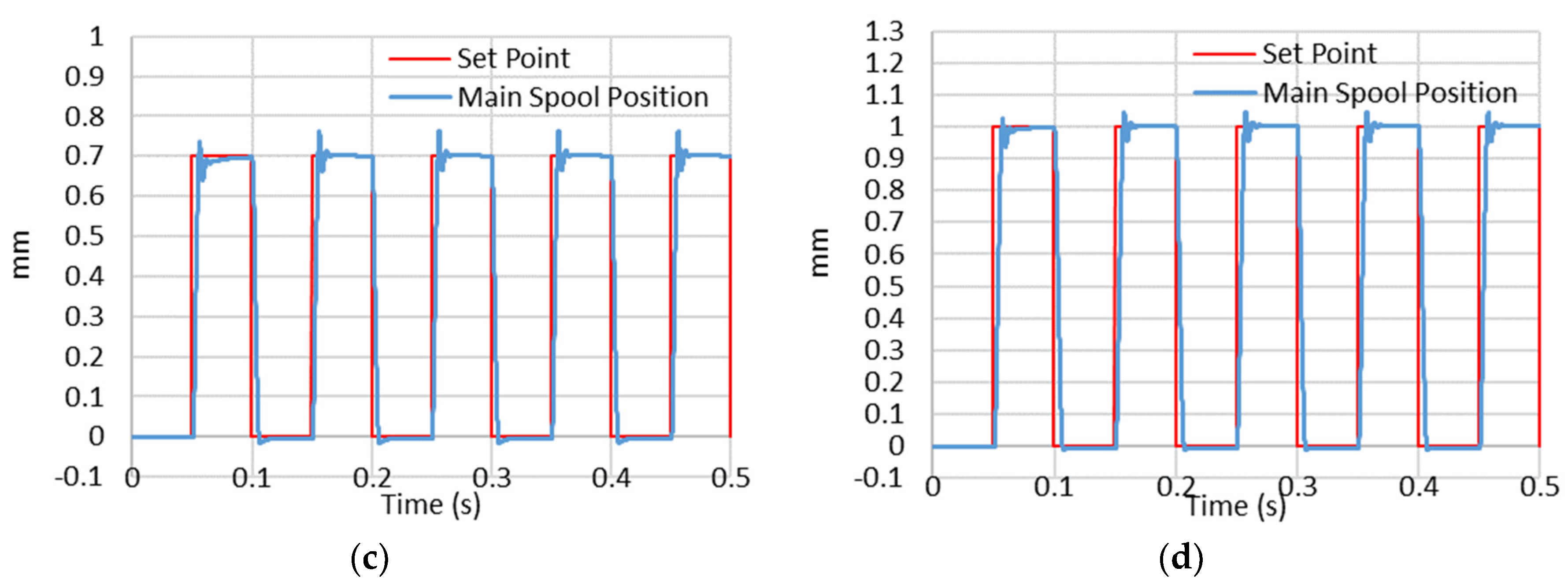
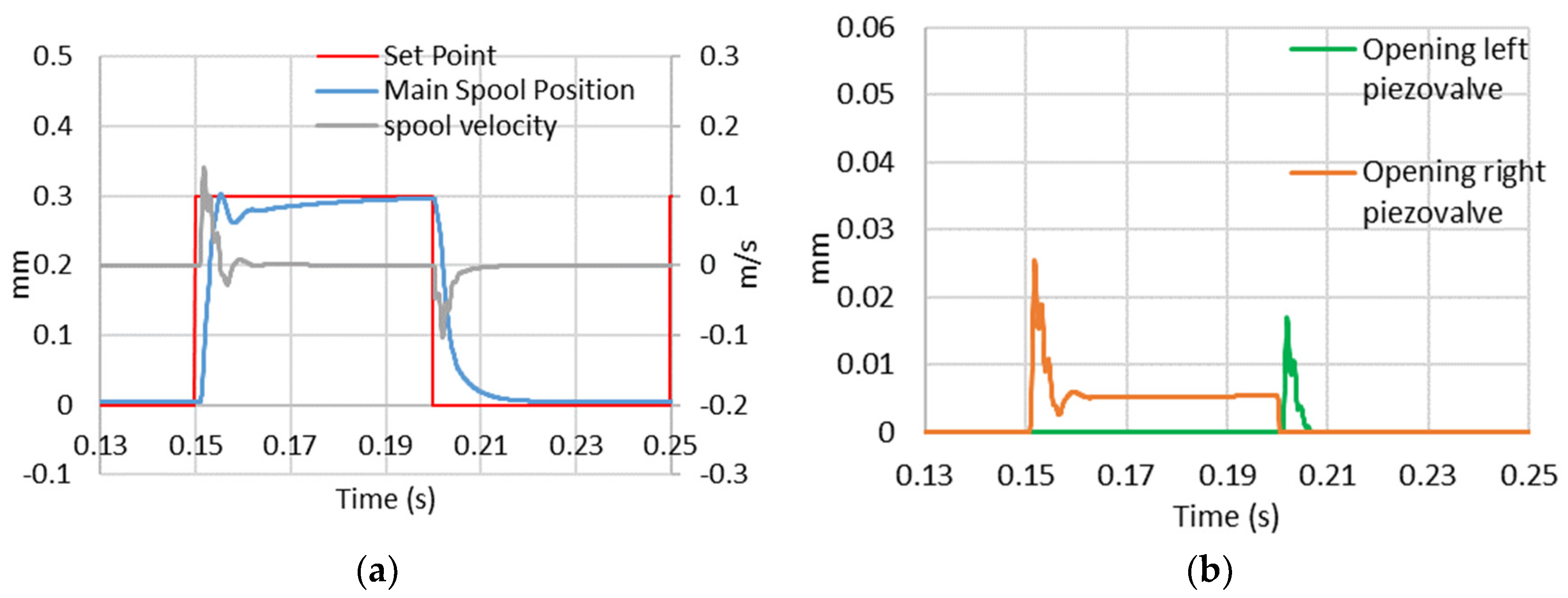
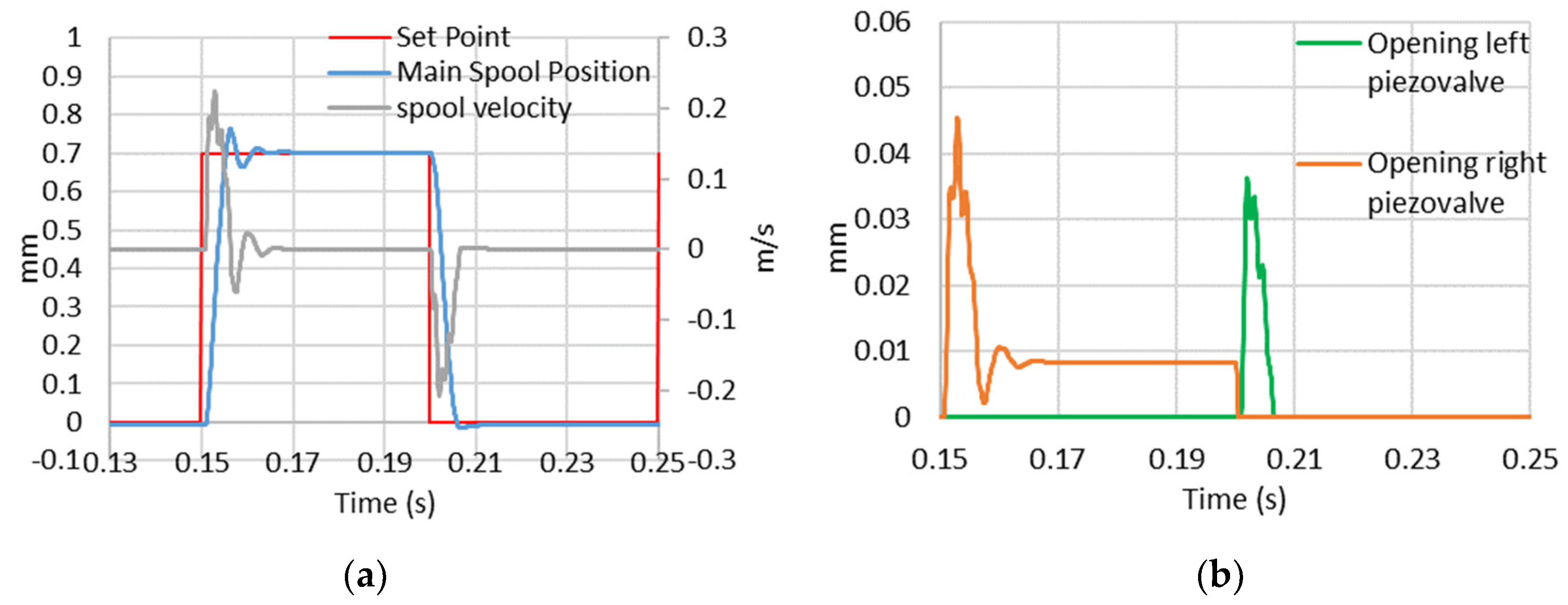
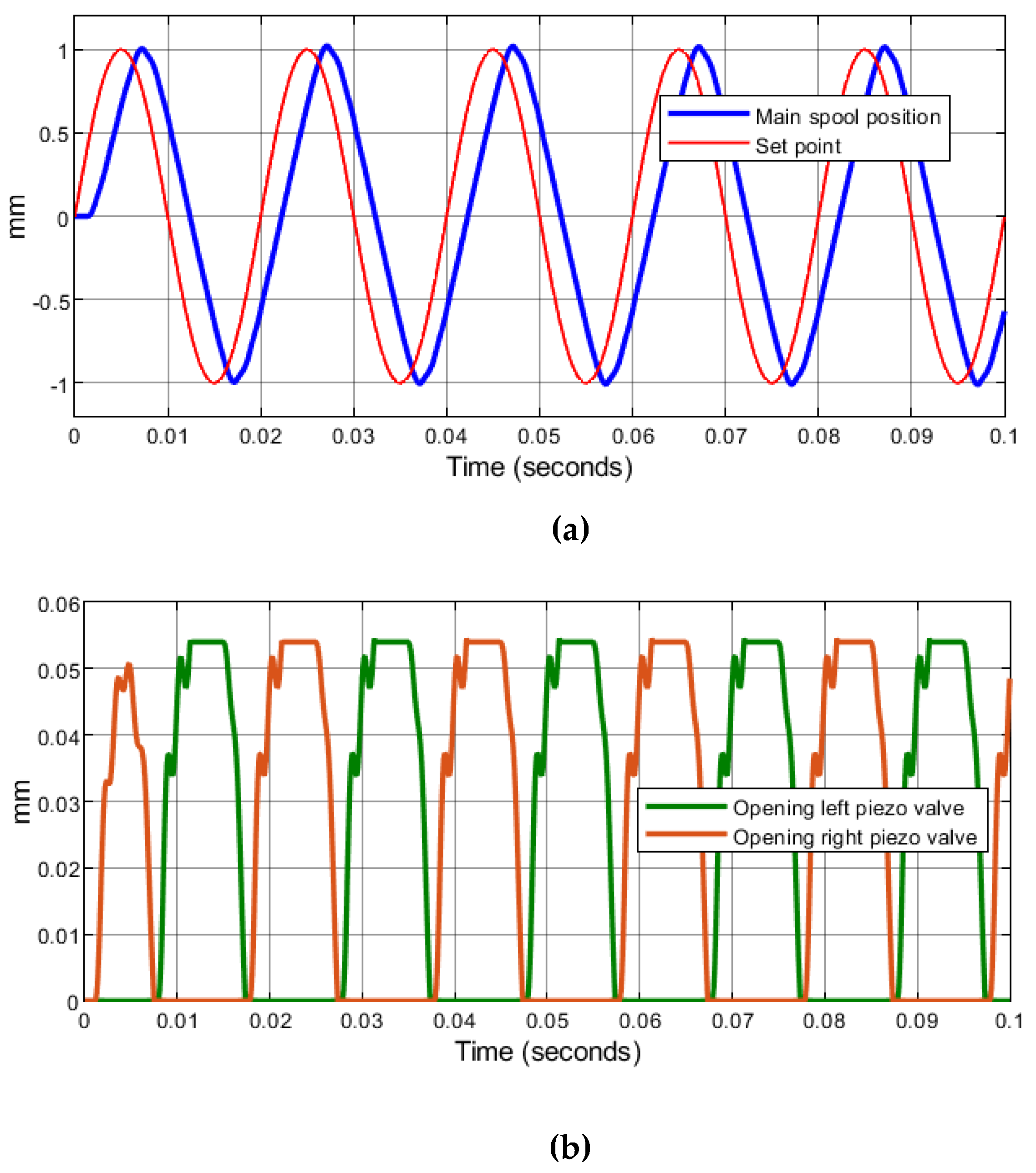
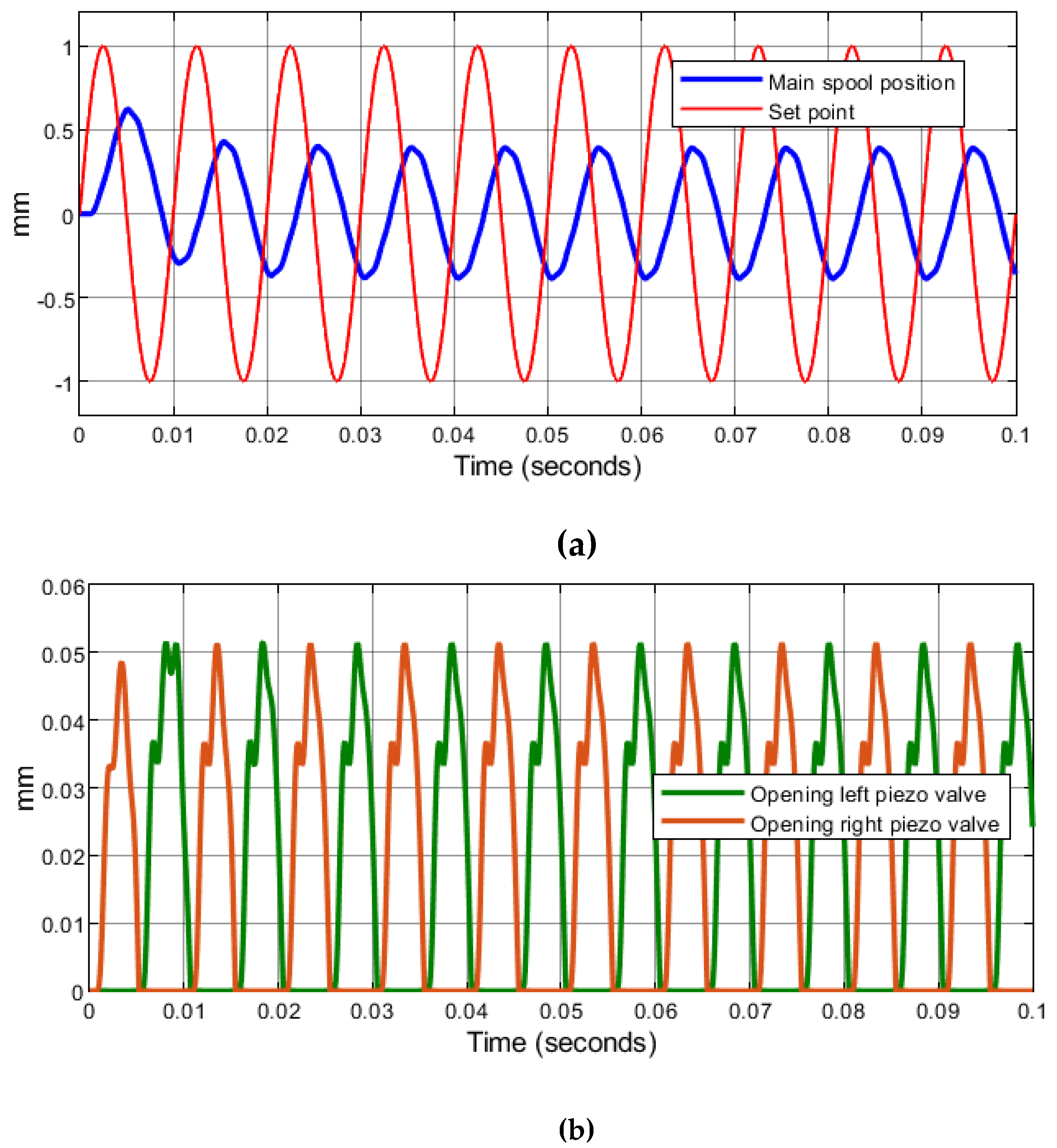
5.2. Performance Prediction
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A | Valve port connected to the actuator |
| Al,s | Leakage area of the main spool (mm2) |
| Al,v | Leakage area of the piezo-valve (mm2) |
| Ar,0 | Restricted area of the fixed orifice (mm2) |
| Ar,s | Restriction area of the main spool (mm2) |
| Ar,v | Restriction area of the piezo-valve (mm2) |
| As | Spool end area (mm2) |
| B | Valve port connected to the actuator |
| b | Width of the slots (mm) |
| C | Damping coefficient of the main spool (Ns/m) |
| c | Clearance (μm) |
| Cap | Capacitance of the ring bender (nF) |
| CD | Discharge coefficient |
| Crb | Damping factor of the ring bender (Ns/m) |
| Cstop | Damping coefficient hard stop (Ns/m) |
| Ds | Main spool diameter (mm) |
| D0 | Diameter of the hydraulic chamber (mm) |
| d | Diameter of the piezo-valve nozzle (mm) |
| E | Bulk modulus (N/m2) |
| E0 | Pure liquid bulk modulus (N/m2) |
| e | Error |
| Fb | Blocking force (N) |
| Ff,s | Flow force acting on the spool (N) |
| Ff,rb | Flow force acting on the ring bender (N) |
| Imax | Maximum current of the amplifier (A) |
| Ka | Gain of the amplifier |
| KD | Derivative gain |
| Kd,v | Max. blocking force over max. voltage (N/V) |
| KI | Integral gain |
| Kp | Proportional gain |
| krb | Stiffness of the ring bender (N/m) |
| Kstop | Stiffness hard stop (N/m) |
| Lmax | Maximum free stroke of the ring bender (mm) |
| L0 | Length of the hydraulic chamber (mm) |
| M | Main spool mass (kg) |
| m0 | Mass of the moving parts (kg) |
| n | Hysteresis non-linear term (V) |
| P | Valve port connected to the pump |
| p | Pressure (N/m2) |
| pA | Pressure at port A (N/m2) |
| pB | Pressure at port B (N/m2) |
| pl | Pressure acting on the left surface of the spool (N/m2) |
| pr | Pressure acting on the right surface of the spool (N/m2) |
| p0 | Ambient pressure (N/m2) |
| pP | Supply pressure (N/m2) |
| pT | Discharge pressure (N/m2) |
| Q | Flow rate through the main valve (m3/s) |
| qc,l | Flow rate entering the left hydraulic chamber because of oil compressibility (m3/s) |
| qc,r | Flow rate entering the right hydraulic chamber because of oil compressibility (m3/s) |
| q0,l | Flow rate through the left orifice (m3/s) |
| q0,r | Flow rate through the right orifice (m3/s) |
| qs,l | Flow rate inside the left external chamber of the spool (m3/s) |
| qs,r | Flow rate inside the right external chamber of the spool (m3/s) |
| qv,l | Flow rate exiting the left piezo-valve (m3/s) |
| qv,r | Flow rate exiting the right piezo-valve (m3/s) |
| r | Roughness (μm) |
| T | Valve port connected to the tank |
| t | Time (s) |
| V | Volume at the left or right of the main spool (mm3) |
| Vamp | Voltage from the amplifier (V) |
| Vc | Control Voltage (V) |
| Vdead | Dead volume (mm3) |
| Vo | Volume of the hydraulic chamber (mm3) |
| X | Main spool displacement (mm) |
| Xmax | Maximum opening of the main valve (mm) |
| x | Ring bender displacement (mm) |
| xmax | Maximum opening of the piezo-valve (mm) |
| xmin | Minimum opening of the piezo-valve (mm) |
| x0 | Pre-compression of the ring bender (mm) |
| α | Parameter for the hysteresis formula |
| β | Parameter for the hysteresis formula |
| γ | Ratio of the specific heats |
| δ | Parameter for the hysteresis formula |
| ε | Relative gas content at atmospheric pressure |
| θ | Flow angle (rad) |
| ξ | Damping factor of the amplifier |
| ρ | Actual density of the oil (kg/m3) |
| ρ0 | Density of the oil at ambient pressure (kg/m3) |
| ωn | Natural frequency of the amplifier (rad/s) |
References
- Tamburrano, P.; Plummer, A.R.; Distaso, E.; Amirante, R. A review of electro-hydraulic servovalve research and development. Int. J. Fluid Power 2019, 20, 53–98. [Google Scholar] [CrossRef]
- Xu, B.; Shen, J.; Liu, S.; Su, Q.; Zhang, J. Research and Development of Electro-hydraulic Control Valves Oriented to Industry 4.0: A Review. Chin. J. Mech. Eng. 2020, 33, 1–20. [Google Scholar] [CrossRef] [Green Version]
- Liu, C.; Wang, Y.; Pan, T.; Zheng, G. Fault diagnosis of electro-hydraulic servo valve using extreme learning machine. Int. Trans. Electr. Energy Syst. 2020. [Google Scholar] [CrossRef]
- Tamburrano, P.; Plummer, A.R.; Distaso, E.; Amirante, R. A review of direct drive proportional electrohydraulic spool valves: Industrial state-of-the-art and research advancements. J. Dyn. Syst. Meas. Control 2019, 141. [Google Scholar] [CrossRef]
- Li, L.; Yan, H.; Zhang, H.; Li, J. Numerical simulation and experimental research of the flow force and forced vibration in the nozzleflapper valve. Mech. Syst. Signal Process. 2018, 99, 550–566. [Google Scholar] [CrossRef]
- Li, S.; Aung, N.Z.; Zhang, S.; Cao, J.; Xue, X. Experimental and numerical investigation of cavitation phenomenon in flapper-nozzle pilot stage of an electrohydraulic servo-valve. Comput. Fluids 2013, 88, 590–598. [Google Scholar] [CrossRef]
- Aung, N.Z.; Li, S. A numerical study of cavitation phenomenon in a flapper-nozzle pilot stage of an electrohydraulic servo-valve with an innovative flapper shape. Energy Convers. Manag. 2014, 77, 31–39. [Google Scholar] [CrossRef]
- Zhang, S.; Li, S. Cavity shedding dynamics in a flapper-nozzle pilot stage of an electro-hydraulic servo-valve: Experiments and numerical study. Energy Convers. Manag. 2015, 100, 370–379. [Google Scholar] [CrossRef]
- Yang, H.; Wang, W.; Lu, K.; Chen, Z. Cavitation reduction of a flapper-nozzle pilot valve using continuous microjets. Int. J. Heat Mass Transf. 2019, 133, 1099–1109. [Google Scholar] [CrossRef]
- Saha, B.K.; Peng, J.; Li, S. Numerical and Experimental Investigations of Cavitation Phenomena inside the Pilot Stage of the Deflector Jet Servo-Valve. IEEE Access 2020, 8, 64238–64249. [Google Scholar] [CrossRef]
- Yang, Q.; Aung, N.Z.; Li, S. Confirmation on the effectiveness of rectangle-shaped flapper in reducing cavitation in flapper–nozzle pilot valve. Energy Convers. Manag. 2015, 98, 184–198. [Google Scholar] [CrossRef]
- Zhang, S.; Aung, N.Z.; Li, S. Reduction of undesired lateral forces acting on the flapper of a flapper–nozzle pilot valve by using an innovative flapper shape. Energy Convers. Manag. 2015, 106, 835–848. [Google Scholar] [CrossRef]
- Bang, Y.B.; Joo, C.S.; Lee, K.I.; Hur, J.W.; Lim, W.K. Development of a two-stage high speed electrohydraulic servovalve systems using stack-type piezoelectric elements. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, AIM (2003), Kobe, Japan, 20–24 July 2003; Volume 1, pp. 131–136. [Google Scholar] [CrossRef]
- Lindler, J.E.; Anderson, E.H. Piezoelectric direct drive servovalve. In Proceedings of the SPIE’s 9th Annual International Symposium on Smart Structures and Materials, San Diego, CA, USA, 17–21 March 2002. [Google Scholar]
- Jeon, J.; Han, C.; Han, Y.M.; Choi, S.B. A new type of a direct-drive valve system driven by a piezostack actuator and sliding spool. Smart Mater. Struct. 2014, 23. [Google Scholar] [CrossRef]
- Karunanidhi, S.; Singaperumal, M. Mathematical modelling and experimental characterization of a high dynamic servo valve integrated with piezoelectric actuator. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2010, 224, 419–435. [Google Scholar] [CrossRef]
- Milecki, A. Modelling and investigation of electrohydraulic servovalve with piezo element. Proc. Inst. Mech. Technol. 2006, 26, 181–188. [Google Scholar]
- Lihui, Z.; Shiju, E.; Xilin, Z.; Chunfu, G. Development of hydroelectric servovalve based on piezoelectric elements. In Proceedings of the 2010 International Conference on Mechanic Automation and Control Engineering MACE2010, Wuhan, China, 26–28 June 2010; pp. 3330–3333. [Google Scholar]
- Guang-Ming, C.; Peng, L.I.; Zhi-Gang, Y.; Shi-ju, E.; Jian-fang, L.I. Double-nozzle piezoelectric servovalve. Guangxue Jingmi Gongcheng. Opt. Precis. Eng. 2005, 13, 276–282. [Google Scholar]
- Sangiah, D.K.; Plummer, A.R.; Bowen, C.R.; Guerrier, P. A novel piezohydraulic aerospace servovalve. Part 1: Design and modelling. Proc. Inst. Mech. Eng. Part I J. Syst. Control Eng. 2013, 227, 371–389. [Google Scholar] [CrossRef]
- Persson, L.J.; Plummer, A.R.; Bowen, C.R.; Brooks, I. Design and Modelling of a Novel Servovalve Actuated by a Piezoelectric Ring Bender. In Proceedings of the ASME/BATH 2015 Symposium on Fluid Power and Motion Control, ASME/BATH 2015 Symposium on Fluid Power and Motion Control, Chicago, IL, USA, 12–14 October 2015. [Google Scholar]
- Tamburrano, P.; Amirante, R.; Distaso, E.; Plummer, A.R. Full simulation of a piezoelectric double nozzle flapper pilot valve coupled with a main stage spool valve. Energy Procedia 2018, 148, 487–494. [Google Scholar] [CrossRef]
- Bertin, M.J.F.; Plummer, A.R.; Bowen, C.R.; Johnston, D.N. An Investigation of Piezoelectric Ring Benders and Their Potential for Actuating Servo Valves. In Proceedings of the ASME/BATH 2014 Symposium on Fluid Power and Motion Control, Bath, UK, 10–12 September 2014. [Google Scholar]
- Mathworks. Matlab & Simulink. SimscapeTM User’s Guide R2018a; Mathworks: Natick, MA, USA, 2018. [Google Scholar]
- Noliac. Available online: http://www.noliac.com/products/actuators/plate-stacks/ (accessed on 1 September 2017).
- Tamburrano, P.; Amirante, R.; Distaso, E.; Plummer, A.R. A novel piezoelectric double-flapper servovalve pilot stage: Operating principle and performance prediction. In Proceedings of the BATH/ASME 2018 Symposium on Fluid Power and Motion Control, Bath, UK, 12–14 September 2018. [Google Scholar]
- Tamburrano, P.; Plummer, A.R.; De Palma, P.; Distaso, E.; Amirante, R. A Novel Servovalve Pilot Stage Actuated by a Piezo-electric Ring Bender: A Numerical and Experimental Analysis. Energies 2020, 13, 671. [Google Scholar] [CrossRef] [Green Version]
- Tamburrano, P.; Plummer, A.R.; Elliott, P.; Morris, W.; Page, S.; Distaso, E.; Amirante, R.; De Palma, P. 2D CFD Analysis of Servovalve Main Stage Internal Leakage. In Proceedings of the ASME/BATH 2019 Symposium on Fluid Power and Motion Control, Longboat Key, FL, USA, 7–9 October 2019. [Google Scholar]
- Blackburn, J.F.; Reethof, G.; Shearer, J.L. Fluid Power Control; The MIT Press: Cambridge, MA, USA; Wiley: Hoboken, NJ, USA, 1960. [Google Scholar]
- Merritt, H. Hydraulic Control System; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1967. [Google Scholar]
- Pan, X.D.; Wang, G.L.; Zhang, L. Simulation study on spool edge’s round angle effects on spool valve orifice discharge characteristic. In Applied Mechanics and Materials; Trans Tech Publications Ltd.: Baech, Switzerland, 2008; Volume 10, pp. 918–922. [Google Scholar]
- Yaobao, Y.; Jiayang, Y.; Shengrong, G. Numerical study of solid particle erosion in hydraulic spool valves. Wear 2017, 392, 174–189. [Google Scholar] [CrossRef]
- Moog. 2017. Available online: http://www.moog.com/products/servovalves-servo-proportional-valves.html (accessed on 1 September 2017).

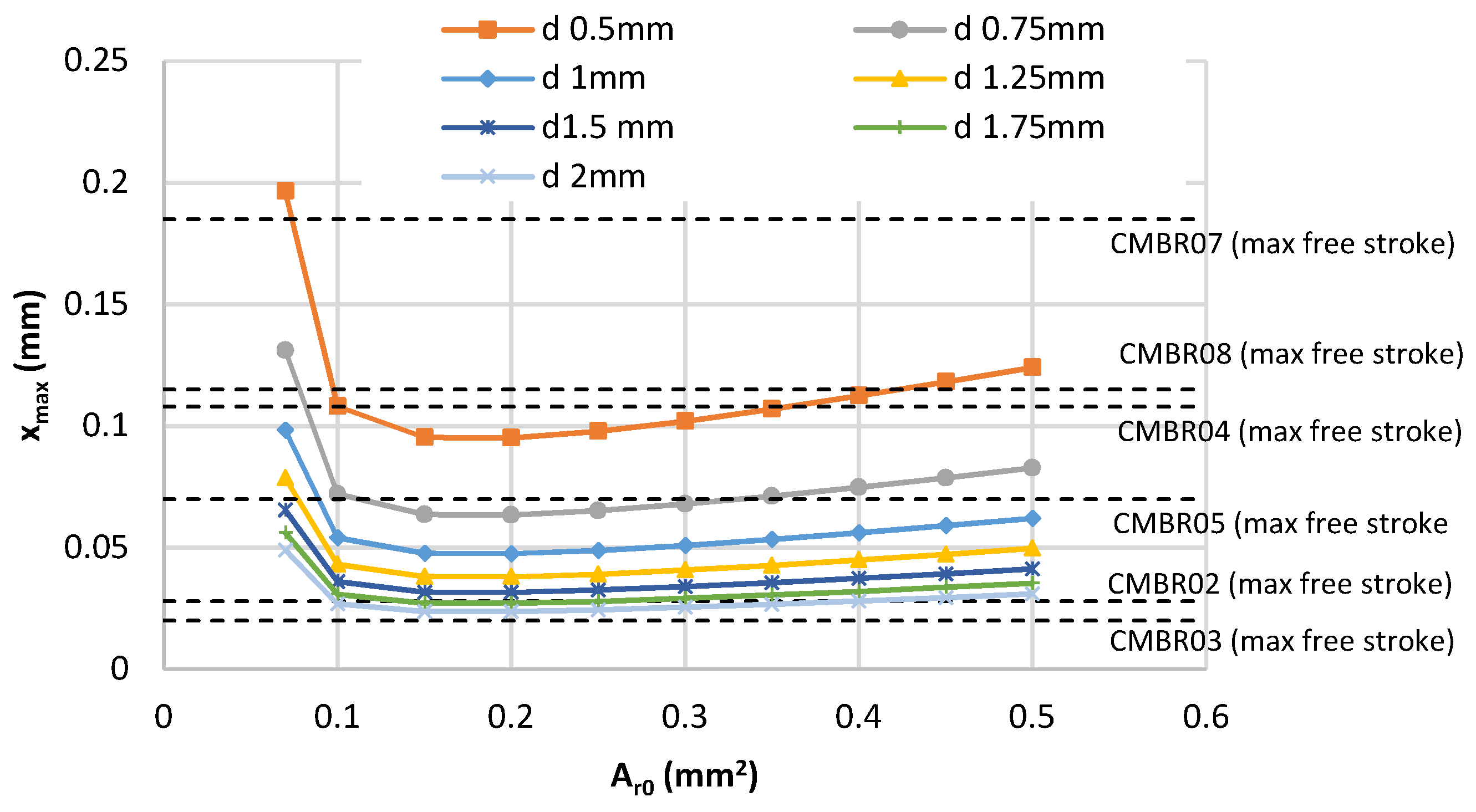
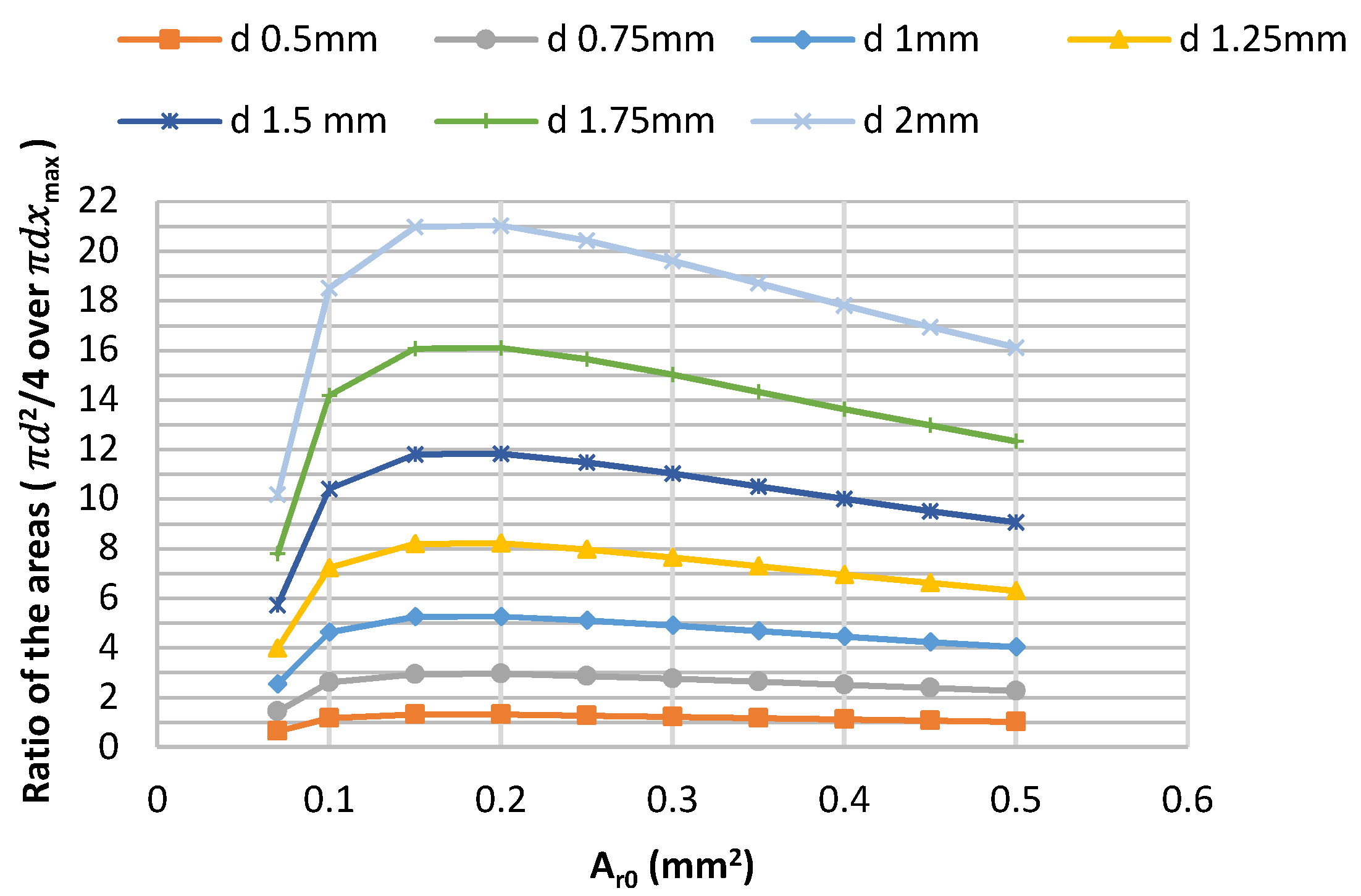
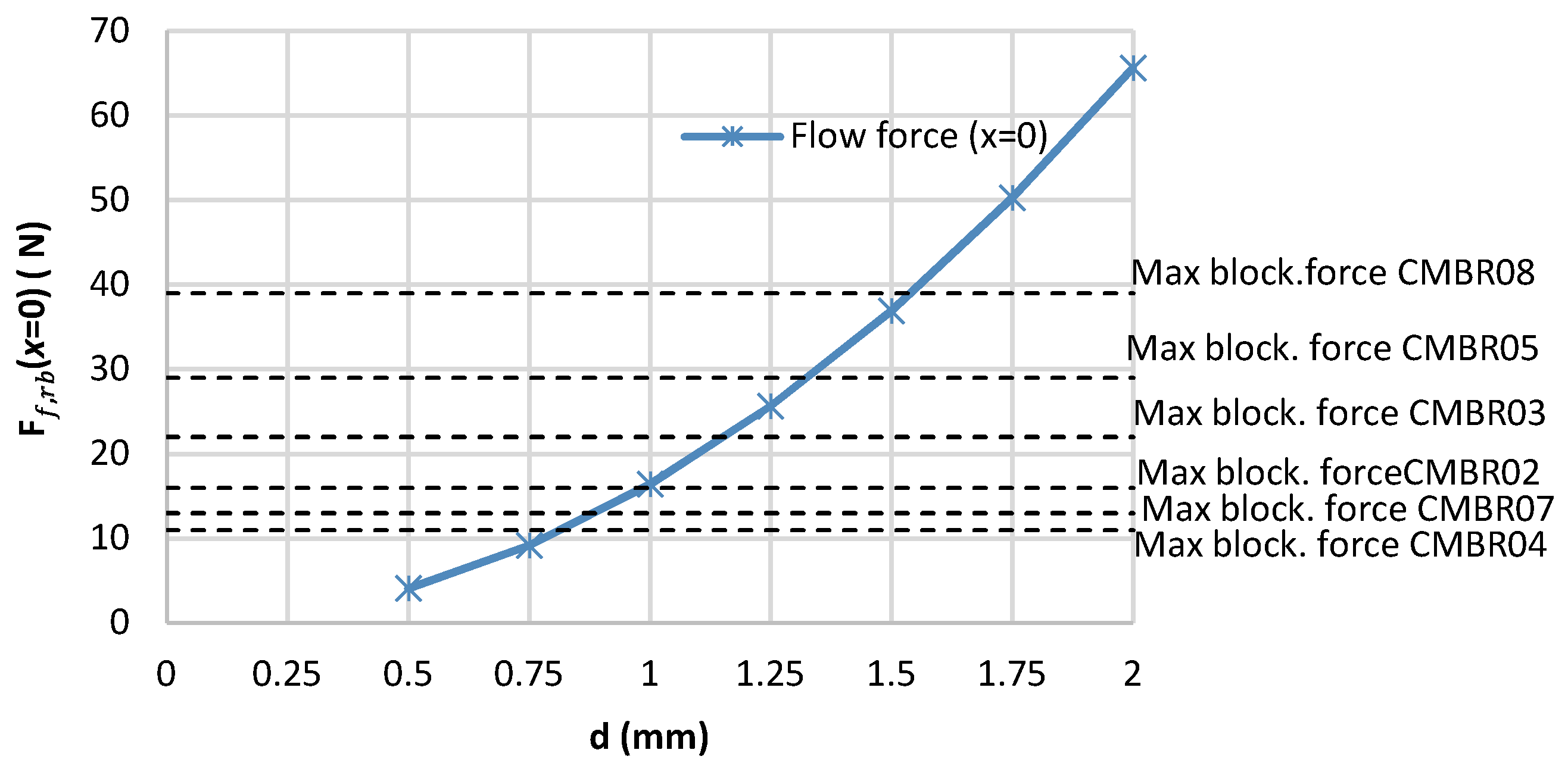
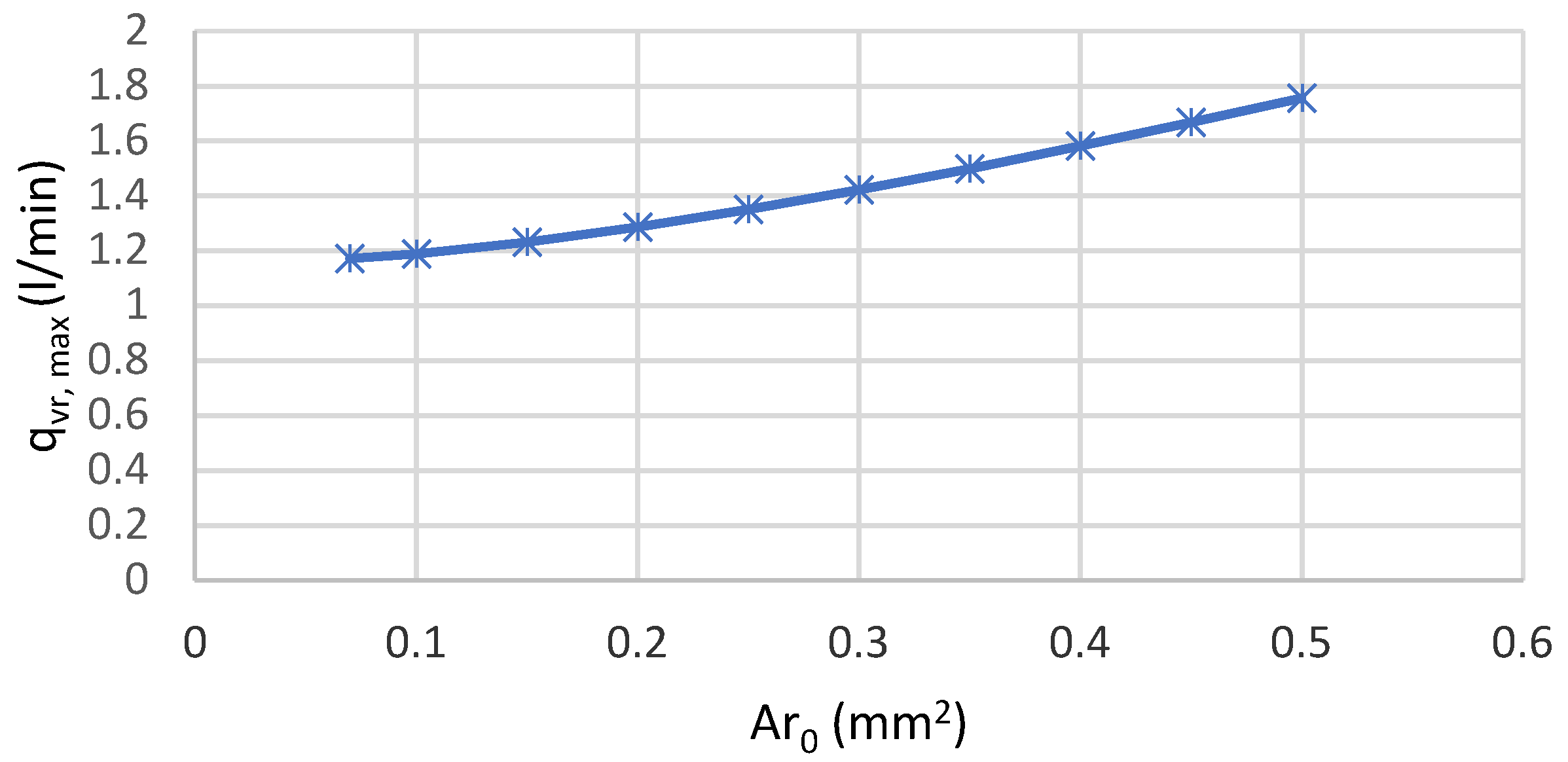
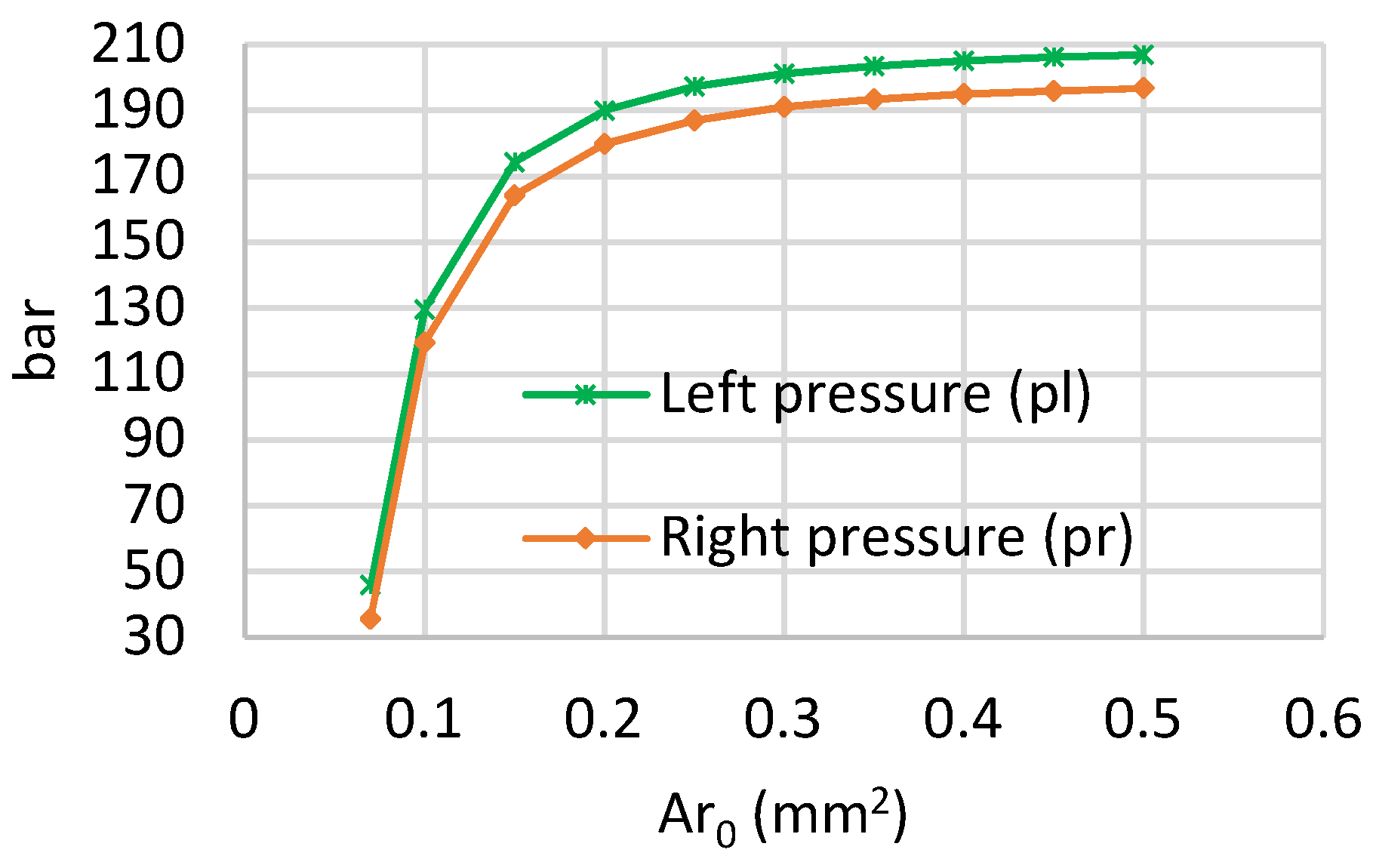



| Product Type | Outer Diameter (mm) | Inner Diameter (mm) | Height (mm) | Operating Voltage (V) | Max. Free Stroke (µm) | Max. Block. Force (N) | Stiffness (N/µm) |
|---|---|---|---|---|---|---|---|
| CMBR02 | 20 | 4 | 1.25 | ±100 | ±28 | ±16 | 0.57 |
| CMBR03 | 20 | 4 | 1.8 | ±100 | ±20 | ±22 | 1.10 |
| CMBR04 | 30 | 6 | 0.7 | ±100 | ±108 | ±11 | 0.10 |
| CMBR05 | 30 | 6 | 1.25 | ±100 | ±70 | ±29 | 0.41 |
| CMBR07 | 40 | 8 | 0.7 | ±100 | ±185 | ±13 | 0.07 |
| CMBR08 | 40 | 8 | 1.25 | ±100 | ±115 | ±39 |
| Parameter | Symbol | Value |
|---|---|---|
| Main spool diameter | 7 mm | |
| Main spool lateral surface | 38.50 mm2 | |
| Width of the slots | b | 10 mm |
| Maximum spool displacement | 1 mm | |
| Maximum spool velocity | 0.25 m/s | |
| Maximum flow rate | 65.8 L/min |
| Parameter | Symbol | Value |
|---|---|---|
| Area of the fixed orifice | 0.1 mm2 | |
| Diameter of the piezo-valve nozzle | 1 mm | |
| Maximum opening of the piezo- valve | 0.05406 mm | |
| Pre-compression of the ring bender | 0.05793 mm | |
| Ring bender model | - | CMBR08 |
| Predicted maximum flow rate through the piezo-valve | 1.190 L/min | |
| Predicted left pressure (at ) | 129.6 bar | |
| Predicted right pressure (at ) | 119.4 bar |
| Component | Parameter | Symbol | Value |
|---|---|---|---|
| Main valve | Main spool diameter | 7 mm | |
| Main spool lateral surface | 38.5 mm2 | ||
| Width of the slots | b | 10 mm | |
| Main spool mass | M | 20 g | |
| Dead volume | Vdead | 38.5 mm3 | |
| Damping coefficient | C | 10 Ns/m | |
| Leakage area | 3 × 10−8 m2 | ||
| Discharge coefficient | CD | 0.7 | |
| Piezo-valve | Diameter of the nozzle | d | 1 mm |
| Discharge coefficient | CD | 0.7 | |
| Max free stroke of the ring bender | Lmax | 0.115 mm | |
| Max blocking force of the ring bender | Fb,max | 39 N | |
| Mass of the moving parts | 20 g | ||
| Damping coefficient | Crb | 26 Ns/m | |
| Ring bender stiffness | krb | 340,000 N/m | |
| Stop stiffness | 108 N/m | ||
| Stop damping coefficient | 500 Ns/m | ||
| Pre-compression of the ring bender | x0 | 0.05793 mm | |
| Minimum opening of the piezo-valve | xmin | 0 | |
| Maximum opening of the piezo-valve | xmax | 0.05406 mm | |
| Leakage area | 3.14159 × 10−9 m2 | ||
| Fixed orifices | Restricted area | Ar,0 | 0.1 mm2 |
| Discharge coefficient | CD | 0.7 | |
| Hydraulic chamber | Diameter | 3 mm | |
| Length | 40 mm | ||
| PI parameters | Proportional gain | 9 | |
| Integral gain | 450 | ||
| Derivative gain | 0.012 | ||
| Saturation limits | ±5 V | ||
| Pump | Supply pressure | pP | 210 bar |
| Reservoir | Pressure | pT | 1 bar |
| Oil (ISO VG 32 50 °C) | Density | ρ0 | 851 kg/m3 |
| Relative gas content | ε | 0.005 | |
| Amplifier | Natural frequency | ωn | 1400 rad/s |
| Damping factor | ξ | 1.5 | |
| Maximum current | Imax | 1 A | |
| Ring bender capacitance | 2 × 1740 nF | ||
| Gain of the amplifier | 20 |
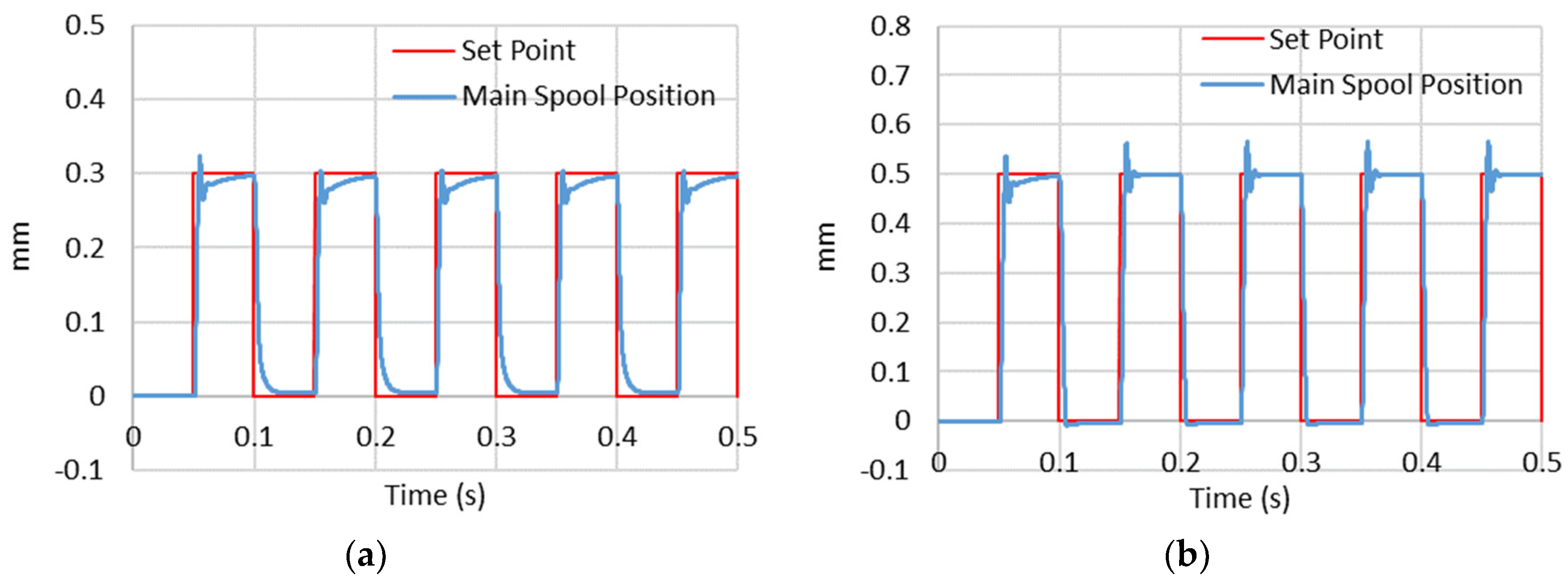
| Set point | X = 0.3 mm | X = 0.5 mm | X = 0.7 mm | X = 1 mm |
| Flow rate at set point | Q = 19.4 L/min | Q = 32.8 L/min | Q = 46 L/min | Q = 65.8 L/min |
| Rise time to reach 90% of the output | Δt = 4.1 ms | Δt = 4.3 ms | Δt = 4.8 ms | Δt = 5.9 ms |
| Flow rate through the piezo valves at null | qv(X = 0) = 0.02930 L/min | qv(X = 0) = 0.02930 L/min | qv(X = 0) = 0.02930 L/min | qv(X = 0) = 0.02930 L/min |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tamburrano, P.; Plummer, A.R.; De Palma, P.; Distaso, E.; Amirante, R. A Novel Servovalve Pilot Stage Actuated by a Piezo-Electric Ring Bender (Part II): Design Model and Full Simulation. Energies 2020, 13, 2267. https://doi.org/10.3390/en13092267
Tamburrano P, Plummer AR, De Palma P, Distaso E, Amirante R. A Novel Servovalve Pilot Stage Actuated by a Piezo-Electric Ring Bender (Part II): Design Model and Full Simulation. Energies. 2020; 13(9):2267. https://doi.org/10.3390/en13092267
Chicago/Turabian StyleTamburrano, Paolo, Andrew R. Plummer, Pietro De Palma, Elia Distaso, and Riccardo Amirante. 2020. "A Novel Servovalve Pilot Stage Actuated by a Piezo-Electric Ring Bender (Part II): Design Model and Full Simulation" Energies 13, no. 9: 2267. https://doi.org/10.3390/en13092267
APA StyleTamburrano, P., Plummer, A. R., De Palma, P., Distaso, E., & Amirante, R. (2020). A Novel Servovalve Pilot Stage Actuated by a Piezo-Electric Ring Bender (Part II): Design Model and Full Simulation. Energies, 13(9), 2267. https://doi.org/10.3390/en13092267









