LLC LED Driver with Current-Sharing Capacitor Having Low Voltage Stress

Abstract

In this paper, an LLC light-emitting diode (LLC LED) driver based on the current-sharing capacitor is presented. In the proposed LED driver, the LLC resonant converter is used to step down the high input voltage, to provide galvanic isolation, to offer a constant current for LEDs. Moreover, the current-sharing capacitor connected to the central-tapped point of the secondary-side winding is used to balance the currents in two LED strings. By doing so, the voltage stress on this capacitor is quite low. Above all, the equivalent forward voltages of the two LED strings are generally influenced by the temperature and the LED current, and this does not affect the current-sharing performance, as will be demonstrated by experiment on the difference in number of LEDs between the two LED strings. In addition, only the current in one LED string is sensed and controlled by negative feedback control, while the current in the other LED string is determined by the current-sharing capacitor. Moreover, this makes the current control so easy. Afterwards, the basic operating principles and analyses are given, particularly for how to derive the effective resistive load from the LED string. Eventually, some experimental results are provided to validate the effectiveness of the proposed LED driver.

1. Introduction

As compared with the traditional lighting sources, like the incandescent lights, fluorescent lights, and halogen lights, etc., the high-brightness lighting-emitting diodes (LEDs) have become promising due to their long life, compact size, and eco-friendly characteristics [1]. The LED lights are widely used in the indoor lighting, outdoor lighting, and display backlighting. In these applications, multiple LEDs are connected to increase the luminous flux. The LEDs can be connected in series and parallel, depending on the output voltage and current of the LED driver. In general, multiple LEDs are connected in series to form an LED string, and then the LED strings are connected in parallel with each other. Since each LED has different voltage and current characteristics, the constant current control is required to equalize each LED string current. Therefore, LED current sharing technique is necessary. The LED current sharing can be classified into two methods. One is the active method [2,3,4,5,6,7,8,9], and the other is the passive method [10,11,12,13,14,15].

Generally, the active method uses semiconductor devices and integrated circuits to achieve LED current sharing. The active method has some disadvantages, such as complexity and high cost. The passive method, which features low cost and simplicity, is developed as another LED current sharing method. The passive method can be subdivided into inductive and capacitive methods. The inductive method usually uses the current-sharing transformers. For the current-sharing transformer method, the differential transformer with a 1:1 turns ratio is used to balance the LED current. On the other hand, the capacitive method uses the capacitors to achieve LED current balance. The current sharing is achieved based on the capacitor ampere-second balance. In Figure 1, the literatures [14] and [15] display the low-power two-channel LED drivers using the capacitor to achieve LED current balance. They are suitable for low-input voltage and low-power applications. These two LED drivers are based on step-up converters. The output voltage of the two-channel LED driver is the sum of the voltages across two LED strings, and this is different from the parallel connection. Thus, these kinds of LED drivers are called pseudo multi-string LED drivers. However, if the resonance behavior is taken into account, then the soft switching of the switch and diode will happen, causing the overall efficiency can be upgraded. Consequently, the non-isolated boost resonant LED driver shown in [16] is presented. In this circuit, only the diode in the resonant path can have zero-current-switching (ZCS) turn-off. In addition, if the resonance behavior as well as galvanic isolation taking into consideration, then the isolated voltage-bucking resonant LED driver as displayed in [17] is proposed. In this circuit, only all the diodes on the secondary side have ZCS.

Therefore, an isolated LED driver based on the LLC resonant converter is proposed herein. Both switches have zero-voltage-switching (ZVS) turn-on and both the diodes on the secondary side have ZCS turn-off except at light load. The proposed LED driver is based on the current-sharing capacitor with a quite low voltage stress. In this paper, the basic operating principles, steady-state analyses, and experimental results will be given in the following sections.

2. Basic Analysis of the Proposed LED Driver

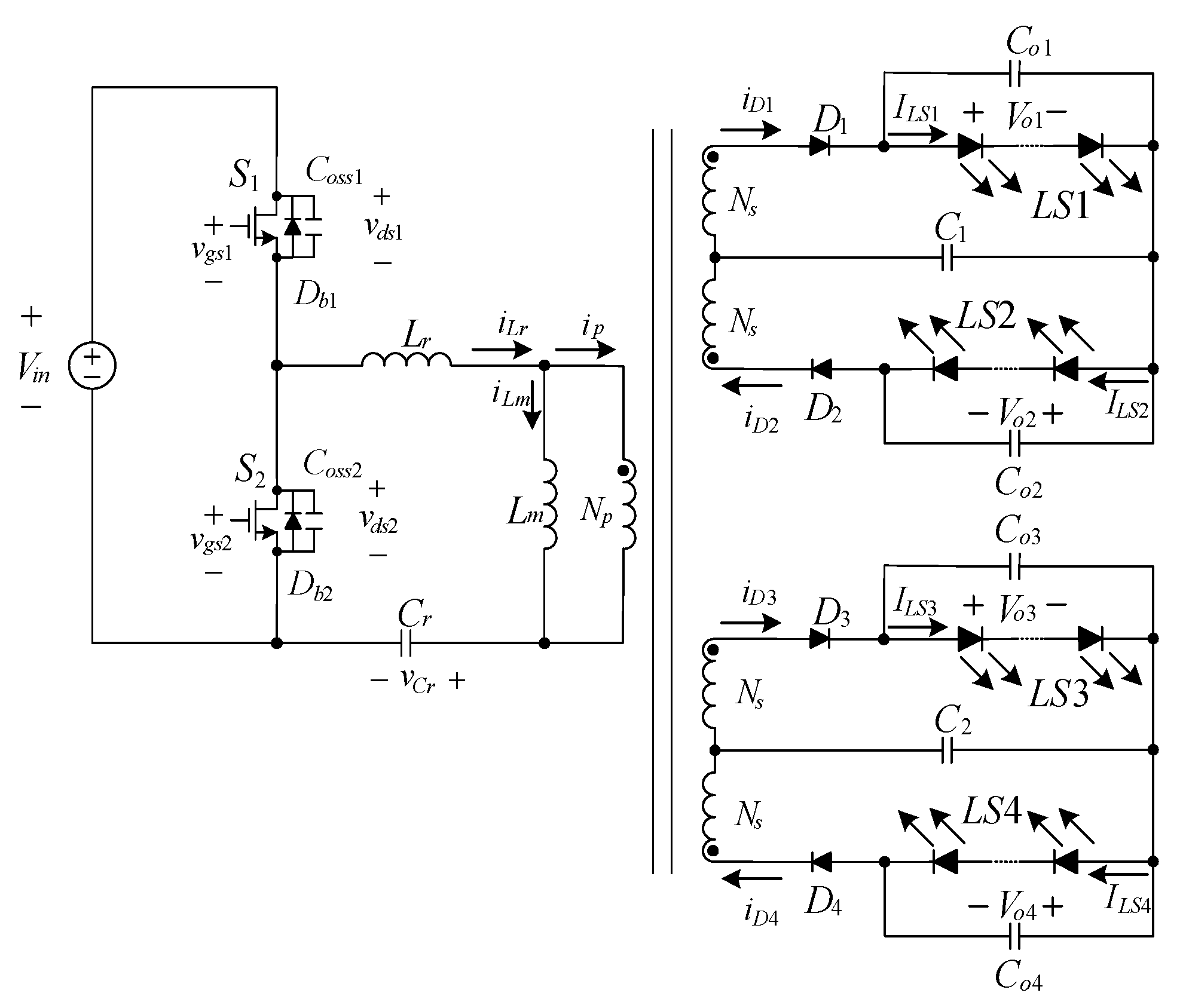
Figure 2 shows the proposed two-channel LED driver. For analysis convenience, there are some assumptions to be made as follows.

(1)

The switches and components are ideal except for the metal-oxide-semiconductor field-effect transistor (MOSFET) switches and the transformer.

(2)

The values of all the capacitors are large enough. Thus, the voltages across them are regarded as constant.

(3)

The two output voltages are identical, namely, V_o1 = V_o2.

The following analyses contain the (a) operating principles; (b) LED modeling; (c) LED load characteristics; (d) voltage gain characteristics; and (e) extension of the proposed LED driver.

2.1. Operating Principles

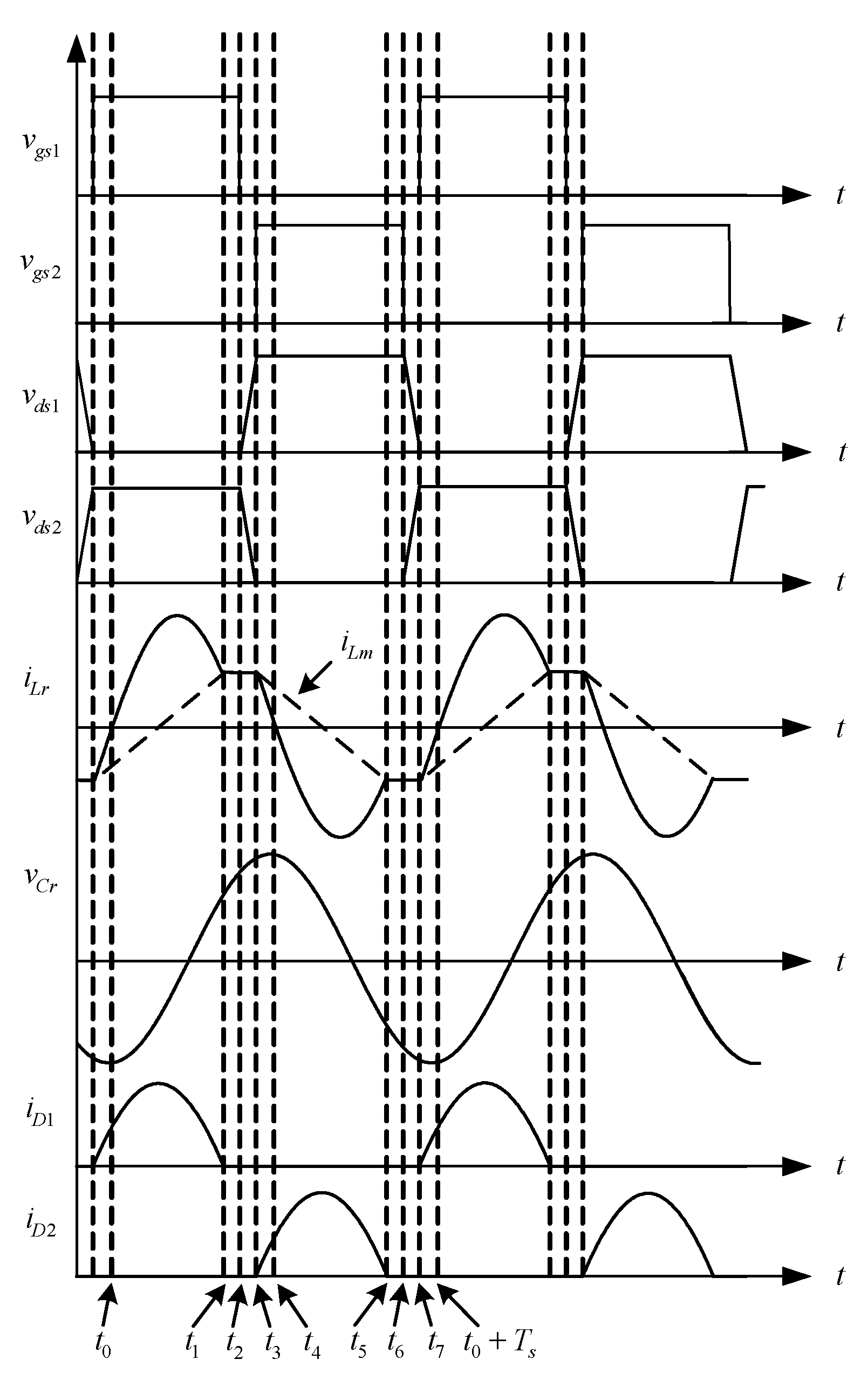
There are 8 operating states in the proposed LED driver. Figure 3 shows the key waveforms over one switching period.

2.1.1. State 1 (t₀, t₁)

As shown in Figure 4a, S₁ is ON, but S₂ is OFF. Thus, L_r and C_r resonate with each other and i_Lr increases from zero. During this state, i_Lr is larger than i_Lm. Therefore, the current i_p is transferred from the primary side to the secondary side, thus making D₁ forward biased and hence providing energy to C_o1 and LS1. As for LS2, it is powered by C_o2. At the same time, the voltage nV_o1 is across L_m, thus causing i_Lm to be increased linearly. This state ends when i_Lr equals i_Lm at t₁.

2.1.2. State 2 (t₁, t₂)

As shown in Figure 4b, S₁ is still ON, but S₂ is still OFF. During this state, since i_Lr is equal to i_Lm, there is no current flowing through the secondary side, thereby causing the energy required by LS1 and LS2 to be provided by C_o1 and C_o2, respectively. At the same time, C_r, L_r, and L_m resonate together, thus causing i_Lr to be increased quite slowly. This state ends when S₁ turns off at t₂.

2.1.3. State 3 (t₂, t₃)

As shown in Figure 4c, S₁ is turned OFF and S₂ still keeps OFF. During this state, C_oss1 is charged and C_oss2 is discharged, thus causing the energy required by LS1 and LS2 to be still provided by C_o1 and C_o2, respectively. This state ends when C_oss1 is charged to V_in, and C_oss2 is discharged to zero at t₃.

2.1.4. State 4 (t₃, t₄)

As shown in Figure 4d, S₁ keeps OFF, but S₂ is turned ON with zero voltage switching (ZVS) due to i_Lr flowing through D_b2. During this state, i_Lr is smaller than i_Lm. Therefore, the current -i_p is reflected from the secondary side to the primary side, thereby making D₂ forward biased and hence providing energy to C_o2 and LS2. As for LS1, it is powered by C_o1. At the same time, the voltage −nV_o2 is across L_m, thereby causing i_Lm to be decreased linearly. This state ends when i_Lr reaches zero at t₄.

2.1.5. State 5 (t₄, t₅)

As shown in Figure 4e, S₁ still keeps OFF, but S₂ keeps ON. During this state, i_Lr changes the direction. The voltage -nV_o2 is still across L_m. Thus, i_Lm is still decreased linearly. This state ends when i_Lr equals i_Lm at t₅.

2.1.6. State 6 (t₅, t₆)

As shown in Figure 4f, S₁ still keeps OFF, but S₂ still keeps ON. Since i_Lr is equal to i_Lm, there is no current flowing through the secondary side, thereby causing the energy required by LS1 and LS2 to be provided by C_o1 and C_o2, respectively. At the same time, C_r, L_r and L_m resonate together, thus causing i_Lr to be decreased quite slowly. This state ends when S₂ turns off at t₆.

2.1.7. State 7 (t₆, t₇)

As shown in Figure 4g, S₁ still keeps OFF, and S₂ is turned OFF. During this state, C_oss1 is charged and C_oss2 is discharged, thus causing the energy required by LS1 and LS2 to be still provided by C_o1 and C_o2, respectively. This state ends when C_oss1 is discharged to zero, and C_oss2 is charged to V_in at t₇.

2.1.8. State 8 (t₇, t₀ + T_s)

As shown in Figure 4h, S₂ keeps OFF, but S₁ is turned ON with ZVS due to i_Lr flowing through D_b1. During this state, −i_Lr is smaller than −i_Lm. Therefore, the current i_p is transferred from the primary side to the secondary side, thus making D₁ forward biased and hence providing energy to C_o1 and LS1. As for LS2 it is powered by C_o2. At the same time, the voltage nV_o1 is across L_m, thus causing i_Lm to be increased linearly. This state ends when i_Lr reaches zero at t = t₀ + T_s.

2.2. LED Modeling

The LED string can be modeled as a piecewise linear model as shown in Figure 5. The equivalent LED string model contains one ideal diode D_ideal, one equivalent on-resistance R_LED and one equivalent forward voltage V_F, with all the three connected in series. Also, the LED string current is defined as I_LED. Hence, the LED string voltage V_LED can be expressed as

$$V_{LED}=V_F+I_{LED}{R}_{LED}$$

(1)

2.3. LED Load Characteristics

The AC equivalent load can be modeled by using the fundamental harmonic approximation (FHA). The AC equivalent circuit of the proposed LLC resonant LED driver is shown in Figure 6. The derivation is shown as follows.

The current i_ac(fund) is defined as a fundamental sinusoidal wave on the secondary side. That is,

$$i_{ac(fund)}(t)=I_p\sin ({\omega }_{s}t)$$

(2)

where I_p is the maximum value of i_ac(fund)(t).

The expression of V_LED can be changed to

$$V_{LED}=V_F+R_{LED}{I}_{LED}=V_F+R_{LED}{\langle i_{D1}(t)\rangle }_{T_s}$$

(3)

where ${\langle i_{D1}(t)\rangle }_{T_s}$ is the average current of i_D1 and equal to I_LED.

Therefore, ${\langle i_{D1}(t)\rangle }_{T_s}$ can be expressed to be

$${\langle i_{D1}(t)\rangle }_{T_s}=\frac{1}{T_s}{\displaystyle {\int }_0^{T_s/2}{I}_p\left|\sin ({\omega }_{s}t)\right|}dt=\frac{1}{\pi }{I}_p$$

(4)

By substituting (4) into (3), V_LED can be rewritten to be

$$V_{LED}=V_F+R_{LED}(1/\pi )I_p$$

(5)

In addition, the voltage on the secondary side, v_ac(t), can be expressed to be

$$v_{ac}(t)=\{\begin{array}{l}{V}_{o1}, i_{D1}(t)>0\\ -V_{o2}, i_{D2}(t) > 0\end{array}$$

(6)

Also, the voltage v_ac(t) can be represented by a Fourier series as follows:

$$v_{ac}(t)=a_0+{\displaystyle \sum _{h=1}^{\infty }[a_h\cos (h{\omega }_{s}t)+b_h\sin (h{\omega }_{s}t)]}$$

(7)

Since v_ac(t) is an odd function waveform, a_n is zero. Thus,

$$v_{ac}(t)={\displaystyle \sum _{h=1,3,5,\dots }^{\infty }\frac{4V_{o1}}{h\pi }}\sin (h{\omega }_{s}t)$$

(8)

The fundamental waveform of v_ac(t), called v_ac(fund)(t), is

$$v_{ac(fund)}(t)=(\frac{4V_{o1}}{\pi })\sin ({\omega }_{s}t)$$

(9)

Based (4) and V_o1 = V_LED, the effective resistive load R_o,ac can be signified by

$$R_{o,ac}=\frac{v_{ac(fund)}\left(t\right)}{i_{ac(fund)}\left(t\right)}=\frac{(\frac{4V_{o1}}{\pi })\sin ({\omega }_{s}t)}{I_p\sin ({\omega }_{s}t)}=\frac{4V_{o1}}{\pi I_p}=\frac{4}{{\pi }^2}(\frac{V_{o1}}{I_{LED}})=\frac{4}{{\pi }^2}(\frac{V_{LED}}{I_{LED}})$$

(10)

2.4. Voltage Gain Characteristics

Figure 7 shows the two-port model of the FHA resonant circuit. The output load resistor R_out can be regarded as the equivalent static resistance of the LED string at a given forward current, that is, V_LED divided by I_LED. In addition, the voltage gain is

$$M(j2\pi f_s)=\frac{n{V}_{o,FHA}(j2\pi f_s)}{V_{in,FHA}(j2\pi f_s)}$$

(11)

where $V_{in,FHA}(j2\pi f_s)$ is the fundamental component of the input voltage in the phasor domain and $V_{o,FHA}(j2\pi f_s)$ is the fundamental component of the output voltage in the phasor domain.

The input voltage waveform of the AC resonant tank is

$$v_{in}(t)=\frac{V_{in}}{2}+{\displaystyle \sum _{h=1,3,5,\dots }^{\infty }\frac{2V_{in}}{h\pi }\sin (h{\omega }_{s}t)}$$

(12)

From (12), it can be seen that the fundamental component of the input voltage is

$$v_{in,FHA}(t)=\frac{2V_{in}}{\pi }\sin ({\omega }_{s}t)$$

(13)

As derived in (9), the output voltage fundamental component is

$$v_{o,FHA}(t)=v_{ac(fund)}(t)=(\frac{4V_{o1}}{\pi })\sin ({\omega }_{s}t)$$

(14)

Based on (11), (13), and (14), the DC-DC input-to-output voltage conversion ratio can be derived as follows:

$$\left|M(j2\pi f_s)\right|=\frac{n\left|V_{o,FHA}(j2\pi f_s)\right|}{\left|V_{i,FHA}(j2\pi f_s)\right|}=\frac{n(\frac{4V_{o1}}{\pi })}{\frac{2V_{in}}{\pi }}$$

(15)

From (15), the DC-DC input-to-output voltage conversion ratio is

$$\frac{V_{o1}}{V_{in}}=\frac{1}{2n}\left|M(j2\pi f_s)\right|$$

(16)

In Figure 6, by transferring the time domain to the s domain and let $s=j2\pi f_s$, the magnitude of the voltage gain $M(j2\pi f_s)$, called M, can be derived as follows:

$$M=\left|M(j2\pi f_s)\right|=\frac{K\times {(\frac{f_s}{f_r})}^2}{\sqrt{{\left[(K+1)\times {(\frac{f_s}{f_r})}^2-1\right]}^2+{\left\{[{(\frac{f_s}{f_r})}^3-1]\times \frac{f_s}{f_r}\times Q\times K\right\}}^2}}$$

(17)

where $K=\frac{L_m}{L_r}$, $f_r=\frac{1}{2\pi \sqrt{L_r{C}_r}}$, $Q=\frac{Z_o}{n^2{R}_{o,ac}}$, and $Z_o=\sqrt{\frac{L_r}{C_r}}$.

From (17), it can be seen that Q and K will affect the voltage gain.

The output resistance in Figure 7 is replaced with the LED equivalent model as shown in Figure 8. Based on (1),

$$I_{LED}=\frac{V_{LED}(=V_{o1})-V_F}{R_{LED}}$$

(18)

Based on (16), Equation (19) can be rewritten as

$$I_{LED}=\frac{\left|M(j2\pi f_s)\right|\cdot \frac{V_{in}}{2n}-V_F}{R_{LED}}$$

(19)

From (19), it can be seen that the LED current can be regulated by changing the switching frequency f_s, and this means that the gain adjustment is made by frequency modulation. As seen in Figure 9, by giving an LED current command I_{LED_command}, the frequency modulator will change the switching frequency f_s, and v_o,FHA will be varied to a corresponding value according to the designed voltage gain M.

2.5. System Control

Figure 10 shows the control strategy of the proposed LED driver. From Figure 10a, it can be seen that one of the LED strings is sensed and the current signal is transformed to the voltage signal and then sent to UCD3138, which contains an error ADC, a filter, and a digital PWM as shown in Figure 10b. The sensed current signal will be sent to the error ADC and compared with the prescribed reference value. After this, the error signal will be sent to the filter, called the PID controller. Eventually, the calculated duty cycle and frequency will control the MOSFETs to regulate the LED string currents.

2.6. Effect of Variations in Equivalent forward Voltage on Current Sharing

As shown in Figure 10a, since the voltages across the two central-tapped windings are the same, this means that

$$V_{D1}+V_{o1}-V_{C1}=V_{D2}+V_{o2}+V_{C1}$$

(20)

Assuming that the diodes D₁ and D₂ are two-in-one, V_D1 can be regarded as almost equal to V_D2. Therefore, (20) can be simplified to (21):

$$V_{C1}=0.5\times (V_{o1}-V_{o2})$$

(21)

Based on (21), if the two LED strings are identical, then V_C1 is zero; otherwise, V_C1 is not zero. This means that the difference in equivalent forward voltage between the two LED strings can be absorbed by the current-sharing capacitor C₁.

2.7. Circuit Extension

Figure 11 shows the four-channel LED driver, which can be derived from the proposed two-channel LED driver. However, in practice, the effective resistive load R_o,ac will be changed. Consequently, the design of the associated parameters will be repeated if necessary.

3. Design Considerations

To verify the effectiveness of the proposed LED driver, a prototype is built up and tested.

Table 1. System specifications of the proposed LED driver.

System Parameters	Specifications
Normal input voltage (Vin_nor)	400 V
Maximum input voltage (Vin_max)	410 V
Minmimum input voltage (Vin_min)	390 V
Nominal LED channel voltage (Vo1, Vo2)	3.45 V × 12 = 41.4 V
Nominal LED channel current (io1, io2)	350 mA
Nominal LED power value (PLED)	30 W
Resonant frequency (fr)	100 kHz
Ratio of magnetizing inductance to resonant inductance (K)	5
Quality factor (Q)	0.48

shows the system specifications of the proposed converter, whereas

Table 2. Components used in the proposed LED driver.

Components	Specifications
MOSFET switches (Q1, Q2)	SPA20N60C3
Diodes (D1, D2)	80 CPQ 150 PbF
Resonant capacitor (Cr)	3.3 nF
Transformer (T1)	Core: PQ35/35 n = Np/Ns = 60/12, Lm = 230.074 μH, Llk = 9.88 μH,
Resonant inductor (Lr)	Core: PQ20/20 L r = 965.8 μH
Current-sharing capacitor (C1)	10 μF
Output capacitors (Co1, Co2)	10 μF

shows the component specifications used in the proposed converter. Moreover, the design procedures of (a) LED selection; (b) transformer turns ratio (n); (c) maximum voltage conversion ratio (M_max) and minimum voltage conversion ratio (M_min); (d) effective resistive load reflected to the primary side of the transformer (n²R_o,ac); (e) ratio of magnetizing inductance to resonant inductance ratio (K) and quality factor (Q); and (f) resonant capacitance (C_r), resonant inductance (L_r), and magnetizing inductance (L_m).

3.1. Selection of LED String

The high-power LEDs, used as load for the proposed LED driver, are made by Everlight Electronics Ltd. The corresponding product name is EHP-AX08EL/GT01H-P01/5670/Y/K42. From the associated datasheet, it can be seen that the forward voltage is about 3.45 V if the constant current flowing through the LED is 350 mA. In the proposed two-channel LED driver, 12 pieces of LEDs are connected in series for each string. Also, the LED string can be constructed by as an approximately linear model as shown in Figure 5. The equivalent forward voltage V_F is about 41.4 V (= 2.73·12), and the equivalent on-resistance R_LED is about 24.68 Ω (= 2.057·12).

3.2. Determination of Transformer Turns Ratio

The turns ratio of the transformer can be figured out under normal input voltage and unity voltage gain, namely, M_nor = 1:

$$n=M_{nor}\times \frac{1}{2}\times \frac{V_{in\_nor}}{V_{o\_rated}}=1\times \frac{1}{2}\times \frac{400}{41.4}\approx 4.83$$

(22)

Based on the above calculation, the turns ratio n is selected to be 5. Via recalculation, the new voltage gain is 1.04.

3.3. Maximum and Minimum Voltage Gains

The maximum voltage gain and the minimum voltage gain are calculated as follows:

$$M_{max}=2\times n\times \frac{V_{o\_rated}}{V_{in\_min}}=2\times 5\times \frac{41.4}{390}\approx 1.06$$

(23)

$$M_{min}=2\times n\times \frac{V_{o\_rated}}{V_{in\_max}}=2\times 5\times \frac{41.4}{410}\approx 1.01$$

(24)

To prevent the operating point from going into the capacitive region, the maximum voltage gain should have a margin. The corresponding margin is 0.15 times M_max. Therefore, the value of M_max is changed to

$$M_{max}=1.06\times 1.15\approx 1.22$$

(25)

3.4. Effective Resistive Load on the Primary Side

Based on (10), the effective resistive load on the primary side, R_ac, is calculated as follows:

$$R_{ac}=n^2{R}_{o,ac}=n^2\frac{4}{{\pi }^2}\frac{V_{o\_rated}}{I_{LED}}=5^2\times \frac{4}{{\pi }^2}\times \frac{41.4}{0.35}\approx 1198.49 \Omega$$

(26)

3.5. Selection of K and Q and Determination of Switching Frequency Range

In the proposed LED driver, the value of K is selected to be 5. From Figure 12, it can be seen that the values of M change with different values of Q. In this paper, Q is selected to be 0.48. The minimum switching frequency f_{s_min} and the maximum switching frequency f_{s_max} are shown below:

$$f_{s\_min}=\frac{f_r}{\sqrt{1+K(1-\frac{1}{M_{max}^2})}}=\frac{100\times {10}^3}{\sqrt{1+5\times (1-\frac{1}{{1.22}^2})}}=61.5 \mathrm{kHz}$$

(27)

$$f_{s\_max}=\frac{f_r}{\sqrt{1+K(1-\frac{1}{M_{min}})}}=\frac{100\times {10}^3}{\sqrt{1+5\times (1-\frac{1}{1.01})}}=97.7 \mathrm{kHz}$$

(28)

3.6. Resonant Capacitance, Resonant Inductance and Magnetizing Inductance

Based on the effective resistive load calculated in (26), the selected resonant frequency f_r = 100 kHz, and the selected quality factor Q = 0.48, the resonant capacitance C_r can be worked out from (29). Moreover, based on (29), the resonant inductance L_r can be figured out from (30). Finally, based on the selected K = 5, the magnetizing inductance can be found from (31):

$$\begin{array}{l}Q=\sqrt{\frac{L_r}{C_r}}\times \frac{1}{R_{ac}}=\frac{1}{2\pi \times f_r\times R_{ac}\times C_r}\\ \Rightarrow C_r=\frac{1}{2\pi \times Q\times f_r\times R_{ac}}\\ \Rightarrow C_r=\frac{1}{2\pi \times 0.48\times 100\times {10}^3\times 1198.49}=2.767 \mathrm{nF}\end{array}$$

(29)

$$\begin{array}{l}{f}_r=\frac{1}{2\pi \sqrt{L_r\times C_r}}\\ \Rightarrow L_r=\frac{1}{{(2\pi \times f_r)}^2\times C_r}\\ \Rightarrow L_r=\frac{1}{{(2\pi \times 100\times {10}^3)}^2\times 2.767\times {10}^{-9}}=915.6 \mathsf{\mu }\mathrm{H}\end{array}$$

(30)

$$L_m=K\times L_r=5\times 915.6\mathsf{\mu }=4578 \mathsf{\mu }\mathrm{H}$$

(31)

4. Experimental Results

Figure 13, Figure 14, Figure 15, Figure 16, Figure 17 and Figure 18 show the measured waveforms at rated loads. Figure 13 shows the gate driving signals for the switches Q₁ and Q₂, and the voltage stresses v_ds1 and v_ds2. From this figure, it can be seen that the voltage stresses on Q₁ and Q₂ are around 400 V.

Figure 14 displays the resonant inductor current i_Lr, and the resonant capacitor voltage v_Cr. From this figure, it can be seen that the switching frequency f_s is smaller than the resonant frequency f_r. Also, when the resonant inductance current equals the magnetizing inductance current, there is no current transferring to the secondary side. During this period, C_r, L_r and L_m resonate together, resulting in a slow increase of the resonant current.

Figure 15 shows the diode currents. From this figure, it can be seen that the diode currents reach zero before the MOSFET switches are turned on, and this means that the diodes are turned off with zero-current switching (ZCS).

Figure 16 shows the voltages on the two LED strings, named V_o1 and V_o2, and the currents in the two LED strings, named I_LS1 and I_LS2. From this figure, it can be seen that V_o1 and V_o2 are both about 41 V, and I_SL1 and I_SL2 are regulated to be 350 mA.

Figure 17 displays the voltage across C₁, named V_C1, and current flowing through C₁, named i_C1. From this figure, it can be seen that V_C1 is zero due to V_o1 almost equal to V_o2.

Figure 18 displays the efficiency. From this figure, it can be seen that the rated-load efficiency is around 94.8%, and the highest efficiency is around 96.6%.

Furthermore, in order to verify the current-sharing performance of variations in forward voltage due to the temperature and the LED current, the number of LEDs for LS₁ is 12 LEDs and the number of LEDs for LS₂ is 9 LEDs. From Figure 19, it can be seen that two currents in LS1 and LS2 are almost the same, about 350 mA, but the difference in voltage between LS1 and LS2 is 10 V (= V_o1 − V_o2 = 40 V − 30 V = 10 V). From this result, it is obvious that if the forward voltage is varied due to the temperature and the LED current, the current sharing is still performed well.

In Figure 20, it can be seen that the voltage across C₁ is not zero, equal to about 5 V, which can be obtained based on (21).

In addition, as shown in Figure 18, the current consumed by the system can be calculated based on output power divided by efficiency and input voltage. Accordingly, the current consumed at 25% load current with 91.6% efficiency is 0.02047 A, the current consumed at 70% load current with 96.6% efficiency is 0.05435 A, and the current consumed at 100% load current with 94.8% efficiency is 0.07911 A.

5. Comparison of Waveforms and Efficiencies

In the following, Figure 17 is compared with Figure 21 and Figure 22, whereas Figure 18 is compared with Figure 23 and Figure 24. From Figure 17, Figure 21 and Figure 22, it can be seen that the currents in two LED strings for each figure are almost the same. Since the input voltages in [14] and [15] are of $3.3 \mathrm{V}\pm 10\%$, the number of efficiency curves for each of these two literatures is three. The highest efficiency among Figure 18, Figure 23 and Figure 24 is 96.6% from Figure 18, whereas the lowest efficiency among them is 86.5% from Figure 24.

6. Conclusions

An isolated LED driver based on the LLC resonant converter is presented herein. In the proposed LED driver, the current-sharing capacitor is used to balance the LED currents. Therefore, the active current sharing circuits are not required. From the experimental results, it can be seen that the currents in the two LED strings are identical without considering the difference in equivalent forward voltage between the two LED strings. Furthermore, the number of the LED channels can be increased. A detailed design of the proposed LED driver is shown in this paper, particularly for how to obtain the effective resistive load from the LED string. As for current control, only the current in one LED string is sensed and controlled by negative feedback control, and the current in the other LED string is determined by the current-sharing capacitor. By doing so, this makes the current control quite easy. Moreover, the measured efficiency shows that the efficiency at rated load is around 94.8%, and the efficiency can be up to 96.6%.