Very Low Sampling Frequency Model Predictive Control for Power Converters in the Medium and High-Power Range Applications
Abstract
:1. Introduction
2. Power Converter Model
2.1. Stationary abc Reference Frame Model
2.2. Stationary αβ Reference Frame Model
2.3. Model Discretization
3. Predictive Control Strategy
3.1. Model Discretization
3.2. Rectifier Injected Voltage
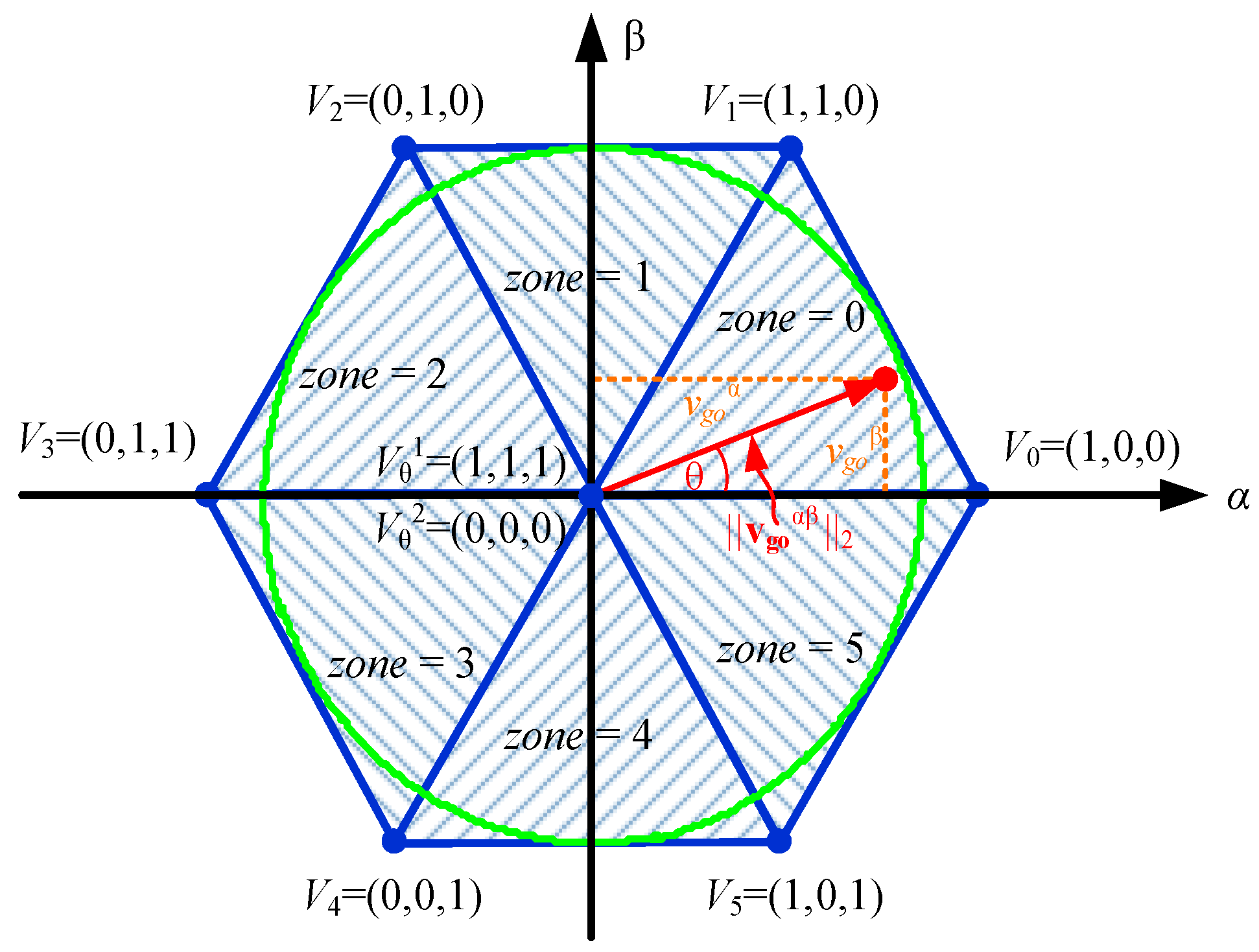
3.3. Required Voltage Based on Space Vector
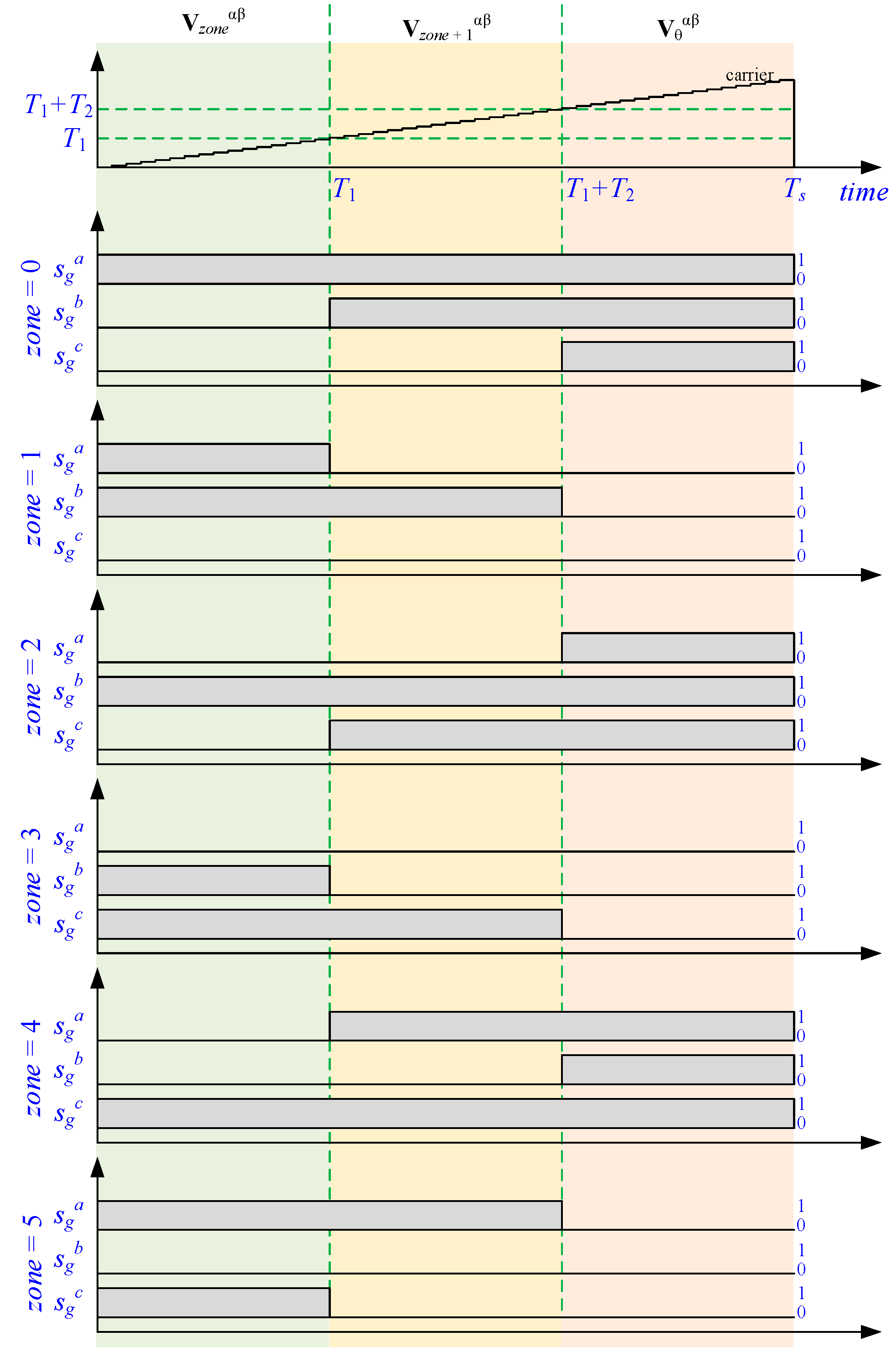
3.4. Switching Generation for a PWM Implementation
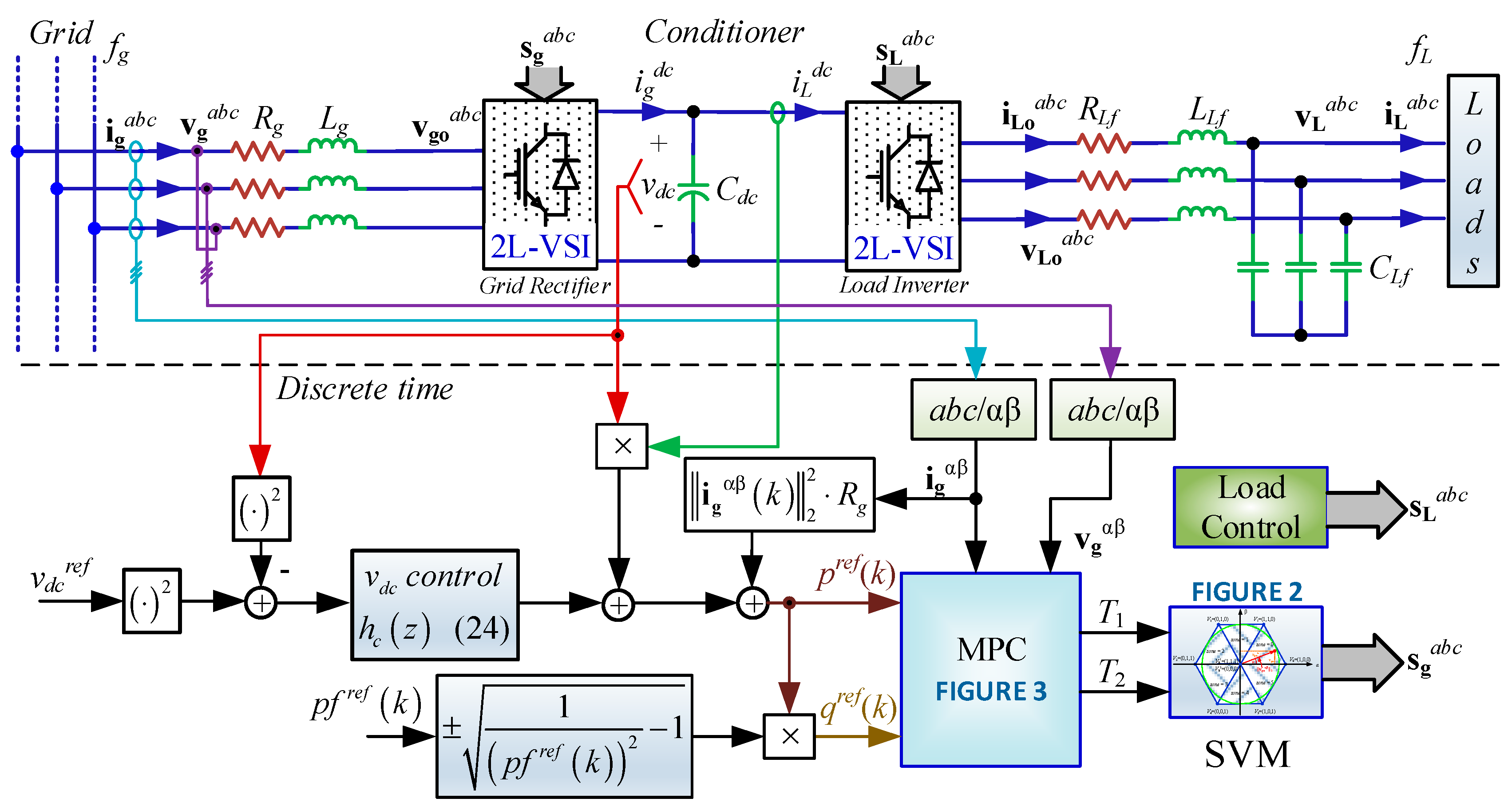
4. Materials and Methods
5. Results
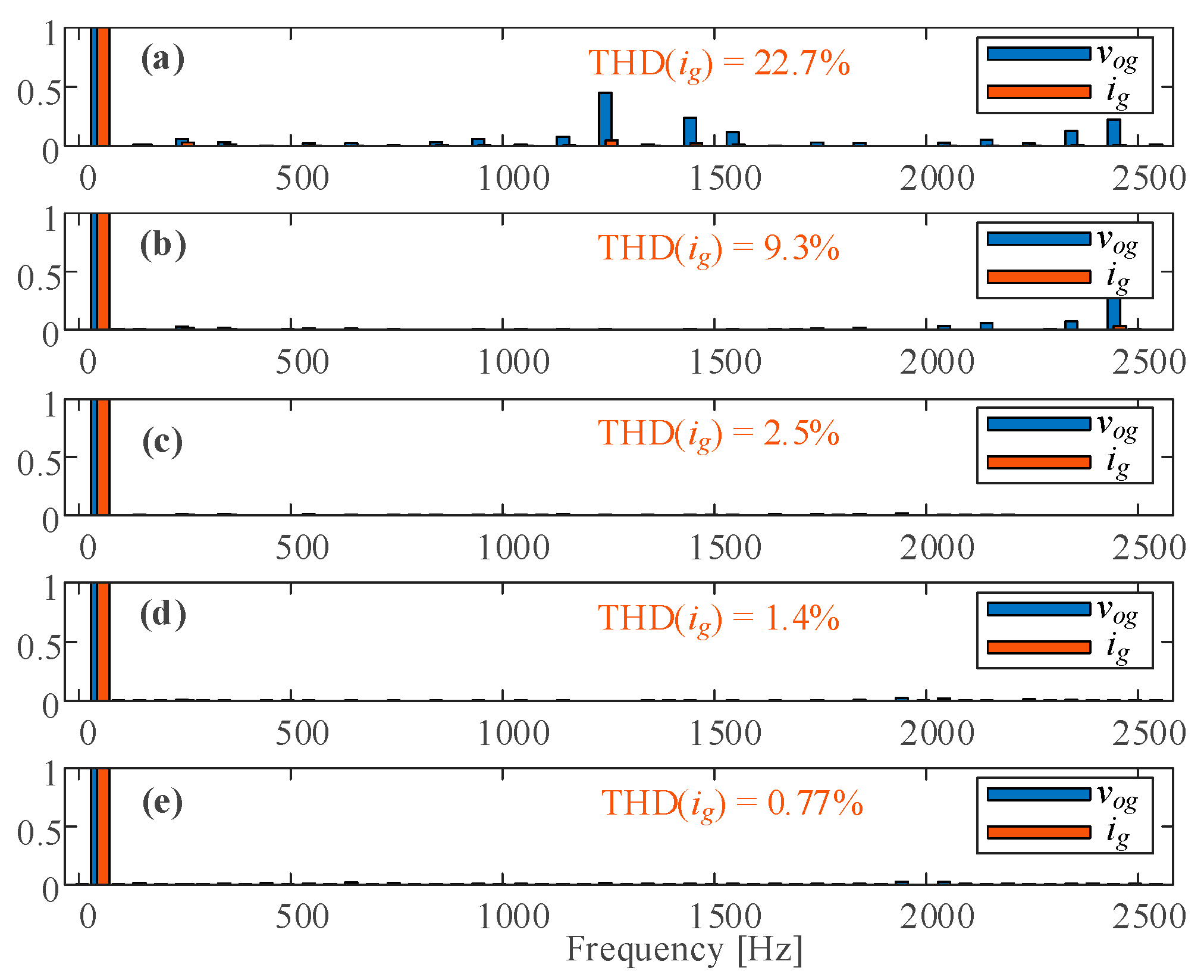
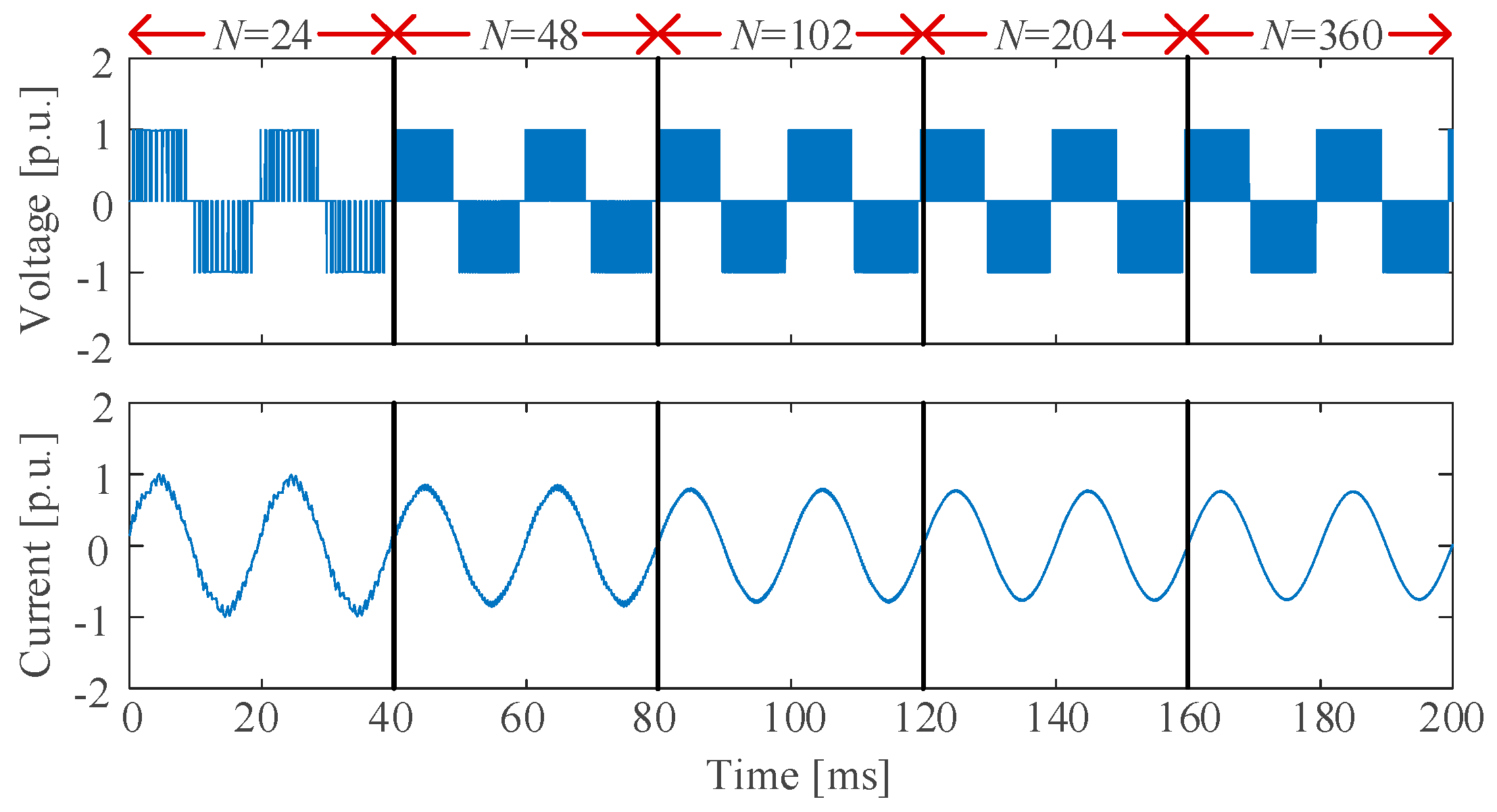
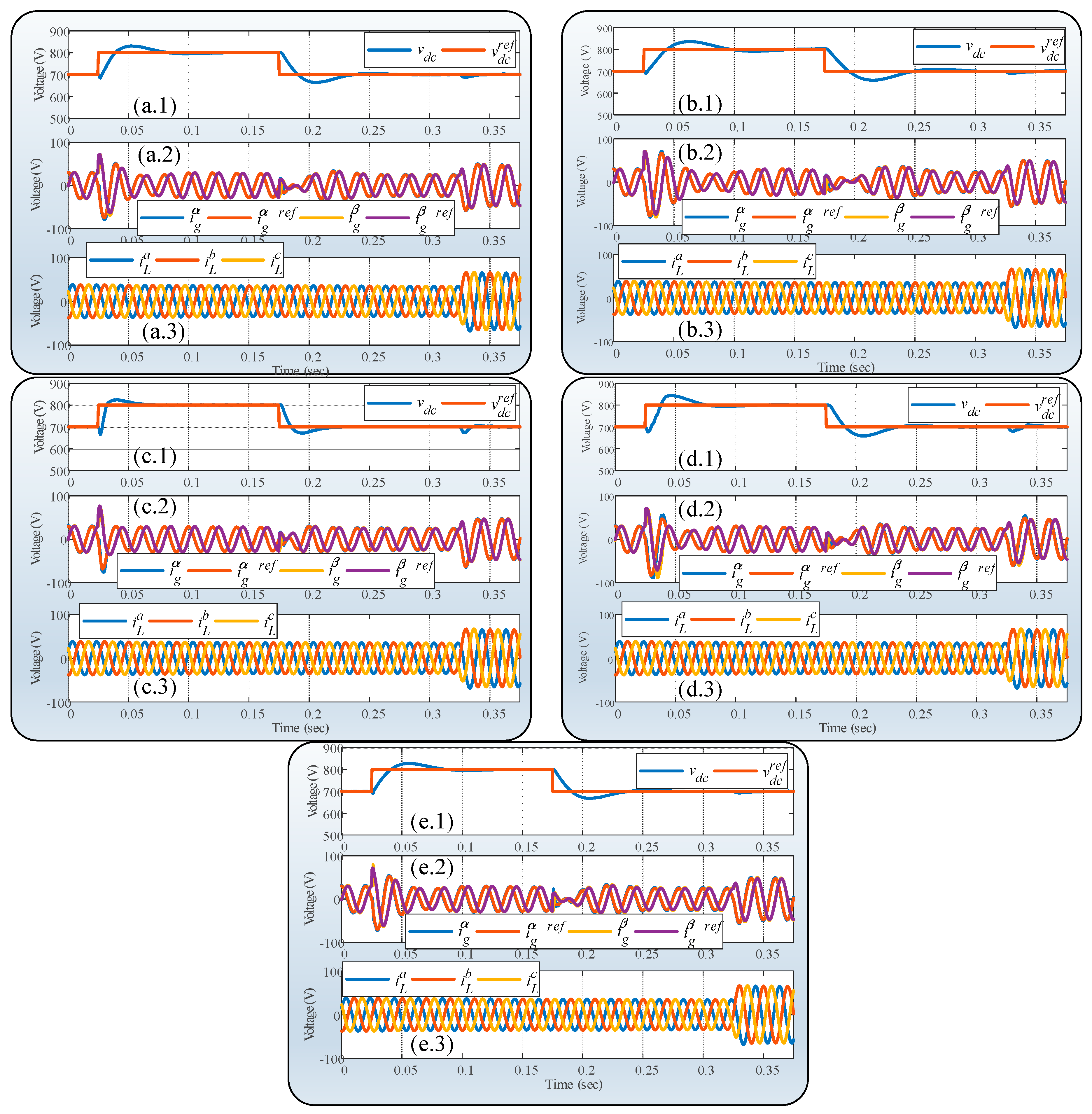
5.1. Simulated Results
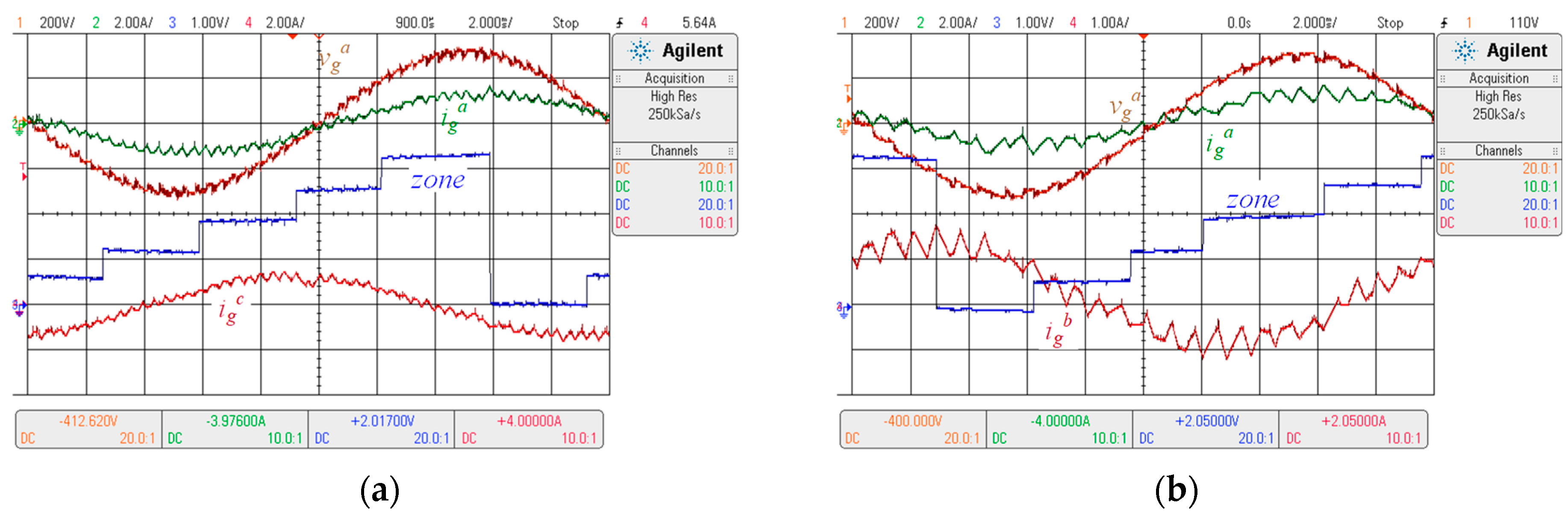
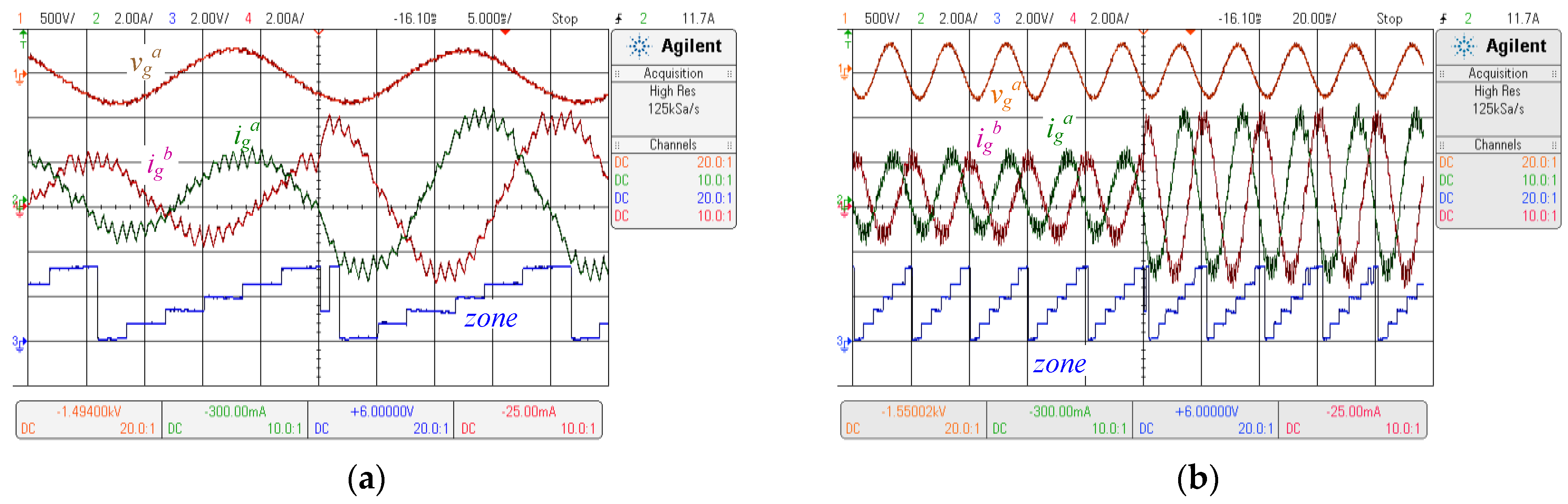
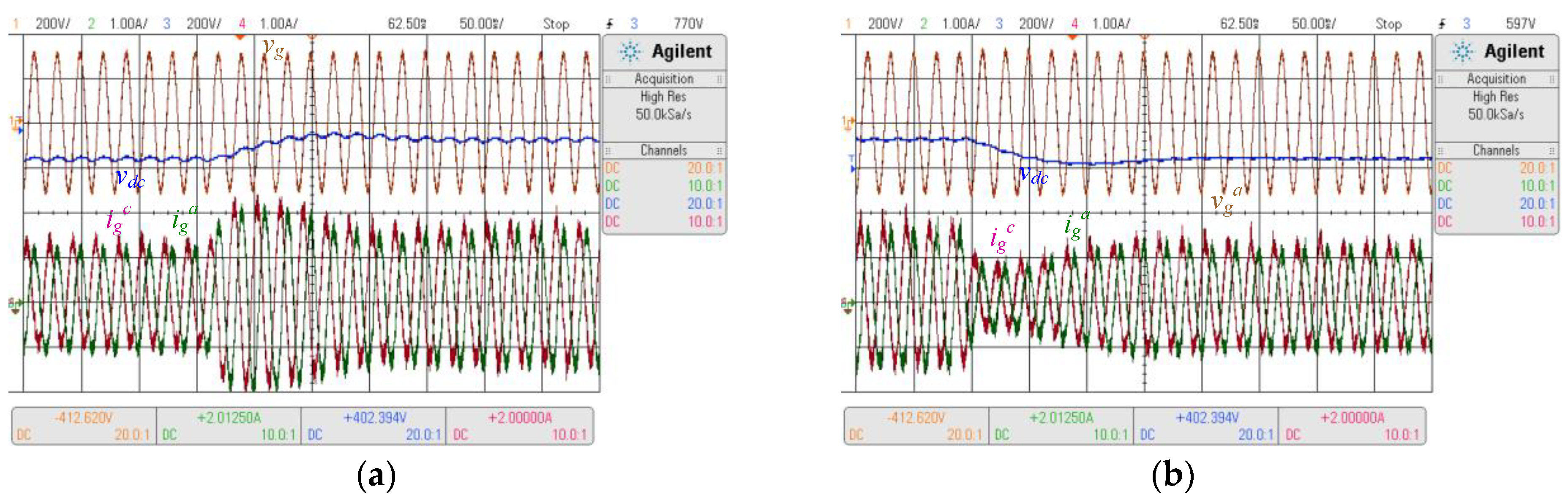
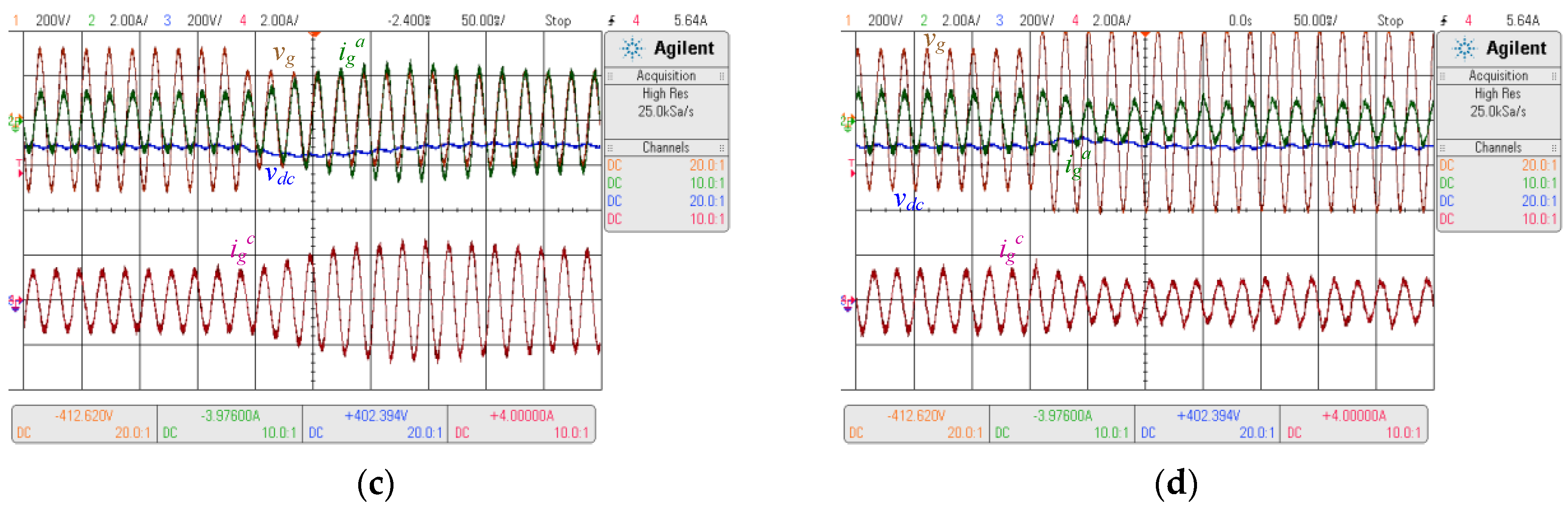
5.2. Experimental Results
6. Discussion
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| PWM | Pulse-width modulation |
| SVM | Space vector modulation |
| UPQC | Unified power quality conditioner |
| MPC | Model predictive control |
| FS-MPC | Finite-Set MPC |
| AFE | Active front end rectifier |
| VSI | Voltage source inverter |
Nomenclature
| Variable | |
| Vector of variables | |
| Complex number | |
| Conjugate complex number of | |
| Estimated variable of | |
| Variable in abc reference frame | |
| Variable in αβ reference frame | |
| Reference of |
References
- Mohammed, S.R.; Teh, J.; Kamarol, M. Upgrading of the Existing Bi-Pole to the New Four-Pole Back-to-Back HVDC Converter for Greater Reliability and Power Quality. IEEE Access 2019, 7, 145532–145545. [Google Scholar] [CrossRef]
- Ramírez, R.O.; Baier, C.R.; Espinoza, J.; Villarroel, F. Finite Control Set MPC with Fixed Switching Frequency Applied to a Grid Connected Single-Phase Cascade H-Bridge Inverter. Energies 2020, 13, 5475. [Google Scholar] [CrossRef]
- Sun, Y.; Zhao, Y.; Dou, Z.; Li, Y.; Guo, L. Model Predictive Virtual Synchronous Control of Permanent Magnet Synchronous Generator-Based Wind Power System. Energies 2020, 13, 5022. [Google Scholar] [CrossRef]
- Naderi, M.; Khayat, Y.; Shafiee, Q.; Dragicevic, T.; Bevrani, H.; Blaabjerg, F. Interconnected Autonomous ac Microgrids via Back-to-Back Converters—Part II: Stability Analysis. IEEE Trans. Power Electron. 2020, 35, 11801–11812. [Google Scholar] [CrossRef]
- de Lacerda, R.P.; Jacobina, C.B.; Fabricio, E.L.L.; Rodrigues, P.L.S. Six-Leg Single-Phase AC–DC–AC Multilevel Converter With Transformers for UPS and UPQC Applications. IEEE Trans. Ind. Appl. 2020, 56, 5170–5181. [Google Scholar] [CrossRef]
- Koroglu, T.; Tan, A.; Savrun, M.M.; Cuma, M.U.; Bayindir, K.C.; Tumay, M. Implementation of a Novel Hybrid UPQC Topology Endowed with an Isolated Bidirectional DC–DC Converter at DC link. IEEE J. Emerg. Sel. Top. Power Electron. 2020, 8, 2733–2746. [Google Scholar] [CrossRef]
- Silva, J.J.; Espinoza, J.R.; Rohten, J.A.; Pulido, E.S.; Villarroel, F.A.; Torres, M.A.; Reyes, M.A. MPC Algorithm With Reduced Computational Burden and Fixed Switching Spectrum for a Multilevel Inverter in a Photovoltaic System. IEEE Access 2020, 8, 77405–77414. [Google Scholar] [CrossRef]
- Xu, C.; Chen, J.; Dai, K. Carrier-Phase-Shifted Rotation Pulse-Width-Modulation Scheme for Dynamic Active Power Balance of Modules in Cascaded H-Bridge STATCOMs. Energies 2020, 13, 1052. [Google Scholar] [CrossRef] [Green Version]
- Muduli, U.R.; Beig, A.R.; Al Jaafari, K.; Alsawalhi, J.Y.; Behera, R.K. Interrupt Free Operation of Dual Motor Four-Wheel Drive Electric Vehicle Under Inverter Failure. IEEE Trans. Transp. Electrif. 2020. [Google Scholar] [CrossRef]
- Kumar, V.; Pandey, A.S.; Sinha, S.K. Stability Improvement of DFIG-Based Wind Farm Integrated Power System Using ANFIS Controlled STATCOM. Energies 2020, 13, 4707. [Google Scholar] [CrossRef]
- Li, Z.; Hao, Q.; Gao, F.; Wu, L.; Guan, M. Nonlinear Decoupling Control of Two-Terminal MMC-HVDC Based on Feedback Linearization. IEEE Trans. Power Deliv. 2019, 34, 376–386. [Google Scholar] [CrossRef]
- Rohten, J.A.; Espinoza, J.R.; Munoz, J.A.; Perez, M.A.; Melin, P.E.; Silva, J.J.; Espinosa, E.E.; Rivera, M.E. Model Predictive Control for Power Converters in a Distorted Three-Phase Power Supply. IEEE Trans. Ind. Electron. 2016, 63, 5838–5848. [Google Scholar] [CrossRef]
- Zhang, X.; Foo, G.H.B.; Jiao, T.; Ngo, T.; Lee, C.H.T. A Simplified Deadbeat Based Predictive Torque Control for Three-Level Simplified Neutral Point Clamped Inverter Fed IPMSM Drives Using SVM. IEEE Trans. Energy Convers. 2019, 34, 1906–1916. [Google Scholar] [CrossRef]
- Rizk, G.; Salameh, S.; Kanaan, H.Y.; Rachid, E.A. Design of passive power filters for a three-phase semi-controlled rectifier with typical loads. In Proceedings of the 2014 9th IEEE Conference on Industrial Electronics and Applications, Hangzhou, China, 9–11 June 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 590–595. [Google Scholar]
- Riedemann Aros, J.; Pena Guinez, R.; Cardenas Dobson, R.; Blasco Gimenez, R.; Clare, J. Indirect matrix converter modulation strategies for open-end winding induction machine. IEEE Lat. Am. Trans. 2014, 12, 395–401. [Google Scholar] [CrossRef]
- Podder, A.K.; Habibullah, M.; Tariquzzaman, M.; Hossain, E.; Padmanaban, S. Power Loss Analysis of Solar Photovoltaic Integrated Model Predictive Control Based On-Grid Inverter. Energies 2020, 13, 4669. [Google Scholar] [CrossRef]
- Zheng, C.; Dragicevic, T.; Blaabjerg, F. Current-Sensorless Finite-Set Model Predictive Control for LC -Filtered Voltage Source Inverters. IEEE Trans. Power Electron. 2020, 35, 1086–1095. [Google Scholar] [CrossRef]
- Kazmierkowski, M.P.; Jasinski, M.; Wrona, G. DSP-Based Control of Grid-Connected Power Converters Operating Under Grid Distortions. IEEE Trans. Ind. Inform. 2011, 7, 204–211. [Google Scholar] [CrossRef]
- Danayiyen, Y.; Lee, K.; Choi, M.; Lee, Y. Model Predictive Control of Uninterruptible Power Supply with Robust Disturbance Observer. Energies 2019, 12, 2871. [Google Scholar] [CrossRef] [Green Version]
- Yfoulis, C.; Papadopoulou, S.; Voutetakis, S. Robust Linear Control of Boost and Buck-Boost DC-DC Converters in Micro-Grids with Constant Power Loads. Energies 2020, 13, 4829. [Google Scholar] [CrossRef]
- Gonzalez-Prieto, I.; Zoric, I.; Duran, M.J.; Levi, E. Constrained Model Predictive Control in Nine-Phase Induction Motor Drives. IEEE Trans. Energy Convers. 2019, 34, 1881–1889. [Google Scholar] [CrossRef]
- Villarroel, F.; Espinoza, J.R.; Rojas, C.A.; Rodriguez, J.; Rivera, M.; Sbarbaro, D. Multiobjective Switching State Selector for Finite-States Model Predictive Control Based on Fuzzy Decision Making in a Matrix Converter. IEEE Trans. Ind. Electron. 2013, 60, 589–599. [Google Scholar] [CrossRef]
- Vazquez, S.; Leon, J.I.; Franquelo, L.G.; Carrasco, J.M.; Martinez, O.; Rodriguez, J.; Cortes, P.; Kouro, S. Model Predictive Control with constant switching frequency using a Discrete Space Vector Modulation with virtual state vectors. In Proceedings of the 2009 IEEE International Conference on Industrial Technology, Bordeaux, France, 21–23 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 1–6. [Google Scholar]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Clare, J.C.; Degano, M.; Bifaretti, S. Modulated Model Predictive Control for a Three-Phase Active Rectifier. IEEE Trans. Ind. Appl. 2015, 51, 1610–1620. [Google Scholar] [CrossRef]
- Aguirre, M.; Kouro, S.; Rojas, C.A.; Rodriguez, J.; Leon, J.I. Switching Frequency Regulation for FCS-MPC Based on a Period Control Approach. IEEE Trans. Ind. Electron. 2018, 65, 5764–5773. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, J.; Yang, H.; Fan, S. New Insights into Model Predictive Control for Three-Phase Power Converters. IEEE Trans. Ind. Appl. 2019, 55, 1973–1982. [Google Scholar] [CrossRef]
- Rivera, M.; Wilson, A.; Rojas, C.A.; Rodriguez, J.; Espinoza, J.R.; Wheeler, P.W.; Empringham, L. A Comparative Assessment of Model Predictive Current Control and Space Vector Modulation in a Direct Matrix Converter. IEEE Trans. Ind. Electron. 2013, 60, 578–588. [Google Scholar] [CrossRef]
- Jin, N.; Pan, C.; Li, Y.; Hu, S.; Fang, J. Model Predictive Control for Virtual Synchronous Generator with Improved Vector Selection and Reconstructed Current. Energies 2020, 13, 5435. [Google Scholar] [CrossRef]
- Sadie, A.; Mouton, T.; Dorfling, M.; Geyer, T. Model Predictive Control with Space-Vector Modulation for a Grid-Connected Converter with an LCL-Filter. In Proceedings of the 2019 21st European Conference on Power Electronics and Applications (EPE ’19 ECCE Europe), Genova, Italy, 2–5 September 2020; IEEE: Piscataway, NJ, USA, 2019; pp. P.1–P.9. [Google Scholar]
- Romero, M.E.; Seron, M.M.; Goodwin, G.C. A combined model predictive control/space vector modulation (MPC-SVM) strategy for direct torque and flux control of induction motors. In Proceedings of the IECON 2011—37th Annual Conference of the IEEE Industrial Electronics Society, Victoria, Australia, 7–10 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 1674–1679. [Google Scholar]
- Landers, P.H. Automatic control systems, B.C. Kuo, Prentice Hall International, 1986. Price: £15.95. ISBN: 13-05 5070-1. Int. J. Adapt. Control Signal Process. 1988, 2, 145–146. [Google Scholar] [CrossRef]
- Roger, D.M.F.G. IEEE Recommended Practice and Requirements for Harmonic Control in Electric Power Systems; IEEE: New York, NY, USA, 2014; Volume 2014. [Google Scholar]
- Jiao, Y.; Lee, F.C. LCL Filter Design and Inductor Current Ripple Analysis for a Three-Level NPC Grid Interface Converter. IEEE Trans. Power Electron. 2015, 30, 4659–4668. [Google Scholar] [CrossRef]



| Parameters | Value | P.U. |
|---|---|---|
| vg | 220 V, rms | 1 |
| ZL | 8.8 Ω | 1 |
| RL—LL | 7 Ω—17 mH | 0.80—0.61 |
| Rg—Lg | 0.4 Ω—12 mH | 0.011—0.43 |
| Cdc | 2.35 mF | 0.677 |
| RLf—LLf—CLf | 1 mΩ—3 mH—10 μF | 0.12 m 0.36 m—3.183 |
| fg—fL | 50 Hz—50 Hz | 1 |
| fs | 1.2 kHz | 24 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rohten, J.A.; Muñoz, J.E.; Pulido, E.S.; Silva, J.J.; Villarroel, F.A.; Espinoza, J.R. Very Low Sampling Frequency Model Predictive Control for Power Converters in the Medium and High-Power Range Applications. Energies 2021, 14, 199. https://doi.org/10.3390/en14010199
Rohten JA, Muñoz JE, Pulido ES, Silva JJ, Villarroel FA, Espinoza JR. Very Low Sampling Frequency Model Predictive Control for Power Converters in the Medium and High-Power Range Applications. Energies. 2021; 14(1):199. https://doi.org/10.3390/en14010199
Chicago/Turabian StyleRohten, Jaime A., Javier E. Muñoz, Esteban S. Pulido, José J. Silva, Felipe A. Villarroel, and José R. Espinoza. 2021. "Very Low Sampling Frequency Model Predictive Control for Power Converters in the Medium and High-Power Range Applications" Energies 14, no. 1: 199. https://doi.org/10.3390/en14010199
APA StyleRohten, J. A., Muñoz, J. E., Pulido, E. S., Silva, J. J., Villarroel, F. A., & Espinoza, J. R. (2021). Very Low Sampling Frequency Model Predictive Control for Power Converters in the Medium and High-Power Range Applications. Energies, 14(1), 199. https://doi.org/10.3390/en14010199









