Effect of Renewable Energy to Reduce Carbon Emissions under a Flexible Production System: A Step Toward Sustainability
Abstract
:1. Introduction
2. Literature Review
2.1. Renewable Energy
2.2. Sustainable Smart Production System (SSPS)
2.3. Variable Demands under the Effect of Energy
2.4. Flexible Production Rate
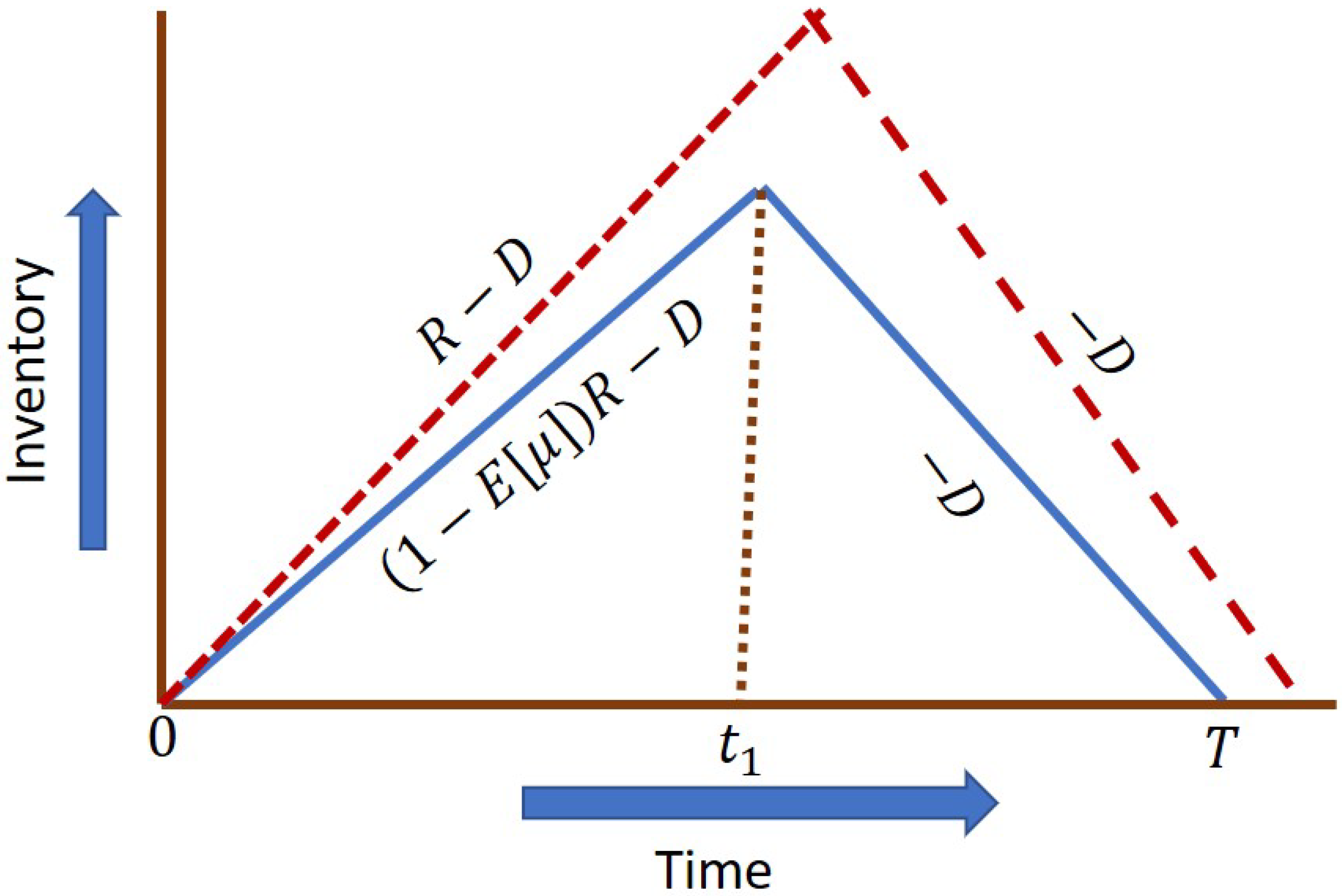
3. Mathematical Model
| Notation | |
| Decision variables | |
| selling price of unit product ($/unit) | |
| T | cycle time of the production system (year) |
| R | flexible production rate of the SSPS (unit) |
| C | investment to reduce CE from the SSPS ($) |
| Parameters | |
| setup cost of the SSPS ($/setup) | |
| energy cost to set up the SSPS ($/setup) | |
| cost for holding the product ($/unit/year) | |
| energy cost for holding the inventory ($/unit/year) | |
| scrap cost for obsolete inventory ($/scrap item) | |
| demand of products (units) | |
| carbon cap of SSPS (kg/year) | |
| carbon emitted for holding the product (kg/year) | |
| carbon emitted for obsolete item (kg/year) | |
| carbon emitted during the setup of the system (kg/year) | |
| carbon emitted during production (kg/year) | |
| environmental effect of CE (kg/year) | |
| shape parameter related to CE reduction | |
| fraction of CE reduction due to investment | |
| obsolesce rate of inventory | |
| tool/die cost of the SSPS ($/unit) | |
| energy cost during production ($/unit) | |
| development cost of the SSPS ($) | |
| energy cost to develop the SSPS ($) | |
| material cost for the products ($/production lot) | |
| expected value of imperfect products | |
| cost for imperfect products ($/imperfect product) | |
| cost of energy due to imperfect production ($/imperfect product) | |
| tax paid for CE ($/unit emission) | |
3.1. Model Formulation
3.2. Solution Methodology
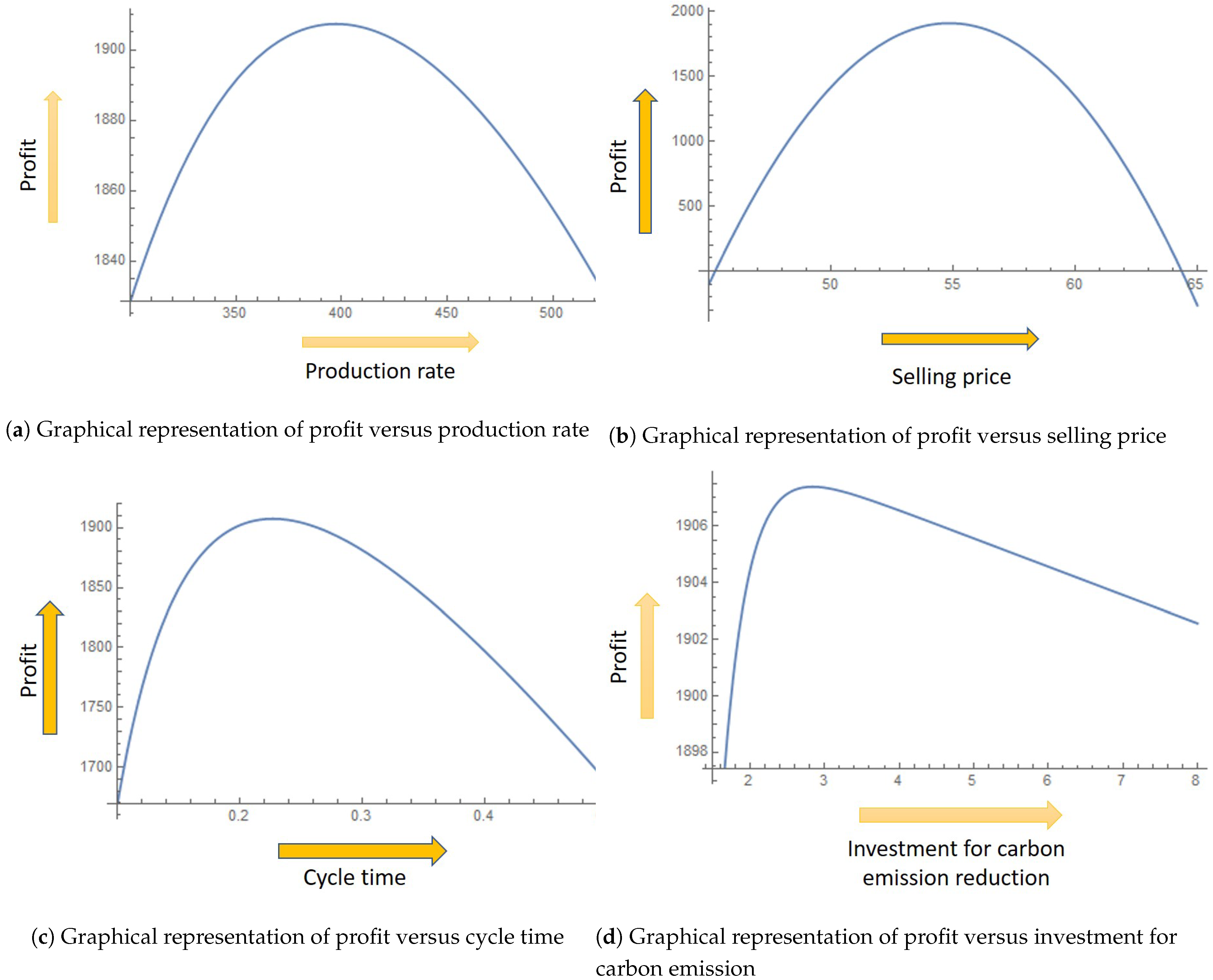
4. Numerical Analysis
4.1. Numerical Experiments
4.1.1. Example 1
4.1.2. Example 2
4.1.3. Example 3
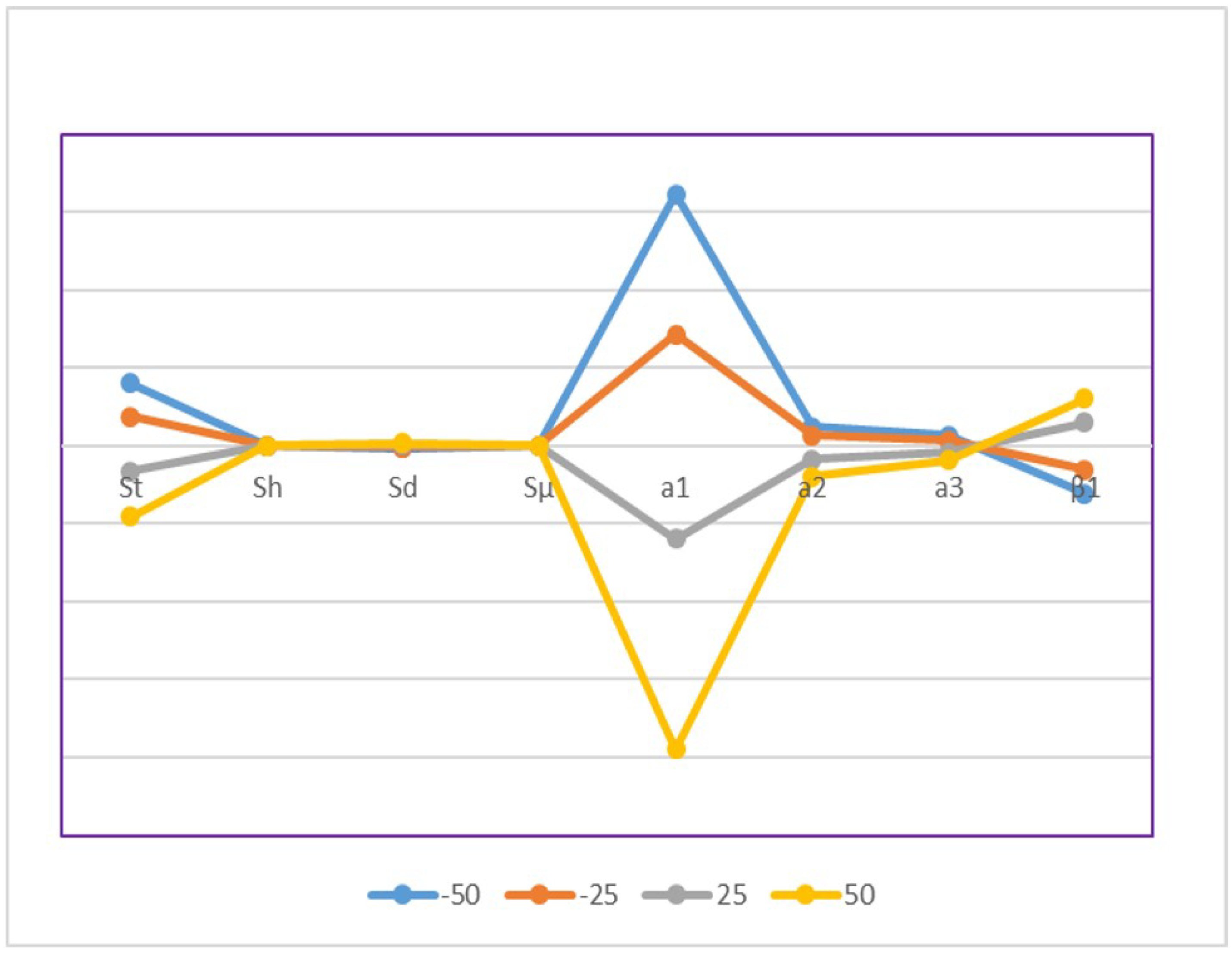
4.2. Sensitivity Analysis
4.3. Managerial Insights
- By utilizing flexible PS, the manager can control the rate of defective production and CE. The manager can plan to sell excess carbon cap to other companies by reducing CE. Hence, it is better to choose a flexible production system rather than a traditional production system. In Mishra et al. [16], the constant production gave less total profit and more CE than the proposed study.
- It is deemed fruitful to invest to reduce the CE in any SSPS. However, it is better to use the investment in the technological growth of the SSPS, which can increase CE reduction. Therefore, it is recommended that managers implement an investment policy for the technological growth of the SSPS to achieve flexible or smart production to control the CE in a sustainable manner. This is strong recommendation from the findings of the sensitivity of this study. It shows the effectiveness of the shape parameter .
- The selling price of any product is essential for the marketability of the product. Therefore, the price should be fixed based on the market survey of similar products in the market. By maintaining the same quality, the optimal selling price should be identified, which can maximize the profit. It can be demanded from the same study of Mishra et al. [16] that variable selling price with energy effect makes more profit rather than the constant demand without energy consideration.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SSPS | sustainable smart production system |
| SSCM | sustainable supply chain management |
| SCM | supply chain management |
| SCM | supply chain |
| GSCM | green supply chain management |
| SMPS | smart production system |
| SPS | sustainable production system |
| EOQ | economic order quantity |
| CE | carbon emission |
| PS | production system |
Appendix A
References
- Ahmed, W.; Sarkar, B. Management of next-generation energy using a triple bottom line approach under a supply chain framework. Resour. Conserv. Recycl. 2019, 150, 104431. [Google Scholar] [CrossRef]
- Sarkar, M.; Sarkar, B. How does an industry reduce waste and consumed energy within a multi-stage smart sustainable biofuel production system? J. Clean. Prod. 2020, 262, 121200. [Google Scholar] [CrossRef]
- Dong, F.; Li, J.; Wang, Y.; Zhang, X.; Zhang, S.; Zhang, S. Drivers of the decoupling indicator between the economic growth and energy-related CO2 in China: A revisit from the perspectives of decomposition and spatiotemporal heterogeneity. Sci. Total Environ. 2019, 685, 631–658. [Google Scholar] [CrossRef] [PubMed]
- Jemai, J.; Chung, B.D.; Sarkar, B. Environmental effect for a complex green supply-chain management to control waste: A sustainable approach. J. Clean. Prod. 2020, 277, 122919. [Google Scholar] [CrossRef]
- Sarkar, B.; Sarkar, M.; Ganguly, B.; Cárdenas-Barrón, L.E. Combined effects of carbon emission and production quality improvement for fixed lifetime products in a sustainable supply chain management. Int. J. Prod. Econ. 2021, 231, 107867. [Google Scholar] [CrossRef]
- Sarkar, B.; Guchhait, R.; Sarkar, M.; Pareek, S.; Kim, N. Impact of safety factors and setup time reduction in a two-echelon supply chain management. Robot. Comput.-Integr. Manuf. 2019, 55, 250–258. [Google Scholar] [CrossRef]
- Khan, I.; Jemai, J.; Han, L.; Sarkar, B. Effect of electrical energy on the manufacturing setup cost reduction, transportation discounts, and process quality improvement in a two-echelon supply chain management under a service-level constraint. Energies 2020, 12, 3733. [Google Scholar] [CrossRef] [Green Version]
- Wang, Z.; Bui, Q.; Zhang, B.; Nawarathna, C.L.K.; Mombeuil, C. The nexus between renewable energy consumption and human development in BRICS countries: The moderating role of public debt. Renew. Energy 2021, 165, 381–390. [Google Scholar] [CrossRef]
- Lee, J.H.; Moon, I. Modeling and optimization of energy efficient routing in wireless sensor networks. Appl. Math. Model. 2014, 38, 2280–2289. [Google Scholar] [CrossRef]
- Sarkar, B.; Omair, M.; Choi, S.B. A Multi-Objective Optimization of Energy, Economic, and Carbon Emission in a Production Model under Sustainable Supply Chain Management. Appl. Sci. 2018, 8, 1744. [Google Scholar] [CrossRef] [Green Version]
- Sarkar, M.; Sarkar, B.; Iqbal, M.W. Effect of energy and failure rate in a multi-item smart production system. Energies 2018, 11, 2958. [Google Scholar] [CrossRef] [Green Version]
- Rasti-Barzoki, M.; Moon, I. A game theoretic approach for car pricing and its energy efficiency level versus governmental sustainability goals by considering rebound effect: A case study of South Korea. Appl. Energy 2020, 271, 115196. [Google Scholar] [CrossRef]
- Dong, F.; Pan, Y. Evolution of renewable energy in BRI countries: A combined econometric and decomposition approach. Int. J. Environ. Res. Public Health 2020, 17, 8668. [Google Scholar] [CrossRef] [PubMed]
- Sarkar, M.; Pan, L.; Dey, B.K.; Sarkar, B. Does the Autonomation Policy Really Help in a Smart Production System for Controlling Defective Production? Mathematics 2020, 8, 1142. [Google Scholar] [CrossRef]
- Mishra, M.; Hota, S.K.; Ghosh, S.K.; Sarkar, B. Controlling Waste and Carbon Emission for a Sustainable Closed-Loop Supply Chain Management under a Cap-and-Trade Strategy. Mathematics 2020, 8, 466. [Google Scholar] [CrossRef] [Green Version]
- Mishra, U.; Wu, J.Z.; Sarkar, B. A sustainable production-inventory model for a controllable carbon emissions rate under shortages. J. Clean. Prod. 2020, 256, 120268. [Google Scholar] [CrossRef]
- Dong, F.; Yu, B.; Pan, Y. Examining the synergistic effect of CO2 emissions on PM2.5 emissions reduction: Evidence from China. J. Clean. Prod. 2019, 223, 759–771. [Google Scholar] [CrossRef]
- Dong, F.; Wang, Y.; Su, B.; Hua, Y.; Zhang, Y. The process of peak CO2 emissions in developed economies: A perspective of industrialization and urbanization. J. Clean. Prod. 2019, 141, 61–75. [Google Scholar] [CrossRef]
- Moon, I.; Xu, J.; Feng, X.; Ruan, X. Cooperative sales promotion with a point-sharing policy: Advantages and limitations. Omega 2020, 94, 102038. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Mokhtarzadeh, M. Pricing and two-dimensional warranty policy of multi-products with online and offline channels using a value-at-risk approach. Comput. Ind. Eng. 2020, 148, 106674. [Google Scholar] [CrossRef]
- Taleizadeh, A.A.; Hazarkhani, B.; Moon, I. Joint pricing and inventory decisions with carbon emission considerations, partial backordering and planned discounts. Ann. Oper. Res. 2020, 290, 95–113. [Google Scholar] [CrossRef]
- Mashud, A.H.M.; Wee, H.M.; Sarkar, B.; Li, Y.H.C. A sustainable inventory system with the advanced payment policy and trade-credit strategy for a two-warehouse inventory system. Kybernetes 2020. [Google Scholar] [CrossRef]
- Tseng, S.H.; Wee, H.M.; Song, P.S.; Jeng, S. Optimal green supply-chain model design considering full truckload. Kybernetes 2019, 48, 2150–2174. [Google Scholar] [CrossRef]
- Sarkar, B.; Dey, B.K.; Pareek, S.; Sarkar, M. A single-stage cleaner production system with random defective rate and remanufacturing. Comput. Ind. Eng. 2020, 150, 106861. [Google Scholar] [CrossRef]
- Saxena, N.; Sarkar, B.; Singh, S.R. Selection of remanufacturing/production cycles with an alternative market: A perspective on waste management. J. Clean. Prod. 2020, 245, 118935. [Google Scholar] [CrossRef]
- Sarkar, M.; Chung, B.D. Flexible work-in-process production system in supply chain management under quality improvement. Int. J. Prod. Res. 2020, 58, 3821–3838. [Google Scholar] [CrossRef]
- Sarkar, B. Mathematical and analytical approach for the management of defective items in a multi-stage production system. J. Clean. Prod. 2019, 218, 896–919. [Google Scholar] [CrossRef]
- Dey, B.K.; Pareek, S.; Tayyab, M.; Sarkar, B. Autonomation policy to control work-in-process inventory in a smart production system. Int. J. Prod. Res. 2020. [Google Scholar] [CrossRef]
- Kang, C.W.; Babar, B.M.; Sarkar, B.; Imran, M. Effect of inspection performance in smart manufacturing system based on human quality control system. Int. J. Adv. Manuf. Tech. 2018, 94, 4351–4364. [Google Scholar] [CrossRef]
- Glock, C.H. A comment: Integrated single vendor single buyer model with stochastic demand and variable lead time. Int. J. Prod. Econ. 2009, 122, 790–792. [Google Scholar] [CrossRef]
- Sarkar, B.; Guchhait, R.; Sarkar, M.; Cárdenas-Barrón, L.E. How does an industry manage the optimum cash flow within a smart production system with the carbon footprint and carbon emission under logistics framework? Int. J. Prod. Econ. 2019, 213, 243–257. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E.; Melo, R.A. A fast and effective MIP-based heuristic for a selective and periodic inventory routing problem in reverse logistics. arXiv 2020, arXiv:2004.04188. [Google Scholar]
- Sarkar, B.; Tayyab, M.; Kim, N.; Habib, M.S. Optimal production delivery policies for supplier and manufacturer in a constrained closed-loop supply chain for returnable transport packaging through metaheuristic approach. Comput. Ind. Eng. 2019, 135, 987–1003. [Google Scholar] [CrossRef]
- Gautam, P.; Kishore, A.; Khanna, A.; Jaggi, C.K. Strategic defect management for a sustainable green supply chain. J. Clean. Prod. 2019, 233, 226–241. [Google Scholar] [CrossRef]
- Cárdenas-Barrón, L.E. Economic production quantity with rework process at a single-stage manufacturing system with planned backorders. Comput. Ind. Eng. 2009, 57, 1105–1113. [Google Scholar] [CrossRef]
- Sarkar, B.; Cárdenas-Barrón, L.E.; Sarkar, M.; Singgih, M.L. An economic production quantity model with random defective rate, rework process and backorders for a single stage production system. J. Manuf. Syst. 2014, 33, 423–435. [Google Scholar] [CrossRef]
| Author(s) | Model Type | Production Rate | Defective Rate | Carbon Emission |
|---|---|---|---|---|
| Sarkar et al. [5] | SSCM | Constant | Constant | Considered |
| Sarkar et al. [6] | SCM | Flexible | − | − |
| Mishra et al. [16] | SPS | Constant | − | Considered |
| Taleizadeh et al. [21] | EOQ | − | Considered | |
| Tseng et al. [23] | SCM | Constant | − | Considered |
| Saxena et al. [25] | SCM | Constant | Constant | Considered |
| Dey et al. [28] | Production | Constant | Random | − |
| Proposed research | SSPS | Flexible | Random | Considered |
| Parameters | Changes (in %) | Changes of (in %) | Parameters | Changes (in %) | Changes of (in %) |
|---|---|---|---|---|---|
(Setup cost) | −50 | (Holding cost) | −50 | ||
| −25 | −25 | ||||
| +25 | +25 | ||||
| +50 | +50 | ||||
(Scrap cost) | −50 | (Defective item cost) | −50 | ||
| −25 | −25 | ||||
| +25 | +25 | ||||
| +50 | +50 | ||||
(Tool/die cost) | −50 | (Development cost) | −50 | ||
| −25 | −25 | ||||
| +25 | +25 | ||||
| +50 | +50 | ||||
(Material cost) | −50 | (Carbon emission reduction parameter) | −50 | ||
| −25 | −25 | ||||
| +25 | +25 | ||||
| +50 | +50 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sarkar, M.; Chung, B.D. Effect of Renewable Energy to Reduce Carbon Emissions under a Flexible Production System: A Step Toward Sustainability. Energies 2021, 14, 215. https://doi.org/10.3390/en14010215
Sarkar M, Chung BD. Effect of Renewable Energy to Reduce Carbon Emissions under a Flexible Production System: A Step Toward Sustainability. Energies. 2021; 14(1):215. https://doi.org/10.3390/en14010215
Chicago/Turabian StyleSarkar, Mitali, and Byung Do Chung. 2021. "Effect of Renewable Energy to Reduce Carbon Emissions under a Flexible Production System: A Step Toward Sustainability" Energies 14, no. 1: 215. https://doi.org/10.3390/en14010215
APA StyleSarkar, M., & Chung, B. D. (2021). Effect of Renewable Energy to Reduce Carbon Emissions under a Flexible Production System: A Step Toward Sustainability. Energies, 14(1), 215. https://doi.org/10.3390/en14010215





