Impact of Energy and Carbon Emission of a Supply Chain Management with Two-Level Trade-Credit Policy

Abstract

Supply chain management aims to integrate environmental thinking with efficient energy consumption into supply chain management. It includes a flexible manufacturing process, more product delivery to customers, optimum energy consumption, and reduced waste. The manufacturing process can be made more flexible through volume agility. In this scenario, production cannot be constant, and with the concept of volume agility, production is taken as a decision variable under the effect of optimum energy consumption. Considering a two-echelon supply chain, we consider a producer and supplier with two-level-trade-credit policies (TLTCP) with the optimum consumption. To reduce the integrated total inventory cost, we believe that demand is a function of the credit period and selling price. The cost function is analyzed, either with the credit period dependent demand rate or with the selling price dependent demand rate through the numerical examples under energy costs. Energy and carbon emission costs are introduced in setup/ordering cost, holding cost, and item cost for producer and supplier. The effect of inflation on the total cost cannot be ignored; this model is being developed for deteriorating items with the simultaneous impact of volume agility, energy, carbon emission cost, and two-level-trade-credit policies with inflation. This supply chain model was solved analytically and obtained the optimum decision variables in a quasi-closed form solution. An illustrative theorem is being utilized to analyze the optimum result for all the decision parameters. The convexity of the objective function is being obtained analytically as well as graphically. Finally, numerical examples and sensitivity analysis are employed to illustrate the present study and with managerial insights.

1. Introduction

The efficient use of energy can make a supply chain more efficient. Supply chain management (SCM) is characterized by complementing the traditional economic (cost) focus on environmental (emissions) considerations only without the concept of carbon emission. This research gap for the effect of energy and carbon emission can be conducted in this study. It is challenging to reduce carbon emission and energy consumption in traditional production, but energy consumption can be reduced by controlling the production rate. Due to a lack of coordination in the supply chain, the impact of deterioration from one stage to other increases. Effects of carbon emission in a global sustainable supply chain play an important role. Carbon emission and energy cost may happen in many different production stages while holding the produced stock, placing the order, and item cost.

Consequently, due to the deterioration of products, waste is generated in every supply chain stage. It poses a severe risk to nature and human health. It introduces global warming to the environment. Global warming is increasing due to the greenhouse gas emissions (GHGs), such as carbon dioxide (CO₂), methane, and nitrous oxide. Cárdenas-Barrón and Sana [1] introduced a model to show the payment policies and reduce costs without considering waste items. Taleizadeh et al. [2] introduced a reworked strategy within a production model. They proved that multiple shipments could reduce the waste quickly compared to a single shipment with a large lot. Taleizadeh et al. [3] developed an improved strategy to repair defective products to reduce waste, but they did not consider controllable production rates. They just thought of a fixed production rate. Chen et al. [4] formulated a model on management of warehouses with low carbon under the effect of the cap-and-trade policy. This model proved that by utilizing cap and trade policy within production management, the carbon emission could be controlled, which is significant support for an environmental issue. Sarkar et al. [5] formulated a model based on the effect of multi-delay-in-payments and variable carbon emission cost. The single-setup-multiple-delivery policy is also discussed for the reduction of waste production. Khanna et al. [6] introduced a two-level-trade-credit policy (TLTCP) in an integrated model. However, they did not consider the reduction of those defective items by any strategy. Aljazzar et al. [7] formulated a delay-in-payment policy model to decrease carbon emission from the integrated model. Many researchers have tried to manage and reduce the cost of transportation and the cost of carbon emission. Tiwari et al. [8] established a multi-item sustainable green production process with the effect of partial backordering and payment delay policy. Sarkar [9] developed a model for defective goods with a multi-stage production system. Tayyab and Sarkar [10] investigated a model on optimal quantity under a multi-stage production with a random defective rate without any waste reduction policy or cost reduction policy. Kim and Sarkar [11] analyzed a model for upgrading the quality of items with a multi-stage cleaner production process. In this model, lead time-dependent ordering cost is assumed. Ahmed and Sarkar [12] formulated a model on sustainable supply chain management (SSCM) for a second-generation biofuel on carbon emission in an integrated model. Sarkar and Chung [13] developed a flexible work-in-process production system in SCM under quality improvement.

Agile manufacturing has also been applied to the economic production quantity (EPQ) model. The controllable production rate can be easily used through agile manufacturing to increase or decrease the production rate based on the management’s necessity or based on the system required. It indicates that the production rate must vary with the situation, whatever is necessary at the right time with the right judgment. This production rate is assumed as a decision variable. Sana and Chaudhuri [14] formulated a model using stock-dependent demand with volume flexibility for deteriorating items. According to the authors, the unit production cost is a function of the finite production rate, treated as a decision variable. Sana and Chaudhuri [15] extended this model by using a time-dependent demand rate. Physical delay of the stocked item over time is taken into account, and inventory shortages are allowed. Singh et al. [16] formulated a supply chain model with variable holding costs for a flexible manufacturing system. Singh et al. [17] inspected an ordering model with volume agility, variable demand, and inflation. Dem and Singh [18] studied an ordering system with multiple items and greening under the flexible production rate assumption. Sangal and Gupta [19] formulated a two-warehouse vendor-supplier framework with volume agility. Singh and Gupta [20] discussed the theory based on the supply chain model with error in quality inspection with selling price dependent demand rate under the effect of volume agility. Gautam et al. [21] examined a model on sustainable production policies under the impact of volume agility, preservation technology, and price-reliant demand.

An EPQ model depends on the supposition that as the supplier receives the producer’s goods, he must pay the goods’ cost. Nevertheless, in today’s scenario, it is very general to observe that the producer will allocate a specific time interval for paying the total price of items that the producer owes to the supplier for the goods, known as the trade-credit period (TCP). Generally, interest is not charged if it is reimbursed during the time given by the producer. There are two benefits of this credit-period, which the producer offers.

• This price reduction policy for green products attracts new customers.
• It should cause a decline in sales since it takes time to profit from this delay period more often, and some customers will pay more rapidly.

In supply chain management, TLTCP plays an important role. In this credit policy, the producer offers a credit period to the supplier, and the supplier also provides some credit period to his customers. Ouyang et al. [22] analyzed a strategy with TCP and non-instantaneous delivery. Jaggi et al. [23] proposed a model with TLTCP to assume that the demand rate is a function of that period given for paying the money. Sarkar [24] proposed a model that is based on TCP. Here deterioration rate depends on time, but he did not consider any idea regarding agile manufacturing or its effect. The author just developed a delay-period concept on the basic inventory model and did not find any waste reduction in the inventory system. Khanra et al. [25] extended this idea with the effect of shortages and time-varying demand rates. Here, the impact of TCP is also discussed. Chung [26] developed a production model based on TLTCP instead of the basic inventory model with limited storage capacity in an integrated system. Sarkar et al. [27] finally established a model with a price-discount offer, finite replenishment rate, and credit-period policy. Sarkar et al. [28] formulated a model for defective units. In this model, variable lead time and TCP are also discussed without reducing those faulty products. Sarkar et al. [29] analyzed the TCP policy’s effect on outcomes with a fixed lifetime. Here deterioration rate is taken as a variable. Yadav et al. [30] explained a retailer’s optimal policy under inflation in a fuzzy environment with TCP. The TLTCP is considered, and the demand rate depends on the selling price and credit period. An integrated total cost function is evaluated in three different cases and analyzes varying cost function parameters’ effects.

The concept of energy and carbon emission cost with agile manufacturing for product management is the significant study gap in inventory models. The planned model fulfills this study gap within an integrated model. Thus, TLTCP is utilized for this purpose. The energy and carbon emission costs can be reduced, production can be decided as per the situation, and the total cost can be globally minimized.

Research Gap

At the producer’s end, different production rates are considered to formulate the model more effective in the literature. Agile manufacturing received little attention in the literature at the producer’s end in the SCM. If the producer will decide the production rate as per the market situation, this affects the whole supply chain to reduce the holding cost and minimize the total cost. Here, to increase the demand, the producer offers some credit period to the supplier, and the supplier also provides some credit period to the customer. In all the above papers, the effect of TLTCP with an integrated model is unobserved. Therefore, a new agile manufacturing model has been developed to determine the supplier’s optimal TCP when producer and supplier propose a time-period to motivate their customers. In this research, the demand rate is a function of the credit period offered by the supplier and selling price, which is not considered with agile manufacturing in the above literature review. This study highlights agile manufacturing and TLTCP in the supply chain.

Further, it develops an assessment of the energy and carbon emission in setup/ordering cost, holding cost, and item cost. In this model, there is an analysis of total integrated cost with different cases of demand rate by numerical examples. Here production rate, credit period offered by the supplier, and complete cycle length are taken as decision variables. From the above literature review, the research gap is shown in contribution to

Table 1. Contribution from various researchers.

Researcher (s)	Model Type	Manufacturing Type	Financial Policy	Demand Pattern	Environmental Effect
Cárdenas-Barrón [1]	EPQ	Traditional	Trade-credit	Variable	Not applicable
Taleizadeh et al. [2,3]	EOQ	Not applicable	Not applicable	Constant	Not applicable
Sarkar et al. [5]	SSCM	Traditional	Trade-credit	Constant	Carbon emission
Tiwari et al. [8]	EPQ	Traditional	Trade-credit	Constant	Not applicable
Sarkar [9]	SCM	Traditional	Not applicable	Constant	Not applicable
Kim and Sarkar [11]	EPQ	Traditional	Not applicable	Constant	Carbon emission
Ahmed and Sarkar [12]	SSCM	Traditional	Not applicable	Constant	Carbon emission
Sana and Chaudhuri [14]	EPQ	Agile	Not applicable	Variable	Not applicable
Ouyang et al. [22]	EOQ	Not applicable	Trade-credit	Constant	Not applicable
Jaggi et al. [23]	Integrated inventory	Traditional	Trade-credit	Constant	Not applicable
Chung [26]	EPQ	Traditional	Trade-credit	Constant	Not applicable
This model	GSCM	Agile	Trade-credit	Variable	Carbon emission

.

The rest of this paper is ordered as follows: Section 2 shows the notations and assumptions. Section 3 shows the material and methods for producer and supplier. Illustrative examples, which explain the numerical verifications, sensitivity analysis, and observations, are provided in Section 4. Discussion and managerial insights represent the outcomes of this study in Section 5. Conclusion and suggestions for further research shown in Section 6 and Appendix A.

2. Problem Description, Notations, and Assumptions

2.1. Problem Description

A supply chain coordination is studied to minimize the energy and carbon emission cost with agile manufacturing. In agile manufacturing, per unit production cost is different from the raw material, and production rate is assumed as a decision variable. Here the demand rate varies with the credit period and selling price. The carbon emission and energy cost are found during setup/ordering cost, item cost, and holding cost. This research aims to control the energy and carbon emission cost, minimize the total cost, and maintain an improved strategy towards the integrated model. In this study, TLTCP plays a vital role in motivating the customers and increasing the demand.

2.2. Notation

2.2.1. Decision Variables

• T: Producer’s cycle length;
• N: Credit period offered by supplier;
• P: Production rate for the producer.

2.2.2. Producer’s Parameters

• C_1p: Producer’s stock holding cost ($/unit/week);
• C_p: Producer’s item cost ($/unit/week);
• C_2p: Producer’s setup cost ($/set up);
• C’_1p: Cost which include energy and carbon emission due to holding items ($/unit/week);
• C’_p: Cost which include energy and carbon emission due to deterioration ($/unit/week);
• C’_2p: Cost which include energy and carbon emission due to setup ($/setup);
• φ(P): Production cost.

2.2.3. Supplier’s Parameters

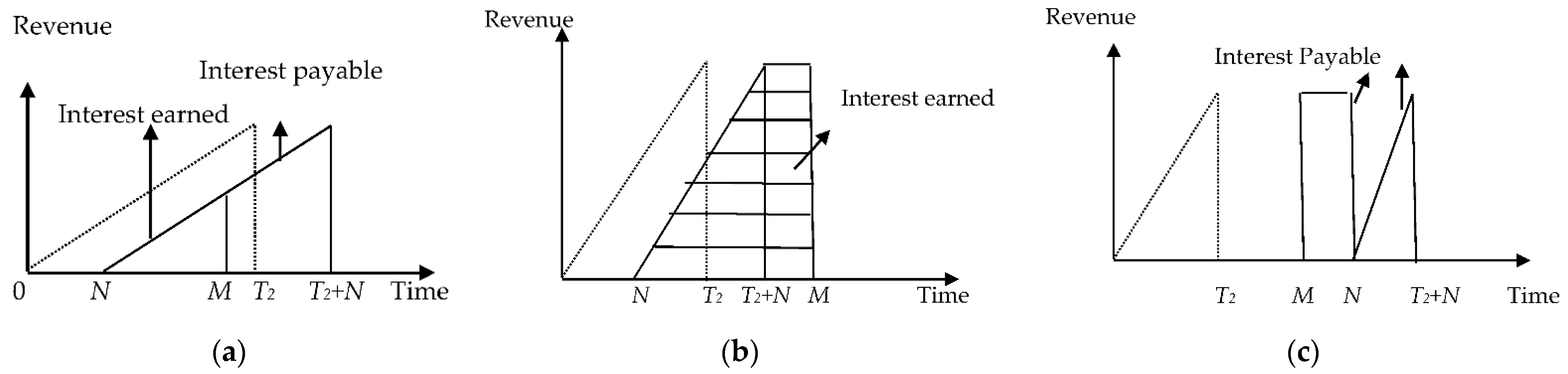
• M: Credit period offered by producer;
• i_e: Interest rate earned by supplier;
• i_p: Interest rate payable by supplier;
• C_1s: Holding cost of supplier ($/unit/week);
• C_s: Item cost of supplier ($/unit);
• C_2s: Ordering cost ($/order);
• C’_1s: Cost which include energy and carbon emission due to holding items ($/unit/week);
• C’_2s: Cost which include energy and carbon emission due to ordering items ($/order);
• C’_s: Cost which include carbon emission and energy due to deterioration ($/unit/week);
• c: Purchasing cost ($/unit);
• r: Inflation rate;
• n: Number of cycles;
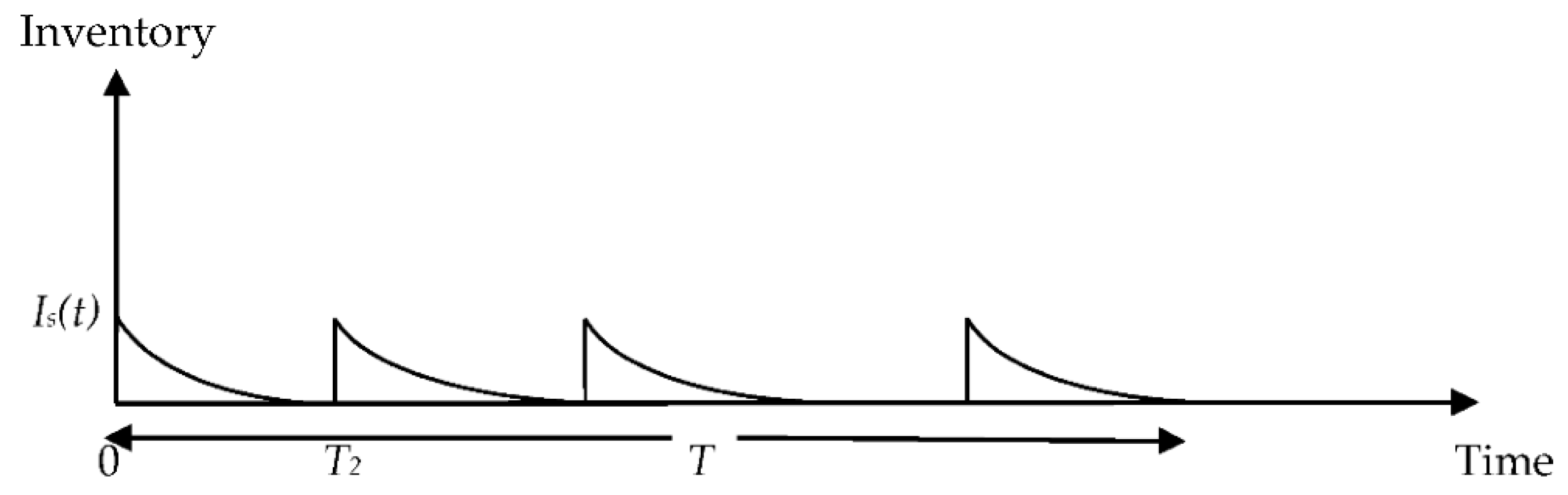
• T₂: Per delivery cycle length; T₂= T/n.

2.3. Assumptions

• As for the environment requirements, this paper assumed the carbon emission and energy cost in holding cost, item cost, and setup/ordering costs for producer and supplier (Ahmed and Sarkar [12]).
• Due to agile manufacturing, a controllable production rate controls the excess holding or shortage any time during the whole cycle-length. There is no shortage, since the production rate is considered a decision variable (Sana and Chaudhuri [2]).
• Here, the demand rate is variable, and demand varies with the supplier’s credit period and selling price. Therefore, D = W − (W − f)(1 − z)^N + α p^−τ, where W and f are the maximum and initial demand of products (unit/week), respectively, z is the demand saturation rate (unit/week). α and τ are the scaling parameter and price elasticity parameter of the selling price p, respectively (Jaggi et al. [13]).
• The deterioration rate (0 ≤ θ ≤ 1) exists and is very small.
• In this paper, TLTCP is applied. In this policy, the producer gives a fixed time M to the supplier, and the supplier also proposes a period N to their clients for the settlement of the account (Jaggi et al. [13]).
• A complete model is studied in the inflationary environment (Yadav et al. [20]).
• Due to agile manufacturing, production cannot be constant. That is why production cost is given below (Sana and Chaudhuri [3]):

$$\varphi (P)=\left(\mu +(k/P)+sP+\beta (P-P_c) .g(P-P_c)\right), \mathrm{where} g (P-P_c)=\{\begin{array}{l}1\\ 0\end{array}\begin{array}{l}P>P_c\\ P\le P_c.\end{array}$$

Here,

• µ is the material cost.
• The second term is $(k/P)$ is associated with labor and energy cost. As the production rate (P) increases, this cost decreases.
• The term (sP) represents a tool or die costs.
• The last term represents a critical value of the production rate (P_c) for the machine. The formed stock is to be defective for a very high production rate (P > P_c).

3. Material and Methods

In this section, we proposed a two-echelon integrated model for a producer and a supplier. Here the producer produces the goods with a production rate (P). These goods are transferred to the supplier in the number of shipments. The demand rate depends on the credit-period and selling price. The credit period is given to the supplier by the producer to return the number of goods. The retailer also allows a credit period to its customers.

3.1. Producer’s Model

The producer’s production model is formulated under agile manufacturing. The production process starts at t = 0 time and goes up to t = T₁ time, where the stock level goes to its highest level. At this time, the inventory level goes up because of production and declines because of deterioration and demand. At time T₁, production stops, and inventory level decreases because of demand and deterioration rate. The level of the stock goes down to zero at t = T. For the duration of [0, T], the stock system’s behavior is exhibited in Figure 1.

It is observed that the rate of inventory level increases due to the production rate and decreases due to demand and deterioration rate. The inventory position can be represented as follows:

$$\frac{d{I}_{p1}(t)}{dt}=-\theta I_{p1}(t)-D+P, 0\le t\le T_1,$$

(1)

At the time duration, $T_1\le t\le T,$ we observe that the inventory level rate decreases due to the demand and deterioration rate. The inventory position can be represented as follows:

$$\frac{d{I}_{p2}(t)}{dt}=-\theta I_{p2}(t)-D, T_1\le t\le T,$$

(2)

On solving the above equations by using boundary conditions $I_{p1}(0)=0$ and $I_{p2}(T)=0,$ we have, inventory level during the production time at any time t is as follows:

$$I_{p1}(t)=\left(\frac{P-D}{\theta }\right)(1-e^{-\theta t}),$$

(3)

Inventory level during the non-production time at any time t is as follows:

$$I_{p2}(t)=\left(\frac{D}{\theta }\right)\left(e^{\theta (T-t)}-1\right)\hspace{0.17em},$$

(4)

With the initial condition I_p1(T₁) = I_m, the maximum inventory after production is

$$I_m=\left(\frac{P-D}{\theta }\right)(1-e^{\theta T_1}),$$

(5)

Using the equation of continuity of inventory $I_{p1}\left(T_1\right)=I_{p2}\left(T_1\right)$, we have

$$\left(\frac{P-D}{\theta }\right)(1-e^{-\theta T_1})=\left(\frac{D}{\theta }\right)\left(e^{\theta (T-T_1)}-1\right)\hspace{0.17em}.$$

(6)

This gives the products production time as

$$T_1=\frac{1}{\theta }\log \left(\frac{D{e}^{\theta T}+P-D}{P}\right).$$

(7)

The producer bears the material setup cost, holding cost, item cost, and production cost. The setup cost, holding cost, and item cost include energy and carbon emission cost. The following components give the total cost function:

3.1.1. Holding Cost

For maintaining the EURO-14, the industry must take care of the environmental cost and the extra amount of investment. Therefore, the holding cost consists of two components. One is associated due to the holding of the products as C_1p, and the other part is due to the energy consumption and carbon emission as C’_1p. Finally, the total holding cost under the effect of the environment is

$$\begin{gathered} H{C}_p=\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\left[{\displaystyle \underset{0}{\overset{T_1}{\int }}{I}_{p1}(t)}{e}^{-rt}dt+{\displaystyle \underset{T_1}{\overset{T}{\int }}{I}_{p2}(t)}{e}^{-rt}dt\right], \\ =\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\left[\left(\frac{P-D}{\theta }\right)\left\{\frac{\theta -(\theta +r)e^{-r{T}_1}+r{e}^{-(\theta +r)T_1}}{r\left(\theta +r\right)}\right\}\hspace{0.17em}+\frac{D}{\theta }\left(\frac{e^{-rT}-e^{-r{T}_1}}{r}+\frac{e^{\theta T-(\theta +r)T_1}-e^{-rT}}{\theta +r}\right)\right]. \end{gathered}$$

(8)

3.1.2. Setup Cost

The producer’s setup cost consists of two components one is associated due to the setup of the products as C_2p, and the other component is the energy consumption and carbon emission as C’_2p. Finally, the total setup cost under the effect of the environment is

$$S{C}_p=\frac{(C_{2p}+{C^{\prime }}_{2p})}{T}.$$

(9)

3.1.3. Item Cost

The producer’s item cost consists of two components. One is associated with the deterioration and items sold as C_p and other components due to the energy consumption and carbon emission as C’_p. Finally, the total item cost under the effect of the environment is

$$I{C}_p=\frac{(C_p+{C^{\prime }}_p)}{T}{\displaystyle \underset{0}{\overset{T_1}{\int }}P}{e}^{-rt}dt=\frac{(C_p+{C^{\prime }}_p)}{T}P(1-e^{-r{T}_1}).$$

(10)

3.1.4. Production Cost

The producer’s production cost includes labor cost, material cost, tool/die cost, and some excess labor and energy cost.

$$PC=\varphi (P)\left[{\displaystyle \underset{0}{\overset{T_1}{\int }}P}{e}^{-rt}dt\right]=\left(\mu +(k/P)+sP+\beta (P-P_c)g(P-P_c)\right)\left(\frac{(1-e^{-r{T}_1})P}{r}\right).$$

(11)

3.1.5. Producer’s Total Cost

The producer’s total cost can be represented by:

$$\begin{gathered} T{C}_p=PC+D{C}_p+S{C}_p+H{C}_p, \\ \begin{array}{l}T{C}_p=\left(\mu +\frac{k}{P}+sP+g(P-P_c)\beta (P-P_c)\right)\left(\frac{(1-e^{-r{T}_1})P}{Tr}\right)+\frac{(C_{2p}+{C^{\prime }}_{2p})}{T}+\frac{(C_p+{C^{\prime }}_p)}{T}P(1-e^{-r{T}_1})\\ +\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\left[\left(\frac{P-D}{\theta }\right)\left\{\frac{\theta -(\theta +r)e^{-r{T}_1}+r{e}^{-(\theta +r)T_1}}{r\left(\theta +r\right)}\right\}\hspace{0.17em}+\frac{D}{\theta }\left(\frac{e^{-rT}-e^{-r{T}_1}}{r}+\frac{e^{\theta T-(\theta +r)T_1}-e^{-rT}}{\theta +r}\right)\right].\end{array} \end{gathered}$$

(12)

3.2. Supplier’s Model for Selling Strategy of Products

The supplier’s inventory storage and demand pattern can be represented as in Figure 2. At the starting of the period, I_s(t) is stock received from the producer. It is supposed that the supplier has a credit-period which the producer offers, and the supplier also gives a time interval to his clients. The level of stock I_s(t) continuously goes down to meet the demand due to the deterioration and demand, and inventory level goes down to zero at t = T₂. Here, the supplier supplies the inventory to their customers in n different orders.

During the time interval, $0\le t\le T_2,$ the inventory level decreases due to the demand and deterioration rate. Hence, the variation in the level of inventory versus time t is given below:

$$\frac{d{I}_s\left(t\right)}{dt}=-\theta I_s(t)-D\hspace{1em}0\le t\le T_2,$$

(13)

With the inventory status $I_s\left(T_2\right)$ = 0, current inventory at any time t in the period $0\le t\le T_2$ is as follows:

$$I_s\left(t\right)=\left(D/\theta \right)\left(e^{\theta (T_2-t)}-1\right)\hspace{0.17em}.$$

(14)

The supplier bears the ordering cost, holding cost, item cost, interest payable cost, and interest earned. The ordering cost, holding cost, and item cost include energy and carbon emission cost. The following components give the total cost function.

3.2.1. Holding Cost for Items

Here holding cost consists of two components. One is associated with the holding of the products as C_1s, and the other component is the energy consumption and carbon emission as C’_1s. Finally, the total holding cost under the effect of the environment is

$$H{C}_s=\frac{n(C_{1s}+{C^{\prime }}_{1s})}{T}{\displaystyle \underset{0}{\overset{T_2}{\int }}{e}^{-rt}{I}_s\left(t\right)dt}=\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right).$$

(15)

3.2.2. Ordering Cost for Items

The supplier’s ordering cost consists of two components. One is associated with the ordering of the products as C_2s, and the other component is the energy consumption and carbon emission as C’_2s. Finally, the total ordering cost under the effect of the environment is

$$S{C}_s=\frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}.$$

(16)

3.2.3. Item Cost

The supplier’s item cost consists of two components. One is associated due to the deterioration and item sold as C_s, and the other component is due to the energy consumption and carbon emission as C’_s. Finally, the total item cost under the effect of the environment is

$$I{C}_s=\frac{n(C_s+{C^{\prime }}_s)}{T}{I}_s(0)=\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{W - \left(W-f\right){\left(1-z\right)}^N+ \tau p^{-\rho }}{\theta }\right)\left(e^{\theta (T_2)}-1\right)\hspace{0.17em}.$$

(17)

There are different possibilities of permissible delay payment period. Variation of revenue versus time is shown in Figure 3a–c.

3.2.4. Supplier’s Total Cost

The supplier’s total cost can be represented by:

$$\begin{array}{l}T{C}_s=H{C}_s+I{C}_s+S{C}_s,\\ =\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right)+\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{D}{\theta }\right)\left(e^{\theta (T_2)}-1\right)+\frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}\end{array}$$

3.2.5. Supplier’s Total Cost in Two Different Credit Policy

Case I-When N ≤ M ≤ T₂ + N

Here, TCP offered by the supplier to his clients is significantly less than the TCP proposed by the producer to the supplier. After getting the revenue, the supplier earns interest on the average sales revenue in the time interval (M–N). The finances are arranged to make the payment to the producer at time M. It is shown in Figure 3a.

Interest earned for the products can be expressed as:

$$I{E}_1=\frac{n{i}_{e}p}{T}{\displaystyle \underset{N}{\overset{M}{\int }}D{e}^{-rt}}dt=\frac{n{i}_{e}pD(e^{-rN}-e^{-rM})}{rT},$$

(18)

Interest payable for the products can be defined as:

$$I{P}_1=\frac{n{i}_{p}c}{T}{\displaystyle \underset{M}{\overset{N+T}{\int }}{e}^{-tr}{I}_s\left(t\right)}dt=\frac{n{i}_{p}cD}{T\theta }\left[\frac{e^{\theta T_2}(e^{-(r+\theta )M}-e^{-(r+\theta )(T_2+N)})}{\theta +r}+\frac{(e^{-r(T_2+N)}-e^{-rM})}{r}\right],$$

(19)

Supplier’s total cost TC_s1 for the inventory per unit time can be expressed as:

$$\begin{array}{l}T{C}_{s1}=T{C}_s+I{P}_1-I{E}_1,\\ =\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right)+\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{D}{\theta }\right)\left(e^{\theta (T_2)}-1\right)+\frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}\\ +\frac{n{i}_{p}cD}{T\theta }\left[\frac{e^{\theta T_2}(e^{-rM-\theta M}-e^{-(T_2+N)(r+\theta )})}{\theta +r}+\frac{(e^{-r{T}_2-rN}-e^{-rM})}{r}\right]-\frac{n{i}_{e}pD(e^{-rN}-e^{-rM})}{r.T}.\end{array}$$

(20)

Case II-N ≤ T₂ + N ≤ M

Here, TCP offered by the producer to the supplier is more than the cycle length of the supplier and the TCP provided by the supplier to his customers, and the supplier earns interest on the received average sales revenue during (N, T₂ + N) and on total sales revenue for (M–(T₂ + N)), but there is no interest payable by the supplier. It is represented in Figure 3b.

Interest earned for the inventory can be express as:

$$\begin{gathered} I{E}_2=\frac{n{i}_{e}p}{T}\left[{\displaystyle \underset{N}{\overset{T_2+N}{\int }}D{e}^{-r{t}_2}}d{t}_2+D{T}_2{\displaystyle \underset{T_2+N}{\overset{M}{\int }}{e}^{-r{t}_2}d{t}_2}\right], \\ =\frac{n{i}_{e}p}{T}\left[\frac{D{e}^{-rN}}{r}\left(1-\frac{e^{-r{T}_2}}{r}\right)+D{T}_2\left(\frac{e^{-r(T_2+N)}}{r}-\frac{e^{-rM}}{r}\right)\right], \end{gathered}$$

(21)

Supplier’s total cost TC_s2 of inventory product per cycle can be express as:

$$\begin{array}{l}T{C}_{s2}=T{C}_s-I{E}_2,\\ =\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right)+\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{D}{\theta }\right)\left(e^{\theta (T_2)}-1\right)\hspace{0.17em}+\\ \frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}-\frac{n{i}_{e}p}{T}\left[\frac{D{e}^{-rN}}{r}\left(1-\frac{e^{-r{T}_2}}{r}\right)+D{T}_2\left(\frac{e^{-r(T_2+N)}}{r}-\frac{e^{-rM}}{r}\right)\right].\end{array}$$

(22)

Case III-M ≤ N ≤ T₂ + N

Here, TCP offered by the supplier to his customers is more than that period provided by the producer to the supplier, and the supplier has no interest, but pays interest on the full order of products for a time (N–M) and average product held during the cycle T₂. It is represented in Figure 3c.

Interest payable for a product is expressed as:

$$I{P}_2=\frac{n{i}_{p}c}{T}\left[D{T}_2(N-M)+{\displaystyle \underset{N}{\overset{T_2+N}{\int }}D{e}^{-r{t}_3}}d{t}_3\right]=\frac{n{i}_{p}cD}{T}\left[T_2(N-M)+\frac{e^{-rN}}{r}\left(1-\frac{e^{-r{T}_2}}{r}\right)\right],$$

(23)

Supplier’s total cost TC_s3 for product per unit time can be express as:

$$\begin{array}{l}T{C}_{s3}=H{C}_s+I{C}_s+S{C}_s+I{P}_2,\\ =\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right)+\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{D}{\theta }\right)\left(e^{\theta (T_2)}-1\right)+\\ \frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}+\frac{n{i}_{p}cD}{T}\left[T_2(N-M)+\frac{e^{-rN}}{r}\left(1-\frac{e^{-r{T}_2}}{r}\right)\right],\end{array}$$

(24)

Therefore, the total cost is

$$T{C}_{sc}=\{\begin{array}{ccc}T{C}_{s1}& if& N \le M \le T_2+N \\ T{C}_{s2}& if& N \le T_2+N \le M \\ T{C}_{s3}& if& M \le N \le T_2+N \end{array}.$$

(25)

where $T{C}_{s1}$, $T{C}_{s2}$, and $T{C}_{s3}$ are given by Equations (20), (22) and (24) for products.

Finally, the system’s integrated cost comprises the producer’s cost (TC_p) and the supplier’s cost (TC_sc). The relevant cost for the whole model is different in various cases.

3.3. Integrated Cost Function for Two-Echelon Supply Chain Management

Three cases of the joint total cost are formed because of different situations of the supply chain, and can be developed as:

$$\begin{array}{l}TC{S}_1\left(P, N, T\right)=T{C}_p+T{C}_{s1},N\le M\le T_2+N,\\ TC{S}_2\left(P, N, T\right)=T{C}_p+T{C}_{s2},N\le T_2+N\le M,\\ TC{S}_3\left(P, N, T\right)=T{C}_p+T{C}_{s3},M\le N\le T_2+N.\end{array}$$

This theory develops a production model for items with a specific credit period for the supplier. The inventory cost model is derived from the policy of optimal production and credit-period.

3.3.1. The Total Integrated Cost in Case I

$$\begin{array}{l}TC{S}_1\left(P, N, T\right)=b\left(\frac{P(1-e^{-r{T}_1})}{Tr}\right)+\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\left[\left(\frac{P-D}{\theta }\right)\left\{\frac{\theta -(\theta +r)e^{-r{T}_1}+r{e}^{-(\theta +r)T_1}}{r\left(\theta +r\right)}\right\}\hspace{0.17em}+\frac{D}{\theta }\left(\frac{e^{-rT}-e^{-r{T}_1}}{r}+\frac{e^{\theta T-(\theta +r)T_1}-e^{-rT}}{\theta +r}\right)\right]\\ +\frac{(C_{2p}+{C^{\prime }}_{2p})}{T}+\frac{(C_p+{C^{\prime }}_p)}{T}P(1-e^{-r{T}_1})+\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right)+\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{D}{\theta }\right)\left(e^{\theta (T_2)}-1\right)\hspace{0.17em}+\\ \frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}+\frac{n{i}_{p}cD}{T\theta }\left[\frac{e^{\theta T_2}(e^{-rM-\theta M}-e^{-(T_2+N)(r+\theta )})}{\theta +r}+\frac{(e^{-r{T}_2-rN}-e^{-rM})}{r}\right]-\frac{n{i}_{e}pD(e^{-rN}-e^{-rM})}{rT}.\end{array}$$

(26)

3.3.2. The Total Integrated Cost in Case II

$$\begin{array}{l}TC{S}_2\left(P, N, T\right)=b\left(\frac{P(1-e^{-r{T}_1})}{Tr}\right)+\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\left[\left(\frac{P-D}{\theta }\right)\left\{\frac{\theta -(\theta +r)e^{-r{T}_1}+r{e}^{-(\theta +r)T_1}}{r\left(\theta +r\right)}\right\}\hspace{0.17em}+\frac{D}{\theta }\left(\frac{e^{-rT}-e^{-r{T}_1}}{r}+\frac{e^{\theta T-(\theta +r)T_1}-e^{-rT}}{\theta +r}\right)\right]\\ +\frac{(C_{2p}+{C^{\prime }}_{2p})}{T}+\frac{(C_p+{C^{\prime }}_p)}{T}P(1-e^{-r{T}_1})+\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right)+\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{D}{\theta }\right)\left(e^{\theta (T_2)}-1\right)\hspace{0.17em}+\frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}\\ -\frac{n{i}_{e}pD}{Tr}\left[e^{-rN}\left(1-\left(\frac{e^{-r{T}_2}}{r}\right)\right)+T_2\left(e^{-r(T_2+N)}-e^{-rM}\right)\right].\end{array}$$

(27)

3.3.3. The Integrated Total Cost in Case III

$$\begin{array}{l}TC{S}_3\left(P, N, T\right)=b\left(\frac{P(1-e^{-r{T}_1})}{Tr}\right)+\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\left[\left(\frac{P-D}{\theta }\right)\left\{\frac{\theta -(\theta +r)e^{-r{T}_1}+r{e}^{-(\theta +r)T_1}}{r\left(\theta +r\right)}\right\}\hspace{0.17em}+\frac{D{e}^{-r{T}_1}}{\theta }\left(\frac{e^{-rT}-e^{-r{T}_1}}{r}+\frac{e^{\theta T-(\theta +r)T_1}-e^{-rT}}{\theta +r}\right)\right]\\ +\frac{(C_{2p}+{C^{\prime }}_{2p})}{T}+\frac{(C_p+{C^{\prime }}_p)}{T}P(1-e^{-r{T}_1})+\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{\theta T_2}-e^{-r{T}_2}}{\theta +r}+\frac{e^{-r{T}_2}-1}{r}\right)+\frac{n(C_s+{C^{\prime }}_s)}{T}\left(\frac{D}{\theta }\right)\\ \left(e^{\theta (T_2)}-1\right)+\frac{n(C_{2s}+{C^{\prime }}_{2s})}{T}+\frac{n{i}_{p}cD}{T}\left[T_2(N-M)+\frac{e^{-rN}}{r}\left(1-\frac{e^{-r{T}_2}}{r}\right)\right].\end{array}$$

(28)

3.4. Solution Methodology

Kuhn-Tucker’s method is the best approach to prove the convexity of this model. From the necessary conditions of optimization, one can obtain:

$$\begin{array}{l}\frac{\partial TC{S}_1}{\partial P}=\frac{(C_p+{C^{\prime }}_p)}{T}\left((1-m)-\frac{mrD\left(e^{\theta T}-1\right)}{P\theta }\right)+\frac{P(1-m)}{rT}\left(-\frac{k}{P^2}+s+\beta \right)+\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\\ \left\{\frac{\left(l{e}^{\theta T}-m\right)D^2\left(e^{\theta T}-1\right)}{P^2{\theta }^2}+\frac{lr+\theta -m(r+\theta )}{r\theta \left(\theta +r\right)}+\frac{(P-D)D\left(e^{\theta T}-1\right)(l-m)}{\theta P^2\theta }\right\}+\frac{(1-m)b}{rT}-\frac{mbD\left(e^{\theta T}-1\right)}{TP\theta }=0,\end{array}$$

(29)

$$\begin{array}{l}\frac{\partial TC{S}_1}{\partial N}=\frac{D{e}^{-rN}np{i}_e}{T}+\frac{n{i}_{p}cD{K}_4}{T\theta }+\frac{Knp{i}_e{D}_1}{rT}-\frac{(C_p+C_p{}^{\prime })D{l}_{2}r}{T\theta }-\frac{(C_s+C_s{}^{\prime })(e^{\frac{T\theta }{n}}-1)n{D}_1}{T\theta }\\ -\frac{n{i}_{p}c{D}_1}{T\theta }\left(\frac{K_2}{r}+\frac{e^{T\theta /n}{K}_1}{r+\theta }\right)+\frac{n(C_{1s}+C_{1s}{}^{\prime })D_1}{T\theta }\left(\frac{e^{-r(T/n)}-1}{r}+\frac{K_3}{r+\theta }\right)-\frac{Db{l}_2}{T\theta }+\frac{(C_{1p}+C_{1p}{}^{\prime })}{T}\\ \left[-\left(\frac{e^{-rT}-m}{r}+\frac{-e^{-rT}+l{e}^{T\theta }}{r+\theta }\right)\frac{D_1}{\theta }+\frac{\left(rl+\theta -m(r+\theta )\right)D_1}{r(r+\theta )\theta }+\frac{D}{\theta }\left(-\frac{l_2}{P\theta }+\frac{e^{T\theta }{l}_1}{P\theta }\right)+\frac{\left(P-D\right)\left(l_1-l_2\right)}{P{\theta }^2}\right]=0,\end{array}$$

(30)

$$\begin{array}{l}\frac{\partial TC{S}_1}{\partial T}=-\frac{(C_p+C_p{}^{\prime })P(1-m)}{T^2}-\frac{(C_{2p}+{C^{\prime }}_{2p})}{T^2}-\frac{n(C_{2s}+{C^{\prime }}_{2s})}{T^2}+\frac{(C_s+{C^{\prime }}_s)e^{\theta T/n}D}{T}+\frac{Knp{i}_{e}D}{r{T}^2}+\frac{(C_p+C_p{}^{\prime })rDm{e}^{T\theta }}{T}\\ -\frac{n(C_s+{C^{\prime }}_s)(e^{\frac{T\theta }{n}}-1)D}{T^2\theta }-\frac{n{i}_{p}cD}{T^2\theta }\left(\frac{K_2}{r}+\frac{e^{T\theta /n}{K}_1}{r+\theta }\right)+\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T^2\theta }\left(\frac{e^{-r(T/n)}-1}{r}+\frac{e^{T\theta /n}-e^{-r(T/n)}}{r+\theta }\right)+\frac{n{i}_{p}cD}{T\theta }\left(\frac{K_4}{n}+\frac{\theta e^{\theta T/n}{K}_1}{n(r+\theta )}\right)\\ +\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{e^{-r(T/n)}}{n}-\frac{r{e}^{-r(T/n)}+\theta e^{-\theta (T/n)}}{n(r+\theta )}\right)-\frac{(C_{1p}+C_{1p}{}^{\prime })}{T^2}\left\{\frac{D}{\theta }\left(\frac{e^{-rT}-m}{r}+\frac{-e^{-rT}+l{e}^{T\theta }}{r+\theta }\right)+\frac{\left(P-D\right)(l-m)}{r\theta }\right\}\\ +\frac{(C_{1p}+C_{1p}{}^{\prime })}{T^2}\left\{\frac{\left(P-D\right)Dr{e}^{T\theta }(l-m)}{Pr\theta }+\frac{D}{\theta }\left(-e^{-rT}+\frac{l{e}^{T\theta }D}{P}+\frac{r{e}^{-rT}+m{e}^{T\theta }}{r+\theta }\right)\right\}=0.\end{array}$$

(31)

The sufficient condition must be satisfied to prove the globality of the optimal solution. Now, to acquire the optimal solution, a theorem is formulated as follows:

Theorem 1.

If${\xi }_1>0,{\xi }_1{\xi }_2-{\xi }_4{}^2>0,\left({\xi }_1{\xi }_2{\xi }_3-{\xi }_1{\xi }_6{}^2-{\xi }_3{\xi }_4{}^2+2{\xi }_4{\xi }_5{\xi }_6-{\xi }_2{\xi }_5{}^2\right) >0,$then TCS₁ (P, N, T) will be minimum at point (P*, N*, T*)

Proof. 

To find the sufficient condition of the global optimality, taking second-order derivatives of Equations (29)–(31) versus P, T, and N, one can find:

$$\begin{array}{l}\frac{{\partial }^{2}TC{S}_1}{\partial N^2}=-\frac{D{e}^{-rN}nrp{i}_e}{T}+\frac{n{i}_{p}cD(-r{K}_4-\theta e^{(-r-\theta )(N+T/n)+T\theta /n})}{T\theta }-\frac{2D_1{e}^{-rN}np{i}_e}{T}-\frac{2n{i}_{p}c{D}_1{K}_4}{T\theta }+\frac{nK{i}_{e}p{D}_1}{Tr}-\frac{2(C_p+C_p{}^{\prime })l_{2}r}{T\theta }\\ -\frac{2(C_s+C_s{}^{\prime })(e^{\frac{T\theta }{n}}-1)n{D}_1}{T\theta }-\frac{2n{i}_{p}c{D}_1}{T\theta }\left(\frac{K_2}{r}+\frac{e^{T\theta /n}{K}_1}{r+\theta }\right)+\frac{2n(C_{1s}+C_{1s}{}^{\prime })D_1}{T\theta }\left(\frac{e^{-r(T/n)}-1}{r}+\frac{K_3}{r+\theta }\right)-\frac{2l_{2}b}{T\theta }\\ +\frac{(C_{1p}+C_{1p}{}^{\prime })}{T}\left[-\left(\frac{e^{-rT}-m}{r}+\frac{-e^{-rT}+l{e}^{T\theta }}{r+\theta }\right)\frac{2D_1}{\theta }+\frac{2\left(rl+\theta -m(r+\theta )\right)D_1}{r(r+\theta )\theta }+\frac{D}{\theta }\left(-\frac{2l_2}{P\theta }+\frac{2e^{T\theta }{l}_1}{P\theta }\right)+\frac{\left(P-D\right)\left(l_1-l_2\right)}{P{\theta }^2}\right]= {\xi }_1(say),\end{array}$$

$$\begin{array}{l}\frac{{\partial }^{2}TC{S}_1}{\partial P^2}=\frac{2(1-m)(s+\beta )}{rT}-\frac{mD\left(e^{\theta T}-1\right)}{P\theta T}\left(2\left(-\frac{k}{P^2}+s+\beta \right)+\frac{(C_p+{C^{\prime }}_p)\left(e^{\theta T}-1\right)r^{2}D}{P^2}\right)\\ +\frac{(C_{1p}+{C^{\prime }}_{1p})}{T}\left\{\begin{array}{l}\frac{D}{\theta }\left(\frac{D^2{\left(e^{\theta T}-1\right)}^2\left(l(r+\theta )e^{\theta T}-mr\right)}{P^4{\theta }^2}+\frac{2\left(m-l{e}^{\theta T}\right)D\left(e^{\theta T}-1\right)}{P^3\theta }\right)+\frac{(P-D)D\left(e^{\theta T}-1\right)}{\theta }\\ \left(\frac{D\left(e^{\theta T}-1\right)\left(l(r+\theta )-mr\right)}{P^4{\theta }^2}-\frac{2\left(l-m\right)}{P^3\theta }\right)+\frac{2\left(l-m\right)D\left(e^{\theta T}-1\right)}{P^2{\theta }^2}\end{array}\right\}\\ -\frac{mrb{D}^2{\left(e^{\theta T}-1\right)}^2}{P^3{\theta }^{2}T}={\xi }_2(say),\end{array}$$

$$\begin{array}{l}\frac{{\partial }^{2}TC{S}_1}{\partial T^2}=\frac{2(C_p+C_p{}^{\prime })P(1-m)}{T^3}+\frac{2(C_{2p}+{C^{\prime }}_{2p})}{T^3}+\frac{2n(C_{2s}+{C^{\prime }}_{2s})}{T^3}-\frac{2(C_s+{C^{\prime }}_s)e^{\theta T/n}D}{T^2}-\frac{2Knp{i}_{e}D}{r{T}^3}-\frac{(C_p+C_p{}^{\prime })rDm{e}^{T\theta }}{T^2}\\ +\frac{2n(C_s+{C^{\prime }}_s)(e^{\frac{T\theta }{n}}-1)D}{T^3\theta }+\frac{2(C_s+{C^{\prime }}_s)n(e^{\theta T/n}-1)D}{T^3\theta }+\frac{\theta (C_s+{C^{\prime }}_s)e^{\theta T/n}D}{nT}+\frac{(C_p+C_p{}^{\prime })rDm{e}^{T\theta }}{T}\left(\theta -\frac{rD{e}^{T\theta }}{T}\right)+\\ \frac{2n{i}_{p}cD}{T^3\theta }\left(\frac{e^{-r(N+T/n)}-e^{-rM}}{r}+\frac{e^{T\theta /n}{K}_1}{r+\theta }\right)+\frac{2n(C_{1s}+{C^{\prime }}_{1s})D}{T^3\theta }\left(\frac{e^{-r(T/n)}-1}{r}+\frac{e^{T\theta /n}-e^{-r(T/n)}}{r+\theta }\right)-\frac{2n{i}_{p}cD}{T^2\theta }\left(\frac{K_4}{n}+\frac{\theta e^{T\theta /n}{K}_1}{n(r+\theta )}\right)+\\ \frac{n{i}_{p}cD}{T\theta }\left(\frac{r{e}^{-r(N+T/n)}+\theta e^{(-r-\theta )(N+T/n)+T\theta /n}}{n^2}+\frac{{\theta }^2{e}^{\theta T/n}{K}_1}{n^2(r+\theta )}-\frac{r{e}^{(-r-\theta )(N+T/n)+T\theta /n}}{n^2}\right)-\frac{2n(C_{1s}+{C^{\prime }}_{1s})D}{T^2\theta }\left(-\frac{e^{-r(T/n)}}{n}-\frac{r{e}^{-r(T/n)}+\theta e^{-\theta (T/n)}}{n(r+\theta )}\right)\\ +\frac{n(C_{1s}+{C^{\prime }}_{1s})D}{T\theta }\left(\frac{r{e}^{-r(T/n)}}{n^2}+\frac{-r^2{e}^{-r(T/n)}+{\theta }^2{e}^{-\theta (T/n)}}{n^2(r+\theta )}\right)+\frac{2(C_{1p}+C_{1p}{}^{\prime })}{T^3}\left\{\frac{D}{\theta }\left(\frac{e^{-rT}-m}{r}+\frac{-e^{-rT}+l{e}^{T\theta }}{r+\theta }\right)+\frac{\left(P-D\right)(l-m)}{r\theta }\right\}\\ -\frac{2(C_{1p}+C_{1p}{}^{\prime })}{T^2}\left\{\frac{\left(P-D\right)D{e}^{T\theta }(l-m)}{P\theta }+\frac{D}{\theta }\left(-e^{-rT}+\frac{l{e}^{T\theta }D}{P}+\frac{r{e}^{-rT}+l{e}^{T\theta }(\theta -e^{T\theta }D(r+\theta ))/P}{r+\theta }\right)\right\}+\frac{(C_{1p}+C_{1p}{}^{\prime })}{T}\\ \left\{\frac{\left(P-D\right)}{P\theta }\left(e^{T\theta }mD\left(\theta -\frac{r{e}^{T\theta }D}{P}\right)+\frac{l{e}^{T\theta }D}{P}\left(\theta +\frac{(r+\theta )e^{T\theta }D}{P}\right)\right)+\frac{D}{\theta }\left(\begin{array}{l}{r}^2{e}^{-rT}+\frac{mr{e}^{T\theta }D}{P}\left(\theta -\frac{r{e}^{T\theta }D}{P}\right)+\\ \frac{1}{r+\theta }\left(\begin{array}{l}-r^2{e}^{-rT}-\frac{l{e}^{2T\theta }D\theta (r+\theta )}{P}\\ +e^{T\theta }l{\left(\theta -\frac{(r+\theta )e^{T\theta }D}{P}\right)}^2\end{array}\right)\end{array}\right)\right\}\\ +\frac{2Pb(1-m)}{r{T}^3}-\frac{2e^{T\theta }mDb}{T^2}+\frac{e^{T\theta }mDb}{T}\left(\theta -\frac{r{e}^{T\theta }D}{P}\right)={\xi }_3(say),\end{array}$$

$$\begin{array}{l}\frac{{\partial }^{2}TC{S}_1}{\partial N\partial T}=-\frac{Knp{i}_e}{T^2}\left(-D{e}^{-rN}+\frac{K{D}_1}{r}\right)+\frac{i_{p}c}{T\theta }\left(\frac{-n{K}_{4}D}{T}-r{K}_{4}D+\frac{n{D}_1}{T}\left(\frac{K_2}{r}+\frac{K_1{e}^{T\theta /n}}{r+\theta }\right)-n{D}_1\left(K_4+\frac{K_1\theta e^{T\theta /n}}{r+\theta }\right)\right)\\ -\frac{D_1{e}^{T\theta }(rm(C_p+C_p{}^{\prime })+(C_s+{C^{\prime }}_s))}{T}+\frac{n(C_s+{C^{\prime }}_s)D_1(e^{\frac{T\theta }{n}}-1)}{T^2\theta }+\frac{(C_p+C_p{}^{\prime })r{l}_2}{T\theta }\left(\frac{1}{T}+\frac{D{r}^2{e}^{T\theta }}{P}\right)+\frac{n(C_{1s}+{C^{\prime }}_{1s})D_1}{T\theta }\\ \left(\frac{e^{-r(T/n)}}{n}+\frac{r{e}^{-r(T/n)}+\theta e^{-\theta (T/n)}}{n(r+\theta )}-\frac{(e^{-r(T/n)}-1)}{r}-\frac{K_3}{r+\theta }\right)-\frac{mb{e}^{T\theta }{D}_1}{T}+\frac{b{l}_2}{T\theta }\left(\frac{1}{T}+\frac{r{e}^{T\theta }}{P}\right)-\frac{(C_{1p}+C_{1p}{}^{\prime })}{T^2}\\ \left\{\frac{-D_1}{\theta }\left(\frac{e^{-rT}-m}{r}+\frac{-e^{-rT}+l{e}^{T\theta }}{r+\theta }\right)+\frac{D_1(lr+\theta -mr-m\theta )}{r\theta (r+\theta )}-\frac{D(l_2+l_1{e}^{T\theta })}{P{\theta }^2}+\frac{\left(P-D\right)(l_1-l_2)}{\theta }\right\}\\ +\frac{(C_{1p}+C_{1p}{}^{\prime })}{T^2}\left\{\frac{D_1{e}^{T\theta }(-l_1+l_2)}{\theta }-\frac{D_1}{\theta }\left(e^{-rT}+\frac{mD{e}^{T\theta }}{P}\right)-\frac{\left(P-D\right)D_1{e}^{T\theta }(l+m)}{\theta P}+\frac{D}{\theta }\left(-\frac{m{e}^{T\theta }{D}_1}{P}+\frac{l{e}^{T\theta }{D}_1}{P}\right)\right\}={\xi }_5(say),\end{array}$$

$$\begin{array}{l}\frac{{\partial }^{2}TC{S}_1}{\partial N\partial P}=-\frac{r^{2}D{l}_2\left(b+(C_p+{C^{\prime }}_p)\right)}{P{\theta }^2}-\frac{l_2}{r}\left(\frac{-k}{P^2}+s+\beta \right)+\frac{(C_{1p}+C_{1p}{}^{\prime })}{T}\\ \left\{\begin{array}{l}\frac{-D\left(l_1{e}^{T\theta }-l_2\right)}{P^2{\theta }^2}+\frac{D\left(l_1-l_2\right)}{\theta }+\frac{D}{\theta }\left(\frac{\left(-l_1{e}^{T\theta }+l_2\right)}{P^2\theta }+\frac{(e^{T\theta }-1)D\left(l_1{e}^{T\theta }(r+\theta )-r{l}_2\right)}{P^2{\theta }^2}\right)\\ +\frac{\left(P-D\right)}{P^2{\theta }^2}\left(l_1+l_2+\frac{(e^{T\theta }-1)D}{\theta }\left(-r{l}_2+(r+\theta )l_1\right)\right)+\frac{\left(l_1-l_2\right)}{P{\theta }^2}\end{array}\right\}={\xi }_6(say).\end{array}$$

To minimize the total integrated cost function of inventory management, the principle minors must be positive in sign. Hence, the conditions are made this way: (i) Satisfy; then, the total costs function contains a global minimum at the decision variables’ optimum value. This model is tested through numerical experiments, and at the optimal points, the optimality is tested.

Similarly, we can check for Case II and Case III. □

4. Numerical Examples

This section used data to demonstrate the application of the model. The integrated model consists of improvement over procurement, manufacturing, and distribution. The model is formulated to examine the effect of controllable production rate and permissible delay in payment policy to minimize energy and carbon emission costs. The model is reviewed by the following numerical example. The numerical data is considered from Jaggi et al. [5] and Sarkar and Chung [26].

4.1. Numerical Example 1

This numerical considers the TCP offered by the supplier to his clients is significantly less than the TCP proposed by the producer to the supplier. The data values are:

Let C_p = $6.7/unit/week, C_1p = $2.8/unit/week, C_2p = $990/set up, C’_1p = $0.2/unit/week, C’_p = $0.3/unit/week, C’_2p = $10/set up, θ = 0.02, r = 0.01, W = 100 units/week, f = 20 units/week, z = 0.2, τ = 0.03, α = 0.11, p = $5/unit, c = $11/unit, M = 12week, P_c = 220 units, μ = $90/week, k = $3500/week, s = $0.01/week, β = $0.04/week, C_s = $5.5/unit/week, C_1s = $2.7/unit/week, C_2s = $298/order, C’_1s = $0.3/unit/week, C’_s = $0.5/unit/week, C’_2s = $2/order, n = 3, r = 0.01, i_e = 0.15/year, i_p = 0.10/year.

The best possible value of TCS₁ is $11,356.2, P is 182.436 units, N is 8.995 weeks, and T is 10.1445 weeks. T₁ and T₂ can be found out from the Equation (7) and T₂ = T/n. Complete numerical is analyzed with the help of Mathematica software.

Using the above values of all parameters and optimal values of decision parameters, we can validate our numerical through the Hessian matrix.

$$\frac{{\partial }^2(TCS)}{\partial T^2}=31.5807>0,|\begin{array}{cc}{\xi }_3& {\xi }_4\\ {\xi }_4& {\xi }_2\end{array}|=|\begin{array}{cc}31.581& 1.439\\ 1.439& -0.006105\end{array}|=2.123>0and\left|\left|\begin{array}{ccc}{\xi }_3& {\xi }_4& {\xi }_5\\ {\xi }_4& {\xi }_2& {\xi }_6\\ {\xi }_5& {\xi }_6& {\xi }_1\end{array}\right|\right|=\left|\begin{array}{ccc}31.581& 1.439& 25.517\\ 1.439& -0.006105& 0.3925\\ 25.517& 0.3925& -110.635\end{array}\right|=506.112>0$$

Therefore, at the critical point, the total integrated cost TCS₁ is minimum.

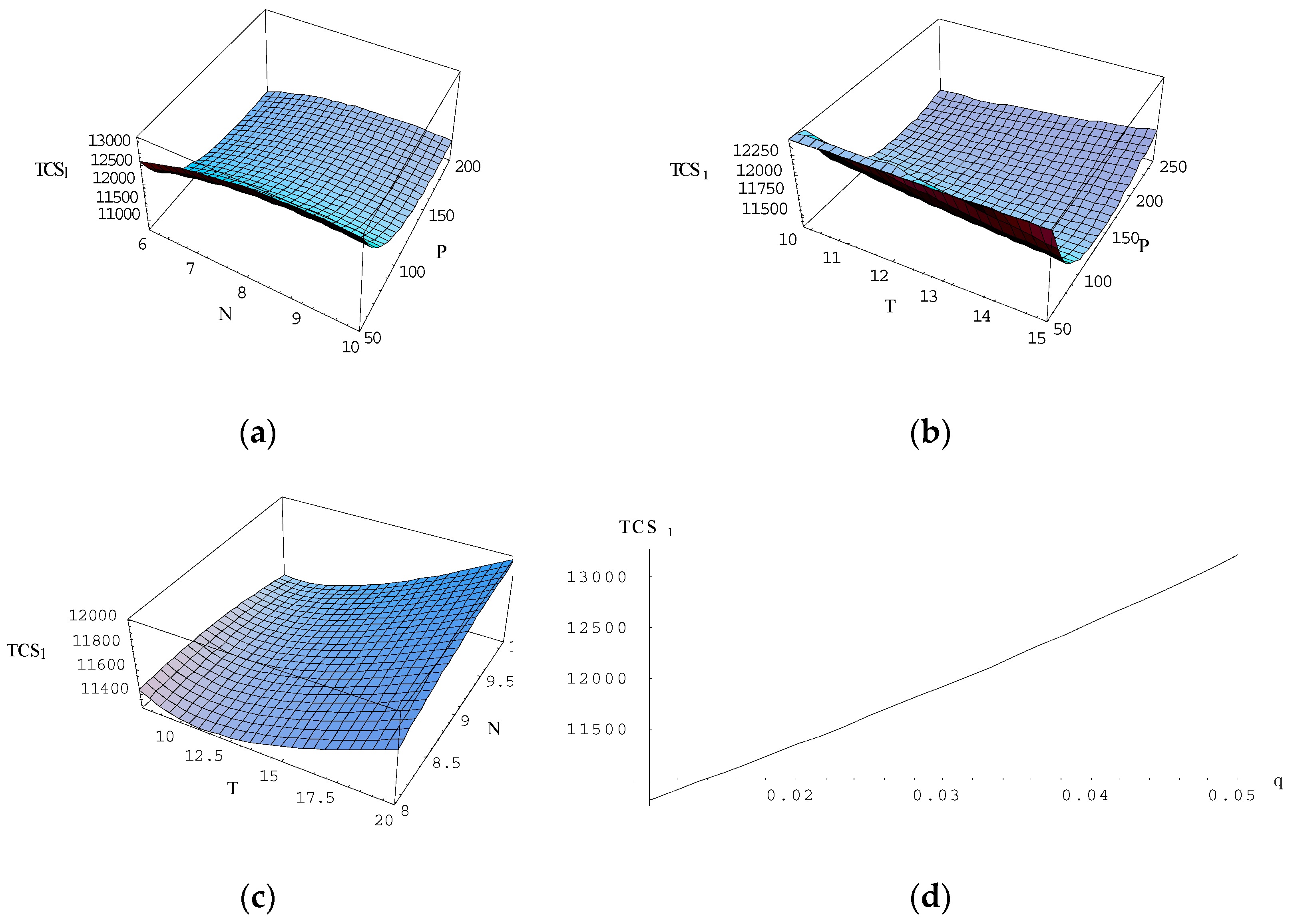
4.1.1. Nature of Total Cost Concerning Two Decision Variables and the Third One Is Fixed

Here, graphical representations of the convexity of the integrated cost function with respect to the pair of decision variables are shown in Figure 4a–c. The impact of the producer’s cycle length and production rate on total cost is illustrated in Figure 4a. Here, credit period N is fixed on its optimal value. The total cost function shows the convexity for two decision variables. Figure 4b shows the convexity of the objective function with respect to production rate P and credit period N when the producer’s cycle length T is fixed. Figure 4c provides the impact of variation in the producer’s cycle length T and credit period N on the complete system’s total cost. Here, production rate is fixed. It shows the convexity of the cost function.

4.1.2. Effect of the Various Parameters on the Decision Variables and the Total Integrated Cost

Table 2. Sensitivity analysis of key parameters of the model.

Parameter Changes		T (week)	N (week)	P	TCS2 ($)
n	2	8.1689	9.4597	199.611	10,867.2
	3	10.1445	8.994	182.435	11,356.2
	4	12.1536	8.7306	164.183	11,760.5
	5	14.483	8.5827	142.532	12,103.6
	6	18.637	8.6091	105.998	12,127.4
Demand rate	D = W − (W − f)(1 − z)N	10.1342	8.996	182.629	12,155.3
	D = W + α p−τ	18.7961	0.47419	84.6265	14,451.6
	D = W − (W − f)(1 − z)N ++ α p−τ	10.1445	8.995	182.436	11,356.2
C’1p	0.2	10.1445	8.995	182.436	11,356.2
	0.3	9.920	8.950	182.023	11,374.1
	0.4	9.7421	8.912	181.629	11,396.3
	0.5	9.5324	8.88	181.147	11,405.2
	0.6	9.2456	8.85	180.843	11,422.8
C’p	0.1	10.2312	9.120	182.36	11,356.0
	0.2	10.1445	8.995	182.436	11,356.1
	0.3	10.0123	8.812	182.148	11,356.2
	0.4	9.8245	8.723	181.962	11,356.3
	0.5	9.7310	8.621	181.823	11,356.4
C’2p	8	10.1421	8.992	182.421	11,356.0
	10	10.1445	8.995	182.436	11,356.2
	12	10.1462	8.999	182.446	11,356.4
	14	10.1483	9.002	182.459	11,356.6
	16	10.1494	9.014	182.463	11,356.8

shows the impact of the number of shipments on the decision variables and the total integrated cost. As the number of shipments increases, the producer’s cycle length and the integrated cost increases, and the production rate and credit period decrease. It also shows the effect of different demand rates on the decision variables and the integrated cost function. As the demand rate is credit period dependent, total cost and production rate increase, and there is a slight decrement in the producer’s cycle length. As the demand rate is selling price dependent, then the producer’s cycle length and integrated cost increases, and the production rate and credit period decrease. An increase in the value of all energy and carbon emission parameters increases the integrated total cost function.

Figure 4d shows the impact of deterioration rate θ on an integrated cost function; as the deterioration rate increases, the total cost increases accordingly.

4.2. Numerical Example 2

This numerical considers the TCP offered by the producer to the supplier is more than the cycle length of the supplier and the TCP provided by the supplier to his customers. The data values are:

Let C_p = $4.5/unit/week, C_1p = $2.1/unit/week, C_2p = $1000/set up, C’_1p = $0.9/unit/week, C’_p = $1.5/unit/week, C’_2p = $30/set up, θ = 0.03, r = 0.01, W = 100 units/week, f = 20 units/week, z = 0.2, τ = 0.03, α = 0.11, p = $6/unit, c = $10/unit, M = 30week, P_c = 220 units, μ = $90/week, k = $3200/week, s = $0.02/week, β = $0.03/week, C_s = $4.5/unit/week, C_1s = $2.1/unit/week, C_2s = $290/order, C’_1s= $0.9/unit/week, C’_s = $0.4/unit/week, C’_2s = $11/order, n = 2, r = 0.01, i_e = 0.15/year, i_p = 0.10/year.

The best possible value of TCS₂ is $146,438, P is 12,849.9 units, N is 13.0415 weeks, and T is 22.9585 weeks. T₁ and T₂ values can be found out from the Equation (7) and T₂ = T/n.

By using the above values of all parameters and optimal values of decision parameters, we can validate our numerical through Hessian matrix.

$${\xi }_3=2173.69>0,|\begin{array}{cc}{\xi }_3& {\xi }_4\\ {\xi }_4& {\xi }_2\end{array}|=|\begin{array}{cc}2173.69& 209\\ 209& -201.526\end{array}|=450280>0and\left|\begin{array}{ccc}{\xi }_3& {\xi }_4& {\xi }_5\\ {\xi }_4& {\xi }_2& {\xi }_6\\ {\xi }_5& {\xi }_6& {\xi }_1\end{array}\right|=\left|\begin{array}{ccc}2173.69& 209& -16.7189\\ 209& -201.526& 30.24\\ -16.7189& 30.24& -2238.89\end{array}\right|=1076410000>0$$

Therefore, at the critical point, the total integrated cost TCS₂ is minimum.

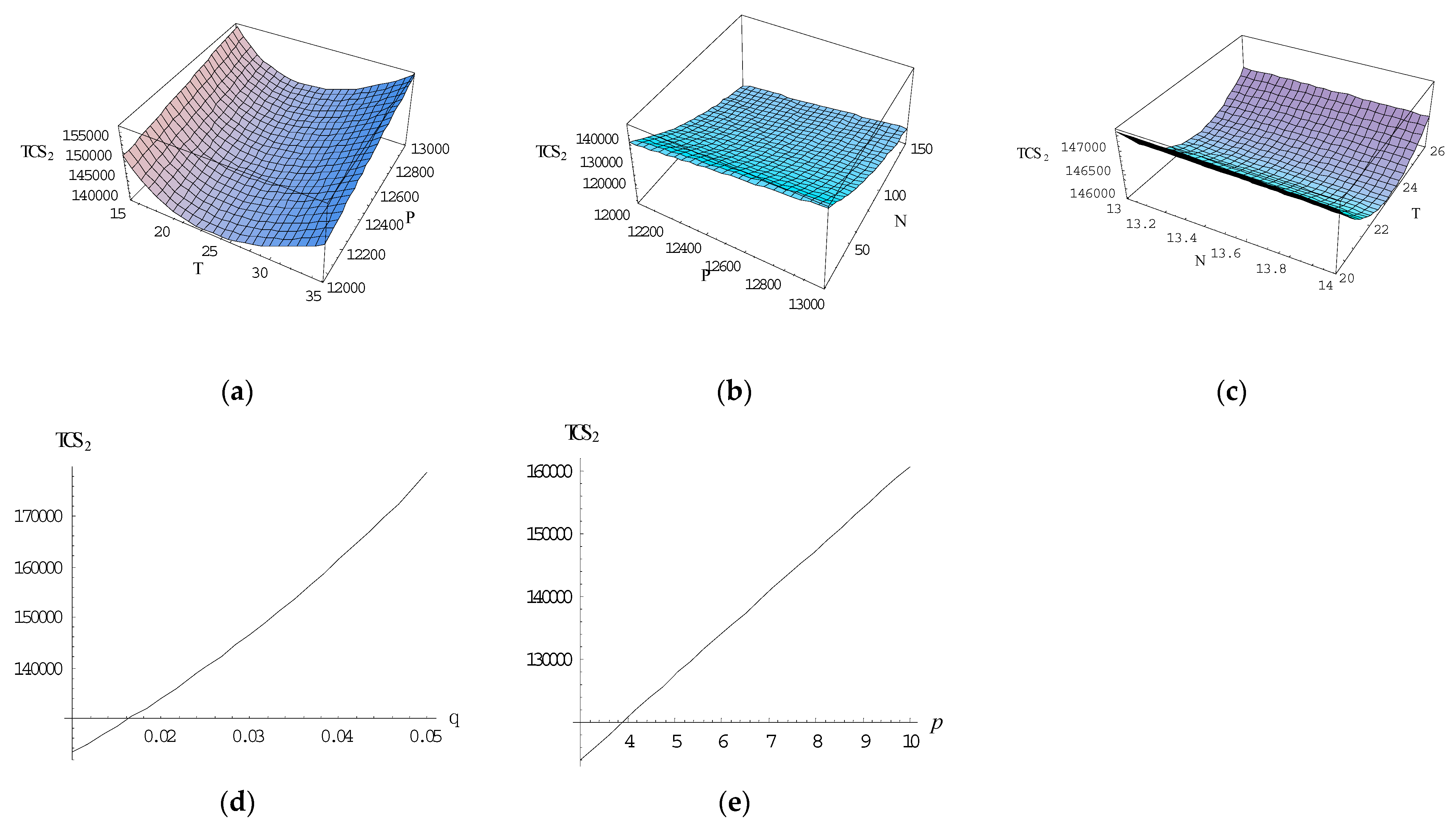
4.2.1. Nature of Total Cost with Respect to Two Decision Variables and the Third One Is Fixed

Here, graphical representations of the convexity of the integrated cost function with respect to the pair of decision variables are shown in Figure 5a–c. The impact of the producer’s cycle length and production rate on the total cost is illustrated in Figure 5a, here credit period N is fixed. It shows the convexity for two decision variables. Figure 5b shows the convexity of the objective function for production rate P and credit period N when the producer’s cycle length T is fixed. Figure 5c provides the impact of variation in the producer’s cycle length T and credit period N on the integrated cost. This shows the convexity with respect to the pair of decision variables.

4.2.2. Effect of the Various Parameters on the Decision Variables and the Total Integrated Cost

Table 3. Sensitivity analysis of key parameters of the model.

Parameter Changes		T (week)	N (week)	P	TCS2 ($)
n	2	22.9585	13.0415	12,849.9	146,438
	3	28.2951	12.504	11,061.8	153,318
	4	31.5985	12.2168	11,052.3	170,615
	5	33.9561	12.0324	11,497.2	190,263
	6	36.1785	11.8809	11,650.9	206,448
Demand rate	D = W − (W − f)(1 − z)N	22.8706	13.052	12,991.3	147,304
	D = W + α p−τ	6.1727	4.84	1238.7	168,514
	D = W − (W − f)(1 − z)N ++ α p−τ	22.9585	13.0415	12,849.9	146,438
C’1p	0.6	23.7101	13.641	12,906.1	146,369
	0.7	23.5245	13.610	12,884.3	126,401
	0.8	23.0124	13.370	12,860.1	146,438
	0.9	22.9559	13.041	12,849.9	146,461
	1.0	22.5157	12.880	12,812.3	146,492
C’p	1.3	23.3410	13.44	12,852.3	146,425
	1.4	23.0120	13.28	12,851.2	146,435
	1.5	22.9511	13.04	12,849.9	146,438
	1.6	22.8147	12.84	12,847.0	146,440
	1.7	22.6312	12.51	12,846.6	146,443
C’2p	26	22.95.3	12.315	12,818.4	146,420
	28	22.9574	12.712	12,824.1	146,426
	30	22.9585	13.041	12,849.9	146,438
	32	22.9591	13.512	12,855.6	146,445
	34	22.9600	14.143	12,901.2	146,450

shows the impact of the number of shipments, different demand rates, and cost parameters of energy and carbon emission on the decision variables and the integrated cost. As the number of shipments increases, the producer’s cycle length and the integrated cost increases, and the production rate and credit period decrease. As the demand rate is credit period dependent, total cost and production rate increase, and there is a slight decrement in the producer’s cycle length. As the demand rate is selling price-dependent, the producer’s cycle length and integrated cost increases, and the production rate and credit period decrease. An increase in the value of all energy and carbon emission parameters increases the integrated total cost function.

4.2.3. Effect of the Deterioration Rate and Selling Price on the Total Integrated Cost

Figure 5d shows that as the deterioration rate increases, the total cost increases accordingly. Figure 5e shows that as the selling price increases, demand decreases, holding cost increases, and the total cost increases.

5. Discussion and Managerial Insights

• The result presents the strategy and critical implication for producers in managing inventory systems under agile manufacturing to incorporate energy and carbon emissions costs. The producer should also focus on the deterioration and demand rates, as it is susceptible to the total cost. Since the deterioration rate increases, the total cost of the model increases. In numerical 1 and 2, it has been proved that if the demand rate changes, then the total cost is very much affected, which is shown in Table 2 and Table 3, respectively. Here the total cost is analyzed in three cases. One is demand depends on selling price and credit period. Second, demand depends on the credit period only, and the third one is that demand depends on the price of sale only. It is observed that the total cost is minimum in case one. Thus, it is suggested to the manager to balance the different studies regarding the demand parameter.
• The producer can adjust the production rate during production to meet the customer’s demand since it is a decision variable. The producer must be vigilant about the demands of the market. This model gives the fundamental insight for planning his credit period as per the production to fulfill all the requirements.
• The inventory model can benefit from creating decisions to progress the inventory system by incorporating energy and carbon emission costs. The decision-maker should take care of energy and carbon emission costs while modeling as different rules impose regularity authorities.
• To acquire more demand, TLTCP is used, due to which, both producer and supplier can earn more interest. Different cases of credit periods are shown through numerical examples. The results revealed that the TCP offered to the customer has a good effect on demand, reducing the total integrated cost. Offering TCP is the supply chain’s motivational tool, so the decision-maker should take care of this issue.

6. Conclusions

Energy and carbon emission is inevitable in every manufacturing system. Machining operations, chemical reactions, storage, and transportation are the main activities that emit carbon significantly. In the present paper, the author analyzes a production-inventory model under energy and carbon emission. The study formulated a two-level integrated model containing a producer and a supplier. The production process is assumed to be agile to depict a more realistic production model. Here production rate is considered to be a decision variable. This model has been developed based on the inventory management theory and examined how all optimal decision variables and the supply chain’s total cost are affected by critical parameters. Our computational results supply managerial insights to the production and marketing managers to help plan the supply chain’s successful coordination. The problem addressed in this model is applied to a wide array of production practices and motivated by real business concerns. Future research can be extended with a fuzzy environment for a multi-echelon integrated model with additive or flexible manufacturing to make zero waste for saving the environment.