Geomechanics in Depleted Faulted Reservoirs
Abstract
:1. Introduction
2. Geometry, Materials, and Methods
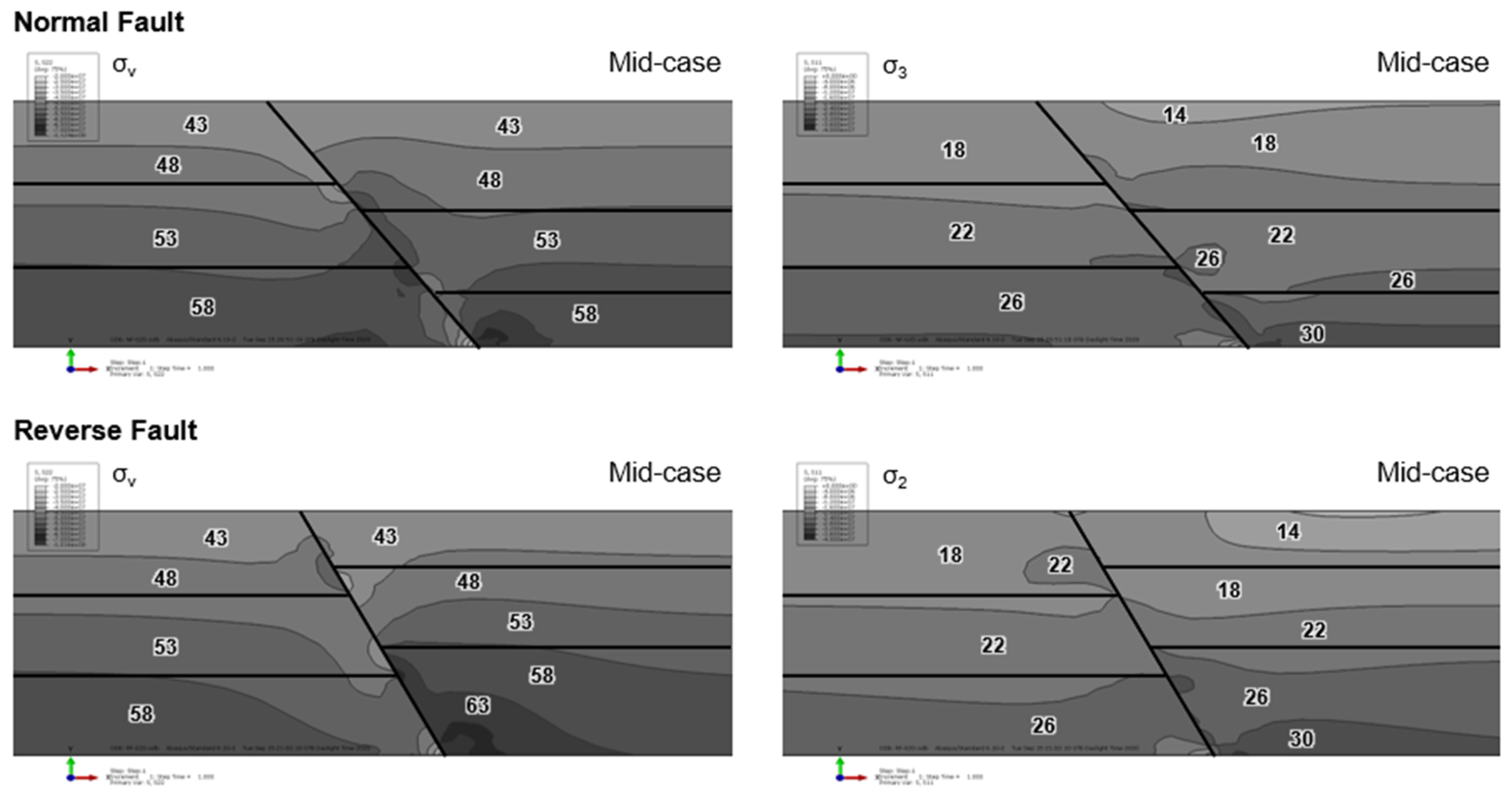
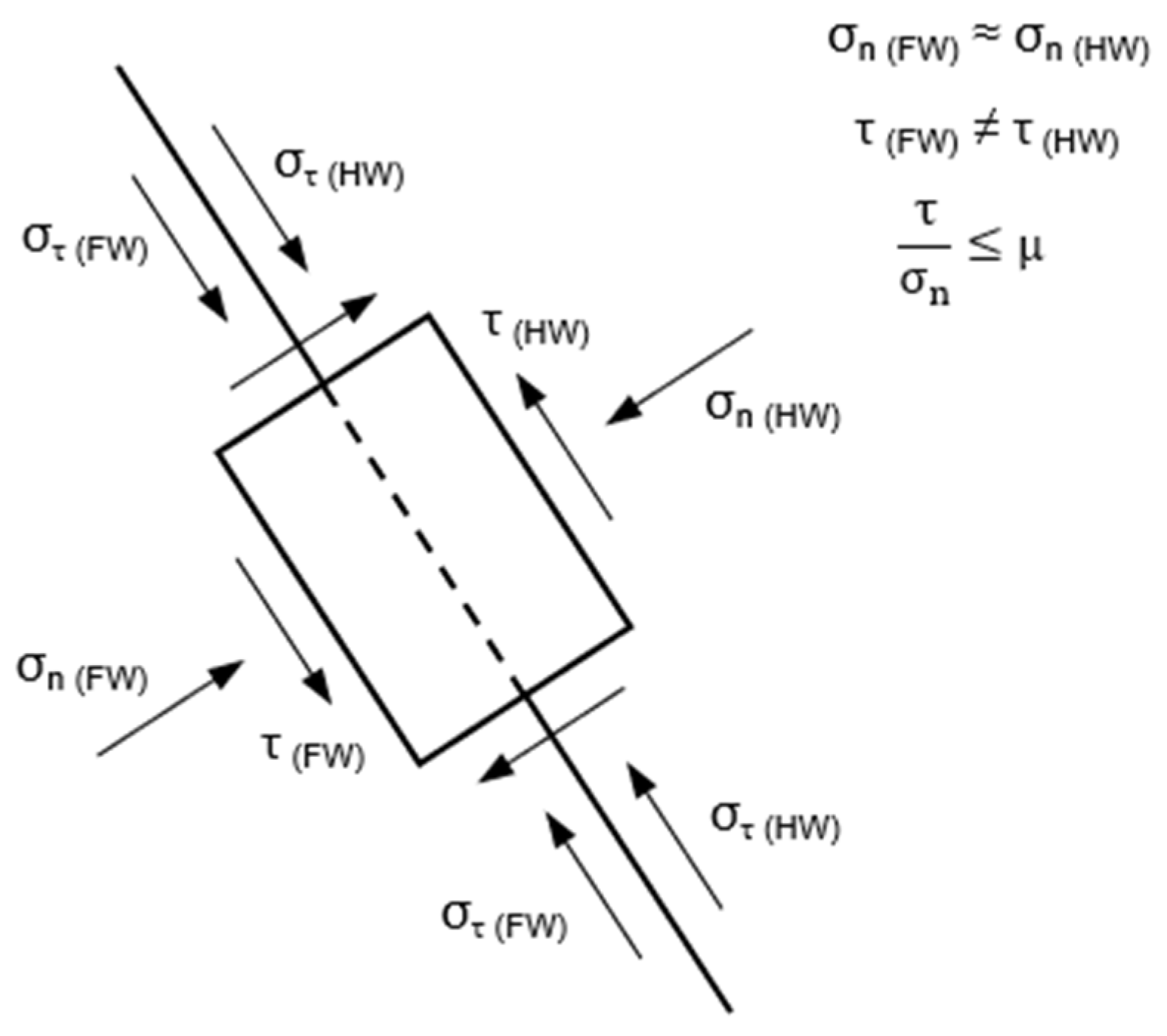
2.1. Faults
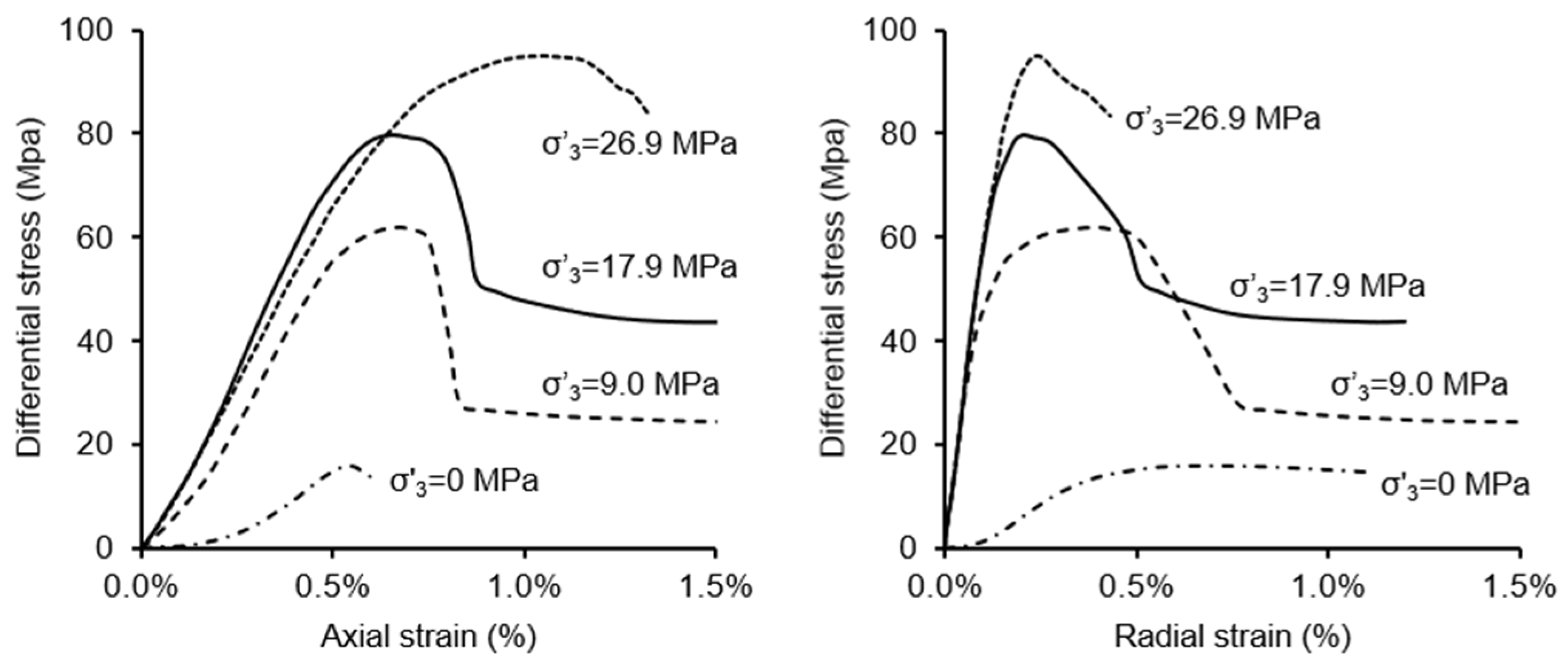
2.2. Elastoplasticity
3. Results
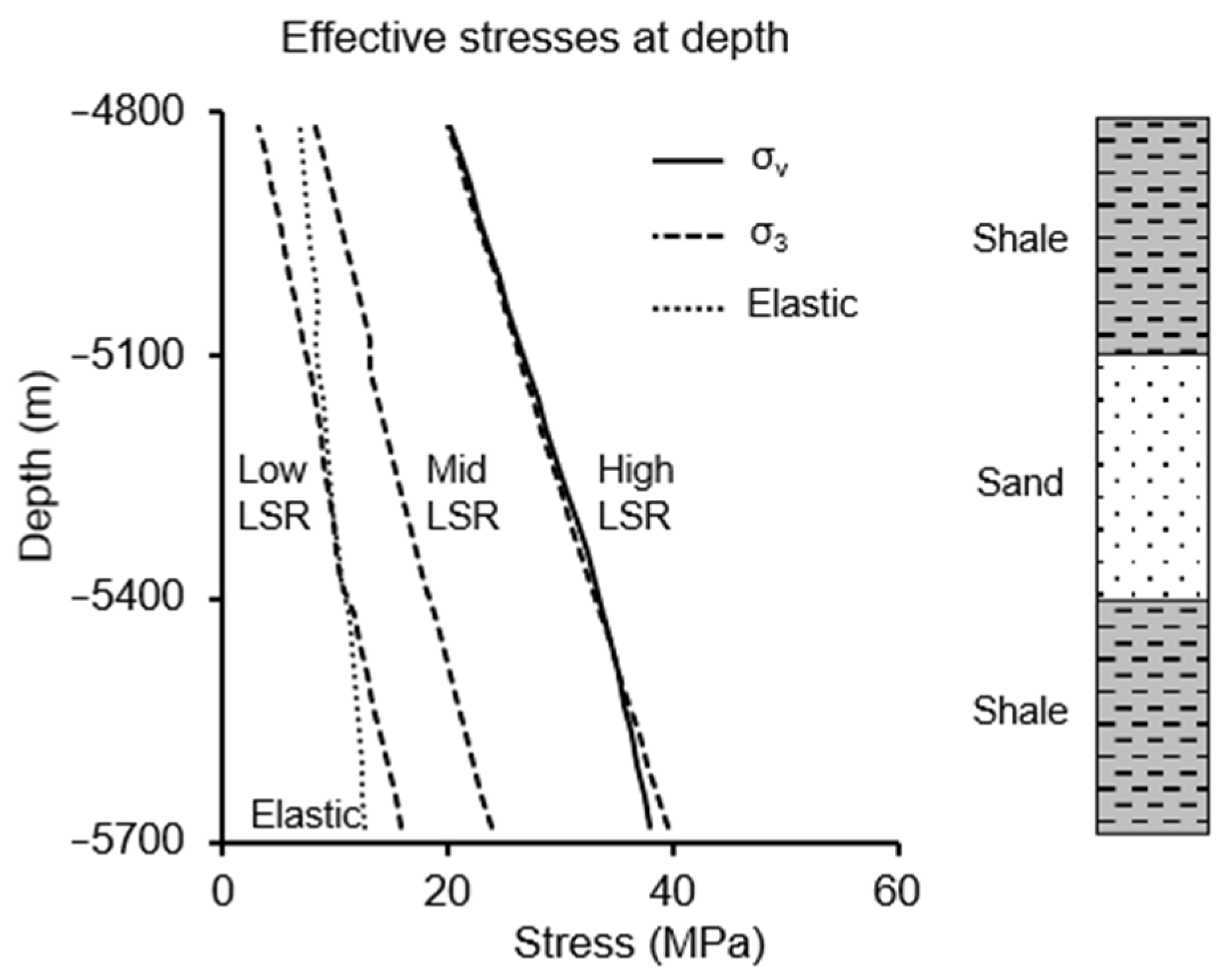
3.1. Effective Stresses
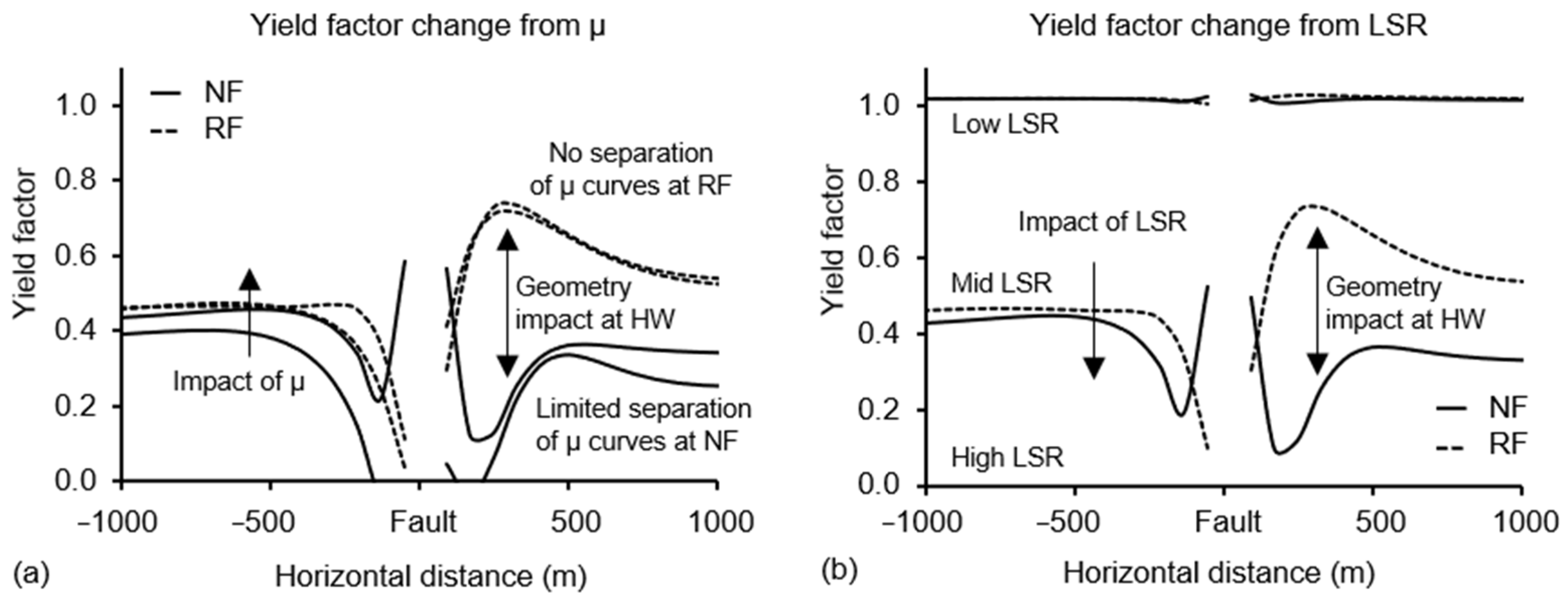
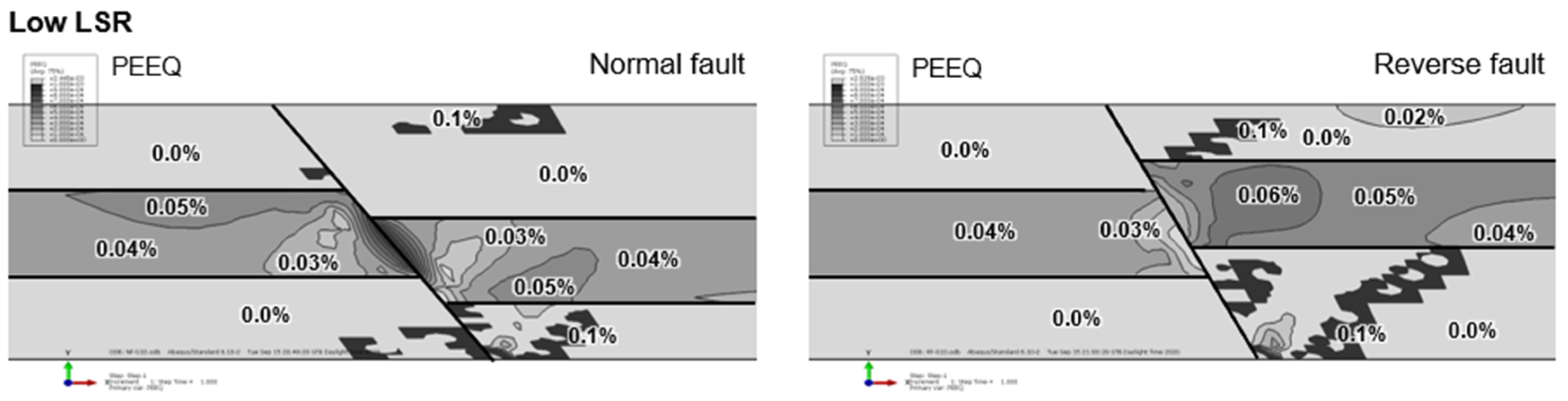
3.2. Yield Factor and Plastic Deformation
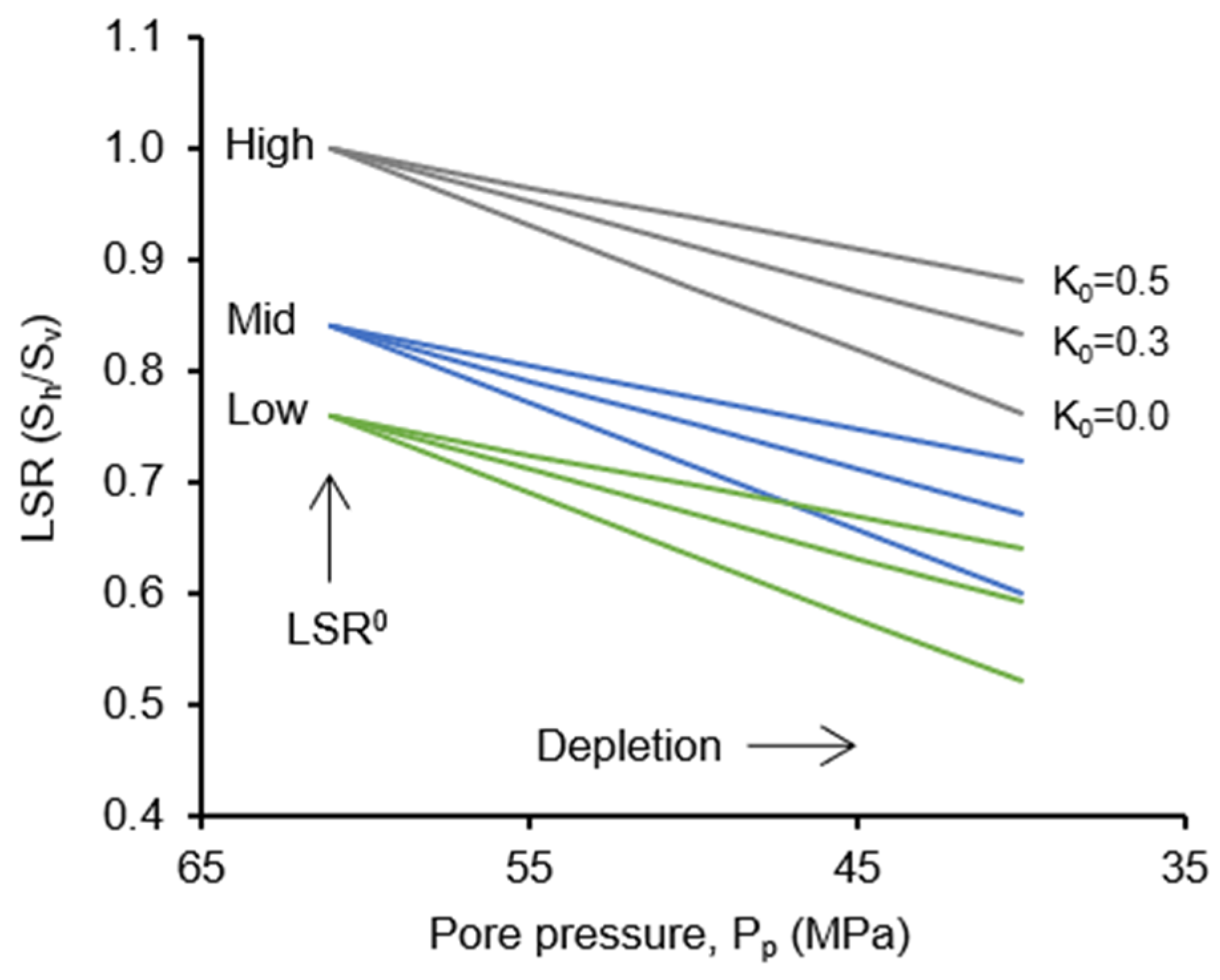
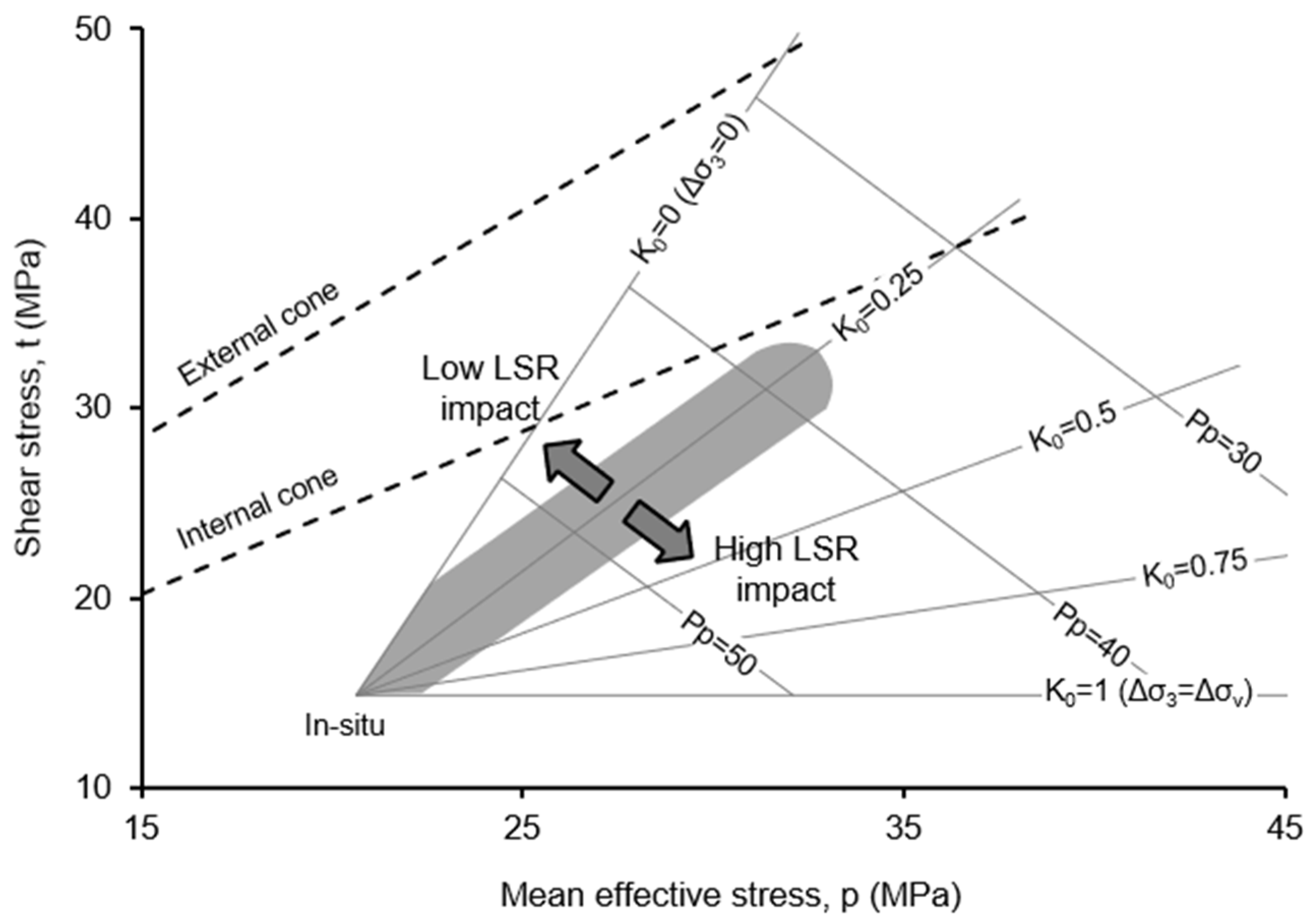
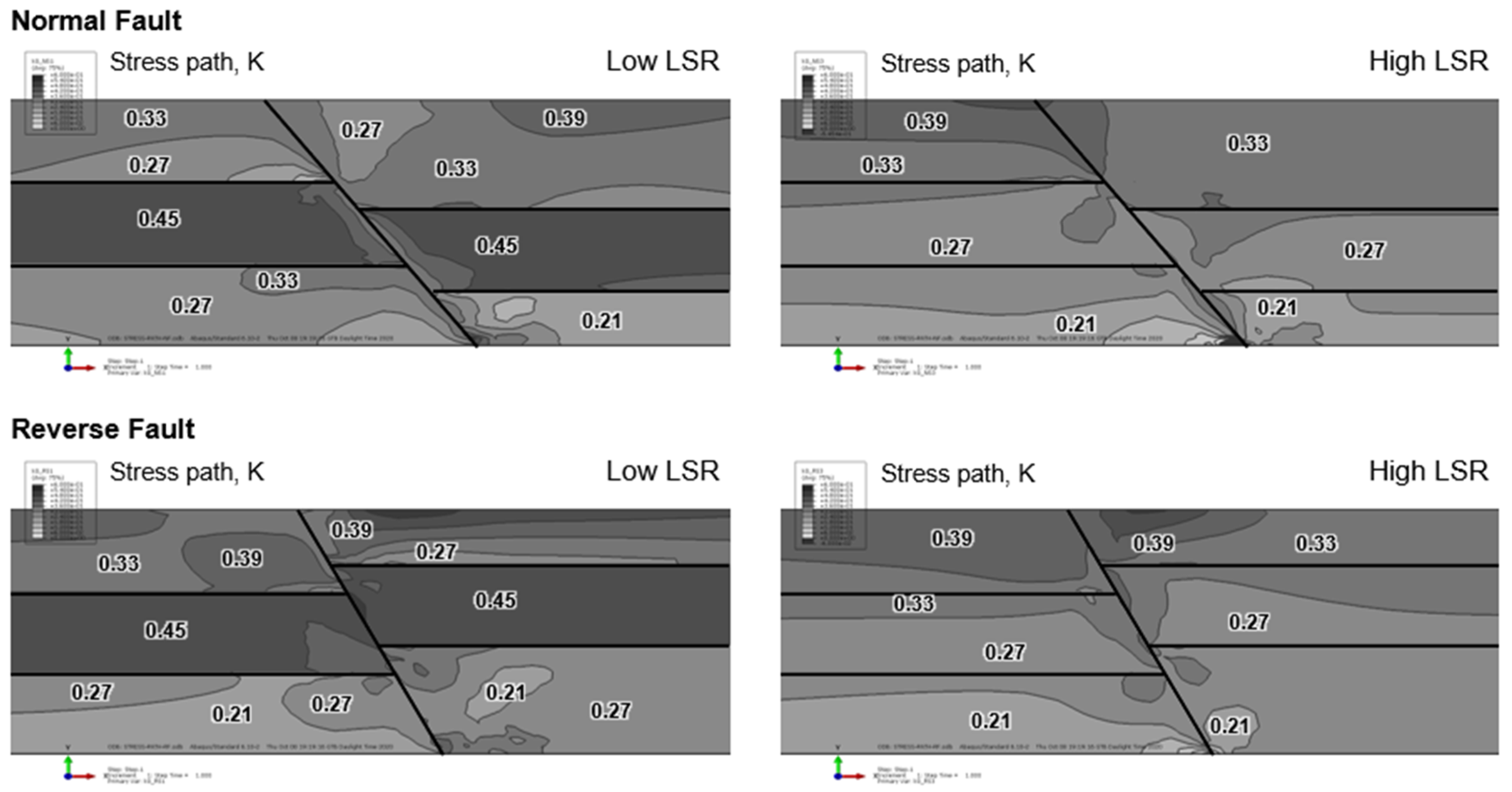
3.3. Stress Path
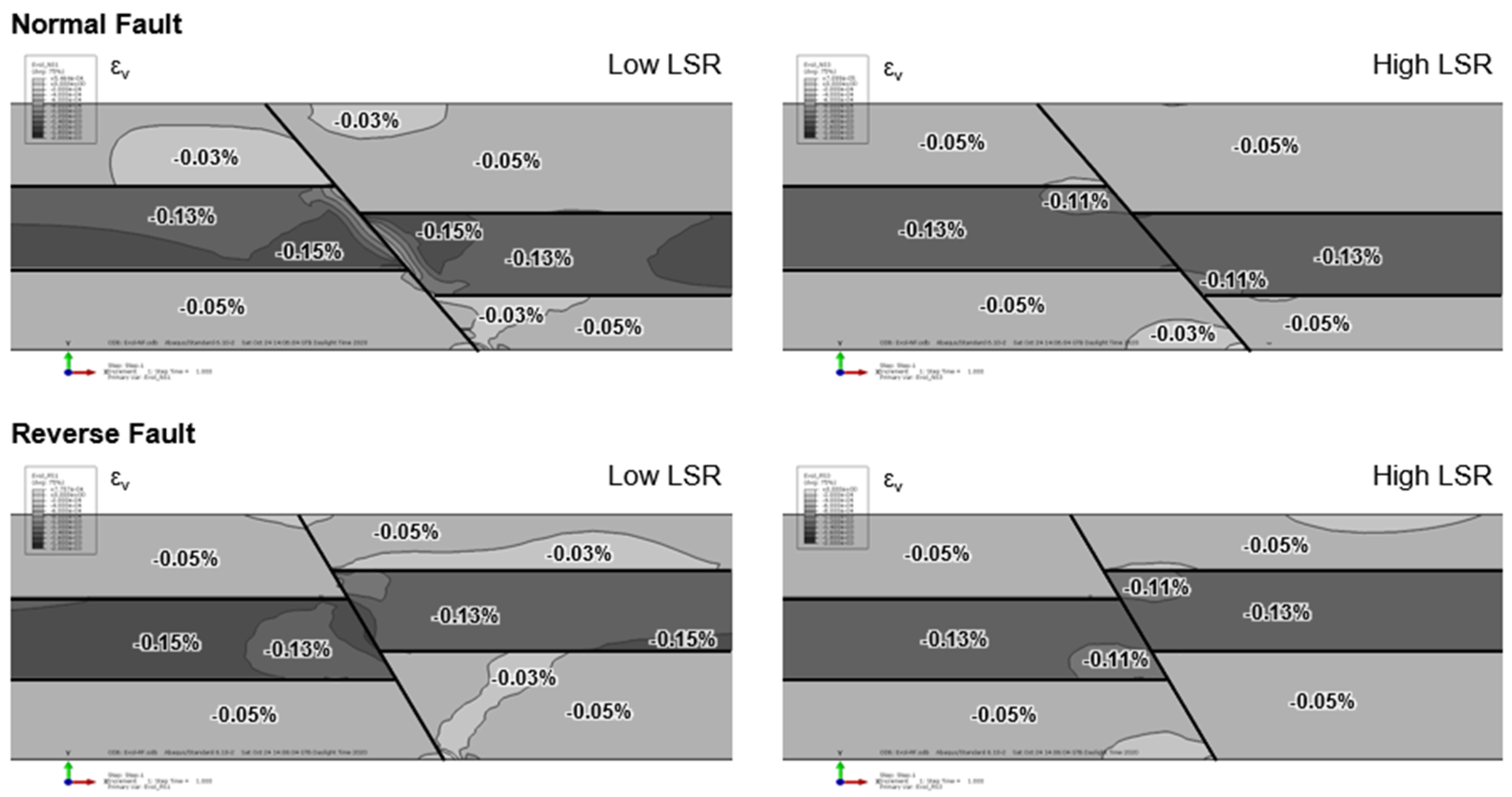
3.4. Volumetric Strain
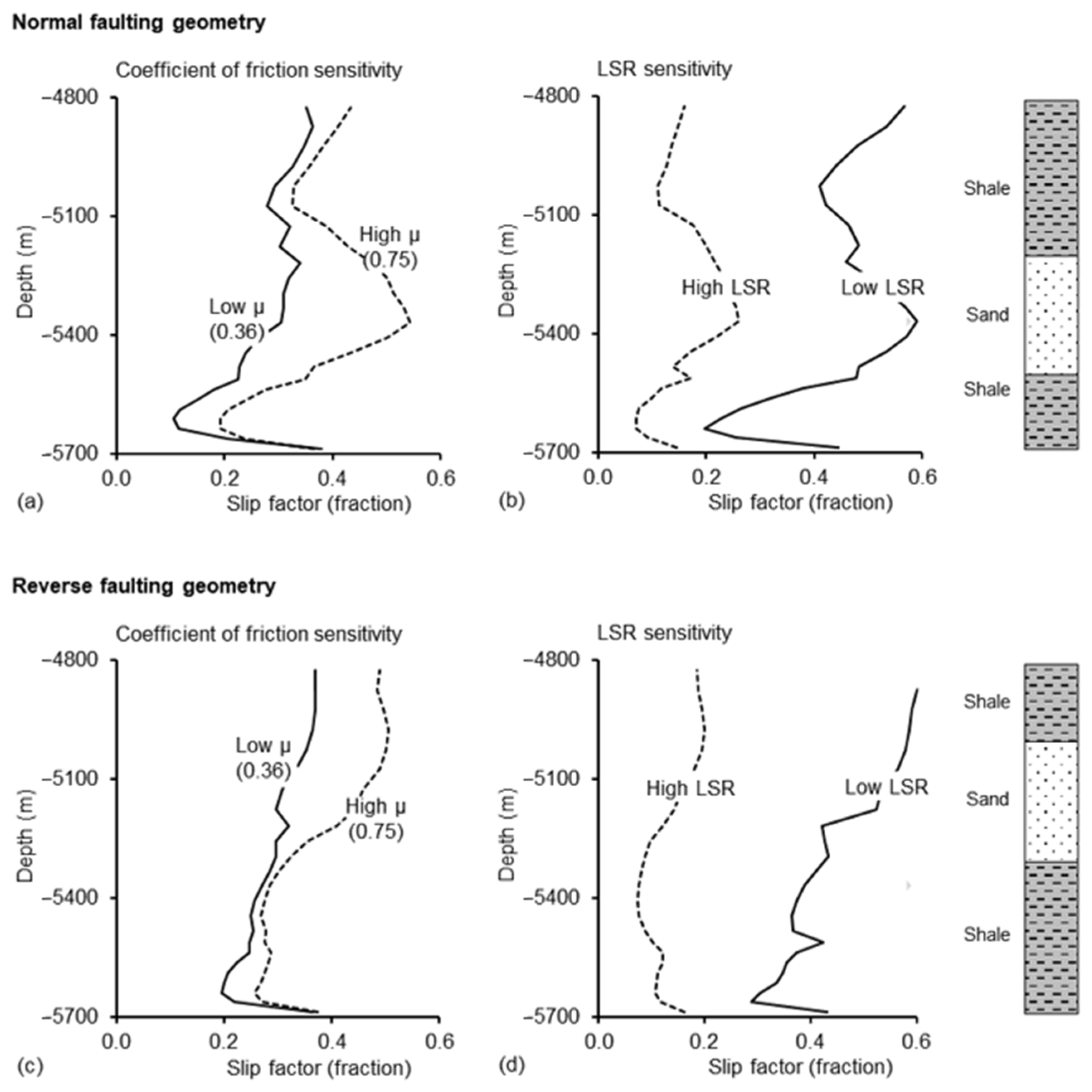
3.5. Slip Factor
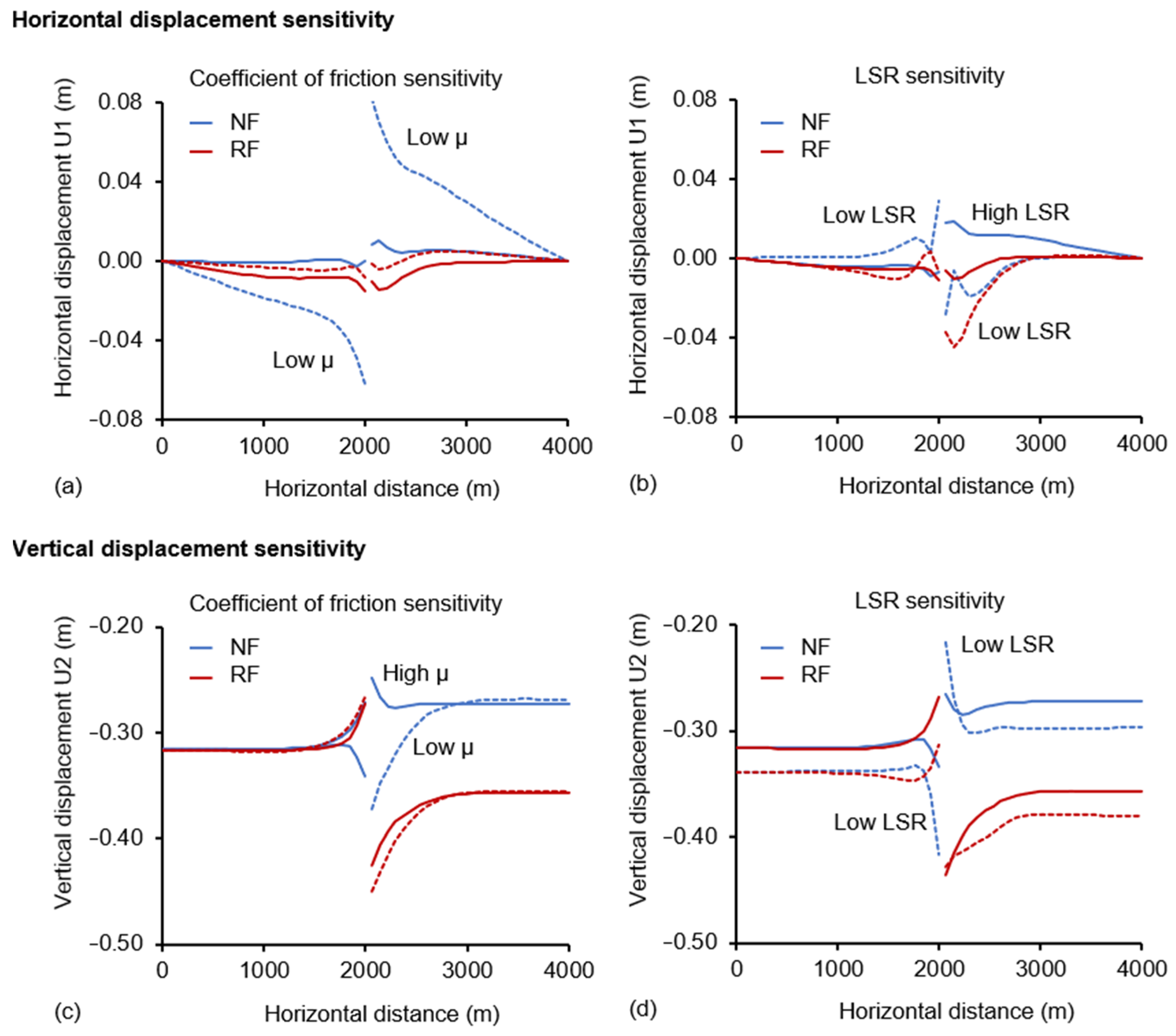
3.6. Displacement
4. Conclusions
- The developed effective stresses with the depletion of the field are influenced by the fault geometry of the compartmentalized blocks.
- Plastic deformation develops for low LSR and increases as the reservoir is depleted affecting mainly the region near the fault. Plastic regions are most pronounced in the shale formation, rather than in the sandstone. More volatile conditions in relation to change of the friction coefficient and LSR were found for the normal fault geometry.
- Lower values of the LSR increases the slip tendency at the fault surface.
- The reservoir deformation is dominated by vertical displacement. The horizontal displacements are relatively small and only in the case of the normal fault it exceeds 0.07 m in the HW. The higher vertical displacements develop in the near fault region. In the remote fault area, the vertical displacement is clearly governed by the reservoir depletion and it is nearly uniform.
- The volumetric strain predominantly indicates that compaction takes place. The higher volume decreases developed for low LSR.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Wayne, N.; Schechter, S.D.; Thompson, B.L. Naturally Fractured Reservoir Characterization; Society of Petroleum Engineers: Richardson, TX, USA, 2006. [Google Scholar]
- Schutjens, P.M.T.M.; Hanssen, T.H.; Hettema, M.H.H.; Merour, J.; de Bree, P.; Coremans, J.W.A.; Helliesen, G. Compaction-Induced Porosity/Permeability Reduction in Sandstone Reservoirs: Data and Model for Elasticity-Dominated Deformation. SPE Reserv. Eval. Eng. 2004, 7, 202–216. [Google Scholar] [CrossRef]
- Holt, R.M.; Gheibi, S.; Lavrov, A. Where Does the Stress Path Lead? Irreversibility and Hysteresis in Reservoir Geomechanics. In 50th US Rock Mechanics/Geomechanics Symposium; American Rock Mechanics Association: Houston, TX, USA, 2016; Volume 2, pp. 1020–1032. [Google Scholar]
- Hu, T.; Fournier, F.; Royer, J.J. Combining Geostatistics with Finite Element Modelling for Geomechanical Risk Assessment. In Proceedings of the VIII International Geostatistics Congress, Santiago, Chile, 1–5 December 2008; p. 10. [Google Scholar]
- Chan, A.W.; Zoback, M.D. Deformation Analysis in Reservoir Space (DARS): A Simple Formalism for Prediction of Reservoir Deformation with Depletion. In SPE/ISRM Rock Mechanics Conference; Society of Petroleum Engineers: Houston, TX, USA, 2002. [Google Scholar] [CrossRef]
- Chang, K.W.; Segall, P. Seismicity on Basement Faults Induced by Simultaneous Fluid Injection-Extraction. Pure Appl. Geophys. 2016, 173, 2621–2636. [Google Scholar] [CrossRef]
- Haug, C.; Nüchter, J.A.; Henk, A. Assessment of Geological Factors Potentially Affecting Production-Induced Seismicity in North German Gas Fields. Geomech. Energy Environ. 2018, 16, 15–31. [Google Scholar] [CrossRef]
- Zoback, M.D.; Zinke, J.C. Production-Induced Normal Faulting in the Valhall and Ekofisk Oil Fields. Pure Appl. Geophys. 2002, 159, 403–420. [Google Scholar] [CrossRef]
- Haddad, M.; Eichhubl, P. Poroelastic Models for Fault Reactivation in Response to Concurrent Injection and Production in Stacked Reservoirs. Geomech. Energy Environ. 2020, 24, 100181. [Google Scholar] [CrossRef]
- Lozovyi, S.; Yan, H.; Holt, R.M.; Bakk, A. Effect of Non-Linear Elasticity on Stress Paths in Depleted Reservoirs and Their Surroundings. In 54th US Rock Mechanics/Geomechanics Symposium; American Rock Mechanics Association: Golden, Colorado, 2020; pp. 1–8. [Google Scholar]
- Teatini, P.; Zoccarato, C.; Ferronato, M.; Franceschini, A.; Frigo, M.; Janna, C.; Isotton, G. About Geomechanical Safety for UGS Activities in Faulted Reservoirs. Proc. Int. Assoc. Hydrol. Sci. 2020, 382, 539–545. [Google Scholar] [CrossRef] [Green Version]
- ter Heege, J.H.; Pizzocolo, F.; Osinga, S.; Van der Veer, E. Geomechanical Production Optimization in Faulted and Fractured Reservoirs. In EAGE/SPE Workshop on Integrated Geomechanics in Exploration and Production; European Association of Geoscientists & Engineers: Abu Dhabi, UAE, 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Markou, N.; Papanastasiou, P. Petroleum Geomechanics Modelling in the Eastern Mediterranean Basin: Analysis and Application of Fault Stress Mechanics. Oil Gas Sci. Technol. Rev. d’IFP Energ. Nouv. 2018, 73, 57. [Google Scholar] [CrossRef]
- Markou, N.; Papanastasiou, P. Geomechanics of Compartmentalized Reservoirs with Finite Element Analysis: Field Case Study from the Eastern Mediterranean. In SPE Annual Technical Conference and Exhibition; Society of Petroleum Engineers: Houston, TX, USA, 2020; p. 23. [Google Scholar] [CrossRef]
- Hettema, M. Analysis of Mechanics of Fault Reactivation in Depleting Reservoirs. Int. J. Rock Mech. Min. Sci. 2020, 129, 104290. [Google Scholar] [CrossRef]
- Fjaer, E.; Holt, R.M.; Raaen, A.M.; Risnes, R.; Horsrud, P. Petroleum Related Rock Mechanics, 2nd ed.; Elsevier Science: Oxford, UK, 2008. [Google Scholar]
- Jaky, J. The Coefficient of Earth Pressure at Rest. J. Soc. Hung. Arch. Eng. 1944, 78, 355–388. [Google Scholar]
- Papanastasiou, P.; Sarris, E.; Kyriacou, A. Constraining the In-Situ Stresses in a Tectonically Active Offshore Basin in Eastern Mediterranean. J. Pet. Sci. Eng. 2017, 149, 208–217. [Google Scholar] [CrossRef]
- Hibbitt, K. Sorensen, Abaqus Theory Manual; Simulia: Johnston, RI, USA, 1992. [Google Scholar]
- Horsrud, P. Estimating Mechanical Properties of Shale from Empirical Correlations. SPE Drill. Complet. 2001, 16, 68–73. [Google Scholar] [CrossRef] [Green Version]
- Hettema, M.H.H.; Schutjens, P.M.T.M.; Verboom, B.J.M.; Gussinklo, H.J. Production-Induced Compaction of a Sandstone Reservoir: The Strong Influence of Stress Path. SPE Reserv. Eval. Eng. 2000, 3, 342–347. [Google Scholar] [CrossRef]
- Santarelli, F.J.; Tronvoll, J.T.; Svennekjaier, M.; Skeie, H.; Henriksen, R.; Bratli, R.K. Reservoir Stress Path: The Depletion and the Rebound. In SPE/ISRM Rock Mechanics in Petroleum Engineering; Society of Petroleum Engineers: Trondheim, Norway, 1998; p. 7. [Google Scholar] [CrossRef]
- Gheibi, S.; Holt, R.M.; Vilarrasa, V. Effect of Faults on Stress Path Evolution during Reservoir Pressurization. Int. J. Greenh. Gas Control 2017, 63, 412–430. [Google Scholar] [CrossRef] [Green Version]
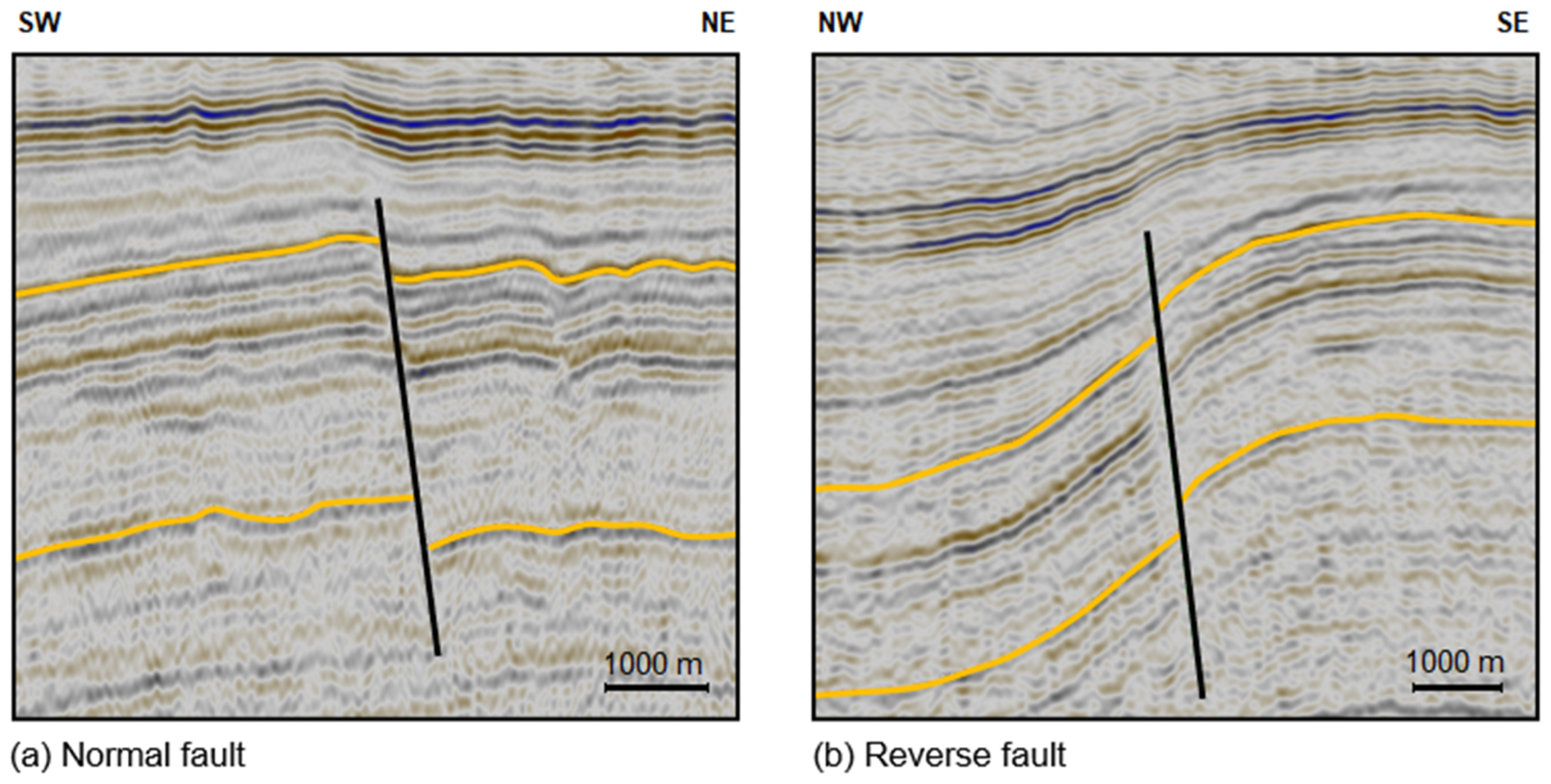
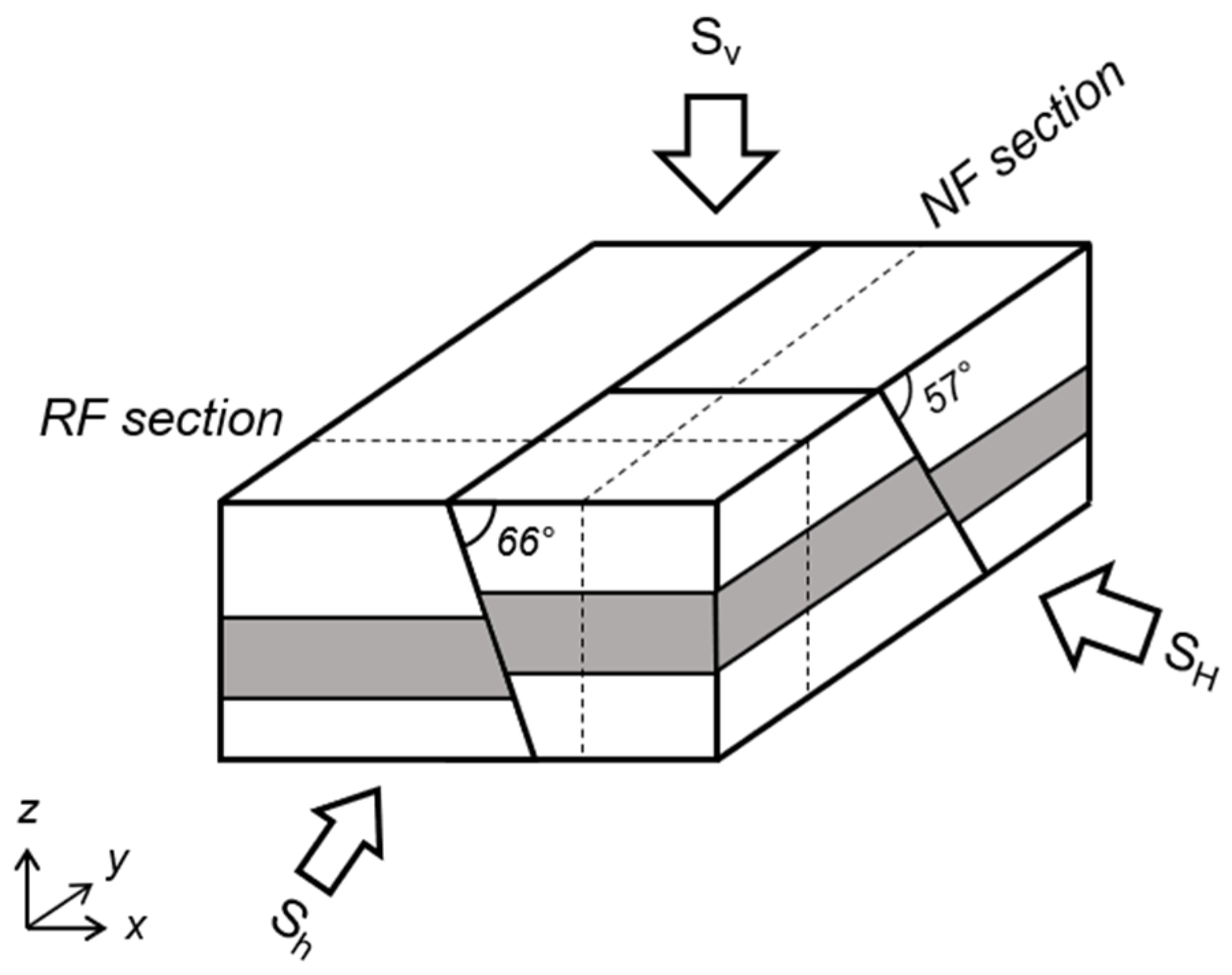
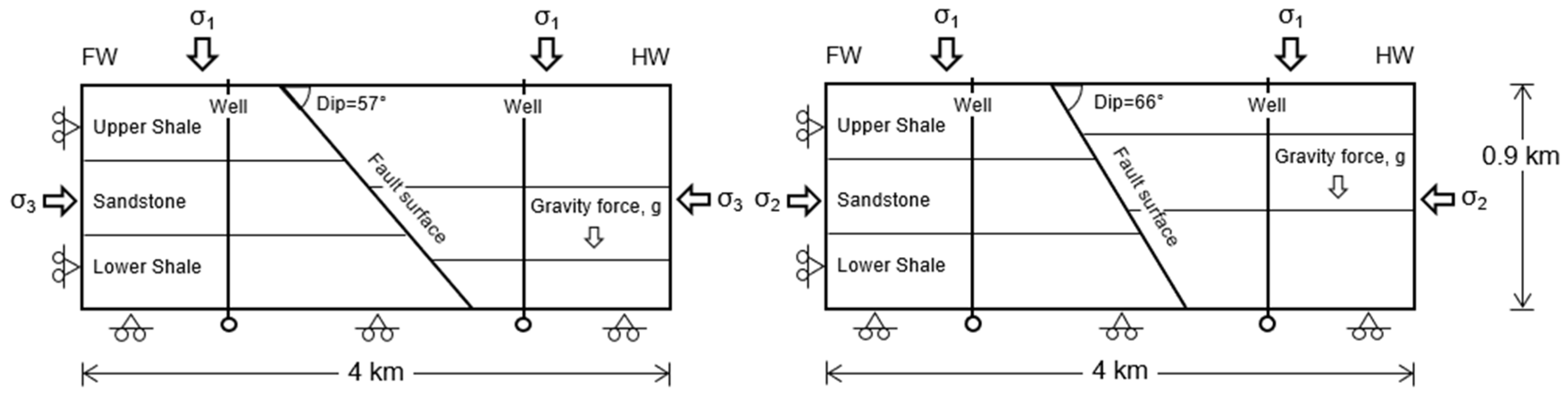
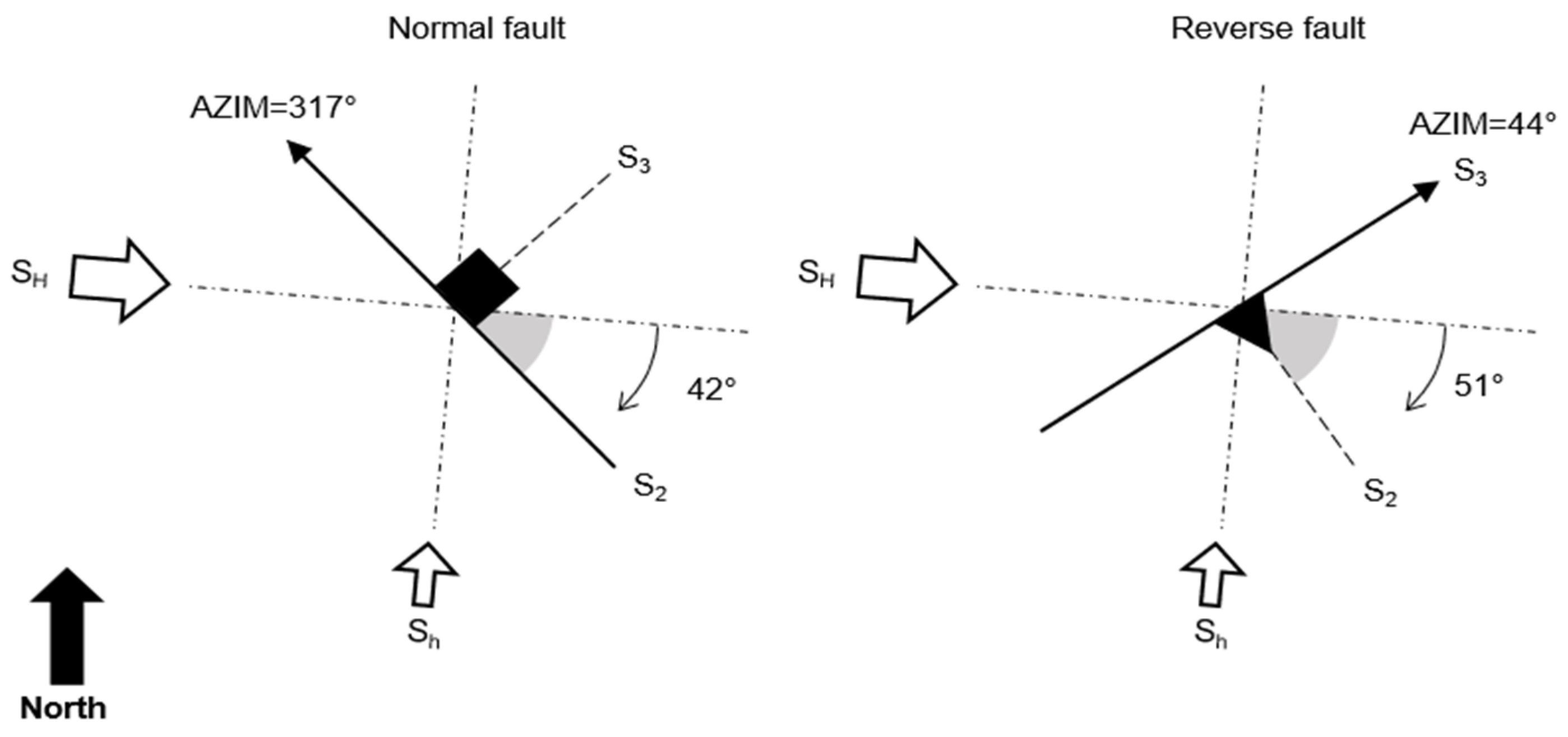

| Parameter | Normal Fault | Reverse Fault |
|---|---|---|
| Dip | 57° | 66° |
| Strike azimuth angle relative to North | 317° | 44° |
| Transformation angle relative to SH | 42° clockwise | 51° clockwise |
| LSR Scenarios | Low | Mid | High |
| S3 (MPa) | 67.3 | 74.4 | 88.6 |
| LSR | 0.76 | 0.84 | 1.0 |
| Friction Scenarios | Low | Mid | High |
| Coefficient of Friction, μ | 0.36 | 0.58 | 0.75 |
| Parameter | Sandstone | Shale |
|---|---|---|
| Porosity, φ (fraction) | 0.20 | 0.10 |
| Young modulus, E (GPa) | 14.5 | 41.8 |
| Poisson’s ratio, ν | 0.24 | 0.25 |
| Drucker–Prager angle, β (degrees) | 40.6° | 31.6° |
| Peak strength, d (MPa) | 17.8 | 17.7 |
| Dilation angle, ψ (degrees) | 18.2° | 0.0° |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Markou, N.; Papanastasiou, P. Geomechanics in Depleted Faulted Reservoirs. Energies 2021, 14, 60. https://doi.org/10.3390/en14010060
Markou N, Papanastasiou P. Geomechanics in Depleted Faulted Reservoirs. Energies. 2021; 14(1):60. https://doi.org/10.3390/en14010060
Chicago/Turabian StyleMarkou, Nikolaos, and Panos Papanastasiou. 2021. "Geomechanics in Depleted Faulted Reservoirs" Energies 14, no. 1: 60. https://doi.org/10.3390/en14010060
APA StyleMarkou, N., & Papanastasiou, P. (2021). Geomechanics in Depleted Faulted Reservoirs. Energies, 14(1), 60. https://doi.org/10.3390/en14010060






