WAMS-Supported Power Mismatch Optimization for Secure Intentional Islanding
Abstract
:1. Introduction
2. Problem Description
2.1. Network
2.2. UFLS Protection
2.3. Phasor Measurement Units and Wide-Area Monitoring System
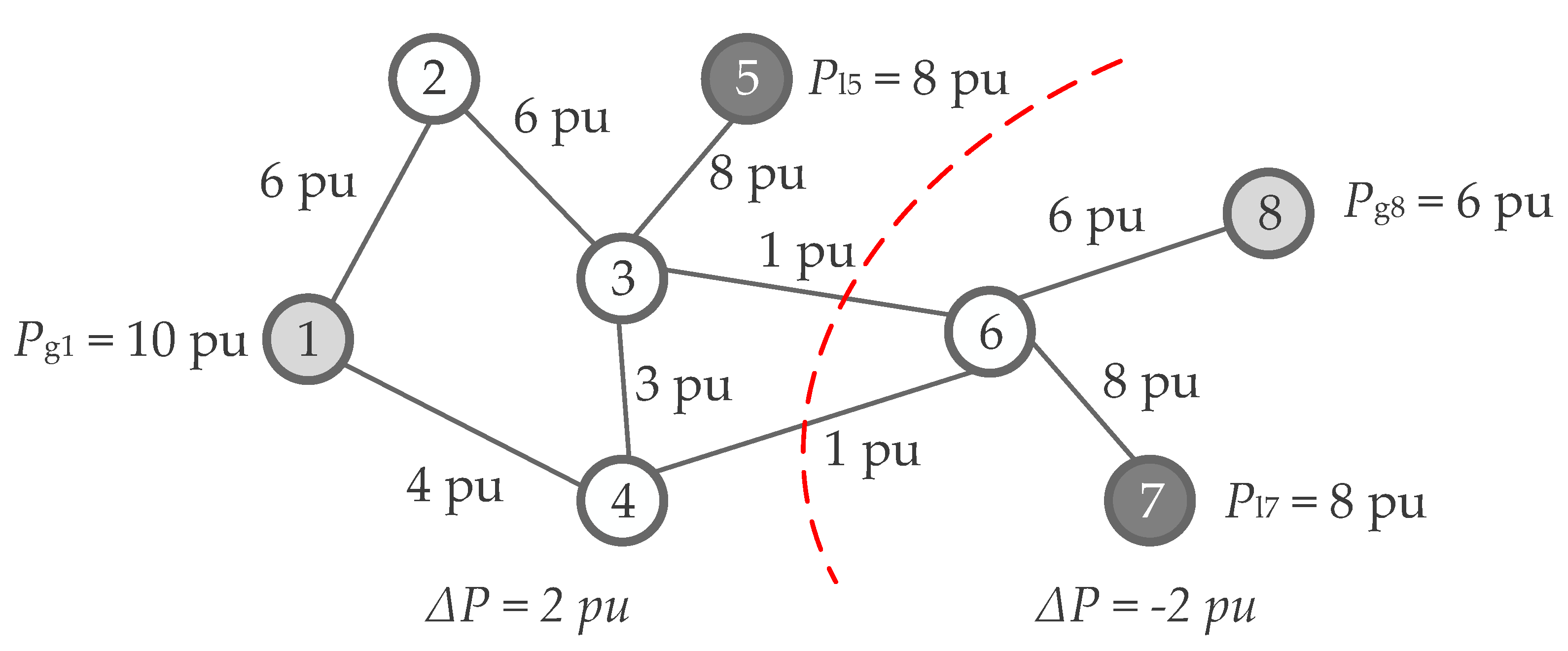
3. Methodology
Intentional Controlled Islanding
4. Case Study
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| EPS | Electric power system |
| ICI | Intentional controlled islanding |
| MILP | Mixed-integer linear programming |
| RoCoF | Rate of change of frequency |
| SIPS | System integrity protection schemes |
| UFLS | Under-frequency load shedding |
| UVLS | Under-voltage load shedding |
| WAMS | Wide-area monitoring system |
| G | Undirected graph |
| V | Graph vertices |
| E | Graph edges |
| ei,j | Edge from node i to node j |
| wi,j | Weight edge from node i to node j |
| Binary variable showing edge status between node i and node j | |
| Pi,j | Active power flow from node i to node j |
| Xi,j | Reactance between nodes i and j |
| δi | Voltage angle of ith node |
| Load active power at node i after UFLS activation | |
| Load active power at node i in steady state | |
| Generator active power at node i after UFLS activation | |
| Exponential coefficient for voltage dependence of active power | |
| Exponential coefficient for voltage dependence of reactive power | |
| Frequency dependency coefficient for active power | |
| Frequency dependency coefficient for reactive power | |
| {•}0 | Subscript for variables in steady state |
| {•}(t) | Time-dependent variables |
| Minimum value for a load in pu in island transition | |
| Maximum value for a load in pu in island transition |
References
- Taylor, P.K.C.; Pourbeik, P. IEEE Task Force on Blackout Experience, Mitigation, and Role of New Technologies; IEEE Power and Energy Society: Piscataway, NJ, USA, 2007; Volume 238. [Google Scholar]
- ENTSO-E. Continental Europe Synchronous Area Separation on 8 January 2021, Interim Report 2021. Available online: https://eepublicdownloads.azureedge.net/clean-documents/Publications/Position%20papers%20and%20reports/entso-e_CESysSep_interim_report_210225.pdf (accessed on 12 January 2021).
- AEMO. Black System South Australia, 28 September 2016: Final Report; Australian Energy Market Operator: Sydney, Australia, 2017. [Google Scholar]
- Final Report of the Investigation Committee on the 28 September 2003 Blackout in Italy 2004. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/pre2015/publications/ce/otherreports/20040427_UCTE_IC_Final_report.pdf (accessed on 12 January 2021).
- Naglic, M.; Popov, M.; van der Meijden, M.A.M.M.; Terzija, V. Synchronized Measurement Technology Supported Online Generator Slow Coherency Identification and Adaptive Tracking. IEEE Trans. Smart Grid 2020, 11, 3405–3417. [Google Scholar] [CrossRef] [Green Version]
- Dabbaghjamanesh, M.; Wang, B.; Kavousi-Fard, A.; Mehraeen, S.; Hatziargyriou, N.D.; Trakas, D.N.; Ferdowsi, F. A Novel Two-Stage Multi-Layer Constrained Spectral Clustering Strategy for Intentional Islanding of Power Grids. IEEE Trans. Power Deliv. 2020, 35, 560–570. [Google Scholar] [CrossRef]
- Babaei, M.; Muyeen, S.M.; Islam, S. Transiently Stable Intentional Controlled Islanding Considering Post-Islanding Voltage and Frequency Stability Constraints. Int. J. Electr. Power Energy Syst. 2021, 127, 106650. [Google Scholar] [CrossRef]
- Quiros-Tortos, J.; Demetriou, P.; Panteli, M.; Kyriakides, E.; Terzija, V. Intentional Controlled Islanding and Risk Assessment: A Unified Framework. IEEE Syst. J. 2018, 12, 3637–3648. [Google Scholar] [CrossRef] [Green Version]
- Tyuryukanov, I.; Popov, M.; van der Meijden, M.A.M.M.; Terzija, V. Slow Coherency Identification and Power System Dynamic Model Reduction by Using Orthogonal Structure of Electromechanical Eigenvectors. IEEE Trans. Power Syst. 2021, 36, 1482–1492. [Google Scholar] [CrossRef]
- Teymouri, F.; Amraee, T. An MILP Formulation for Controlled Islanding Coordinated with under Frequeny Load Shedding Plan. Electr. Power Syst. Res. 2019, 171, 116–126. [Google Scholar] [CrossRef]
- New, W.C. Load Shedding, Load Restoration, and Generator Protection Using Solid-State and Electromechanical Underfrequency Relays; General Electric Company, Power Systems Management: Atlanta, GA, USA, 1974. [Google Scholar]
- Awadalla, M.; Papadopoulos, P.N.; Milanovic, J.V. An Approach to Controlled Islanding Based on PMU Measurements. In 2017 IEEE Manchester PowerTech; IEEE: Manchester, UK, 2017; pp. 1–6. [Google Scholar]
- Demetriou, P.; Quiros-Tortos, J.; Kyriakides, E. When to Island for Blackout Prevention. IEEE Syst. J. 2019, 13, 3326–3336. [Google Scholar] [CrossRef]
- You, H.; Vittal, V.; Wang, X. Slow Coherency-Based Islanding. IEEE Trans. Power Syst. 2004, 19, 483–491. [Google Scholar] [CrossRef]
- Xu, G.; Vittal, V. Slow Coherency Based Cutset Determination Algorithm for Large Power Systems. IEEE Trans. Power Syst. 2010, 25, 877–884. [Google Scholar] [CrossRef]
- Xu, G.; Vittal, V.; Meklin, A.; Thalman, J.E. Controlled Islanding Demonstrations on the WECC System. IEEE Trans. Power Syst. 2011, 26, 334–343. [Google Scholar] [CrossRef]
- Esmaeilian, A.; Kezunovic, M. Prevention of Power Grid Blackouts Using Intentional Islanding Scheme. IEEE Trans. Ind. Appl. 2017, 53, 622–629. [Google Scholar] [CrossRef]
- Rezaee, M.; Moghadam, M.S.; Ranjbar, S. Online Estimation of Power System Separation as Controlled Islanding Scheme in the Presence of Inter-Area Oscillations. Sustain. Energy Grids Netw. 2020, 21, 100306. [Google Scholar] [CrossRef]
- Singh, M.; Meera, K.S.; Joshi, P.; Prakash, P. Islanding Scheme for Power Transmission Utilities. In Proceedings of the 2017 6th International Conference on Computer Applications in Electrical Engineering-Recent Advances (CERA), Roorkee, India, 5–7 October 2017; pp. 69–73. [Google Scholar]
- Lu, W.; Bésanger, Y.; Zamaï, E.; Radu, D. Blackouts: Description, Analysis and Classification. In Proceedings of the WSEAS International Conference on Electric Power Systems, Lisbon, Portugal, 22–24 September 2006; pp. 429–434. [Google Scholar]
- Teymouri, F.; Amraee, T.; Saberi, H.; Capitanescu, F. Toward Controlled Islanding for Enhancing Power Grid Resilience Considering Frequency Stability Constraints. IEEE Trans. Smart Grid 2019, 10, 1735–1746. [Google Scholar] [CrossRef]
- Shao, H.; Norris, S.; Lin, Z.; Bialek, J. Determination of When to Island by Analysing Dynamic Characteristics in Cascading Outages. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013; pp. 1–6. [Google Scholar]
- Adibi, M.M.; Kafka, R.J. Power System Restoration Issues. IEEE Comput. Appl. Power 1991, 4, 19–24. [Google Scholar] [CrossRef]
- Adibi, M.M.; Kafka, L.R.J.; Milanicz, D.P. Expert System Requirements for Power System Restoration. IEEE Trans. Power Syst. 1994, 9, 1592–1600. [Google Scholar] [CrossRef]
- Bahrami, M.; Vakilian, M.; Farzin, H.; Lehtonen, M. Multi-Step Island Formation and Repair Dispatch Reinforced by Mutual Assistance after Natural Disasters. Int. J. Electr. Power Energy Syst. 2021, 126, 106572. [Google Scholar] [CrossRef]
- Feng, Z.; Niu, W.; Wang, S.; Cheng, C.; Song, Z. Mixed Integer Linear Programming Model for Peak Operation of Gas-Fired Generating Units with Disjoint-Prohibited Operating Zones. Energies 2019, 12, 2179. [Google Scholar] [CrossRef] [Green Version]
- Alavi, S.A.; Ilea, V.; Saffarian, A.; Bovo, C.; Berizzi, A.; Seifossadat, S.G. Feasible Islanding Operation of Electric Networks with Large Penetration of Renewable Energy Sources Considering Security Constraints. Energies 2019, 12, 537. [Google Scholar] [CrossRef] [Green Version]
- Porzio, G.F.; Nastasi, G.; Colla, V.; Vannucci, M.; Branca, T.A. Comparison of Multi-Objective Optimization Techniques Applied to off-Gas Management within an Integrated Steelwork. Appl. Energy 2014, 136, 1085–1097. [Google Scholar] [CrossRef]
- SPD—Inertia TF Inertia and Rate of Change of Frequency (ROCOF) 2020. Available online: https://eepublicdownloads.azureedge.net/clean-documents/SOC%20documents/Inertia%20and%20RoCoF_v17_clean.pdf (accessed on 12 January 2021).
- Demetriou, P.; Asprou, M.; Quiros-Tortos, J.; Kyriakides, E. Dynamic IEEE Test Systems for Transient Analysis. IEEE Syst. J. 2017, 11, 2108–2117. [Google Scholar] [CrossRef]
- SAFA for RGCE, E.-E. Annex 5: Policy on Emergency and Restoration 2019. Available online: https://eepublicdownloads.entsoe.eu/clean-documents/Publications/SOC/safa/5_-_Policy__on_Emergency_and_Restoration.pdf (accessed on 12 January 2021).
- Commision Regulation (EU). 2017/2196—Establishing a Network Code on Electricity Emergency and Restoration; Official Journal of the European Union, EU: Luxembourg, 2017. [Google Scholar]
- Rudez, U.; Mihalic, R. WAMS-Based Underfrequency Load Shedding with Short-Term Frequency Prediction. IEEE Trans. Power Deliv. 2016, 31, 1912–1920. [Google Scholar] [CrossRef]
- Machowski, J.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley & Sons, Ltd.: Abingdon, UK, 2008. [Google Scholar]
- Castello, P.; Lixia, M.; Muscas, C.; Pegoraro, P.A. Impact of the Model on the Accuracy of Synchrophasor Measurement. IEEE Trans. Instrum. Meas. 2012, 61, 2179–2188. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Synchrophasor Measurements for Power Systems; IEEE Std C371181-2011 Revis. IEEE Std C37118-2005; IEEE: Piscataway, NJ, USA, 2011; pp. 1–61. [Google Scholar] [CrossRef]
- IEEE. IEEE Standard for Synchrophasor Data Transfer for Power Systems; IEEE Std C371182-2011 Revis. IEEE Std C37118-2005; IEEE: Piscataway, NJ, USA, 2011; pp. 1–53. [Google Scholar] [CrossRef]
- Esmaili, M.; Ghamsari-Yazdel, M.; Amjady, N.; Chung, C.Y. Convex Model for Controlled Islanding in Transmission Expansion Planning to Improve Frequency Stability. IEEE Trans. Power Syst. 2021, 36, 58–67. [Google Scholar] [CrossRef]




| Stage | I. | II. | III. | IV. | V. | VI. | ICI |
|---|---|---|---|---|---|---|---|
| Load shed (% of total load) | 10 | 10 | 10 | 5 | 5 | 5 | / |
| Frequency threshold (Hz) | 59.5 | 59.3 | 59 | 58.6 | 58.3 | 58.0 | 57.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Grozdanovski, J.; Mihalic, R.; Rudez, U. WAMS-Supported Power Mismatch Optimization for Secure Intentional Islanding. Energies 2021, 14, 2790. https://doi.org/10.3390/en14102790
Grozdanovski J, Mihalic R, Rudez U. WAMS-Supported Power Mismatch Optimization for Secure Intentional Islanding. Energies. 2021; 14(10):2790. https://doi.org/10.3390/en14102790
Chicago/Turabian StyleGrozdanovski, Jovancho, Rafael Mihalic, and Urban Rudez. 2021. "WAMS-Supported Power Mismatch Optimization for Secure Intentional Islanding" Energies 14, no. 10: 2790. https://doi.org/10.3390/en14102790
APA StyleGrozdanovski, J., Mihalic, R., & Rudez, U. (2021). WAMS-Supported Power Mismatch Optimization for Secure Intentional Islanding. Energies, 14(10), 2790. https://doi.org/10.3390/en14102790






