Realistic Optimization of Parallelogram-Shaped Offshore Wind Farms Considering Continuously Distributed Wind Resources
Abstract
:1. Introduction
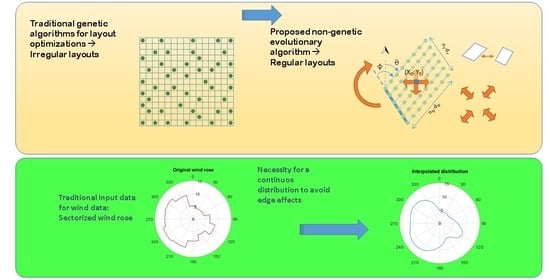
1.1. Genetic and Non-Genetic Evolutive Algorithms
- Defining a discrete computational domain in the form of a grid in which the turbines can be located in the centre of each cell. This is the most popular method. For example, Kunakote et al. in [14] conduct a comparative performance of twelve metaheuristics to optimize the layout of a wind farm after discretizing the studied area into grids. Binary reasoning is applied to discriminate whether each cell includes a turbine or not.
- Assuming a predefined number of wind turbines in the wind farm and optimizing the value of the two geographic coordinates of each wind turbine.
1.1.1. Contribution 1. Non-Genetic Evolutionary Algorithm Searching in a Vast Concession Area
1.1.2. Contribution 2. Analysis of the Optimal Orientation for Rows and Columns
1.2. Wake Loss Model
Contribution 3. Continuous Interpolation of Sectorized Wind Data
- Section 2 lists the expressions for two of the most popular economic indicators used to assess the profitability of a investment, presents a brief but complete description of the Park model to evaluate the wind speed deficit, introduces a new method to interpolate a continuous distribution of the wind rose and the Weibull parameters when data for a reduced number of sectors are given, and presents the basis of the NGEA used to solve the WFOP.
- Section 3 presents and discusses the results obtained after testing it in the HR-I site;
- Finally last Section exposes the conclusions extracted from the work.
2. Materials and Methods
2.1. Economic Indicators
- A positive value is indicative of a profitable investment but does not give an idea of its quality since, in general, NPV will increase with the OWF size. It cannot be used to compare two OWFs with different sizes, locations or bid prices.
- The value of LCOE is strongly influenced by the discount rate, while the value of IRR is influenced by the sale price of the energy produced. The calculation of NPV is determined by both data, and the variation in one of them will not only produce an erroneous value in the objective function but will also distort the selection between individuals. For example, if a too low energy price or a too high discount rate have been taken, then the best solution found will tend to reduce the distances between turbines more than what is ideal.
2.2. Annual Energy Production (AEP)
2.3. Continuous Distribution of Magnitudes Given by the Wind Rose and Averaged Values
- Obtain from the wind rose.
- Calculate the accumulated sum of the probabilities along the sectors from (22).
- Obtain the cubic spline S.
- An estimation of p can be found as the derivative of S.
2.4. Description of the Non-Genetic Evolutionary Algorithm
- All of the turbines are of the same type and the rotors are at the same height. Therefore, it is only valid for offshore sites.
- Turbines are uniformly distributed forming a parallelogram-shaped OWF. All of the rows have the same number of turbines.
- The cable size and the substation position are optimized, but not the connection between turbines; i.e, all of the turbines of a row must be connected from the last one to the first one following a radial cable arrangement as in HR-I [37].
- The HV cable trajectory from the offshore substation to the coast transition is not optimized.
- A maximum of 80 turbines are allowed.
- The turbine positions are limited to the shallow waters plotted in clear blue in Figure 1 (Note: the shallow waters at the right of the dashed line is considered as forbidden zone and hence disregarded). The search area in this study is limited to a reduced space, but in general the search area can be enlarged to thousands of km2, without compromising the computation time.
- For the first optimization, distances between turbines in a row dtr, and between rows dr are fixed and equal to 7 D. For the second optimization .
3. Optimization Results
3.1. Anticipation of the Optimal Orientation and Inclination Angle
- The wind rose and the Weibull parameters are those specified for the HR-I site during the period 1999–2002, obtained from [36] and reproduced in Table 1. Data have been interpolated according to the method explained in Section 2.3 to estimate a continuous distribution of the density of probability and Weibull parameters.
- The number of rows and turbines per row are and , respectively.
- The separation between turbines of a row as well as between rows is D.
3.2. Possibility to Limit the Speed Range for the Deficit Calculation
3.3. Results of the Layout Optimization Search
4. Conclusions and Discussion
- that takes into account all of the factors (or at least more than any other paper found) required for the economic evaluation;
- that fully defines the position, size and configuration of the optimal OWF with regularly distributed turbines and shaped like a parallelogram;
- that, alternatively, indicates what should be the orientation and inclination of the concession area to make it more attractive to potential developers of wind farms.
- discussion on the optimal orientation of the concession area for HR-I,
- recommendation to reduce the range of speeds to be studied when evaluating the orientation and inclination of the OWF during the optimization algorithm execution,
- possibility to deduce the optimal orientation and inclination replacing the original layout into a scaled version of the OWF, with half of the rows and half of the turbines per row,
- the evaluation of a quincunx configuration, which does not entail an increase in the energy produced, mainly if the position of the turbines must be limited to a certain concession area.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Glossary
| OPEX | operational expenditure |
| CAPEX | capital expenditure |
| NPV | net present value |
| IRR | internal rate of return |
| LCOE | levelized cost of energy |
| T | wind farm life time |
| a | annuity factor |
| AEP | annual energy production |
| price per kWh | |
| annual inflation | |
| r | discount rate |
| nominal interest rate | |
| decommissioning cost | |
| WACC | weighted average cost of capital |
| number of sectors | |
| number of rows | |
| number of turbines per row | |
| distance between rows, in diameters | |
| distance between turbines in a row, in diameters | |
| orientation of an array with respect to North, in deg, sense CW | |
| parallelogram angle; equal to for rectangle | |
| surface roughness length | |
| A | scale factor of the Weibull distribution |
| K | shape factor of the Weibull distribution |
| wind speed deficit at a downwind turbine | |
| wake decay constant | |
| h | tower hub height |
| D | rotor diameter of the upwind turbine |
| diameter of the wake | |
| thrust coefficient | |
| s | projection of the distance between turbines onto the wind direction |
| y | transversal separation between turbines |
| effective surface of the downwind rotor affected by the upstream weak | |
| GA | genetic algorithm |
| OWF | offshore wind farm |
| WFOP | wind farm optimization problem |
| NGEA | non-genetic evolutionary algorithm |
| HR-I | Horns Rev I |
References
- Walsh, C. Offshore wind in Europe. Refocus 2019, 3, 14–17. [Google Scholar]
- Serrano González, J.; Burgos Payán, M.; Santos, J.M.R.; González-Longatt, F. A review and recent developments in the optimal wind-turbine micro-siting problem. Renew. Sustain. Energy Rev. 2014, 30, 133–144. [Google Scholar] [CrossRef]
- Herbert-Acero, J.F.; Probst, O.; Réthoré, P.E.; Larsen, G.C.; Castillo-Villar, K.K. A review of methodological approaches for the design and optimization of wind farms. Energies 2014, 7, 6930–7016. [Google Scholar] [CrossRef]
- Kirchner-Bossi, N.; Porté-Agel, F. Realistic wind farm layout optimization through genetic algorithms using a Gaussian wake model. Energies 2018, 11, 3268. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Yang, H.; Lin, L.; Koo, P. Wind turbine layout optimization using multi-population genetic algorithm and a case study in Hong Kong offshore. J. Wind. Eng. Ind. Aerodyn. 2015, 139, 89–99. [Google Scholar] [CrossRef]
- Pookpunt, S.; Ongsakul, W. Design of optimal wind farm configuration using a binary particle swarm optimization at Huasai district, Southern Thailand. Energy Convers. Manag. 2016, 108, 160–180. [Google Scholar] [CrossRef]
- Chowdhury, S.; Zhang, J.; Messac, A.; Castillo, L. Optimizing the arrangement and the selection of turbines for wind farms subject to varying wind conditions. Renew. Energy 2013, 52, 273–282. [Google Scholar] [CrossRef]
- Hou, P.; Hu, W.; Soltani, M.; Chen, Z. Optimized Placement of Wind Turbines in Large-Scale Offshore Wind Farm Using Particle Swarm Optimization Algorithm. IEEE Trans. Sustain. Energy 2015, 6, 1272–1282. [Google Scholar] [CrossRef] [Green Version]
- Salcedo-Sanz, S.; Gallo-Marazuela, D.; Pastor-Sanchez, A.; Carro-Calvo, L.; Portilla-Figueras, A.; Prieto, L. Offshore wind farm design with the Coral Reefs Optimization algorithm. Renew. Energy 2014, 63, 109–115. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Solving the wind farm layout optimization problem using random search algorithm. Renew. Energy 2015, 78, 182–192. [Google Scholar] [CrossRef]
- Mittal, P.; Kulkarni, K.; Mitra, K. A novel hybrid optimization methodology to optimize the total number and placement of wind turbines. Renew. Energy 2016, 86, 133–147. [Google Scholar] [CrossRef] [Green Version]
- Mayo, M.; Daoud, M. Informed mutation of wind farm layouts to maximise energy harvest. Renew. Energy 2016, 89, 437–448. [Google Scholar] [CrossRef] [Green Version]
- Neshat, M.; Alexander, B.; Sergiienko, N.Y.; Wagner, M. Optimisation of large wave farms using a multi-strategy evolutionary framework. In Proceedings of the 2020 Genetic and Evolutionary Computation Conference, Cancun, Mexico, 8–12 July 2020; pp. 1150–1158. [Google Scholar]
- Kunakote, T.; Sabangban, N.; Kumar, S.; Tejani, G.G.; Panagant, N. Comparative Performance of Twelve Metaheuristics for Wind Farm Layout Optimisation. Arch. Comput. Methods Eng. 2021. [Google Scholar] [CrossRef]
- Serrano González, J.; Trigo García, Á.L.; Burgos Payán, M.; Riquelme Santos, J.; González Rodríguez, Á.G. Optimal wind-turbine micro-siting of offshore wind farms: A grid-like layout approach. Appl. Energy 2017, 200, 28–38. [Google Scholar] [CrossRef]
- Neubert, A.; Shah, A.; Schlez, W. Maximum Yield From Symmetrical Wind Farm Layouts. In Proceedings of the DEWEK 2010, Bremen, Germany, 17–18 November 2010; pp. 1–4. [Google Scholar]
- Feng, J.; Shen, W.Z. Co-optimization of the shape, orientation and layout of offshore wind farms. J. Phys. Conf. Ser. 2020, 1618. [Google Scholar] [CrossRef]
- Stanley, A.P.; Ning, A. Massive simplification of the wind farm layout optimization problem. Wind Energy Sci. 2019, 4, 663–676. [Google Scholar] [CrossRef] [Green Version]
- Lv, M.; Li, J.; Du, H.; Zhu, W.; Meng, J. Solar array layout optimization for stratospheric airships using numerical method. Energy Convers. Manag. 2017, 135, 160–169. [Google Scholar] [CrossRef]
- Gerdes, G.; Albrecht, T.; Zeelenberg, S. Case Study: European Offshore Wind Farms—A Survey for the Analysis of the Experiences and Lessons Learnt by Developers of Offshore Wind Farms; Technical Report; Deutsche WindGuard GmbH: Varel, Germany, 2005. Available online: https://tethys.pnnl.gov/publications/case-study-european-offshore-wind-farms-survey-analysis-experienceslessons-learnt (accessed on 14 May 2021).
- Musial, W.; Parker, Z.; Fields, J.; Scott, G.; Elliott, D.; Draxl, C. Assessment of Offshore Wind Energy Leasing Areas for the BOEM Massachusetts Wind Energy Area; Technical Report October; National Renewable Energy Laboratory, 2012. Available online: https://www.nrel.gov/docs/fy14osti/60942.pdf (accessed on 14 May 2021).
- Archer, C.L.; Vasel-Be-Hagh, A.; Yan, C.; Wu, S.; Pan, Y.; Brodie, J.F.; Maguire, A.E. Review and evaluation of wake loss models for wind energy applications. Appl. Energy 2018, 226, 1187–1207. [Google Scholar] [CrossRef]
- Katic, I.; Højstrup, J.; Jensen, N. A Simple Model for Cluster Efficiency Publication date. In Proceedings of the European wind energy association conference and exhibition, Rome, Italy, 7–9 October 1987; Volume 1, pp. 407–410. [Google Scholar]
- Barthelmie, R.J.; Folkerts, L.; Larsen, G.C.; Rados, K.; Pryor, S.C.; Frandsen, S.T.; Lange, B.; Schepers, G. Comparison of Wake Model Simulations with Offshore Wind Turbine Wake Profiles Measured by Sodar. J. Atmos. Ocean Technol. 2006, 23, 888–901. [Google Scholar] [CrossRef]
- Walker, K.; Adams, N.; Gribben, B.; Gellatly, B.; Nygaard, N.G.; Henderson, A.; Marchante Jimemez, M.; Schmidt, S.R.; Rodriguez Ruiz, J.; Paredes, D.; et al. An evaluation of the predictive accuracy of wake effects models for offshore wind farms. Wind Energy 2016, 19, 979–996. [Google Scholar] [CrossRef]
- Feng, J.; Shen, W.Z. Modelling wind for wind farm layout optimization using joint distribution of wind speed and wind direction. Energies 2015, 8, 3075–3092. [Google Scholar] [CrossRef] [Green Version]
- Rodrigues, S.; Restrepo, C.; Katsouris, G.; Pinto, R.T.; Soleimanzadeh, M.; Bosman, P.; Bauer, P. A multi-objective optimization framework for offshorewind farm layouts and electric infrastructures. Energies 2016, 9, 216. [Google Scholar] [CrossRef] [Green Version]
- Levitt, A.C.; Kempton, W.; Smith, A.P.; Musial, W.; Firestone, J. Pricing offshore wind power. Energy Policy 2011, 39, 6408–6421. [Google Scholar] [CrossRef]
- Voormolen, J.A.; Junginger, H.M.; van Sark, W.G. Unravelling historical cost developments of offshore wind energy in Europe. Energy Policy 2016, 88, 435–444. [Google Scholar] [CrossRef]
- Danish Energy Authority, Amaliegade 44 1256 Copenhagen K. Offshore Wind Power- Danish Experiences and Solutions; Technical Report; Danish Energy Authority: Amaliegade, Denmark, 2005; ISBN 87-7844-560-4. Available online: https://discomap.eea.europa.eu/map/Data/Milieu/OURCOAST_097_DK/OURCOAST_097_DK_Doc4_ExpSolutionsDK.pdf (accessed on 14 May 2021).
- Shao, Z.; Wu, Y.; Li, L.; Han, S.; Liu, Y. Multiple wind turbine wakes modeling considering the faster wake recovery in overlapped wakes. Energies 2019, 12, 680. [Google Scholar] [CrossRef] [Green Version]
- Sørensen, T.; Lybech, M.; Nielsen, P. Adapting and Calibration of Existing Wake Models to Meet the Conditions Inside; Technical Report 27491529; EMD International A/S: Aalborg, Denmark, 2008; Available online:https://www.emd.dk/files/PSO%20projekt%205899.pdf (accessed on 14 May 2021).
- Hansen1, K.; Barthelmie, R.J.; Jensen, L.E.; Sommer, A. The impact of turbulence intensity and atmospheric stability on power deficits due to wind turbine wakes at Horns Rev wind farm. Wind Energy 2012, 15, 183–196. [Google Scholar] [CrossRef] [Green Version]
- Barthelmie, R.J.; Pryor, S.C.; Frandsen, S.T.; Hansen, K.S.; Schepers, J.G.; Rados, K.; Schlez, W.; Neubert, A.; Jensen, L.E.; Neckelmann, S. Quantifying the impact of wind turbine wakes on power output at offshore wind farms. J. Atmos. Ocean Technol. 2010, 27, 1302–1317. [Google Scholar] [CrossRef]
- Tian, L.; Zhu, W.; Shen, W.; Song, Y.; Zhao, N. Prediction of multi-wake problems using an improved Jensen wake model. Renew. Energy 2017, 102, 457–469. [Google Scholar] [CrossRef]
- Li, S. Wind Array Performance Evaluation Model for Large Wind Farms and Wind Farm Layout Optimization. Thesis, 2014. Available online: https://etd.ohiolink.edu/apexprod/rws_etd/send_file/send?accession=case1405080318 (accessed on 14 May 2021).
- Lingling, H.; Yang, F.; Xiaoming, G. Optimization of electrical connection scheme for large offshore wind farm with genetic algorithm. In Proceedings of the 2009 International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–4. [Google Scholar] [CrossRef]
- Pedersen, M.M.; van der Laan, P.; Friis-Moller, M.; Rinker, J.; Rethore, P.E. DTUWindEnergy/PyWake: PyWake. 2019. Available online: https://topfarm.pages.windenergy.dtu.dk/PyWake/ (accessed on 14 May 2021). [CrossRef]
- Wu, Y.T.; Porte-Agel, F. Atmospheric Turbulence Effects on Wind-Turbine Wakes: An LES Study. Energies 2012, 5, 5340–5362. [Google Scholar] [CrossRef]
- Gonzalez-Rodriguez, A.G. Review of offshore wind farm cost components. Energy Sustain. Dev. 2016. [Google Scholar] [CrossRef]















| Sector | N | NNE | NEE | E | EES | ESS | S | SSW | SWW | W | WWN | WNN |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| freq (%) | 3.8 | 4.3 | 5.5 | 8.3 | 8.7 | 6.7 | 8.4 | 10.5 | 11.4 | 12.2 | 13.9 | 6.1 |
| (m/s) | 8.71 | 9.36 | 9.29 | 10.27 | 10.89 | 10.49 | 10.94 | 11.23 | 11.93 | 11.94 | 12.17 | 10.31 |
| 2.08 | 2.22 | 2.41 | 2.37 | 2.51 | 2.75 | 2.61 | 2.51 | 2.33 | 2.35 | 2.58 | 2.01 |
| Wind Speed (m/s) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| Power (kW) | 0 | 0 | 0 | 66 | 154 | 282 | 460 | 696 | 996 | 1341 | 1661 | 1866 | 1958 |
| Thrust coef | 0 | 0 | 0 | 0.818 | 0.806 | 0.804 | 0.81 | 0.81 | 0.807 | 0.793 | 0.739 | 0.709 | 0.409 |
| Wind speed (m/s) | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
| Power (kW) | 1988 | 1997 | 1999 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | 2000 | |
| Thrust coef | 0.314 | 0.249 | 0.202 | 0.17 | 0.14 | 0.119 | 0.102 | 0.088 | 0.077 | 0.067 | 0.06 | 0.05 |
| Actual | Optim | Optim | Actual | Optim | Optim | ||
|---|---|---|---|---|---|---|---|
| Layout | Layout | ||||||
| dtr (D) | 7 | 7 | 5.35 | Turbines | 154.8 | 154.8 | 154.8 |
| dr (D) | 7 | 7 | 19.98 | Foundations | 48.18 | 49.08 | 48.51 |
| ntr | 8 | 5 | 16 | Electrical Offshore | 58.04 | 60.04 | 58.04 |
| nr | 10 | 16 | 5 | Electrical Onshore | 15.88 | 15.88 | 15.88 |
| θ (deg) | 173 | 71.05 | 62.5 | Others | 16.60 | 16.60 | 16.60 |
| ϕ (deg) | 83 | 91.16 | 99.97 | OPEX | 14.24 | 14.47 | 14.97 |
| AEP (GWh) | 712.47 | 723.55 | 748.60 | LCOE (€/MWh) | 61.26 | 60.95 | 59.34 |
| Elect. losses (GWh) | 9.83 | 8.53 | 16.35 | IRR | 13.78% | 13.99% | 14.41% |
| Wake losses (GWh) | 76.81 | 64.35 | 40.68 | NPV (M€) | 72.93 | 77.47 | 86.09 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonzalez-Rodriguez, A.G.; Serrano-González, J.; Burgos-Payán, M.; Riquelme-Santos, J.M. Realistic Optimization of Parallelogram-Shaped Offshore Wind Farms Considering Continuously Distributed Wind Resources. Energies 2021, 14, 2895. https://doi.org/10.3390/en14102895
Gonzalez-Rodriguez AG, Serrano-González J, Burgos-Payán M, Riquelme-Santos JM. Realistic Optimization of Parallelogram-Shaped Offshore Wind Farms Considering Continuously Distributed Wind Resources. Energies. 2021; 14(10):2895. https://doi.org/10.3390/en14102895
Chicago/Turabian StyleGonzalez-Rodriguez, Angel G., Javier Serrano-González, Manuel Burgos-Payán, and Jesús Manuel Riquelme-Santos. 2021. "Realistic Optimization of Parallelogram-Shaped Offshore Wind Farms Considering Continuously Distributed Wind Resources" Energies 14, no. 10: 2895. https://doi.org/10.3390/en14102895
APA StyleGonzalez-Rodriguez, A. G., Serrano-González, J., Burgos-Payán, M., & Riquelme-Santos, J. M. (2021). Realistic Optimization of Parallelogram-Shaped Offshore Wind Farms Considering Continuously Distributed Wind Resources. Energies, 14(10), 2895. https://doi.org/10.3390/en14102895