A Mobile Energy Storage Unit Serving Multiple EV Charging Stations
Abstract
:1. Introduction
2. Proposed Approach
2.1. Problem Statement
2.2. Assumptions
- Customers’ requirements are received day-ahead.
- Visiting order of the charging station is known based on the forecasted load profile.
- The time segment is hourly and changes within the hour are averaged.
3. Problem Formulation
3.1. Power Flow Constraints
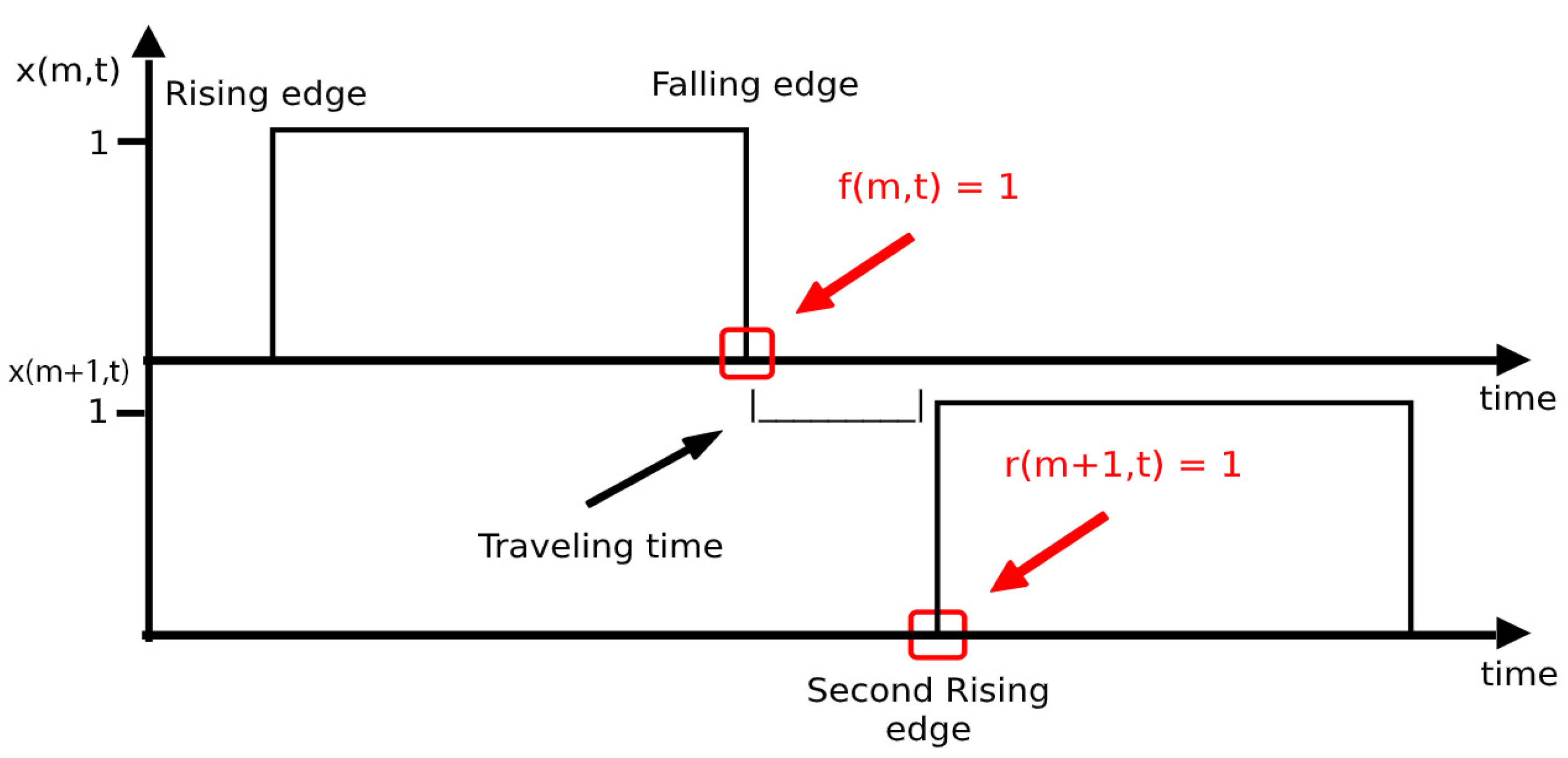
3.2. EVs Charging Constraints
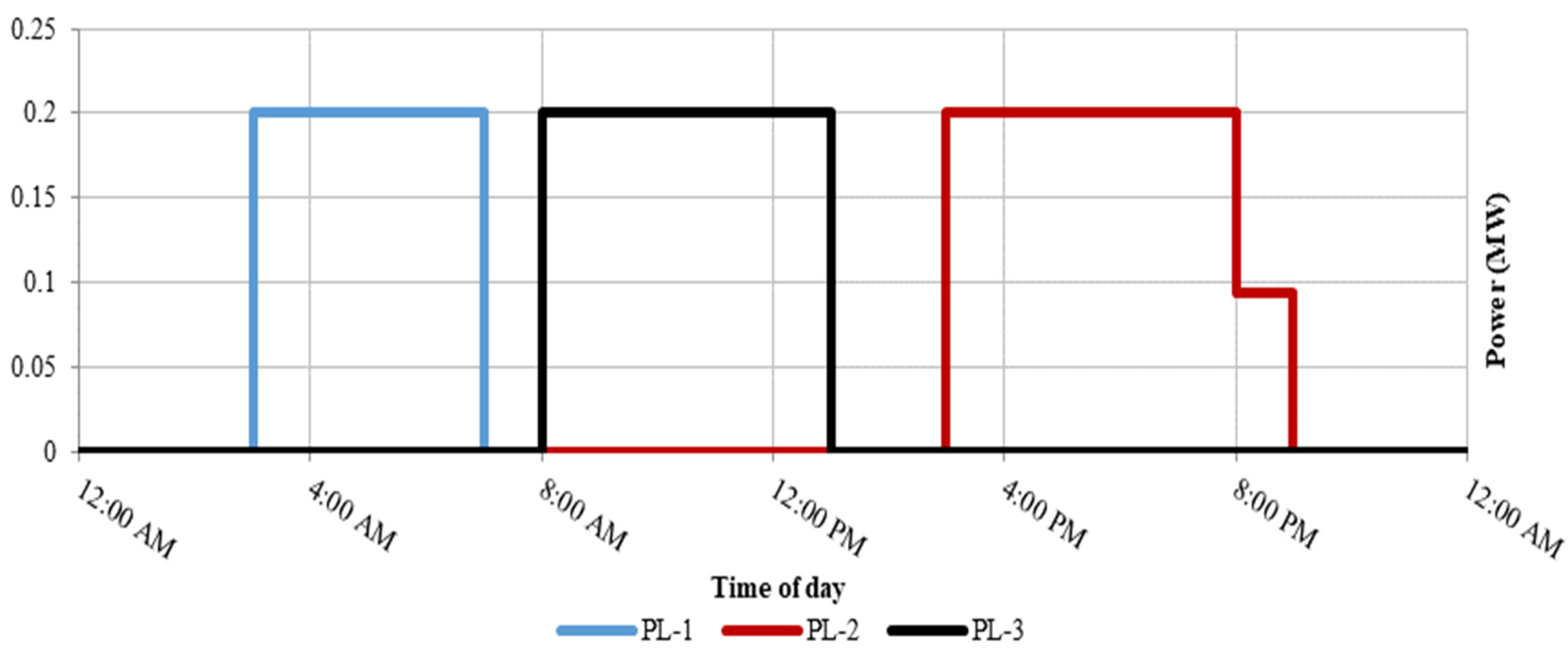
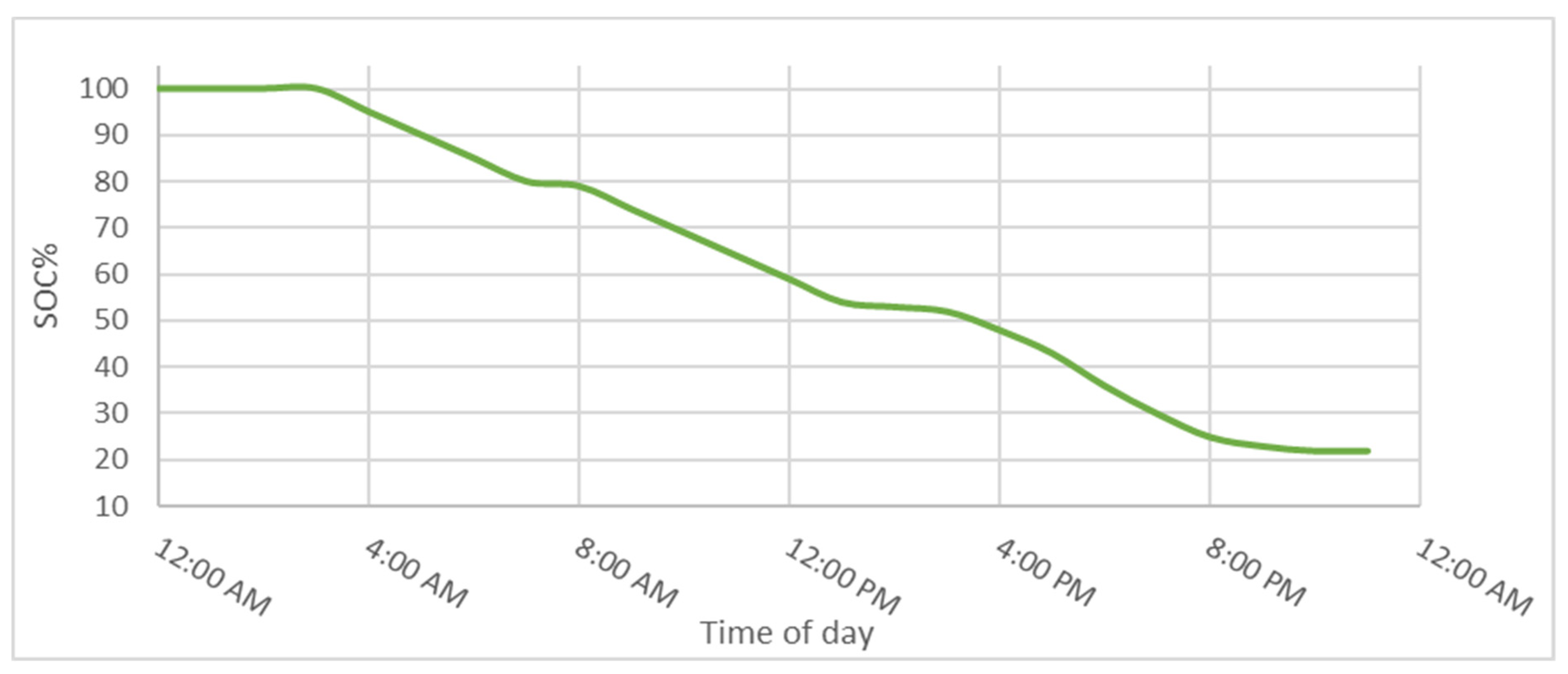
3.3. Mobile Storage Modeling
3.4. Decision Variables Constraints
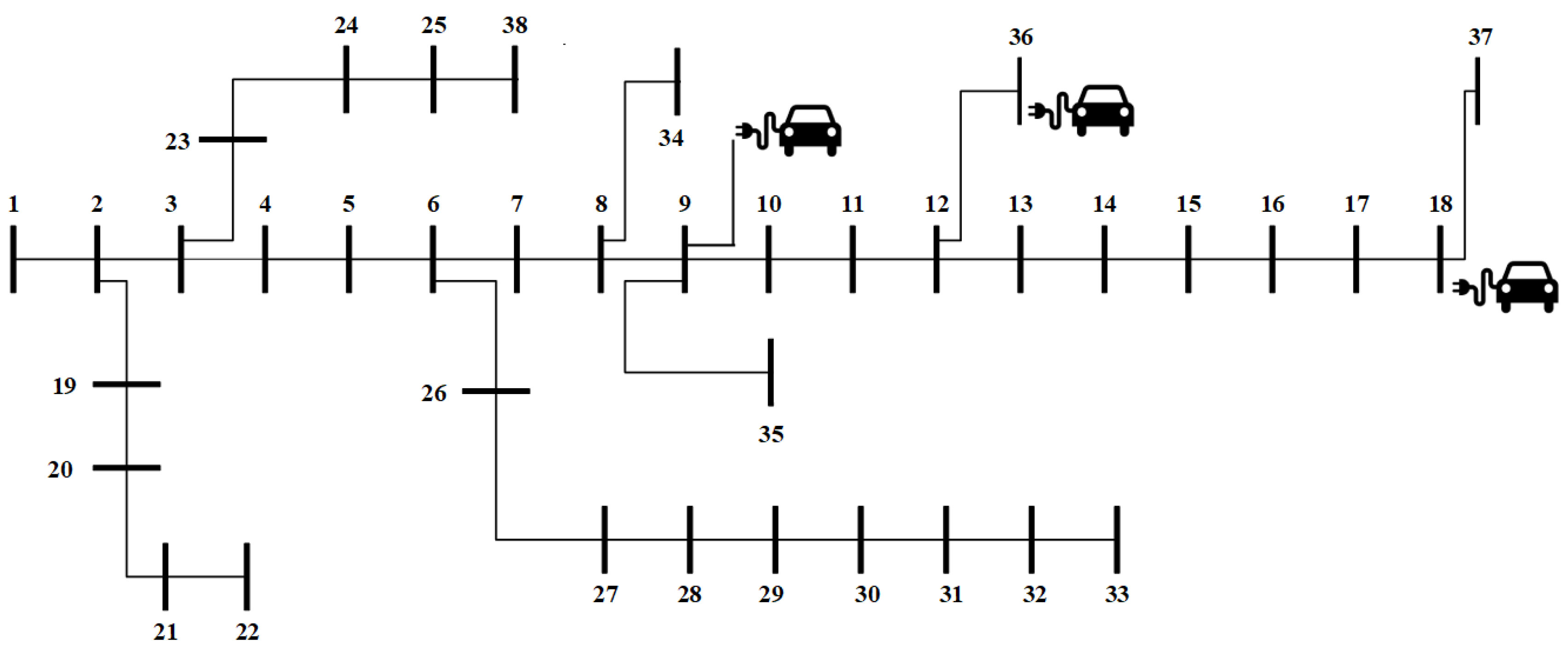
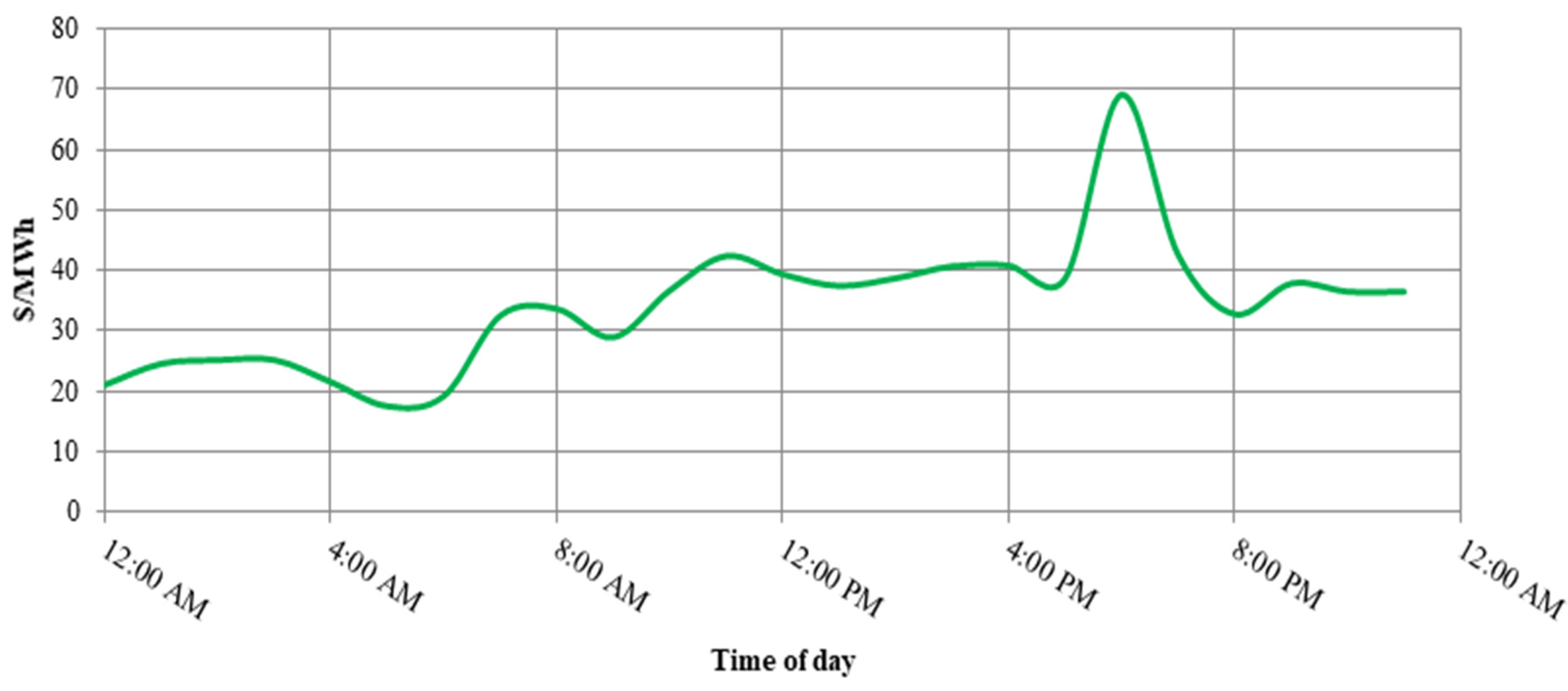
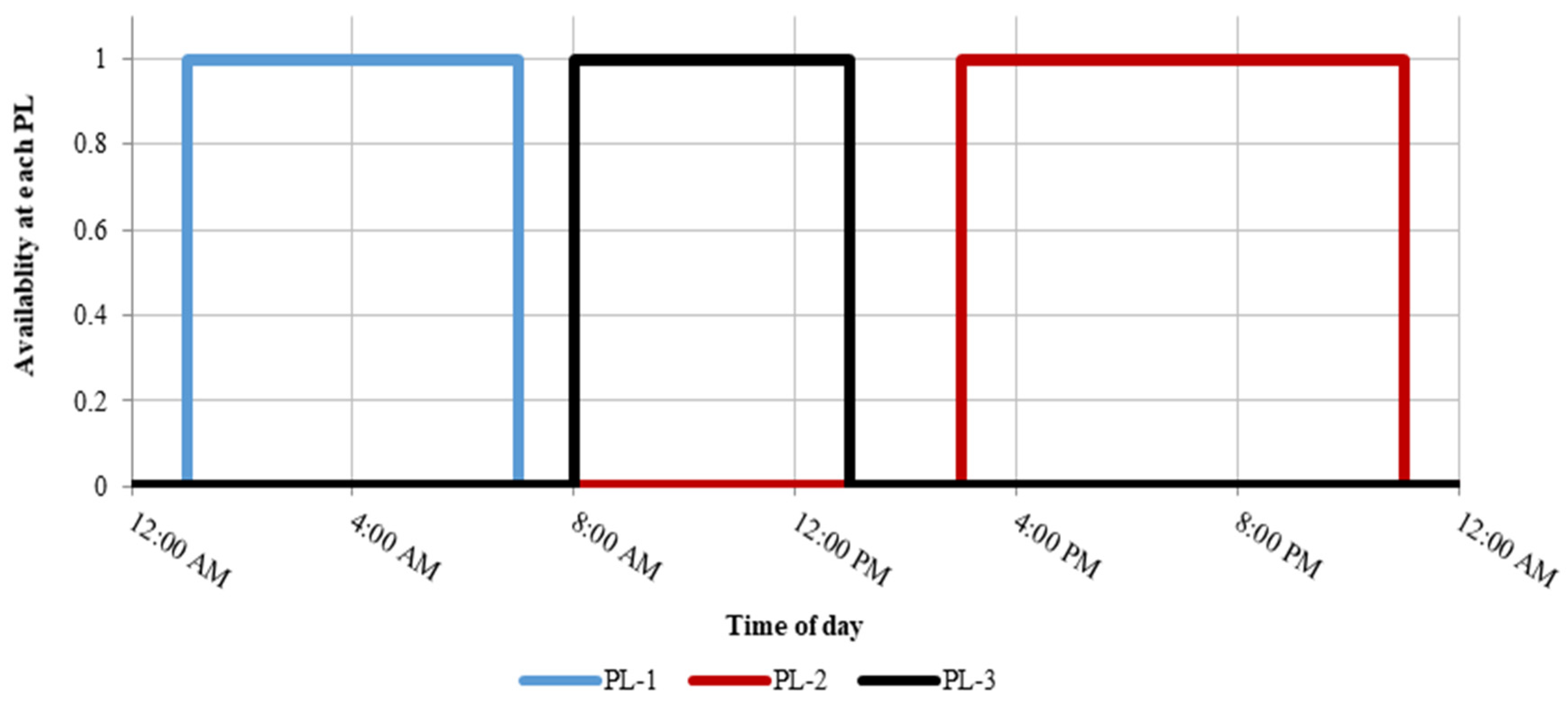
4. Case Studies
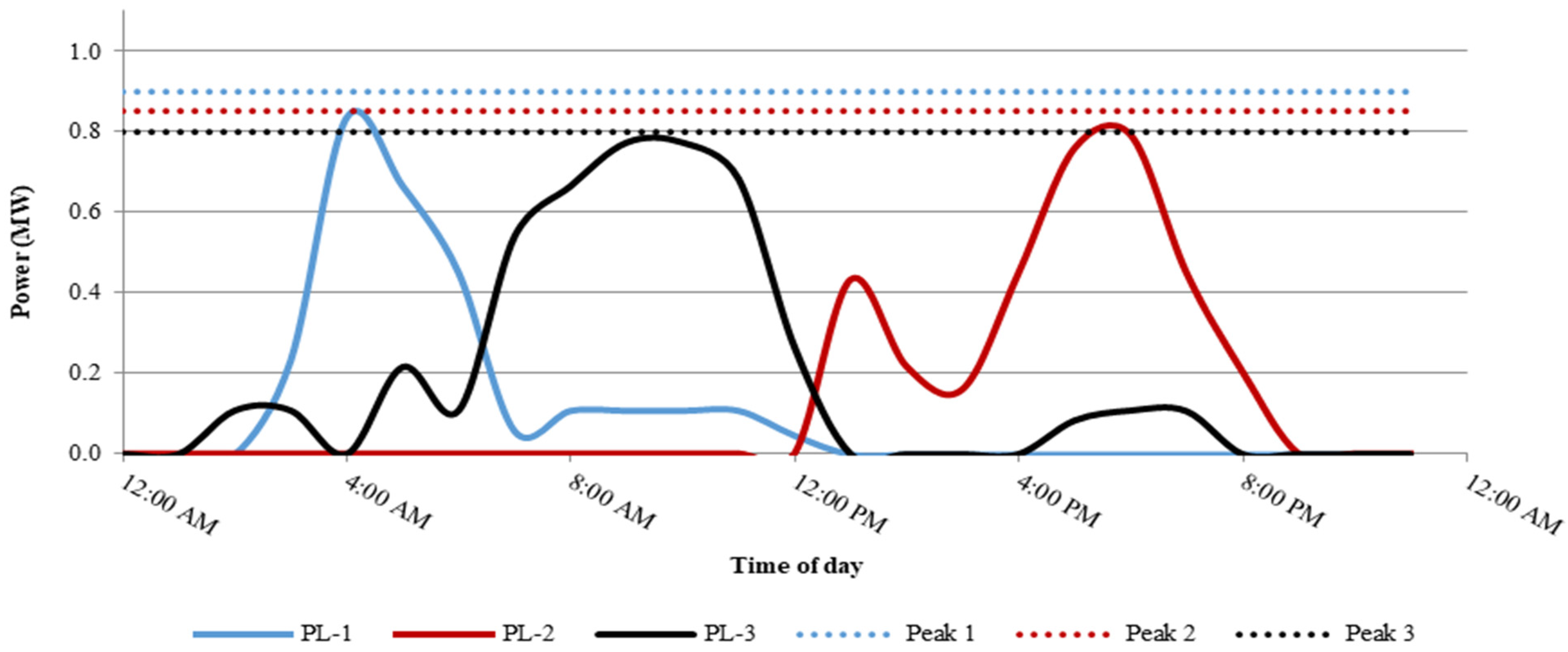
4.1. Case Study-1
4.2. Case Study-2
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Olabi, A.G.; Wilberforce, T.; Abdelkareem, M.A.; Ramadan, M. Critical Review of Flywheel Energy Storage System. Energies 2021, 14, 2159. [Google Scholar] [CrossRef]
- Hesse, H.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-Ion Battery Storage for the Grid—A Review of Stationary Battery Storage System Design Tailored for Applications in Modern Power Grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef] [Green Version]
- Babaei, S.; Steen, D.; Le, T.A.; Carlson, O.; Bertling, L. Effects of plug-in electric vehicles on distribution systems: A real case of Gothenburg. In Proceedings of the 2010 IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenburg, Sweden, 11–13 October 2010; pp. 1–8. [Google Scholar]
- Shalaby, A.A.; Shaaban, M.F.; Mokhtar, M.; Zeineldin, H.H.; El-Saadany, E.F. Optimal Day-ahead Operation for a PV-based Battery Swapping Station for Electric Vehicles. In Proceedings of the 2021 6th International Symposium on Environment-Friendly Energies and Applications (EFEA), Sofia, Bulgaria, 24–26 March 2021; pp. 1–8. [Google Scholar]
- Deshmukh, R.R.; Ballal, M.S. An energy management scheme for grid connected EVs charging stations. In Proceedings of the 2018 International Conference on Power, Instrumentation, Control and Computing (PICC), Thrissur, India, 18–20 January 2018; pp. 1–6. [Google Scholar]
- Chaudhari, K.; Ukil, A.; Kumar, K.N.; Manandhar, U.; Kollimalla, S.K. Hybrid Optimization for Economic Deployment of ESS in PV Integrated EV Charging Station. IEEE Trans. Ind. Inform. 2017, 14, 106–116. [Google Scholar] [CrossRef]
- Shojaabadi, S.; Abapour, S.; Abapour, M.; Nahavandi, A. Optimal planning of plug-in hybrid electric vehicle charging station in distribution network considering demand response programs and uncertainties. IET Gener. Transm. Distrib. 2016, 10, 3330–3340. [Google Scholar] [CrossRef]
- Panwar, L.K.; Reddy, S.; Verma, A.; Panigrahi, B.K.; Kumar, R. Optimal schedule of plug in electric vehicles in smart grid with constrained parking lots. In Proceedings of the 2016 IEEE 6th International Conference on Power Systems (ICPS), New Delhi, India, 4–6 March 2016; pp. 1–6. [Google Scholar]
- Sortomme, E.; El-Sharkawi, M.A. Optimal charging strategies for unidirectional vehicle-to-grid. IEEE Trans. Smart Grid 2011, 2, 131–138. [Google Scholar] [CrossRef]
- Oceano, A.; Rodella, G.; Rizzo, R.; di Noia, L.P.; Brusaglino, G. Grid balancing support through Electric Vehicles mobile storage. In Proceedings of the 2020 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Sorrento, Italy, 24–26 June 2020; pp. 108–113. [Google Scholar]
- SSamara, M.; Shaaban, M.F.; Osman, A. Management of Mobile Energy Generation and Storage System. In Proceedings of the 2019 IEEE PES GTD Grand International Conference and Exposition Asia (GTD Asia), Bangkok, Thailand, 19–23 March 2019; pp. 450–454. [Google Scholar]
- Abdeltawab, H.; Mohamed, Y.A.I. Mobile Energy Storage Sizing and Allocation for Multi-Services in Power Distribution Systems. IEEE Access. 2019, 7, 176613–176623. [Google Scholar] [CrossRef]
- Yu, R.; Zhong, W.; Xie, S.; Yuen, C.; Gjessing, S.; Zhang, Y. Balancing Power Demand Through EV Mobility in Vehicle-to-Grid Mobile Energy Networks. IEEE Trans. Ind. Inform. 2016, 12, 79–90. [Google Scholar] [CrossRef]
- Yan, Y.; Yu, B.; Ouyang, F.; Zhu, W.; Li, H. Study on the Control Strategy of Mobile Battery Energy Storage for the Overload Elimination of Distribution Transformer. In Proceedings of the 2020 12th IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Nanjing, China, 17–19 April 2020; pp. 1–5. [Google Scholar]
- Nakhodchi, N.; Aghli, N.; Alishahi, S.; Pourarab, M.H. Design and successful utilisation of the first multi-purpose mobile distributed energy storage system in Iran. CIRED Open Access Proc. J. 2017, 2017, 109–111. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Dvorkin, Y. Enhancing Distribution System Resilience with Mobile Energy Storage and Microgrids. IEEE Trans. Smart Grid 2019, 10, 4996–5006. [Google Scholar] [CrossRef]
- Sanchez-Martin, P.; Sanchez, G.; Morales-Espana, G. Direct Load Control Decision Model for Aggregated EV Charging Points. IEEE Trans Power Syst. 2012, 27, 1577–1584. [Google Scholar] [CrossRef]
- Kronqvist, J.; Bernal, D.; Lundell, A.; Grossmann, I. A review and comparison of solvers for convex MINLP. Optim. Eng. 2019, 20, 397–455. [Google Scholar] [CrossRef] [Green Version]
- Haidl, P.; Buchroithner, A.; Schweighofer, B.; Bader, M.; Wegleiter, H. Lifetime Analysis of Energy Storage Systems for Sustainable Transportation. Sustainability 2019, 11, 6731. [Google Scholar] [CrossRef] [Green Version]
- Toronto Parking Authority, City of Toronto. 2021. Available online: https://www.toronto.ca/city-government/accountability-operations-customer-service/city-administration/city-managers-office/agencies-corporations/agencies/toronto-parking-authority/ (accessed on 2 March 2021).
- Le, X.-H.; Ho, H.V.; Lee, G.; Jung, S. Application of Long Short-Term Memory (LSTM) Neural Network for Flood Forecasting. Water 2019, 11, 1387. [Google Scholar] [CrossRef] [Green Version]
- Nikola One. Available online: https://nikolamotor.com/one (accessed on 1 May 2021).
- BU-1003: Electric Vehicle (EV)—Battery University, Batteryuniversity.com. Available online: https://batteryuniversity.com/learn/article/electric_vehicle_ev (accessed on 2 May 2021).
- Mongird, K.; Viswanathan, V.V.; Balducci, P.J.; Alam, M.J.E.; Fotedar, V.; Koritarov, V.S.; Hadjerioua, B. Hydro Wires, Energy Storage Technology and Cost Characterization Report; U.S. Department of Energy: Washington, DC, USA, 2019.
- Zhao, Y.; Pohl, O.; Bhatt, A.I.; Collis, G.E.; Mahon, P.J.; Rüther, T.; Hollenkamp, A.F. A Review on Battery Market Trends, Second-Life Reuse, and Recycling. Sustain. Chem. 2021, 2, 167–205. [Google Scholar] [CrossRef]


| PLs Specifications | Value |
|---|---|
| EVs battery capacity | 40 kWh |
| Maximum charging rate | 9.6 kW |
| Maximum depth of discharge (MDOD) | 80% |
| Chargers Available in PL1 | 121 |
| Chargers Available in PL2 | 144 |
| Chargers Available in PL3 | 168 |
| TT between PL1 and PL2 | 1 h |
| TT between PL2 and PL3 | 2 h |
| TT between PL1 and PL3 | 1 h |
| MESS Specifications | Value |
|---|---|
| Maximum discharge rate of MESS | 200 kW |
| Total batteries capacity | 4 MWh |
| Battery packs weights | 26,000 kg |
| Truck payload capacity | >29,000 kg |
| Average speed assumption | 60 km/h |
| Label | Historical Peaks | Demand Charge Rate | Case Study-1 | Case Study-2 | |||
|---|---|---|---|---|---|---|---|
| Energy Cost | Extra Demand Charges | Energy Cost | Extra Demand Charges | Battery Degredation Cost | |||
| Parking lot 1 | 0.9 MW | $4.1/kW | $89.97 | $533 | $60.847 | 0 | $151.848 |
| Parking lot 2 | 0.85 MW | $205.512 | $450 | $139.869 | 0 | ||
| Parking lot 3 | 0.8 MW | $214.88 | $697 | $156.13 | 0 | ||
| Total | - | - | $510.307 | $1680 | $356.846 | 0 | $151.848 |
| $2190.307 | $508.694 | ||||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Elmeligy, M.M.; Shaaban, M.F.; Azab, A.; Azzouz, M.A.; Mokhtar, M. A Mobile Energy Storage Unit Serving Multiple EV Charging Stations. Energies 2021, 14, 2969. https://doi.org/10.3390/en14102969
Elmeligy MM, Shaaban MF, Azab A, Azzouz MA, Mokhtar M. A Mobile Energy Storage Unit Serving Multiple EV Charging Stations. Energies. 2021; 14(10):2969. https://doi.org/10.3390/en14102969
Chicago/Turabian StyleElmeligy, Mohamed M., Mostafa F. Shaaban, Ahmed Azab, Maher A. Azzouz, and Mohamed Mokhtar. 2021. "A Mobile Energy Storage Unit Serving Multiple EV Charging Stations" Energies 14, no. 10: 2969. https://doi.org/10.3390/en14102969
APA StyleElmeligy, M. M., Shaaban, M. F., Azab, A., Azzouz, M. A., & Mokhtar, M. (2021). A Mobile Energy Storage Unit Serving Multiple EV Charging Stations. Energies, 14(10), 2969. https://doi.org/10.3390/en14102969









