Next Article in Journal
Short Term Active Power Load Prediction on A 33/11 kV Substation Using Regression Models
Previous Article in Journal
Assessing the Link between Vessel Size and Maritime Supply Chain Sustainable Performance
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Energies
Volume 14
Issue 11
10.3390/en14112978
energies-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

The Impact of Low-Resource Periods on the Reliability of Wind Power Systems for Rural Electrification in Africa

by
Hanieh Seyedhashemi
1,2,*,
Benoît Hingray
1,*,
Christophe Lavaysse
1,3 and
Théo Chamarande
1
1
CNRS, Grenoble Alpes University, Grenoble-INP, IRD, IGE, 38000 Grenoble, France
2
UR RiverLy, Centre de Lyon-Villeurbanne, INRAE, 5 rue de la Doua CS 20244, 69625 Villeurbanne, France
3
IRD, Grenoble, FR and JRC, European Commission, 21027 Ispra, Italy
*
Authors to whom correspondence should be addressed.
Energies 2021, 14(11), 2978; https://doi.org/10.3390/en14112978
Submission received: 14 April 2021 / Revised: 18 May 2021 / Accepted: 19 May 2021 / Published: 21 May 2021
(This article belongs to the Section A3: Wind, Wave and Tidal Energy)
Browse Figures
Versions Notes

Abstract

:
Decentralized electricity systems based on variable renewable energy (VRE) sources such as wind power can provide affordable, dependable, and modern energy in a manner consistent with the Paris Agreement. Such sources are, however, sensitive to extreme values of climatic factors—an issue that may jeopardize power system reliability. As a resource-rich region with a high proportion of rural population without access to electricity, Africa has been of wide interest in studies on VRE-based electricity generation. Nevertheless, there is still a major gap in our continent-scale understanding of the wind power potential and its variability at different time scales, as well as the influence of low-wind-resource periods in Africa. Using ERA5 hourly estimates of wind speed, the present study investigated the adequacy and temporal variability of local wind power potential across Africa over the 2000–2017 period. The results indicated that design requirements of wind power systems are, on average, fulfilled in regions in the North, South, and Horn of Africa at different time scales. However, low-resource periods were shown to have a significant impact on the reliability of wind power potential in the majority of the continent. Demand flexibility can reduce the severity of these periods and help to achieve design requirements.

1. Introduction

1.1. Application of Decentralized Energy Systems for Electrification in Remote Regions

One key objective of the Sustainable Development Goals set by the United Nations General Assembly in 2015 for future decades is to provide access to affordable, reliable, and modern energy to all. From another angle, compliance with the objectives of the Paris Agreement to limit global warming well below 2 °C requires that electrification systems be reliant upon VRE or carbon-free resources such as wind and solar energy [1]. On top of environmental concerns over centralized power systems, which mostly burn fossil fuels, the (high) cost of the distribution of energy from such systems to remote regions needs to be taken into account. A viable alternative to centralized electricity generation would be decentralized off-grid energy solutions. If for most decentralized systems, power production was historically obtained with fuel gensets, today many of them include production from renewable energy sources. The possibility of developing systems where the production is mainly or only obtained from renewable energy sources would be obviously ideal, but the feasibility of such systems is still an open question in many regions worldwide [2].

1.2. Reliability and Serviceability of Decentralized Energy Systems in Low-Resource Periods

Autonomous micro-grids, which are partly or entirely reliant on VRE sources such as wind and solar energy, should be capable of delivering a reliable power service that could satisfy consumers’ demand at any time, or most of the time [3]. Nevertheless, delivering a reliable power service based on VRE sources faces some challenges such as the (large) extent of the intermittency driven by the natural variability of climate factors such as air temperature, wind velocity, solar radiation, etc. [4]. Many previous studies have explored the spatial and/or temporal variability of VRE resources across the globe (see [5,6,7,8,9,10]). The intermittency of VRE can typically lead to drastic and sudden changes in power production over the year–an issue that is critical for the reliability of the power system [11].
VRE resources also exhibit significant sensitivity to extreme values of climatic variables. This can be disadvantageous to the sustainable (day-to-day, seasonal, etc.) power production, and may lead to “energy droughts”, i.e., periods of low power production or high energy demand/supply imbalance [12,13]. Although low-power-production periods may not exert a critical influence on power production in some regions [14], in a setting where energy supply comes from a local VRE power production system, such periods can lead to energy supply failures when the demand cannot be fully met [9,15]. Resource variability and low-power-production periods are typically dealt with by using energy storage facilities, by increasing the power generation capacity or introducing backup systems, and by demand flexibility (see [9,15,16,17,18,19,20]).

1.3. Wind-Based Decentralized Power Systems for Electrification in Africa

According to the International Energy Agency, as of 2019, only 38% of people in rural regions in Africa have access to electricity (www.iea.org accessed on 20 May 2021), and universal access to electricity is not going to be reached by 2030 in Sub-Saharan Africa by using the usual technologies [21]. However, many areas in Africa have been proven to be capable of meeting this challenge, since they are endowed with a potential for renewable energy resources that covers many times their current energy consumption [7] (see also Table 1 for Sub-Saharan countries). A 100% renewable resource-based system can provide sufficient power for all electricity demand at a low cost in Sub-Saharan Africa [22]. Indeed, decentralized wind and solar power systems can expand energy access to millions of people in many remote and rural areas in Africa [23,24,25].
The interest in solar energy is obviously large over the whole continent, but [7,27] have shown that wind energy should also be attractive and promising for a considerable number of regions. In certain regions, wind energy can even exceed the current electrical power consumption [7]. In regions with relatively high average wind speeds, wind power can be economically competitive compared to solar photovoltaic and/or diesel power [27].
In regions with suitable wind resources, utility-scale wind farms are globally increasing in number [28,29,30] thanks to their relatively high capacity of energy generation at low cost [31]. At smaller scales, it is expected that more and more stand-alone wind energy systems will be used to feed off-grid power systems [32,33]. While some techno-economic analyses of the performance of stand-alone wind micro-grids (on their own or in comparison with other VRE resources such as photovoltaic) in Africa have been conducted [27,34,35], large-scale empirical assessments of the reliability of wind power systems across the continent remain scarce. In particular, previous studies have taken little or no notice of low-power-production periods and reliability for the quality level of power services that can be delivered (a noticeable exception is the work of [11], which is restricted to South Africa). Hence, there is still a major gap in our continent-scale understanding of the wind power potential and its variability at different time scales, as well as the impact of low-wind-resource periods on wind power in Africa.
The present paper aims to fill this gap by providing a continent-wide evaluation of the reliability of hypothetical autonomous power systems that would only rely on the local wind resource for power production. Relying on a meteorological reanalysis dataset for the 2000–2017 period, we characterize the adequacy and temporal variability of the local wind power potential and assess the reliability of the resource with a focus on low-wind days with the help of an applicative yet intuitive approach. We also assess how demand flexibility (deferring a fraction of demand of one day to the next day) would help in coping with low-power-production periods.
Overall, our research contributes in multiple ways to the existing literature on wind power reliability and variability. First, to the best of the author’s knowledge, no previous study has used large-scale data of comparable quality to the data used in the present work. Owing to this data, we were able to provide a comprehensive analysis of wind resource variability in Africa at the continent level. Second, this study is the first to take into account the impacts of low-wind-resource periods on the service quality of a power system at a continent-scale. Our study offers an innovative yet simple framework for the identification of low-wind-resource regions in Africa and investigates the influence of resource scarcity on the reliability of wind power potential. Finally, by offering a simple demand-side management solution, we assess whether the issue of low-power-production periods could be addressed.
The paper is organized as follows. Section 2 presents data and methods. Results are presented in Section 3 and discussed in Section 4. Section 5 concludes.

2. Materials and Methods

Our study area extends over the whole continent of Africa, from a latitude of about −35° in South Africa to around 40° in Tunisia and from a longitude of around −20° in Senegal to 50° in Somalia. Earth’s Equator passes through the middle of Africa, splitting it into regions with diverse climatic conditions from equatorial, tropical wet and dry and desert or semi-arid to mountain climate. We used hourly estimates of wind speed at an elevation of 10 m in the ERA5 meteorological reanalysis dataset, the latest generation of ECMWF (European Centre for Medium-Range Weather Forecasts, https://www.ecmwf.int/ (accessed on 20 May 2021)) atmospheric reanalyzes of the global climate [36,37]. The wind speed data with a spatial resolution of 0.250 × 0.250 (a 30 km grid) have been extracted for an 18-year period, from 2000 to 2017.
The power produced by a wind turbine is a non-linear function of wind speed. Each wind turbine has its own “power curve”, a graph that relates the wind power production to the wind speed. This curve is typically characterized by three wind speed values: cut-in speed, rated speed, and cut-out speed. The cut-in speed is the minimum wind speed required to activate the wind turbine; no production is obtained for a wind speed lower than the cut-in speed. The rated speed is the wind speed at which the wind turbine reaches its rated power, i.e., the maximum power that the turbine can produce. The cut-out speed is the maximum wind speed that a wind turbine can manage, i.e., the turbine has to be turned off at speeds beyond the cut-out speed.
Converting wind speed to wind power thus necessitates the selection of an appropriate wind turbine that could be used in stand-alone energy systems in Africa. Wind speed thresholds do not vary a lot from one wind turbine to another. In other words, there is not much variation among wind turbines in terms of the critical wind speed values coupled with them. In most cases, wind turbines start generating electricity power when the wind speed is between 3 and 5 m/s, reach their maximum power at 11–12 m/s, and cut out, for security reasons, when wind speed is equal to or larger than the cut-out threshold around 25 m/s [30].
In low wind regions, extracting as much wind power as possible requires wind turbines with low cut-in thresholds [27]. One of these turbines is the FL 30 wind turbine, a product of the German manufacturer Fuhrländer AG, with 2.5, 12, and 25 m/s as cut-in, rated, and cut-out wind speeds, respectively [38]. This turbine was further used for our work to characterize the resource. It is rather a conservative choice. To our knowledge, it has indeed one of the least possible cut-in wind speeds among the commercial wind turbines available today. Note that these thresholds are close to the ones used in a previous study [35] on small wind energy systems in South Africa (cut-in wind speed: 2.5 and 4 m/s; rated wind speed: 10.5 and 12 m/s).
Fuhrländer FL 30, with rated power of 30 kW, can work at hub heights of 18, 24, and 27 m, which often offers the best techno-economic compromise for small/frugal installations such as those required for isolated MGs.
In this study, we fixed the desired hub height to the middle value of 24 m. Since the wind speed data have been recorded at an elevation of 10 m, we employed the logarithmic power law interpolation to convert wind speed at 10 m to speed at 24 m. The power law interpolation can be expressed as follows [39]:
log ( U ( z ) U ( z r ) ) = α ∗ log ( z z r )
where U(z) is the wind speed at the height of z and U(zr) is the wind speed at the height of zr; α is the power law exponent, which depends on the atmosphere stability. Consistent with [27], in the present study, we set the exponent to the constant value of 1/7, proposed by [36] for well-exposed sites and open areas.
To characterize the wind energy resource, we use the capacity factor (CF) of wind power for the above-mentioned turbine. The CF of a wind turbine for a given time is the ratio of the actual power generated by the turbine for the wind conditions at that time to the rated (peak) power of the turbine. The CF is thus a function of wind speed and varies in time.
Using the CF time series instead of the original power values allows for the transferability of the results to any other wind turbine that shares the same (or a similar) power curve, i.e., cut-in, rated, and cut-off wind speeds. For each grid point in the data, the wind power potential in terms of CF was calculated using hourly estimates of wind speed values over the study period. For our analysis, we then calculated for each day the daily average of hourly estimates of CF. The time series of mean daily CF was then used for characterizing the wind resource adequacy and its reliability. The adequacy of the wind power resource is typically evaluated with the mean CF value estimated over a period of time, assumed to be representative of the current climate context. In the following, we estimate for each location the mean CF value over the 18-year period of available wind data (2000 to 2017). We provide the interannual mean estimates for the annual, seasonal, and monthly time scales. Note that the least possible value of the mean CF (0) is obtained when the instantaneous wind speed at that site is always lower than the cut-in wind speed. The highest possible value of Mean CF (1) is achieved when wind conditions allow the wind turbine to produce its rated power without interruption. This would require that the wind speed always continuously remain between the rated and the cut-out speeds. In a study of the synergies of solar and wind power in West Africa, [40] have considered CF = 0.15 (a threshold stricter than the one proposed by [41]) as the minimum wind power potential required for an adequate resource. In the present study, the resource is considered to be adequate if CF is greater or equal to 0.2. This is a more conservative choice, but the sensitivity of our results to this choice is low (see discussion section).
In a 100% wind micro-grid configuration where the total demand is supposed to be satisfied by the generated wind power, low-resource days may have major impacts on the adequacy and reliability of the power system. Inadequacy of the wind power potential causes disruption to demand satisfaction. The storage of energy generated during high-resource periods for use in critically low-resource periods is one option to redress the imbalance between demand and power production. However, this might not always be feasible, especially where low-resource periods last several weeks or even months, a phenomenon that is frequently observed in some parts of the world due to the persistence of weather events. Increasing the size of the wind turbine fleet to produce more and ultimately sufficient energy can be another option for dealing with low-resource periods. The higher the number of wind turbines, the larger the production, the easier it should be to satisfy the demand each day, especially for days where the wind resource is low (provided the resource is not zero). Therefore, in a 100% wind MG, a way to increase the service quality level in low-resource days is to oversize the wind turbine fleet.
In the current study, we assumed a hypothetical configuration in which the available energy storage allows only for satisfying intraday demand-supply mismatch. In such a configuration, the service quality level is therefore contingent upon the amount of energy produced in low-wind days. We considered a low percentile of daily wind power potential (i.e., fifth percentile of CFs) to be a rough estimate of the minimum level of demand satisfaction. Let us assume that, in order for an energy system to attain the required level of service quality, it should satisfy the daily demand (kWh) in at least 95% of the days of the year. The daily wind power (kWh) production of one turbine for any given day j is 24 *Prated *CFj where Prated is the rated power (kW) of the turbine and where CFj is the mean capacity factor for that day. The daily wind power production of one turbine is therefore expected to be greater than 24 *Prated *CF5 in more than 95% of the days of the year, where CF5 is the fifth percentile of the mean daily CF values observed in the considered period. In the configuration where the daily demand is constant and equal to E0 (kWh), the number of wind turbines required to meet E0 in at least 95% of the days of the year would then be N = E0/(24 *Prated *CF5).
In the following, we will estimate for each location the 5th percentile of daily CF values from hourly time series of wind speed in the ERA5 data. We additionally examine the duration of low-wind-power periods for which CF is less than CF5, since short but numerous low-wind periods may have different impacts upon energy systems than long but rare low-wind-power periods. For this, we calculate the maximum number of consecutive days where the daily capacity factor falls below the CF5 value.
Finally, we additionally provide a map of the number of 30 kW wind turbines that would be required to satisfy an assumed constant demand of 100 kW for 95% of the days. From a socio-economical point of view, the number of wind turbines obtained will obviously be non-realistic for many locations. Nevertheless, for the sake of consistency and to provide a complete picture of the relevance or irrelevance of the wind power option for micro-grids development in Africa, we calculated the number of turbines for the whole continent.

3. Results

3.1. Mean Wind Power Resource at Annual and Seasonal Scales

The annual mean wind power potential (CF) and variability of daily CF values for 12 sample grid points across Africa over the 2000–2017 period are presented in Figure 1. This figure clearly illustrates the spatial and temporal variability of wind power potential in terms of CF. At the annual scale, the mean CF varies from values less than 0.1 in Central African countries near the Equator (from the latitude of around −10° to 10°), West Africa, Western Ethiopia, Morocco, and Madagascar, to 0.4 in large parts of North Africa, Horn of Africa, and Southern Africa (mostly in South Africa, Namibia, and Botswana). In a number of regions in Northwest Africa (particularly in Western Sahara and Mauritania), the mean CF even reaches 0.6.
Regardless of the location, the resource presents seasonality (see Figure S1 in Supplementary Materials). In some regions, the seasonality is rather moderate. Mean CF values are in the range of 0.2 to 0.4 in all seasons in large parts of Southern Africa (e.g., Namibia and Botswana). They are below 0.1 whatever the season in Ethiopia and a large area of Central Africa. The seasonality can be conversely rather important in some other regions. This is especially the case in the Horn of Africa, with mean CF between 0.2 and 0.4 in MAM (March, April, May) and SON (September, October, November) and up to 0.6 in JJA (June, July, August). This is also the case to a lesser extent in West and North Africa.
Overall, countries in the North, South, and Horn of Africa exhibit adequate mean wind power potential (CF ≥ 0.2) at the annual and seasonal scales, although there are some locally low values of CF in some seasons, especially in Morocco and Northern Algeria. Other regions highlight a likely insufficient resource despite a local rise of CF for some seasons. This is the case of Western Africa or in countries located in the South and the Southeast part of Central Africa (e.g., Angola, Kenya).

3.2. Mean Wind Power Resource at Monthly Scale

A more comprehensive evaluation of the wind power potential variability is presented in Figure 2 with the mean capacity factor (CFM) for each month. The spatial and monthly variability follows those already discussed in previous sections. Countries in the North, South, and Horn of Africa with adequate wind power potential (CF ≥ 0.2) at annual and seasonal scales satisfy the adequacy requirement of wind power production at the monthly scale as well.
Figure 3 presents the minimum and maximum values of CFM across the continent, and the corresponding month in which these two values are realized in each location. In Central and Western Africa, Ethiopia, and some local spots (e.g., in local sites in Morocco, Northern Algeria, Angola), the maximum mean monthly CFM values are quite low (close to zero in most parts). In these areas, the wind power potential is low all the time.
The wind resource is conversely very promising whatever the month in many regions. The minimum monthly mean CFM remains for instance within the range of 0.2–0.4 in the North, some local spots in Namibia, many local spots in South Africa and Botswana, and in the Horn of Africa. Very few regions with the good wind power potential at annual and seasonal scales actually fail at the monthly time scale (minimum CFM < 0.2).
At least 56% of grid points have adequate CF (CF ≥ 0.2) at annual and seasonal scales (see Table 2). This value decreases to 40% at the monthly scale. Despite the failure of some regions at the monthly scale, a considerable number of regions still exhibit great potential for accommodating wind power systems, provided that mean capacity factor is used as a tool for assessing the adequacy of wind power potential.
A clear North–South segmentation is observed for corresponding months of CFM extremes. In the Northern Hemisphere, the minimum CFM is achieved in the second half of the year (typically from August to November), while in the Southern Hemisphere, this minimum is realized in earlier months (typically from December to May). For both areas, the month with the maximum CFM is in the opposite “season”. This observation is almost consistent with the results of the seasonal analysis.

3.3. Daily Variability of Wind Power Resource

The daily resource variability is a key variability feature for assessing system reliability. It is illustrated in Figure 1 for a sample of 16 grid points across Africa. The daily resource variability obviously varies from one location to the other and from one season to the other for one location. For instance, for the location in Namibia, the variability is much less in DJF than in the other seasons. In Morocco, it is conversely much less in JJA.
To understand better, the daily variability of the resource is estimated for each location with the coefficient of variation (CV) of the daily mean CF values. It is estimated at the annual scale, from all daily values of the considered period, and for each season separately (Figure 4). Disregarding central Africa and central Ethiopia where the mean resource is very low, the CV at the annual scale varies from 0.45 in large parts of Northern and Southern Africa to values above 0.8 in Northwest and West Africa, Madagascar, and some Southeastern regions. Overall, most areas present a significant day-to-day variability of the resource for at least one season. Exceptions have to be mentioned in the parts of the Sahara, the Atlantic northern coast, or the Horn of Africa, suggesting some promising reliability of the wind resource. In other regions, the resource seems to be also rather reliable for two or three seasons, such as in parts of Southwest Africa and most parts of Sahara.
Part of this variability obviously derives from the seasonality of the resource. As highlighted in Figure 4, part of the variability also derives from the day-to-day variability of the weather. This is illustrated with the large CV values obtained in Northwest and Southeast Africa in almost all seasons, or in West Africa in JJA and SON or in Madagascar in DJF and MAM.
The fraction of daily variability explained by seasonality (and in symmetry by the weather day-to-day variability) is given in Figure 5. As already suggested by previous figures, this fraction obviously depends a lot on the region. For most countries in the North and South, seasonality explains not more than 40%, whereas in Central and West Africa, it increases to 70%, and in the Horn of Africa to 90%. It is interesting to note that this pattern is the opposite of the one presented by [14] for solar energy.

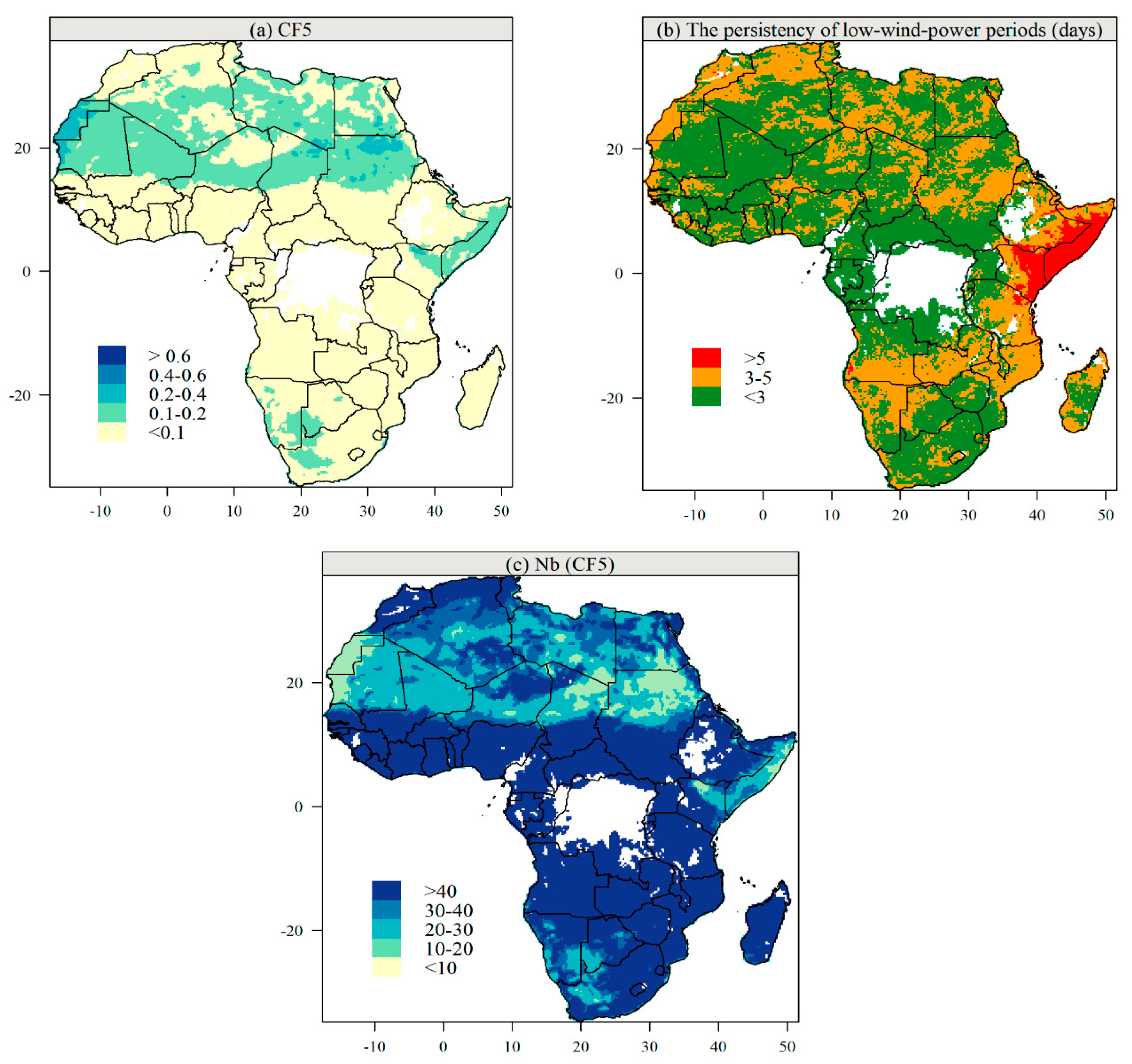
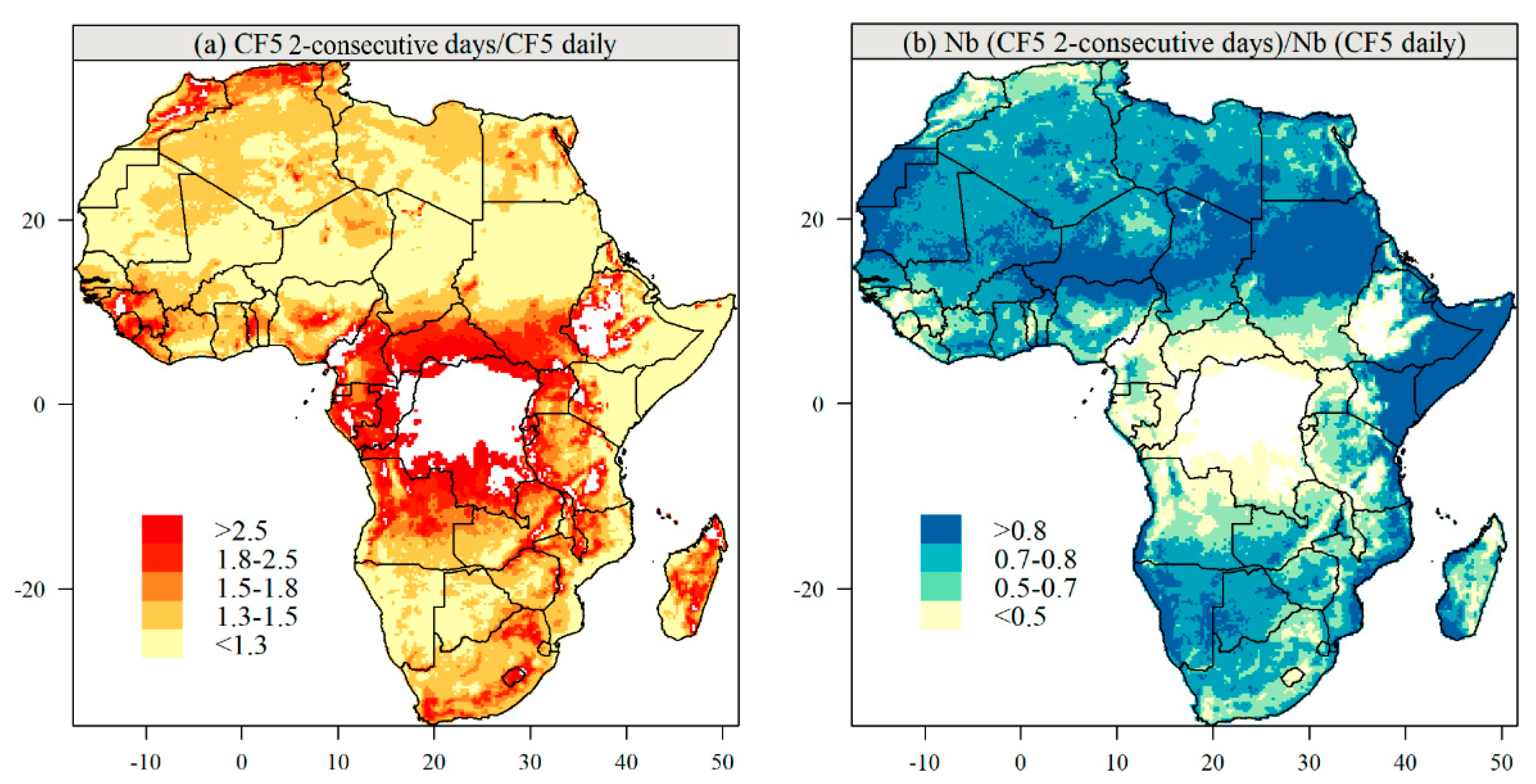
3.4. Low-Wind-Power Days and Periods

The spatial pattern of the fifth percentile of daily CF values (CF5) is presented in Figure 6a. Many locations in the North and a number of local spots in the South have CF5 values in the range of 0.1–0.2. There are also few spots with CF5 in the range of 0.2–0.4 in the North. Other areas exhibit CF5 values below 0.1. This means that, if we consider the value of CF5 (instead of mean CF) as the criterion for assessing the adequacy of wind resource potential, almost the whole continent fails (i.e., has a CF5 value below the minimum threshold of 0.2).
According to Table 2, only a small fraction of the continent area (2%) could reach the required level of CF in low-wind-power periods. This highlights the importance of taking into account low-wind-resource days and their potential impact on power production. Indeed, most regions that had shown great potential for wind power production in the first stage proved not to be adequate in terms of the wind power potential if a low CF percentile is used to assess the adequacy.
Another challenge posed by low-resource periods is their persistency. Low-resource periods in many regions last between two and three days (see Figure 6b). However, even in regions with relatively high (yet generally low) power potential (0.1 ≤ CF5 < 0.2), like some parts in Sudan or in the Horn of Africa, low-resource periods can last longer than three days. The maximum recorded duration is 10 days in the Horn of Africa. This observation reveals that, although low-resource days are rare, they can last for several days and lead to the failure of the power system.

3.5. Economic Viability of 100% Wind MGs: A Rough Guess

The minimum number of 30 kW wind turbines required to meet a constant 100 kW demand in at least 95% of days follows the same spatial pattern as the one for CF5. The greater the value of CF5, the smaller the required number of wind turbines. In a handful of areas such as Sudan, Chad, and Western Sahara, this number is smaller than 20 (see Figure 6c). In large parts of the North and a small region in the South, this number is between 20 and 30, and in Central, Southern, and Southeastern Africa, from Angola to Tanzania, the required number of wind turbines is greater than 40. In our configuration, this indicates that the number of required wind turbines is rather large in almost all locations across the continent. Consequently, the use of MG that are entirely reliant on wind may not be economically viable in a considerable part of the continent.

4. Discussion

4.1. Adequacy of Mean Wind Power Potential (CF ≥ 0.2) and Its Reliability

Mean wind power potential (at the hub height of 24 m) at local spots can reach 0.4 in the North, South, and the Horn of Africa at annual and seasonal scales. Nevertheless, in many regions, the value of mean CF is heavily season-dependent. Our results are consistent with the results of [12], who found that the highest technical power potential is achieved in Northern Africa, followed by the South and East.
The results of our study indicated that both the seasonal mean CF (~0.3–0.5 ≥ 0.2) and the minimum CFM (~0.3 ≥ 0.2) can be adequate for operating a wind power system in many parts in the North and South and the Horn of Africa. However, in many areas, the wind power potential is low all the time; examples are Central African countries, a large area of Western Ethiopia, and some local spots in Morocco and Northern Algeria.
Our findings for mean wind power are in agreement with the results of [27], who found that wind power systems are likely to be economically advantageous over solar photovoltaic and diesel systems in Somalia, Western Sahara, Chad, and South Africa, but not in many regions, especially in Central Africa, due to low wind speeds. Wind power production is obviously not relevant in a large latitudinal band around the Equator or in several specific regions such as Morocco and Northern Algeria. However, [27] only considered the mean daily wind resource and its variability for one whole year in their simulation and disregarded the seasonal and inter-annual dynamics of wind speeds. In contrast with them, we studied the resource seasonal variability. We showed that the resource seasonal variations can lead to a potentially large difference in required design or resource adequacy from one season to the other.
In addition to the adequacy of mean CF in the North and South (especially in the West and South along the coast) and in the Horn of Africa, the resource is reliable in these regions. We observed that the annual and seasonal mean capacity factors were not very variable over the study period, hence making the power system reliable for serviceability provided that the value of mean CF is the criterion for assessing the adequacy. Needless to say, the requirements of adequacy were not met in Central Africa, where the wind power potential was low and the wind resource variability was high.
Consistent with the findings of [11], we also observed that South Africa’s wind power potential varied across different timescales, with a higher reliability in summer (DJF) than winter (JJA). Overall, South Africa has moderate to high wind power potential, especially in the west and the south along the coast.

4.2. Coping with Low-Wind-Power Periods

Relying solely on mean capacity factor values and refusing to take notice of low-resource periods and their persistency when assessing the adequacy of wind power potential could be misleading. As previously shown, in many regions, the mean wind power potential (CF) satisfies the requirements of adequacy at annual, seasonal, and monthly scales. However, in the very same areas, not only is the fifth percentile of daily power potential (CF5) below the minimum threshold (0.2), but low resource conditions can also present significant persistence. To assess the reliability of a wind power system in a robust way, the adequacy of the power produced in low-resource periods as well as the persistency and duration of such periods should be accounted for in addition to the “average” adequacy of wind power potential.
The first option that comes to mind for addressing the problem of low-wind-power periods is to oversize the power system. This option, however, may not be economically relevant. Another possibility is to postpone some uses of electricity for use at a later time. The following section discusses such an option in more detail.

4.2.1. Demand Flexibility and Its Effects on the Micro-Grid Design

As shown in the results section, there is an inverse relationship between the values of CF5 and the number of wind turbines required to meet the demand. Assuming that micro-grids are designed such that they satisfy demand in at least 95% of the days of the year, and that there is no possibility for increasing the power system fleet size, one alternative option is to consider some flexibility of the demand. Indeed, consumers may adapt their daily demand and postpone a part of it to subsequent days when the resource is greater. This option can be preferable where oversizing the power system fleet is technically or economically unviable.
As demonstrated by [9], for 100% solar power-based micro-grids, day-to-day demand flexibility would help to achieve the required level of service quality with a smaller micro-grid system. In the present study, we implemented the same demand-side solution to a 100% wind power-based micro-grid. In this new configuration where demand flexibility is present, we considered that a part of the demand can be deferred until the next day.
In this regard, we calculated two-consecutive-day wind power potential (CF), which is the moving average of the energy potential over two days in sequence (i.e., the CF at day n is the average of the CF at days n and n−1). To assess the serviceability of the power system, we considered a configuration similar to the baseline configuration, where demand is expected to be satisfied in at least 95% of days of the year.
Therefore, in the first step, we calculated the ratio of the fifth percentile of two-consecutive-day CF values to the fifth percentile of daily CF values (CF5). Next, we calculated the number of 30 kW wind turbines required to meet a constant 100 kW demand in 95% of days of the year using the mean energy potential over the two consecutive days (and divided this number by the number of wind turbines required to meet demand in 95% of days of the year using the mean daily energy potential) to assess the service quality level in the configuration with day-to-day demand flexibility. In the other similar study of Africa [27], the resource persistency was disregarded, and the possibility of demand flexibility was not considered.
The CF5 value of the mean power potential over two consecutive days is obviously always greater than the CF5 value estimated previously for one day (Figure 7a). At some coastline areas as well as a considerable number of spots in Angola, the Central African Republic, and South Sudan, CF5 over two consecutive days is at least 1.8 times greater than daily CF5. Even a large part of the North, especially in the Maghreb, the West, and the South exhibit considerable proportions in the range of 1.3–1.5. This proportion increases to 1.8 in some local spots in these regions. The number of grid points with adequate CF (CF ≥ 0.0.2) increases by 150% compared to daily CFs (see Table 2).
Consequently, the flexibility of demand can significantly decrease the size of the power system in areas with low daily CF5 values. Indeed, the number of wind turbines required to meet demand decreases by up to 50% in many regions around Central Africa. In numerous local spots in the South and in Madagascar, as well as a few local spots in the North, this number decreases by about 40%. Even in the North, especially in the Maghreb, the number of required wind turbines decreases by about 20%. In large parts of Sudan, Chad, Niger, Western Sahara, and West Africa, no considerable change can be observed (Figure 7b).

4.2.2. Mixing Variable Renewable Energy (VRE) Resources

Another solution to the problem of the low VRE resource periods (like wind) and the mismatch between the demand and the production is to combine two or more different VRE resources that could be complementary in a power system [12,42]. For instance, power systems that rely entirely on solar energy may fail, at sub-daily time scales, to keep pace with demand during the night or in winter and fall, where high cloud cover prevents solar radiation from passing to the surface. In such a setting, combining solar and wind energy resources in a hybrid power system could address this problem. Mixing VRE sources has been found to allow for a significant reduction of the severity and frequency of low VRE resource periods [12].
Many studies have investigated the combination of different VRE resources with the aim of reducing imbalances between energy supply and energy demand [12,42,43,44], reducing the variability of power output [45,46,47], cost optimization [48,49,50,51] and enhancing the stability of the power system [40].
Within the context of this study, such a solution may be used in regions where the wind power potential is not always sufficient. [40] have already shown the feasibility of hybrid power systems in West Africa, a region characterized by low wind energy potential. The influence of hybridization for improving the reliability of the production would be worth investigating in the following.

4.3. Sensitivity of the Results to the Capacity Factor Threshold

Having set the minimum threshold of mean CF to 0.2, we showed that, at annual and seasonal scales, at least 40% of grid points, and at the monthly scale, around 56% of the grid points have mean CF ≥ 0.2. In addition, our findings demonstrated that only 2% of grid points have CF5≥ 0.2 (see Table 2). In order to test the robustness of our results to the threshold selection, we performed the analyses again using the threshold proposed by [40]. In the new configuration, we considered the threshold of 0.15 for the minimum level of power production adequacy. The results did not change significantly. At least 64% of grid points at annual and seasonal scales and around 48% of the grid points at the monthly scale have CF ≥ 0.15, and only 9% of grid points have CF5 ≥ 0.15. In conclusion, the significant impact of low-resource periods on wind power production was still present, and our findings were robust to the threshold selection.

5. Conclusions and Perspectives

In this applied study, we used hourly estimates of wind speed provided by the ERA5 climate reanalysis dataset to evaluate the adequacy, sustainability, and thus reliability of wind power resources across Africa at different time scales, and to assess the impact of low-power-production periods over an 18-year period. We considered the threshold of 0.2 as the minimum wind power potential (capacity factor) required for operating a power system.
The results of our study indicated that the annual and seasonal mean wind power potential (~0.3–0.5 ≥ 0.2), and the minimum monthly mean capacity factor (~0.3 ≥ 0.2) can be adequate for operating a wind power system in many parts in the North and South and in the Horn of Africa. The wind power potential is even less variable in these regions, and thus the reliability requirement of the power system is satisfied. However, in the very same areas, not only is the wind power resource in low-power-production periods below the minimum threshold (0.2), but the persistence of these low resource periods (i.e., the number of consecutive days with low resource) is also noticeable. In this regard, our analysis showed that in a considerable number of locations, 30 or more 30 kW wind turbines would be required to meet a 100 kW constant demand for at least 95% of days. If some demand flexibility is considered, this number can decrease by 20% to 50%.
This research highlights the critical impact of low-power-production periods on wind power potential and the key role that might be played by energy storage facilities, issues and/or demand flexibility that need to be addressed by policymakers in preliminary analyses of micro-grid design.
This study made use of a reanalysis dataset with relatively high spatiotemporal resolution at a large scale. A more in-depth analysis of the adequacy, sustainability, and technical and economic feasibility of wind power systems (especially during low-resource periods) at a local scale would require observational data, preferably with a higher resolution than that of the data used in the current study. In a recently published article, [52] examined wind potential characteristics and carried out a techno-economic feasibility analysis of wind turbines in Mauritania by relying on observational data collected from eight sites. Such detailed studies are obviously required at the end.
We assessed the relevance of 100% wind power systems during low-wind periods. Future research might explore the feasibility of hybrid systems (in which the complementarity of different VRE’s can reduce the problem of intermittency), especially during low-resource periods in Africa [12].
The inter- and intra-annual variability of wind resources can change due to global climate change. Climate change could provide favorable conditions for some regions in terms of the possibility of exploiting wind power, while the opposite may occur in other places [53]. The future potential of wind energy over Africa under a warming climate is actually uncertain [54], and different models can typically project changes of different signs in specific regions (as shown by [55] for Europe; see also [56]). The last multi model ensemble of projections from the high-resolution CORDEX-Africa climate experiments would be worth investigation in this respect as in [57,58] for the possible evolutions of the solar resource potential over the continent. For wind resources, a methodology similar to the one used in this paper can be applied to future projections of wind speed to examine the sensitivity of the reliability of wind power systems to climate change.
The minimum capacity factor threshold that was used in this study for assessing the adequacy of wind power potential (0.2) was rather a strict threshold that enabled us to avoid overestimating the wind power potential in Africa. The power generation capacity of wind turbines has experienced an increase owing to innovative constructive solutions [59] and technological improvements to the average hub height, turbine rating, and rotor diameters, and a rising trend in R&D investments [30,60]. Such solutions can increase energy efficiency and may have major implications for sustainable growth and environmental development [59]. With the latest technology advancements in the design and manufacturing of onshore wind turbines, a less strict threshold might therefore be used in future research to evaluate the adequacy of wind power potential in different regions of the world, including but not limited to Africa.

Supplementary Materials

The following is available online at https://www.mdpi.com/article/10.3390/en14112978/s1, Figure S1: The mean wind power potential in terms of CF over the 2000–2017 period.

Author Contributions

Conceptualization and methodology: H.S., B.H. and C.L.; software, formal analysis, writing—original draft preparation: H.S.; writing—review and editing: H.S., B.H., C.L. and T.C. All authors have read and agreed to the published version of the manuscript.

Funding

This research received no external funding.

Institutional Review Board Statement

Not applicable.

Informed Consent Statement

Not applicable.

Data Availability Statement

The data presented in this study are openly available at https://doi.org/10.24381/cds.adbb2d47 (accessed on 20 May 2021).

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Fay, M.; Hallegatte, S.; Vogt-Schilb, A.; Rozenberg, J.; Narloch, U.; Kerr, T. Decarbonizing Development: Three Steps to a Zero-Carbon Future; The World Bank: Washington, DC, USA, 2015. [Google Scholar]
  2. Kaundinya, D.P.; Balachandra, P.; Ravindranath, N. Grid-connected versus stand-alone energy systems for decentralized power—A review of literature. Renew. Sustain. Energy Rev. 2009, 13, 2041–2050. [Google Scholar] [CrossRef]
  3. Marnay, C.; Venkataramanan, G. Microgrids in the evolving electricity generation and delivery infrastructure. In Proceedings of the 2006 IEEE Power Engineering Society General Meeting, Montreal, QC, Canada, 18–22 June 2006; p. 5. [Google Scholar] [CrossRef] [Green Version]
  4. Engeland, K.; Borga, M.; Creutin, J.-D.; François, B.; Ramos, M.-H.; Vidal, J.-P. Space-time variability of climate variables and intermittent renewable electricity production—A review. Renew. Sustain. Energy Rev. 2017, 79, 600–617. [Google Scholar] [CrossRef]
  5. Lave, M.; Kleissl, J.; Arias-Castro, E. High-frequency irradiance fluctuations and geographic smoothing. Sol. Energy 2012, 86, 2190–2199. [Google Scholar] [CrossRef] [Green Version]
  6. Sørensen, P.E.; Cutululis, N.A.; Vigueras-Rodriguez, A.; Jensen, L.E.; Hjerrild, J.; Donovan, M.H.; Madsen, H. Power Fluctuations from Large Wind Farms. IEEE Trans. Power Syst. 2007, 22, 958–965. [Google Scholar] [CrossRef]
  7. Mentis, D.; Hermann, S.; Howells, M.; Welsch, M.; Siyal, S.H. Assessing the technical wind energy potential in Africa a GIS-based approach. Renew. Energy 2015, 83, 110–125. [Google Scholar] [CrossRef]
  8. Kariuki, B.W.; Sato, T. Interannual and spatial variability of solar radiation energy potential in Kenya using Meteosat satellite. Renew. Energy 2018, 116, 88–96. [Google Scholar] [CrossRef]
  9. Plain, N.; Hingray, B.; Mathy, S. Accounting for low solar resource days to size 100% solar microgrids power systems in Africa. Renew. Energy 2019, 131, 448–458. [Google Scholar] [CrossRef]
  10. Schindler, D.; Behr, H.D.; Jung, C. On the spatiotemporal variability and potential of complementarity of wind and solar resources. Energy Convers. Manag. 2020, 218, 113016. [Google Scholar] [CrossRef]
  11. Fant, C.; Gunturu, B.; Schlosser, A. Characterizing wind power resource reliability in southern Africa. Appl. Energy 2016, 161, 565–573. [Google Scholar] [CrossRef] [Green Version]
  12. Raynaud, D.; Hingray, B.; François, B.; Creutin, J. Energy droughts from variable renewable energy sources in European climates. Renew. Energy 2018, 125, 578–589. [Google Scholar] [CrossRef]
  13. van der Wiel, K.; Stoop, L.; van Zuijlen, B.; Blackport, R.; Broek, M.V.D.; Selten, F. Meteorological conditions leading to extreme low variable renewable energy production and extreme high energy shortfall. Renew. Sustain. Energy Rev. 2019, 111, 261–275. [Google Scholar] [CrossRef]
  14. Sinden, G. Characteristics of the UK wind resource: Long-term patterns and relationship to electricity demand. Energy Policy 2007, 35, 112–127. [Google Scholar] [CrossRef]
  15. Huld, T.; Moner-Girona, M.; Kriston, A. Geospatial Analysis of Photovoltaic Mini-Grid System Performance. Energies 2017, 10, 218. [Google Scholar] [CrossRef] [Green Version]
  16. Celli, G.; Pilo, F.; Pisano, G.; Soma, G. Optimal participation of a microgrid to the energy market with an intelligent EMS. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005; pp. 663–668. [Google Scholar] [CrossRef]
  17. Chen, S.X.; Gooi, H.B.; Wang, M.Q. Sizing of Energy Storage for Microgrids. IEEE Trans. Smart Grid 2012, 3, 142–151. [Google Scholar] [CrossRef]
  18. Hedegaard, K.; Meibom, P. Wind power impacts and electricity storage—A time scale perspective. Renew. Energy 2012, 37, 318–324. [Google Scholar] [CrossRef]
  19. Al-Falahi, M.D.; Jayasinghe, S.; Enshaei, H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
  20. Perez, M.; Perez, R.; Rábago, K.R.; Putnam, M. Overbuilding & curtailment: The cost-effective enablers of firm PV generation. Sol. Energy 2019, 180, 412–422. [Google Scholar] [CrossRef]
  21. Van Ruijven, B.J.; Schers, J.; van Vuuren, D.P. Model-based scenarios for rural electrification in developing countries. Energy 2012, 38, 386–397. [Google Scholar] [CrossRef] [Green Version]
  22. Barasa, M.; Bogdanov, D.; Oyewo, A.S.; Breyer, C. A cost optimal resolution for Sub-Saharan Africa powered by 100% renewables in 2030. Renew. Sustain. Energy Rev. 2018, 92, 440–457. [Google Scholar] [CrossRef]
  23. Deichmann, U.; Meisner, C.; Murray, S.; Wheeler, D. The economics of renewable energy expansion in rural Sub-Saharan Africa. Energy Policy 2011, 39, 215–227. [Google Scholar] [CrossRef] [Green Version]
  24. Johnson, N.G.; Bryden, K.M. Energy supply and use in a rural West African village. Energy 2012, 43, 283–292. [Google Scholar] [CrossRef]
  25. Xu, Z.; Nthontho, M.; Chowdhury, S. Rural electrification implementation strategies through microgrid approach in South African context. Int. J. Electr. Power Energy Syst. 2016, 82, 452–465. [Google Scholar] [CrossRef]
  26. Wheeler, D.; That, T.T.; Meisner, C.; Deichmann, U.; Buys, P. Country Stakes in Climate Change Negotiations: Two Dimensions of Vulnerability; Policy Research Working Paper Series; The World Bank: Washington, DC, USA, 2007. [Google Scholar]
  27. Gabra, S.; Miles, J.; Scott, S.A. Techno-economic analysis of stand-alone wind micro-grids, compared with PV and diesel in Africa. Renew. Energy 2019, 143, 1928–1938. [Google Scholar] [CrossRef]
  28. Sayas, F.C.; Allan, R. Generation availability assessment of wind farms. IEE Proc. Gener. Transm. Distrib. 1996, 143, 507–518. [Google Scholar] [CrossRef]
  29. Billinton, R.; Gao, Y. Multistate Wind Energy Conversion System Models for Adequacy Assessment of Generating Systems Incorporating Wind Energy. IEEE Trans. Energy Convers. 2008, 23, 163–170. [Google Scholar] [CrossRef]
  30. IRENA. Renewable Power Generation Costs in 2017; IRENA: Masdar City, Abu Dhabi, United Arab Emirates, 2018. [Google Scholar]
  31. Dimitrovski, A.; Tomsovic, K. Impact of Wind Generation Uncertainty on Generating Capacity Adequacy. In Proceedings of the 2006 International Conference on Probabilistic Methods Applied to Power Systems, Stockholm, Sweden, 11–15 June 2006; pp. 1–6. [Google Scholar] [CrossRef]
  32. López-González, A.; Ranaboldo, M.; Domenech, B.; Ferrer-Martí, L. Evaluation of small wind turbines for rural electrification: Case studies from extreme climatic conditions in Venezuela. Energy 2020, 209, 118450. [Google Scholar] [CrossRef]
  33. Ferrer-Martí, L.; Garwood, A.; Chiroque, J.; Ramirez, B.; Marcelo, O.; Garfí, M.; Velo, E. Evaluating and comparing three community small-scale wind electrification projects. Renew. Sustain. Energy Rev. 2012, 16, 5379–5390. [Google Scholar] [CrossRef]
  34. Szabó, S.; Bódis, K.; Huld, T.; Moner-Girona, M. Energy solutions in rural Africa: Mapping electrification costs of distributed solar and diesel generation versus grid extension. Environ. Res. Lett. 2011, 6, 034002. [Google Scholar] [CrossRef]
  35. Olatayo, K.I.; Wichers, J.H.; Stoker, P.W. Energy and economic performance of small wind energy systems under different climatic conditions of South Africa. Renew. Sustain. Energy Rev. 2018, 98, 376–392. [Google Scholar] [CrossRef]
  36. Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 global reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
  37. ECMWF. Advancing Global NWP through International Collaboration. Available online: https://www.ecmwf.int/ (accessed on 5 April 2021).
  38. Fuhrländer FL 30—30.00 kW—Wind Turbine. Available online: https://en.wind-turbine-models.com/turbines/278-fuhrlaender-fl-30 (accessed on 5 April 2021).
  39. Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application; John Wiley & Sons: Hoboken, NJ, USA, 2010. [Google Scholar]
  40. Sterl, S.; Liersch, S.; Koch, H.; Van Lipzig, N.P.M.; Thiery, W. A new approach for assessing synergies of solar and wind power: Implications for West Africa. Environ. Res. Lett. 2018, 13, 094009. [Google Scholar] [CrossRef]
  41. Jacobson, M.Z.; Delucchi, M.A.; Bauer, Z.A.; Goodman, S.C.; Chapman, W.E.; Cameron, M.A.; Bozonnat, C.; Chobadi, L.; Clonts, H.A.; Enevoldsen, P.; et al. 100% Clean and Renewable Wind, Water, and Sunlight All-Sector Energy Roadmaps for 139 Countries of the World. Joule 2017, 1, 108–121. [Google Scholar] [CrossRef] [Green Version]
  42. Jurasz, J.; Canales, F.; Kies, A.; Guezgouz, M.; Beluco, A. A review on the complementarity of renewable energy sources: Concept, metrics, application and future research directions. Sol. Energy 2020, 195, 703–724. [Google Scholar] [CrossRef]
  43. Heide, D.; von Bremen, L.; Greiner, M.; Hoffmann, C.; Speckmann, M.; Bofinger, S. Seasonal optimal mix of wind and solar power in a future, highly renewable Europe. Renew. Energy 2010, 35, 2483–2489. [Google Scholar] [CrossRef]
  44. Francois, B.; Borga, M.; Creutin, J.; Hingray, B.; Raynaud, D.; Sauterleute, J. Complementarity between solar and hydro power: Sensitivity study to climate characteristics in Northern-Italy. Renew. Energy 2016, 86, 543–553. [Google Scholar] [CrossRef]
  45. Danso, D.K.; François, B.; Hingray, B.; Diedhiou, A. Assessing hydropower flexibility for integrating solar and wind energy in West Africa using dynamic programming and sensitivity analysis. Illustration with the Akosombo reservoir, Ghana. J. Clean. Prod. 2021, 287, 125559. [Google Scholar] [CrossRef]
  46. François, B.; Hingray, B.; Raynaud, D.; Borga, M.; Creutin, J. Increasing climate-related-energy penetration by integrating run-of-the river hydropower to wind/solar mix. Renew. Energy 2016, 87, 686–696. [Google Scholar] [CrossRef]
  47. Zhang, H.; Cao, Y.; Zhang, Y.; Terzija, V. Quantitative synergy assessment of regional wind-solar energy resources based on MERRA reanalysis data. Appl. Energy 2018, 216, 172–182. [Google Scholar] [CrossRef]
  48. Bekele, G.; Tadesse, G. Feasibility study of small Hydro/PV/Wind hybrid system for off-grid rural electrification in Ethiopia. Appl. Energy 2012, 97, 5–15. [Google Scholar] [CrossRef]
  49. Budischak, C.; Sewell, D.; Thomson, H.; Mach, L.; Veron, D.E.; Kempton, W. Cost-minimized combinations of wind power, solar power and electrochemical storage, powering the grid up to 99.9% of the time. J. Power Sources 2013, 225, 60–74. [Google Scholar] [CrossRef] [Green Version]
  50. Adaramola, M.S.; Agelin-Chaab, M.; Paul, S.S. Analysis of hybrid energy systems for application in southern Ghana. Energy Convers. Manag. 2014, 88, 284–295. [Google Scholar] [CrossRef]
  51. Gils, H.C.; Scholz, Y.; Pregger, T.; de Tena, D.L.; Heide, D. Integrated modelling of variable renewable energy-based power supply in Europe. Energy 2017, 123, 173–188. [Google Scholar] [CrossRef] [Green Version]
  52. Bilal, B.; Adjallah, K.H.; Yetilmezsoy, K.; Bahramian, M.; Kıyan, E. Determination of wind potential characteristics and techno-economic feasibility analysis of wind turbines for Northwest Africa. Energy 2021, 218, 119558. [Google Scholar] [CrossRef]
  53. Pryor, S.; Barthelmie, R.J. Climate change impacts on wind energy: A review. Renew. Sustain. Energy Rev 2010, 14, 430–437. [Google Scholar] [CrossRef]
  54. Sawadogo, W.; Reboita, M.S.; Faye, A.; Da Rocha, R.P.; Odoulami, R.C.; Olusegun, C.F.; Adeniyi, M.O.; Abiodun, B.J.; Sylla, M.B.; Diallo, I.; et al. Current and future potential of solar and wind energy over Africa using the RegCM4 CORDEX-CORE ensemble. Clim. Dyn. 2020. [Google Scholar] [CrossRef]
  55. Moemken, J.; Reyers, M.; Feldmann, H.; Pinto, J.G. Future Changes of Wind Speed and Wind Energy Potentials in EURO-CORDEX Ensemble Simulations. J. Geophys. Res. Atmos. 2018, 123, 6373–6389. [Google Scholar] [CrossRef]
  56. Wang, S.; Yang, H.; Pham, Q.B.; Khoi, D.N.; Nhi, P.T.T. An Ensemble Framework to Investigate Wind Energy Sustainability Considering Climate Change Impacts. Sustainability 2020, 12, 876. [Google Scholar] [CrossRef] [Green Version]
  57. Bichet, A.; Hingray, B.; Evin, G.; Diedhiou, A.D.; Kebe, C.M.F.; Anquetin, S. Potential impact of climate change on solar resource in Africa for photovoltaic energy: Analyses from CORDEX-AFRICA climate experiments. Environ. Res. Lett. 2019, 14, 124039. [Google Scholar] [CrossRef]
  58. Soares, P.M.M.; Brito, M.C.; Careto, J. Persistence of the high solar potential in Africa in a changing climate. Environ. Res. Lett. 2019, 14, 124036. [Google Scholar] [CrossRef]
  59. Florescu, A.; Barabas, S.; Dobrescu, T. Research on Increasing the Performance of Wind Power Plants for Sustainable Development. Sustainability 2019, 11, 1266. [Google Scholar] [CrossRef] [Green Version]
  60. Miller, L.M.; Keith, D.W. Corrigendum: Observation-based solar and wind power capacity factors and power densities (2018 Environ. Res. Lett. 13 104008). Environ. Res. Lett. 2019, 14, 079501. [Google Scholar] [CrossRef]
Energies 14 02978 g001 550
Figure 1. The mean wind power potential in terms of CF at annual scale over the 2000–2017 period in the center. The mean seasonal CFs are presented in Figure S1 in Supplementary Materials. The figures around the Annual CF show the variability of daily CF values (unitless) for 16 sample grid points in different climates. The y-axis and x-axis in small graphs exhibit the values of CF (from 0 (no wind power) to 1 (wind power equal to rated power of the turbine)) and time of the year (days from January to December), respectively. All the figures have the same scale. The solid grey line is the mean and the boundaries are showing 10th and 90th percentiles of CF values over the study period (2000–2017). Note that the wind resource (mean and variability) can vary a lot from one location to the other within a country.
Figure 1. The mean wind power potential in terms of CF at annual scale over the 2000–2017 period in the center. The mean seasonal CFs are presented in Figure S1 in Supplementary Materials. The figures around the Annual CF show the variability of daily CF values (unitless) for 16 sample grid points in different climates. The y-axis and x-axis in small graphs exhibit the values of CF (from 0 (no wind power) to 1 (wind power equal to rated power of the turbine)) and time of the year (days from January to December), respectively. All the figures have the same scale. The solid grey line is the mean and the boundaries are showing 10th and 90th percentiles of CF values over the study period (2000–2017). Note that the wind resource (mean and variability) can vary a lot from one location to the other within a country.
Energies 14 02978 g001
Energies 14 02978 g002 550
Figure 2. The monthly mean wind power potential in terms of CF over the 2000–2017 period.
Figure 2. The monthly mean wind power potential in terms of CF over the 2000–2017 period.
Energies 14 02978 g002
Energies 14 02978 g003 550
Figure 3. (a,b): minimum CFM and the corresponding month of occurrence; (c,d): maximum CFM and the corresponding month of occurrence.
Figure 3. (a,b): minimum CFM and the corresponding month of occurrence; (c,d): maximum CFM and the corresponding month of occurrence.
Energies 14 02978 g003
Energies 14 02978 g004 550
Figure 4. The annual and seasonal variability of daily CF in terms of coefficient of variation over the study period (2000–2017): (a) over the year; (b) DJF (December, January, February); (c) MAM (March, April, May); (d) JJA (June, July, August) and (e) SON (September, October, November). The coefficient of variation is calculated by dividing the standard deviation by mean (σ/μ, where µ and σ are the mean and the standard deviation of daily CF for a desired season over the study period). For the sake of readability, CV values greater than 1 were set to 1.
Figure 4. The annual and seasonal variability of daily CF in terms of coefficient of variation over the study period (2000–2017): (a) over the year; (b) DJF (December, January, February); (c) MAM (March, April, May); (d) JJA (June, July, August) and (e) SON (September, October, November). The coefficient of variation is calculated by dividing the standard deviation by mean (σ/μ, where µ and σ are the mean and the standard deviation of daily CF for a desired season over the study period). For the sake of readability, CV values greater than 1 were set to 1.
Energies 14 02978 g004
Energies 14 02978 g005 550
Figure 5. Percentage of the daily variability of CF at the annual scale that can be explained by the annual cycle of CF. The calculation of the statistic is inspired by the work of [9]. The percentage is expressed as α = σ1/σ0, where σ0 is the standard deviation of daily CF values calculated from all daily data in the 2000–2017 period (σ02 = 1/(n − 1) Σj=1..n(CF(j) − µ)2, where CF(j) is the daily CF value at day j, µ is the mean daily CF for the period and n is the number of days in the period), σ1 is the standard deviation of daily CF values calculated from the 365 daily values of an average year (σ12 = 1/(365 − 1) Σd=1..365(CF(d) − µ)2 where CF(d) is the inter-annual mean CF (mean over 18 years)) for the calendar day d = 1, 365 (i.e., value for d on the solid curve in Figure 1).
Figure 5. Percentage of the daily variability of CF at the annual scale that can be explained by the annual cycle of CF. The calculation of the statistic is inspired by the work of [9]. The percentage is expressed as α = σ1/σ0, where σ0 is the standard deviation of daily CF values calculated from all daily data in the 2000–2017 period (σ02 = 1/(n − 1) Σj=1..n(CF(j) − µ)2, where CF(j) is the daily CF value at day j, µ is the mean daily CF for the period and n is the number of days in the period), σ1 is the standard deviation of daily CF values calculated from the 365 daily values of an average year (σ12 = 1/(365 − 1) Σd=1..365(CF(d) − µ)2 where CF(d) is the inter-annual mean CF (mean over 18 years)) for the calendar day d = 1, 365 (i.e., value for d on the solid curve in Figure 1).
Energies 14 02978 g005
Energies 14 02978 g006 550
Figure 6. Low-wind-power days: (a) the fifth percentile of daily capacity factor for the 2000–2017 period (CF5); (b) the persistency of low-wind days; (c) the number of 30 kW wind turbines required to meet a constant 100 kW demand in at least 95% of days of the year (Nb (CF5)). The areas for which the fifth percentile of daily capacity factor is zero are masked (white color).
Figure 6. Low-wind-power days: (a) the fifth percentile of daily capacity factor for the 2000–2017 period (CF5); (b) the persistency of low-wind days; (c) the number of 30 kW wind turbines required to meet a constant 100 kW demand in at least 95% of days of the year (Nb (CF5)). The areas for which the fifth percentile of daily capacity factor is zero are masked (white color).
Energies 14 02978 g006
Energies 14 02978 g007 550
Figure 7. Low-wind days: (a) the ratio of the fifth percentile of capacity factor over two consecutive days to fifth percentile of daily capacity factor (CF5) for the 2000–2017 period; (b) the proportion of the number of wind turbines required to meet demand in at least 95% of days of the year when two-consecutive-day mean CF is used to the case where daily CF5 values are used. The areas for which the fifth percentile of the capacity factor is zero are masked (white color).
Figure 7. Low-wind days: (a) the ratio of the fifth percentile of capacity factor over two consecutive days to fifth percentile of daily capacity factor (CF5) for the 2000–2017 period; (b) the proportion of the number of wind turbines required to meet demand in at least 95% of days of the year when two-consecutive-day mean CF is used to the case where daily CF5 values are used. The areas for which the fifth percentile of the capacity factor is zero are masked (white color).
Energies 14 02978 g007
Table
Table 1. Potential annual production of renewable energy relative to current annual domestic energy consumption for Sub-Saharan countries. A ratio of 1 corresponds to a configuration where the estimated potential equals the current energy consumption. Source: [23,26].
Table 1. Potential annual production of renewable energy relative to current annual domestic energy consumption for Sub-Saharan countries. A ratio of 1 corresponds to a configuration where the estimated potential equals the current energy consumption. Source: [23,26].
CountryRatioCountryRatioCountryRatio
Namibia100.5Burkina Faso15.9Kenya6.5
Central Afr. Rep.90.9Madagascar14.6Malawi6.4
Mauritania86.2Guinea-Bissau14.2Ghana5.7
Chad77.3Tanzania14.1Uganda3.1
Mali58.4Cameroon12.7Gambia2.7
Niger50.4Senegal12.5Burundi2.2
Congo43.6Benin12.5Nigeria2.0
Angola27.9Sierra Leone10.1Swaziland1.6
Sudan27.6Côte d’Ivoire9.6Lesotho1.4
Zambia25.2Eritrea9.5South Africa1.3
Congo, Dem Rep24.7Guinea9.0Equatorial Guinea0.9
Mozambique23.4Togo8.9Cape Verde0.9
Botswana22.4Ethiopia8.5Rwanda0.7
Gabon20.3Zimbabwe8.0Comoros0.2
Table
Table 2. The percentage of grid points exhibit adequate wind power potential (CF ≥ 0.2) at different time scales (annual, seasonal, and monthly) on average, and in low-wind-power periods. Three-letter acronyms denote different trimesters: DJF (December, January, February); MAM (March, April, May); JJA (June, July, August); SON (September, October, December).
Table 2. The percentage of grid points exhibit adequate wind power potential (CF ≥ 0.2) at different time scales (annual, seasonal, and monthly) on average, and in low-wind-power periods. Three-letter acronyms denote different trimesters: DJF (December, January, February); MAM (March, April, May); JJA (June, July, August); SON (September, October, December).
VariableProportion of Grid Points (%)
Adequacy at Annual and Seasonal Scales
Annual57.71
DJF57.27
MAM56.92
JJA60.75
SON56.92
Adequacy at Monthly Scale
Minimum CFM40.07
Maximum CFM73.20
Low-Wind-Power Periods
CF52.15
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations.

Share and Cite

MDPI and ACS Style

Seyedhashemi, H.; Hingray, B.; Lavaysse, C.; Chamarande, T. The Impact of Low-Resource Periods on the Reliability of Wind Power Systems for Rural Electrification in Africa. Energies 2021, 14, 2978. https://doi.org/10.3390/en14112978

AMA Style

Seyedhashemi H, Hingray B, Lavaysse C, Chamarande T. The Impact of Low-Resource Periods on the Reliability of Wind Power Systems for Rural Electrification in Africa. Energies. 2021; 14(11):2978. https://doi.org/10.3390/en14112978

Chicago/Turabian Style

Seyedhashemi, Hanieh, Benoît Hingray, Christophe Lavaysse, and Théo Chamarande. 2021. "The Impact of Low-Resource Periods on the Reliability of Wind Power Systems for Rural Electrification in Africa" Energies 14, no. 11: 2978. https://doi.org/10.3390/en14112978

APA Style

Seyedhashemi, H., Hingray, B., Lavaysse, C., & Chamarande, T. (2021). The Impact of Low-Resource Periods on the Reliability of Wind Power Systems for Rural Electrification in Africa. Energies, 14(11), 2978. https://doi.org/10.3390/en14112978

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop