Combined Optimal Planning and Operation of a Fast EV-Charging Station Integrated with Solar PV and ESS

Abstract

Sufficient and convenient fast-charging facilities are crucial for the effective integration of electric vehicles. To construct enough fast electric vehicle-charging stations, station owners need to earn a reasonable profit. This paper proposed an optimization framework for profit maximization, which determined the combined planning and operation of the charging station considering the vehicle arrival pattern, intermittent solar photovoltaic generation, and energy storage system management. In a planning horizon, the proposed optimization framework finds an optimal configuration of a grid-connected charging station. Besides, during the operation horizon, it determines an optimal power scheduling in the charging station. We formulated an optimization framework to maximize the expected profit of the station. Four types of costs were considered during the planning period: the investment cost, operational cost, maintenance cost, and penalties. The penalties arose from vehicle customers’ dissatisfaction associated with waiting time in queues and rejection by the station. The simulation results showed the optimal investment configuration and daily power scheduling in the charging station in various environments such as the downtown, highway, and public stations. Furthermore, it was shown that the optimal configuration was different according to the environments. In addition, the effectiveness of solar photovoltaic, energy storage system, and queue management was demonstrated in terms of the optimal solution through a sensitivity analysis.

1. Introduction

The electrification of the transport sector is expected to play a vital role in mitigating the environmental damages caused by the broad usage of fossil fuels, especially in the power-generation and transportation sectors. It has also stimulated increasing attention towards electric vehicles (EVs) [1]. For instance, the U.K.’s Committee on Climate Change stated that all new cars and vans in the U.K. should be EVs by 2035 [2]. Moreover, about 30% of car passengers’ vehicle kilometers will be provided by electricity in 2040 [3]. Generally, replacing conventional gas-based vehicles with EVs can reduce the emission of harmful gases, increase the penetration of renewable energy resources, and alleviate the issues of the accessibility and affordability of fossil fuels [4,5,6,7,8]. Consequently, with the modern development of battery technologies, countries and industries around the world are looking to elevate their policies and incentives to expedite the large-scale market share of EVs [9,10].

However, the utmost concern over the high penetration of EVs correlates with the limited availability of EVs’ fast-charging facilities and EV owners’ range anxiety resulting from both the EVs’ short driving distance and the long waiting time at charging stations [11,12,13]. To overcome these challenges, ensuring that EVs operate solely on electric power, it is indispensable to establish sufficient fast-charging stations conveniently accessible to satisfy the charging demand [14,15,16,17]. Therefore, optimal planning is required to ensure the cost-effective operation of the fast-charging station and accelerate the ubiquitous usage of EVs.

In recent years, issues with EV-charging infrastructure deployment have received extensive attention from researchers. The existing literature focused on optimal placement and planning problems, specifically from the sides of the siting and sizing of charging stations [18,19,20,21,22,23,24]. The authors in [18] proposed optimal planning for plug-in EV fast-charging stations based on the characterization of charging demand using a Markov chain and queueing theory. Additionally, an optimization approach was presented for optimal placement and sizing of the EV-charging stations to minimize the total cost, including station development, electrification costs, and both the EV and electric grid energy loss cost [19]. Another optimization model for optimal sizing and placement of plug-in electric vehicle fast-charging stations was proposed to minimize the social cost related to both the transportation and distribution network [20]. Further, a profit optimization problem was proposed in [21] for charging service providers wanting to build or expand their charging networks based on the time-varying and location-dependent demands from vehicles and the constraints of the power grid. Using the capacitated flow refueling location model to describe the EV charging demand in [22], the authors proposed an approach for the optimal planning of EV fast-charging stations considering the interaction between the transportation and electrical networks. A multi-objective model to maximize the traffic flow and to minimize the power loss was presented in [23] for the optimal location and sizing of the charging station. In [24], the authors proposed an optimization framework to minimize the cost for the charging station by sizing infrastructure and by scheduling the charging session for the EVs while maintaining the quality of service.

For the profitable operation of fast-charging infrastructures, the usage of an energy storage system (ESS) to coordinate the impact of the station and the main grid was studied [25,26,27,28]. An approach to determine the optimal size of the ESS to minimize the energy and the ESS cost of a fast-charging station was proposed [25]. In [26], a method was presented that determines the size of the ESS considering the average waiting time of EVs arriving at a fast-charging station. Moreover, an optimization approach was presented in [27] for the sizing of the ESS in a fast-charging station considering cost minimization, peak shaving, and resilience enhancement. To analyze the economic scenario, in [28], the authors studied a network of charging stations equipped with an ESS and an allocation scheme concerning power and customer routes.

Fast-charging station operators look to maximize their profits while meeting EV charging demand. To this end, the optimal operation of external main grid power and internal power from solar photovoltaic (PV) systems and ESSs is essential. A study proposed a mixed-integer programming method to minimize the cost of PV-powered EV-charging stations [29]. Additionally, a design criterion for fast-charging facilities was studied to supplement the residential and public slow-charging infrastructure for covering Flemish mobility needs in [30]. The concept of a virtual energy hub for the integration of an electric transportation system combined with solar PV generation and an ESS from a power electronics point of view was proposed in [31]. In our previous work [32], we developed an optimization technique using solar PV and an ESS for the fast EV-charging station (FECS) operation based on the commute and errand distributed trips.

In this study, we extended our previous research by considering an FECS- planning problem. We developed an optimization framework for profit maximization considering both the optimal configuration of the FECS with solar PV and an ESS and the daily power scheduling in the FECS. During the long-term planning horizon, the FECS owner decides the number of fast chargers and waiting spaces, as well as the capacities of the solar PV system and the ESS. In the short-term operational horizon, the FECS schedules its power (solar PV, ESS, and main grid power) to maximize its operational profit while supplying EV charging demand. Further, we formulated an optimization model that combines the planning and daily operation in their respective horizons and maximizes the profit of the FECS over the entire planning horizon. The revenue of the FECS comes from the EVs’ charging fees. The overall cost includes four types of costs: (i) the FECS construction cost, (ii) the daily operational cost, (iii) the maintenance cost of the FECS, and (iv) the penalty from EV customers’ inconvenience. We also considered two penalty terms from EV owner’s inconvenience: waiting time in FECS queue and rejection by FECS. To model the EV mobility and calculate these penalties numerically, we used an approximation M/G/N/K queueing system [33,34,35]. We showed the effectiveness of solar PV, ESS, and queue management and the impact of various parameters on the optimal solution by sensitivity analysis through case studies.

The remainder of this paper is organized as follows. Section 2 describes the integrated FECS model. In Section 3, we formulate the planning and operation optimization model and demonstrate the solution methodology. Section 4 presents the case study results to verify the effectiveness of the proposed model. Finally, we present the conclusion in Section 5.

2. FECS System Model

An integrated FECS is shown in Figure 1. The FECS is equipped with a set of fast chargers $\{1,\dots ,N\}$ that use electric power from the solar PV, the ESS, and the main grid and operates at a fixed charging power rate. Further, the number of waiting spaces R is preserved in the FECS for EVs when all chargers are occupied. Based on the capacity of the FECS, at most N EVs can be charged simultaneously. In this study, we considered that during long-term planning, the FECS decides an investment on its charging capacity, which includes the numbers of chargers N and waiting space R, and the power capacity, which includes the sizes of the PV ${\gamma }_{PV}$ and ESS ${\gamma }_{ESS}$.

Each fast charger $n\in N$ can serve at most one EV during a time slot. The EV charging process starts at the beginning of a time slot and finishes at the end of the time slot. The FECS purchases power from the main grid or uses solar PV and ESS power to supply the EV charging demand. Considering that one day consists of $\{1,\dots ,T\}$ time slots, we set the duration of one time slot as 10 min, which resulted in $T=144$.

2.1. Power Supply

The FECS receives power supply from both the solar PV generator and the main grid. Since the solar PV power output is unknown during the planning, we assumed that the FECS can estimate its solar PV output for the next day with reasonable accuracy (recent research on day-ahead solar power forecasting showed that its mean absolute percentage error (MAPE) varied from 6% to 13% [36,37]). We used a set of scenarios of solar PV output $\Omega$ to represent different days in a year. After the FECS invests in the capacity of the solar PV generator ${\gamma }_{PV}$, the power supplied by the solar PV generator in scenario $\omega \in \Omega$ at time t is obtained by:

$$0\le P_{PV}^{\omega ,t}\le {\gamma }_{PV},\forall t\in T$$

(1)

To meet the charging demand, the FECS utilizes power from the main grid when the solar PV power generator and ESS provide an insufficient power supply. The amount of power purchased from the main grid in scenario $\omega$ at time slot t is limited and is modeled as:

$$P_{mg}^{min}\le P_{mg}^{\omega ,t}\le P_{mg}^{max},\forall t\in T$$

(2)

where the upper limit is associated with the capacity of the distribution network, such as the power line to which the FECS is connected. In this study, we assumed that the FECS cannot feed the power back to the main grid, that is $P_{mg}^{min}=0$.

2.2. Energy Storage System

The FECS controls the ESS charging/discharging power and exploits its flexibility to smooth out the intermittent nature of solar PV generation; thus, it balances the EV charging demand and power supply. In the planning stage, the FECS decides the ESS capacity ${\gamma }_{ESS}$ with a C-rate of 1. Therefore, in scenario $\omega$, the upper bounds of the ESS charging and discharging power are limited to ${\gamma }_{ESS}$. that is:

$$0\le P_{ch}^{\omega ,t}\le \frac{{\gamma }_{ESS}}{\Delta t},\forall t\in T$$

(3)

$$0\le P_d^{\omega ,t}\le \frac{{\gamma }_{ESS}}{\Delta t},\forall t\in T$$

(4)

Upon including the power loss during the charging and discharging of the ESS, the state of charge (SoC) at time t is defined as follows:

$$S^{\omega ,t}=S^{\omega ,t-1}+({\eta }_{ch}{P}_{ch}^{\omega ,t}-\frac{P_d^{\omega ,t}}{{\eta }_d})\Delta t,\forall t\in T$$

(5)

where $S^{\omega ,t}$ denotes the SoC of the ESS. The SoC is bounded as:

$$S^{min}{\gamma }_{ESS}\le S^{\omega ,t}\le S^{max}{\gamma }_{ESS},\forall t\in T$$

(6)

We added one more constraint on the SoC whose level should be equal at the beginning and the end of the operation period, that is,

$$S^{\omega ,1}=S^{\omega ,T}.$$

(7)

2.3. EV Arrival at the FECS and Charging Demand

The arrival of the EV at the FECS was modeled by a Poisson random process with an expected arrival rate ${\lambda }^t$ [21]. We assumed that the EV charging demand was fulfilled in one time slot $\Delta t$. A Gaussian distribution function $\mathcal{N}(\mu ,{\sigma }^2)$ was used to approximate the probability density function (PDF) of the charging demand for each arriving EV, where $\mu$ and $\sigma$ are the mean and standard deviation of the distribution, respectively.

Let D be a random variable that represents the charging demand of an EV; hence, the expected charging demand for the FECS during (t, $t+\Delta t$) is obtained by:

$$\mathbb{E}\left[D\right]{\lambda }^t\Delta t,\forall t\in T$$

(8)

Unfortunately, the FECS may not fulfill all the EVs’ charging demands due to the limited capacity of its chargers and waiting spaces. If the number of EVs arriving simultaneously at the FECS is greater than the number of chargers, some EVs are queued in the waiting spaces and are served when chargers are available. Moreover, EVs that arrive when the waiting spaces are fully occupied usually have to leave the FECS and are referred to as rejected with blocking probability $p_b^t$. Therefore, the actual expected energy to be supplied by the FECS at t is lower than that in Equation (8), and it is denoted as:

$$\mathbb{E}\left[D\right]{\lambda }^t(1-p_b^t)\Delta t,\forall t\in T$$

(9)

Accordingly, given the invested number of chargers N, we can obtain the total expected power utilization by the FECS to meet the expected energy demand during the charging time, that is:

$$N{P}_n^t=\mathbb{E}\left[D\right]{\lambda }^t(1-p_b^t),\forall t\in T$$

(10)

Let $\mu =\frac{1}{\Delta t}$ and $P^{rate}$ be the fast charger average charging service rate and the rate at which power is delivered by a fast charger, respectively. We obtained an analogous expression for the energy delivered by the FECS to supply the average energy demand of an EV during the charging process as $\mathbb{E}\left[D\right]=\frac{P^{rate}}{\mu }$. Thus, we can obtain the expected amount of power necessary for a fast charger n to supply the EV demand in time t as:

$$P_n^t=\frac{{\lambda }^t}{N\mu }{P}^{rate}(1-p_b^t).\forall t\in T$$

(11)

Note that the FECS utilization factor is defined by $\rho =\frac{{\lambda }^t}{N\mu }$.

To obtain the expected power utilization for a fast charger $P_n^t$, the blocking probability $p_b^t$ is required. We used the first-come, first-served M/G/N/K model in queueing theory to explore the charging process of the FECS and analytically describe its performance metrics.

Furthermore, for a safe operation, the charging power of each fast charger is constrained by the upper-bound as shown below:

$$0\le P_n^t\le P_n^{max},\forall t\in T$$

(12)

2.4. M/G/N/K Queueing System Performance Evaluation

To validate the accuracy of the M/G/N/K queueing system, we compared the results of the analytical approximation and queue simulation of the FECS. We obtained the blocking probability in Equation (13), the average queue length in Equation (14), and the average waiting time in Equation (15) for the analytical approximation using the queueing analysis from existing research [35]. They are mathematically defined as:

$$p_b=\frac{{\left(N\rho \right)}^N}{N!}{\zeta }^{K-N}{p}_0,i=K,$$

(13)

$$\mathbb{E}\left(L_q\right)\approx \sum _{i=N}^K(i-N)p_i\cong \frac{{\left(N\rho \right)}^N}{N!}\frac{\zeta }{(1-\rho )(1-\zeta )}\{1-{\zeta }^R-R(1-\zeta )\rho {\zeta }^{R-1}\}{p}_0,$$

(14)

$$\mathbb{E}\left(W\right)\approx \frac{\mathbb{E}\left(L_q\right)}{\lambda },$$

(15)

respectively. The detailed procedure of this approximation solution is presented in Appendix A.

Further, we performed simulations using SimEvent in Simulink/MATLAB. Parameters were set as $N=6$, $R=3$, and $\mu =6$. Figure 2 shows the analytical (lines) and simulation (dots) results of the blocking probability, average queue length, and average waiting time for $\rho <1$.

The results appeared very similar; moreover, their mean absolute percentage errors (MAPEs) were 55.3%, 11.4%, and 12.2% for the blocking probability, queue length, and waiting time, respectively. These values were non-negligible because minor errors usually gave rise to high percentage errors due to very small values; for example, the blocking probability of $\lambda =1$ was 0.0000012. Therefore, the mean absolute error (MAE) was an adequate metric for confirming the closeness between the analytical and simulation results. The MAEs for the blocking probability, average queue length, and average waiting time were 0.0035, 0.035, and 0.087. Therefore, it was sufficient to use the queueing analysis to model the EVs’ behavior in the FECS.

3. Combined Planning and Operation Problem

In this paper, we proposed a framework to maximize the average profit of an integrated FECS. The FECS connected to the main grid consisted of fast chargers, waiting spaces, solar PV generators, and an ESS. The FECS tried to maximize its expected profit while providing adequate charging services, where profit refers to the difference between revenue and cost. The revenue was generated from the EV charging fee. In contrast, the total cost included the investment cost (fast chargers, waiting spaces, solar PV, and ESS), daily operation cost during the planning period, maintenance cost, and penalties associated with EV users’ inconvenience.

3.1. FECS Investment

First, for a long-term planning horizon, the FECS had to decide its configuration, wherein the numbers of fast chargers, waiting space, and both the solar PV generator and ESS capacities were the decision variables of this stage: ${\chi }_{inv}=\{N,R,{\gamma }_{PV},{\gamma }_{ESS}\}$. The long-term investment cost of the FECS is:

$$C_{inv}\left({\chi }_{inv}\right)=C^{FC}N+C^{L}R+C^{PV}{\gamma }_{PV}+C^{ESS}{\gamma }_{ESS},$$

(16)

where $C^{FC}N,C^{L}R,C^{PV}{\gamma }_{PV},\mathrm{and}{C}^{ESS}{\gamma }_{ESS}$ are the investment costs of fast chargers, waiting spaces, solar PV, and ESS, respectively.

Ideally, the investment cost of the FECS should be less than the total budget, and the decision variables should be non-negative, as:

$$C^{FC}N+C^{L}R+C^{PV}{\gamma }_{PV}+C^{ESS}{\gamma }_{ESS}\le B,$$

(17)

$$0<N\le N^{max},0<R\le R^{max},{\gamma }_{PV}\ge 0,{\gamma }_{ESS}\ge 0.$$

(18)

3.2. Daily Operation

After deciding the configuration of the FECS, the FECS operates daily for EV charging. The FECS prepares its power scheduling at one day ahead of an operational day to maximize its revenue. The FECS earns revenue and pays operational costs daily. The revenue implies the income from the EV charging fee, defined as $R_{op}^t=C^{ev}N{P}_n^t$, whereas the operational cost involves the expenses of purchasing the power from the main grid and the cost from ESS degradation, which is defined as $C_{op}^t=C^t{P}_{mg}^{\omega ,t}+C^{\omega ,s}(P_{ch}^{\omega ,t}+P_d^{\omega ,t})$. The FECS highly prioritizes the use of output power from the solar PV generator because it does not incur an operational cost. However, when more power supply is required, the FECS uses the ESS and/or main grid power. If the solar PV output is higher than the charging demand, the surplus power goes to the ESS provided that it has sufficient space to store it; otherwise, it is dumped. Therefore, the FECS should schedule its power carefully to maximize its profit.

The decision variables of daily power scheduling are ${\chi }_{op}=\{P_{mg}^{\omega ,t},P_{PV}^{\omega ,t},P_{ch}^{\omega ,t},\mathrm{and}{P}_d^{\omega ,t}\}$, and the expected daily operational profit over all possible scenarios $\omega \in \Omega$ is expressed as:

$$P_{op}\left({\chi }_{op}\right)=\sum _{\omega \in \Omega }\sum _{t\in T}{\pi }^{\omega }(R_{op}^t-C_{op}^{\omega ,t})$$

(19)

An important constraint for daily operation is the power balance equation. The FECS manages its power to balance the supply and demand, which is given by:

$$P_{ch}^{\omega ,t}+\sum _{n=1}^N{P}_n^t=P_{mg}^{\omega ,t}+P_{PV}^{\omega ,t}+P_d^{\omega ,t},\forall t\in T$$

(20)

where the left and right sides of Equation (20) represent demand and supply, respectively.

3.3. Penalties from Discomfort

Because of the limited number of fast chargers and waiting space, some EVs wait in the queue while others may be rejected, causing user inconvenience. Therefore, the objective function captures this discomfort as a penalty function, regarded as a cost term and defined as:

$$C_{pen}\left({\chi }_{inv}\right)=\sum _{t\in T}\left(C^W\mathbb{E}\left[W^t\right]+C^{rej}\mathbb{E}\left[R_{ej}^t\right]\right)$$

(21)

where the first and second terms represent the penalties associated with the waiting time and rejection at the FECS, respectively. These penalties correlate with the investment decision ${\chi }_{inv}$. Further details on the calculation of $\mathbb{E}\left[W^t\right]$ and $\mathbb{E}\left[R_{ej}^t\right]$ are shown in Appendix A.

3.4. Maintenance Costs

Regular maintenance is required to safely operate the FECS (fast charger, waiting spaces, solar PVs, and ESS) during the planning period. The maintenance costs are defined as:

$$C_{main}\left({\chi }_{inv}\right)=C_{FC}^{M}N+C_L^{M}R+C_{PV}^M{\gamma }_{PV}+C_{ESS}^M{\gamma }_{ESS},$$

(22)

The maintenance cost depends on the investment decision, ${\chi }_{inv}$. It is important to note that the maintenance cost for the waiting space is related to the cost of leasing the land.

3.5. Combined Planning and Operation Problem

With all the above analyses, the formulation of an optimization problem to maximize the profit of the integrated FECS considering planning and daily operation is now possible. Revenue comes from the charging fee of EVs. The total cost consists of the sum of the long-term investment cost, expected daily operational cost, penalties, and maintenance cost. A set of decision variables is represented by $\chi ={\chi }_{inv}\cup {\chi }_{op}$. The profit maximization problem for the FECS over all possible scenarios $\omega \in \Omega$ is formulated as:

$$\begin{array}{cc}\hfill \underset{\chi }{max}& \left[\delta \left(P_{op}\left({\chi }_{op}\right)-C_{pen}\left({\chi }_{inv}\right)-C_{main}\left({\chi }_{inv}\right)\right)-C_{inv}\left({\chi }_{inv}\right)\right],\hfill \\ \hfill s.t.& \left(1\right)-\left(7\right),\left(11\right),\left(12\right),\left(17\right),\left(18\right),\left(20\right)\hfill \end{array}$$

(23)

The objective Equation (23) obtains the optimal configuration to maximize the FECS profit under all scenarios in the entire planning horizon. The other costs are normalized by the net present value at the investment decision stage while excluding the investment cost. The time discount $\delta$ is defined as:

$$\delta =\sum _{m=1}^M\frac{1}{{(1+r_m)}^m},$$

(24)

where M and $r_m$ denote the FECS’s planning horizon and the interest rate in period m, respectively.

4. Case Study and Simulation Results

This section evaluates the proposed profit maximization scheme for the FECS, where the optimization problem was solved using AMPL with a Gurobi solver [38].

4.1. Case Study Parameters

We considered a decade-long planning period for a grid-connected FECS with a solar PV generator and an ESS. However, there was limited data on fast EV charging as the use of EVs is still low. Therefore, we assumed that the EV charging demand followed the distribution of general vehicle travel profiles from the summary of travel trends of the 2009 National Household Travel Survey [39]. We used two prominent scenarios: commute distribution and errand distribution, to discuss the validity of our proposed optimization scheme. We added some randomness to the distributions ensuring that the EVs’ arrival was modeled per the Poisson process with a rate of $\lambda$[number of EV arrivals/$\Delta t$]. The average energy consumption of EVs per kilometer is 0.15 kWh/km [18]. Hence, we assumed that the maximum one-time charging demand was up to 20 kWh within one charging process. The power generation of the solar PV was derived from real data [40].

We used a time-of-use (ToU) pricing scheme of San Diego Gas & Electric (SDGE) during summer as the purchasing price of the main grid power (SDG&E EV time-of-use summer pricing plan, available online: https://www.sdge.com/residential/pricing-plans/about-our-pricing-plans/electric-vehicle-plans, accessed on 20 May 2021).

Table 1. SDGE time-of-use pricing rate in summer.

Period	Time	Price (USD/kWh)
Super Off-Peak	00:00–06:00	0.21364
Off-Peak	06:00–16:00	0.29171
	21:00–00:00
On-Peak	16:00–21:00	0.37774

shows the detail of the TOU tariff. The price of power $C^{ev}$ for EV charging at the FECS was set as 0.33 USD/kWh [41], and the land cost was 407 USD/m${}^2$ [22]. We assumed that one waiting space required 30 m${}^2$ of space. The maintenance costs of the fast chargers, the solar PV, the ESS, and the waiting spaces were obtained by normalizing their respective annualized capital costs with a discount factor of $r_m$ equal to 0.1. Further, the approximation of the costs related to the waiting time and rejection for EVs at the FECS were set based on the travel time cost analysis [42]. The hourly cost associated with EV waiting time in the queue was set to 30% of the average hourly wages. Alternatively, the EV rejection cost was set to 45% of the average hourly wages. The basic minimum wage of California in 2020 [43] was considered for reference.

Table 2. Parameters for the simulations.

Parameter	Value and Unit
$P_{mg}^{max}$	1200 kW
$P^{rate}$	120 kW
${\eta }_{ch}={\eta }_d$	0.95
$N^{max}$	10
$R^{max}$	20
$C^s$	0.01 USD/kW
$C^{PV}$	1830 USD/kW [44]
$C^{ESS}$	271 USD/kWh [45]
$C^{FC}$	35,000 USD/Fast-charger [46]
$C^L$	12,210 USD/Waiting-Space [22]
$C^W$	0.6 USD/h
$C^{rej}$	0.9 USD/h

encapsulates the parameters of the FECS.

4.2. Daily Operation of FECS

We first demonstrated the results of daily operation with a budget of USD 1.3 M. Then, the optimal planning of the FECS was conducted according to the budget in the following section.

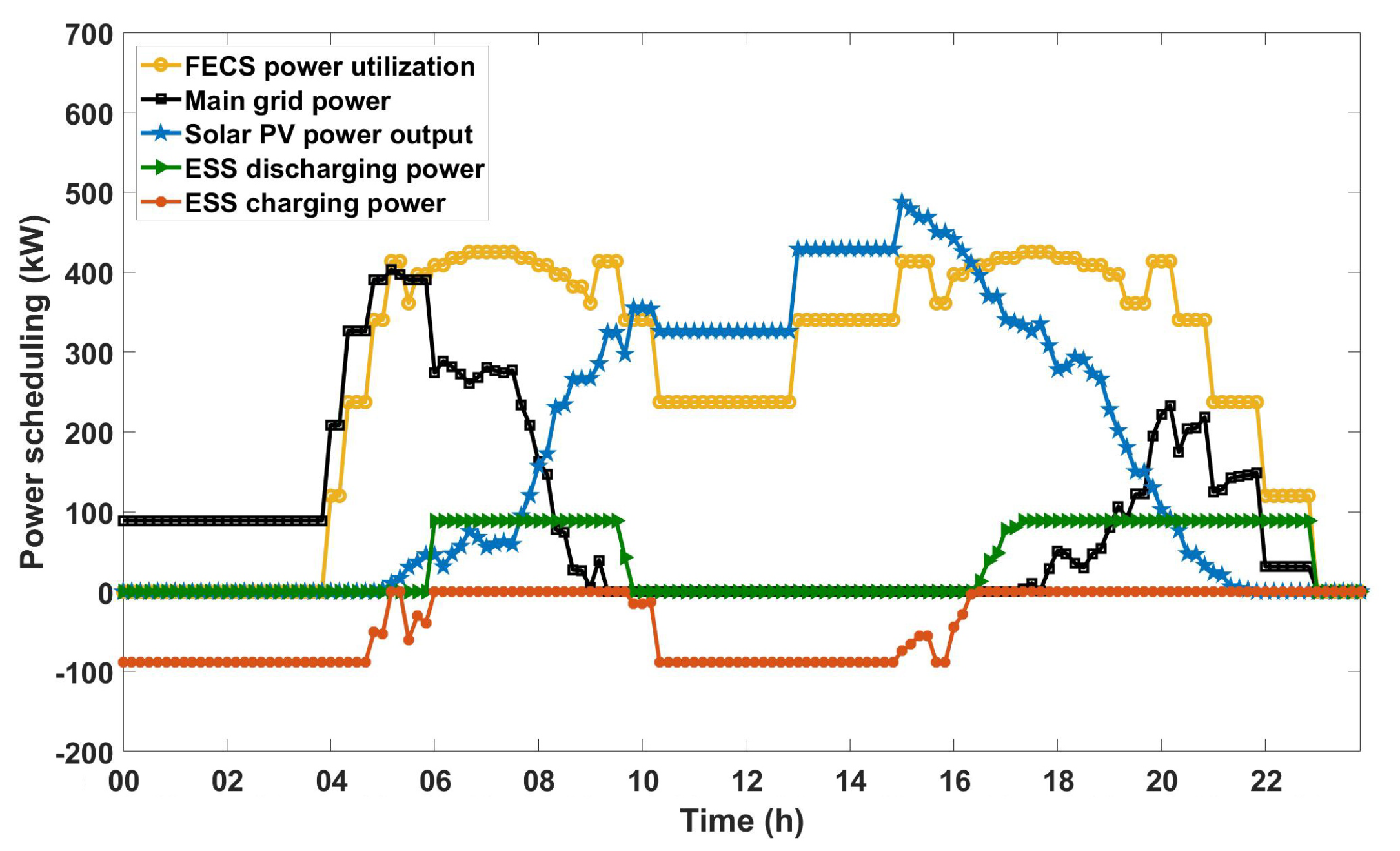
The daily operation of the FECS per the proposed optimization framework using the distribution of a commute trip is shown in Figure 3. With a commute distribution and a budget of USD 1.3 M, the optimal configuration of the FECS, i.e., the number of chargers, waiting spaces, solar PV capacity, and ESS capacity, was 4, 2, 533 kW, and 592 kWh, respectively. The commute trip distributions were indirectly depicted as “FECS Power Utilization”, i.e., load, because the FECS solely supplied charging power to the EVs.

The daily operation results showed that the FECS power utilization with the commute distribution had two peaks: morning and evening. At night, the FECS charged the ESS using the main grid power considering the low price (considering there was no price difference for the main grid during nighttime, any usage pattern can be followed at night. However, flat power usage during the night had the smallest peak. Therefore, in our simulations, we added a quadratic form of the main grid power having a very small weight, that is: $\beta {\left(P_{mg}^t\right)}^2$ to $C_{op}^t$, and set $\beta$ to less than 0.000001. Thus, the optimization result did not change.) until 6:00, after which the ESS discharged its power to supply the charging demand because the purchasing price of the main grid power increased. When the solar PV output was higher than charging demand (between 9:50 and 16:20), the surplus energy was stored in the ESS and was released in the evening, that is during the highest-priced period.

Figure 4 illustrates the power scheduling of the FECS with the errand distribution having a budget of USD 1.3 M. The number of chargers, waiting spaces, solar PV capacity, and ESS capacity for errand distribution were 6, 1, 589 kW, and 0 kWh, respectively. Herein, the EVs arrived at the FECS in a relatively uniform manner during the daytime, and ESS utilization was limited because of almost no surplus. Therefore, there was no ESS involved in the optimal configuration with a USD 1.3 M budget. Alternatively, investment in solar PV was very important because a significant portion (66%) of the total EVs’ charging demand was supplied solely by the solar PV power, thereby cutting off the expenses of purchasing the main grid power.

4.3. FECS Planning Result

The optimal planning of the FECS was analyzed under different budgets. Figure 5 shows the optimal capacity of the solar PV, ESS, number of fast chargers, and waiting spaces according to the budgets. Under the budget of USD 0.3 M, the FECS had two fast chargers and one waiting space installed, with 119 kW from the solar PV and no ESS, in both the commute and errand distribution scenarios. The fast charger and solar PV were more likely to increase the profit than the waiting space and ESS, respectively. Investments in the ESS for the FECS with the commute distribution started with a budget of USD 1 M, while the FECS with the errand distribution did so later because of the load pattern, as shown in Figure 3 and Figure 4. However, there was a sufficient surplus of solar PV generation during the daytime in the commute scenario. As a result, the FECS prioritized investing in the ESS to absorb the surplus.

By contrast, in the errand scenario, the ESS was sensitive to the price by charging and discharging during the lowest-priced and highest-priced periods, respectively. However, it did not significantly contribute to the daytime profit as the load consumed all the solar PV power. Therefore, the ESS investment was not predominant in the FECS with the errand distributed load under a limited budget. Without budget constraints, all four capacities of the FECS increased to their maximum value, and the commute and errand configurations were the same.

Figure 6 shows the total maintenance cost and penalties according to the budgets for the commute and errand scenarios during the planning period. As the budget increased, the value of every FECS element increased, thereby increasing the maintenance cost. On the other hand, the penalty associated with EV rejection decreased with the number of fast chargers. Additionally, a finite queue length cannot change the EV blocking probability stochastically, as the waiting time increased with the waiting space. Accordingly, the penalty for EVs’ waiting time in the queue increased with the number of waiting spaces.

At a small budget of USD 0.3 M, the penalty for rejection was higher than the maintenance costs because the FECS can invest in a small capacity, causing many EV rejections. However, as the budget increased, the penalty of rejection decreased more in the errand scenario than the commute scenario considering that the FECS invested in many chargers. Further, the maintenance cost of the solar PV and ESS was higher in the commute scenario than in the errand scenario because the FECS invested considerably in the ESS capacity. The penalty associated with the waiting time did not have a tremendous impact considering that the investment in the waiting spaces was not a priority for the FECS to increase the profit.

4.4. Sensitivity Analysis

To analyze the effectiveness of the solar PV and ESS within the FECS, we set four cases with both the commute and errand distributed loads: (i) baseline case, i.e., FECS without solar PV and ESS; (ii) FECS with ESS; (iii) FECS with solar PV; and (iv) FECS with solar PV and ESS.

The numerical results shown in

Table 3. Optimal FECS planning result, commute distribution.

	# of chr.	# of w. sp.	PV cap. (kW)	ESS cap. (kWh)
Baseline	6	1	-	-
FECS with ESS	6	1	-	1800
FECS with PV	5	2	600	-
FECS with PV and ESS	4	2	533	592

represent the optimal FECS planning, that is the solution of (23) at a budget of USD 1.3 M, for the commute scenario. The corresponding optimal profit is presented in

Table 4. The total cost of the FECS with the commute distribution during the planning period for the four cases, which includes the operational cost, penalties, maintenance cost, and investment cost. The total profit is revenue minus total cost. All values are in USD.

	Rev.	Opr. Cost	Pen.	Mnt. Cost	Inv. Cost	Total Profit
Baseline	44,009,500	42,208,200	379,897	228,856	222,210	970,259
FECS with ESS	44,009,500	39,392,000	379,897	460,923	710,010	3,066,633
FECS with PV	40,532,200	18,338,800	467,978	485,781	1,297,420	19,942,287
FECS with PV and ESS	35,377,500	12,390,400	592,773	499,561	1,300,000	20,594,768

.

FECS gained some profit in all four cases, meaning that the revenue was more significant than the cost. Because the revenue of the FECS came from the charging fee paid by the EVs, it increased with the number of fast chargers and waiting spaces. Table 3 shows that both the FECS without the PV and ESS and the FECS with only the ESS had the highest number of fast chargers. As a result, they had high expected revenue, as shown in Table 4. Moreover, they had slight performance penalties. There were two effects of waiting spaces: they decreased the penalty of EV rejection and increased the waiting penalty. Although the penalty of EV rejection was higher than that of waiting, the impact of the waiting space on the penalty was positive, thereby increasing revenue.

However, the FECS with the ESS did not achieve the highest profit owing to its high operational cost. That is, the FECS used the main grid power at a higher price. Considering the generated power by the solar PV, the solar PV was more advantageous than the ESS in terms of profit. Nevertheless, the FECS with only the PV led to the wastage of the surplus solar PV energy. Therefore, the FECS with the PV and ESS delivered the lowest operating cost because of the flexibility of the ESS. Although the FECS led to the lowest revenue, it obtained the highest total profit. Note that we omitted the result of the errand scenario because it showed a similar result. The FECS with the solar PV and ESS was the most profitable for an errand distribution scenario.

We extended our analysis to discuss the impact of the budget on the total profit. The optimization results for the FECS under the public FECS cases are depicted in Figure 7. In the baseline case, the FECS invested only in the charger and waiting space, and its profit did not change with the budget. In the case of the FECS with the ESS, after an ESS of 1800 kWh capacity at the budget of USD 0.8 M, no further investment would be possible even t a higher budget. However, in the FECS with PV, the FECS would require a budget of USD 1.4 M to install an optimal 600 kW solar PV capacity. Finally, the FECS with PV and the ESS required the highest budget of USD 2 M to install the optimal amount of capacity, which also resulted in the highest profit. At the highest budget of USD 2 M, the optimal configurations for the commute and errand distributions were almost the same regardless of the EV charging demand. When the FECS with the solar PV installed the ESS, the profit improvement under the errand distribution was more remarkable than that under the commute distribution at a budget of USD 2 M. This was because the charging demand in the errand distribution absorbed all the available solar PV power, and the ESS covered the high-priced period. While although the EV arrival pattern of the commute distribution was more diverse than that of the errand distribution, the ESS could flatten this diversity, but the unused solar PV power could appear when all the demand was satisfied and the ESS was fully charged.

4.5. FECS in Different Location

Not only EV arrival patterns, but also local characteristics were important factors for an optimal configuration of the FECS. To see the impact of location, we applied our framework to three locations: public, highway, and downtown. The FECS installed in a public space was an ordinary charging station, for which the parameters are given in Table 2. The FECS on the highway was a station built along the highway, which means the land price was minimal, i.e., $C^{PV}$=1830 USD/kW and $C^L=0$ USD/waiting space. On the other hand, the land price was high in the downtown, i.e., $C^{PV}=$5490 USD/kW and $C^L=$20,000 USD/waiting space.

Figure 8 shows the optimal configuration of the FECS according to the locations and EV arriving pattern. The number of fast chargers remained the same for the three locations because it depended more on the arrival pattern. On the other hand, the number of waiting spaces was very different. Because of the high price, the FECS installed in the downtown only prepared the minimum waiting space. In contrast, the FECS installed on the highway had more waiting spaces, i.e., eight and seven waiting spaces with the commute and errand distributions, respectively. Furthermore, the capacities of the solar PV and ESS had a similar trend according to the locations, as shown in Figure 8b. With the errand distribution, no FECS installed the ESS because of its load pattern.

As a result, the profit of the FECS in each location was different. Figure 9 shows the optimal profit for each location. The profit of the FECS on the highway was 2.6 times and 3.3 times higher than that of the FECS in the downtown for the commute and errand distribution, respectively. The high profit of the highway case was relative to the low cost for the solar PV and waiting spaces. On the other hand, the FECS in the downtown invested less in the solar PV, and it had no ESS as there was no surplus.

4.6. Optimal Profit with Uncertainty

So far, the simulation results were based on fixed solar PV output, and the FECS operator knows the output exactly. To simulate this realistically, we added uncertainty, i.e., Gaussian noise, on the solar PV output in this section. The severity of the errors was controlled using the standard deviation of the added Gaussian noise. The FECS used the main grid power to cover the difference between the actual PV production and the expected one because of the variability of solar PV power, which caused an increase in its operational cost. The profits under the uncertainty of solar PV are shown in Figure 10. When the errors were 5%, 10%, 15%, and 20%, the optimal profit decreased 5.59%, 11.15%, 16.67%, and 22.26%, respectively. The optimal profit of the proposed framework still showed a good result assuming that the practical error range was 6% to 13%.

5. Conclusions

Fast EV-charging stations (FECSs) are a critical component for the widespread adoption of electric vehicles (EVs). A well-planned effective configuration and optimization of the operation of the FECS are required to meet the charging demand for profit maximization. Accordingly, an optimization framework was formulated for the combined planning and operation of an FECS integrated with a solar PV generator and an ESS. In the proposed framework, the total cost of the FECS accounted for its installation cost, daily operational cost, maintenance cost, and penalties from the customers’ inconvenience. We used the average waiting time in the FECS and the blocking probability to obtain the customer inconvenience through an M/G/N/K queueing model. Because the numerical result of the queueing analysis was very similar to the simulation result, we used the queueing analysis to model the EV arrival. The simulation result of the FECS showed the optimal configuration for the FECS having a given budget and daily power scheduling to support the EV-charging demand. According to the EV arrival pattern and the FECS’s location, the optimal configuration and scheduling were different. For example, when the EV arrival pattern was similar to the solar PV output, i.e., errand demand, the FECS without the ESS was optimal. On the other hand, the FECS installed the ESS for the commute demand. Our proposed optimization framework gave an intuition about the choice of the parameters for real-world cases resulting in a profitable decision on the investment of the FECS. The FECS in a distribution network and its impact on power quality will be essential for future research.