1. Introduction
The rapid increase in the demand for airline transportation and air traffic has led airline companies to use their resources more effectively. Most commercial airlines, especially flag carriers, aim to maximise their potential to deliver economic and social benefits by increasing their connectivity among spoke cities and market share to grow sustainably in the future. Due to high profitability and high costs, competition in the aviation industry is increasingly fierce and the need for optimal planning has arisen. The AFAP directly affects the profitability of the airline carrier. Assigning an aircraft with a smaller capacity than the passenger demand to a flight directly leads to spill cost due to lack of capacity. Additionally, assigning an aircraft with a higher seat capacity than passenger demand results in extra operating cost, idle capacity, and opportunity costs. For this reason, allocating appropriate aircraft types to predetermined flight legs is an important problem that directly affects profitability for airline companies.
The fleet assignment model commonly aims to minimise the total cost including operating, maintenance, fuel, and spill costs, or to maximise the total profit including fares, revenue of connected flights and spill-over benefits.
According to our knowledge, Abara [
1] first introduced the connection network structure and formulated an integer programming model for solving AFAP. The model solution includes a profit-maximising objective function, considering the limitations of flight coverage, balance, scheduling balance, and the number of aircraft available. Hane et al. [
2] proposed a time-space network structure that reduces the number of decision variables in Abara [
1] by allowing freedom on established connections. Rushmeier and Kontogiorgis [
3] proposed a similar model to Abara [
1] for the formulation of a large-scale fleet assignment problem by focusing on representing flight connection possibilities. Sherali et al. [
4] presented a comprehensive survey of fleet assignment models by reviewing the models and methods in the literature. They summarised the gaps in the fleet assignment literature and listed future research directions for the estimation of model parameters, such as flight fee and demand. In this study, we briefly discuss recent fleet assignment studies in
Section 2; however, one may refer to the surveys of Sherali et al. [
4] and Ng et al. [
5].
This study presents an integer programming model and a heuristic algorithm for AFAP. Based on the connection network model by Abara [
1], we developed a new integer programming model with a preprocessing procedure on flight connections. Additionally, we constructed an effective heuristic algorithm to solve more realistic AFAPs; and we performed a computational study to demonstrate the performance of the proposed algorithm.
The remainder of the paper is organised as follows:
Section 2 provides a recent literature review of studies on the heuristic algorithms for AFAP. The integer programming formulation of the airline fleet assignment model is given in
Section 3. In
Section 4, we introduce the two-phase heuristic algorithm for AFAP.
Section 5 provides a computational study on a set of problem instances derived from a real-life AFAP from Turkey. Finally, in
Section 6, we summarise our contributions, conclude with a discussion and offer suggestions for the direction of future research for airline planners and researchers.
2. Related Literature
The fleet assignment problem is generally solved for maximising the profit and minimising the cost of assignment. Both profit and cost terms include various types of elements such as operating cost, opportunity cost, carrying cost, and spill cost. Although the fleet assignment problem is largely studied in operations research literature, the interactions between fleet assignment and other airline scheduling processes is still attractive for researchers. Sherali et al. [
4] implied that fleet assignment studies generally isolated the problem under restrictive assumptions such as considering the same-every-day schedule, and using point forecasts for flight-based demands instead of itinerary-based demands. The airline fleet assignment problem is becoming more challenging due to the various parameters of each fleet type and the high impact on airline profit as uncertainty in passenger demand increases. The dynamic nature of the problem has led to the need for computationally efficient algorithms to prevent imbalanced assignments.
A considerable number of airside operation research projects using heuristics and meta-heuristics can be found in the current literature [
5]. The fleet assignment problem has been investigated jointly with fleet sizing and flight scheduling problems. The problem is becoming more difficult to solve as the dimensions of the problem increase. Sosnowska [
6] presented the advantage of using a simulated annealing-based heuristic algorithm over the GRASP algorithm for solving a simplified version of the fleet assignment problem. Barnhart et al. [
7] proposed a path-based fleet assignment model by incorporating demand management decisions into fleet assignment. These extensions increased the size and complexity of the original problem. Therefore, heuristic and metaheuristic algorithms were used to solve the fleet assignment problem. Anzoom and Hasin [
8] developed two profit-maximising mathematical models for short-haul and long-haul operations with seat and distance concerns. They used an ant colony algorithm with quick convergence to the optimal solution of the problem. The ant colony algorithm was adapted to solve the fleet assignment problem by Kang et al. [
9] in order to minimise the number of the flights and to maximise maintenance opportunities. They constructed a flight string-based ant colony algorithm and modified the pheromone update mechanism to increase the convergence rate. Dozic and Kalic [
10] developed a robust, comprehensive, three-stage airline fleet planning model to help airlines in their decisions regarding fleet size and mix. In the second stage, they used a heuristic algorithm to determine the size of the airline fleet. Dozic et al. [
11] proposed a model to determine the fleet size and fleet assignment in the case of single-fleet existence. Since the joint problem of fleet sizing and fleet assignment is NP-hard, a metaheuristic approach based on the variable neighbourhood search methodology was proposed by Dozic et al. [
11].
In the literature, the airline fleet assignment problem is often integrated with the flight scheduling problem. Yan et al. [
12] proposed a mixed-stop heuristic procedure for solving the integrated problem of airport selection, fleet routing, and scheduling. Gürkan et al. [
13] considered cruise time control for integrated airline scheduling and the aircraft fleeting problem. They developed two heuristic methods, the discrete approximation and cruise speed control algorithm, and a multi-stage triplet search algorithm for solving the proposed nonlinear mixed integer programming model. Cadarso and Marin [
14] aimed to reduce the number of disconnected passengers in an integrated fleet assignment and flight planning problem. Jamili [
15] proposed a new robust mathematical model to solve integrated aircraft routing and scheduling, considering the fleet assignment problem and developed a heuristic algorithm based on simulated annealing. Kenan et al. [
16] proposed a two-stage stochastic programming model for the integrated flight scheduling and fleet assignment problem. They recommended medium and small airline companies to use sample average approximation algorithm in order to manage a large number of optional legs and different airport conditions. For considering the stochastic demand, Yan et al. [
17] proposed a two-stage stochastic programming and used arc- and route-based strategies to develop two different heuristic algorithms. Pilla et al. [
18] formulated a two-stage stochastic programming model for fleet assignment by considering the uncertainty in revenue and operating costs, passenger demand. and aircraft capacity. To deal with demand uncertainty, the re-fleeting strategy has been frequently investigated. Eltoukhy et al. [
19] conducted a review of re-fleeting and implied the drawbacks of the strategy due to the limited number of re-fleeting options (because all the aircraft belong to the same family, resulting in an inefficient re-fleeting process). Furthermore, researchers stated that the re-fleeting process under heterogeneous fleet assignment with crew-considered scope is promising as it increases the flexibility and efficiency of the re-fleeting process.
Accordingly, the number of proposed algorithms for solving AFAP is increasing rapidly as modifications and extensions are included in the base problem. Since the problem is strongly connected with network design, fleet design, flight scheduling, aircraft routing, and crew management, realistic problems still require efficient algorithms for solving fully integrated airline processes. The complexity of the models and the need for innovative solution methods increase as modifications and extensions become a larger part of the original problem.
3. Mathematical Model
In general, the AFAP aims to assign the most suitable aircraft to the flight legs in order to maximise total profit. Basically, improper assignments have significant consequences on airline profit. Assigning lower-capacity aircraft to high-demand flights will result in a loss of passengers, whereas in the opposite case, leaving the aircraft empty will increase the operational costs. The overall revenue from the assignment of fleets to flight legs is determined by considering the distance of each flight leg and unit revenue per seat mile. Likewise, cost per available seat-mile, the capacities of fleet types, and distances of flight legs are used to define overall cost of fleet assignment. Thus, we formulate the AFAP with a profit maximising objective function as in Equation (1).
where
denotes revenue per available seat kilometre for flight leg
,
denotes cost per available seat kilometre for fleet type
,
denotes the distance of flight leg
and
is the capacity of fleet type
. The binary decision variable
equals 1 if the fleet type
is assigned to leg
and
where a feasible connection exists.
The objective function can be extended by introducing a demand estimation for each flight leg. As real applications encourage the allocation of additional capacity surplus, we employ seat capacity () instead of demand data for calculating the total revenue.
The basic fleet assignment model is defined as a connection network model, which was proposed by Abara [
1]. Let
be the set of fleet type,
denote the set of arrival legs, and
denote the set of departure legs for station
with
. Equation (2) ensures the cover constraints, so each flight is preceded by an arrival or an originating arc that is covered by a fleet type.
Equation (2) implies that all flights are required to be served by a fleet type.
Equation (3) ensures the flow balance of each leg in the network for each fleet type.
Equation (4) ensures the flow balance of each leg in the network for each fleet type. For each station in the network, the number of aircraft for each fleet type remain the same every night, so the same assignment can be used in the succeeding days.
Equation (5) states that the number of assignments cannot exceed the available number of aircraft for fleet type , where denotes number of available aircraft for each fleet type f. Lastly, the decision variables are introduced as binary in Equation (6).
The basic fleet assignment model using a connection network aims to maximise the profit function, which is defined by subtracting operating cost from the expected revenue. The cost factor is accounted as a nominal unit operating cost for any fleet type. In this study, we adapted a novel profit function to the connection network model of Abara [
1] by assessing the revenue per available seat kilometre for all legs and the costs per available seat kilometre for all fleet types.
4. Proposed Two-Phase Heuristic Algorithm
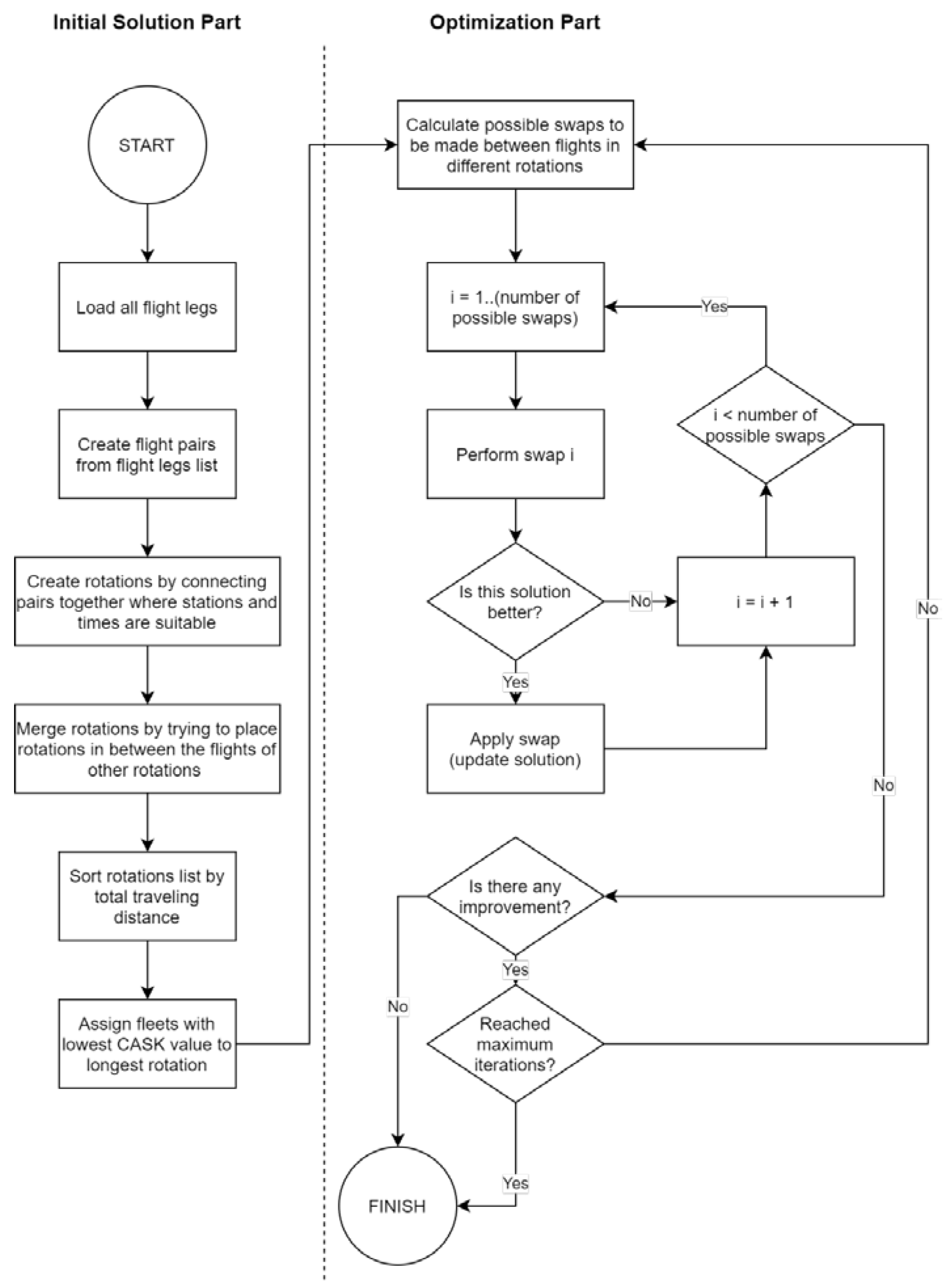
A two-phase heuristic algorithm was developed to solve the airline fleet assignment problem. The first phase of the algorithm generates an initial, basic and feasible solution. In the second phase, we propose a mechanism to improve the solution quality in terms of a predefined objective function. In the first phase, the algorithm aims to generate feasible flight pairs regarding the features of flights. These features can be stated as: origin, destination, arrival time, and departure time of any flight. A general flowchart for the two-phase heuristic algorithm is shown in
Figure 1.
We considered station-related and time-related constraints to determine an initial feasible solution. The general schema of the algorithm is shown in
Figure 2.
FindInitialSolution comprises the first phase of the algorithm that seeks a feasible solution considering the time-related and location-related issues.
A detailed pseudo code for phase 1 is given in
Figure 3. In order to elaborate on the first phase of the algorithm, we provide a numerical example that includes 4 flights with origins/destinations and scheduled departure/arrival times, as shown in
Table 1.
Firstly, we created flight pairs among all flight legs considering time and location-based constraints. For example, the first flight-pair was generated with Flight 1234 and Flight 3456 so that a feasible route was created between BAH-SAW-BAH (1234BAHSAW-3456SAWBAH) airports. Similarly, Flight 6789 and Flight 5678 were paired together and a route was created between SAW-CDG-SAW airports. Next, the algorithm searched for feasible rotations between flight pairs. For example, a feasible rotation could be found by linking two flight pairs with these flights: 1234BAHSAW-6789SAWCDG-5678CDGSAW-3456SAWBAH, which occur between BAH, CDG, and SAW airports.
The second phase of the algorithm aims to increase solution quality toward optimality. We summarise the steps of the second phase in
Figure 4. The second phase optimises the rotation of each aircraft by evaluating the profit function which comprises the revenue of rotations and the cost of assigning a fleet on corresponding route.
In small cases, enumerating possible swaps of flights takes a negligible amount of time. We examined the performance of the proposed heuristics by conducting computational experiments and concluded that the algorithm finds optimal solutions within a reasonable amount of time as the dimension of the problem increases.
5. Computational Study for the Two-Phase Heuristic Algorithm
This section includes a numerical study to examine the computational performance of the proposed algorithm. A real case problem arose as a result of the fleet assignment problem for an airline carrier in Turkey, which flies over 300 destinations. This work focused on flights that based out of SAW airport, where 46 flight legs and 10 destinations (stations) were considered. The data appear to be of moderate size, as only predetermined fleet data and related domestic/international flight data were provided. The detailed information on fleet data is described in
Table 2.
Initially, we generated subproblems based on the real case by adjusting the number of flight legs and stations. In order to reproduce results for evaluating the computational performance of the proposed heuristic algorithm, 17 new data instances were created by randomly removing flights and/or stations from the original data. In order to preserve the flow balance in the data, we utilized a basic procedure that transfers the flights of removed stations randomly to unremoved stations from the data. Therefore, each problem instance has at least one arrival and one departure flight from each station. The mathematical model in
Section 2 was coded in ILOG CPLEX Optimization Studio and the two-phase heuristic algorithm in
Section 3 was coded in Python 3.7. The programs run on a computer with an Intel
® Core i5, 1.70 GHz and 3.0 GB RAM computer. A brief summary of data instances is provided in
Table 3.
For all data instances, the mathematical model and the proposed heuristics achieved the optimal solution. In CPLEX, where the absolute MIP distance tolerance was set to
, we also used the default optimality gap. Therefore, CPLEX terminated when an integer feasible solution was shown to be within 0.01% of optimality. The proposed method also achieved the same optimal solutions as in CPLEX. As the size of the problem increased, solution times required for both methods increased similarly.
Figure 5 illustrates that the two-phase heuristics produced the same results with 85% better run times on average.
The proposed heuristic found the optimal solution quickly for smaller subproblems. For higher dimensions, the proposed heuristic algorithm significantly decreased computation times. We examined the comparative performance of the proposed two-phase heuristic algorithm for 18 problem instances.
Figure 6 shows that increasing the number of stations significantly increased the solution time for CPLEX while it had a limited effect on run time of the proposed heuristics.
As the size of the data increased, the computation times increased substantially while solving the mathematical model. The computation times of the proposed two-phase heuristics outperformed the model for all data instances.
The experimental results indicate that the heuristic approach helps managers/decision-makers better manage the airline fleet assignment problem of minimising costs. We can summarize the benefits of using the proposed heuristics as follows: (1) the heuristic approach is much faster than solving the AFAP mathematical model using a connection network, (2) it is also simpler to adapt the heuristic method to recent changes than transforming mathematical formulations, and (3) the proposed heuristic appears to be more practical than developing/implementing a mathematical model regarding the dynamic structure of airline operations, last-minute changes, and real-time, decision-making requirements in airline systems. The proposed heuristic approach also proved its capability for real-case problems.
6. Conclusions and Future Research
The global demand for flight travel is projected to increase in the future decade. Commercial airlines, especially in developing countries, are strengthening their fleets and increasing their fleet’s use. In the airline industry, two major factors for managing fleets are the projected increase in revenue per passenger per kilometre, and the expected decrease in the cost per passenger per kilometre. The revenue per passenger per kilometre is an important airline profit metric that is strongly connected to the effective assignment of fleets. Thus, airlines may have the opportunity to add new flight legs to the schedule and upgrade or downgrade some of the fleets on a recent assignment.
In this study, we extended the connection network model of AFAP by maximising the profit function with two main industry adopted metrics. As the problem dimensions increase, the mathematical model becomes inadequate in terms of solution times. Therefore, we employed a preprocessing procedure for representing flight connection possibilities to decrease run times for the mathematical model. Additionally, we proposed a two-phase heuristic algorithm for solving AFAPs comprising a higher number of stations and flight legs. The proposed heuristics provide optimal solutions for all AFAP instances with shorter run times.
The contribution of this study is twofold. Firstly, the two key metrics, the revenue per passenger per kilometre and the cost per seat per kilometre, are primarily assessed while solving AFAP instances originating from a real case problem. Secondly, we emphasise the importance of real industry-connected studies to both researchers and practitioners by developing the mathematical model and the two-phase heuristic algorithm based on industry-adopted metrics. For future work, we aim to extend the capabilities of the proposed two-phase heuristic algorithm by integrating hub optimization, rescheduling opportunities, and capacity issues.
Numerous extensions, i.e., path-based demands, network and recapture effects, through-flights, and maintenance issues, can be incorporated to address more realistic versions of the fleet assignment problem encountered in operation (Sherali et al. [
4]). One immediate, future research direction can be the integration of the fleet sizing problem considering the dynamics in demand generation on flight legs. Although there are different studies that proposed integrating these problems, to the best of our knowledge, the fleet sizing and assignment problems are not integrated with the consideration of demand generation. Additionally, another immediate, future study may be conducted to ensure availability for last-minute (higher-fare) passengers. The risk of underestimating the number of spilled passengers and limited availability for lower fare passengers may be included in forthcoming studies. Lastly, the level of fleet use may be re-examined considering the maintenance costs of aircraft and the frequency of maintenance requirements.
Finally, the desire of airlines is to minimise the time aircraft spend on ground because they only create revenue while flying in the air and instead incur cost while standing at the airport. Therefore, airlines are seeking better methods to solve the AFAP to reduce costs, to enable new opportunities, to meet passenger demands as close as possible, and to increase profitability. However, AFAPs are dynamic and can easily be affected by their environment. The environmental factors should be evaluated and specific objectives can be determined to increase the robustness of the assignments, i.e., balanced utilisation of aircraft/fleets.