Machine Learning-Based Small Hydropower Potential Prediction under Climate Change
Abstract
:1. Introduction
2. Data Descriptions and Methods
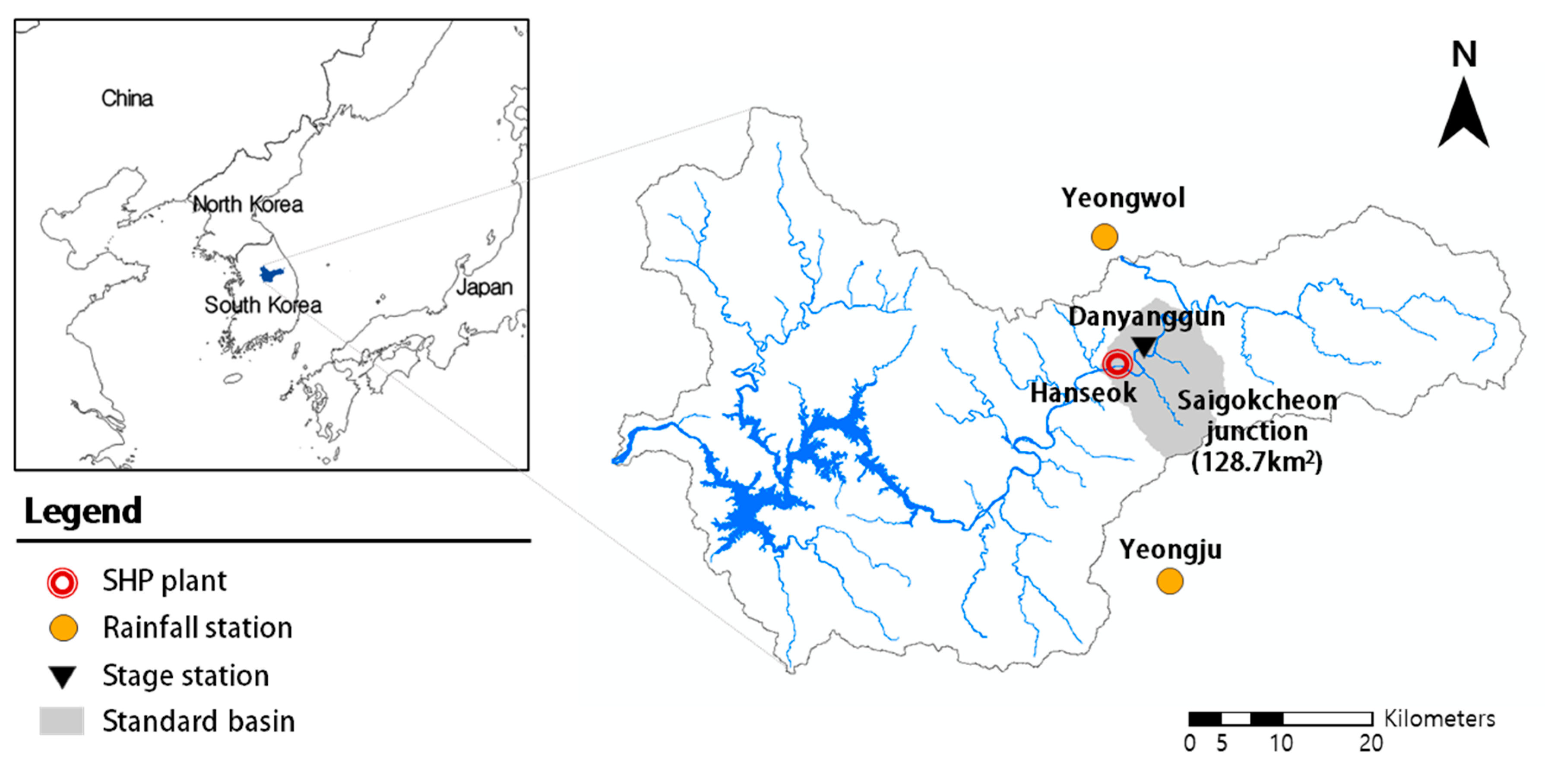
2.1. Target SHP Plant and Data
2.2. Climate Change Scenario
2.3. Artificial Neural Network
2.4. Evaluation Metrics
2.5. SHP Potential Calculation
3. Results
3.1. ANN Model Development
3.2. Runoff Prediction under A Climate Change Scenario Using ANN Model
3.3. SHP Potential Prediction
4. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ANN | Artificial Neural Network |
| CC | Coefficient of Coefficient |
| GCM | Global Climate Model |
| NSE | Nash–Sutcliffe Efficiency |
| PBIAS | Percent Bias |
| RCP | Representative Concentration Pathway |
| SHP | Small Hydropower |
References
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Garrote, L. Water-energy-ecosystem nexus: Balancing competing interests at a run-of-river hydropower plant coupling a hydrologic–ecohydraulic approach. Energy Convers. Manag. 2020, 223, 113267. [Google Scholar] [CrossRef]
- Kuriqi, A.; Pinheiro, A.N.; Sordo-Ward, A.; Bejarano, M.D.; Garrote, L. Ecological impacts of run-of-river hydropower plants—Current status and future prospects on the brink of energy transition. Renew. Sustain. Energy Rev. 2021, 142, 110833. [Google Scholar] [CrossRef]
- Frey, G.W.; Linke, D.M. Hydropower as a renewable and sustainable energy resource meeting global energy challenges in a reasonable way. Energy Policy 2002, 30, 1261–1265. [Google Scholar] [CrossRef]
- Llamosas, C.; Sovacool, B.K. The future of hydropower? A systematic review of the drivers, benefits and governance dynamics of transboundary dams. Renew. Sustain. Energy Rev. 2021, 137, 110495. [Google Scholar] [CrossRef]
- Francisco, M.A.; Myriam, T.; Antonio, Z.S.; Adel, J.; Francisco, G.M. An overview of research and energy evolution for small hydropower in Europe. Renew. Sustain. Energy Rev. 2017, 75, 476–489. [Google Scholar]
- Freitas, M.A.V.; Soito, J.L.S. Vulnerability to climate change and water management: Hydropower generation in Brazil. WIT Trans. Ecol. Environ. 2009, 124, 217–228. [Google Scholar] [CrossRef] [Green Version]
- Hamududu, B.; Killingtveit, A. Assessing Climate Change Impacts on Global Hydropower. Energies 2012, 5, 305–322. [Google Scholar] [CrossRef] [Green Version]
- Van Vliet, M.; van Beek, L.; Eisner, S.; Flörke, M.; Wada, Y.; Bierkens, M. Multi-model assessment of global hydropower and cooling water discharge potential under climate change. Glob. Environ. Chang. 2016, 40, 156–170. [Google Scholar] [CrossRef]
- Chilkoti, V.; Bolisetti, T.; Balachandar, R. Climate change impact assessment on hydropower generation using multi-model climate ensemble. Renew. Energy 2017, 109, 510–517. [Google Scholar] [CrossRef]
- Fan, J.-L.; Hu, J.-W.; Zhang, X.; Kong, L.-S.; Li, F.; Mi, Z. Impacts of climate change on hydropower generation in China. Math. Comput. Simul. 2020, 167, 4–18. [Google Scholar] [CrossRef]
- Kumar, A.; Schei, T.; Ahenkorah, A.; Rodriguez, R.; Devernay, J.; Freitas, M.; Hall, D.; Killingtveit, Å.; Liu, Z.; Edenhofer, O.; et al. (Eds.) IPCC Special Report on Renewable Energy Sources and Climate Change Mitigation; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2011. [Google Scholar]
- Markoff, M.S.; Cullen, A.C. Impact of climate change on Pacific Northwest hydropower. Clim. Chang. 2007, 87, 451–469. [Google Scholar] [CrossRef]
- Minville, M.; Brissette, F.; Krau, S.; Leconte, R. Adaptation to Climate Change in the Management of a Canadian Water-Resources System Exploited for Hydropower. Water Resour. Manag. 2009, 23, 2965–2986. [Google Scholar] [CrossRef]
- Vicuna, S.; Leonardson, R.; Hanemann, M.W.; Dale, L.L.; Dracup, J.A. Climate change impacts on high elevation hydropower generation in California’s Sierra Nevada: A case study in the Upper American River. Clim. Chang. 2007, 87, 123–137. [Google Scholar] [CrossRef]
- Vicuña, S.; Dracup, J.A.; Lund, J.R.; Dale, L.L.; Maurer, E.P. Basin-scale water system operations with uncertain future climate conditions: Methodology and case studies. Water Resour. Res. 2010, 46. [Google Scholar] [CrossRef] [Green Version]
- Raje, D.; Mujumdar, P. Reservoir performance under uncertainty in hydrologic impacts of climate change. Adv. Water Resour. 2010, 33, 312–326. [Google Scholar] [CrossRef]
- Koch, F.; Prasch, M.; Bach, H.; Mauser, W.; Appel, F.; Weber, M. How Will Hydroelectric Power Generation Develop under Climate Change Scenarios? A Case Study in the Upper Danube Basin. Energies 2011, 4, 1508–1541. [Google Scholar] [CrossRef]
- Schaefli, B.; Hingray, B.; Musy, A. Climate change and hydropower production in the Swiss Alps: Quantification of potential impacts and related modelling uncertainties. Hydrol. Earth Syst. Sci. 2007, 11, 1191–1205. [Google Scholar] [CrossRef]
- Majone, B.; Villa, F.; Deidda, R.; Bellin, A. Impact of climate change and water use policies on hydropower potential in the south-eastern Alpine region. Sci. Total. Environ. 2016, 543, 965–980. [Google Scholar] [CrossRef]
- Schaefli, B. Projecting hydropower production under future climates: A guide for decision-makers and modelers to interpret and design climate change impact assessments. Wiley Interdiscip. Rev. Water 2015, 2, 271–289. [Google Scholar] [CrossRef] [Green Version]
- Arriagada, P.; Dieppois, B.; Sidibe, M.; Link, O. Impacts of Climate Change and Climate Variability on Hydropower Potential in Data-Scarce Regions Subjected to Multi-Decadal Variability. Energies 2019, 12, 2747. [Google Scholar] [CrossRef] [Green Version]
- Carvajal, P.E.; Anandarajah, G.; Mulugetta, Y.; Dessens, O. Assessing uncertainty of climate change impacts on long-term hydropower generation using the CMIP5 ensemble—the case of Ecuador. Clim. Chang. 2017, 144, 611–624. [Google Scholar] [CrossRef] [Green Version]
- Eshchanov, B.; Abylkasymova, A.; Overland, I.; Moldokanov, D.; Aminjonov, F.; Vakulchuk, R. Hydropower Potential of the Central Asian Countries. Cent. Asia Reg. Data Rev. 2019, 19, 1–7. [Google Scholar]
- Hu, Y.; Jin, X.; Guo, Y. Big data analysis for the hydropower development potential of ASEAN-8 based on the hydropower digital planning model. J. Renew. Sustain. Energy 2018, 10, 034502. [Google Scholar] [CrossRef]
- Hamududu, B.H.; Killingtveit, Å. Hydropower Production in Future Climate Scenarios; the Case for the Zambezi River. Energies 2016, 9, 502. [Google Scholar] [CrossRef] [Green Version]
- Kim, G.J.; Sun, S.P.; Yeo, G.D.; Kim, H.S. A Study on Variability of Small Hydro Power Generation Considering Climate change. KSCE Conv. Korean Soc. Civ. Eng. 2012, 10, 932–935. [Google Scholar]
- Liu, X.; Tang, Q.; Voisin, N.; Cui, H. Projected impacts of climate change on hydropower potential in China. Hydrol. Earth Syst. Sci. 2016, 20, 3343–3359. [Google Scholar] [CrossRef] [Green Version]
- Wang, H.; Xiao, W.; Wang, Y.; Zhao, Y.; Lu, F.; Yang, M.; Hou, B.; Yang, H. Assessment of the impact of climate change on hydropower potential in the Nanliujiang River basin of China. Energy 2019, 167, 950–959. [Google Scholar] [CrossRef]
- Campolo, M.; Soldati, A.; Andreussi, P. Artificial neural network approach to flood forecasting in the River Arno. Hydrol. Sci. J. 2003, 48, 381–398. [Google Scholar] [CrossRef]
- Kerh, T.; Lee, C. Neural networks forecasting of flood discharge at an unmeasured station using river upstream information. Adv. Eng. Softw. 2006, 37, 533–543. [Google Scholar] [CrossRef]
- Neslihan, S. Modeling flood discharge at ungauged sites across Turkey using neuro-fuzzy and neural networks. J. Hydroinform. 2011, 13, 842–849. [Google Scholar]
- Hidayat, H.; Hoitink, A.J.F.; Sassi, M.G.; Torfs, P.J.J.F. Prediction of Discharge in a Tidal River Using Artificial Neural Networks. J. Hydrol. Eng. 2014, 19, 04014006. [Google Scholar] [CrossRef]
- Jahangir, M.H.; Reineh, S.M.M.; Abolghasemi, M. Spatial predication of flood zonation mapping in Kan River Basin, Iran, using artificial neural network algorithm. Weather. Clim. Extrem. 2019, 25, 100215. [Google Scholar] [CrossRef]
- Bomers, A.; van der Meulen, B.; Schielen, R.M.J.; Hulscher, S.J.M.H. Historic Flood Reconstruction With the Use of an Artificial Neural Network. Water Resour. Res. 2019, 55, 9673–9688. [Google Scholar] [CrossRef] [Green Version]
- Kyoung, M.; Kim, H.S.; Sivakumar, B.; Singh, V.; Ahn, K. Dynamic characteristics of monthly in the Korean Peninsular under climate change. Stoch. Environ. Res. Risk Assess. 2011, 25, 613–625. [Google Scholar] [CrossRef]
- Bodas-Salcedo, A.; Mulcahy, J.P.; Andrews, T.; Williams, K.D.; Ringer, M.A.; Field, P.R.; Elsaesser, G.S. Strong Dependence of Atmospheric Feedbacks on Mixed-Phase Microphysics and Aerosol-Cloud Interactions in HadGEM3. J. Adv. Model. Earth Syst. 2019, 11, 1735–1758. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, J.W. Prediction and Evaluation of Hydro-Ecology, Functions, and Sustainability of a Wetland under Climate Change. Ph.D. Thesis, Inha University, Incheon, Korea, 2019. [Google Scholar]
- Kwak, J.; Kim, S.; Jung, J.; Singh, V.P.; Lee, N.R.; Kim, H.S. Assessment of Meteorological Drought in Korea under Climate Change. Adv. Meteorol. 2016, 2016, 1–13. [Google Scholar] [CrossRef]
- McCulloch, W.S.; Pitts, W. A logical calculus of the ideas immanent in nervous activity. Bull. Math. Biol. 1943, 5, 115–133. [Google Scholar] [CrossRef]
- Jung, S. Estimation and Future Prospect of Small Hydropower Generation Potential for the Ungaged Basin. Ph.D. Thesis, Inha University, Incheon, Korea, 2020. [Google Scholar]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model Evaluation Guidelines for Systematic Quantification of Accuracy in Watershed Simulations. Trans. ASABE 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Xiang, Z.; Yan, J.; Demir, I. A rainfall-runoff model with LSTM-based sequence-to-sequence learning. Water Resour. Res. 2020, 56, e2019WR025326. [Google Scholar] [CrossRef]
- Andrade, C.W.L.; Montenegro, S.M.G.L.; Montenegro, A.A.A.; Lima, J.R.D.S.; Srinivasan, R.; Jones, C.A. Climate change impact assessment on water resources under RCP scenarios: A case study in Mundaú River Basin, Northeastern Brazil. Int. J. Clim. 2021, 41, 1045–1061. [Google Scholar] [CrossRef]
- Tarekegn, N.; Abate, B.; Muluneh, A.; Dile, Y. Modeling the impact of climate change on the hydrology of Andasa watershed. Model. Earth Syst. Environ. 2021, 1–17. [Google Scholar] [CrossRef]
- Jung, J.; Jung, S.; Lee, J.; Lee, M.; Kim, H. Analysis of Small Hydropower Generation Potential: (2) Future Prospect of the Potential under Climate Change. Energies 2021, 14, 3001. [Google Scholar] [CrossRef]




| RCP | Case | |
|---|---|---|
| 2.6 | The Earth is able to recover the effects of human activities (Impossible Scenario) | 420 ppm |
| 4.5 | The green gas reduction policies are implemented significantly | 540 ppm |
| 6.0 | The green gas reduction policies are realized at less than RCP 4.5 | 670 ppm |
| 8.5 | The greenhouse gases are emitted at the current trend (without reduction) | 940 ppm |
| Statistic | Historic (2000–2020) | Future (2021–2030) | Change (%) |
|---|---|---|---|
| Max. | 1581.69 | 855.63 | −45.9% |
| 75% | 657.02 | 467.93 | −28.8% |
| 50% | 371.07 | 328.09 | −11.6% |
| 25% | 201.55 | 235.51 | 16.9% |
| Min. | 9.41 | 78.55 | 734.6% |
| Mean | 491.79 | 364.20 | −25.9% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jung, J.; Han, H.; Kim, K.; Kim, H.S. Machine Learning-Based Small Hydropower Potential Prediction under Climate Change. Energies 2021, 14, 3643. https://doi.org/10.3390/en14123643
Jung J, Han H, Kim K, Kim HS. Machine Learning-Based Small Hydropower Potential Prediction under Climate Change. Energies. 2021; 14(12):3643. https://doi.org/10.3390/en14123643
Chicago/Turabian StyleJung, Jaewon, Heechan Han, Kyunghun Kim, and Hung Soo Kim. 2021. "Machine Learning-Based Small Hydropower Potential Prediction under Climate Change" Energies 14, no. 12: 3643. https://doi.org/10.3390/en14123643






