Vector Modulation-Based Model Predictive Current Control with Filter Resonance Suppression and Zero-Current Switching Sequence for Two-Stage Matrix Converter
Abstract
:1. Introduction
- A vector modulation-based model predictive current control (VMMPCC) strategy is proposed, which features the controllable source reactive power and the controllable output currents with fixed switching frequency output waveforms. The comparison between the proposed VMMPCC and existing methods is shown in Table 1.
- The advantage of the VMMPCC strategy compared with the CMPC is firstly proved using the principle of vector synthesis and the law of sines in the vector distribution area.
- A zero-current switching sequence (ZSS) is proposed, which can guarantee safe zero-current switching operations and reduce the switching losses. This pattern can simplify the commutation of the TSMC and avoid complex commutation strategies (e.g., four-step commutation) in traditional control methods.
- A novel input filter resonance suppression (IFRS) method is proposed and applied in the VMMPCC for the TSMC, featuring good damping performance and easy implementation.
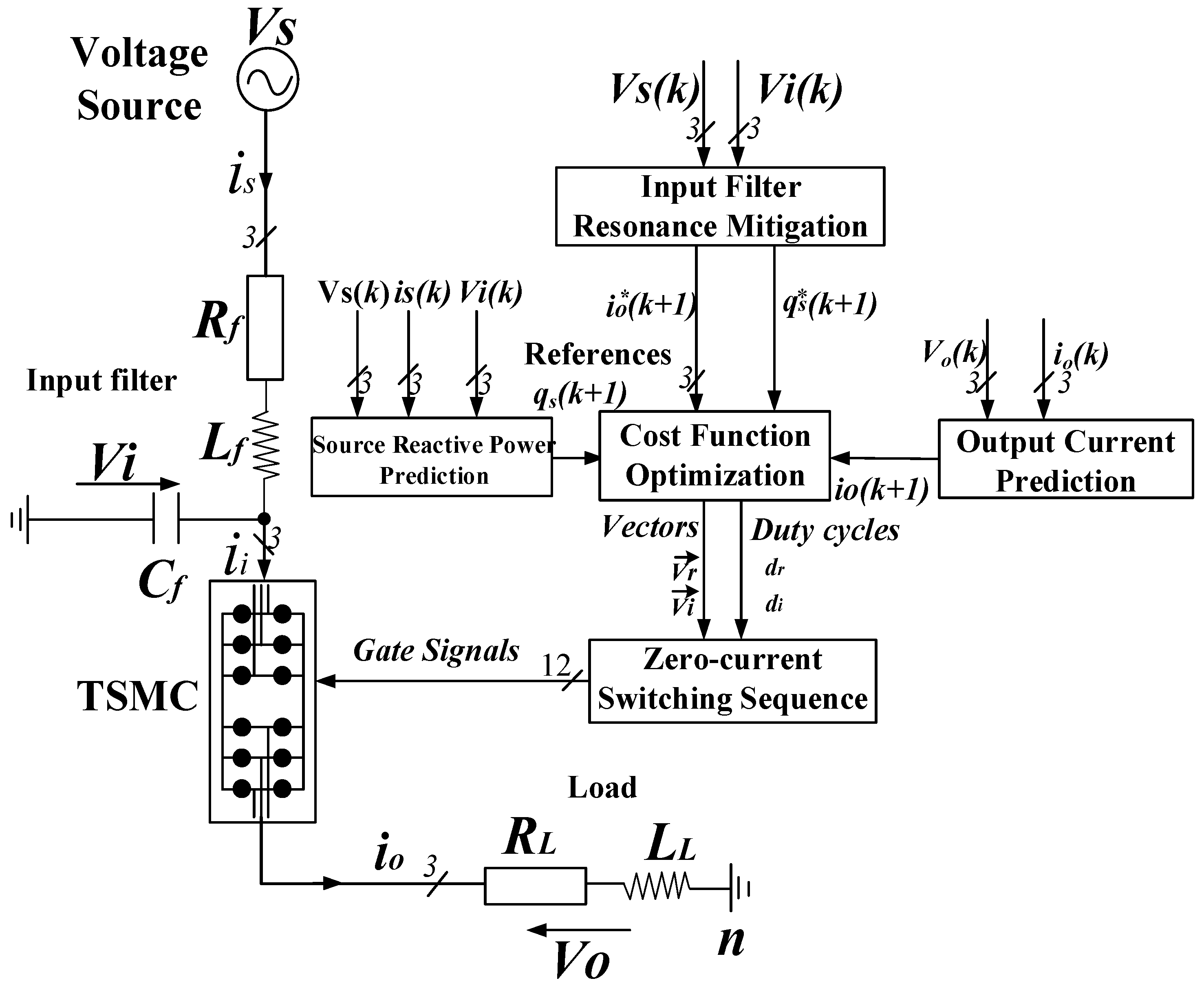
2. TSMC Mathematical System Model
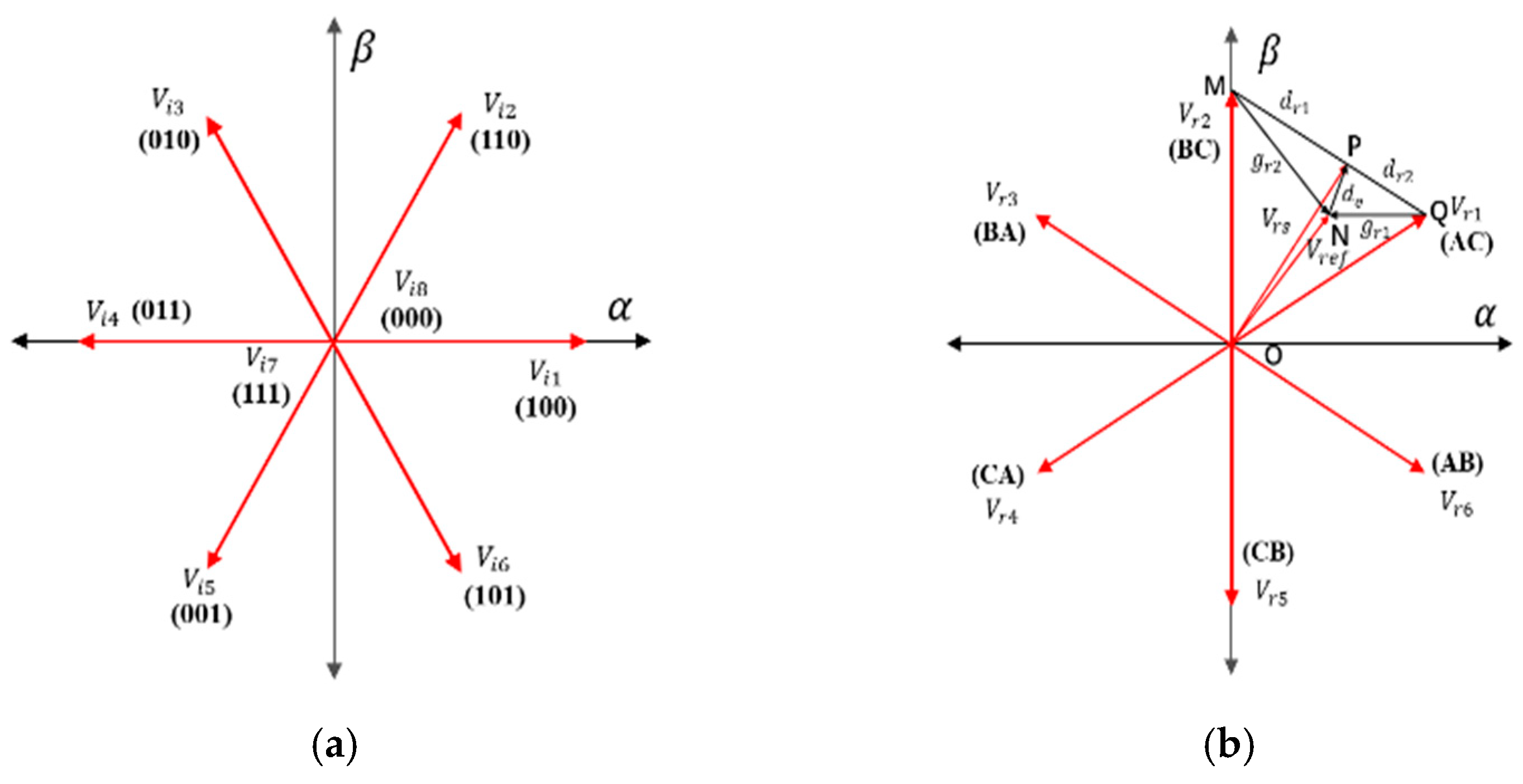
3. Vector Modulation Based Model Predictive Control Strategy with Zero-Current Switching Sequence
3.1. Source Reactive Power Prediction and Output Current Prediction
3.2. Cost Function Optimization
3.3. Comparision between the Proposed VMMPCC and the CMPC
- ; This means that P and Q are the same points and the error between the synthesized vector and the reference vector (equal to the length of PN) is zero;
- In fact, since:
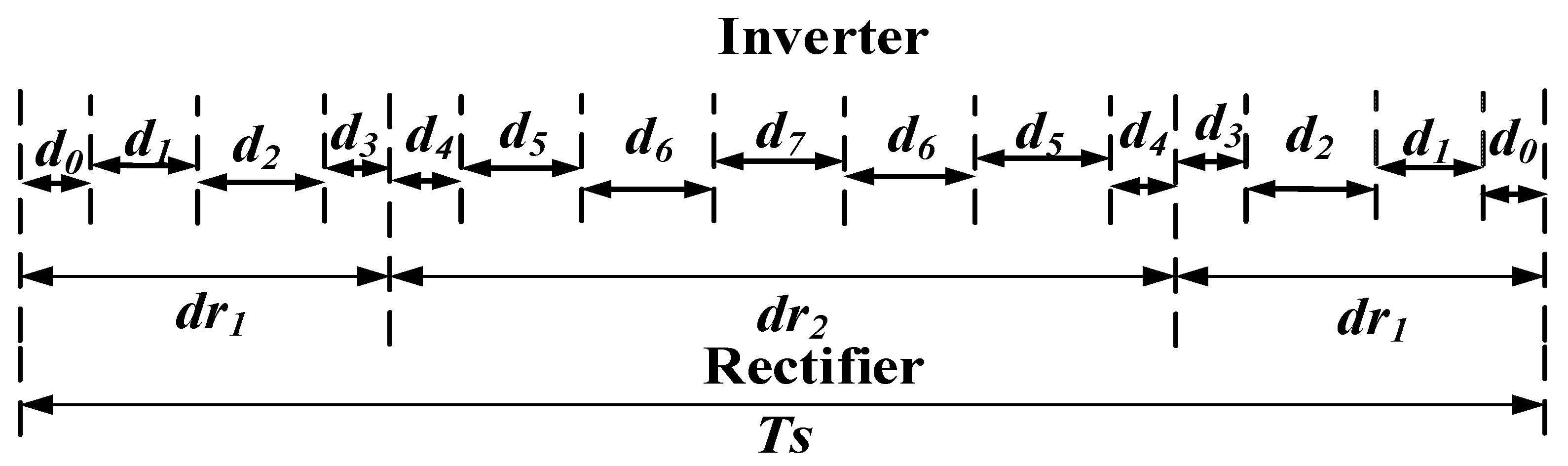
3.4. Zero-Current Switching Sequence
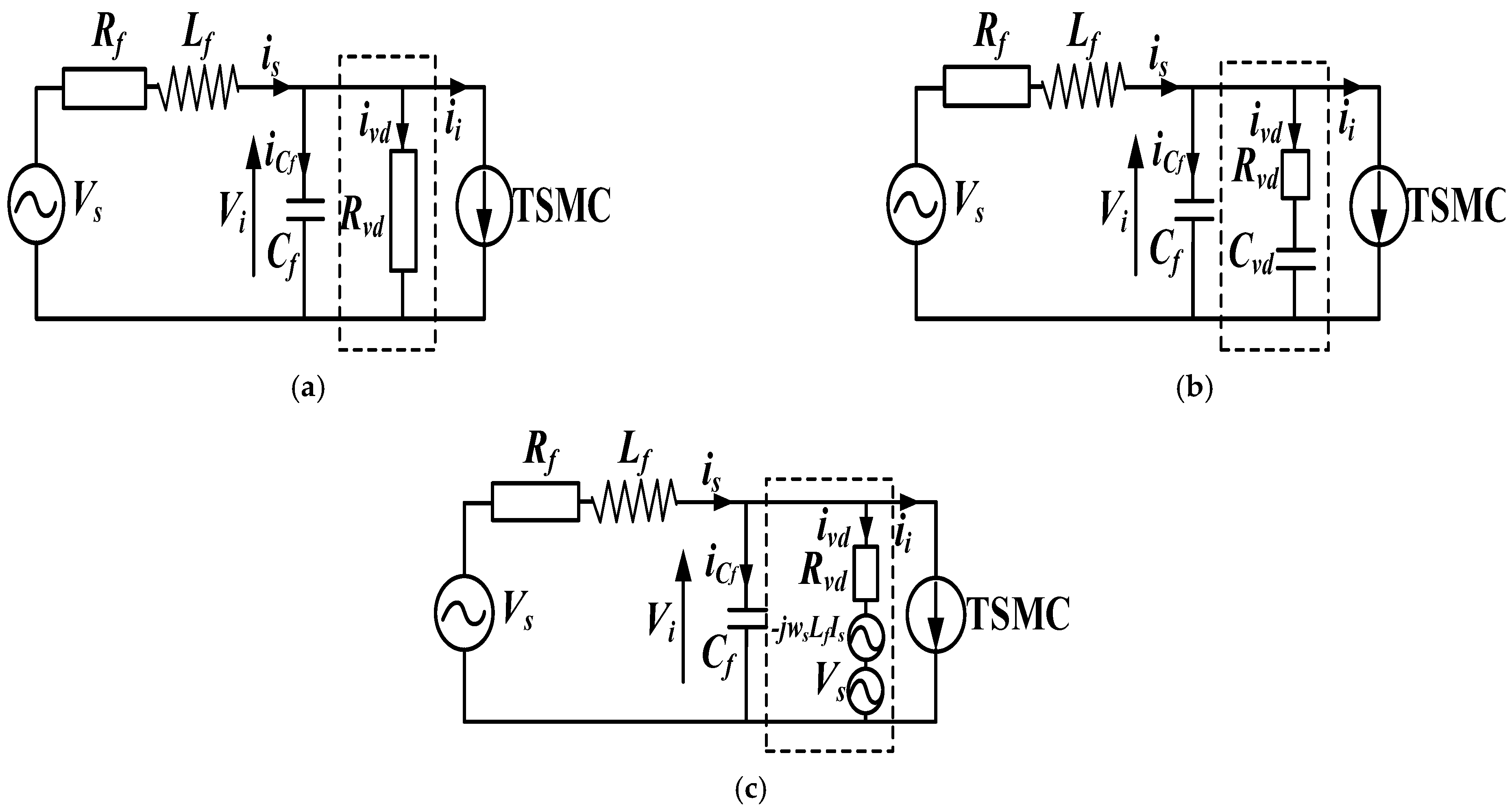
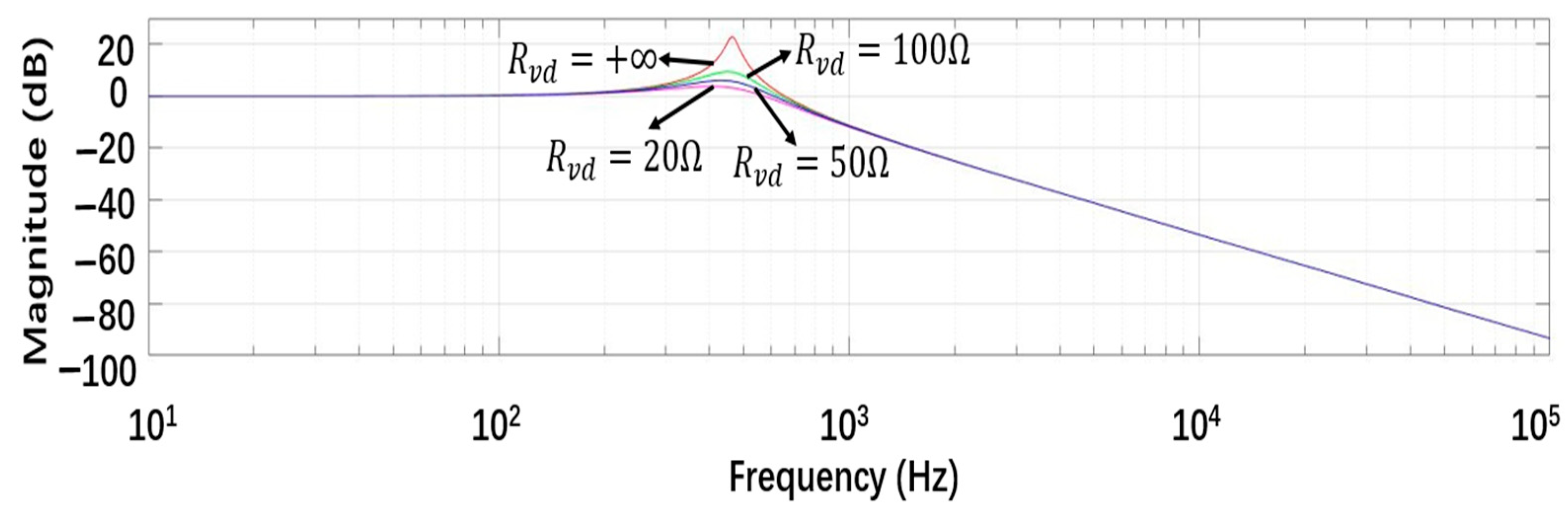
4. Input Filter Resonance Suppression
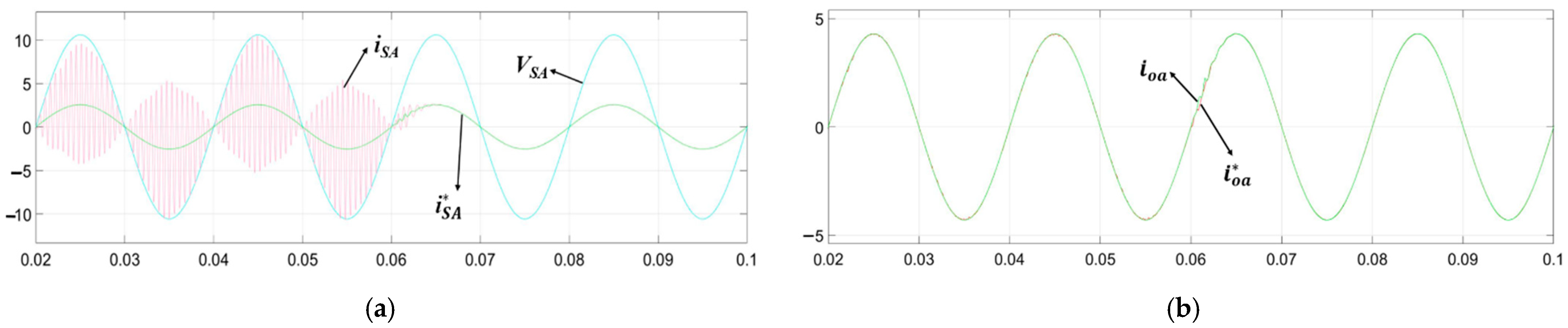
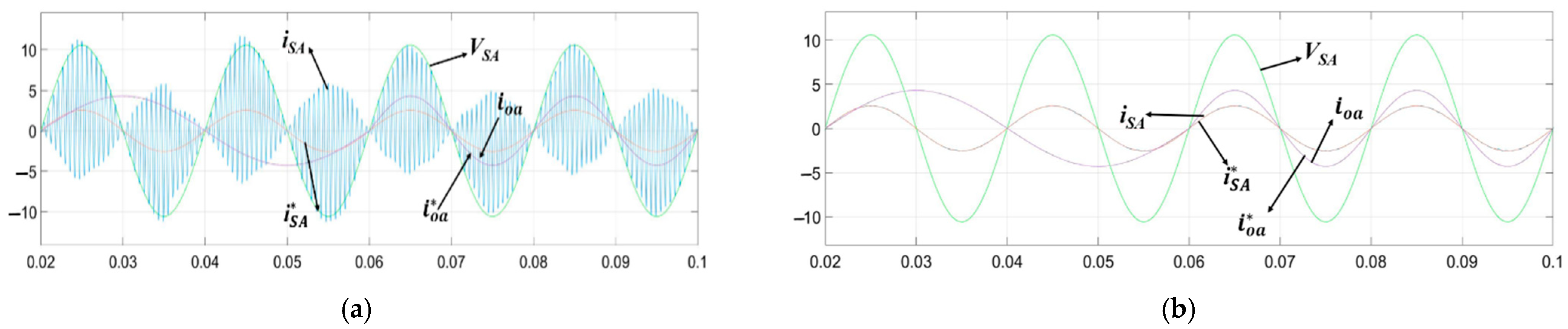
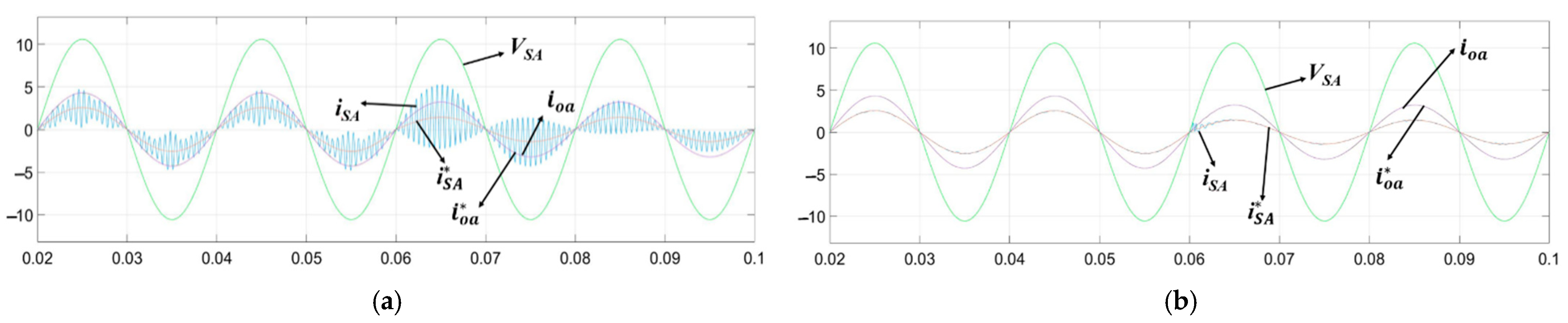
5. Simulation Results
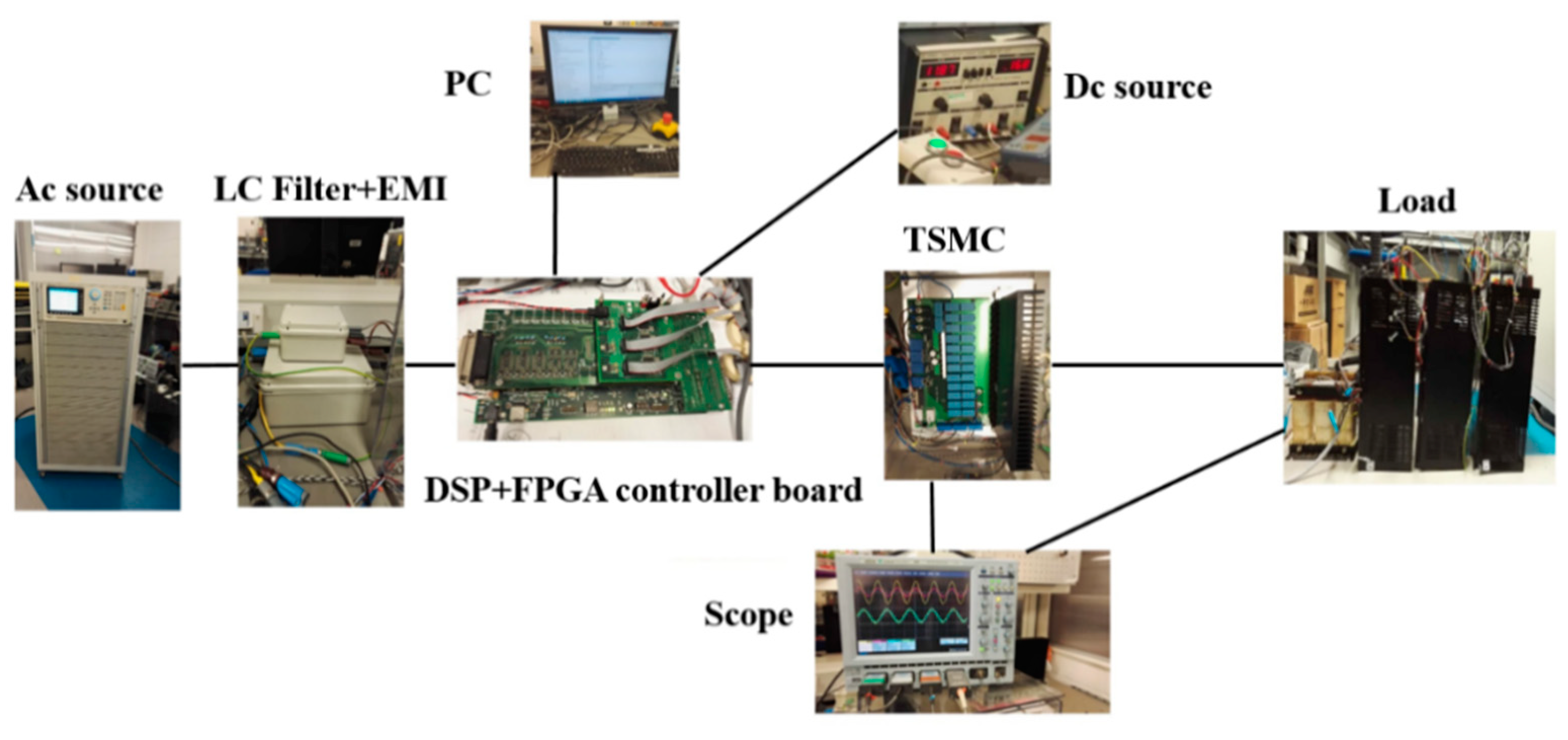
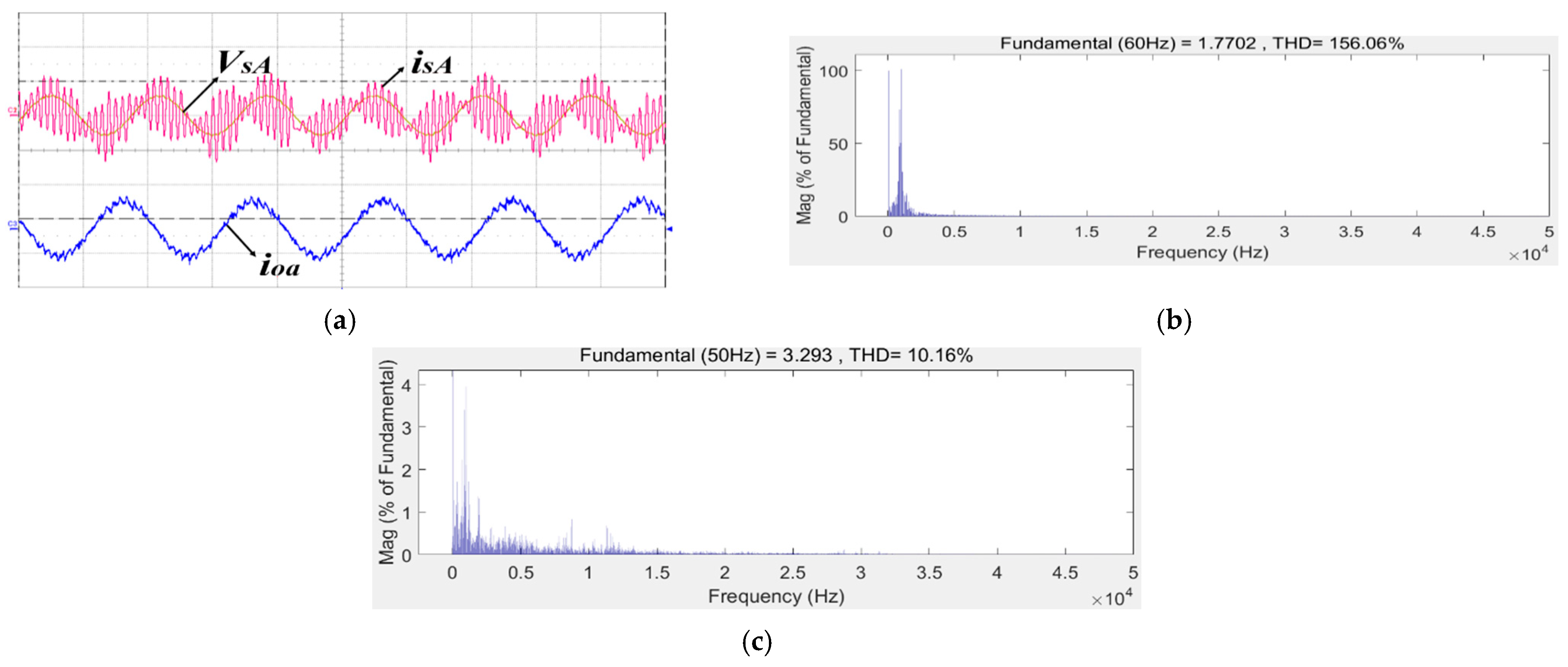
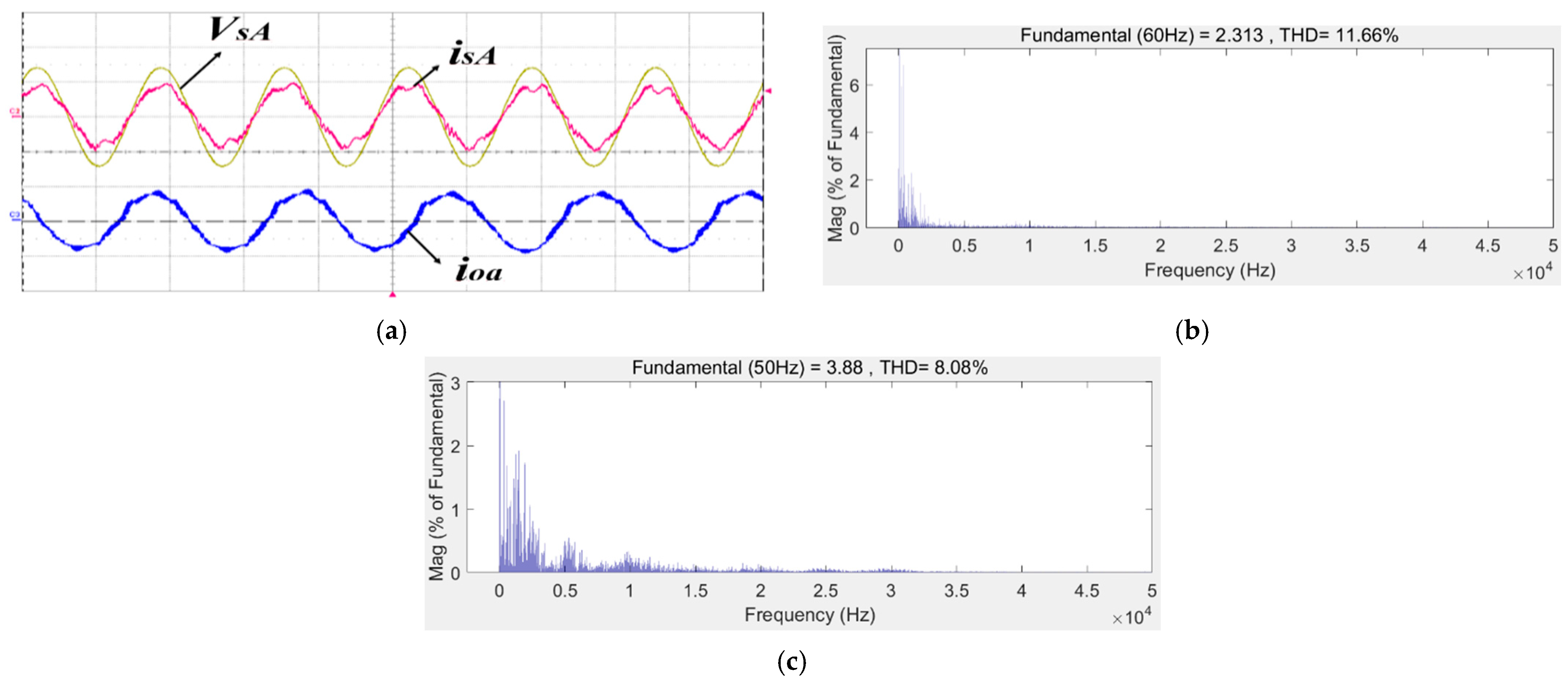
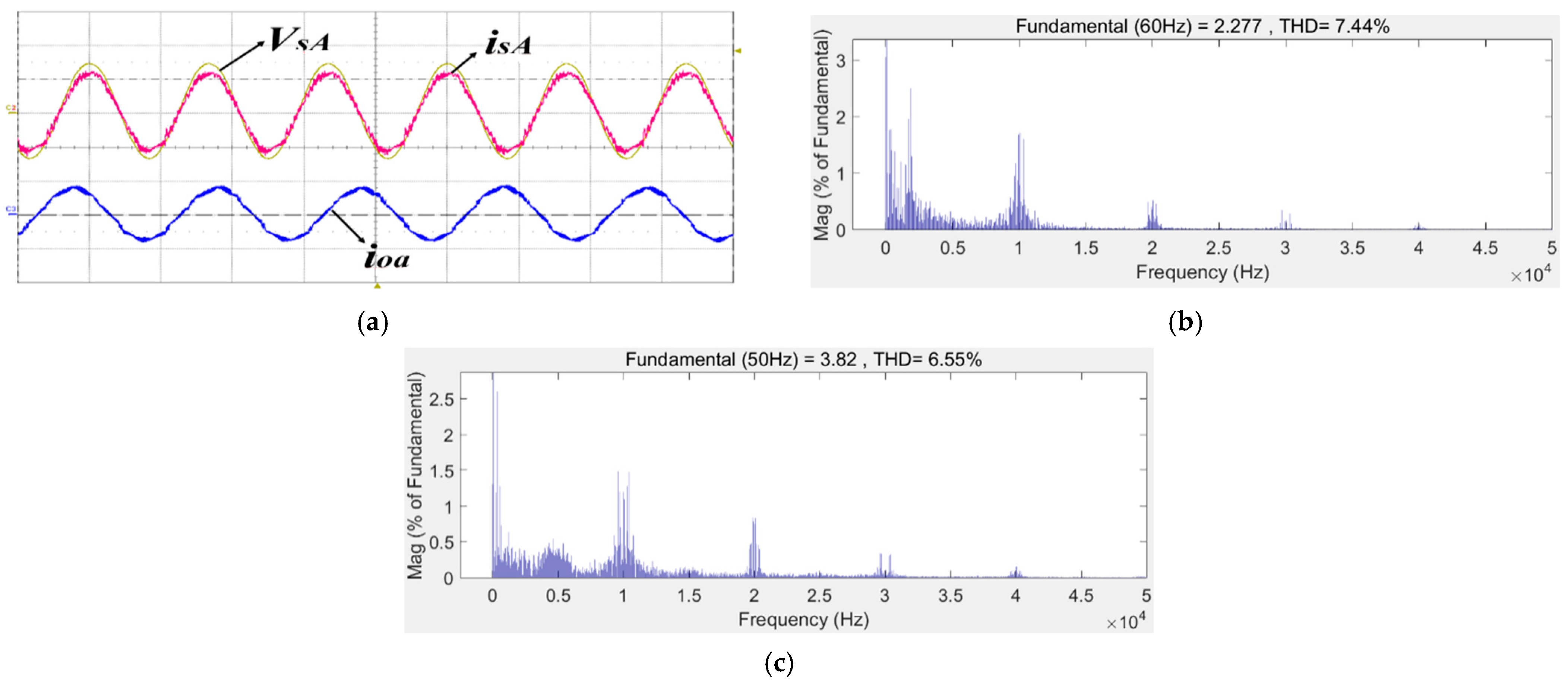
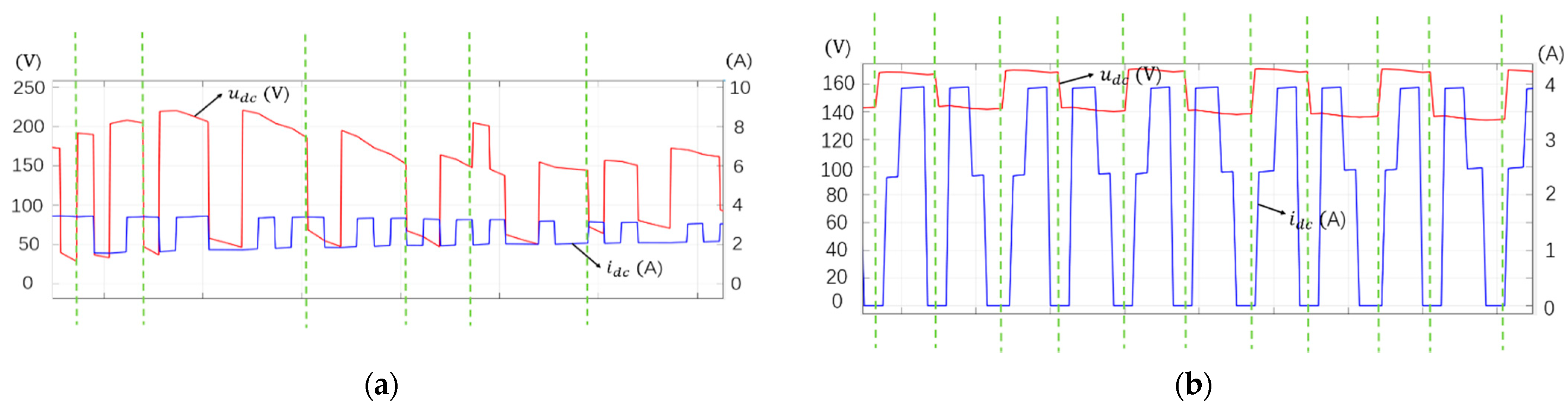
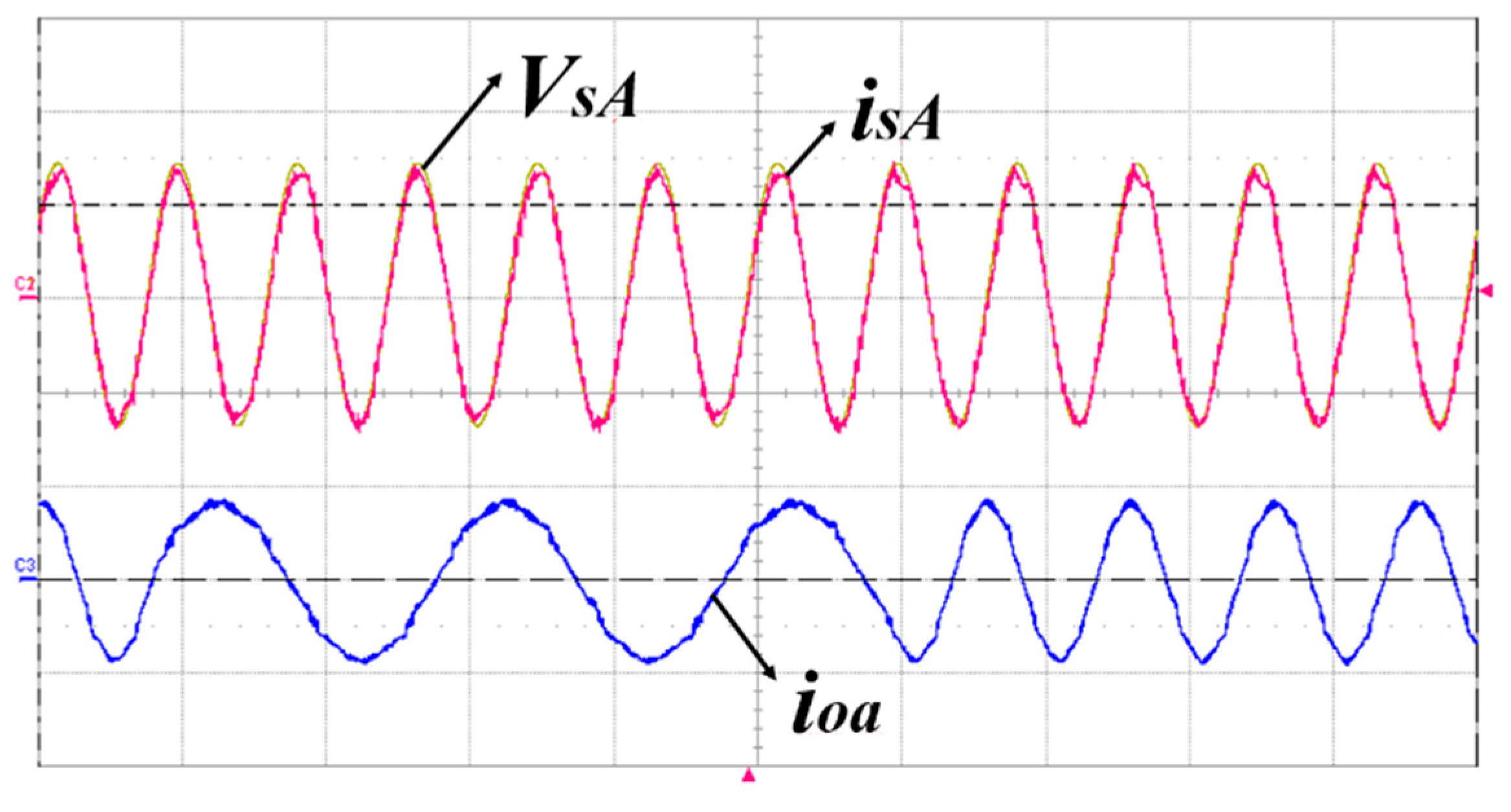
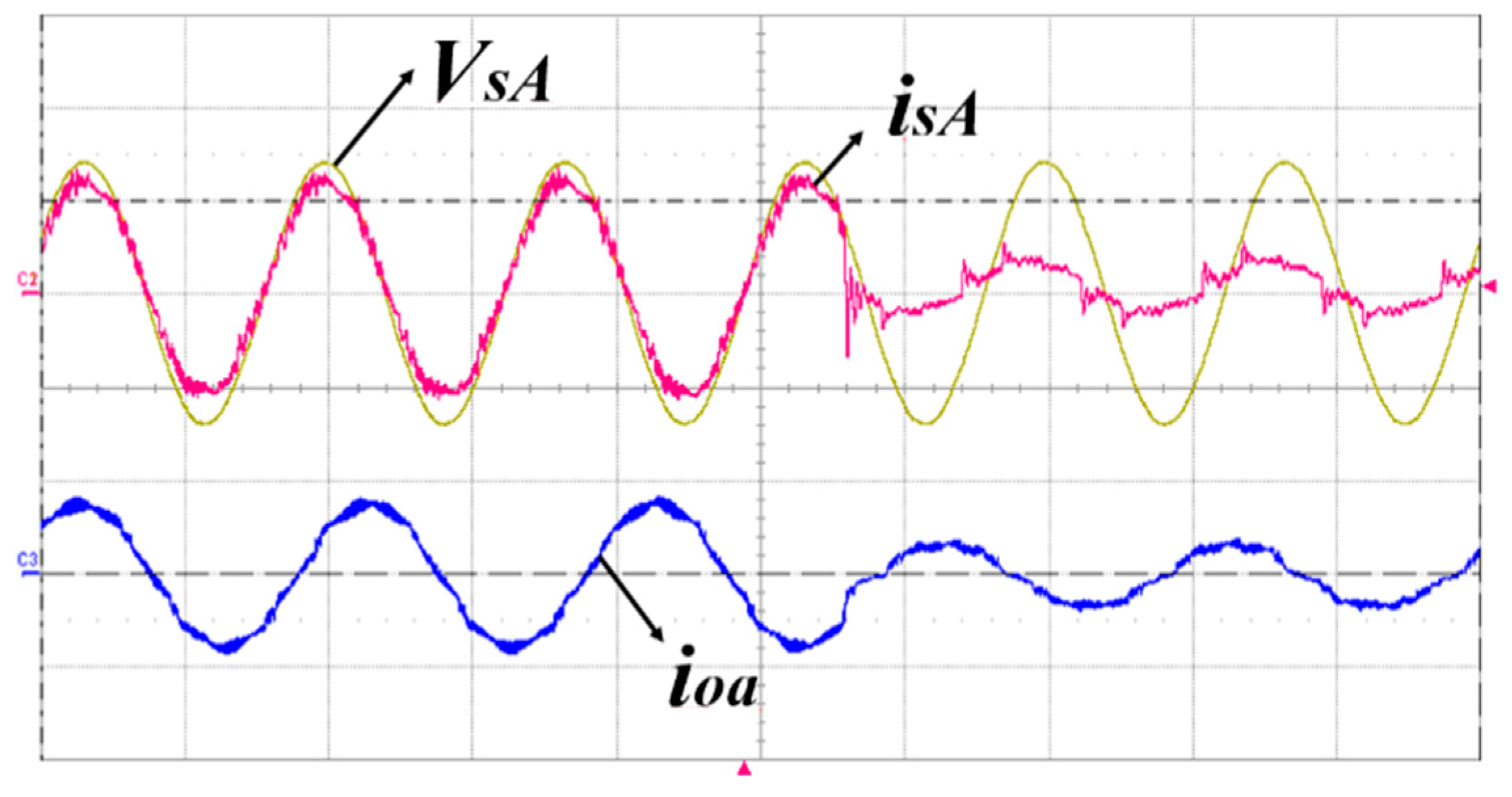
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Friedli, T.; Kolar, J.W.; Rodriguez, J.; Wheeler, P.W. Comparative Evaluation of Three-Phase AC–AC Matrix Converter and Voltage DC-Link Back-to-Back Converter Systems. IEEE Trans. Ind. Electron. 2012, 59, 4487–4510. [Google Scholar] [CrossRef]
- Wheeler, P.; Rodriguez, J.; Clare, J.; Empringham, L.; Weinstein, A. Matrix converters: A technology review. IEEE Trans. Ind. Electron. 2002, 49, 276–288. [Google Scholar] [CrossRef]
- Alesina, A.; Venturini, M.G.B. Analysis and design of optimum-amplitude nine-switch direct AC-AC converters. IEEE Trans. Power Electron. 1989, 4, 101–112. [Google Scholar] [CrossRef]
- Kolar, J.W.; Friedli, T.; Rodriguez, J.; Wheeler, P.W. Review of Three-Phase PWM AC–AC Converter Topologies. IEEE Trans. Ind. Electron. 2011, 58, 4988–5006. [Google Scholar] [CrossRef]
- Lee, M.Y.; Wheeler, P.; Klumpner, C. Space-Vector Modulated Multilevel Matrix Converter. IEEE Trans. Ind. Electron. 2010, 57, 3385–3394. [Google Scholar] [CrossRef]
- Lei, J.; Zhou, B.; Bian, J.; Qin, X.; Wei, J. A Simple Method for Sinusoidal Input Currents of Matrix Converter Under Unbalanced Input Voltages. IEEE Trans. Power Electron. 2015, 31, 21–25. [Google Scholar] [CrossRef]
- Rivera, M.; Wheeler, P.; Olloqui, A.; Khaburi, D.A. A Review of Predictive Control Techniques for Matrix Converters—Part I. In Proceedings of the 2016 7th Power Electronics and Drive Systems Technologies Conference (PEDSTC), Tehran, Iran, 16–18 February 2016; Institute of Electrical and Electronics Engineers (IEEE): Newark, NJ, USA, 2016; pp. 582–588. [Google Scholar]
- Rodriguez, J.; Rivera, M.; Kolar, J.W.; Wheeler, P.W. A Review of Control and Modulation Methods for Matrix Converters. IEEE Trans. Ind. Electron. 2012, 59, 58–70. [Google Scholar] [CrossRef]
- Nguyen, T.; Lee, H.-H. A New SVM Method for an Indirect Matrix Converter with Common-Mode Voltage Reduction. IEEE Trans. Ind. Inform. 2014, 10, 61–72. [Google Scholar] [CrossRef]
- Sun, Y.; Li, X.; Su, M.; Wang, H.; Dan, H.; Xiong, W. Indirect Matrix Converter-Based Topology and Modulation Schemes for Enhancing Input Reactive Power Capability. IEEE Trans. Power Electron. 2015, 30, 4669–4681. [Google Scholar] [CrossRef]
- Tsoupos, A.; Khadkikar, V.M. A Novel SVM Technique with Enhanced Output Voltage Quality for Indirect Matrix Converters. IEEE Trans. Ind. Electron. 2018, 66, 832–841. [Google Scholar] [CrossRef]
- Rivera, M.; Rojas, C.; Wilson, A.; Rodriguez, J.; Espinoza, J.; Baier, C.; Muñoz, J. Review of predictive control methods to improve the input current of an indirect matrix converter. IET Power Electron. 2014, 7, 886–894. [Google Scholar] [CrossRef]
- Ahmed, A.A.; Koh, B.K.; Lee, Y.I. A Comparison of Finite Control Set and Continuous Control Set Model Predictive Control Schemes for Speed Control of Induction Motors. IEEE Trans. Ind. Inform. 2018, 14, 1334–1346. [Google Scholar] [CrossRef]
- Formentini, A.; Trentin, A.; Marchesoni, M.; Zanchetta, P.; Wheeler, P. Speed Finite Control Set Model Predictive Control of a PMSM Fed by Matrix Converter. IEEE Trans. Ind. Electron. 2015, 62, 6786–6796. [Google Scholar] [CrossRef]
- Gulbudak, O.; Santi, E. FPGA-Based Model Predictive Controller for Direct Matrix Converter. IEEE Trans. Ind. Electron. 2016, 63, 4560–4570. [Google Scholar] [CrossRef]
- Siami, M.; Khaburi, D.A.; Rodriguez, J. Simplified Finite Control Set-Model Predictive Control for Matrix Converter-Fed PMSM Drives. IEEE Trans. Power Electron. 2017, 33, 2438–2446. [Google Scholar] [CrossRef]
- Rivera, M.; Yaramasu, V.; Llor, A.; Rodriguez, J.; Wu, B.; Fadel, M. Digital Predictive Current Control of a Three-Phase Four-Leg Inverter. IEEE Trans. Ind. Electron. 2013, 60, 4903–4912. [Google Scholar] [CrossRef]
- Tarisciotti, L.; Zanchetta, P.; Watson, A.; Wheeler, P.W.; Clare, J.C.; Bifaretti, S. Multiobjective Modulated Model Predictive Control for a Multilevel Solid-State Transformer. IEEE Trans. Ind. Appl. 2015, 51, 4051–4060. [Google Scholar] [CrossRef]
- Vijayagopal, M.; Empringham, L.; de Lillo, L.; Tarisciotti, L.; Zanchetta, P.; Wheeler, P. Control of a Direct Matrix Converter Induction Motor Drive with Modulated Model Predictive Control. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; Institute of Electrical and Electronics Engineers (IEEE): Newark, NJ, USA, 2015; pp. 4315–4321. [Google Scholar]
- Vijayagopal, M.; Zanchetta, P.; Empringham, L.; de Lillo, L.; Tarisciotti, L.; Wheeler, P. Control of a Direct Matrix Converter with Modulated Model-Predictive Control. IEEE Trans. Ind. Appl. 2017, 53, 2342–2349. [Google Scholar] [CrossRef]
- Renault, A.; Ayala, M.; Comparatore, L.; Pacher, J.; Gregor, R. Comparative Study of Predictive-Fixed Switching Techniques for a Cascaded H-Bridge Two level STATCOM. In Proceedings of the 2018 53rd International Universities Power Engineering Conference (UPEC), Glasgow, Scotland, 4–7 September 2018; Institute of Electrical and Electronics Engineers (IEEE): Newark, NJ, USA, 4 September 2018; pp. 1–6. [Google Scholar]
- Garcia, C.F.; Silva, C.A.; Rodriguez, J.R.; Zanchetta, P.; Odhano, S.A. Modulated Model-Predictive Control with Optimized Overmodulation. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 404–413. [Google Scholar] [CrossRef]
- He, Z.; Guo, P.; Shuai, Z.; Xu, Q.; Luo, A.; Guerrero, J.M. Modulated Model Predictive Control for Modular Multilevel AC/AC Converter. IEEE Trans. Power Electron. 2019, 34, 10359–10372. [Google Scholar] [CrossRef]
- Fang, F.; Tian, H.; Li, Y. Finite Control Set Model Predictive Control for AC–DC Matrix Converter with Virtual Space Vectors. IEEE J. Emerg. Sel. Top. Power Electron. 2021, 9, 616–628. [Google Scholar] [CrossRef]
- Di, Z.; Rivera, M.; Dan, H.; Tarisciotti, L.; Zhang, K.; Xu, D.; Wheeler, P. Modulated model predictive current control of an indirect matrix converter with active damping. In Proceedings of the IECON 2017—43rd Annual Conference of the IEEE Industrial Electronics Society, Beijing, China, 29 October–1 November 2017; Institute of Electrical and Electronics Engineers (IEEE): Newark, NJ, USA, 2017; pp. 1313–1318. [Google Scholar]
- Wang, F.; Chen, N.; Xia, A.; Rodriguez, J. Modulated Model Predictive Control of Two-Stage Matrix Converter for Reducing Common-mode Voltage. In Proceedings of the IEEE International Symposium on Predictive Control of Electrical Drives and Power Electronics (PRECEDE 2019), Quanzhou, China, 31 May–2 June 2019; Institute of Electrical and Electronics Engineers (IEEE): Newark, NJ, USA, 4 July 2019. [Google Scholar] [CrossRef]
- Salo, M.; Tuusa, H. A vector controlled current-source PWM rectifier with a novel current damping method. IEEE Trans. Power Electron. 2000, 15, 464–470. [Google Scholar] [CrossRef]
- Sun, Y.; Su, M.; Li, X.; Wang, H.; Gui, W. A General Constructive Approach to Matrix Converter Stabilization. IEEE Trans. Power Electron. 2013, 28, 418–431. [Google Scholar] [CrossRef]
- Sato, I.; Itoh, J.-I.; Ohguchi, H.; Odaka, A.; Mine, H. An Improvement Method of Matrix Converter Drives Under Input Voltage Disturbances. IEEE Trans. Power Electron. 2007, 22, 132–138. [Google Scholar] [CrossRef]
- Mariethoz, S.; Morari, M. Explicit Model-Predictive Control of a PWM Inverter with an LCL Filter. IEEE Trans. Ind. Electron. 2008, 56, 389–399. [Google Scholar] [CrossRef]
- Lei, J.; Zhou, B.; Qin, X.; Wei, J.; Bian, J. Active damping control strategy of matrix converter via modifying input reference currents. IEEE Trans. Power Electron. 2015, 30, 5260–5271. [Google Scholar] [CrossRef]
- Rivera, M.; Rodriguez, J.; Wu, B.; Espinoza, J.R.; Rojas, C.A. Current Control for an Indirect Matrix Converter with Filter Resonance Mitigation. IEEE Trans. Ind. Electron. 2011, 59, 71–79. [Google Scholar] [CrossRef]
- Rivera, M.; Rojas, C.; Rodríguez, J.; Wheeler, P.; Wu, B.; Espinoza, J. Predictive Current Control with Input Filter Resonance Mitigation for a Direct Matrix Converter. IEEE Trans. Power Electron. 2011, 26, 2794–2803. [Google Scholar] [CrossRef]
- Akagi, H.; Watanabe, E.; Aredes, M. More power to you (review of Instantaneous Power Theory and Applications to Power Conditioning by Akagi, H. et al.; 2007) [book review]. IEEE Power Energy Mag. 2007, 6, 80–81. [Google Scholar] [CrossRef]
- Wang, X.; Lin, H.; Feng, B.; Lyu, Y. Damping of Input LC Filter Resonance Based on Virtual Resistor for Matrix Converter. In Proceedings of the 2012 IEEE Energy Conversion Congress and Exposition (ECCE), Raleigh, NC, USA, 15–20 September 2012; pp. 3910–3916. [Google Scholar] [CrossRef]
- Trentin, A.; Empringham, L.; de Lillo, L.; Zanchetta, P.; Wheeler, P.; Clare, J. Experimental Efficiency Comparison Between a Direct Matrix Converter and an Indirect Matrix Converter Using Both Si IGBTs and SiC mosfets. IEEE Trans. Ind. Appl. 2016, 52, 4135–4145. [Google Scholar] [CrossRef] [Green Version]
- Zhang, X.; Zhang, L.; Zhang, Y. Model Predictive Current Control for PMSM Drives with Parameter Robustness Improvement. IEEE Trans. Power Electron. 2019, 34, 1645–1657. [Google Scholar] [CrossRef]
- Gulbudak, O.; Gokdag, M. Asymmetrical Multi-Step Direct Model Predictive Control of Nine-Switch Inverter for Dual-Output Mode Operation. IEEE Access 2019, 7, 164720–164733. [Google Scholar] [CrossRef]
- Yu, Y.; Wang, X. Multi-Step Predictive Current Control for NPC Grid-Connected Inverter. IEEE Access 2019, 7, 157756–157765. [Google Scholar] [CrossRef]





| Method | Switching Frequency | Design of the Input Filter | Computational Burden | Control Objective | Verification | Applications |
|---|---|---|---|---|---|---|
| The proposed VMMPCC | Fixed | common | common | Source reactive power and output currents | Simulation and experiment | TSMC |
| CMPC in [12,13,14,15,16,17] | Variable | difficult | common | Currents, voltages, power | Simulation and experiment | Many power converters |
| M2PC in [18,19,20,21,22,23,24] | Fixed | common | Common [18,19,20,21,22], High [23,24] | Currents, lack of Source reactive power control | Simulation and experiment | B2B, VSI, MMC, ADC, OSMC |
| M2PC in [25,26] | Fixed | common | common | Currents, lack of Source reactive power control | Simulation | TSMC |
| 0 | 1 | 1 | 0 | 0 | 0 | 0 | |||
| 0 | 0 | 1 | 1 | 0 | 0 | 0 | |||
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | |||
| 0 | 0 | 0 | 0 | 1 | 1 | 0 | |||
| 0 | 0 | 0 | 0 | 0 | 1 | 1 | |||
| 0 | 1 | 0 | 0 | 0 | 0 | 1 |
| 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||
| 0 | 1 | 1 | 1 | 0 | 0 | 0 | |||
| 0 | 0 | 1 | 1 | 1 | 0 | 0 | |||
| 0 | 0 | 0 | 1 | 1 | 1 | 0 | |||
| 0 | 0 | 0 | 0 | 1 | 1 | 1 | |||
| 0 | 1 | 0 | 0 | 0 | 1 | 1 | |||
| 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 0 |
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 1 |
| The amplitude of source voltage | 141 V | |
| Input filter inductor | 5 mH | |
| Input filter resistor | 0.5 | |
| Input filter capacitor | 21 μF | |
| Load inductor | 5 mH | |
| Load resistor | 5 | |
| Sampling time | 100 μs | |
| Sampling frequency | 10 kHz |
| Method | |||
|---|---|---|---|
| CMPC | 9.37 | 11.66% | 8.08% |
| VMMPCC | 2.49 | 7.44% | 6.55% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Di, Z.; Xu, D.; Zhang, K. Vector Modulation-Based Model Predictive Current Control with Filter Resonance Suppression and Zero-Current Switching Sequence for Two-Stage Matrix Converter. Energies 2021, 14, 3685. https://doi.org/10.3390/en14123685
Di Z, Xu D, Zhang K. Vector Modulation-Based Model Predictive Current Control with Filter Resonance Suppression and Zero-Current Switching Sequence for Two-Stage Matrix Converter. Energies. 2021; 14(12):3685. https://doi.org/10.3390/en14123685
Chicago/Turabian StyleDi, Zhengfei, Demin Xu, and Kehan Zhang. 2021. "Vector Modulation-Based Model Predictive Current Control with Filter Resonance Suppression and Zero-Current Switching Sequence for Two-Stage Matrix Converter" Energies 14, no. 12: 3685. https://doi.org/10.3390/en14123685
APA StyleDi, Z., Xu, D., & Zhang, K. (2021). Vector Modulation-Based Model Predictive Current Control with Filter Resonance Suppression and Zero-Current Switching Sequence for Two-Stage Matrix Converter. Energies, 14(12), 3685. https://doi.org/10.3390/en14123685






