Comparison of Screening Configurations for the Mitigation of Voltages and Currents Induced on Pipelines by HVAC Power Lines
Abstract
:1. Introduction
2. Numerical Methodology
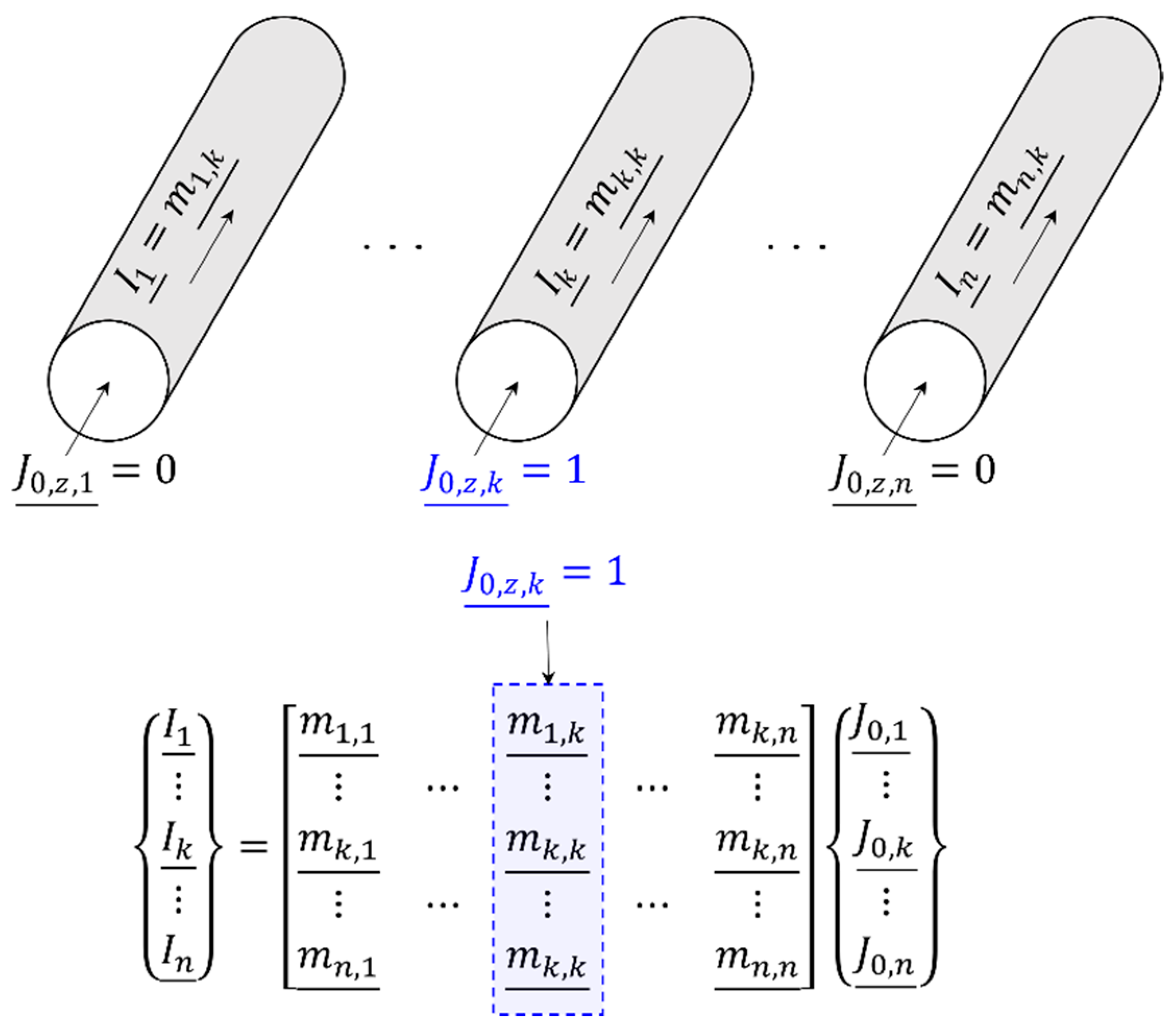
2.1. Mathematical Model
2.2. Finite Element Formulation
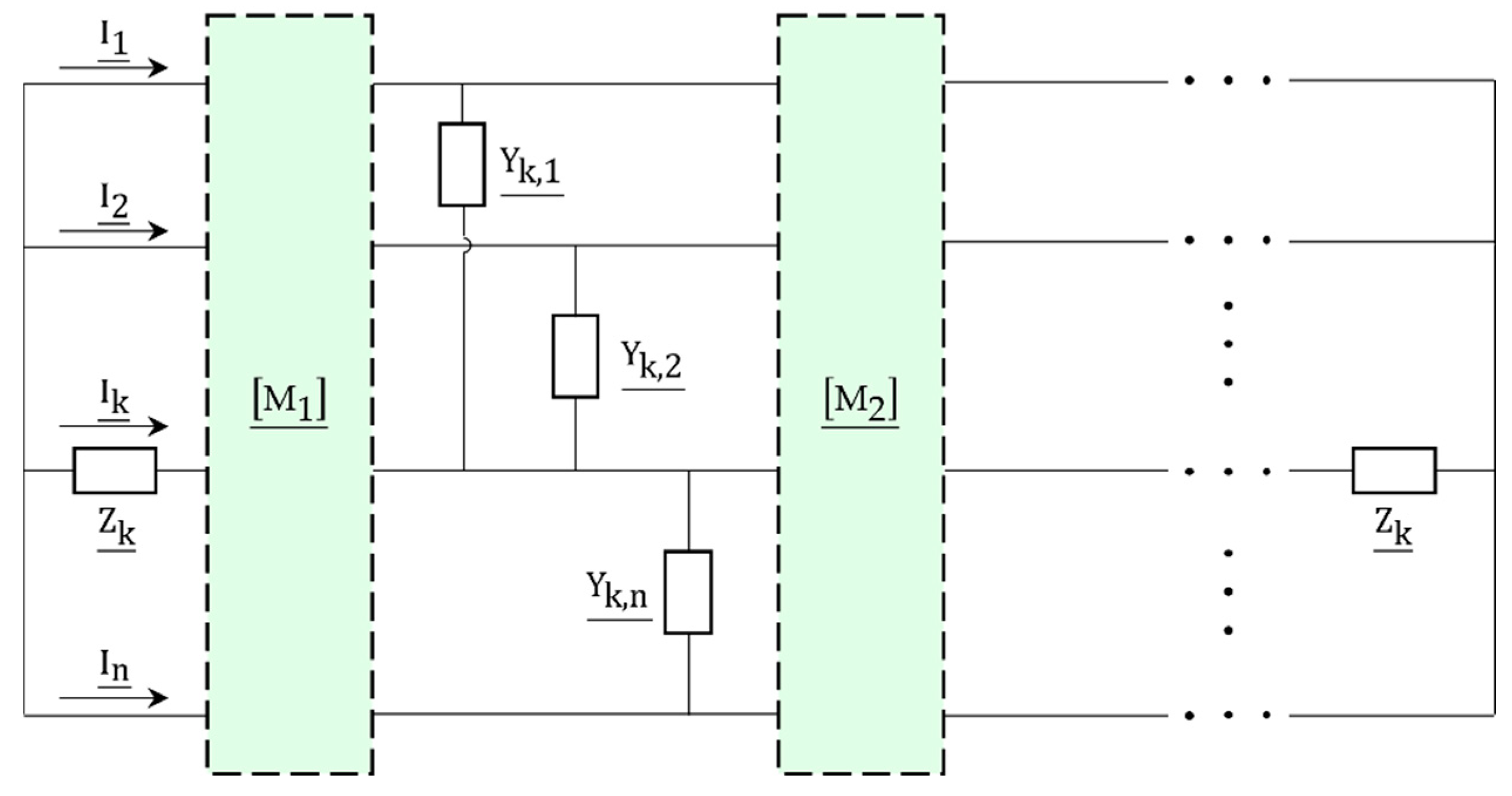
2.3. Equivalent Circuit
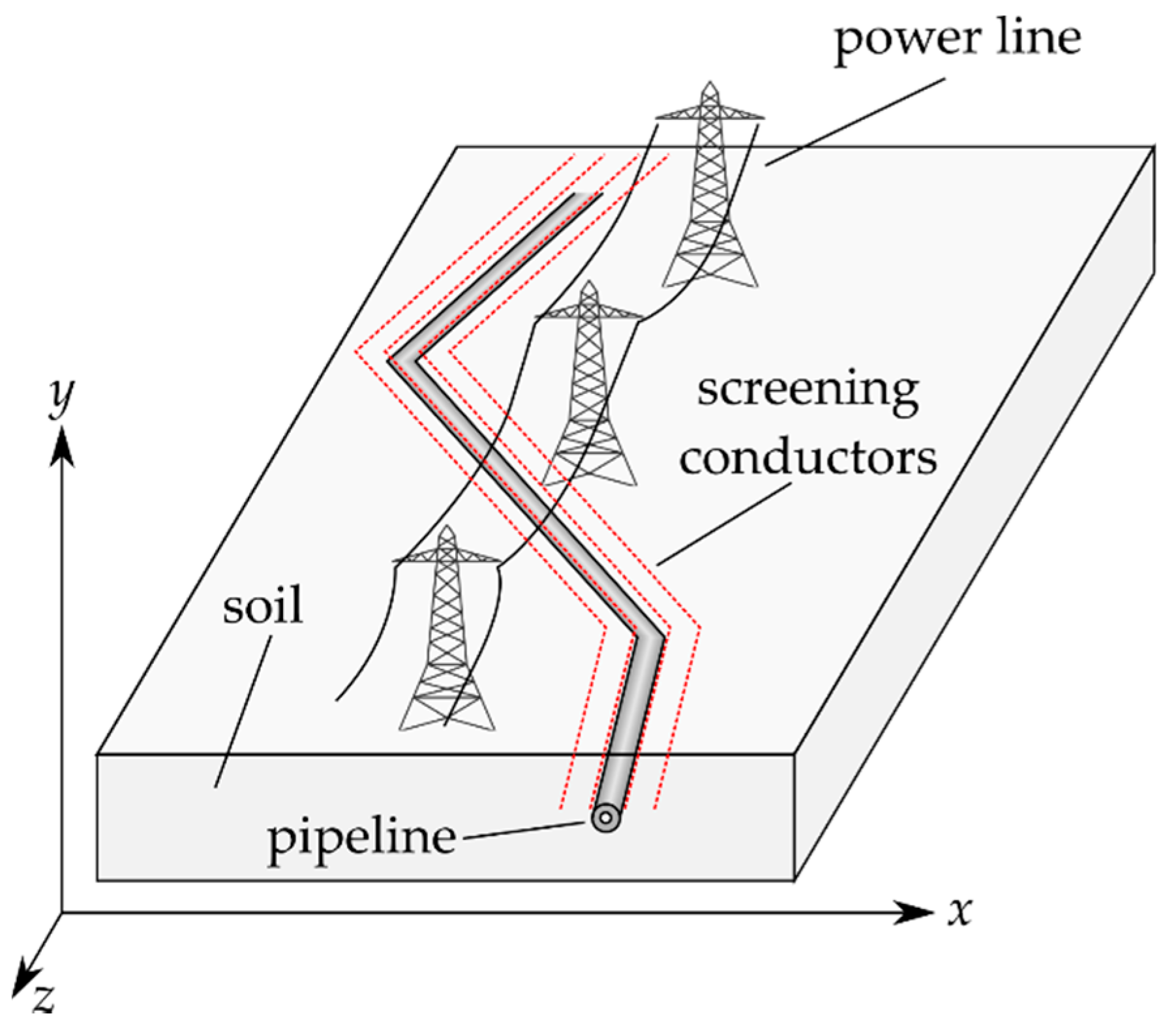
3. Simulation of a Nonparallel Pipeline–Power Line Routing
3.1. Configuration Description
3.1.1. Pipeline–Power Line Routing
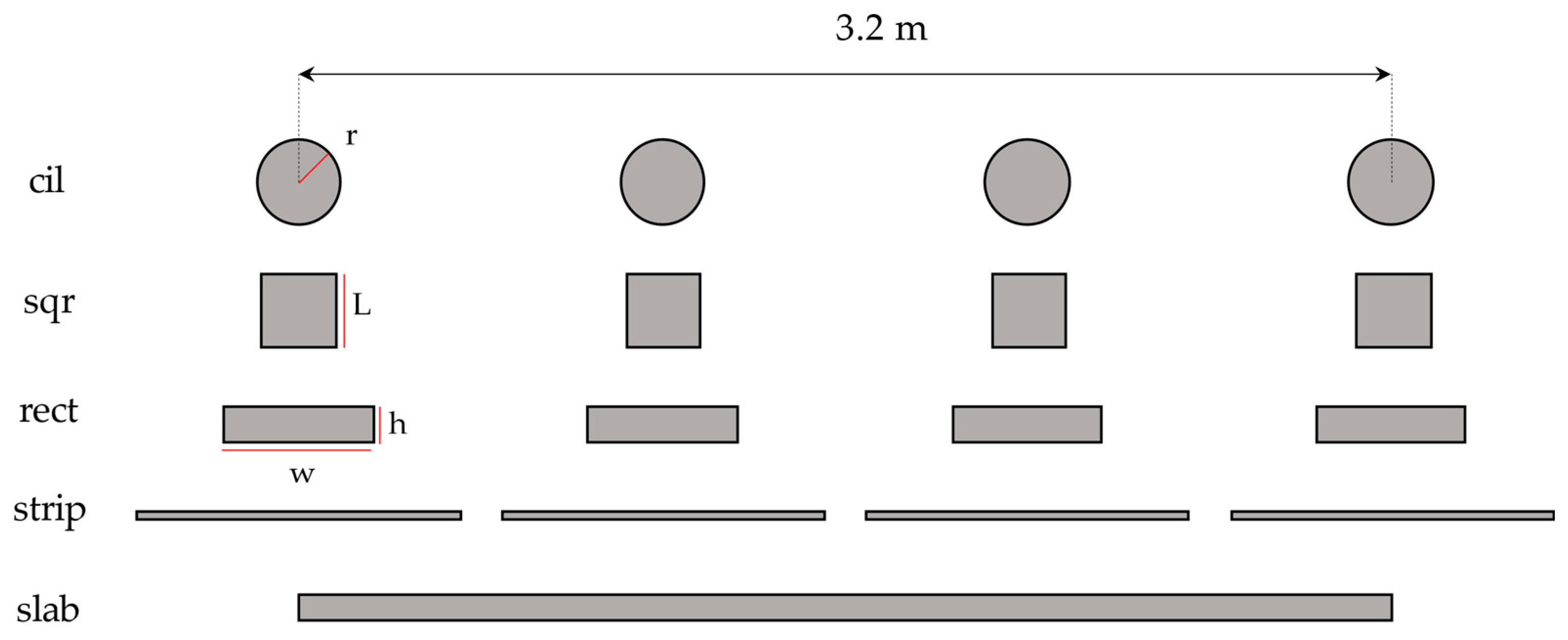
3.1.2. Screening Conductors
3.1.3. Equivalent Circuit, Electrical, and Geometrical Data
3.2. Simulation Results
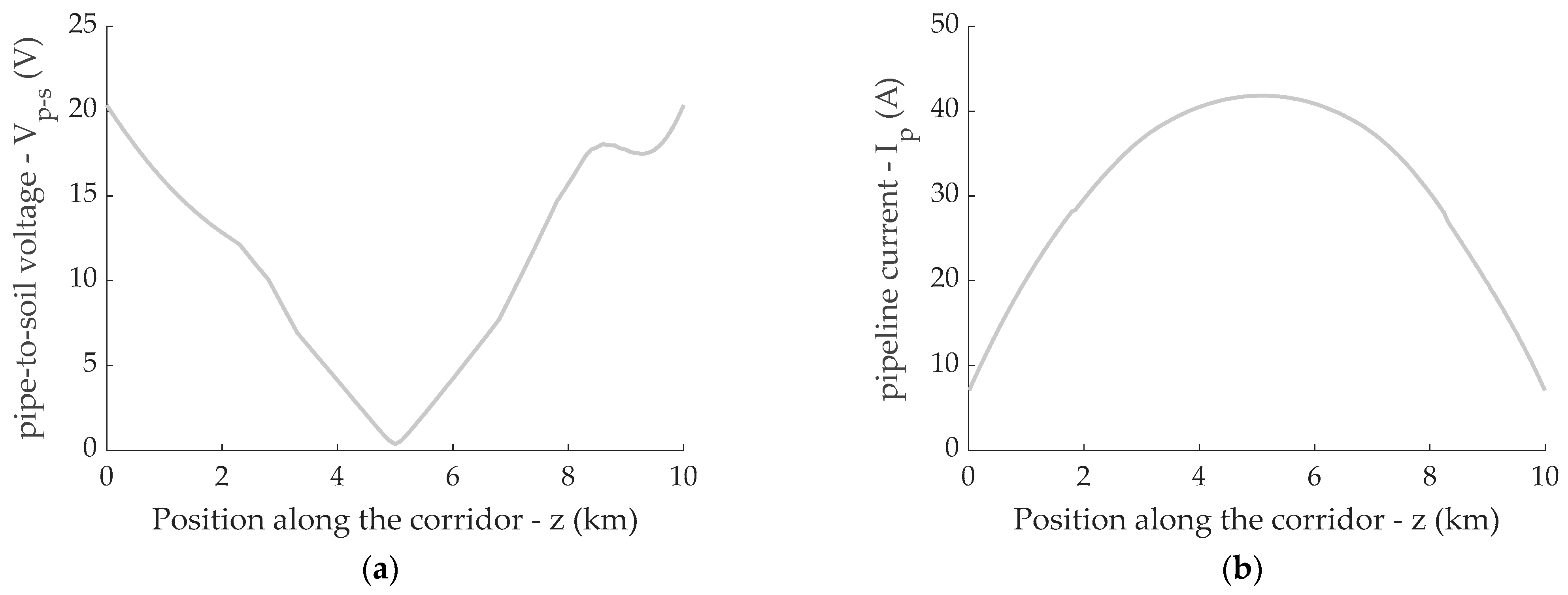
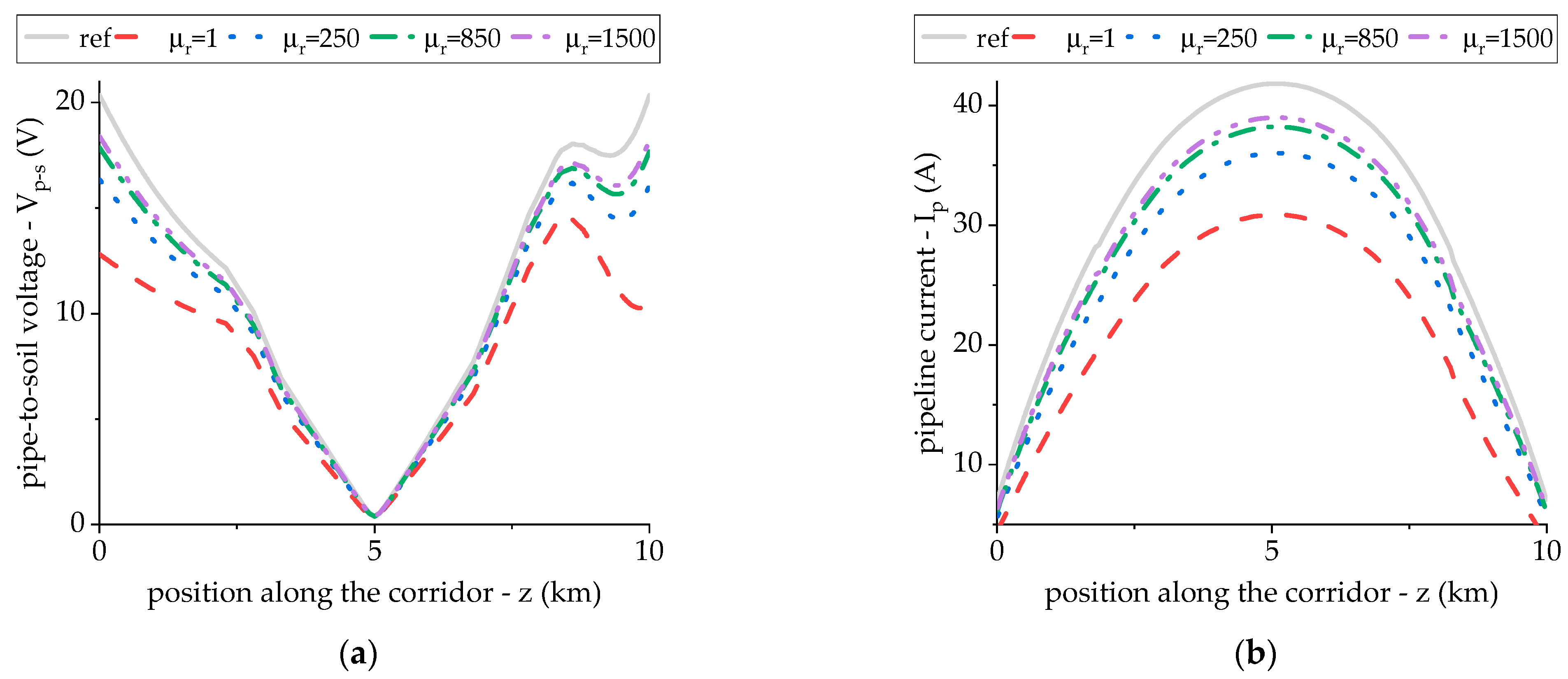
3.2.1. Induced Voltage and Current in Absence of Screening Conductors
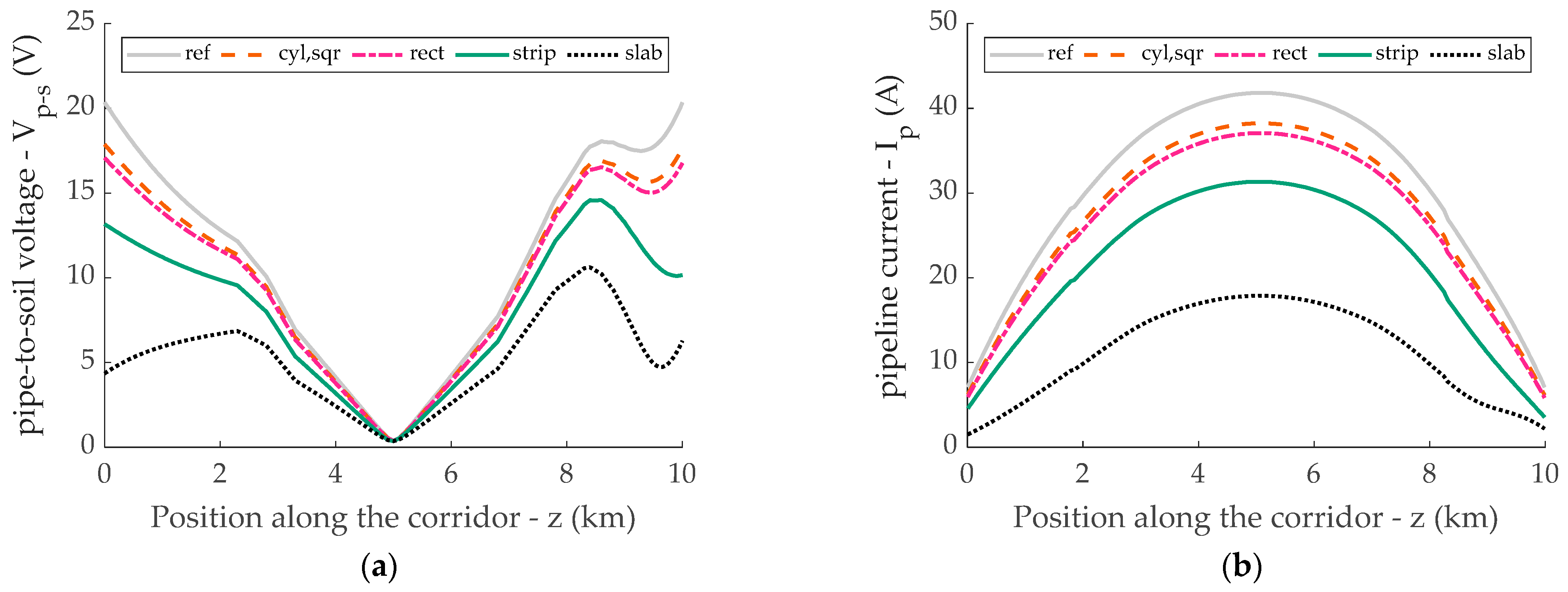
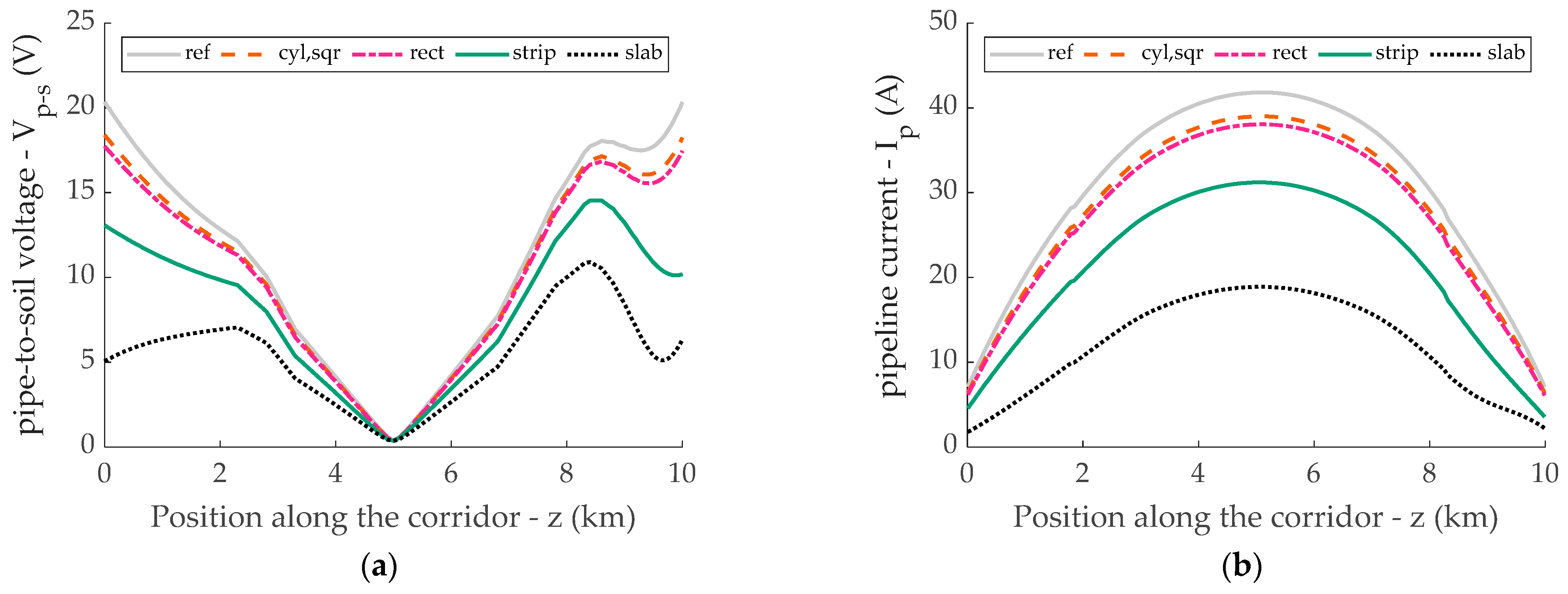
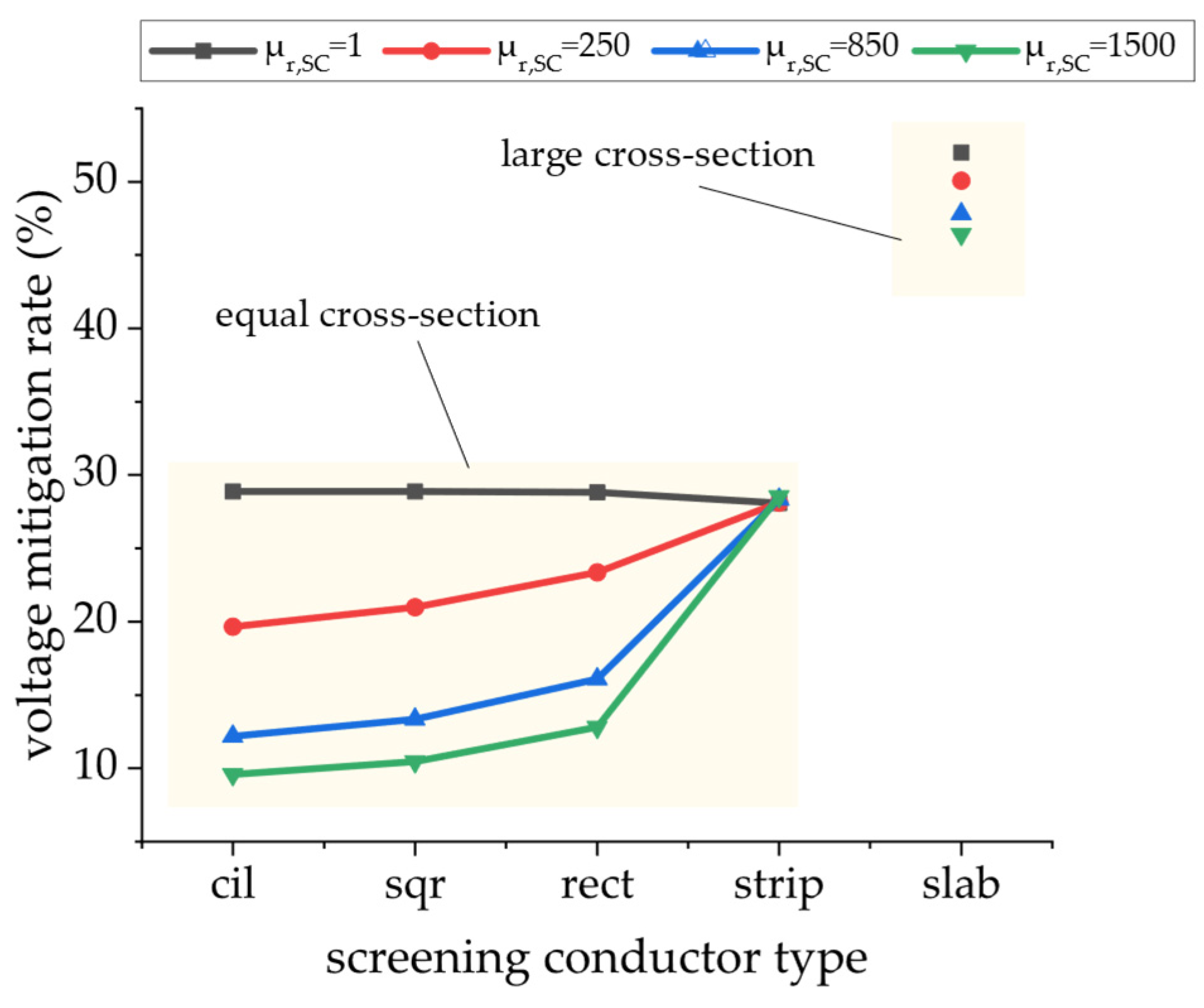
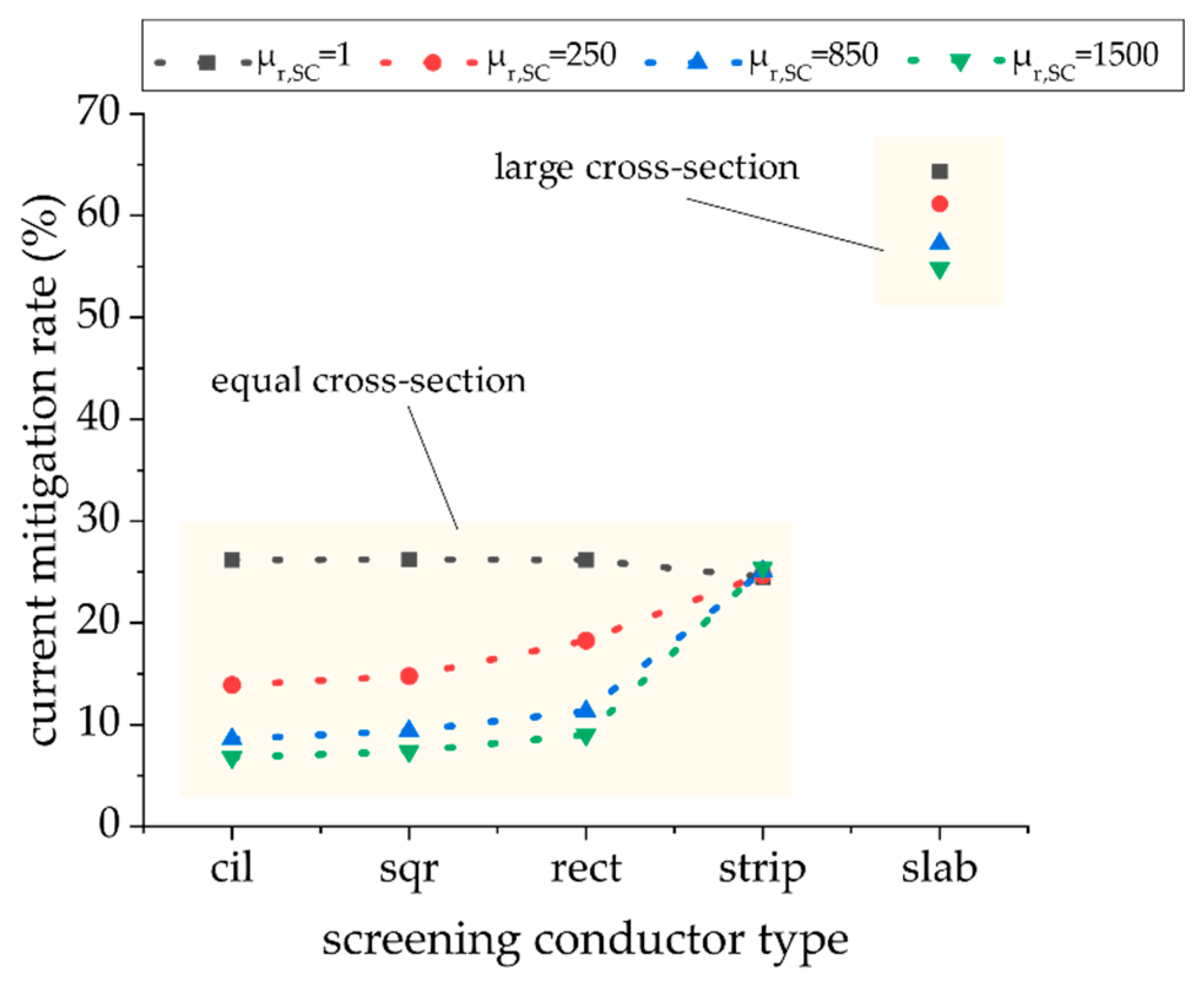
3.2.2. Parametric Analysis of Electromagnetic Screening Effectiveness
3.2.3.
3.2.4.
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
References
- Peabody, A.W.; Verhiel, A.L. The Effects of High-Voltage AC Transmission Lines on Buried Pipelines. IEEE Trans. Ind. Gen. Appl. 1971, IGA-7, 395–402. [Google Scholar] [CrossRef]
- Dabkowski, J.; Taflove, A. Prediction Method for Buried Pipeline Voltages Due to 60 Hz AC Inductive Coupling Part II–Field test Verification. IEEE Trans. Power Appar. Syst. 1979, PAS-98, 788–794. [Google Scholar] [CrossRef]
- Lucca, G. AC interference from a faulty power line on nearby buried pipelines: Influence of the surface layer soil. IET Sci. Meas. Technol. 2020, 14, 225–232. [Google Scholar] [CrossRef]
- Micu, D.D.; Christoforidis, G.C.; Czumbil, L. AC interference on pipelines due to double circuit power lines: A detailed study. Electr. Power Syst. Res. 2013, 103, 1–8. [Google Scholar] [CrossRef]
- Ruan, W.; Southcy, R.D.; Tee, S.; Dawalibi, F.P. Recent advances in the modeling and mitigation of AC interference in pipelines. In Proceedings of the NACE-International Corrosion Conference Series; Nace International: Nashville, TN, USA, 2007; pp. 76521–765210. [Google Scholar]
- Gomes, N.; Almeida, M.E.; Machado, V.M. Series Impedance and Losses of Magnetic Field Mitigation Plates for Underground Power Cables. IEEE Trans. Electromagn. Compat. 2018, 60, 1761–1768. [Google Scholar] [CrossRef]
- Corrosion of Metals and Alloys-Determination of AC Corrosion-Protection Criteria; Standard EN ISO 18086:2017; International Organization for Standardization: Geneva, Switzerland, 2017.
- Abdel-Gawad, N.M.K.; El Dein, A.Z.; Magdy, M. Mitigation of induced voltages and AC corrosion effects on buried gas pipeline near to OHTL under normal and fault conditions. Electr. Power Syst. Res. 2015, 127, 297–306. [Google Scholar] [CrossRef]
- Ouadah, M.; Touhami, O.; Ibtiouen, R.; Benlamnouar, M.F.; Zergoug, M. Corrosive effects of the electromagnetic induction caused by the high voltage power lines on buried X70 steel pipelines. Int. J. Electr. Power Energy Syst. 2017, 91, 34–41. [Google Scholar] [CrossRef]
- Bortels, L.; Parlongue, J.; Fieltsch, W.; Segall, S. Manage Pipeline Integrity by Predicting and Mitigating HVAC Interference. In Proceedings of the NACE-International Corrosion Conference Series; Nace International: San Antonio, TX, USA, 2010; pp. 1–15. [Google Scholar]
- Al-Badi, A.H.; Ellithy, K.; Al-Alawi, S. Prediction of voltages on mitigated pipelines paralleling electric transmission lines using ANN. Int. J. Comput. Appl. 2010, 32, 15–22. [Google Scholar]
- Dabkowski, J. How to predict and mitigate A. C. voltages on buried pipelines. Pipeline Gas J. 1979, 206, 19–21. [Google Scholar]
- Tachick, H. AC mitigation using shield wires and decoupling devices. Mater. Perform. 2008, 47, 36–39. [Google Scholar]
- Popoli, A.; Cristofolini, A.; Sandrolini, L.; Abe, B.T.; Jimoh, A. Assessment of AC interference caused by transmission lines on buried metallic pipelines using F.E.M. In Proceedings of the 2017 International Applied Computational Electromagnetics Society Symposium, Firenze, Italy, 26–30 March 2017. [Google Scholar] [CrossRef]
- Ametani, A.; Yoneda, T.; Baba, Y.; Nagaoka, N. An Investigation of Earth-Return Impedance Between Overhead and Underground Conductors and Its Approximation. IEEE Trans. Electromagn. Compat. 2009, 51, 860–867. [Google Scholar] [CrossRef]
- Lucca, G. Mutual impedance between an overhead and a buried line with earth return. In Proceedings of the Ninth International Conference on Electromagnetic Compatibility, Wroclaw, Poland, 13–17 September 2010; (Conf. Publ. No. 396). pp. 80–86. [Google Scholar]
- Kaboli, A.; Hr, S.; Al Hinai, A.; Al-Badi, A.; Charabi, Y.; Al Saifi, A. Prediction of Metallic Conductor Voltage Owing to Electromagnetic Coupling Via a Hybrid ANFIS and Backtracking Search Algorithm. Energies 2019, 12, 3651. [Google Scholar] [CrossRef] [Green Version]
- Popoli, A.; Sandrolini, L.; Cristofolini, A. A quasi-3D approach for the assessment of induced AC interference on buried metallic pipelines. Int. J. Electr. Power Energy Syst. 2019, 106, 538–545. [Google Scholar] [CrossRef]
- Popoli, A.; Sandrolini, L.; Cristofolini, A. Inductive coupling on metallic pipelines: Effects of a nonuniform soil resistivity along a pipeline-power line corridor. Electr. Power Syst. Res. 2020, 189, 106621. [Google Scholar] [CrossRef]
- CIGRE. Guide on the Influence of High Voltage AC Power Systems on Metallic Pipelines; Cigré Working Group 36.02: Paris, France, 1995. [Google Scholar]
- Cristofolini, A.; Popoli, A.; Sandrolini, L. Numerical Modelling of Interference from AC Power Lines on Buried Metallic Pipelines in Presence of Mitigation Wires. In Proceedings of the 2018 IEEE International Conference on Environment and Electrical Engineering and 2018 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Palermo, Italy, 12–15 June 2018; pp. 1–6. [Google Scholar]
- Popoli, A.; Sandrolini, L.; Cristofolini, A. Finite Element Analysis of Mitigation Measures for AC Interference on Buried Pipelines. In Proceedings of the 2019 IEEE International Conference on Environment and Electrical Engineering and 2019 IEEE Industrial and Commercial Power Systems Europe (EEEIC/I&CPS Europe), Genoa, Italy, 11–14 June 2019; pp. 1–5. [Google Scholar]
- Popoli, A.; Cristofolini, A.; Sandrolini, L. A numerical model for the calculation of electromagnetic interference from power lines on nonparallel underground pipelines. Math. Comput. Simul. 2020. [Google Scholar] [CrossRef]
- Steele, C.W. Numerical Computation of Electric and Magnetic Fields; Springer Science & Business Media: New York, NY, USA, 2012. [Google Scholar]
- Hayashi, T.; Mizuno, Y.; Naito, K. Study on Transmission-Line Arresters for Tower with High Footing Resistance. IEEE Trans. Power Deliv. 2008, 23, 2456–2460. [Google Scholar] [CrossRef]
- Yadee, P.; Premrudeepreechacharn, S. Analysis of Tower Footing Resistance Effected Back Flashover across Insulator in a Transmission System. In Proceedings of the International Conference on Power Systems Transients, Lyon, France, 4–7 June 2007. [Google Scholar]
- ITU-T. CCITT Directives Volume {III}: Calculating Induced Voltages and Currents in Pratical Cases; ITU-T: Geneva, Switzerland, 1989. [Google Scholar]
- Geuzaine, C.; Remacle, J.-F. Gmsh: A three-dimensional finite element mesh generator with built-in pre- and post-processing facilities. Int. J. Numer. Methods Eng. 2009, 79, 1309–1331. [Google Scholar] [CrossRef]





| Quantity | Value | Units |
|---|---|---|
| —phase I current | 1500 | A |
| —phase II current | 1500 | A |
| —phase III current | 1500 | A |
| —soil conductivity | ||
| —pipeline conductivity | ||
| —OGW conductivity | ||
| —screening conductor conductivity | S/m | |
| —pipeline external radius | m | |
| —pipeline internal radius | 0.375 | m |
| —OGW radius | m | |
| —soil relative magnetic permeability | - | |
| —OGW relative magnetic permeability | 1 | - |
| —pipeline relative magnetic permeability | 250 | - |
| —screening conductors’ relative magnetic permeability | [1, 1500] | - |
| —P.U.L. pipe-to-soil admittance 1 | S/m | |
| —P.U.L. OGW-to-soil admittance 2 | S/m | |
| —pipe-to-soil terminal impedance | ||
| —OGW-to-soil terminal impedance | 1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Popoli, A.; Sandrolini, L.; Cristofolini, A. Comparison of Screening Configurations for the Mitigation of Voltages and Currents Induced on Pipelines by HVAC Power Lines. Energies 2021, 14, 3855. https://doi.org/10.3390/en14133855
Popoli A, Sandrolini L, Cristofolini A. Comparison of Screening Configurations for the Mitigation of Voltages and Currents Induced on Pipelines by HVAC Power Lines. Energies. 2021; 14(13):3855. https://doi.org/10.3390/en14133855
Chicago/Turabian StylePopoli, Arturo, Leonardo Sandrolini, and Andrea Cristofolini. 2021. "Comparison of Screening Configurations for the Mitigation of Voltages and Currents Induced on Pipelines by HVAC Power Lines" Energies 14, no. 13: 3855. https://doi.org/10.3390/en14133855
APA StylePopoli, A., Sandrolini, L., & Cristofolini, A. (2021). Comparison of Screening Configurations for the Mitigation of Voltages and Currents Induced on Pipelines by HVAC Power Lines. Energies, 14(13), 3855. https://doi.org/10.3390/en14133855








