Induction Heating of Gear Wheels in Consecutive Contour Hardening Process †
Abstract
:1. Introduction
- -
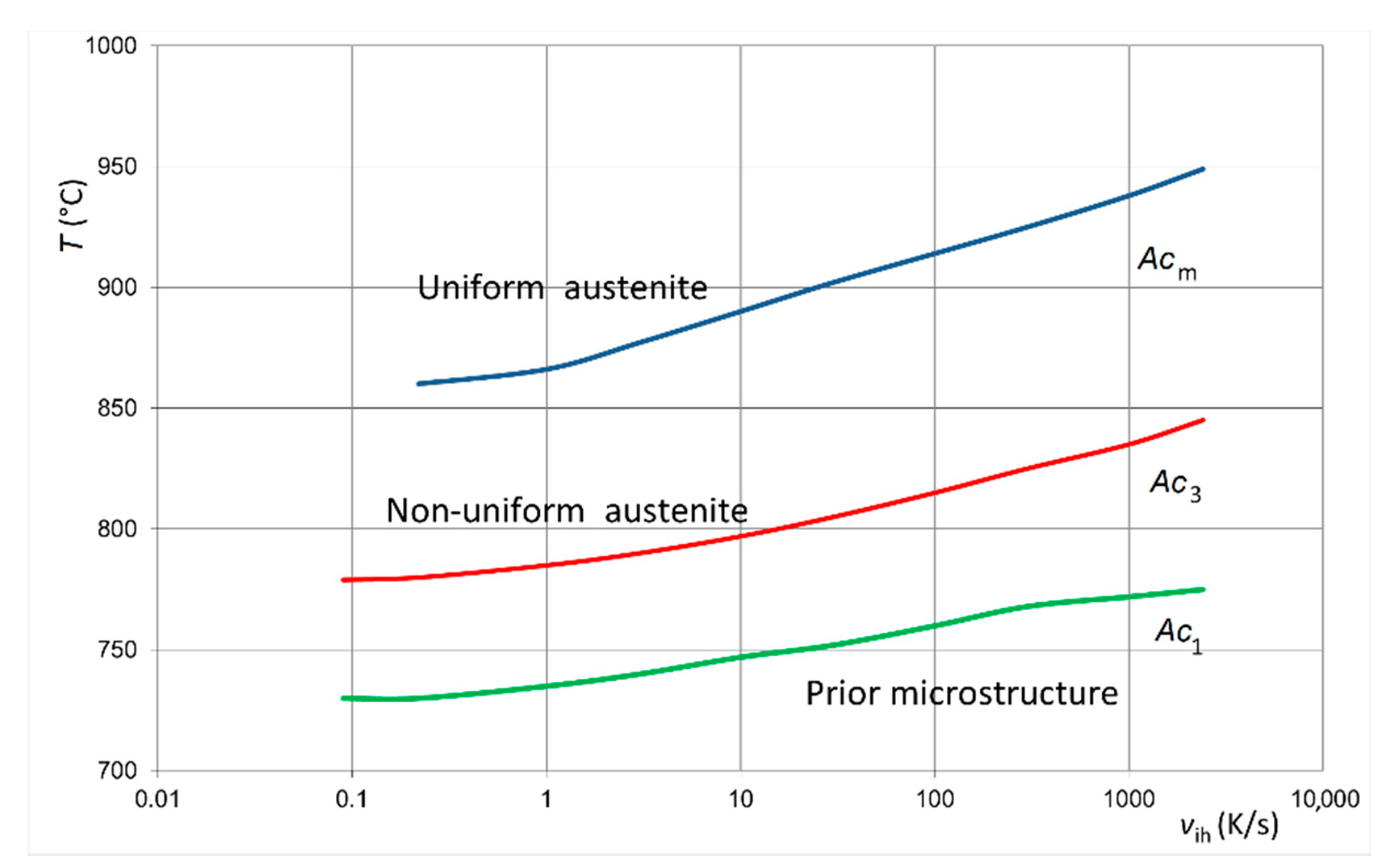
- The dependence of the critical temperatures for the investigated steel on velocity of induction heating strongly influences upon accurate determination of the hardening temperature;
- -
- The material properties of the investigated steel as non-linear dependences on the temperature;
- -
- The dependence of hardness on the velocity of cooling should be elaborated based upon a set of continuous-cooling-transformation diagrams for the investigated steel starting at different hardening temperatures.
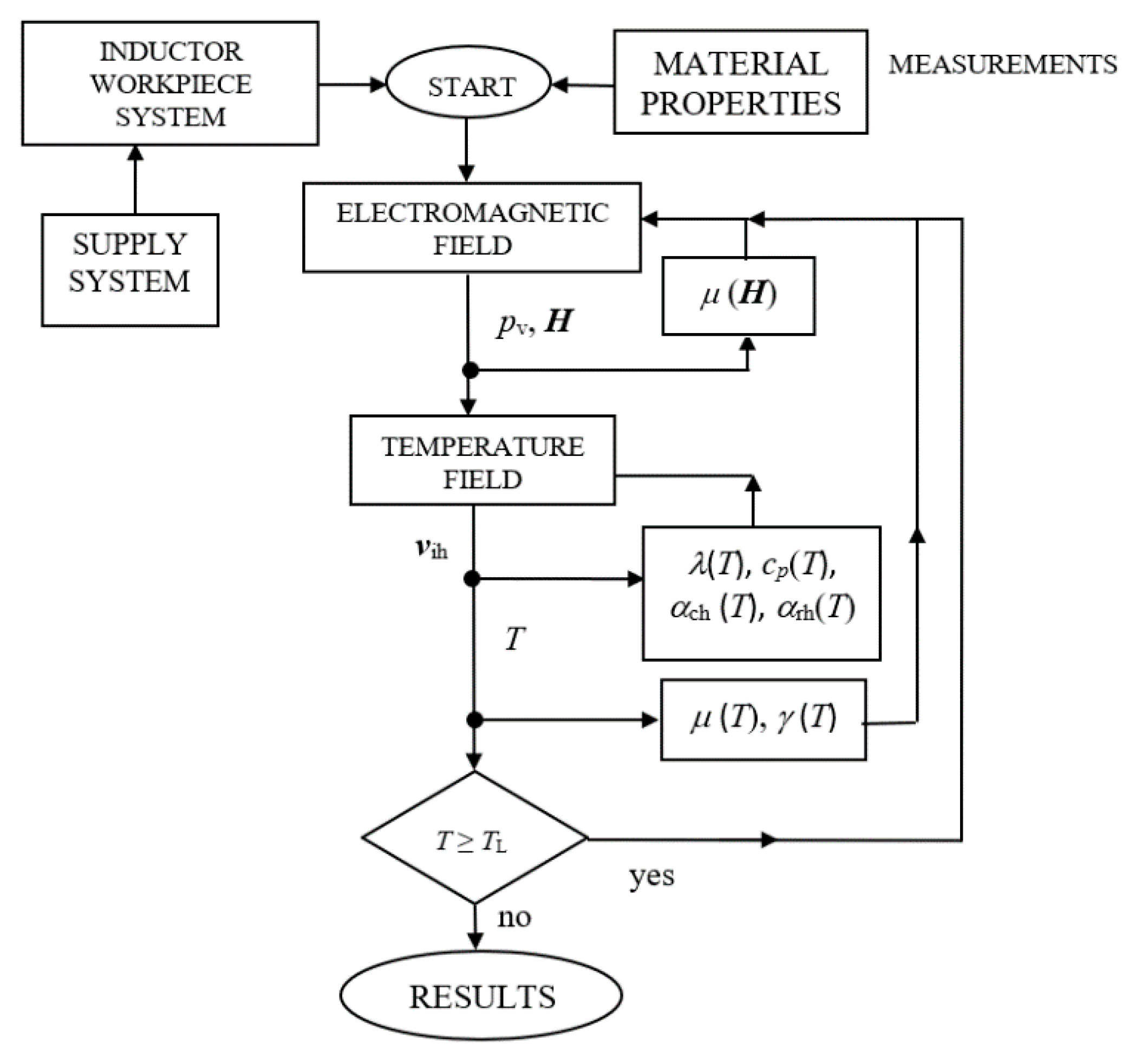
2. Mathematical Model of ICH process
2.1. Induction Heating for CDFIH Approach
- -
- Electric supply parameters: Inductor current or voltage and its frequency;
- -
- Geometry of inductor-gear wheel system;
- -
- Material properties of investigated steel and their dependences on field quantities (magnetic field intensity H, temperature T);
- -
- Distribution of volumetric power density in the heated element;
- -
- Dependence of specific heat, thermal conductivity, convection and radiation heat transfer coefficients on temperature;
- -
- Time-temperature-austenitization diagram for the investigated steel;
- -
- Expected hardening temperature guaranteeing uniform austenite microstructure.
- -
- MF heating—time tMF;
- -
- Short break for shifting workpiece between inductors—time tb;
- -
- HF heating—time tHF.
2.2. Cooling
- -
- Geometry of sprayer-gear wheel system;
- -
- Cooling parameters (parameters of cooling medium, its pressure, flow-rate and temperature);
- -
- Initial temperature distribution in the workpiece;
- -
- CCT (Continuous-Cooling-Transformation) diagram for investigated steel;
- -
- Convection heating transfer coefficient for intensive cooling.
3. Formulation of the Problem
- Gear wheel: teeth number—16, width of the tooth ring—6 mm, top diameter—35.6 mm, root diameter—26.9 mm, hole diameter—16 mm.
- MF inductor: external diameter—54 mm, internal diameter—39.5 mm, height—7 mm.
- HF inductor: external diameter—61 mm, internal diameter—39.5 mm, height—21 mm, flux concentrator made of Fluxtrol 50: its external diameter—81.5 mm, its internal diameter 39 mm, thickness of upper and lower cylinder—5 mm.
- Sprayer: distance between inductor and sprayer—20 mm, external diameter—85 mm, internal diameter—61 mm.
- MF induction heating: current—1450 A, heating time—4.4 s, frequency—36 kHz.
- Break between MF and HF heating: —0.1 s.
- HF induction heating: current—520 A, time—0.4 s, frequency—242 kHz.
- Parameters of cooling: quenchant—polymer solution Aqua Quench 140, concentration—10%, temperature—25 °C, pressure—89 kPa, flow-rate—2·10−5 m3/s, convection heat transfer coefficient at external surface—400 W/(m2·K).
- Heating rate and critical temperatures: velocity of induction heating—205 K/s, modified upper critical temperature—993 °C, hardening temperature—1010 °C.
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Rudnev, V.; Totten, G. Induction Heating and Heat Treatment 4C; ASM International: Materials Park, OH, USA, 2014. [Google Scholar]
- Jones, K.T.; Newsome, M.; Carter, D. Gas carburizing vs. contour induction hardening on bevel gears. Gear Solut. 2010, 8, 38–54. [Google Scholar]
- Chatterjee, M. Comparative Study of Carburizing vs. Induction Hardening of Gear Wheels. 2003. Available online: https://www.heattreattoday.com/processes/carburizing/carburizing-technical-content/comparative-study-of-carburizing-vs-induction-hardening-of-gears/ (accessed on 15 May 2021).
- Schwenck, M.; Schwenck, W. Substitution of case hardening gearbox components in the automotive as well as aeronautical industry through contour induction hardening. In Proceedings of the International Conference on Heating by Electromagnetic Sources, HES-07, Padova, Italy, 20–22 June 2007; pp. 175–182. [Google Scholar]
- Rudnev, V. Induction hardening of gear wheels and critical components Part 1. Gear Technol. 2008, 1, 58–63. [Google Scholar]
- Rudnev, V.; Loveless, D.; Cook, R. Handbook of Induction Heating; CRC Press: London, UK; Taylor and Francis Group: Abingdon, UK, 2018. [Google Scholar]
- Lupi, S. Fundamentals of Electroheat, Electrical Technologies for Process Heating; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Rudnev, V.; Loveless, D.; Cook, R.; Black, M. Induction Hardening of Gear. Heat Treat. Met. 2004, 1, 11–15. [Google Scholar]
- Pleshcheva, Y.; Baldan, N.; Popov, A.; Nikanorov, A.; Rapaport, E.; Nacke, B. Effective methods for optimal design of induction coils on example of surface hardening. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2019, 39, 90–99. [Google Scholar]
- Kwang-Hyung, C.; Chang-Tae, J.; Rae-Young, K. Analysis and evaluation of WBG power device in high frequency induction heating application. Energies 2020, 13, 5351. [Google Scholar]
- Goldstein, R.; Nemkov, V. Design Principles for Induction Heating and Hardening. In Handbook of Metallurgical Process Design; Marcel Dekker: New York, NY, USA, 2004; pp. 591–640. [Google Scholar]
- Szychta, E.; Szychta, L. Comparative Analysis of Effectiveness of Resistance and Induction Turnout Heating. Energies 2020, 13, 5262. [Google Scholar] [CrossRef]
- Rudnev, V. Induction hardening of gear wheels and critical components Part 2. Gear Technol. 2008, 2, 47–53. [Google Scholar]
- Buglaliero, N.; Zimmerman, C.; Richardson, S.; Perkins, R.; McCurdy, D.; Giessel, B. Heat Treatment Processes for Gear Wheels—Gear Solutions. 2010. Available online: https://gearsolutions.com/features/heat-treat-processes-for-gears/ (accessed on 15 May 2021).
- Spezzapria, M.; Forzan, M.; Dughiero, F. Numerical Simulation of Solid-Solid Phase Transformations During Induction Hardening. IEEE Trans. Magn. 2016, 52, 740–743. [Google Scholar] [CrossRef]
- Barglik, J. Mathematical modelling of induction surface hardening. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2016, 35, 1403–1417. [Google Scholar] [CrossRef]
- Barglik, J. Induction contour hardening of gear wheels made of steel 300M. IOP Conf. Ser. Mater. Sci. Eng. 2018, 424, 012062. [Google Scholar] [CrossRef]
- Lupi, S.; Forzan, M.; Alifierov, A. Induction and Direct Resistance Heating: Theory and Numerical Modelling; Springer: Berlin/Heidelberg, Germany, 2015. [Google Scholar]
- Holman, P. Heat Transfer; Mc Graw Hill: New York, NY, USA, 2009. [Google Scholar]
- Barglik, J.; Smalcerz, A. Influence of the magnetic permeability on modelling of induction surface hardening. COMPEL Int. J. Comput. Math. Electr. Electron. Eng. 2017, 36, 555–564. [Google Scholar] [CrossRef]
- Barglik, J.; Czerwiński, M.; Hering, M.; Wesołowski, M. Radiation in Modelling of Induction Heating Systems; IOS Press: Amsterdam, The Netherlands, 2008; pp. 202–211. [Google Scholar]
- Barglik, J.; Smalcerz, A.; Przylucki, R.; Dolezel, I. 3D modeling of induction hardening of gear wheels. J. Comput. Appl. Math. 2014, 270, 231–240. [Google Scholar] [CrossRef]
- Zgraja, J.; Lisowski, G.; Kucharski, J. Autonomous Energy Matching Control in an LLC Induction Heating Generator. Energies 2020, 13, 1860. [Google Scholar] [CrossRef] [Green Version]
- Barglik, J. Induction hardening of steel elements with complex shapes. Przeglad Elektrotechniczny 2018, 94, 51–54. [Google Scholar] [CrossRef] [Green Version]
- WinSite. Cedrat Flux Software. Available online: https://www.winsite.com/cedrat/cedrat+flux/ (accessed on 15 May 2021).
- ITA Technology and Software. QTSteel Software. Available online: http://www.ita-tech.cz/en/products-services/heat-treatment/software-qtsteel (accessed on 15 May 2021).
- Shinozaki, T.; Tomota, Y.; Fukino, T.; Suzuki, T. Microstructure evolution during reverse transformation of austenite from tempered martensite in low alloy steel. ISIJ Int. 2017, 57, 740–743. [Google Scholar] [CrossRef] [Green Version]
- Barglik, J. Induction heating of small gear wheels in the contour hardening process. In Proceedings of the 19th International Symposium on Electromagnetic Fields in Mechatronics, Electrical and Electronic Engineering (ISEF 2019), Nancy, France, 29–31 August 2019; pp. 1–2. [Google Scholar]
- Barglik, J.; Smalcerz, A.; Smagor, A.; Kopec, G. Experimental Stand for Investigation of Induction Hardening of Steel Elements. Metalurgija 2018, 57, 341–344. [Google Scholar]
- Centre for Induction Technology. Fluxtrol 50. Available online: https://fluxtrol.com/inc/pdf/Fluxtrol-50-Specs.pdf (accessed on 15 May 2021).
- Wróbel, T.; Przyszlak, N.; Dulska, A. Technology of Alloy Layers on Surface of Castings. Int. J. Met. 2019, 13, 604–610. [Google Scholar] [CrossRef] [Green Version]

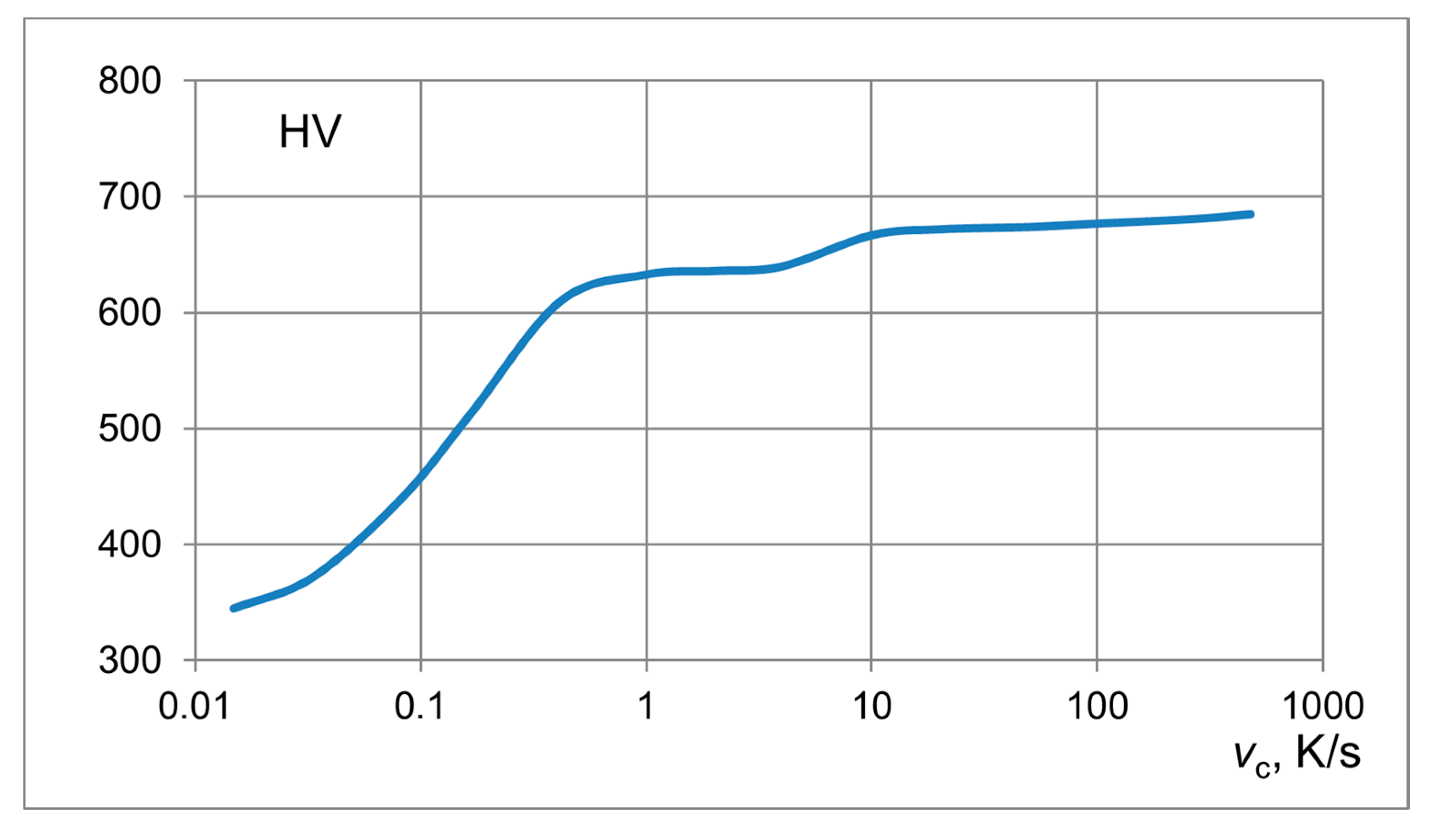


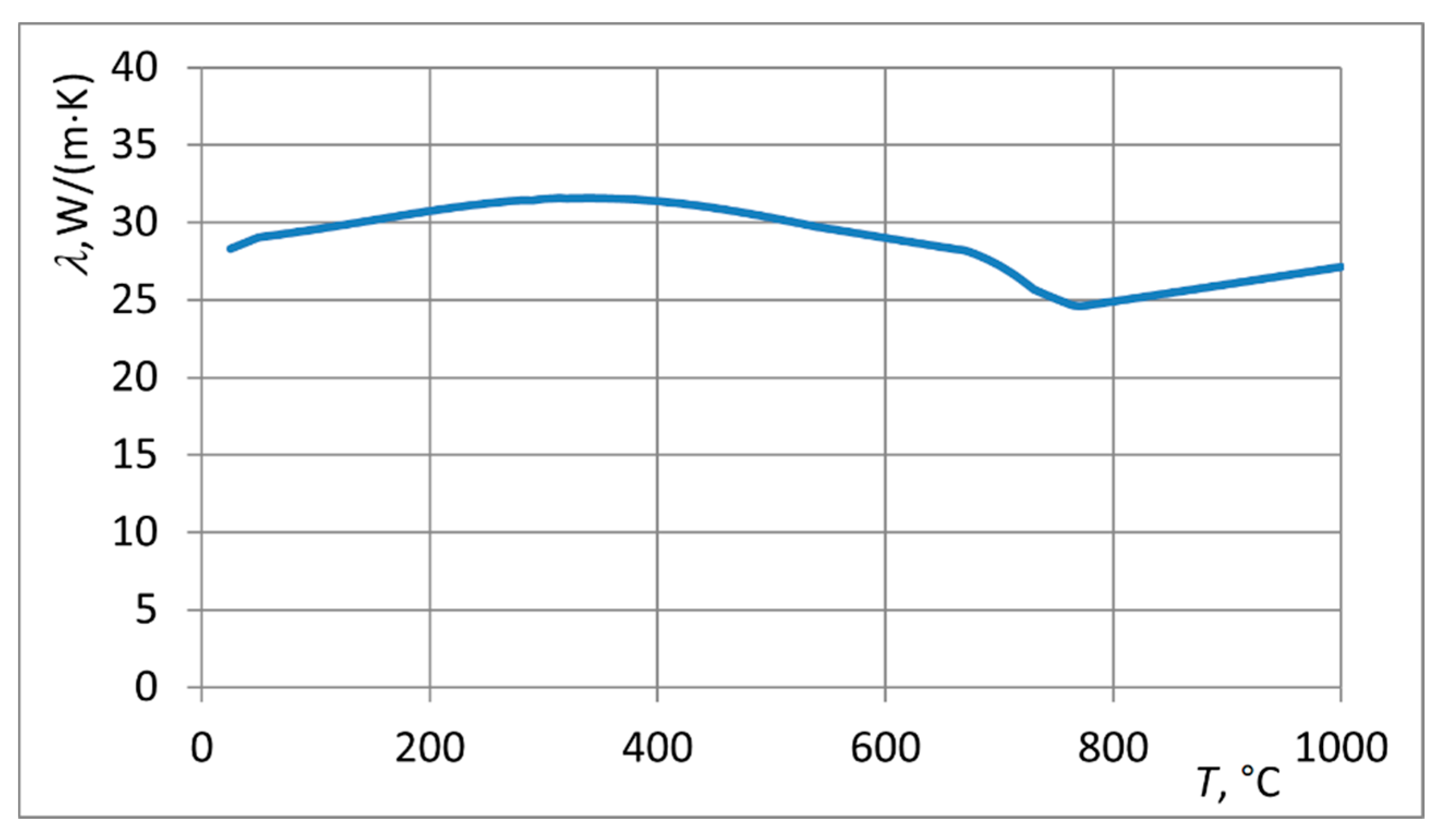


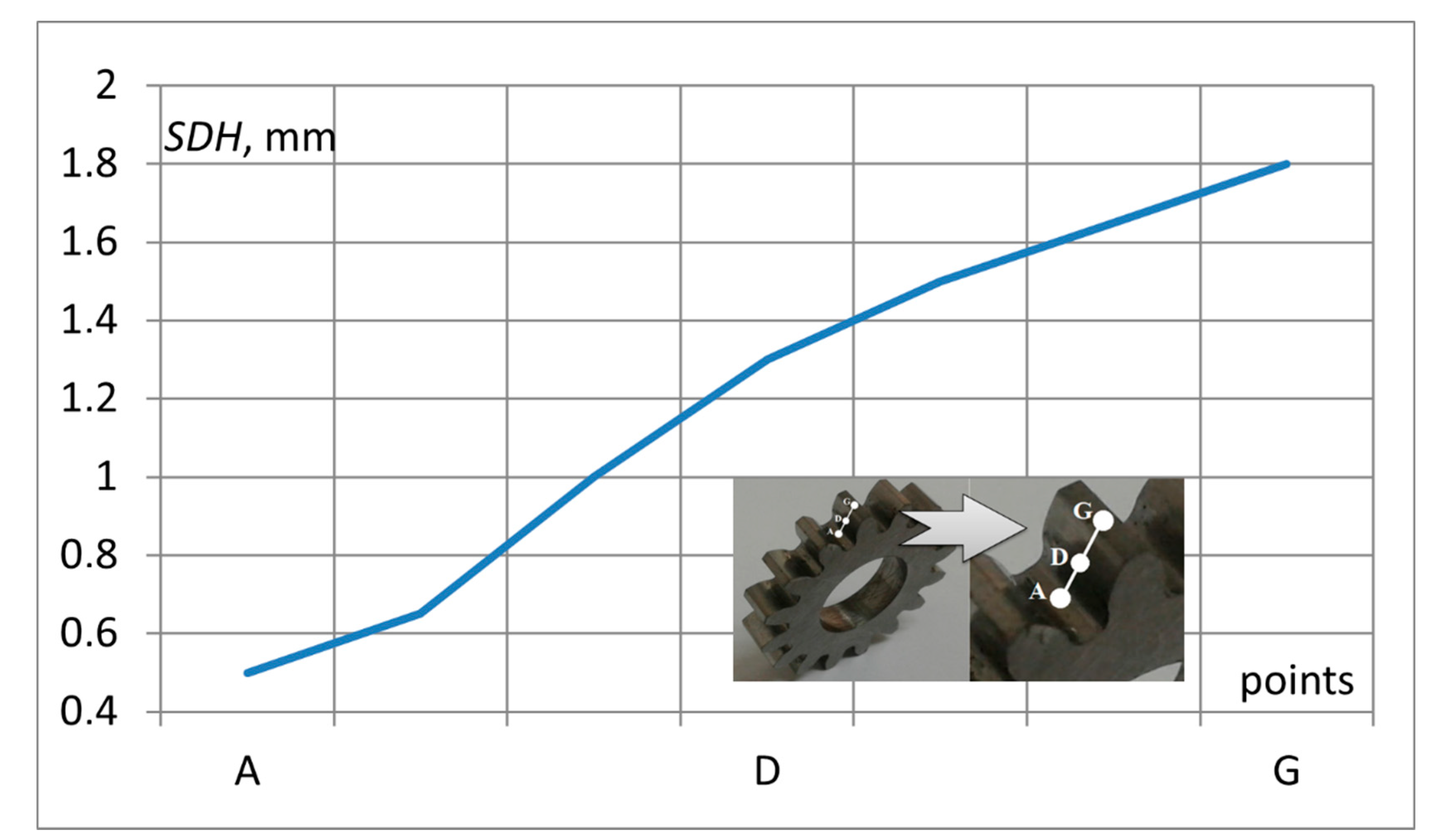
 —computations (line A…G); •••—measurements in points A, D, G.
—computations (line A…G); •••—measurements in points A, D, G.
 —computations (line A…G); •••—measurements in points A, D, G.
—computations (line A…G); •••—measurements in points A, D, G.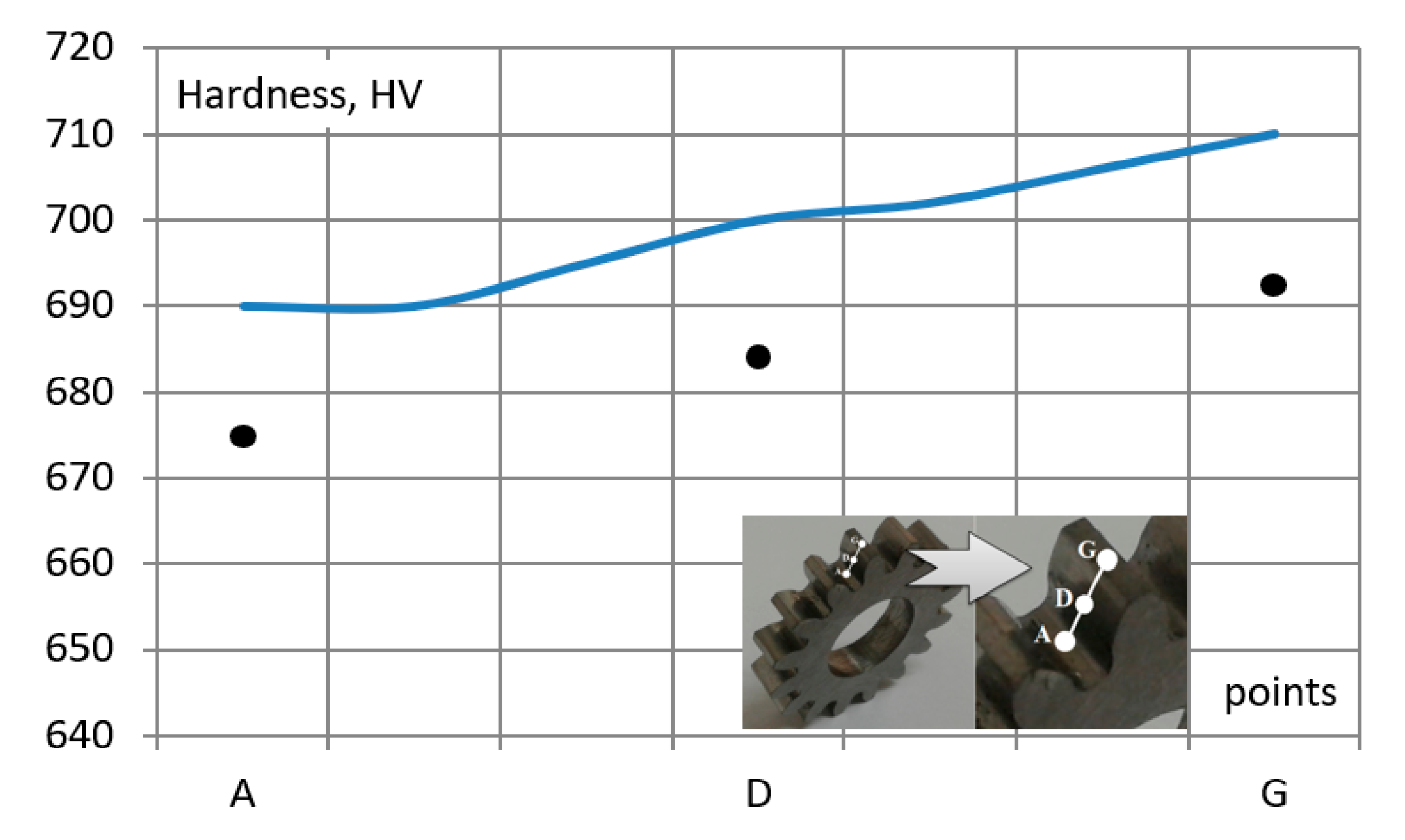
 —computations (line A…G); •••—measurements.
—computations (line A…G); •••—measurements.
 —computations (line A…G); •••—measurements.
—computations (line A…G); •••—measurements.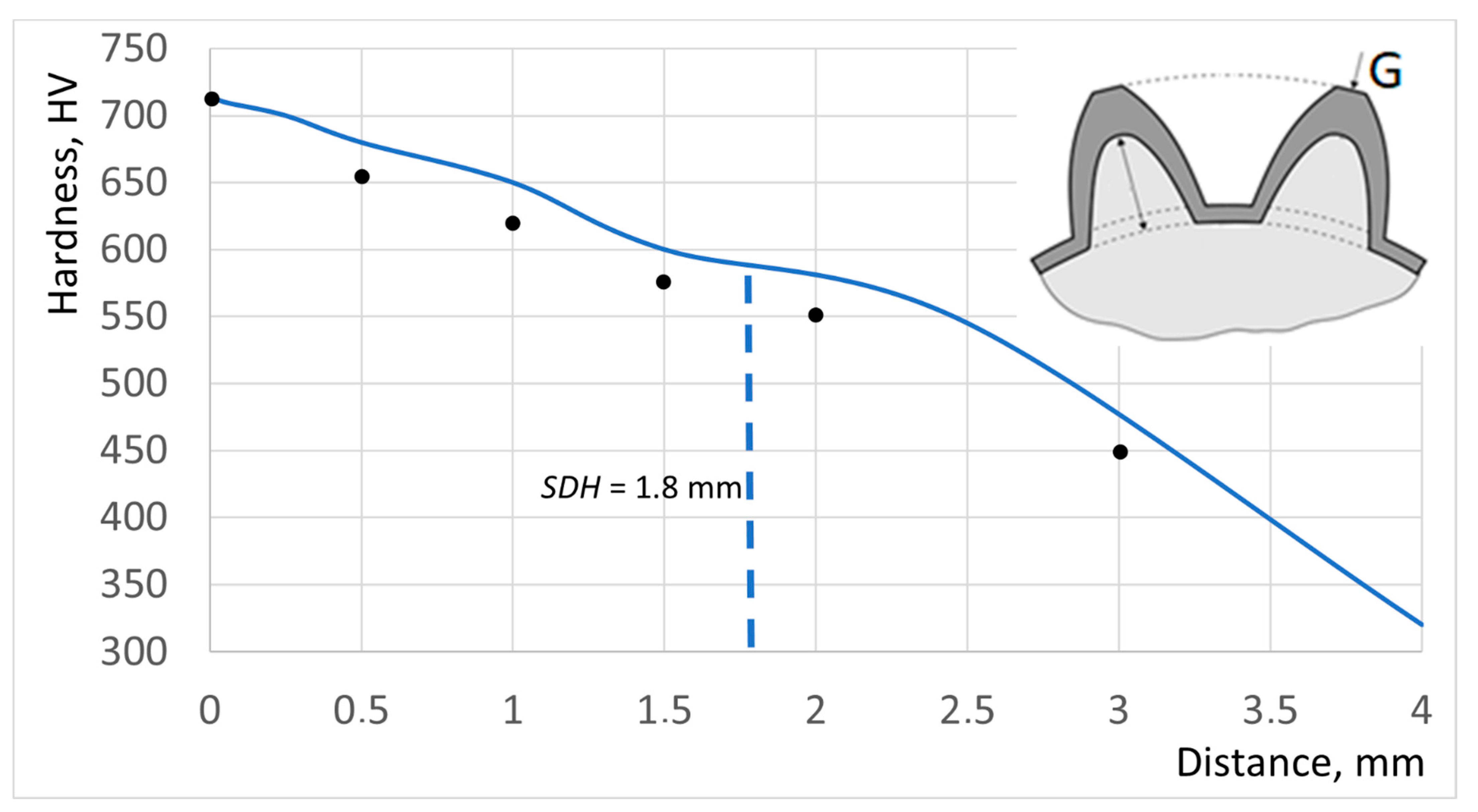
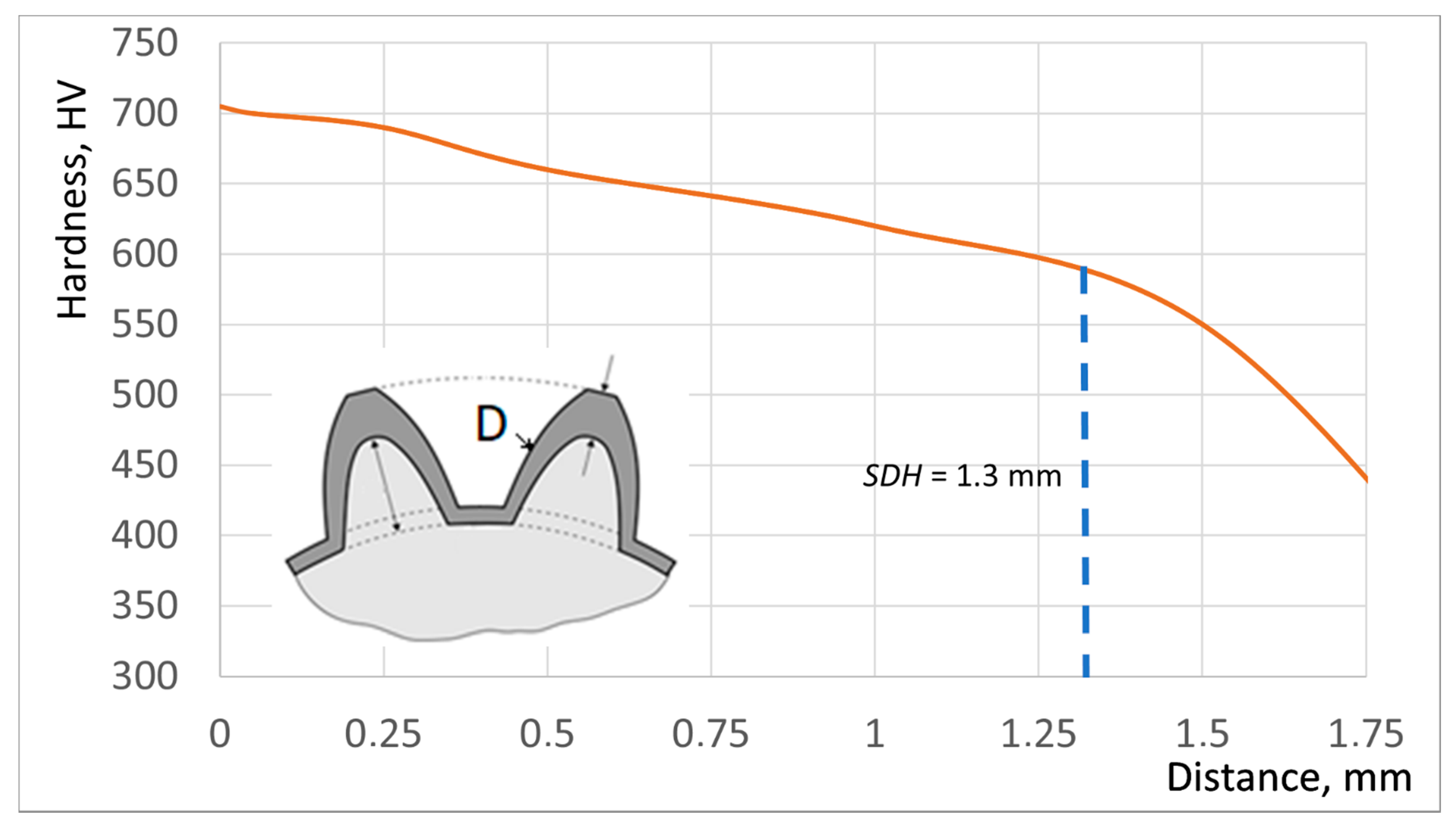
 —computations; •••—measurements.
—computations; •••—measurements.
 —computations; •••—measurements.
—computations; •••—measurements.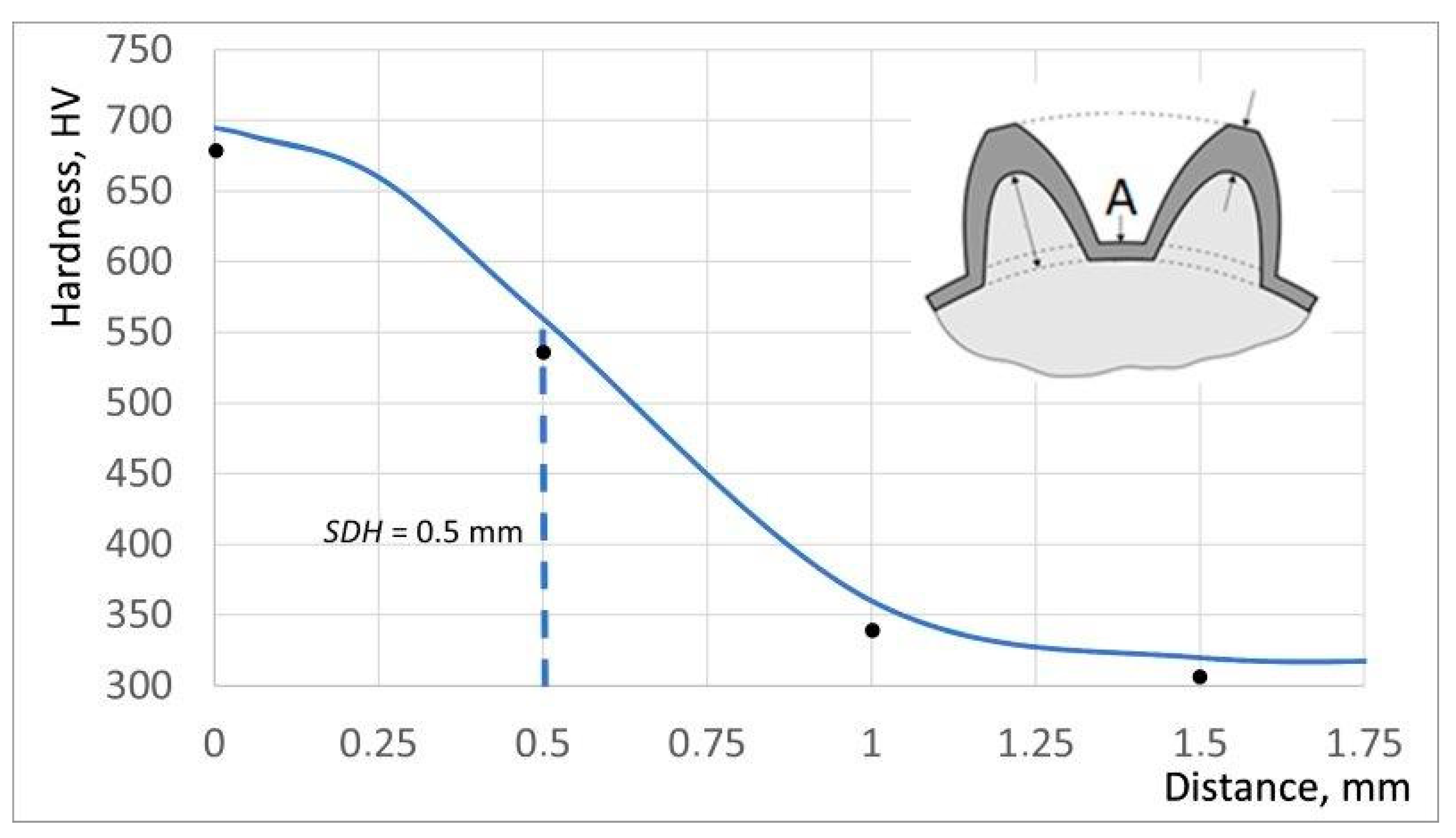

| Element | C | Si | Mn | Cr | Ni | Mo | Fe |
|---|---|---|---|---|---|---|---|
| Mass, % | 0.41 | 1.63 | 0.83 | 0.83 | 1.91 | 0.41 | 95 |
| K/s | 0.1 | 1 | 10 | 100 | 200 | 500 | 1000 |
| Acm, °C | 887 | 899 | 924 | 955 | 985 | 1030 | 1055 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Barglik, J.; Smagór, A.; Smalcerz, A.; Desisa, D.G. Induction Heating of Gear Wheels in Consecutive Contour Hardening Process. Energies 2021, 14, 3885. https://doi.org/10.3390/en14133885
Barglik J, Smagór A, Smalcerz A, Desisa DG. Induction Heating of Gear Wheels in Consecutive Contour Hardening Process. Energies. 2021; 14(13):3885. https://doi.org/10.3390/en14133885
Chicago/Turabian StyleBarglik, Jerzy, Adrian Smagór, Albert Smalcerz, and Debela Geneti Desisa. 2021. "Induction Heating of Gear Wheels in Consecutive Contour Hardening Process" Energies 14, no. 13: 3885. https://doi.org/10.3390/en14133885
APA StyleBarglik, J., Smagór, A., Smalcerz, A., & Desisa, D. G. (2021). Induction Heating of Gear Wheels in Consecutive Contour Hardening Process. Energies, 14(13), 3885. https://doi.org/10.3390/en14133885








