Comprehensive Review of Short-Term Voltage Stability Evaluation Methods in Modern Power Systems

Abstract

The possibility to monitor and evaluate power system stability in real-time is in growing demand. Whilst most stability-related studies focus on long-term voltage stability and frequency stability, very little attention is given to the issue of short-term (voltage) instability. In this paper, the most common evaluation methods present in the literature are summarized, with a focus on their applicability to modern power systems with a large amount of renewable energy integration. The paper presents a first-of-a-kind structured review of this topic. We find that all existing methods have noteworthy limitations that necessitate further improvements. Additionally, the need of having an inclusive short-term instability prediction method is demonstrated, due to strong interactions between various short-term instability mechanisms. These findings provide a good foundation for further research and advancement in the field of real-time stability monitoring.

1. Introduction

Renewable energy integration is advancing rapidly all around the world. For instance, renewable energy surpassed fossil fuels in the total annual electricity production in the European Union in 2020 [1]. Even though this is an important milestone, it is only a fraction of the changes we are about to witness in the next couple of decades. If the world is heading towards meeting the requirements of the Paris Climate Agreement, renewable energy will swiftly become a dominant source of electricity worldwide.

While this is expected to slow down climate change significantly, power system operators will face immense challenges by the unprecedented changes in the dynamics occurring in the power systems. Major challenges in this regard are related to the inertia reduction due to the phasing out of the synchronous generators. There are promising solutions such as synthetic inertia and fast(er) frequency reserves, however, the electrical power system dynamics should inevitably be significantly faster in the future. This will result in a need to use (at least) equally fast monitoring and control solutions in modern grids. Monitoring possibilities have been improved dramatically with the introduction of phasor measurement units (PMUs). Nonetheless, their utilization for advanced grid resilience assessment is still in the early development stage.

Apart from the issues with inertia, systems might experience many other potential dynamic issues with the further integration of renewables. Some of the significant issues that systems are already facing are related to voltage stability [2]. While long-term voltage stability is an extensively researched topic, short-term stability is comparably receiving significantly less attention. Although the issue used to be a low-probability event, with the changes we see in the systems, this might no longer be the case. It can be expected that local voltage-related issues will be more common, and will become a major focus of system operators throughout the energy transition [2,3].

Therefore, there exists a great need to analyze and predict short-term (voltage) instabilities. Nevertheless, the methods for such a task are scarce, with questionable applicability to the modern power system dynamics that incorporate a large amount of inverter-based generation (IBG). This is particularly true for methods that are meant to be used in real-time, which are arguably the most important to have. For the advancements in the field of real-time instability evaluation to be made, shortcomings of the currently available methods should be identified. Furthermore, challenges for obtaining a better solution ought to be presented and analyzed.

The main contributions of this paper can be summarized as follows:

• A comprehensive and critical review of the available short-term instability methods, with the emphasis on real-time solutions;
• Analysis of the methods on selected relevant qualitative measures (e.g., applicability in systems with high IBG penetration, computational complexity, parameter sensitivity, etc.);
• Insights on the necessity for a holistic short-term instability evaluation approach due to inherent similarities between various short-term instability phenomena.

This paper is organized into five main sections. The introduction section highlights the motivation behind this work. The second section describes short-term instability in more detail, supported by the current scientific extent, as well as highlights the necessity for an inclusive short-term instability evaluation. In the third section, several short-term instability evaluation methods are assessed in terms of various relevant qualitative factors. The fourth section summarizes the findings and presents a brief discussion. Finally, conclusions and future work considerations are presented in the fifth section.

2. Short-Term Instability Overview

Short-term voltage instability is defined as a voltage deterioration due to fast-acting load components (i.e., induction motors), electronically controlled loads, HVDC links, and inverter-based generation [4]. Alternatively, it can be understood as the inability of a power system to deliver the required power to the loads [5]. The most common cause has been attributed to motor stalling and HVDC links connected to weak AC systems. Stalling motors draw a very high reactive current, stressing the distribution (and sometimes transmission) grid greatly. Such conditions may cause cascading faults, resulting in a swift voltage collapse with potentially widespread consequences.

Furthermore, rapidly increasing renewable energy sources (RES) penetration is notably affecting short-term voltage instability as well, making the phenomenon much more complex. RES influence can be either positive or negative, depending on many factors. Post-disturbance interplays between motors’ dynamics and distributed energy resources (DER) and their controls leads to an emphasized need to monitor and predict potential instabilities. Some of the factors that may cause short-term instabilities were analyzed in depth in [6,7]. It is expected that these effects will become even more frequent and more severe in modern grids, creating the need for both real-time monitoring and mitigation solutions.

The short-term voltage instability phenomenon occurs in a timeframe of several seconds and has hence been generally hard to analyze or predict in real-time. The voltage deterioration occurs fast, often leaving no time for manual mitigation measures. While this problem has been hard to tackle in the past, the recent improvements in grid monitoring based on synchrophasors open possibilities for fast monitoring and fast automatic mitigation solutions.

In this paper, the wider term of short-term instability is divided into four distinct phenomena: short-term voltage instability (STVI), transient rotor angle instability (TRAI), fault-induced delayed voltage recovery (FIDVR), and converter-driven slow interaction instability (CSII). All of these phenomena are categorized as separate short-term instability events in the most recent power system stability definitions [4]; hence, the division fully reflects those definitions. Furthermore, all four phenomena are often inherently related and they occur in a similar time scale. A more detailed explanation in this regard is presented further in the paper.

Figure 1 shows the proposed division, accompanied by an illustrative voltage trajectory for each of the mechanisms. The graphs are obtained from analyses conducted in [7] and are for illustrative purposes only. It is, of course, possible that the voltage behaviour can be different for diverse systems/faults. However, the essence of the voltage trajectory should remain similar.

Out of the abovementioned four, STVI is the original and the most known (voltage-related) short-term phenomenon, and it is already introduced at the beginning of this section. It is characterized by a rapid voltage deterioration following a large disturbance. The voltage is unable to recover from the fault, rapidly and progressively leading to the voltage collapse. The corresponding graph in Figure 1 illustrates such a voltage collapse in an STVI case.

TRAI is another widely known phenomenon and is often referred to simply as transient instability. It is defined as a loss of synchronism between synchronous machines (or interconnected systems) after a large disturbance [4]. The physics behind the instability is related to the loss of torque equilibrium, which results in the acceleration or deceleration of the rotor. Consequently, the rotor angle can pass the maximum permitted value, resulting in undamped power swings, which lead to the loss of synchronism—also known as the out-of-step condition. Power systems can lose stability either in the first oscillation (first swing instability) or after several undamped swings. The illustrative example in Figure 1 is of the latter case.

FIDVR is a fairly new phenomenon, at least in terms of the attention it receives in the research and industry. It can be described as a (too) slow recovery of the voltage after a large disturbance, often followed by a voltage overshoot. The phenomenon itself occurs due to the interactions of transmission and distribution systems, i.e., a sudden voltage drop in the transmission grid leads to an increased reactive power demand from the distribution grids. The reason behind this increase has been largely attributed to the stalling of air conditioning (A/C) units, although it can be related to the stalling of any induction motors [8]. The stalled motors depress the voltage for several (tens of) seconds, delaying the recovery [9,10]. Eventually, they are tripped by the thermal protection, which is often followed by a spike in voltage. The timeframe of the phenomenon is hence dependent on the thermal protection settings of widespread induction motors in the grid. The event is not an instability on its own, but the main issue with it is the potential for cascading faults, as many system components may disconnect due to the prolonged low voltage conditions. The phenomenon is illustrated by a voltage curve in Figure 1.

CSII is a newly added stability class, designed to reflect any slow instabilities that may arise due to the inverter-based generation (IBG) [4]. As the amount of renewable energy, and therefore IBG, increases rapidly, it is becoming important to consider this form of instability. The slow instability discussed here is related to the slow interactions of the control systems of IBG with each other and with other elements in the system, such as synchronous generators. Despite mainly being a small-signal stability issue, a large disturbance can also excite CSII, resulting in similar consequences as with the other three short-term instability phenomena. Generally, it is a wide classification and it can affect both voltage and frequency stability. In this paper, the phenomenon is addressed as closely related to voltage stability, as IBG control can drastically affect short-term voltage deviations. The instability is illustrated in Figure 1, where interactions of IBG generation and synchronous machines are seen in voltage variations. However, it should be noted that this is merely an illustrative example since one graph cannot describe all the possible converter-driven unstable voltage trajectories.

Slow frequency instability is not explicitly analyzed here, as it is a phenomenon more related to the available active power generation and overall system inertia, rather than voltage deviations [4]. It is, however, possible that events in Figure 1 eventually lead to frequency instability [7,11,12]. This is not within the scope of this paper, as voltage-related instabilities are of interest. For more information regarding frequency instability, see [4]. Except for this, the short-term resonance stability is not explicitly considered here either, due to similar reasons.

As shown in Figure 1, all of the four phenomena occur in a similarly short time interval. This makes it very complicated to distinguish between them, especially in real-time. Furthermore, phenomena are often interconnected. In a practical scenario, it is very plausible that one of these events triggers another one. For instance, FIDVR can lead to widespread voltage instability and/or rotor angle stability [7], while rotor angle instability can initiate short-term voltage instability (or vice versa) [13]. It has been also demonstrated how a FIDVR event can cause a power imbalance, leading to a potential short-term frequency instability [12]. This can be expected for other types of instability as well, especially in systems with a high share of RES that might disconnect during/after severe disturbances. Overall, power systems are very complex dynamical systems, and drawing a clear line between different short-term phenomena is not always possible. Therefore, an inclusive method that can evaluate all of these voltage deviations rapidly would be highly beneficial in modern power systems. Such premise is taken as a basis of the analysis that follows.

3. Analysis of Short-Term Voltage Stability Evaluation Methods

Many methods present in the literature are trying to tackle the issue of short-term instability. It is important to consider that any method should deliver an improved predicting power in comparison to the simple and available voltage measurements. If a method fails to deliver a clear advantage in that sense, its performance-cost trade-off will be unsuitable for practical applications.

In this section, several short-term voltage stability evaluation methods are theoretically analyzed. The focus is on the most common and the most field-applicable real-time methods, as deemed by the authors.

All the methods are evaluated on several qualitative measures that are very relevant for efficacy and practical applicability. First, it is evaluated whether the method is dependent on system model information. Since systems’ complexity is increasing fast and the precise system model is very hard to obtain in real-time, methods that do not rely on such information are considered superior. Furthermore, methods need to be real-time applicable if they are to be used in practice for real-time instability monitoring.

Next, it is assessed whether these methods could perform well for other short-term instability phenomena since a more holistic approach is preferred, as discussed in Section 2. Moreover, it is very important to determine if methods are applicable for power systems with a large amount of renewable energy integration, which may exhibit different dynamics. The major differences arise mainly due to the rapidly increasing penetration of renewable energy in both transmission and distribution grids.

Furthermore, the computational complexity of the methods and their parameter sensitivity is evaluated. Ideally, a method should be as simple as possible so the calculation time is short, leaving sufficient time for control/mitigation measures. The more time the method requires, the less time is left for the actual instability mitigation solution. Finally, methods that exhibit fewer degrees of freedom regarding parameters are favored, as their applicability to various systems and operation scenarios is more robust. Lastly, we acknowledge the possibility that not all relevant evaluation methods and qualitative measures are considered.

3.1. Lyapunov Exponent

The Lyapunov exponent (LE) originates from the ergodic theory, i.e., a branch of mathematics that analyses deterministic dynamical systems and their statistical properties. LE can be used to determine whether a dynamical system is chaotic at any moment in time, by evaluating the rate of divergence of relevant dynamic system variables.

As such, it is applicable to various dynamical systems and has been recently proposed to be used for electric power grid dynamics. The approach is summarized as shown in Equation (1):

$$\left|\Delta V\left(t\right)\right|=e^{\lambda t}\left|\Delta V_0\right|$$

(1)

where $\lambda$ represents the LE, $\Delta V_0$ the initial voltage deviation, and $\Delta V\left(t\right)$ time-dependent deviation of the voltage trajectories [14]. Since only a finite number of voltage values is available in a practical sense, computation of the LE is done employing time-series data, supplied, for instance, from PMU measurements, as shown in Equation (2):

$$\lambda =\frac{1}{k\Delta t}\ln \left(\left|\frac{V^{\prime }\left(\left(n_0+k\right)\Delta t\right)}{V^{\prime }\left(n_0\Delta t\right)}\right|\right)$$

(2)

where $k$ is the size of the data window, $\Delta t$is the sampling interval, $n_0$ is the first data point index, and $V^{\prime }$ is the time derivative of the voltage at the specific data point [14].

The Lyapunov exponent of a positive (negative) value implies an unstable (stable) system condition in the observed busbar. For power systems, if one of the LEs is positive, the system is unstable. It is hence often referred to as the Maximum Lyapunov Exponent (MLE). A more rigorous mathematical derivation of LE for power systems’ applications can be found in [15].

There are two main directions of LE usage in short-term instability monitoring. One approach is to monitor voltages, as shown in Equations (1) and (2). This effectively results in short-term voltage instability monitoring. Another approach is to utilize the same concept and apply it to rotor angle (transient) stability [16,17]. The idea remains the same, while the monitored variables of interest become rotor angles of the synchronous generators in the system, replacing voltage in Equations (1) and (2). As described in Section 2, it is undeniably beneficial if a single approach can be applied to more than one short-term instability phenomenon. For instance, in [18], merged monitoring of short-term voltage stability and rotor angle transient stability is proposed, utilizing Lyapunov exponents.

One of the major benefits of LE is its independence from the system model. It relies solely on voltage measurements and is therefore not affected by any potential system modelling difficulties. Hence, it is a very promising approach considering how systems are growing in complexity and number of elements. Furthermore, the shift towards renewable energy sources should not negatively affect LE’s ability to predict instabilities either. However, the mentioned accelerating dynamics might make it harder to timely complete a reliable evaluation.

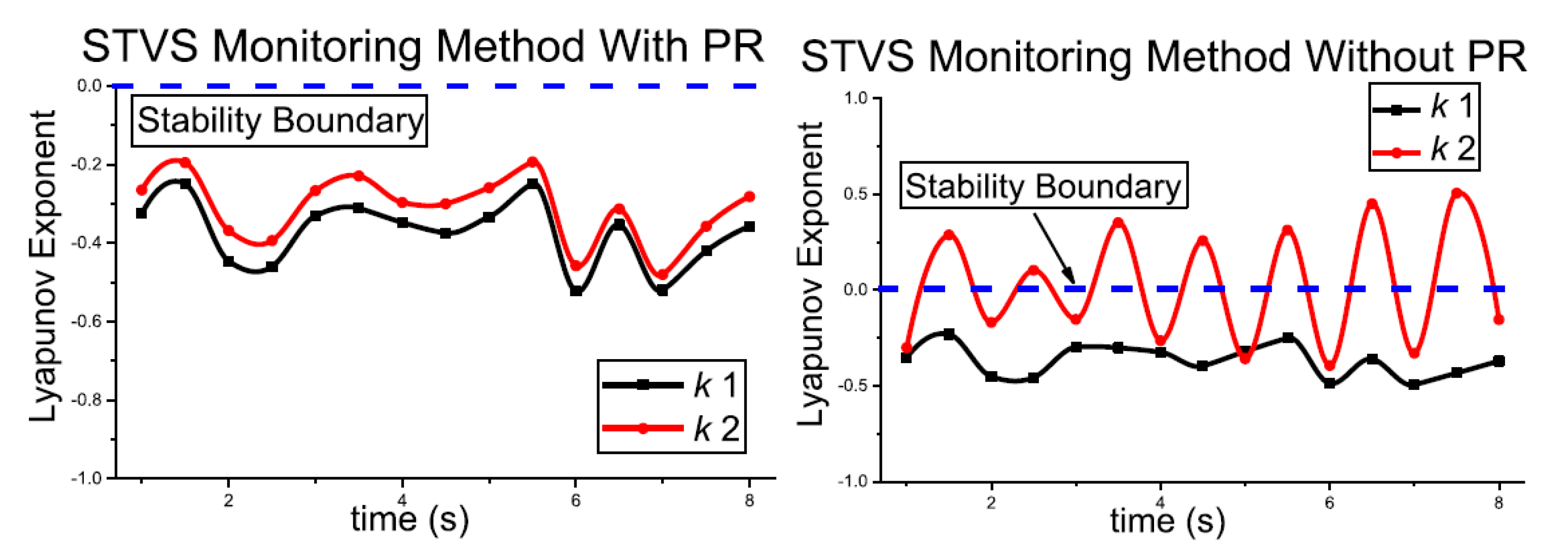
As the LE method utilizes derivatives, which inherently amplify any potential voltage oscillations (that might not be signs of instability), the LE itself can be very oscillatory. This can be seen in almost any application and analysis of LE and might cause problems in terms of parameters settings. The problem of oscillations was addressed in [14], where authors proposed an improved method of LE calculation. The method relies on phase rectification, as a way of smoothening the LE values without sacrificing too much of its predicting potential. The approach is executed using modal analysis, which can rely on Prony’s method, matrix pencil method, or Hankel total least squares (HTLS) method. This results in a longer computational time, slightly reducing the already short time frame for (in)stability evaluation. However, the benefits of smoothening can be very important to avoid false positive or false negative stability evaluations. An example of rectification is shown in Figure 2, where the effect of a different data window size (k) is more pronounced on non-rectified LEs. This may lead to unclear stability evaluation, as shown in the second example.

The LE approach has already been experimentally applied in some systems. In [19], the authors present a framework used to apply LE in a real system, where they address several practical issues on an ad hoc basis, such as parameter settings and noisy measurements. While they do show how LE can successfully and timely issue instability warnings in the observed cases, the challenge remains in generalizing this solution for any system in any operating state.

Finally, the main challenge with any short-term stability evaluation approach, including LE, is that both fast and accurate evaluation is required, which relies on reliable measurements. This is challenging since a smaller time window leads to lower accuracy, while allowing for a larger time window could leave an insufficient amount of time for the suitable control action. Regarding LE, small imprecisions can lead to potentially large errors, considering the computational complexity and the usage of derivatives.

3.2. Transient Voltage Deviation Index

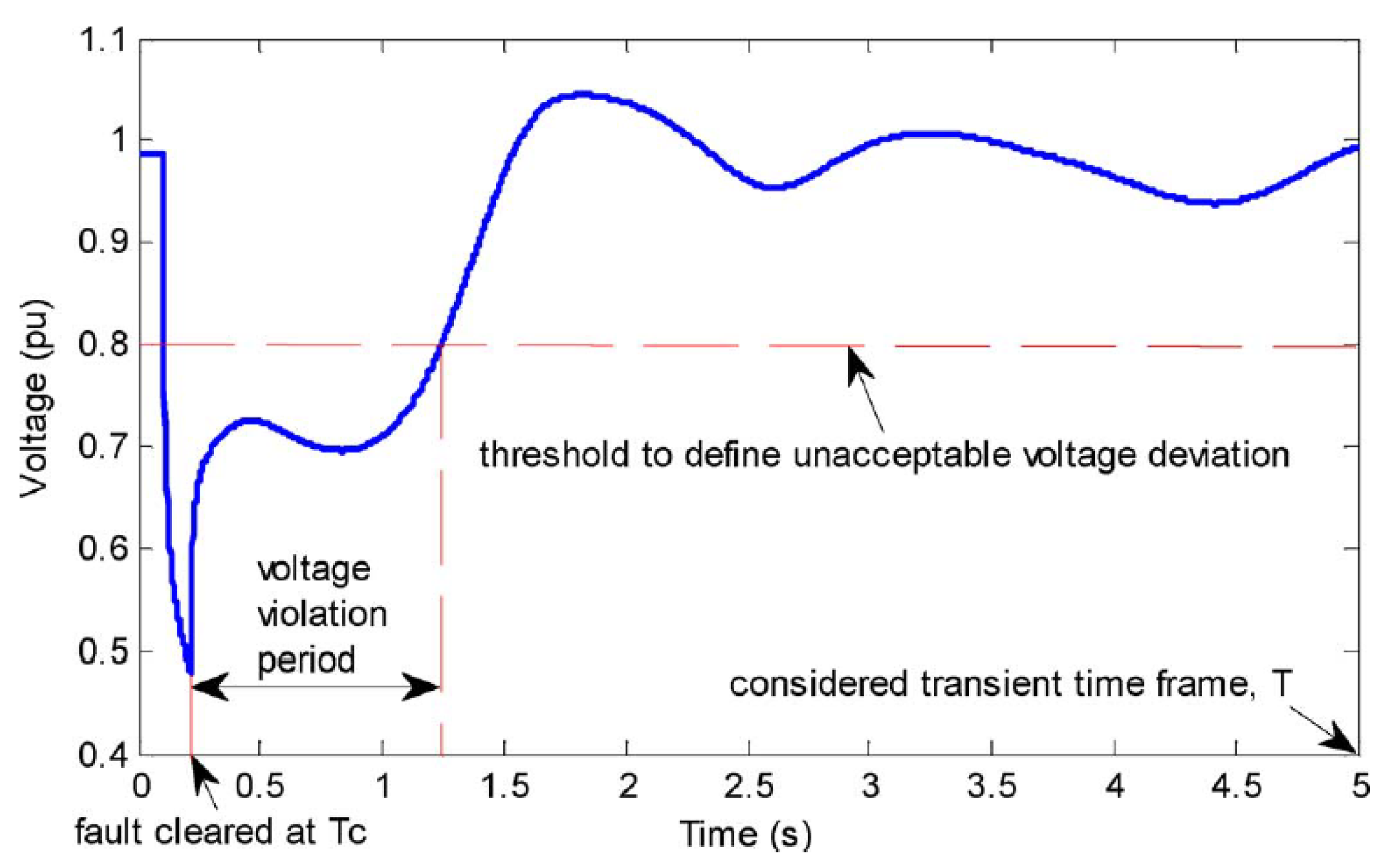
The second short-term voltage stability evaluation method analyzed in this paper is the transient voltage deviation index (TVDI). This quantitative index is proposed in [20], as a technique of measuring the voltage violation magnitude and the corresponding time duration. It provides an assessment of the system transient voltage performance following a disturbance.

The method is mathematically straightforward and it can be described using the following set of Equations (3) and (4):

$$TVSI=\frac{{{\displaystyle \sum }}_{i=1}^N{{\displaystyle \sum }}_{t=Tc}^{T}TVD{I}_{i,t}}{N\left(T-Tc\right)}$$

(3)

where N represents the number of buses in the analyzed system, T is the analyzed transient time frame, Tc is the fault clearing time, and TVDI is the transient voltage deviation index [20]. TVDI is calculated using the following equation:

$$TVDI=\{\begin{array}{c}\frac{\left|V_{i,t}-V_{i,0}\right|}{V_{i,0}}, if \frac{\left|V_{i,t}-V_{i,0}\right|}{V_{i,0}} \ge \mu \\ 0, otherwise \end{array} \forall t\in \left[Tc,T\right]$$

(4)

where $V_{i,t}$ is the voltage magnitude of the bus i at time t, $V_{i,0}$ is the pre-disturbance voltage magnitude of the bus i, and $\mu$ is the threshold used to define unacceptable voltage deviation level. The authors in [20] suggested using $\mu$ = 20%, although it depends on the particular system in question.

For understanding the method better, Figure 3 illustrates the concept and some of the variables from Equations (3) and (4).

Practically, the index is linearly dependent on the depth of the voltage dip and the duration of the dip. Hence, for more severe voltage deviations, either in magnitude or duration, the index will be higher, suggesting that the system’s stability is compromised. The index is used in the literature extensively, for various purposes such as dynamic VAR planning, utilization of demand response, storage, etc. [20]. It has been also useful in more advanced applications, e.g., the essence of a dynamic security assessment in a Hierarchical Intelligent System presented in [21].

The calculation of the index relies on available, accurate, and fast voltage measurements; hence, it is best to base it on PMU measurements. It is consequently sensitive to any measurement imperfections, but not as severely as derivative-based methods. Another benefit is that it is a model-free method, and theoretically, it can be applied to any system.

On the other hand, there are a few downsides. The first and the obvious one is that it only considers low voltage situations as it is focused primarily on short-term voltage stability. However, as discussed in Section 2, short-term instability can manifest in many different ways that are often inherently related. If a system experiences an oscillating voltage profile, TVDI would likely understate the severity of the voltage deviation. This may result in its inability to timely warn the system operators or to be utilized as a signal for predictive/corrective control measures. This could be amended to some extent, by adapting the index to consider overvoltage situations.

Furthermore, if a FIDVR event occurs, TVDI effectiveness is very dependent on the chosen voltage threshold. FIDVR events are not necessarily described by very low voltages, but are rather a prolonged modest undervoltage situation that often ends with an overvoltage spike, and might be quickly followed by voltage instability. Therefore, TVDI would require a relatively high threshold to assess the severity of a FIDVR event appropriately. However, such a high threshold would possibly make the index too sensitive to normal voltage variations, which are not necessarily an instability concern.

Overall, the index is a mathematically straightforward and computationally fast metric to evaluate the severity of a voltage drop. While it is limited by some imperfections mentioned above, it is certainly providing more information than simple voltage monitoring. This is likely true for both current and future power systems, although it requires more research.

3.3. Trajectory Violation Integral

Trajectory Violation Integral (TVI) is a method proposed in [22]. The method can be mathematically described using the following set of equations:

$$TVI=\underset{t_f}{\overset{t_{end}}{{\displaystyle \int }}}{V}_V\left(t\right)dt$$

(5)

where $t_f$ and $t_{end}$ represent fault occurrence time and dynamic simulation window, respectively. Voltage $V_V$ is defined as per Equation (6):

$$V_V\left(t\right)=\{\begin{array}{c}{T}_{low}\left(t\right)-V\left(t\right), if V\left(t\right)<T_{low}\left(t\right) \\ V\left(t\right)-T_{upp}\left(t\right), if V\left(t\right)>T_{upp}\left(t\right)\\ 0, otherwise \end{array}$$

(6)

In Equation (6), $V\left(t\right)$ represents the actual voltage curve, while the upper and lower exponential functions are mathematically derived as shown in Equations (8) and (9):

$$T_{low}\left(t\right)= \frac{{\left(\frac{t}{t_{end}}{e}^{\raisebox{1ex}{$t$}\!\left/ \!\raisebox{-1ex}{$t_{end}$}\right.}\right)}^{\beta }}{e^{\beta }}·V_{st}$$

(7)

$$T_{upp}\left(t\right)=2-T_{low}\left(t\right)$$

(8)

where $\beta$ is a parameter that determines the exponential decay, and $V_{st}$ is the steady-state voltage value. The system-wide measure for $N_b$ buses is calculated as a sum of individual TVI indices from Equation (5), as shown in Equation (9). All the equations are based on [22]:

$$TV{I}_{tot}={\displaystyle \sum }_{i\in N_b}TV{I}_i$$

(9)

For further clarity, Figure 4 presents the methodology graphically.

The concept is novel as it makes use of integral values of voltage deviation, relative to the two exponential curves enveloping the expected recovery trajectory. It can be understood as a metric that evaluates the amount of post-disturbance voltage deviation outside of the pre-set exponential boundaries.

It can evaluate both undervoltage and overvoltage situations, as well as the duration of the voltage violation. Furthermore, unlike fixed thresholds seen in e.g., TVDI, the time-changing exponential thresholds are more intuitive since they are wide in the early post-disturbance period and narrow further as time passes by.

This is more suitable for practical situations, both in current and future systems, as larger voltage deviations in the late (early) post-disturbance phase are more (less) indicative of instabilities. Hence, the index would likely provide good results for other short-term instability mechanisms discussed in Section 2. The time-varying conditionality that results from the usage of exponential functions allows it to put more weight on voltage variations in the late post-fault phase. This is important for all four short-term instability mechanisms and is something that fixed thresholds cannot achieve.

The index does not require any model data, and it is theoretically possible to apply it to any voltage bus with accurate and fast voltage measurements, regardless of the IBG penetration. While the index distinctly quantifies the severity of short-term instability, determining the parameters is not so straightforward, including the instability threshold. Naturally, this depends on the system itself, hence clear stability boundaries are not so easily determined. Finally, the index is sensitive to measurement accuracy, speed, and errors, as its complexity is slightly higher due to the usage of integral values.

3.4. Voltage Instability Predictor

The Voltage instability predictor (VIP) is a relatively well known approach with a long history, based on the Thevenin impedance matching concept. The essence of the method is to detect maximum load power conditions by comparing the impedance of the load and the Thevenin equivalent impedance of the rest of the system, as seen from the busbar of interest. The approach is intuitive and based on the electrical circuit theory, where if assumed that the power factor is constant, the maximum power transfer occurs when the two impedances are equal [23]. This is illustrated in Figure 5.

The difference between the two impedance values can be understood as a margin of (voltage) stability. This can be easily translated to a power margin, effectively showing the maximum power transfer of a measured corridor and the current system operation’s proximity to it. The impedance of the load is calculated as a ratio between the voltage and the current at the bus in question, while the Thevenin impedance is usually evaluated by using a recursive least squares (RLS) algorithm.

The Thevenin impedance matching approach is generally applied to the issue of long-term voltage stability. For instance, some known methods based on this approach can be found in [24,25,26]. While its applicability to the problem of short-term voltage stability is not so frequently addressed, in [23] the authors suggest that the method is also somewhat useful for FIDVR and STVI evaluation. They illustrate this by two simple examples, where the difference between the impedances, accompanied by reactive power margin calculations, can determine whether a system is short-term voltage stable or not.

There are, however, several limitations to the Thevenin impedance matching approach, and some of them are especially relevant for the issue of STVI evaluation. The original and fundamental issue comes from the fact that a simple impedance replaces a complex, nonlinear, and discontinuous system. This may introduce several oversimplifications, as well as issues with the RLS algorithm. Some of these concerns are addressed in [27].

On a more general note, the introduction of renewable energy and inverter-driven dynamics arguably makes the systems excessively complex for such a simplification, on both transmission and distribution levels. Similarly, loads are becoming much more complex and are hardly replicable by a simple impedance in modern systems, which emphasizes the issue further. Sources of reactive power used in regulating the voltage are not as centralized as before, limiting the practical feasibility of Q-margin monitoring. A related issue has been addressed in [28], where it was shown that related PV and QV curves, widely used in industry for maximum loadability and voltage stability, are becoming increasingly inaccurate in modern power systems.

While the approach of Thevenin impedance matching and related methods is still potentially very useful in long-term voltage stability evaluation, applying the same principle to the fast and nonlinearity-driven issue of short-term instability is likely not fully feasible. This is especially true for real-time assessment in systems with accelerating dynamics.

3.5. Contingency Severity Index

The contingency severity index (CSI) was proposed in [29] and was originally based on WECC/NERC standards. The idea behind the metric is to evaluate a voltage dip based on its magnitude as well as its duration. The approach can be summarized with the following equations:

$$CSI\left(t_f\right)= \sum _{i=1}^n\frac{w_{\upsilon i}S{I}_{\upsilon i}\left(t_f\right)+w_{ti}S{I}_{ti}\left(t_f\right)}{n}$$

(10)

where $w_{\upsilon }$ and $w_t$ are weight factors, $n$ is the number of busses, and the two SI indices are defined as follows:

$$S{I}_{\upsilon }\left(t_f\right)= \{\begin{array}{c}\frac{\left|V_0-V_{dev}\right|}{\left|V_0\right|}, if \frac{\left|V_0-V_{dev}\right|}{\left|V_0\right|} \ge 0.3 \left(0.25 if load bus\right)\\ 0, otherwise \end{array}$$

(11)

$$S{I}_t\left(t_f\right)={\displaystyle \sum }_{l_q\in L_{l_q}}\raisebox{1ex}{${\tau }_{l_q}$}\!\left/ \!\raisebox{-1ex}{$\left(t_f-t_{cl}\right)$}\right.$$

(12)

where $V_0$ is the initial pre-disturbance voltage magnitude, $V_{dev}$ is voltage deviation as a result of the disturbance, $t_f$ is the time window of evaluation, and $t_{cl}$ is the fault clearing time. The detailed derivation and explanations can be found in [29].

By comparing CSI with the TVDI presented in Section 3.2, it can be seen that the approach is mathematically very similar. The main difference arises due to the separate calculation of voltage magnitude deviation and the duration of the deviation, which are summed up in the final index. This allows for separate weighting factors to be applied in (10). In [29], the authors utilize this metric to determine the optimal location for voltage support, by using mixed integer dynamic optimization that relies on the inputs of CSI.

In general, a very similar analysis in comparison to TVDI can be written for this method. Hence, to avoid being repetitive, Section 3.2 elaborates on these already. The only clear difference is seen in the possibility to attribute different weights to the duration and amplitude of a voltage deviation, which might be useful for adaptations to other short-term phenomena.

3.6. Voltage Stability Risk Index

The voltage stability risk index (VSRI) was originally developed in [30] as a long-term voltage stability indicator. It is further utilized in [31] to analyze the voltage stability and to propose an optimal location for load shedding.

The index relies on the calculation of a moving average window of voltages, followed by an evaluation of the normalized relative voltage deviation. The final value is derived as a sum of the time-varying values of relative deviations.

Mathematically, VSRI can be derived as follows, based on [31,32]:

$$VSRI{ }_j=\{\begin{array}{c}{\displaystyle {\displaystyle \sum }_{k=1}^j}\frac{\left(d_k-d_{k-1}\right)}{2j} , j\le N\\ {\displaystyle {\displaystyle \sum }_{k=j-N+1}^j}\frac{\left(d_k-d_{k-1}\right)}{2N} , N+1\le j\le M\end{array}$$

(13)

Value $d_j$ is a percentage diversity of the current sample$y_j$, with respect to the moving average based on${\upsilon }_j$. It is calculated as shown in Equation (14):

$$d_j=\left(y_j-{\upsilon }_j\right)·\frac{100}{{\upsilon }_j} , j=1,2,\dots ,M$$

(14)

The moving average value ${\upsilon }_j$ is calculated by taking the N initial samples as a moving window across the total measured sample of M:

$$\upsilon { }_j=\{\begin{array}{c} {\displaystyle {\displaystyle \sum }_{k=1}^j}\frac{y_k}{j} , j=1,2,\dots ,N\\ {\displaystyle {\displaystyle \sum }_{k=j-N+1}^j}\frac{y_k}{N} , j=N+1,\dots ,M\end{array}$$

(15)

A more detailed description of the methodology derivation can be found in [30,31].

When the index converges to zero, the system voltage is considered stable, while otherwise, it might be an indication of instability. An illustrative example is shown in Figure 6, taken from [31], which demonstrates a case of generator outage leading to voltage instability. Voltage and VSRI values of one busbar are shown as a function of time.

While the index is originally developed for a long-term voltage stability evaluation, the authors in [32] have shown that it might be possible to use it in a short-term voltage stability evaluation as well, with good accuracy and predictability in their analyzed scenarios. However, the presented algorithm settings are an ad hoc solution, and it is unclear whether it may be applicable for various systems and situations.

From both a theoretical and practical perspective, a voltage deviation from a moving average can provide useful information about the system state. This holds for both current and future systems, and it does not require any knowledge of the system composition.

Furthermore, whether the algorithm would work for different short-term instability mechanisms in modern power systems is unclear. It is possible that the oscillatory behaviour of the voltage, as seen in the case of transient rotor angle instability and converter-driven slow interaction instability, will not be evaluated as severely as it should be. Similar may occur in a FIDVR situation.

The index itself is not very complex to calculate, but parameter choices such as the window size used for the moving average and the chosen unstable criteria value may affect the efficacy. The authors in [32] address these concerns to some extent, but they still suggest the need for more research.

3.7. Data-Driven Methods

Considering the advancements in data analytics, there have been several attempts of utilizing various advanced data-driven methods to the issue of short-term (voltage) stability. Various methods fit in this category. Several promising ones, as deemed by the authors, are briefly discussed in this chapter.

Numerous learning-based methods can be found for the issue of short-term voltage instability. For instance, in [33], the authors presented a short-term voltage stability assessment method that relies on the time series shapelet classification. The general idea is to collect post-contingency PMU data and utilize such data for classification learning. The approach was further expanded in [34], where voltage stability margin was also considered. In [35], the authors utilized an ensemble-based randomized learning model that is aggregated in a hierarchical and self-adaptive method. The efficacy of the method was showcased on both short-term voltage instability and FIDRV phenomena, with promising results. In [36], an imbalanced learning method was suggested as a way to overcome scarce instability data. In [37], spatial-temporal learning based on visualization of voltage stability dynamics is suggested. A local autopattern assessment scheme was proposed in [38]. A data-fitting method for rapid STVI evaluation was presented in [39]. The authors in [40] summarized many data-driven methods, some of which are applicable for the issue of short-term instability detection. Finally, in [41], a STVI assessment method that can cope with the missing PMU data is proposed.

Another advanced approach in the evaluation of short-term voltage stability is the use of a digital replica (twin) of the system. Such an approach was presented in [42], where the authors utilized a faster than real-time digital twin fed by the real-time system data. The idea is to predict the trajectory of the voltage, rather than derive STVI evaluation based on the already available data. This is only possible if such a framework is able to operate faster than in real-time, which is shown to be the case in an example presented in the paper. The case study related to a FIDVR event was conducted successfully.

Most of these methods can be, in theory, applied to the real-time short-term instability assessment. Furthermore, they are not limited to a single phenomenon but are rather applicable to various phenomena. The increase in renewable energy penetration and the overall change in the dynamics should not, on their own, affect the efficacy of these methods.

However, a common feature for most of the mentioned data-driven methods is that they are still in the early development stage. There are several challenges to apply such methods in real-time. Firstly, the short-term instability is currently not so frequently experienced in the grids, making it challenging to train the models well through any learning algorithms. This can be resolved by utilizing simulation results, but then the mentioned issue of modelling accuracy is faced. Considering the complexity and the uncertainty of large power system models, providing sufficiently accurate data series might be challenging. Secondly, the computational complexity and the parameter settings can be very difficult and time-consuming. Whilst one solution might work well for a specific grid, designing a generalized approach is not straightforward.

Nevertheless, with the computational efficiency and speed increasing drastically, followed by improvements of data-driven (learning) algorithms, these solutions will likely play an important role in future predictions of short-term instabilities.

4. Summary and Discussion

Table 1. Overview of the presented methods.

Method	Abbreviation	Year	References
Lyapunov Exponent	LE	2013	[14,15,16,17,18,19]
Transient Voltage Deviation Index	TVDI	2014	[20,21]
Trajectory Violation Integral	TVI	2015	[22]
Voltage Instability Predictor	VIP	2012	[23]
Contingency Severity Index	CSI	2011	[29]
Voltage Stability Risk Index	VSRI	2007	[30,31,32]
Data-Driven Methods	DDM	2015–2020	[33,34,35,36,37,38,39,40,41,42]

presents an overview of all the analyzed methods, including the year of publishing and the relevant references. Due to the increasing complexity of power systems, a lot of attention in the past years has been given to the usage of LE-based methods. Furthermore, advancements in data analytics and data science prompted the development of various Data-Driven Methods. Nevertheless, the expanding usage of synchrophasors in power systems provides the opportunity for utilization of all the mentioned methods much more accurately than before.

As a summary of Section 3,

Table 2. Qualitative evaluation of the presented methods.

Method	Model-Free	Real-Time Applicability	Applicable to Various ST Phenomena	Useful in IBG-Rich Systems	Computational Complexity	Parameter Sensitivity
LE	✓✓	✓✓	✓✓	✓✓	X	X
TVDI	✓✓	✓✓	X	?	✓✓	✓
TVI	✓✓	✓✓	✓	✓✓	X	?
VIP	?	✓	X	X	✓	✓
CSI	✓✓	✓✓	?	?	✓✓	✓
VSRI	✓✓	✓	?	✓	✓	?
DDM	?	?	✓✓	✓✓	X	X

✓✓: Very good, ✓: Good, X: Bad, ?: More research needed.

presents a qualitative evaluation of all the analyzed methods concerning several relevant characteristics introduced and discussed throughout Section 3.

Based on Table 2, none of the methods is (very) good on all the relevant qualitative factors. Where more advanced methods like LE excel, simpler linear methods are less applicable. On the contrary, these improvements are accompanied by increased complexity and parameter sensitivity, which reflects negatively on the robustness of the method.

Most of the methods, except for the VIP and data-driven methods, are generally model-free and are hence simple in terms of the necessary inputs. The VIP and DDM require more research to evaluate whether they can be used for short-term (ST) instability evaluation without any model inputs, as explained in Section 3. The situation is similar for real-time applicability, where the majority of methods are (very) good. The VIP and VSRI methods are originally developed for long-term voltage stability monitoring and are therefore relatively less suitable for faster real-time stability evaluations. DDM require more research in this regard, as it is questionable whether they can be sufficiently fast and cost-effective with the available solutions and computational possibilities.

Nonetheless, the major challenge for most of the methods is the applicability to modern systems with a high penetration of inverter-based generation, as well as the applicability to other short-term instability phenomena. These are arguably the two most important factors in the analysis. The best-suited methods for these concerns are computationally more complex, such as LE, TVI, and potentially VSRI and DDM. LE was already shown to be applicable to other ST phenomena, such as transient rotor angle stability. Furthermore, the LE concept itself of evaluating if a dynamical system is chaotic does not lose its predicting power if a system integrates more IBG and becomes more complex overall. TVI was not explicitly tested on other phenomena, but the method is practically intuitive with a time-adjustable instability threshold, and it is likely possible to utilize it for various short-term instability mechanisms, irrespective of the IBG penetration. Computationally simpler methods (i.e., TVDI and CSI) are likely to be less useful in modern systems, and their applicability to various ST phenomena is limited. This is mainly the consequence of simplistic linear instability thresholds, which are not adaptable enough and potentially misleading in systems with a high share of IBG. Nevertheless, more research is required in this regard. On the other hand, VSRI applies moving average calculations, which can offer some insights even for IBG-rich systems. However, it is unclear if the method can detect other short-term instabilities or its efficacy is limited to voltage stability. This necessitates further research. The VIP method becomes less effective with the increase in systems’ complexity and is therefore not very suitable for either of these two challenges. Thevenin equivalence on such fast dynamical phenomena is unlikely to yield accurate and useful results. Advanced DDM might overcome these difficulties completely as they are widely applicable for complex dynamical systems in general, but they bring other challenges for real-time assessments.

In terms of complexity and parameter sensitivity, simpler linear methods without too many parameters (i.e., TVDI, CSI, and VIP) are always preferred. The methods that use derivatives or integrals (i.e., LE and TVI) compensate their dominance in efficacy for the increased complexity and parameter sensitivity. This seems to be particularly true for LE, where it was shown that parametrization could be very challenging. VSRI is not exceptionally complex to compute, but its parametrization challenges have not been explored extensively yet. Data-driven methods are generally neither simple to calculate nor easy to parametrize. All the methods also differ in speed of instability detection, which is not explicitly considered in this paper. Some information in that regard can be found in [32].

Finally, various individual challenges are discussed in Section 3 for each of the methods, which are not emphasized in Table 2. Generally, it can be concluded that there exists no single method that can tackle all the necessary challenges. Hence, there is a research gap with potentially high practical impact, that can be confronted in either combining or adapting some of the (parts of) these methods, or deriving a completely new method that addresses all the mentioned points. This requires future work attention.

It is important to highlight that this is a qualitative analysis only. A quantitative analysis that evaluates the efficiency of all these methods on a large data set of (simulated and/or measured) modern power system dynamics would be valuable. This is also an interesting future research consideration.

5. Conclusions

Short-term voltage stability is a phenomenon that at present receives insufficient attention in academia and industry. The transition towards renewable energy implies that system dynamics will inevitably become faster, which will make real-time short-term instability evaluation very important in modern power systems. This paper highlights the necessity of an inclusive short-term instability evaluation, considering the interactions between different phenomena on the same time scale. Such advanced methods (which were unfeasible in the past) are now enabled by fast and accurate PMU measurements.

The paper presents various available evaluation methods. A succinct qualitative analysis of several real-time applicable methods is conducted by highlighting the strengths and weaknesses. The general notion is that there is no single method that can successfully evaluate short-term instability for various systems and events. Some methods are promising; however, they still require additional improvements. Furthermore, computational complexity needs to be carefully addressed, as every second used to evaluate the system stability is a second less for potential emergency control strategies to be deployed. Finally, generally implementable methods without extensive case-by-case parametrization are more desirable.

A method that fulfils all these conditions would provide enormous benefits to the modern power grid dynamic vulnerability assessment, and it is hence an interesting future work consideration.