Numerical Analysis of Melting Process in a Rectangular Enclosure with Different Fin Locations
Abstract
:1. Introduction
2. Model Construction
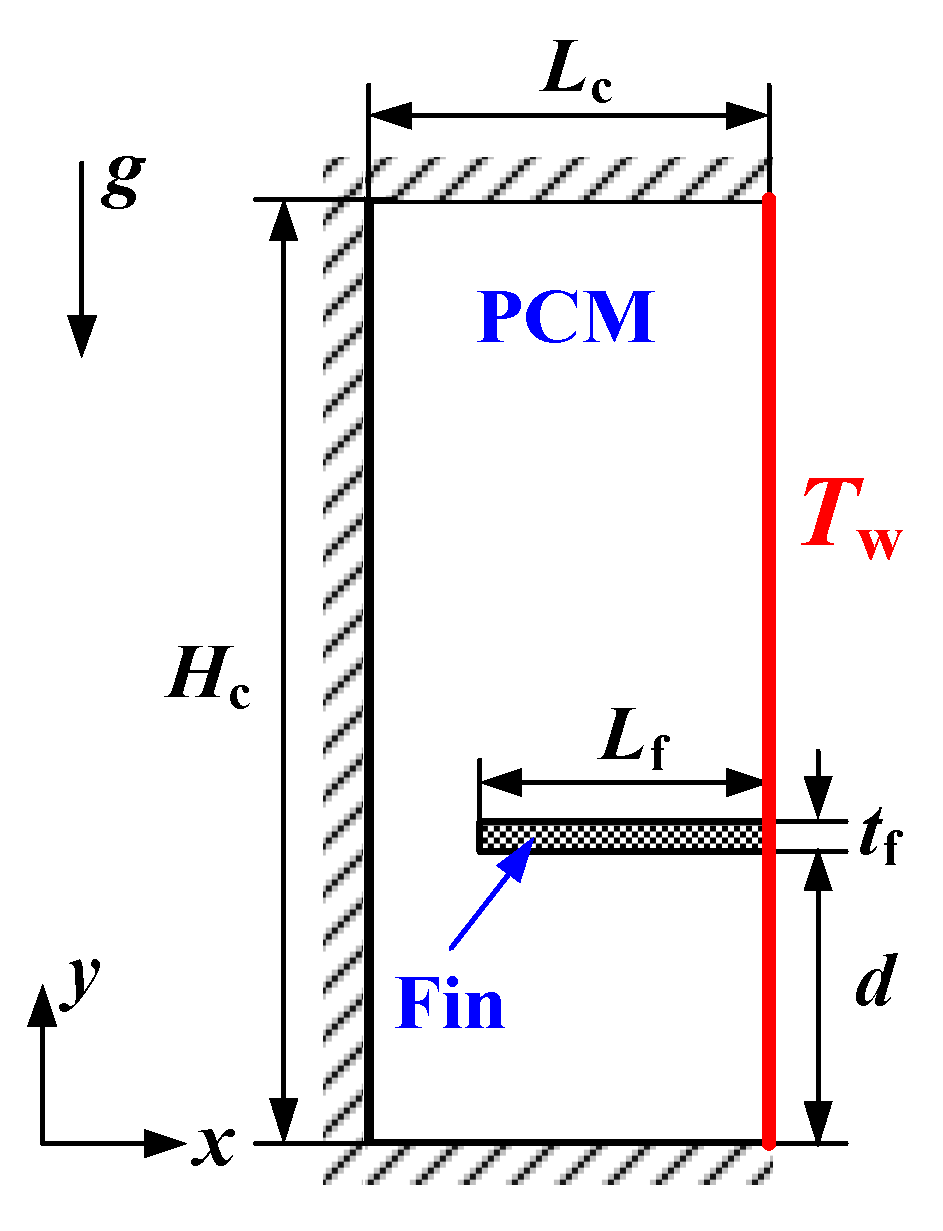
2.1. Physical Model
2.2. Mathematical Model
- The motion of liquid is viewed as a 2D, laminar and incompressible flow.
- Both PCM volume change and radiation are ignored.
- The thermo-physical properties of fin material and PCM are constant, except for PCM density, ρ, in the buoyancy force term of momentum equations where the Boussinesq approximation is used, i.e., ρ varies linearly with temperature, T, as presented by:where ρref and Tref are the reference density and reference temperature which are set as liquid density, ρl, and melting temperature, Tl [22,39].
- Boundary condition:
- Initial condition:
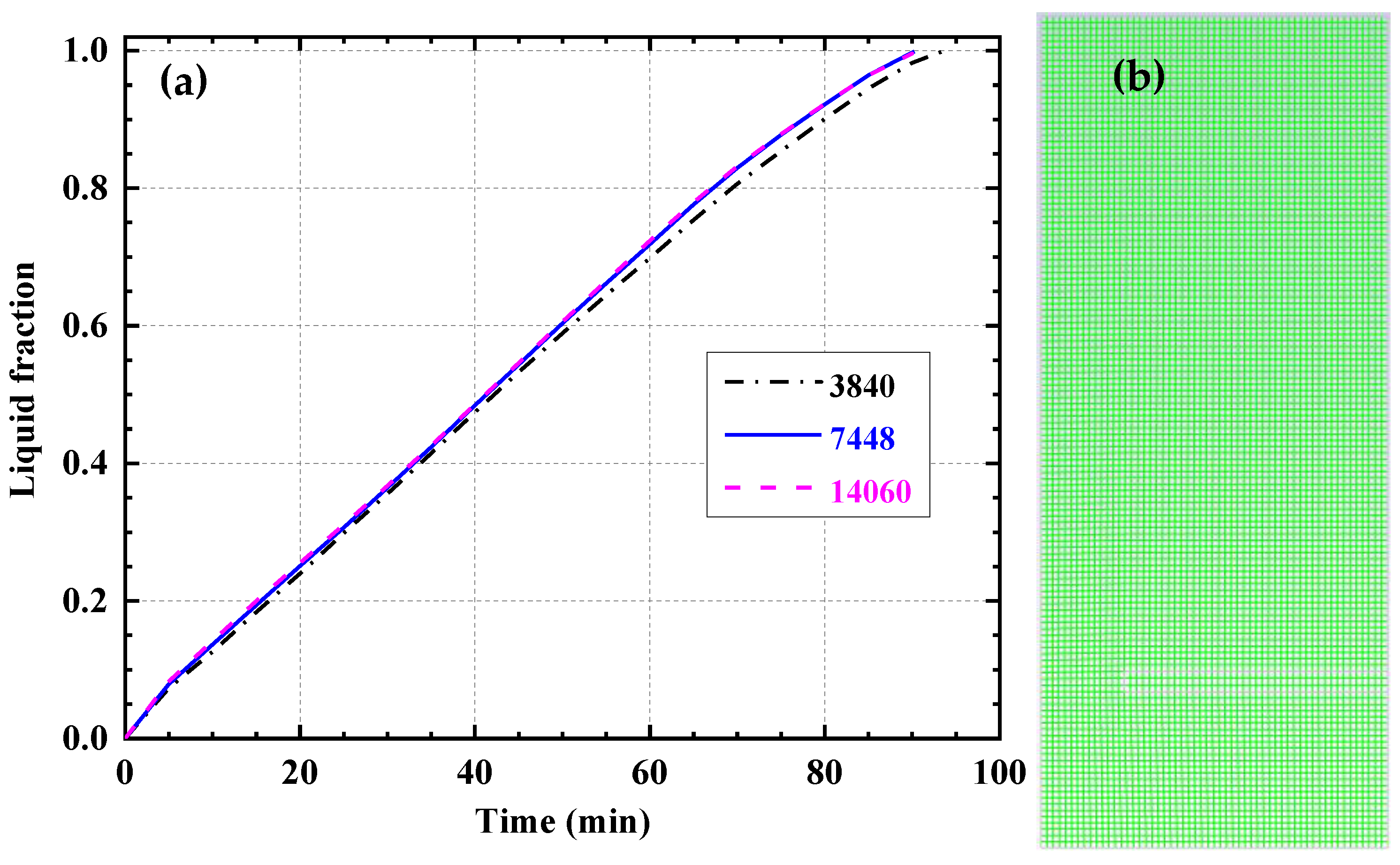
2.3. Independence Tests
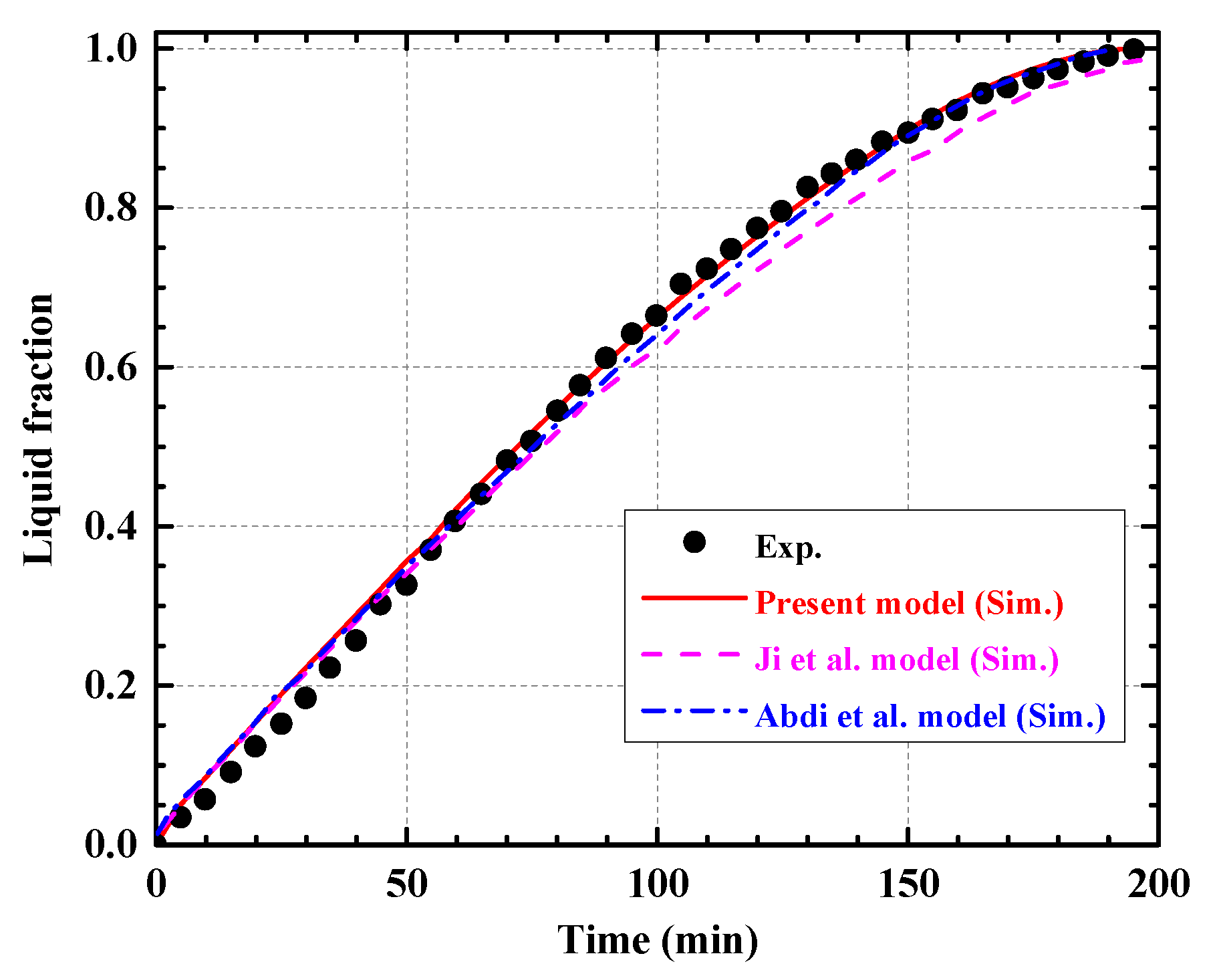
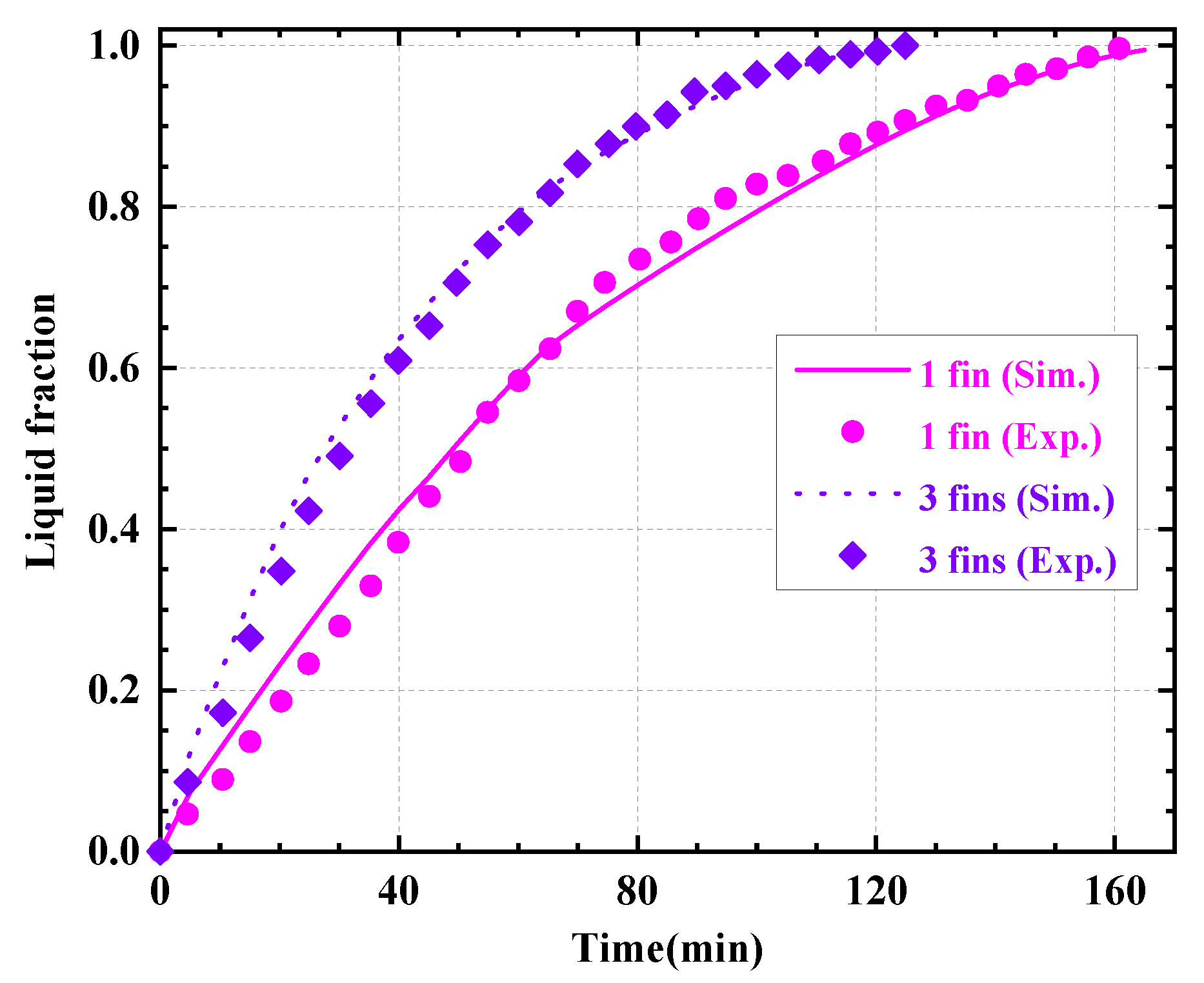
2.4. Model Validation
3. Results and Discussion
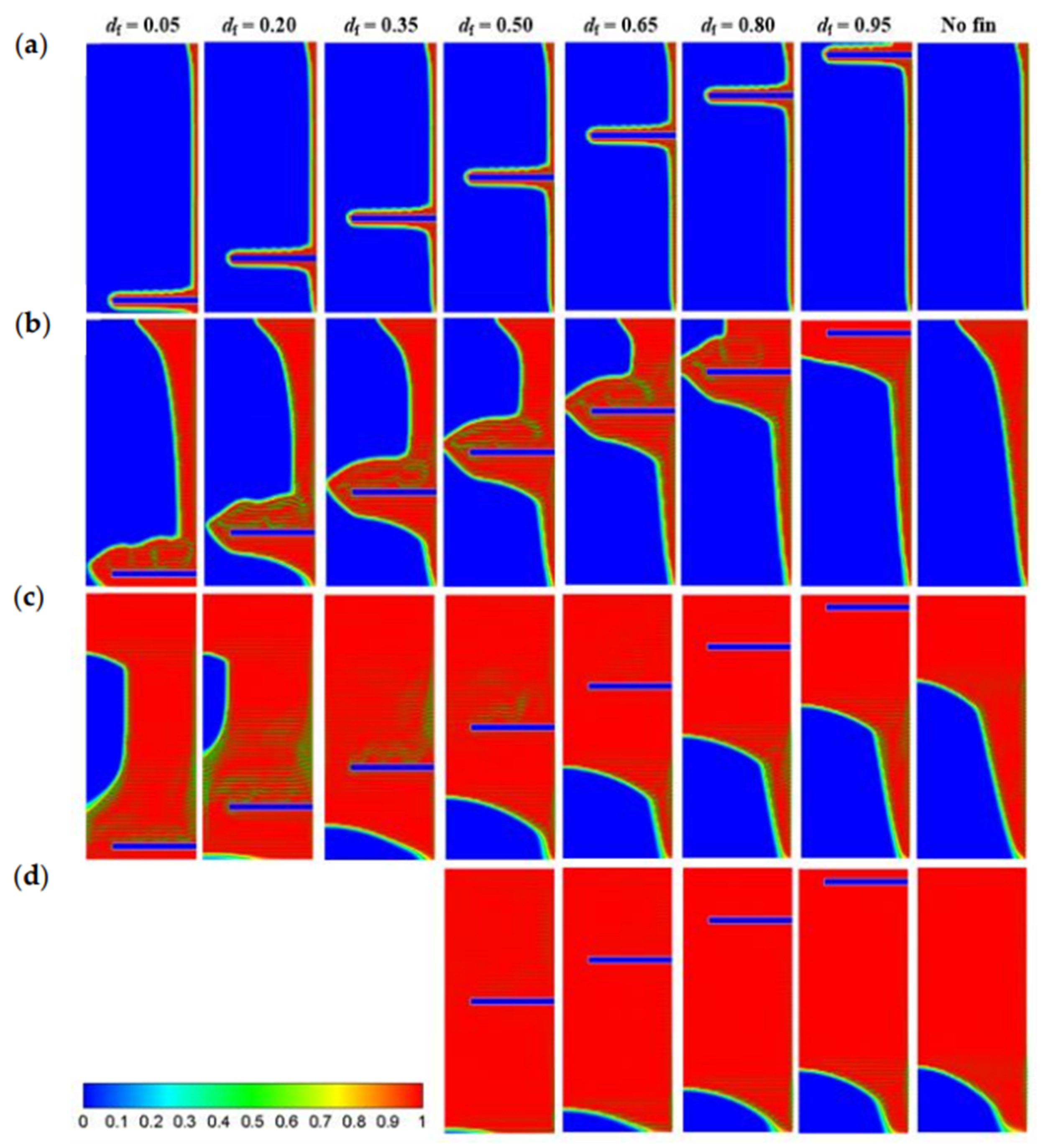
3.1. Patterns of Melting
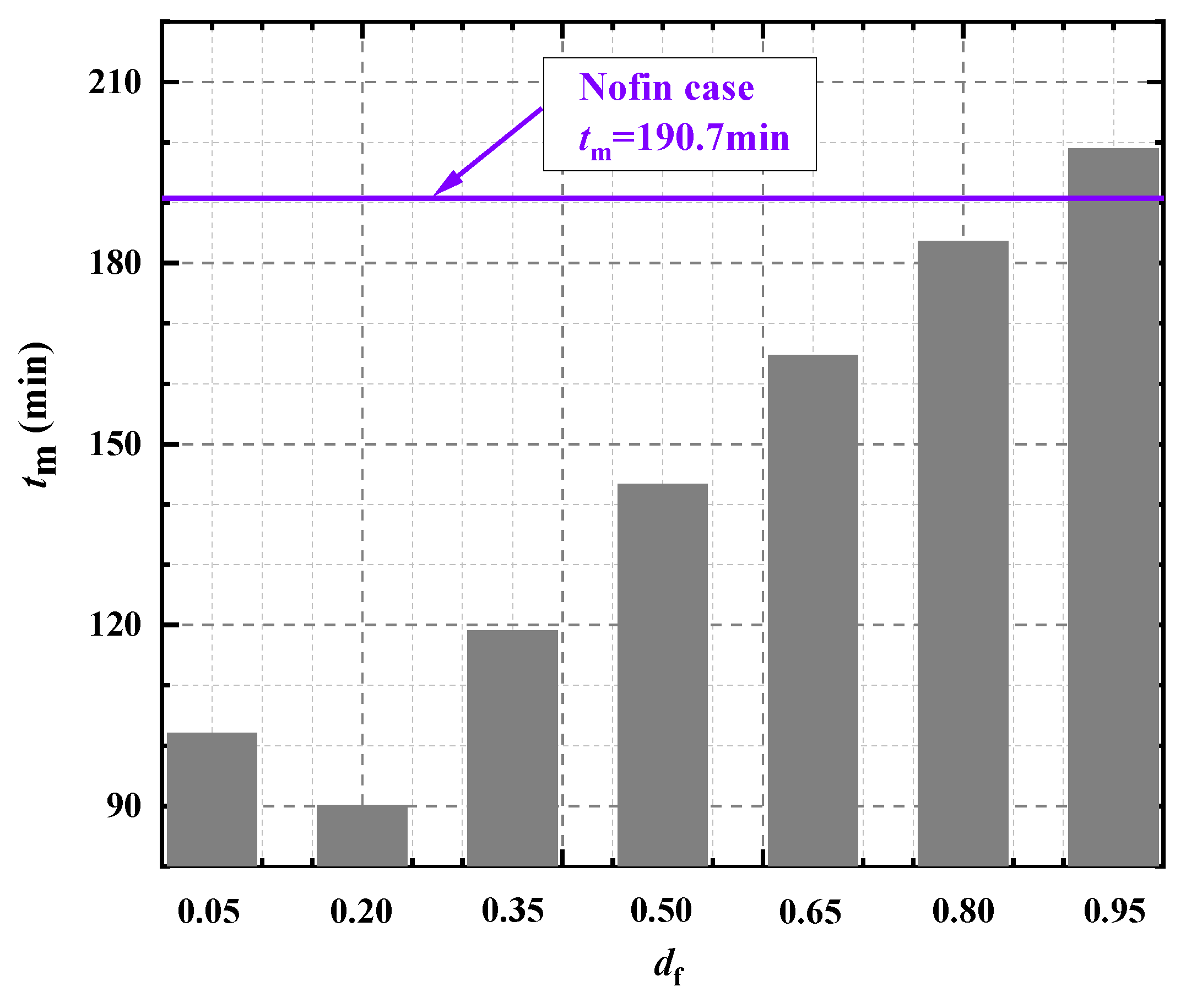
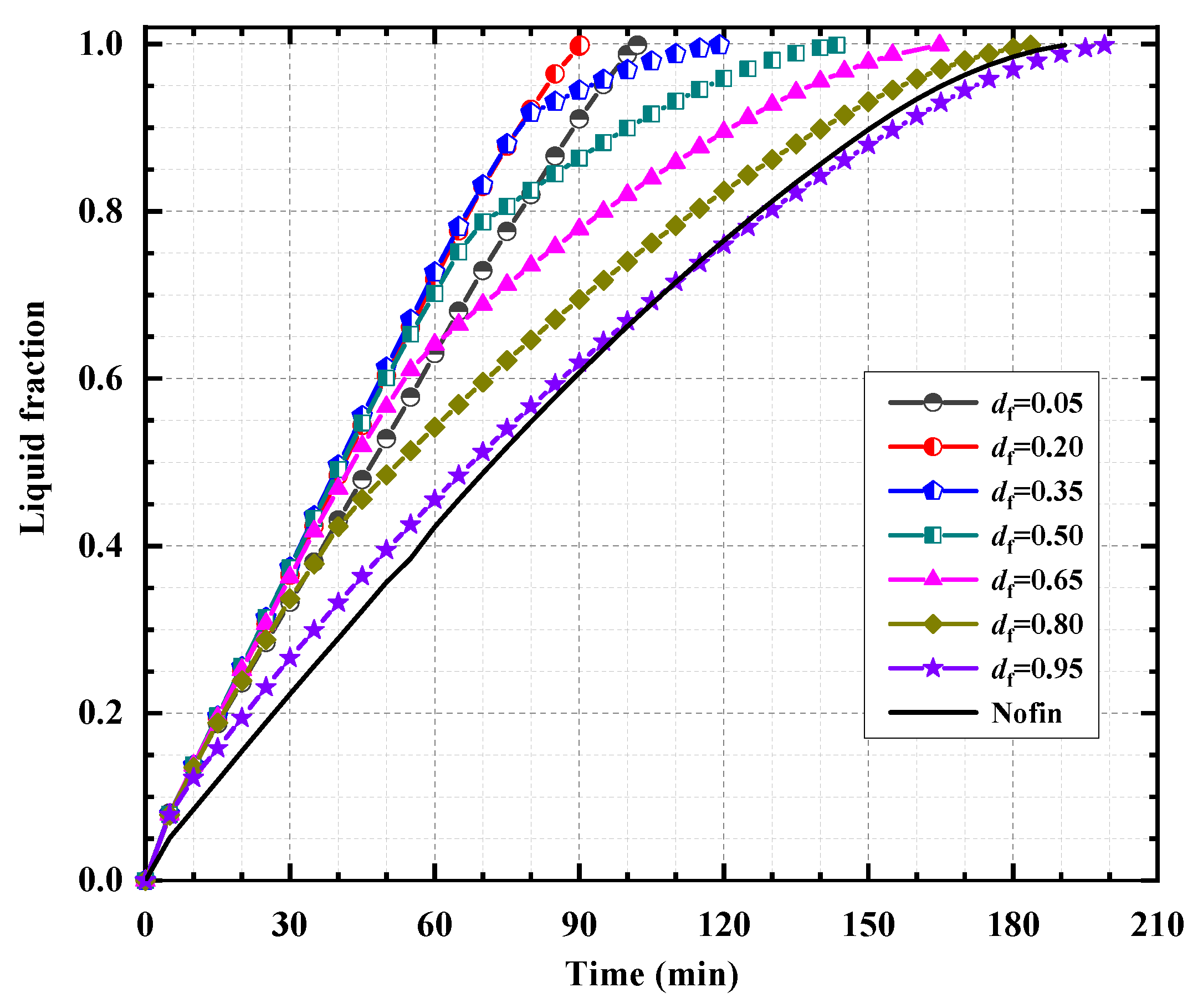
3.2. Melting Time, tm
- For a lower γ (less than 10%), inserting fins is effective to enhance melting; the effect of df is insignificant because the conduction dominates the heat transfer.
- For df = 0.05 and 0.20, the melting rate, quite higher than the no fin case, approximately remains the same with rising γ. It is because the fin mounted at a lower place does not hinder the liquid flow. On account of that the influence range of fins as to heat conduction is limited by the bottom surface for df = 0.05 in comparison to df = 0.20, tm (df = 0.05) > tm (df = 0.20).
- For df = 0.35–0.80, as γ increases, the melting rate decreases to a value lower than the no fin case at a time. Depending on df, the larger the df is, the lower the time is, i.e., the earlier the transition arises. For instance, the transition time is 80 min for df = 0.35 and reduces to 55 min for df = 0.65. This behavior is expected since the mounted fin impedes the liquid flow and the higher it is put, the earlier the impedance takes place. Besides, the thermal stratification region enlarges with moving the fin up, as a result of which tm (df = 0.35) < tm (df = 0.50) < tm (df = 0.65) < tm (df = 0.80).
- For df = 0.95, the liquid flow intensity weakens considerably, because of forming thermal stratification at the upper part, even though the flow resistance as to fins is rather limited. Thus, the transition of melting rate ahead of df = 0.80 is presented and the melting process is longer than the no fin case.
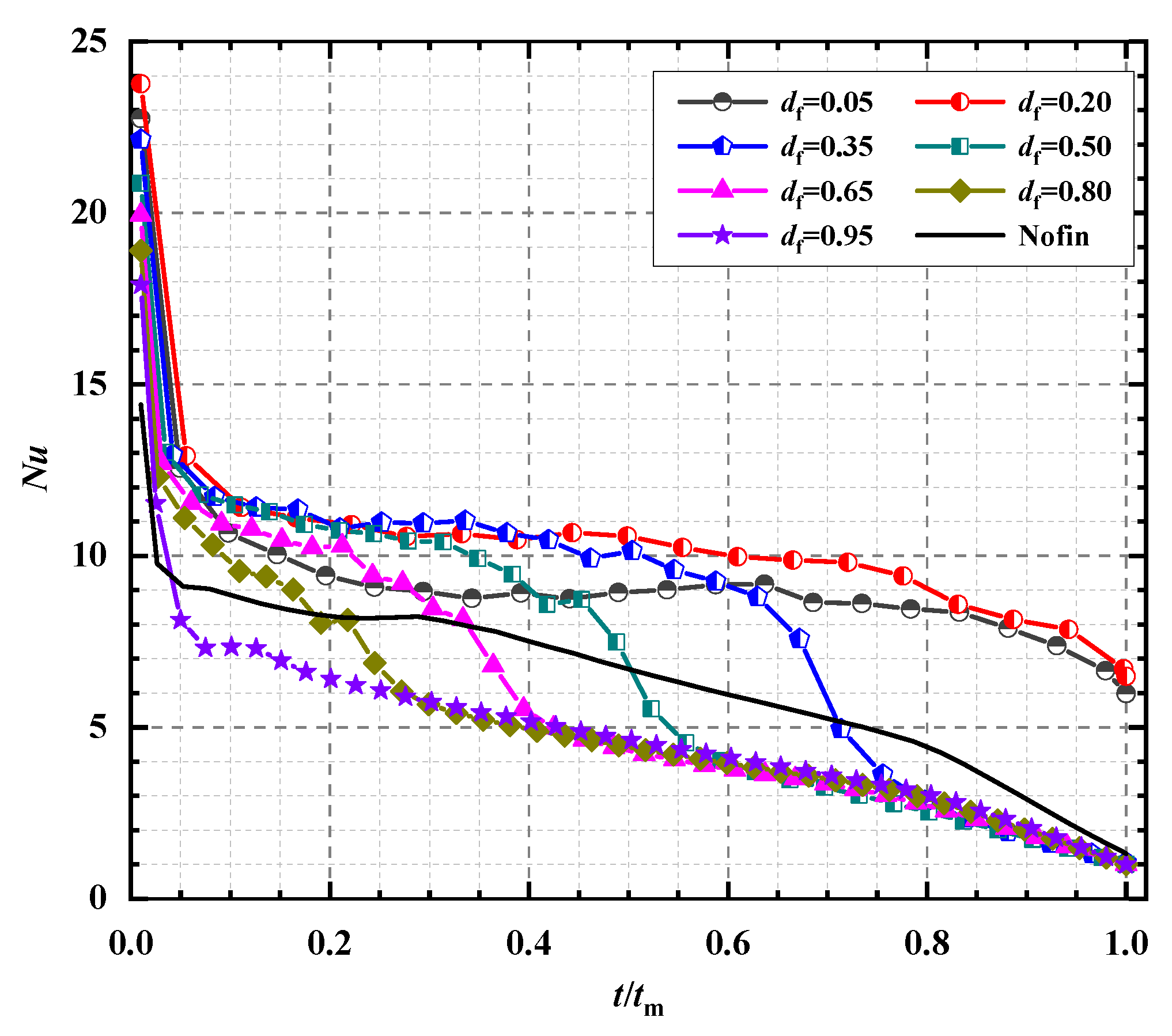
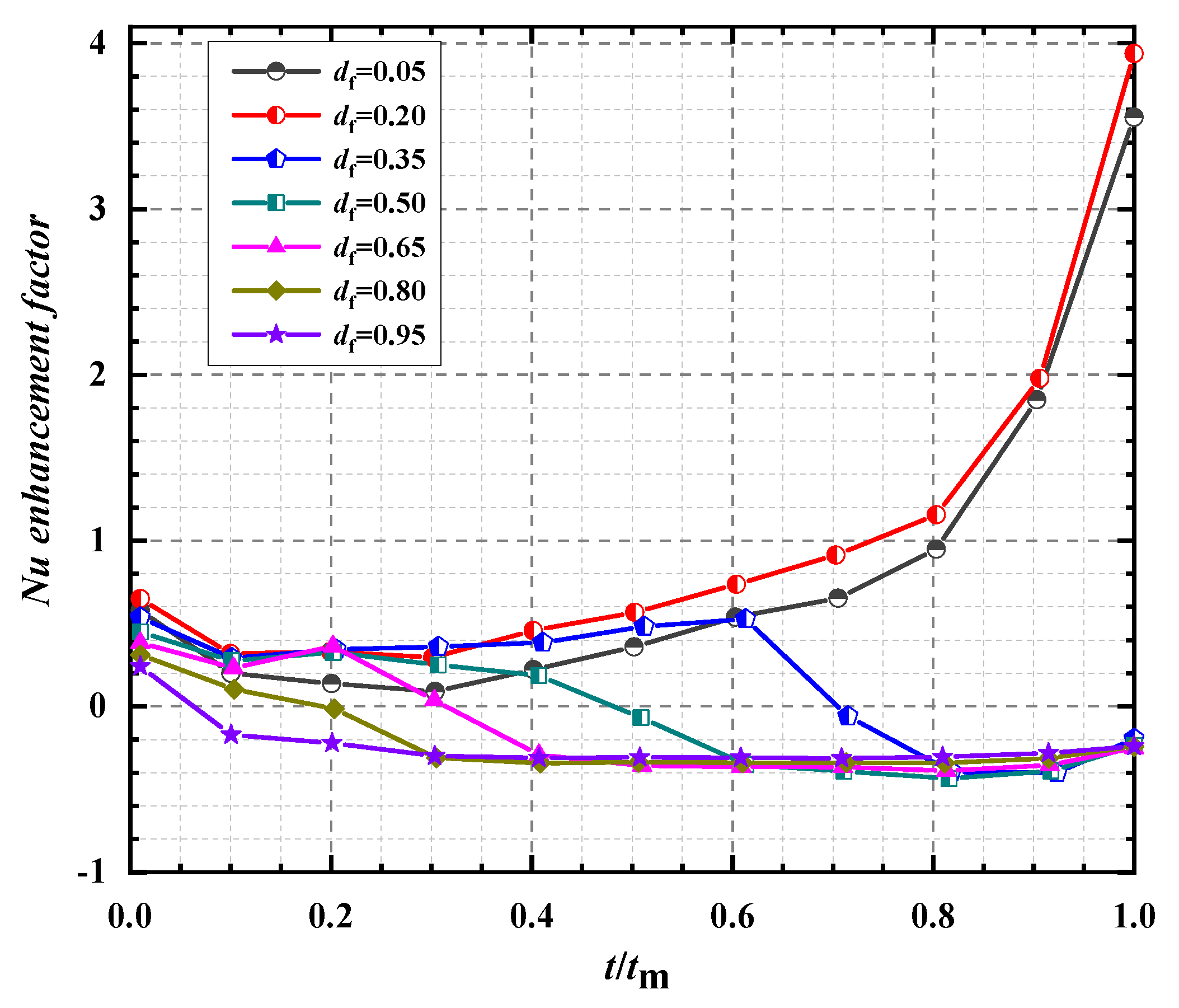
3.3. Surface Averaged Nusselt Number Nu
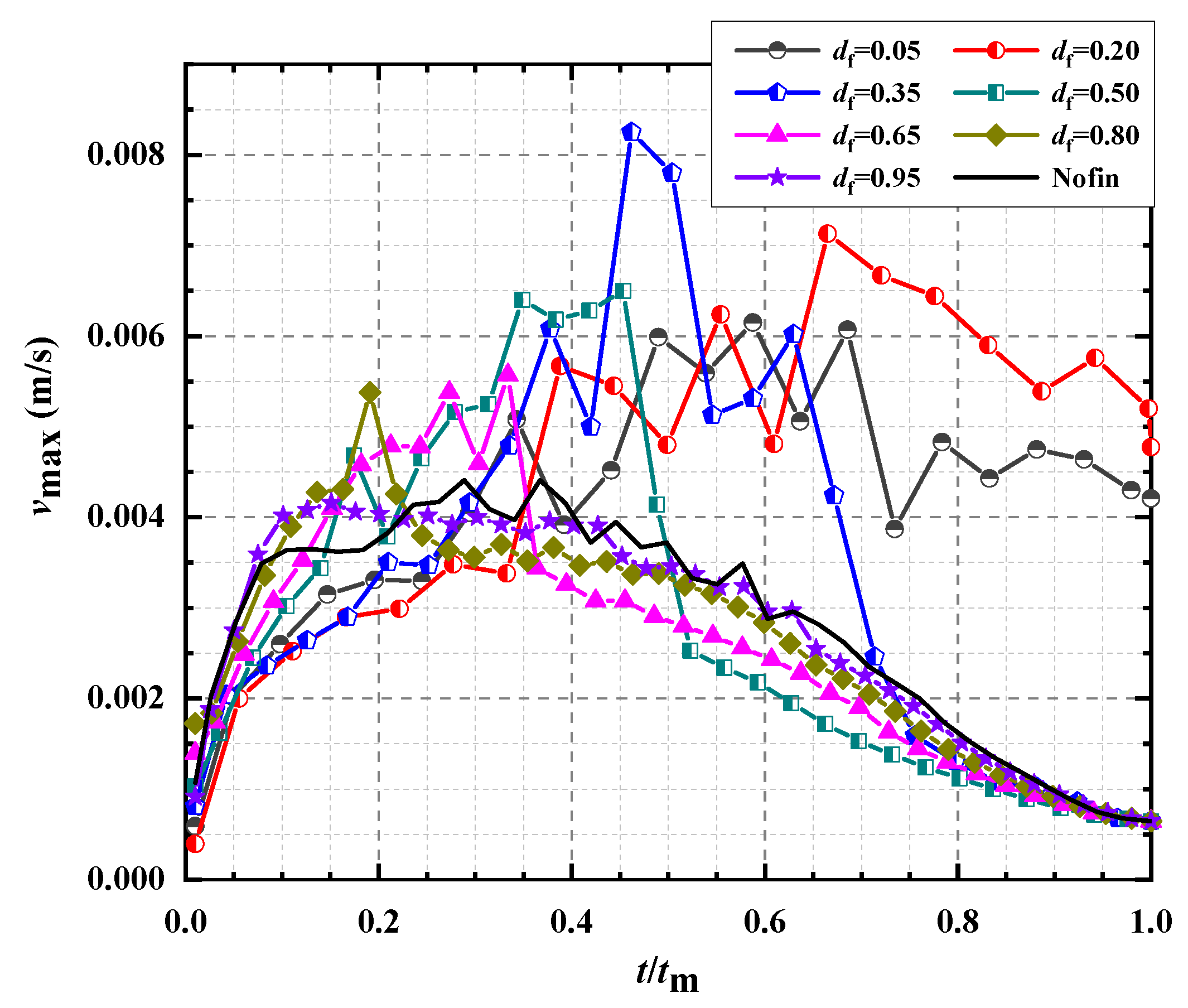
- εNu increases with t/tm in the whole melting process for df = 0.05 and 0.20. It is expected since mounting fin at a lower position enhances conduction at the beginning and facilitates natural convection at the middle and late stages; besides, the melting in the left corner is reinforced by the lower fin significantly, which is extensively regarded as a factor prolonging melting process seriously [28,46]. A testimony that facilitates natural convection is provided by Figure 10 which shows the variation of the maximum liquid flow velocity, vmax, with t/tm. For t/tm > 0.30, the difference between vmax (df) and vmax (no fin) enlarges notably with t/tm, precisely corresponding to the sharp increase of εNu.
- While for df = 0.35–0.80, the transition from εNu > 0 to εNu < 0 arises. That is, the heat transfer is not strengthened all the time. It is because the conduction is improved notably at the early stage or the early and middle stages, depending on df, but after that natural convection is reduced significantly due to the increase of liquid flow resistance as to fins and the formation of thermal stratification. The impedance of fins is verified by the variation of vmax shown in Figure 10. The comparison between Figure 10 and Figure 9 shows that the transition time from vmax (df) > vmax (no fin) to vmax (df) < vmax (no fin) is approximately equal to the transition time from εNu > 0 to εNu < 0.
- As liquid contours of the no fin case shown (Figure 5), the melting is originally much faster at the upper part in comparison to the lower part. As a result, the improvement of mounting fins near the top surface is not obvious and only limited to the very early stage. Besides, mounting fins near the top surface improves the temperature distribution nearby, facilitating the formation of thermal stratification and weakening the convection flow. Hence, on the one hand, εNu > 0 only arises at t/tm < 0.025 and εNu < 0 is presented at the rest of time for df = 0.95; on the other hand, the influence mechanism is different for df = 0.35–0.80 and df = 0.95, even though they share the same trend. As the same to df = 0.05–0.80, the variation of εNu is quite similar to the difference between vmax (df) and vmax (no fin).
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Amush | mushy zone constant, kg/(m3·s) |
| Aw | heat transfer area, m2 |
| cp | specific heat capacity, J/(kg·K) |
| d | distance between the lower surface of fin and the bottom surface of enclosure, m |
| df | fin location, d/H |
| g | gravitational acceleration, m/s2 |
| h | heat transfer coefficient, W/(m2·K) |
| hs | sensible enthalpy, J/kg |
| H | enthalpy, J/kg |
| Hc | height of rectangular enclosure, m |
| ΔH | latent enthalpy, J/kg |
| Lc | length of rectangular enclosure, m |
| Lf | length of fin, m |
| Lh | latent heat, J/kg |
| Nu | Nusselt number |
| p | pressure, Pa |
| Q | heat flux, W |
| t | time, s |
| tf | thickness of fin, m |
| tm | melting time, s |
| T | temperature, °C |
| T0 | initial temperature, °C |
| Tw | surface temperature, °C |
| u | velocity, m/s |
| vmax | maximum liquid flow velocity, m/s |
| Greek symbols | |
| β | Thermal expansion coefficient, 1/K |
| γ | liquid fraction |
| λ | thermal conductivity, W/(m·K) |
| ε | small number |
| εNu | Nu enhancement factor |
| ρ | density, kg/m3 |
| Subscripts | |
| fin | fin |
| l | liquid |
| PCM | PCM |
| ref | reference |
| s | solid |
Abbreviations
| LTES | latent thermal energy storage |
| PCM | phase change material |
References
- Hosenuzzaman, M.; Rahim, N.A.; Selvaraj, J.; Hasanuzzaman, M.; Malek, A.B.; Nahar, A. Global prospects, progress, policies, and environmental impact of solar photovoltaic power generation. Renew. Sust. Energ. Rev. 2015, 41, 284–297. [Google Scholar] [CrossRef]
- Shen, Z.G.; Tian, L.L.; Liu, X. Automotive exhaust thermoelectric generators: Current status, challenges and future prospects. Energy Convers. Manag. 2019, 195, 1138–1173. [Google Scholar] [CrossRef]
- Lin, Y.; Alva, G.; Fang, G. Review on thermal performances and applications of thermal energy storage systems with inorganic phase change materials. Energy 2018, 165, 685–708. [Google Scholar] [CrossRef]
- Wang, F.; Cao, J.; Ling, Z.; Zhang, Z.; Fang, X. Experimental and simulative investigations on a phase change material nano-emulsion-based liquid cooling thermal management system for a lithium-ion battery pack. Energy 2020, 207, 118215. [Google Scholar] [CrossRef]
- Gholamibozanjani, G.; Farid, M. A critical review on the control strategies applied to PCM-enhanced buildings. Energies 2021, 14, 1929. [Google Scholar] [CrossRef]
- Leang, E.; Tittelein, P.; Zalewski, L.; Lassue, S. Impact of a composite trombe wall incorporating phase change materials on the thermal behavior of an individual house with low energy consumption. Energies 2020, 13, 4872. [Google Scholar] [CrossRef]
- Li, Z.; Ma, T.; Zhao, J.; Song, A.; Cheng, Y. Experimental study and performance analysis on solar photovoltaic panel integrated with phase change material. Energy 2019, 178, 471–486. [Google Scholar] [CrossRef]
- Thalib, M.M.; Manokar, A.M.; Essa, F.A.; Vasimalai, N.; Sathyamurthy, R.; Garcia Marquez, F.P. Comparative study of tubular solar stills with phase change material and nano-enhanced phase change material. Energies 2020, 13, 3989. [Google Scholar] [CrossRef]
- Park, S.; Woo, S.; Shon, J.; Lee, K. Experimental study on heat storage system using phase-change material in a diesel engine. Energy 2017, 119, 1108–1118. [Google Scholar] [CrossRef]
- Tao, Y.B.; He, Y.L. A review of phase change material and performance enhancement method for latent heat storage system. Renew. Sustain. Energy Rev. 2018, 93, 245–259. [Google Scholar] [CrossRef]
- Shen, Z.G.; Chen, S.; Liu, X.; Chen, B. A review on thermal management performance enhancement of phase change materials for vehicle lithium-ion batteries. Renew. Sustain. Energy Rev. 2021, 148, 111301. [Google Scholar] [CrossRef]
- Zhang, S.; Feng, D.; Shi, L.; Wang, L.; Jin, Y.; Tian, L.; Li, Z.; Wang, G.; Zhao, L.; Yan, Y. A review of phase change heat transfer in shape-stabilized phase change materials (ss-PCMs) based on porous supports for thermal energy storage. Renew. Sustain. Energy Rev. 2021, 135, 110127. [Google Scholar] [CrossRef]
- Peng, H.; Zhang, D.; Ling, X.; Li, Y.; Wang, Y.; Yu, Q.; She, X.; Li, Y.; Ding, Y. n-Alkanes phase change materials and their microencapsulation for thermal energy storage: A critical review. Energy Fuels 2018, 32, 7262–7293. [Google Scholar] [CrossRef]
- Sardari, P.T.; Mohammed, H.I.; Giddings, D.; Walker, G.S.; Gillott, M.; Grant, D. Numerical study of a multiple-segment metal foam-PCM latent heat storage unit: Effect of porosity, pore density and location of heat source. Energy 2019, 189, 116108. [Google Scholar] [CrossRef]
- Ghalambaz, M.; Zhang, J. Conjugate solid-liquid phase change heat transfer in heat sink filled with phase change material-metal foam. Int. J. Heat Mass Transf. 2020, 146, 118832. [Google Scholar] [CrossRef]
- Gao, Y.; Liu, F.; Wang, J.; Ye, W.; Meng, X. Influence of the copper foam shape on thermal performance of phase-change material. J. Energy Storage 2021, 36, 102416. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Metal foam/PCM melting evolution analysis: Orientation and morphology effects. Appl. Therm. Eng. 2021, 187, 116572. [Google Scholar] [CrossRef]
- Iasiello, M.; Mameli, M.; Filippeschi, S.; Bianco, N. Simulations of paraffine melting inside metal foams at different gravity levels with preliminary experimental validation. J. Phys. Conf. Ser. 2020, 1599, 012008. [Google Scholar] [CrossRef]
- Chen, X.; Xia, X.; Sun, C.; Wang, F.; Liu, R. Performance evaluation of a double-pipe heat exchanger with uniform and graded metal foams. Heat Mass Transf. 2020, 6, 291–302. [Google Scholar] [CrossRef]
- Ghahremannezhad, A.; Xu, H.; Salimpour, M.R.; Wang, P.; Vafai, K. Thermal performance analysis of phase change materials (PCMs) embedded in gradient porous metal foams. Appl. Therm. Eng. 2020, 179, 115731. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.K.; Naso, V. The effects of variable porosity and cell size on the thermal performance of functionally-graded foams. Int. J. Therm. Sci. 2021, 160, 106696. [Google Scholar] [CrossRef]
- Ji, C.; Qin, Z.; Low, Z.; Dubey, S.; Choo, F.H.; Duan, F. Non-uniform heat transfer suppression to enhance PCM melting by angled fins. Appl. Therm. Eng. 2018, 129, 269–279. [Google Scholar] [CrossRef]
- Mehta, D.S.; Vaghela, B.; Rathod, M.K.; Banerjee, J. Heat transfer enhancement using spiral fins in different orientations of latent heat storage unit. Int. J. Therm. Sci. 2021, 169, 107060. [Google Scholar] [CrossRef]
- Cao, X.; Yuan, Y.; Xiang, B.; Sun, L.; Zhang, X. Numerical investigation on optimal number of longitudinal fins in horizontal annular phase change unit at different wall temperatures. Energy Build. 2018, 158, 384–392. [Google Scholar] [CrossRef]
- Huang, M.J.; Eames, P.C.; Norton, B.; Hewitt, N.J. Natural convection in an internally finned phase change material heat sink for the thermal management of photovoltaics. Sol. Energy Mater. Sol. Cells 2011, 95, 1598–1603. [Google Scholar] [CrossRef] [Green Version]
- Acır, A.; Emin Canlı, M. Investigation of fin application effects on melting time in a latent thermal energy storage system with phase change material (PCM). Appl. Therm. Eng. 2018, 144, 1071–1080. [Google Scholar] [CrossRef]
- Kamkari, B.; Shokouhmand, H. Experimental investigation of phase change material melting in rectangular enclosures with horizontal partial fins. Int. J. Heat Mass Transf. 2014, 78, 839–851. [Google Scholar] [CrossRef]
- Kamkari, B.; Groulx, D. Experimental investigation of melting behaviour of phase change material in finned rectangular enclosures under different inclination angles. Exp. Therm. Fluid Sci. 2018, 97, 94–108. [Google Scholar] [CrossRef]
- Joneidi, M.H.; Rahimi, M.; Pakrouh, R.; Bahrampoury, R. Experimental analysis of Transient melting process in a horizontal cavity with different configurations of fins. Renew. Energy 2020, 145, 2451–2462. [Google Scholar] [CrossRef]
- Karami, R.; Kamkari, B. Experimental investigation of the effect of perforated fins on thermal performance enhancement of vertical shell and tube latent heat energy storage systems. Energy Convers. Manag. 2020, 210, 112679. [Google Scholar] [CrossRef]
- Fekadu, B.; Assaye, M. Enhancement of phase change materials melting performance in a rectangular enclosure under different inclination angle of fins. Case Stud. Therm. Eng. 2021, 25, 100968. [Google Scholar] [CrossRef]
- Elmaazouzi, Z.; El Alami, M.; Gounni, A.; Bennouna, E.G. Thermal energy storage with phase change materials: Application on coaxial heat exchanger with fins. Mater. Today Proc. 2020, 27, 3095–3100. [Google Scholar] [CrossRef]
- Abdi, A.; Martin, V.; Chiu, J.N. Numerical investigation of melting in a cavity with vertically oriented fins. Appl. Energy 2019, 235, 1027–1040. [Google Scholar] [CrossRef]
- De Césaro Oliveski, R.; Becker, F.; Rocha, L.A.; Biserni, C.; Eberhardt, G.E. Design of fin structures for phase change material (PCM) melting process in rectangular cavities. J. Energy Storage 2021, 35, 102337. [Google Scholar] [CrossRef]
- Mahood, H.B.; Mahdi, M.S.; Monjezi, A.A.; Khadom, A.A.; Campbell, A.N. Numerical investigation on the effect of fin design on the melting of phase change material in a horizontal shell and tube thermal energy storage. J. Energy Storage 2020, 29, 101331. [Google Scholar] [CrossRef]
- Biwole, P.H.; Groulx, D.; Souayfane, F.; Chiu, T. Influence of fin size and distribution on solid-liquid phase change in a rectangular enclosure. Int. J. Therm. Sci. 2018, 124, 433–446. [Google Scholar] [CrossRef]
- Bouhal, T.; Meghari, Z.; El Rhafiki, T.; Kousksou, T.; Jamil, A.; Ghoulam, E.B. Parametric CFD analysis and impact of PCM intrinsic parameters on melting process inside enclosure integrating fins: Solar building applications. J. Build. Eng. 2018, 20, 634–646. [Google Scholar] [CrossRef]
- ul Hasnain, F.; Irfan, M.; Khan, M.M.; Khan, L.A.; Ahmed, H.F. Melting performance enhancement of a phase change material using branched fins and nanoparticles for energy storage applications. J. Energy Storage 2021, 38, 102513. [Google Scholar] [CrossRef]
- Ji, C.; Qin, Z.; Dubey, S.; Choo, F.H.; Duan, F. Simulation on PCM melting enhancement with double-fin length arrangements in a rectangular enclosure induced by natural convection. Int. J. Heat Mass Transf. 2018, 127, 255–265. [Google Scholar] [CrossRef]
- Zhang, S.; Pu, L.; Xu, L.; Liu, R.; Li, Y. Melting performance analysis of phase change materials in different finned thermal energy storage. Appl. Therm. Eng. 2020, 176, 115425. [Google Scholar] [CrossRef]
- Liu, X.; Huang, Y.; Zhang, X.; Zhang, C.; Zhou, B. Investigation on charging enhancement of a latent thermal energy storage device with uneven tree-like fins. Appl. Therm. Eng. 2020, 179, 115749. [Google Scholar] [CrossRef]
- Shokouhmand, H.; Kamkari, B. Experimental investigation on melting heat transfer characteristics of lauric acid in a rectangular thermal storage unit. Exp. Therm. Fluid Sci. 2013, 50, 201–212. [Google Scholar] [CrossRef]
- Kok, B. Examining effects of special heat transfer fins designed for the melting process of PCM and Nano-PCM. Appl. Therm. Eng. 2020, 170, 114989. [Google Scholar] [CrossRef]
- Tian, L.L.; Liu, X.; Chen, S.; Shen, Z.G. Effect of fin material on PCM melting in a rectangular enclosure. Appl. Therm. Eng. 2020, 167, 114764. [Google Scholar] [CrossRef]
- Kamkari, B.; Shokouhmand, H.; Bruno, F. Experimental investigation of the effect of inclination angle on convection-driven melting of phase change material in a rectangular enclosure. Int. J. Heat Mass Transf. 2014, 72, 186–200. [Google Scholar] [CrossRef]
- Joneidi, M.H.; Hosseini, M.J.; Ranjbar, A.A.; Bahrampoury, R. Experimental investigation of phase change in a cavity for varying heat flux and inclination angles. Exp. Therm. Fluid Sci. 2017, 88, 594–607. [Google Scholar] [CrossRef]
- Diani, A.; Campanale, M. Transient melting of paraffin waxes embedded in aluminum foams: Experimental results and modeling. Int. J. Therm. Sci. 2019, 144, 119–128. [Google Scholar] [CrossRef]
| Property | Symbol | Value |
|---|---|---|
| Melting temperature | Tl (°C) | 48.2 |
| Solidification temperature | Ts (°C) | 43.5 |
| Latent heat | Lh (kJ/kg) | 187.21 |
| Specific heat capacity of solid | cp,s (kJ/(kg·K)) | 2.18 |
| Specific heat capacity of liquid | cp,l (kJ/(kg·K)) | 2.39 |
| Density of solid | ρs (kg/m3) | 940 |
| Density of liquid | ρl (kg/m3) | 885 |
| Thermal conductivity of solid | λs (W/(m·K)) | 0.16 |
| Thermal conductivity of liquid | λl (W/(m·K)) | 0.14 |
| Thermal expansion coefficient | β (1/K) | 0.0008 |
| Property | Symbol | Value |
|---|---|---|
| Specific heat capacity | cp,fin (kJ/(kg·K)) | 0.871 |
| Thermal conductivity | λfin (W/(m·K)) | 130 |
| Density | Ρfin (kg/m3) | 2179 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, B.; Tian, L.-L.; Yu, Q.-H.; Liu, X.; Shen, Z.-G. Numerical Analysis of Melting Process in a Rectangular Enclosure with Different Fin Locations. Energies 2021, 14, 4091. https://doi.org/10.3390/en14144091
Huang B, Tian L-L, Yu Q-H, Liu X, Shen Z-G. Numerical Analysis of Melting Process in a Rectangular Enclosure with Different Fin Locations. Energies. 2021; 14(14):4091. https://doi.org/10.3390/en14144091
Chicago/Turabian StyleHuang, Bin, Lin-Li Tian, Qing-Hua Yu, Xun Liu, and Zu-Guo Shen. 2021. "Numerical Analysis of Melting Process in a Rectangular Enclosure with Different Fin Locations" Energies 14, no. 14: 4091. https://doi.org/10.3390/en14144091
APA StyleHuang, B., Tian, L.-L., Yu, Q.-H., Liu, X., & Shen, Z.-G. (2021). Numerical Analysis of Melting Process in a Rectangular Enclosure with Different Fin Locations. Energies, 14(14), 4091. https://doi.org/10.3390/en14144091







