DC-Link Current Harmonic Mitigation via Phase-Shifting of Carrier Waves in Paralleled Inverter Systems

Abstract

DC-connected parallel inverter systems are gaining popularity in industrial applications. However, such parallel systems generate excess current ripple (harmonics) at the DC-link due to harmonic interactions between the inverters in addition to the harmonics from the PWM switching. These DC-link harmonics cause the failure of fragile components such as DC-link capacitors. This paper proposes an interleaving scheme to minimize the current harmonics induced in the DC-link of such a system. First, the optimal phase-shift angle for the carrier signal is investigated using the analytical equations, which provides maximum capacitor current ripple cancellation (i.e., at the main switching frequency harmonic component). These optimally phase-shifted switching cycles lead to variations of the output current ripples, which, when summed together at the DC-link, result in the cancellations of the DC-link current ripples. The results show that when the carrier waves of the two inverters are phase-shifted by a 90° angle, the maximum high-frequency harmonic ripple cancellation occurs, which reduces the overall root-mean-square (RMS) value of the DC-capacitor current by almost 50%. The outcome of this proposed solution is a cost-effective DC-harmonics mitigating strategy for the industrial designers to practically configure multi-inverter systems, even when most of the drives are not operating at rated power levels. The experimental and simulation results presented in this paper verify the effectiveness of the proposed carrier-based phase-shifting scheme for two different configurations of common DC connected multi-converter systems.

1. Introduction

To improve the power delivering capacity, and reliability of power electronic converters, many researchers have directed attention towards the parallel connection of these converter units. Indeed, the parallel connection of converters have received increased attention in the past few years, due to several reasons; increased reliability through reduced number of conversion stages, modularity, ease of maintenance through the operation of identical units, scalable designs, and reduced size of the overall system [1]. More significantly, such systems enable the integration of renewable energy sources and storage with the bulk electric grid [2]. Analytical, and experimental verification of a scenario, in which multiple generators are connected in parallel, and how an interleaving scheme reduced the harmonics at the common point of connection, is discussed in [3]. It explains how the parallel connection of multiple lower power units is used as a solution to design high power converters with better flexibility and higher reliability. However, one drawback of this kind of parallel-connected system [2,3,4] is that, due to the common AC point of connection, the integration of renewable resources becomes difficult. Additionally, in the multi-converter systems explained in [1,5,6,7], each inverter has its own individual rectifier system and shares the common DC-link, an example of which is shown in Figure 1a. Hence the total number of rectifiers needed in the whole system increases, eventually increasing the overall size and reducing reliability.

Even though in industrial applications, DC-connected parallel inverter systems are gaining popularity, such parallel systems generate excess current ripple (harmonics) at the DC-link due to the harmonic interactions between the inverters, in addition to the harmonics from the pulse width modulation switching. This harmonic interaction at the DC-link causes the failure of fragile components such as DC-link capacitors [1,4]. This is of significant importance as the current ripple causes a decrease in the capacitor lifetime due to an increase in the internal temperature. The power loss of the capacitor, which is a function of the current harmonic spectrum and its Equivalent Series Resistance (ESR), also increases as the capacitor current increases [8]. Several studies show that 30% of the total failure root causes in the power electronic systems are due to capacitor failures [9], and hence, they are considered the most fragile components in a power electronic system [9,10,11,12]. In order to extend the lifetime of the DC-link capacitor, two possible solutions are considered. One practical solution in the market is to use higher capacitance and a higher rated current capacitor at the DC-link, but the total volume, weight and cost will significantly increase. Another way is to actively reduce the current stresses of the DC-link capacitor. This method is considered in this paper for a parallel-connected inverter system, which is more cost efficient and convenient to use due to no hardware change being needed. Because in a parallel system the DC-link current is generated by a summation of the current harmonics from the connected converter, the phase-shifted switching cycles lead to variations of the current ripple [5]. Thus, using an interleaving (i.e., phase-shifting) of the PWM carrier waves of the inverters at an optimal angle is a possible solution to effectively reduce the total DC-current ripple at the DC-link.

A plethora of research has been conducted on interleaving the carrier waves of the parallel-connected PWM inverters to reduce the DC-link current harmonics [1,2,3,4,5,7,13]. Lowering the DC-link harmonics reduces the power losses within the capacitor [14]. In a parallel-connected system, the phase-shifted switching cycles of the carrier waves can effectively reduce the current ripple; as a result [7], the size and weight of passive components, such as the DC-link capacitors and EMI-filters, can be reduced. A detailed study of a harmonic reduction technique using synchronized phase-shifted PWM voltage source inverter (VSI) units having an individual DC-source has been provided in [1]. Alternatively, ref. [5] presents the effect of an optimal phase-shift angle on reducing DC-current ripples under unequal DC-link voltage scenarios in two parallel three-phase grid-connected voltage-source inverters (VSIs). The effect of the size of the DC-link components and the grid configuration in three-phase multi-drive systems, similar to the topology shown in Figure 1a, on the resonant frequencies, have been studied in [6]. In [7], analytical modeling of paralleled and interleaved 3-level neutral point clamped inverters using space vector modulation is discussed. It explains how interleaving helps to reduce both AC and DC-side harmonics and reduces the EMI harmonics in parallel-connected inverter systems. To minimise the DC-capacitor size, a coordinated PCC voltage harmonics mitigation strategy is discussed in [15] for parallel inverters by properly shaping inverter output impedance. Similarly, a harmonic damping approach using a point of common-coupling (PCC) voltage control for multi-parallel inverters is discussed in [16]. Even though these techniques seem to be promising solutions to mitigate DC-link harmonics, complexity has become the main obstacle for these harmonic elimination approaches in multidrive systems.

As mentioned above, the existing methods for multi-converter systems, to the best of the authors’ knowledge, have the following two limitations: Firstly, most of them consider common AC-grid connection for the parallel inverters, which limits the integration with the DC-grid system, and renewable energy resources. Secondly, there is no DC-link current harmonic elimination method proposed for multiple drive systems with a common DC-link in any of the pieces of literature so far. To address these research gaps, this work presents a carrier phase-shifting strategy for two different configurations of common DC-connected multi-converter systems. The two key contributions of this paper are:

• A family of common DC-link structures is proposed, where one topology is a multi-converter system with an individual DC-bank (shown in Figure 1b), and another topology is a multi-converter system with a common DC-bank (shown in Figure 1c). In a traditional system, as seen in Figure 1a, each inverter has its own individual rectifier system and shares the common AC link. Compared to this kind of system, the proposed systems in Figure 1b,c have the following advantages. In the proposed multidrive system, the overall system cost would be less: in the traditional system each inverter has its own rectifier, and the cost for two rectifiers has to be considered, which will increase the overall cost. However, in the proposed systems, due to the implementation of a centralized rectifier, the cost would be less. Secondly, due to the reduced number of power electronic components (rectifiers) in the proposed system, the reliability will be higher. Moreover, a centralised rectifier provides the flexibility for plug-and-play of the number of inverters connected to the DC-grid in parallel-connected systems. Notably, this kind of operation allows for the easy integration of DC sources at the common DC link in a system, compared to the conventional parallel-connected system.
• Besides that, this paper proposes a new modulation method to reduce the DC-link capacitor requirement via phase-shifting of the carrier waves, which is a value-added technology. It does not need to change any hardware in the system, while the DC-link ripple and capacitance can be reduced, which benefits the cost, volume and weight of the system. The optimally phase-shifted switching cycles lead to variations of the output current ripples, which, when summed together in the common DC, results in the minimization of ripples at the DC-link current. Thereby, the switching frequency harmonics reduce, which reduces the overall DC-capacitor RMS current; hence, reducing the overall stress (electro-thermal stress and hot-spot temperature) at the DC-link, leading to an improved lifetime of the DC-link capacitor.

This paper is structured as follows. The overall system description is presented in Section 2. Section 3 discusses the harmonic analysis of the capacitor current based on the conventional system, and Section 4 explains the proposed system. The lifetime estimation is discussed in Section 5. The effectiveness of the developed analysis is demonstrated by the results and discussions in Section 6. Finally, conclusions are drawn in Section 7.

2. Proposed System Description

In this study, a diode rectifier with a boost power factor corrector (PFC) and a DC-filter (consisting of a DC-choke and a large electrolytic DC-link capacitor) is implemented due to its simplicity, cost-effectiveness, and reliability advantages [6]. Aluminium electrolytic capacitors (El-caps) are used as DC-link capacitors, due to their advantage of providing a high capacitance per unit volume at low costs compared to other types of capacitors [17]. The boost PFC employed improves the power factor, as well as facilitates power supply hold-up, which ensures that the system can maintain the DC voltage until the backup power supply is connected, in case of a power supply disruption [18,19].

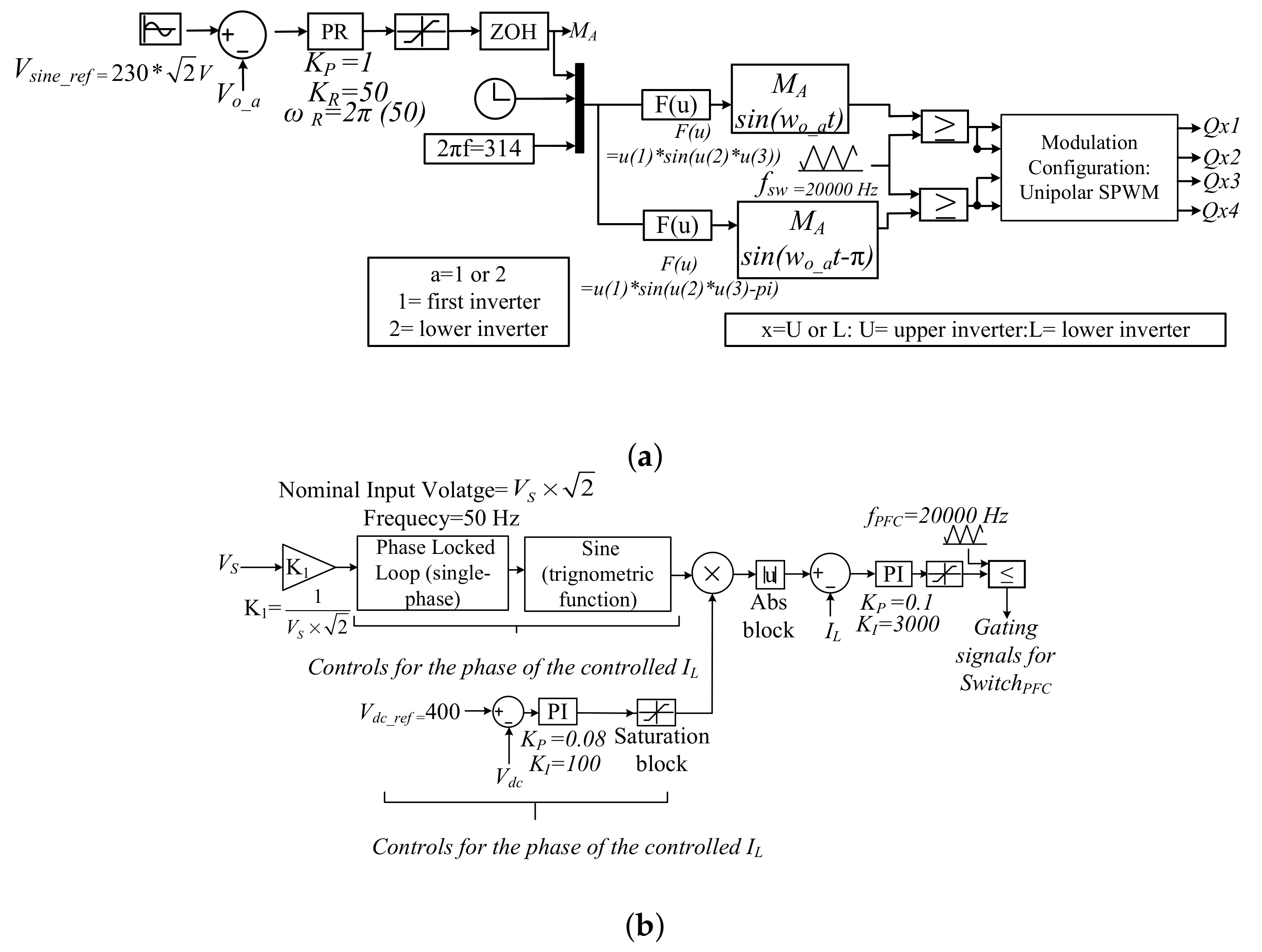
The proposed topologies in this paper, shown in Figure 2 (hereby referred to as the multi-converter system with individual DC-bank) and Figure 3 (hereby referred to as the multi-converter system with common DC-bank), have a centralized rectifier and a common DC point to connect the parallel inverters. The two inverters in the proposed system are in the same phase and have the same output waveforms, as they are to be used for a single application process, for example, in a sugar production plant, where multiple motors are operating at the same speed, frequency and power, or for applications such as the air conditioning and cooling systems in a dairy factory. More importantly, a DC-link current harmonics mitigation strategy is introduced via phase-shifting of the inverter carrier waves in these two topologies. Using a centralized rectifier eliminates the need for each inverter to have its rectifier, as shown in Figure 1a. For the proposed multi-converter system with individual DC-banks, each of the parallel-connected inverters has its individual capacitor bank to limit the DC-link voltage fluctuation. This kind of connection provides more flexibility to the industrial designers to plug-and-play with the number of inverters connected to the DC-grid in parallel-connected systems. On the other hand, the proposed multi-converter system with a common DC-bank has a common capacitor bank consisting of individual capacitors, which are connected in parallel to ensure the equal distribution of the ripple current ($I_{cap}$) flowing through the the DC-link capacitor bank ($C_{DC-bank}$). The total ripple current flowing through ($C_{DC-bank}$) is denoted by ($I_{capbank}$), and through a single capacitor by ($I_{cap}$).

The four switches $Q_{x1}$, $Q_{x2}$, $Q_{x3}$, $Q_{x4}$ of the VSI units, shown in both Figure 2 and Figure 3, are controlled using the unipolar sinusoidal PWM (SPWM) technique, explained in detail in [20,21]. The specifications of the inverter system and output filter (designed according to [21]) are given in

Table 1. Specifications of the output load.

Parameter	Symbol	Value
Rated power (kW)	$P_o$	2.5
Load ($\Omega$)	$R_L$	20
Rated RMS load voltage (V)	$V_{sine-ref}$	230
Load frequency (Hz)	$f_o$	50
Rated DC-link voltage (V)	$V_{dc-ref}$	400
Switching frequency (kHz)	$f_{sw}$	20
Modulation amplitude index	$M_A$	0.8

and

Table 2. Specifications of the inverter output filter.

Parameter	Symbol	Value
Inductor filter ripple current limit	$I_{f\_ripple}$	20%
Inductor (H)	$L_f$	2$\times {10}^{-3}$
Filter cutoff frequency (kHz)	$f_{cutoff}$ ( $f_{cutoff}$<$f_{sw}$/10)	2
Filter capacitor (F)	$C_f$	6$\times {10}^{-6}$

. Both the topologies (in Figure 2 and Figure 3) have the same parameters and loading conditions. The rated output voltage of 230 V (RMS value) for each inverter unit is maintained by its own specific Proportional–Resonant (PR) controller, which is designed according to [22,23]. The control algorithm for the inverter is shown in Figure 4a, and for the boost, PFC is shown in Figure 4b. The parameters for the controllers have the same value, as both VSI units are synchronized and controlled using unipolar SPWM to obtain the same $V_{o-rated}$. The parameters for the boost PFC are shown in

Table 3. Specifications of the boost PFC.

Parameter	Symbol	Value
Power rating (kW)	$P_{PFC}$	2.5
RMS AC−input voltage (V)	$V_S$	230
RMS AC−input current (A)	$I_S$	10.58
PFC switching frequency (kHz)	$f_{PFC}$	20
PFC inductor current ripple	$I_{PFC\_ripple}$	30%
PFC inductor current maximum (A)	$I_{PFC}$	16
PFC inductor minimum (H)	$L_{PFC}$	$3\times {10}^{-3}$
Ripple output peak to peak (p−p) voltage (V)	$V_{PFC\_p-p}$	20
Hold-up time (s)	$t_{hold}$($=1$/$f_o$)	2$\times {10}^{-3}$
PFC capacitor minimum (F)	$C_{PFC}$	3.3$\times {10}^{-3}$

, designed according to [24,25]. The data for the DC-link capacitor are from the data sheet in [26] and are shown in

Table 4. Specifications of the DC-capacitor (KEMET−AlS8(1)(2)392NF500).

Parameter	Symbol	Value
Single capacitance $\left(\mathsf{\mu }F\right)$	$C_{dc}$	3900
Equivalent series resistance $(\mathrm{m}\Omega )$	ESR	61 (100 Hz), 46 (10 kHz)
Thermal resistance (${}^{\circ }$C/W)	$R_{th}$	3.8
Rated lifetime (hours)	$L_o$	9000 (at $T_{rated}$ & $I_{rated}$)
Rated upper category temperature (${}^{\circ }$C)	$T_{rated}$	105
Rated ripple current (A)	$I_{rated}$	12.2 (100 Hz), 19.0 (10 kHz)
Rated voltage (V)	$V_{rated}$	500
Operating temperature (${}^{\circ }$C)	$T_a$	45

.

3. Conventional Method without Any Phase-Shift

In this section, the DC-current harmonics generated by the PWM switching of each of the parallel-connected inverters are analyzed. Let us take the system with two parallel inverters shown in Figure 3 for analysis. For simplicity, it is assumed that both inverters have the same loading conditions, hence, draw the same output current. Conventionally, the two output current ripples and carrier waves (Triangle Wave 1 for upper inverter and Triangle Wave 2 for lower inverter) appear as seen in Figure 5. These output current ripples sum up to produce higher ripples in the DC-current. These ripples (harmonics) degrade the efficiency of the whole system as well as decrease the lifetime of the DC-link capacitors [3]. As the number of inverters increases, more DC-current ripples would be generated by a summation of the current harmonics from the connected converters. To solve the aforementioned issue, it is important to reduce the DC-current harmonics to improve the reliability and lifetime of the DC-link capacitors at an optimized cost.

4. Proposed Method with an Optimal Carrier Phase-Shift

For the multi-converter systems shown in Figure 2 and Figure 3, one of the effective methods to reduce the DC-current ripple is interleaving the carrier signals of the parallel converters. Both the inverters connected to the common DC-link are considered to be in synchronisation with each other, and have the same operating conditions mentioned in Table 1. To apply the proposed DC-link harmonic mitigation method, it is necessary to first find the optimal phase-shift angle (${\theta }_{fsw\_optimal}$) for the carrier signal, which provides maximum capacitor current ripple cancellation (i.e., at the main switching frequency harmonic component which appears at $f_{sw\_harmonic}$= 40 kHz). The optimally phase-shifted switching cycles lead to variations of the output current ripples, which when summed together result in the minimization of ripples at the DC-link current. This is analytically explained in (1)–(9), provided below, for inverters that have unipolar PWM [27]. In this paper, the phase shift is applied to the lower inverter carrier signal, therefore the phase angle of the upper inverter carrier signal is ${\theta }_{fsw1}=0^{\circ }$, whereas the phase angle of lower inverter carrier signal is ${\theta }_{fsw2}$ = ${\theta }_{fsw\_optimal}$.

$$V_{o\_1}=M_A{V}_{dc}sin({\omega }_{o1}t+{\theta }_{o1})+\frac{4V_{dc}}{\pi }\sum _{m=2,4,6...}^{\infty }\sum _{n=\pm 1,\pm 3,\pm 5...}^{\pm \infty }\frac{J_n(m{M}_A\pi /2)}{m}cos\left(\frac{m\pi }{2}\right)sin(n({\omega }_{o1}t+{\theta }_{o1})+m({\omega }_{c1}t+{\theta }_{fsw1}))$$

(1)

$$I_{o\_1}=I_{o\_peak\_1}sin({\omega }_{o1}t+{\theta }_{o1})$$

(2)

$$I_{dc\_1}=I_{o\_1}\times \underset{SwitchingFunction}{\underbrace{\left(\frac{V_{o\_1}}{V_{dc}}\right)}}$$

(3)

$$I_{capbank\_1}=I_{dc\_1}-I_{dc\_avg\_1}$$

(4)

$$V_{o\_2}=M_A{V}_{dc}sin({\omega }_{o2}t+{\theta }_{o2})+\frac{4V_{dc}}{\pi }\sum _{m=2,4,6...}^{\infty }\sum _{n=\pm 1,\pm 3,\pm 5...}^{\pm \infty }\frac{J_n(m{M}_A\pi /2)}{m}cos\left(\frac{m\pi }{2}\right)sin(n({\omega }_{o2}t+{\theta }_{o2})+m({\omega }_{c2}t+{\theta }_{fsw2}))$$

(5)

$$I_{o\_2}=I_{o\_peak\_2}sin({\omega }_{o2}t+{\theta }_{o2})$$

(6)

$$I_{dc\_2}=I_{o\_2}\times \underset{SwitchingFunction}{\underbrace{\left(\frac{V_{o\_2}}{V_{dc}}\right)}}$$

(7)

$$I_{capbank\_2}=I_{dc\_2}-I_{dc\_avg\_2}$$

(8)

$$I_{capbank\_2}=I_{capbank\_1}+I_{capbank\_2}.$$

(9)

In the above equations, $V_{o\_1},V_{o\_2},I_{o\_1},I_{o\_2},$ present upper and lower inverter output voltages and output currents. The peak value of the output currents of upper and lower inverters is $I_{o\_peak\_1},I_{o\_pea{k}_2}.$ The DC-current source and the average value of its upper and lower inverters are represented by $I_{dc\_1},I_{dc\_2},I_{dc\_avg\_1},I_{dc\_avg\_2}.$ The capacitor bank current for upper and lower inverters is denoted by $I_{capbank\_1},I_{capbank\_2}.$ Finally, the fundamental frequency and switching frequency of the upper inverter are symbolised by ${\omega }_{o1},{\omega }_{c1},$ and that of the lower inverter is designated by ${\omega }_{o2},{\omega }_{c2}.$ (1)–(4) describe the upper inverter, while (5)–(8) is for the lower inverter. (3) and (7) are derived based of the power balance equation of the inverter, which states that the input power on the DC-side $(P_{dc}=V_{dc}\times I_{dc})$ of the converter relates to the output apparent power on the AC-side $(P_{ac}=V_o\times I_o)$.

The method used in this paper is as follows: firstly, various phase-shift angles are applied for the carrier signal of the lower inverter (${\theta }_{fsw\_2}$), and the multi-converter system with individual DC-banks (shown in Figure 2) is simulated using PLECS, under the rated operating conditions mentioned in Table 1. Then, the harmonic spectrum (Figure 6b) and the ripples in the time domain waveform (Figure 7b) of the total capacitor current are studied to find the phase-shift angle at which maximum high-frequency harmonic ripple cancellation occurs, which produces the minimum of the overall RMS value of the DC-capacitor current. This will be the optimal ${\theta }_{fsw\_optimal}.$ The same method is applied to the multi-converter system with a common DC-bank shown in Figure 3 to obtain its optimal carrier phase-shift angle.

The switching frequency harmonic component $f_{sw\_harmonic}$ = 40 kHz is shown for various phase-shift angles (${\theta }_{fsw\_2}$) applied to the carrier frequency of the lower inverter for the multi-converter system with a common DC-bank in Figure 6a and the multi-converter system with individual DC-banks in Figure 6b. At ${\theta }_{fsw\_2}=0^{\circ }$ (violet colour bar), there is no phase-shift applied and this case scenario is taken for the system using the conventional method. Among the various phase-shift angles analyzed, it can be seen that the harmonic ripple ($f_{sw\_harmonic}$ = 40 kHz ) is at a minimum when ${\theta }_{fsw\_2}={90}^{\circ }$, denoted by the red color bar in Figure 6a, and the green color in Figure 6b. Thereby, it can be observed from Figure 6 that both the topologies (shown in Figure 2 and Figure 3) have a minimum main switching frequency harmonic component ($f_{sw\_harmonic}$ = 40 kHz) and a maximum DC-capacitor current ripple cancellation at ${90}^{\circ }.$ Furthermore, at a ${90}^{\circ }$ carrier phase-shift angle, there is maximum ripple cancellation in the DC-capacitor bank current as illustrated in Figure 7. It can be understood that the capacitor current ripple is almost half the value (red dotted line) when compared to the scenario in which there is no phase-shift applied (violet line) in both the multi-converter system with individual DC-banks and with a common DC-bank. Accordingly, from Figure 6 and Figure 7, it can be concluded that the optimal phase angle is found to be when the two carrier signals for the two inverters are phase-shifted by ${90}^{\circ }.$

The optimally phase-shifted switching cycles lead to variations of the output current ripples, which when summed together result in the minimization of ripples at the DC-link current as shown in Figure 8e. The reduction of the DC-capacitor current ripples means that the switching frequency harmonics reduce (since a unipolar SPWM is used, for $f_{sw}$ = 20 kHz, the main switching frequency harmonic component appears at $f_{sw\_harmonic}$ = 40 kHz). Consequently, the overall DC-capacitor RMS current decreases, thus reducing the overall stress (electro-thermal stress and hot-spot temperature) at the DC-link. Hence, the proposed scheme shown in Figure 8 (in red line) helps to reduce harmonics, and thereby the total harmonic distortion (THD) in the DC-capacitor current. Without any phase-shift, the THD =5.8% for the capacitor current and, after applying the proposed optimal phase-shifting, the THD reduces to 2.7%, calculated as in [28].

5. Lifetime Estimation of DC-Link Capacitor

Reducing the harmonics ripples in the DC-capacitor current helps to improve the lifetime $L_x$ of the DC-capacitor as the overall electrical and thermal stress in the capacitor significantly decreases [17]. The lifetime prediction model used in this paper is shown in Section 5 and explained in detail (including the equivalent circuit model of capacitor) in [28].

$$L_x=L_o\times \underset{K_V}{\underbrace{{\left(\frac{V}{V_{rated}}\right)}^{-p}}}\times \underset{K_T}{\underbrace{2^{\frac{(T_{rated}-T_h)}{10}}}}.$$

(10)

$L_o$ is the rated lifetime of the capacitor at rated voltage $V_{rated}$, and rated upper category temperature $T_{rated}$ (given in Table 4). $K_T$ is the temperature factor and $K_V$ is the voltage ripple factor. V is the actual operating voltage. The value of the exponent p is between 3 and 5 for El-caps [17]. The hot-spot temperature $T_h$ of the DC-capacitor, estimated by (11), depends upon the operating temperature and $P_{loss}$ on the power loss of the capacitor (which is a function of ripple current and ESR). Considering the heat dissipation from the diode bridge, DC-link filter, and inverter, the operating temperature $T_a$ is defined as 40–60 ${}^{\circ }$C instead of room temperature [14]. $P_{loss}$ can be estimated by (12).

$$T_h=T_a+(P_{loss}\times R_{th})$$

(11)

$$P_{loss}=\sum _{i=1}^n{\left(I_{rms\left(f_i\right)}\right)}^2\times ESR\left(f_i\right),$$

(12)

where $I_{rms\left(f_i\right)}$ is the RMS value of the harmonic ripple current at frequency $f_i$, obtained from the harmonic spectrum of the capacitor current. $ESR\left(f_i\right)$ is the ESR at the $i^{th}$ frequency $f_i$. $R_{th}$ is the thermal resistance of the capacitor between the hot spot and the ambient temperature. The rated values for the chosen capacitor (KEMET AlS8(1)(2)392NF500) in this paper are given in Table 4.

6. Results and Discussion

In this section, the effectiveness of the proposed harmonic mitigation for both the multi-converter system with a common DC-bank and the multi-converter system with individual DC-banks is analyzed through experimental and simulation results.

As shown in Figure 2 and Figure 3, the multi-converter system with a common DC-bank differs from the multi-converter system with individual DC-banks mainly in terms of the DC-link capacitor bank configuration. In the common DC-bank topology (shown in Figure 3), the current harmonics from both inverters flow through the common capacitor bank, consisting of two parallel capacitors. This means that the harmonics from all the parallel-connected inverters flow into this common capacitor bank. Hence, there is the constraint of having a large DC-link capacitor to absorb the harmonics at DC-link, when numerous inverters are connected in parallel in the multi-converter system with a common DC-bank. Alternatively, in the multi-converter system with individual DC-banks, each inverter has its own DC-bus, meaning that harmonics from each inverter are absorbed by its own individual DC-capacitor bus. This topology has the advantage that a greater number of inverters can be connected to a common DC-bus without the need to increase the bulkiness of the DC-bank. Therefore, due to the aforementioned reasons, when a greater number of inverters need to be connected in parallel to the DC grid with a centralized rectifier, the multi-converter system with individual DC-banks (Figure 2) is preferred.

6.1. Experimental Verification (With Scaled-Down Parameters)

In order to validate the proposed optimal carrier phase-shift angle for the topologies, referring to Figure 2 and Figure 3, a downscale experimental platform is built, where resistors are used as the loads as shown in Figure 9. The scaled-down main circuit parameters are listed in

Table 5. Experimental system specifications.

Module	Part Number/Parameter	Symbol
SEMITEACH IGBT module stack	SEMIKRON 08753450	-
AC-filter inductors	4mH, 20A rated current	$L_{f1}$,$L_{f2}$
AC-filter capacitors	1$\mathsf{\mu }$F, 1600V, 19.1A @ 40${}^{\circ }$C	$C_{f1}$,$C_{f2}$
Voltage comparators	LM393	-
PLECS controller box	RT-box 2	-
Resistor Banks	10 $\Omega$–80 $\Omega$	$R_1$,$R_2$

. Compared to the simulation result, the operating conditions are scaled down to enable lab-scale experimentation. For both the inverters, the operating conditions are kept the same throughout the experiment, as explained in

Table 6. Operating conditions (scaled-down) for the experimental analysis.

Parameter	Symbol	Value
Rated power of each inverter (W)	$P_o$	50
Load ($\Omega$)	$R_L$	20
Rated RMS load voltage (V)	$V_{sine-ref}$	40
Load frequency (Hz)	$f_o$	50
Rated DC-link voltage (V)	$V_{dc-ref}$	50
Switching frequency (kHz)	$f_{sw}$	5
Modulation amplitude index	$M_A$	0.8

. Both the SEMIKRON power stacks are connected to a common DC-bus, and the PWM signals for each of these are controlled by the PLECS-RT box 2. Since RT-box PWM signals have only 5V, LM393 comparators are used to shift this voltage level to 15V (the minimum requirement for the gate drivers to operate). A constant DC-voltage source of 50V is supplied at the common DC-point for both the power stacks by the DC-power supplier.

One of the ways to validate the effectiveness of the proposed harmonic mitigation strategy is to observe the switching frequency harmonics (i.e., at 10 kHz) for various carrier phase-shift angles in the $I_{dc}$ for the multi-converter system with a common DC-bank, and $I_{dc\_1}$ for the multi-converter system with individual DC-banks. It is difficult to obtain these two wave-forms directly. Due to the presence of a large DC-link capacitor in the power stack, only low harmonics of $I_{dc}$ and $I_{dc\_1}$ can be measured, as all higher harmonics are absorbed by the DC-capacitor. So, the CSV data for $I_{dc}$ and the capacitor current $I_{capbank}$ were obtained from the oscilloscope measurements for the multi-converter system with a common DC-bank, and the harmonic spectrum was obtained in MATLAB. Similarly, for the multi-converter system with individual DC-banks, the CSV data for $I_{dc\_1}$ and the capacitor current $I_{capbank\_1}$ were obtained from the oscilloscope measurements, and the harmonic spectrum was obtained in MATLAB. The obtained results are shown in Figure 10a,b, respectively. It shows that the switching frequency harmonics (at 10 kHz) are at a minimum when a carrier phase-shift of ${\theta }_{fsw\_2}={90}^{\circ }$ is applied for the proposed two multi-converter systems, making it the optimal carrier phase-shift angle. These results are, hence, in agreement with the proposed DC-link harmonic mitigation method explained in Section 4.

The output voltage and current waveforms at ${\theta }_{fsw\_2}=0^{\circ },$ and ${\theta }_{fsw\_2}={90}^{\circ },$ for the multi-converter system with a common DC-bank captured in the oscilloscopes, are shown in Figure 11. Since the output voltage and current waveforms are not affected by the phase-shift in carrier waves, they overlap each other at ${\theta }_{fsw\_2}=0^{\circ },$ and ${\theta }_{fsw\_2}={90}^{\circ }.$

6.2. DC-Harmonic Analysis Using Optimal Phase-Shift Angle for the Carrier Signal

To illustrate the DC-link harmonic mitigation method, the optimal phase-shift angle for the carrier signal (i.e., ${\theta }_{fsw\_optimal}={90}^{\circ }$) is applied to both the topologies shown in Figure 2 and Figure 3. Each of the two inverters (of two topologies) is simulated (in PLECS) under a rated output power of 2.5 kW and have the same the rated operating conditions given in Table 1. The effect of applying interleaving to the carrier signals of the parallel-connected inverters is illustrated in Figure 12.

It can be seen that adopting the proposed method helps to reduce the dominant switching harmonic components ($f_{sw\_harmonic}$ = 40 kHz, 80 kHz, 120 kHz) in the DC-capacitor bank current, and the overall RMS capacitor bank current. As a result, the electro-thermal stress for each capacitor reduces, thereby increasing its life expectancy calculated using (5)–(12), as shown in

Table 7. Power-loss, and life-expectancy of the DC-link capacitor calculated using the experimental results.

Topology	${\mathit{P}}_{\mathit{loss}}\mathbf{\left(}\mathit{Watts}\mathbf{\right)}$	${\mathit{L}}_{\mathit{x}}\mathbf{\left(}\mathit{Hours}\mathbf{\right)}$	${\mathit{P}}_{\mathit{loss}}\mathbf{\left(}\mathit{Watts}\mathbf{\right)}$	${\mathit{L}}_{\mathit{x}}\mathbf{\left(}\mathit{Hours}\mathbf{\right)}$
	${\mathbf{\theta }}_{\mathit{fsw}\mathbf{\_}\mathbf{2}}\mathbf{=}{\mathbf{0}}^{\mathbf{\circ }}$	${\mathbf{\theta }}_{\mathit{fsw}\mathbf{\_}\mathbf{2}}\mathbf{=}{\mathbf{0}}^{\mathbf{\circ }}$	${\mathbf{\theta }}_{\mathit{fsw}\mathbf{\_}\mathbf{2}}\mathbf{=}{\mathbf{90}}^{\mathbf{\circ }}$	${\mathbf{\theta }}_{\mathit{fsw}\mathbf{\_}\mathbf{2}}\mathbf{=}{\mathbf{90}}^{\mathbf{\circ }}$
The multi-converter system with common DC-bank	1.27	1.35 × ${10}^5$	0.41	1.70 × ${10}^5$
The multi-converter system with individual DC-bank	0.33	1.73 × ${10}^5$	0.12	1.85 × ${10}^5$

. From the industry point of view, it is important to have a lower DC-capacitor bank current as a lesser number of capacitors will be needed, which helps to lower the cost of the overall system.

However, it is necessary to take into consideration the fact that, from a practical application standpoint, it is almost impossible to achieve the loading of two drives according to operation at rated conditions [29]. So, to further demonstrate the effectiveness of the proposed method under such scenarios, for the topologies shown in Figure 2 and Figure 3, the output load of the lower inverter is varied between 0 W and 2500 W (rated power), while the upper inverter is at a rated output power of 2500 W. In each case, the first ($f_{sw\_harmonic}$ = 40 kHz) and second switching frequency harmonic component ($f_{sw\_harmonic}$ = 80 kHz) are observed when ${\theta }_{fsw\_2}=0^{\circ }$ (conventional method) and ${\theta }_{fsw\_2}={90}^{\circ }$ (proposed method) as shown in Figure 13.

It is demonstrated in by Figure 13a–d that, as the output power of the lower inverter ($P_{o2}$) varies from 500 W to 2500 W, the first and switching frequency harmonic component amplitude reduces, due to the impact of the intervention of the carrier waves. The only time when there is no harmonic ripple cancellation is when $P_{o2}=$0 W, the scenario in which the lower inverter is not operating, due to which there is no interleaving (phase-shifting) occurring. Alternatively, the maximum ripple cancellation (or in other words, the minimum amplitude of switching frequency harmonic components) is achieved when each of the two inverters has the same output power (i.e., the case in which $P_{o2}=$ 2500 W in Figure 13a–d. This is because, at the same output loading scenarios, the DC-ripples will be equal (due to the same output power) and opposite (due to ${\theta }_{fsw\_2}={90}^{\circ }$). Remarkably, even in cases where the inverters do not have the same output power ($P_{o2}$ is between 500 W and 2000 W), the DC-current harmonic (ripple) reductions occur. This result is of particular importance in industrial applications where parallel-connected inverters do not run at the same rated power. Applying the proposed method will help to reduce the harmonic content at the DC-link, thereby reducing the requirement to use a large number of DC-link capacitors (which saves costs).

Among the two topologies, the multi-converter system with individual DC-banks is preferred due to the flexibility it gives the industrial designers to play with the number of inverters being connected to the centralized rectifier, and also due to the better lifetime of its DC-link capacitors (Table 7). Notably, one of the advantages of having a centralized rectifier is that, in the event of power failure, it is easy to connect a backup battery at the common DC link connecting the parallel inverter systems. Finally, in the future, it will also be possible to integrate renewable energy resources without much difficulty at the common DC link in these kinds of systems.

A few of the future works related to this paper include the following: a design approach to size the DC-link capacitor for the proposed topologies and compare how it is different from the DC-capacitor in the conventional multidrive systems. Further, more study needs to be conducted on how to optimise the phase-shift angles when two inverters have different speeds and different switching frequency waves, as well as different output frequencies. Including a greater number of inverters and then finding the optimal phase-shift angle in such scenarios can also be a topic for future work.

7. Conclusions

In this paper, a carrier-based phase-shifting scheme is presented to minimize the DC-link current harmonics in the two proposed configurations of common DC-connected multi-converter systems that have a centralized rectifier. Using a centralized rectifier is more compact and reliable due to the reduction of conversion stages in the power system. The analyzed results showed that the maximum high-frequency harmonic ripple cancellation in the DC-capacitor bank current is when the carrier waves of the paralleled-inverters are phase-shifted by a ${90}^{\circ }$ angle (optimal phase angle). This helps to reduce the overall DC-capacitor bank current by almost 50%, thereby improving the lifetime of the DC-link capacitors due to less power loss within the DC-link capacitor. Thereby, the cost of the overall system will be lower as a lesser number of capacitors are needed in the DC-link. Remarkably, even in cases where the inverters do not have the same output power, the DC-current harmonic (ripple) reduction occurs at the optimal phase angle. The outcome of this paper is a simple and effective solution for industrial designers to practically configure multi-inverter systems with reduced DC-link current harmonics, even when most of the drives are not operating at rated power levels.