An Energy Management Optimization Method for Community Integrated Energy System Based on User Dominated Demand Side Response
Abstract
:1. Introduction
1.1. Background and Motivation
1.2. Novelty and Contribution
- (1)
- The interruptible power load, shiftable power load, and adjustable thermal load are modeled, respectively, and are optimized by UDDSR scheme in order to obtain the aggregated IDR bids.
- (2)
- An aggregated buildings thermal model is introduced to measure the temperature requirements of the entire community of users for heating. The adjustable thermal loads of the IDR bids submitted by users are modeled within the context of air temperature, and can be optimized by regulating the indoor temperature of users.
- (3)
- From the overall perspective of system operation, a day-ahead scheduling optimization model for the community IES based on UDDSR is established, and the CVaR theory is introduced to deal with the uncertainties in IES.
2. Demand Response Load Modeling Based on UDDSR
2.1. UDDSR Optimization with Adjustable Thermal Loads
2.2. Adjustable Thermal Loads Model Based on UDDSR
2.3. Electric Loads Model Based on UDDSR
3. Distributed Generator and Co-Supply Equipment Model
3.1. PV Model
3.2. Power Supply Equipment Model
3.2.1. Microgas Turbine (MT) Model
3.2.2. Gas Boiler (GB) Model
3.2.3. Waste Heat Recovery (WHR) Device Model
3.2.4. Heat Exchanger (HE) Model
3.3. Energy Storage Equipment Model
3.3.1. Battery (BT) Model
3.3.2. Thermal Storage Tank (TST) Model
4. Community CHP System Model Based on UDDSR
4.1. Day-Ahead Energy Optimization Model
- Energy balancing constraints
- 2.
- Energy supply constraints
- 3.
- Energy storage constraints
4.2. CVaR-Based Energy Optimization Model
4.2.1. CVaR Model
4.2.2. Day-Ahead Energy Optimization Model Based on CVaR
5. Case Study
5.1. Day-Ahead Energy Optimization Based on UDDSR
5.1.1. Energy Optimization Results without UDDSR Response
5.1.2. Energy Optimization Results with UDDSR Response
5.2. CVaR-Based Energy Optimization
5.2.1. Energy Risk Optimization Results Based on CVaR
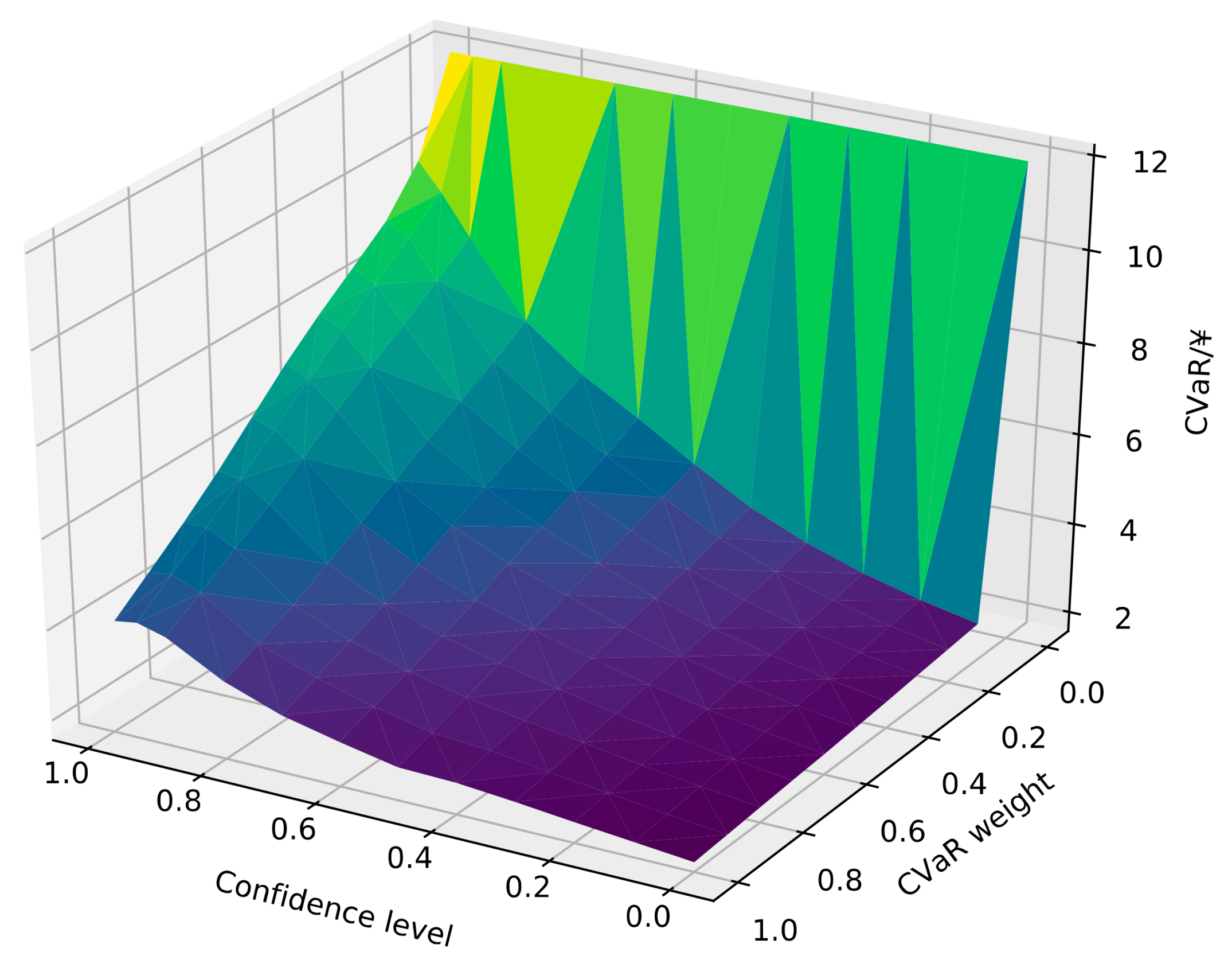
5.2.2. Impact of Confidence Level and Uncertainty Coefficient of CVaR on Energy Use Optimization
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Time period | Electricity Price (RMB/kWh) | Power Load Response Subsidy (RMB/kWh) | Thermal Load Response Subsidy (RMB/kWh) | Imbalance Response Penalty (RMB/kWh) | Gas Price (RMB/m³) |
|---|---|---|---|---|---|
| Peak time ((09:00–13:00], [17:00–20:00)) | 1.19 | 0.3 | 0.2 | 0.6 | 3 |
| Normal time ((06:00–08:00], [14:00–16:00)) | 0.75 | 0.1 | 0.2 | 0.4 | 3 |
| Valley time ((00:00–05:00], [21:00–23:00)) | 0.36 | 0.05 | 0.2 | 0.18 | 3 |
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| MT generating efficiency | 0.36 | TST heat releasing efficiency | 0.95 |
| MT maximum output power | 500 kW | TST self-loss rate of thermal energy | 0.04 |
| MT minimum output power | 10 kW | TST maximum capacity | 100 kWh |
| GB heat production efficiency | 0.85 | TST minimum capacity | 0 kWh |
| GB maximum thermal output power | 600 kW | TST maximum heat storage/release power | 50 kW |
| GB minimum thermal output power | 0 kW | Maximum power purchased from the grid | 1000 kW |
| BT charging efficiency | 0.95 | Minimum power purchased from the grid | 0 kW |
| BT discharging efficiency | 0.95 | Maximum power of interruptible power load | |
| BT self-loss rate of electrical energy | 0.04 | Maximum power of shiftable power load | / |
| BT maximum capacity | 100 kWh | Maximum indoor temperature | 26 |
| BT minimum capacity | 0 kWh | Minimum indoor temperature | 18 |
| BT maximum charging/discharging power | 50 kW | Optimum indoor temperature | 21 |
| TST heat storing efficiency | 0.95 | Maximum adjustable temperature | Tadj |
| Equipment | Operation and Maintenance Cost (RMB/kWh) | Equipment | Subsidy (RMB/kWh) |
|---|---|---|---|
| MT | 0.075 | BT | 0.01 |
| GB | 0.08 | TST | 0.01 |
| PV | 0.01 |
References
- Jia, B.; Li, F.; Sun, B. Design of energy management platform for integrated energy system. In Proceedings of the 2019 14th IEEE Conference on Industrial Electronics and Applications (ICIEA), Xi’an, China, 19–21 June 2019; pp. 1593–1597. [Google Scholar]
- Tao, H.; Fang, L.; YaLou, L.; Xiaoxin, Z. The Design of the Simulation System for the Integrated Energy System. In Proceedings of the 2018 International Conference on Power System Technology (POWERCON), Guangzhou, China, 6–9 November 2018; pp. 410–416. [Google Scholar]
- Zhou, X.; Bao, Y.-Q.; Chen, P.-P.; Ji, T.; Deng, W.; Jin, W. Integrated Electricity and Natural Gas Energy System Scheduling Model Considering Multi-Energy Storage Systems. In Proceedings of the 2018 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Sabah, Malaysia, 7–10 October 2018; pp. 178–182. [Google Scholar]
- Miao, B.; Lin, J.; Li, H.; Liu, C.; Li, B.; Zhu, X.; Yang, J. Day-Ahead Energy Trading Strategy of Regional Integrated Energy System Considering Energy Cascade Uti-lization. IEEE Access 2020, 8, 138021–138035. [Google Scholar] [CrossRef]
- Chen, Y.; Wei, W.; Liu, F.; Sauma, E.E.; Mei, S. Energy Trading and Market Equilibrium in Integrated Heat-Power Distri-bution Systems. IEEE Trans. Smart Grid 2019, 10, 4080–4094. [Google Scholar] [CrossRef]
- Tedesco, F.; Mariam, L.; Basu, M.; Casavola, A.; Conlon, M.F. Economic Model Predictive Control-Based Strategies for Cost-Effective Supervision of Community Microgrids Considering Battery Lifetime. IEEE J. Emerg. Sel. Top. Power Electron. 2015, 3, 1067–1077. [Google Scholar] [CrossRef]
- Qinwei, D. A price-based demand response scheduling model in day-ahead electricity market. In Proceedings of the 2016 IEEE Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Junhui, L.; Hongkun, B.; Hujun, L.; Qinchen, Y.; Fangzhao, D.; Wenjie, Z. Optimal Decomposition of Flexible Load Resource Reserve Target Based on Power Demand Response. In Proceedings of the 2021 IEEE International Conference on Power Electronics, Computer Applications (ICPECA), Shenyang, China, 22–24 January 2021; pp. 1046–1049. [Google Scholar]
- Parisio, A.; Rikos, E.; Glielmo, L. A Model Predictive Control Approach to Microgrid Operation Optimization. IEEE Trans. Control Syst. Technol. 2014, 22, 1813–1827. [Google Scholar] [CrossRef]
- Du, Y.; Zheng, N.; Cai, Q.; Li, Y.; Li, Y.; Shi, P. Research on Key Technologies of User Side Integrated Demand Response for Multi-Energy Coordination. In Proceedings of the 2020 IEEE 4th Conference on Energy Internet and Energy System Integration (EI2), Wuhan, China, 30 October–1 November 2020; pp. 2461–2464. [Google Scholar]
- Bahrami, S.; Sheikhi, A. From Demand Response in Smart Grid toward Integrated Demand Response in Smart Energy Hub. IEEE Trans. Smart Grid 2015, 7, 650–658. [Google Scholar] [CrossRef]
- Liu, P.; Ding, T.; Zou, Z.; Yang, Y. Integrated demand response for a load serving entity in multi-energy market considering network constraints. Appl. Energy 2019, 250, 512–529. [Google Scholar] [CrossRef]
- Wang, J.; Zhong, H.; Ma, Z.; Xia, Q.; Kang, C. Review and prospect of integrated demand response in the multi-energy system. Appl. Energy 2017, 202, 772–782. [Google Scholar] [CrossRef]
- Ren, S.; Dou, X.; Wang, Z.; Wang, J.; Wang, X. Medium- and Long-Term Integrated Demand Response of Integrated Energy System Based on System Dynamics. Energies 2020, 13, 710. [Google Scholar] [CrossRef] [Green Version]
- Yang, H.; Li, M.; Jiang, Z.; Zhang, P. Multi-Time Scale Optimal Scheduling of Regional Integrated Energy Systems Con-sidering Integrated Demand Response. IEEE Access 2020, 8, 5080–5090. [Google Scholar] [CrossRef]
- Tahir, M.F.; Haoyong, C.; Mehmood, K.; Ali, N.; Bhutto, J.A. Integrated Energy System Modeling of China for 2020 by Incorporating Demand Response, Heat Pump and Thermal Storage. IEEE Access 2019, 7, 40095–40108. [Google Scholar] [CrossRef]
- Jiang, Z.; Ai, Q.; Hao, R. Integrated Demand Response Mechanism for Industrial Energy System Based on Multi-Energy Interaction. IEEE Access 2019, 7, 66336–66346. [Google Scholar] [CrossRef]
- Stenner, K.; Frederiks, E.R.; Hobman, E.V.; Cook, S. Willingness to participate in direct load control: The role of consumer distrust. Appl. Energy 2017, 189, 76–88. [Google Scholar] [CrossRef]
- Zhou, S.; Zou, F.; Wu, Z.; Gu, W.; Hong, Q.; Booth, C. A smart community energy management scheme considering user dominated demand side response and P2P trading. Int. J. Electr. Power Energy Syst. 2020, 114, 105378. [Google Scholar] [CrossRef]
- Brahman, F.; Honarmand, M.; Jadid, S. Optimal electrical and thermal energy management of a residential energy hub, integrating demand response and energy storage system. Energy Build. 2015, 90, 65–75. [Google Scholar] [CrossRef]
- Wang, C.S.; Hong, B.W.; Guo, L.; Zhang, D.J.; Liu, W.J. A General Modeling Method for Optimal Dispatch of Combined Cooling, Heating and Power Microgrid. Proc. CSEE 2013, 33, 26–33. [Google Scholar]
- Zhang, Q.; Wang, X. Hedge Contract Characterization and Risk-Constrained Electricity Procurement. IEEE Trans. Power Syst. 2009, 24, 1547–1558. [Google Scholar] [CrossRef]
- Sheikhi, A.; Rayati, M.; Bahrami, S.; Ranjbar, A.M. Integrated Demand Side Management Game in Smart Energy Hubs. IEEE Trans. Smart Grid 2015, 6, 675–683. [Google Scholar] [CrossRef]







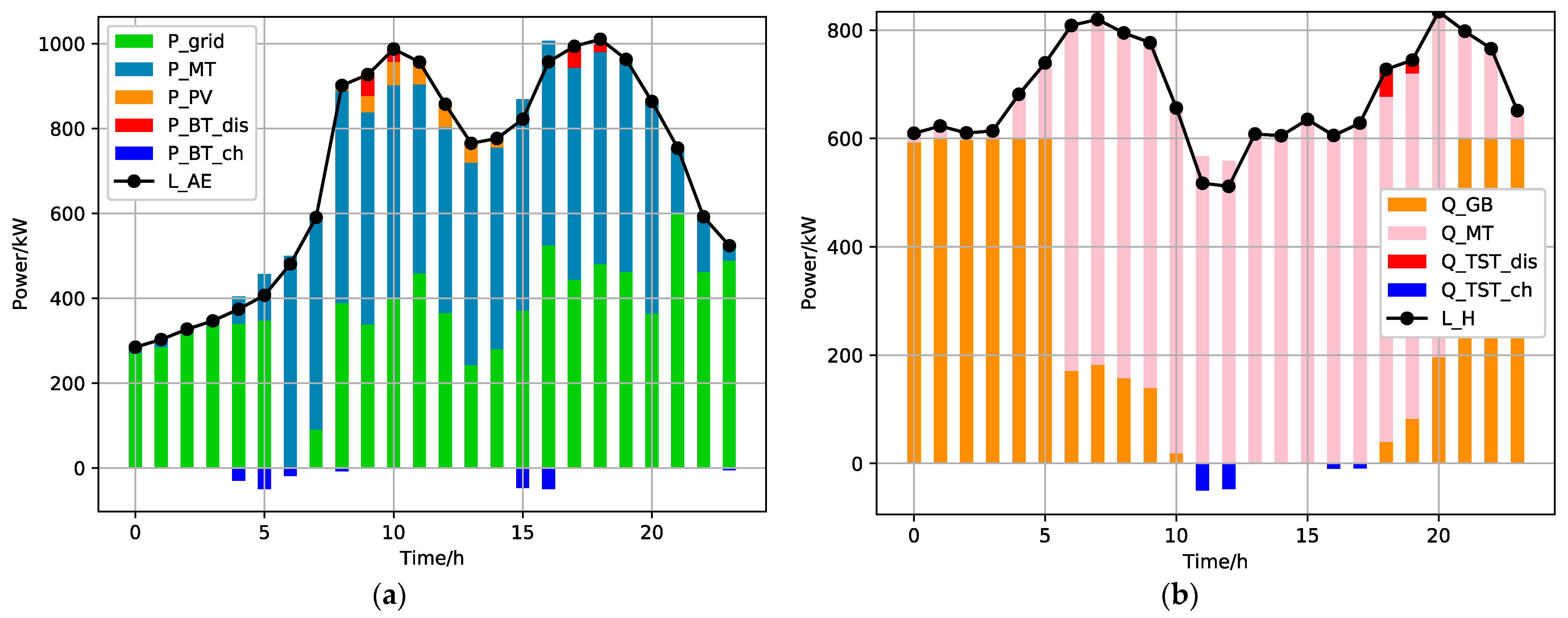








| Before UDDSR | After UDDSR | Saving (%) | |
|---|---|---|---|
| Electricity purchasing cost (RMB) | 7344.90 | 6715.64 | 8.57% |
| Gas purchasing cost (RMB) | 9153.34 | 9001.82 | 1.66% |
| Operation and maintenance (RMB) | 1122.07 | 1108.60 | 1.20% |
| Power load response compensation (RMB) | 0 | 205 | / |
| Thermal load response compensation (RMB) | 0 | 45.49 | / |
| BT subsidies (RMB) | 0 | 5.70 | |
| Adjustable temperature (°C) | 0 | 1 | / |
| Total cost (RMB) | 17,620.31 | 17,076.56 | 3.09% |
| Scenarios | Before UDDSR | 1 | 2 | 3 | 4 |
|---|---|---|---|---|---|
| Maximum risk fluctuation | 0% | ≤5% | ≤10% | ≤15% | >15% |
| Electricity purchasing cost (RMB) | 7344.90 | 6889.18 | 7293.46 | 8048.00 | 11529.32 |
| Gas purchasing cost (RMB) | 9153.34 | 9208.27 | 9177.42 | 9338.93 | 9765.28 |
| Power load response subsidies (RMB) | 0 | 203.25 | 200.87 | 196.98 | 183.88 |
| Thermal load response subsidies (RMB) | 0 | 37.32 | 45.13 | 26.54 | 20.97 |
| BT subsidies (RMB) | 0 | 5.70 | 5.70 | 5.71 | 5.93 |
| Imbalance response penalty (yaun) | 0 | 3.77 | 8.81 | 17.21 | 46.23 |
| Adjustable tmperature (°C) | 0 | 1 | 1 | 1 | 1 |
| Total expected cost of operation (RMB) | 17,620.31 | 17,461.61 | 17,832.64 | 18,739.14 | 22,662.36 |
| CVaR (RMB) | 0 | 4.13 | 5.21 | 17.45 | 41.01 |
| Total cost savings ratio | / | 0.90% | −1.21% | −6.34% | −28.61% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, Y.; Zhang, J.; Ma, Z.; Peng, Y.; Zhao, S. An Energy Management Optimization Method for Community Integrated Energy System Based on User Dominated Demand Side Response. Energies 2021, 14, 4398. https://doi.org/10.3390/en14154398
Li Y, Zhang J, Ma Z, Peng Y, Zhao S. An Energy Management Optimization Method for Community Integrated Energy System Based on User Dominated Demand Side Response. Energies. 2021; 14(15):4398. https://doi.org/10.3390/en14154398
Chicago/Turabian StyleLi, Yiqi, Jing Zhang, Zhoujun Ma, Yang Peng, and Shuwen Zhao. 2021. "An Energy Management Optimization Method for Community Integrated Energy System Based on User Dominated Demand Side Response" Energies 14, no. 15: 4398. https://doi.org/10.3390/en14154398
APA StyleLi, Y., Zhang, J., Ma, Z., Peng, Y., & Zhao, S. (2021). An Energy Management Optimization Method for Community Integrated Energy System Based on User Dominated Demand Side Response. Energies, 14(15), 4398. https://doi.org/10.3390/en14154398





