Lithium Battery SOH Monitoring and an SOC Estimation Algorithm Based on the SOH Result
Abstract
:1. Introduction
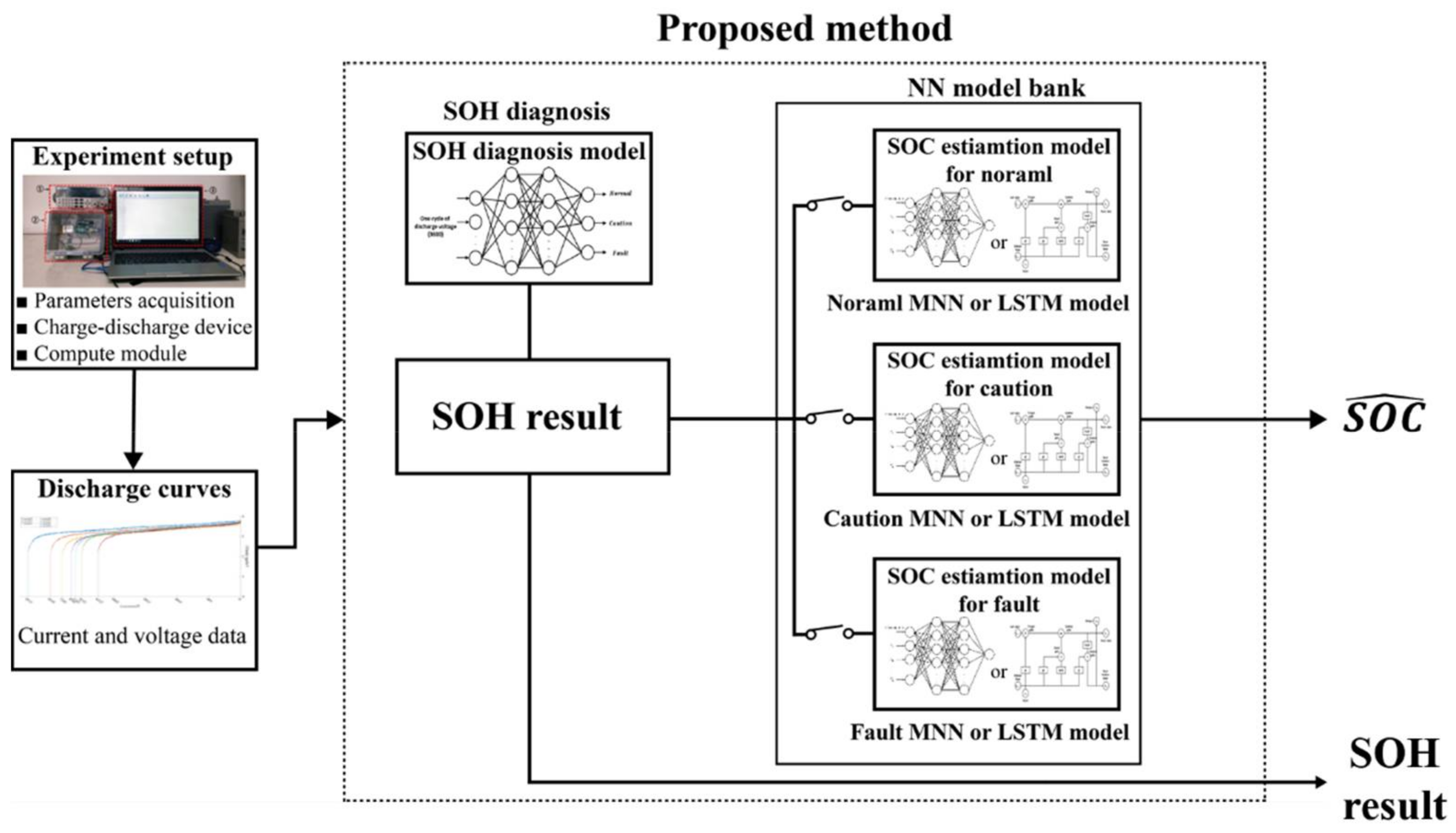
2. Proposed SOC Estimation and SOH Diagnosis Method
2.1. Definition of SOC and SOH
2.2. Proposed SOH Monitoring and the SOC Estimation Algorithm Based on the SOH Results
2.2.1. Proposed SOH Diagnosis Method
2.2.2. Proposed SOC Estimation Based on the SOH
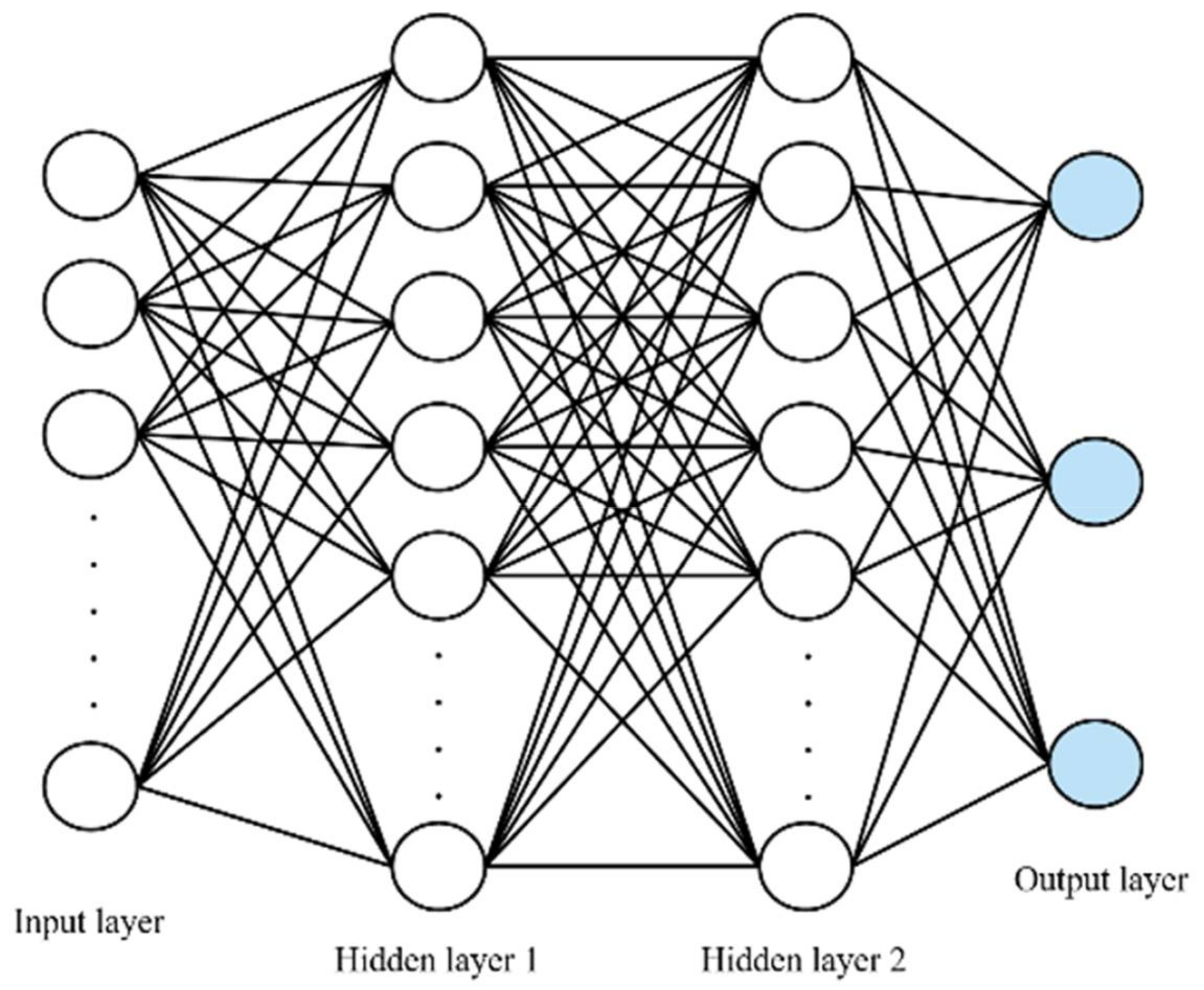
2.3. MNN
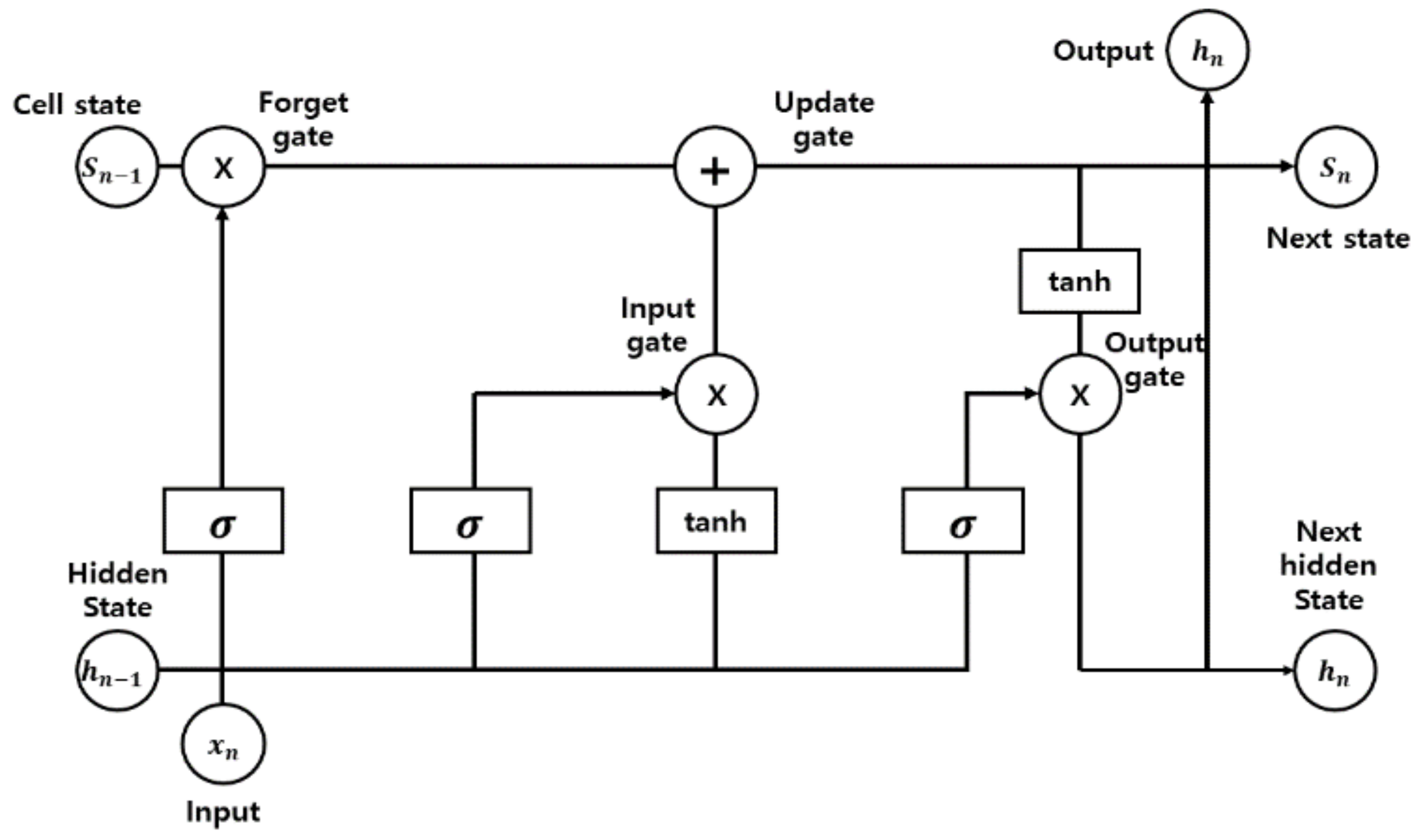
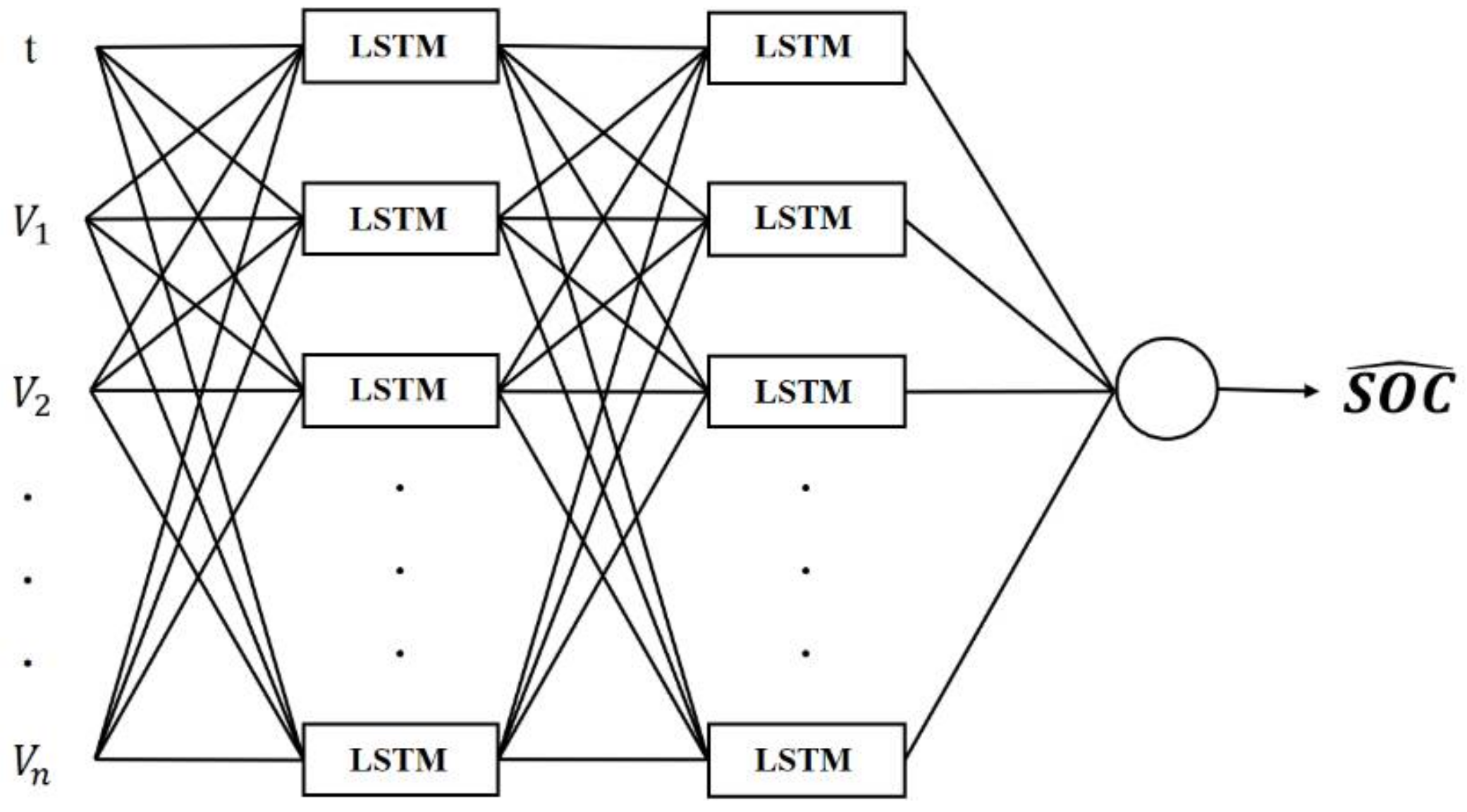
2.4. LSTM
3. Experiment and Results
3.1. Experiment Setup
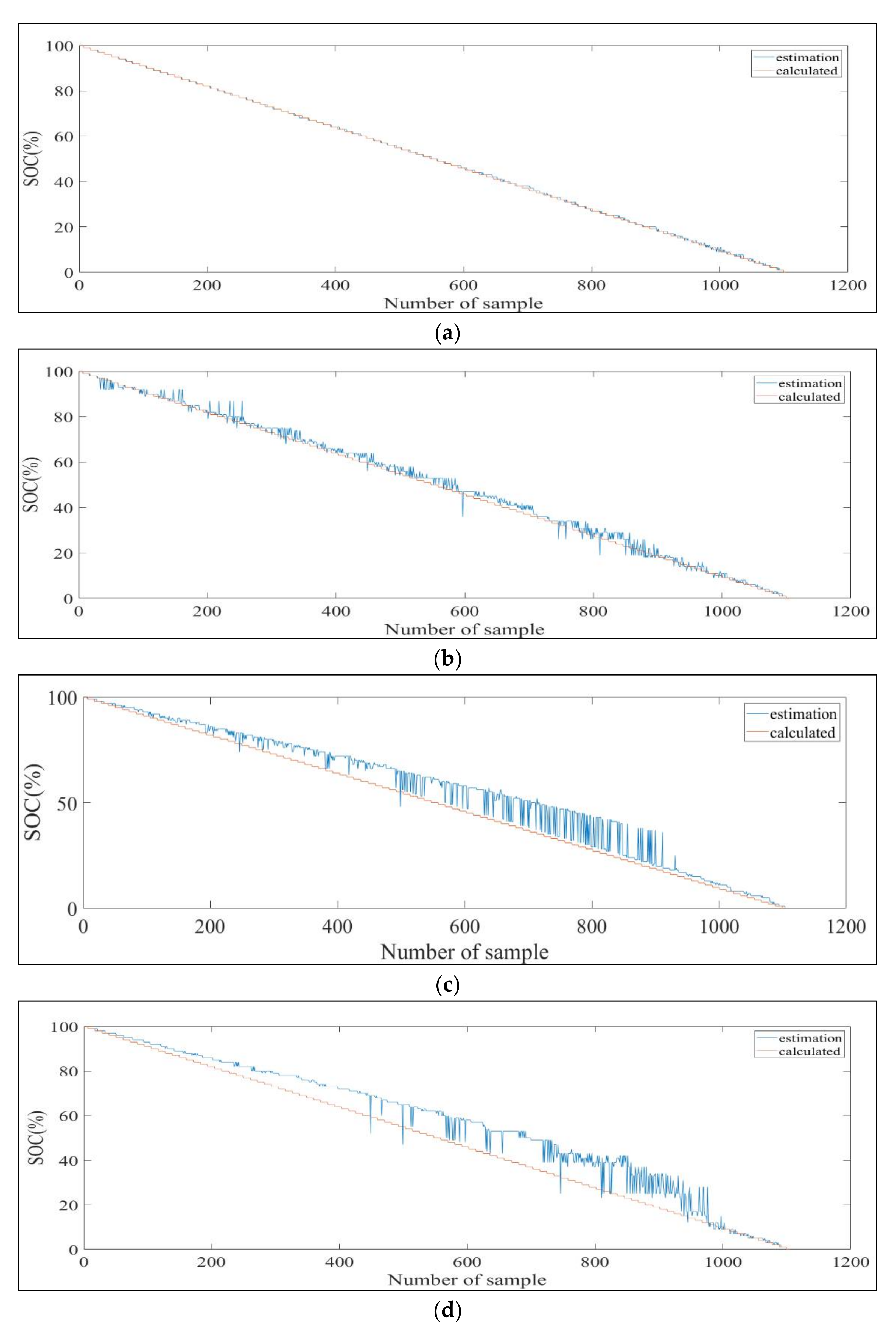
3.2. SOC Estimation Based on the SOH Result
3.2.1. Structure of SOH Diagnosis Using MNN
3.2.2. Structure of SOC Estimation Using a NN Model Bank
3.2.3. Comparison of the Proposed and General Methods
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Gao, Z.; Chin, C.S.; Chiew, J.H.K.; Jia, J.; Zhang, C. Design and Implementation of a Smart Lithium-Ion Battery System with Real-Time Fault Diagnosis Capability for Electric Vehicles. Energies 2017, 10, 1503. [Google Scholar] [CrossRef]
- Cho, T.H.; Hwang, H.R.; Lee, J.H.; Lee, I.S. Comparison of Intelligent Methods of SOC Estimation for Battery of Photovoltaic System. Int. J. Adv. Comput. Sci. Appl. 2018, 9, 49–56. [Google Scholar] [CrossRef]
- Park, J.H.; Lee, J.H.; Kim, S.J.; Lee, I.S. Real-Time State of Charge Estimation for Each Cell of Lithium Battery Pack Using Neural Networks. Appl. Sci. 2020, 10, 8644. [Google Scholar] [CrossRef]
- Seh, Z.W.; Sun, Y.; Zhang, Q.; Cui, Y. Designing high-energy lithium–sulfur batteries. Chem. Soc. Rev. 2016, 4, 383–391. [Google Scholar] [CrossRef]
- Sidhu, A.; Izadian, A.; Anwar, S. Adaptive nonlinear model-based fault diagnosis of Li-ion batteries. IEEE Trans. Ind. Electron. 2014, 62, 1002–1011. [Google Scholar] [CrossRef] [Green Version]
- Zhao, Y.; Liu, P.; Wang, Z.; Zhang, L.; Hong, J. Fault and defect diagnosis of battery for electric vehicles based on big data analysis methods. Appl. Energy 2017, 207, 354–362. [Google Scholar] [CrossRef]
- Chen, Z.; Xiong, R.; Tian, J.; Shang, X.; Lu, J. Model-based fault diagnosis approach on external short circuit of lithium-ion battery used in electric vehicles. Appl. Energy 2016, 184, 365–374. [Google Scholar] [CrossRef]
- How, D.N.; Hannan, M.A.; Lipu, M.H.; Ker, P.J. State of charge estimation for lithium-ion batteries using model-based and data-driven methods: A review. IEEE Access 2019, 7, 136116–136136. [Google Scholar] [CrossRef]
- Corno, M.; Bhatt, N.; Savaresi, S.M.; Verhaegen, M. Electrochemical model-based state of charge estimation for Li-ion cells. IEEE Trans. Control Syst. Technol. 2014, 23, 117–127. [Google Scholar] [CrossRef]
- He, H.; Xiong, R.; Fan, J. Evaluation of lithium-ion battery equivalent circuit models for state of charge estimation by an experimental approach. Energies 2011, 4, 582–598. [Google Scholar] [CrossRef]
- Sun, F.; Hu, X.; Zou, Y.; Li, S. Adaptive unscented Kalman filtering for state of charge estimation of a lithium-ion battery for electric vehicles. Energy 2011, 36, 3531–3540. [Google Scholar] [CrossRef]
- Wu, B.; Han, S.; Shin, K.G.; Lu, W. Application of artificial neural networks in design of lithium-ion batteries. J. Power Sources 2018, 395, 128–136. [Google Scholar] [CrossRef]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Ahmed, R.; Emadi, A. Long short-term memory networks for accurate state-of-charge estimation of Li-ion batteries. IEEE Trans. Ind. Electron. 2017, 65, 6730–6739. [Google Scholar] [CrossRef]
- Shen, P.; Ouyang, M.; Lu, L.; Li, J.; Feng, X. The co-estimation of state of charge, state of health, and state of function for lithium-ion batteries in electric vehicles. IEEE Trans. Veh. Technol. 2017, 67, 92–103. [Google Scholar] [CrossRef]
- Barai, A.; Widanage, W.D.; Marco, J.; McGordon, A.; Jennings, P. A study of the open circuit voltage characterization technique and hysteresis assessment of lithium-ion cells. J. Power Sources 2015, 295, 99–107. [Google Scholar] [CrossRef]
- Ng, M.F.; Zhao, J.; Yan, Q.; Conduit, G.J.; Seh, Z.W. Predicting the state of charge and health of batteries using data-driven machine learning. Nat. Mach. Intell. 2020, 2, 161–170. [Google Scholar] [CrossRef] [Green Version]
- Severson, K.A.; Attia, P.M.; Jin, N.; Perkins, N.; Jiang, B.; Yang, Z.; Chen, M.H.; Aykol, M.; Herring, P.K.; Fraggedakis, D.; et al. Data-driven prediction of battery cycle life before capacity degradation. Nat. Energy 2019, 4, 383–391. [Google Scholar] [CrossRef] [Green Version]
- Attia, P.M.; Grover, A.; Jin, N.; Severson, K.A.; Markov, T.M.; Liao, Y.H.; Chen, M.H.; Cheong, B.; Perkins, N.; Yang, Z.; et al. Closed-loop optimization of fast-charging protocols for batteries with machine learning. Nature 2020, 578, 397–402. [Google Scholar] [CrossRef] [Green Version]
- Ng, K.S.; Moo, C.S.; Chen, Y.P.; Hsieh, Y.C. Enhanced coulomb counting method for estimating state-of-charge and state-of-health of lithium-ion batteries. Appl. Energy 2009, 89, 1506–1511. [Google Scholar] [CrossRef]
- Truchot, C.; Dubarry, M.; Liaw, B.Y. State-of-charge estimation and uncertainty for lithium-ion battery string. Appl. Energy 2014, 119, 218–227. [Google Scholar] [CrossRef]
- Hu, X.; Li, S.; Peng, H. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Lin, C.; Mu, H.; Xiong, R.; Shen, W. A novel multi-model probability battery state of charge estimation approach for electric vehicles using H-infinity algorithm. Appl. Energy 2016, 166, 76–83. [Google Scholar] [CrossRef]
- Gismero, A.; Schaltz, E.; Stroe, D.I. Recursive state of charge and state of health estimation method for lithium-ion batteries based on coulomb counting and open circuit voltage. Energies 2020, 13, 1811. [Google Scholar] [CrossRef] [Green Version]
- Jang, K.-W.; Chung, G.-B. A SOC Estimation using Kalman Filter for Lithium-Polymer Battery. Trans. Korean Inst. Power Electron. 2012, 17, 222–229. [Google Scholar] [CrossRef] [Green Version]
- Chemali, E.; Kollmeyer, P.J.; Preindl, M.; Emadi, A. State-of-charge estimation of Li-ion batteries using deep neural networks: A machine learning approach. J. Power Sources 2018, 400, 242–255. [Google Scholar] [CrossRef]
- Zhang, D.; Dey, S.; Perez, H.E.; Moura, S.J. Remaining useful life estimation of lithium-ion batteries based on thermal dynamics. In Proceedings of the 2017 American Control Conference (ACC), Seattle, WA, USA, 24–26 May 2017; pp. 4042–4047. [Google Scholar]
- El-Dalahmeh, M.; Al-Greer, M.; El-Dalahmeh, M.A.; Short, M. Time-Frequency Image Analysis and Transfer Learning for Capacity Prediction of Lithium-Ion Batteries. Energies 2020, 13, 5447. [Google Scholar] [CrossRef]
- Tang, X.; Wang, Y.; Zou, C.; Yao, K.; Xia, Y.; Gao, F. A novel framework for Lithium-ion battery modeling considering uncertainties of temperature and aging. Energy Convers. Manag. 2019, 180, 162–170. [Google Scholar] [CrossRef]
- Wang, D.; Bao, Y.; Shi, J. Online lithium-ion battery internal resistance measurement application in state-of-charge estimation using the extended Kalman filter. Energies 2017, 10, 1284. [Google Scholar] [CrossRef] [Green Version]
- Song, C.; Shao, Y.; Song, S.; Peng, S.; Zhou, F.; Chang, C.; Wang, D. Insulation resistance monitoring algorithm for battery pack in electric vehicle based on extended Kalman filtering. Energies 2017, 10, 714. [Google Scholar] [CrossRef]
- Hannan, M.A.; Lipu, M.S.H.; Hussain, A.; Saad, M.H.; Ayob, A. Neural network approach for estimating state of charge of lithium-ion battery using backtracking search algorithm. IEEE Access 2018, 6, 10069–10079. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Chang, Z.; Zhang, Y.; Chen, W. Electricity price prediction based on hybrid model of adam optimized LSTM neural network and wavelet transform. Energy 2019, 187, 115804. [Google Scholar] [CrossRef]
- Yu, Y.; Si, X.; Hu, C.; Zhang, J. A review of recurrent neural networks: LSTM cells and network architectures. Neural Comput. 2019, 31, 1235–1270. [Google Scholar] [CrossRef] [PubMed]
- Wu, J.; Zhang, C.; Chen, Z. An online method for lithium-ion battery remaining useful life estimation using importance sampling and neural networks. Appl. Energy 2016, 173, 134–140. [Google Scholar] [CrossRef]







| Method | Advantages | Disadvantages | Example Model |
|---|---|---|---|
| Model-based [9,10] | Reliable and accurate Has universal validity | Requires extensive domain knowledge Longer development time | Equivalent circuit model Electrochemical model Kalman filter |
| Data-driven [11,12,13,14,15,16,17,18] | Shorter development time Does not require very much specialized knowledge. | Requires a large amount of data | Neural network Deep learning Look-up table |
| Coulomb-counter [19,20] | Simple to implement | Errors accumulate over time. | Coulomb-counter |
| Battery Type | Li-Po Battery |
|---|---|
| Capacity | 1.3 Ah |
| Voltage range | 2.4–4.28 V |
| Nominal voltage | 3.7 V |
| Methods | Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | Pattern 5 | Pattern 6 |
|---|---|---|---|---|---|---|
| SOH diagnosis model | normal | normal | caution | caution | fault | fault |
| Methods | Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | Pattern 5 | Pattern 6 |
|---|---|---|---|---|---|---|
| Proposed method using LSTM | 1.31% | 0.18% | 1.59% | 1.19% | 1.13% | 1.68% |
| Proposed method using MNN | 1.59% | 0.33% | 1.09% | 1.65% | 1.23% | 1.55% |
| Only LSTM | 1.96% | 4.12% | 2.65% | 3.19% | 5.83% | 6.05% |
| Only MNN | 1.93% | 4.45% | 2.18% | 2.96% | 6.23% | 6.67% |
| Methods | Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | Pattern 5 | Pattern 6 |
|---|---|---|---|---|---|---|
| Proposed method using LSTM | 0.31% | 0.3% | 0.95% | 1.04% | 0.63% | 0.24% |
| Proposed method using MNN | 1.59% | 0.28% | 1.48% | 1.08% | 0.76% | 1.57% |
| Only LSTM | 2.27% | 4.37% | 2.52% | 2.94% | 5.33% | 5.88% |
| Only MNN | 1.94% | 4.65% | 1.73% | 2.7% | 6.68% | 6.96% |
| Methods | Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | Pattern 5 | Pattern 6 |
|---|---|---|---|---|---|---|
| Proposed method using LSTM | 1.23% | 0.2% | 1.3% | 1.37% | 0.29% | 1.1% |
| Proposed method using MNN | 1.18% | 0.39% | 1.03% | 1.62% | 0.34% | 1.28% |
| Only LSTM | 2.35% | 5.41% | 2.91% | 2.81% | 4.89% | 5.55% |
| Only MNN | 2.05% | 5.15% | 2.07% | 2.98% | 5.86% | 5.99% |
| Methods | Pattern 1 | Pattern 2 | Pattern 3 | Pattern 4 | Pattern 5 | Pattern 6 |
|---|---|---|---|---|---|---|
| Proposed method using LSTM | 1.46% | 0.19% | 0.88% | 1.87% | 0.47% | 0.99% |
| Proposed method using MNN | 1.43% | 0.32% | 1.47% | 0.87% | 0.81% | 1.21% |
| Only LSTM | 2.53% | 5.26% | 2.4% | 2.8% | 5.53% | 5.64% |
| Only MNN | 2% | 4.81% | 1.47% | 2.66% | 6.56% | 6.65% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lee, J.-H.; Lee, I.-S. Lithium Battery SOH Monitoring and an SOC Estimation Algorithm Based on the SOH Result. Energies 2021, 14, 4506. https://doi.org/10.3390/en14154506
Lee J-H, Lee I-S. Lithium Battery SOH Monitoring and an SOC Estimation Algorithm Based on the SOH Result. Energies. 2021; 14(15):4506. https://doi.org/10.3390/en14154506
Chicago/Turabian StyleLee, Jong-Hyun, and In-Soo Lee. 2021. "Lithium Battery SOH Monitoring and an SOC Estimation Algorithm Based on the SOH Result" Energies 14, no. 15: 4506. https://doi.org/10.3390/en14154506
APA StyleLee, J.-H., & Lee, I.-S. (2021). Lithium Battery SOH Monitoring and an SOC Estimation Algorithm Based on the SOH Result. Energies, 14(15), 4506. https://doi.org/10.3390/en14154506





