Electric Field and Temperature Simulations of High-Voltage Direct Current Cables Considering the Soil Environment †
Abstract
:1. Introduction
2. Numerical Computation of the Coupled Electro Thermal Field
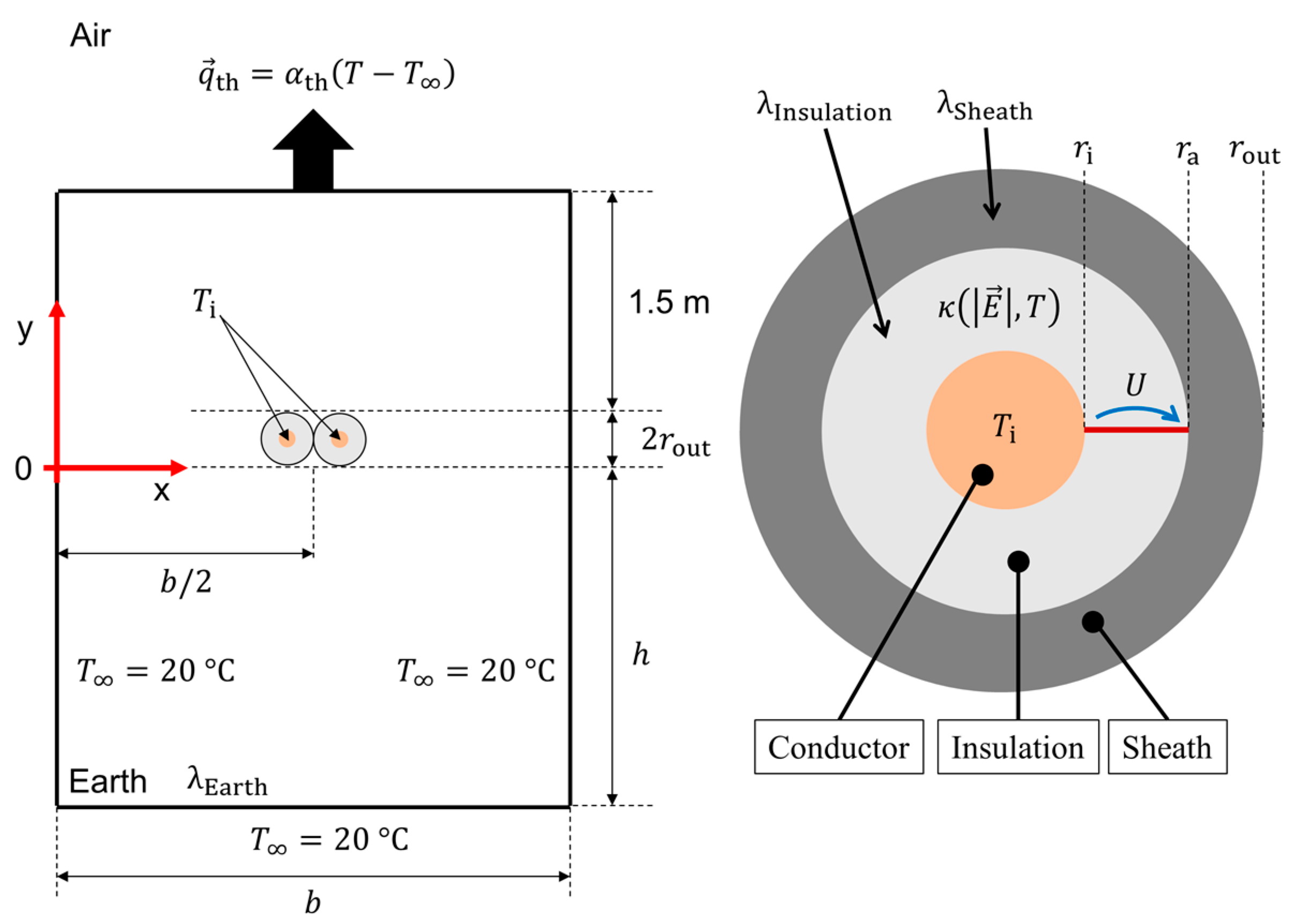
3. Geometric Model Reduction and the Electro-Thermal Coupling
3.1. Single Cable
3.2. Cable Pair Together
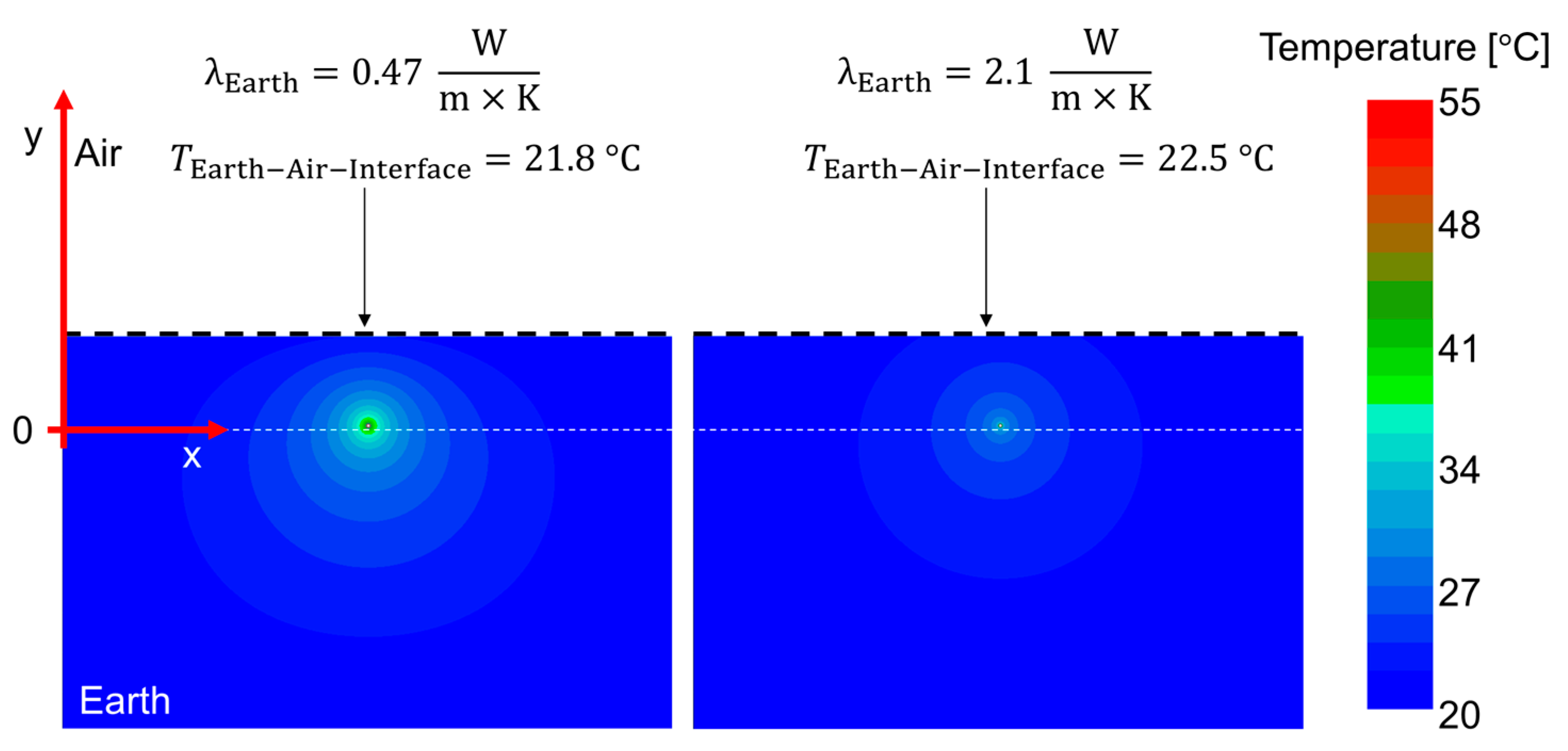
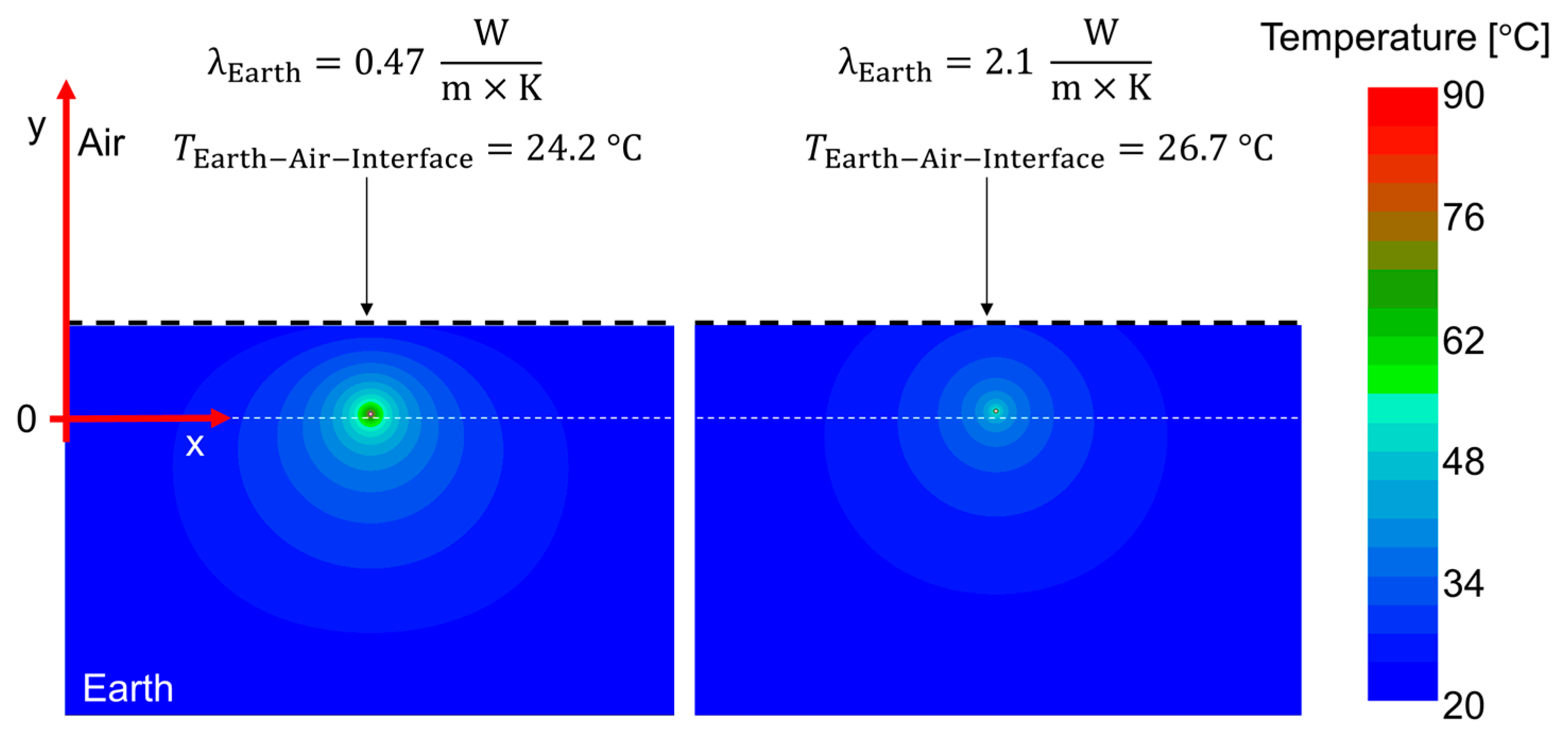
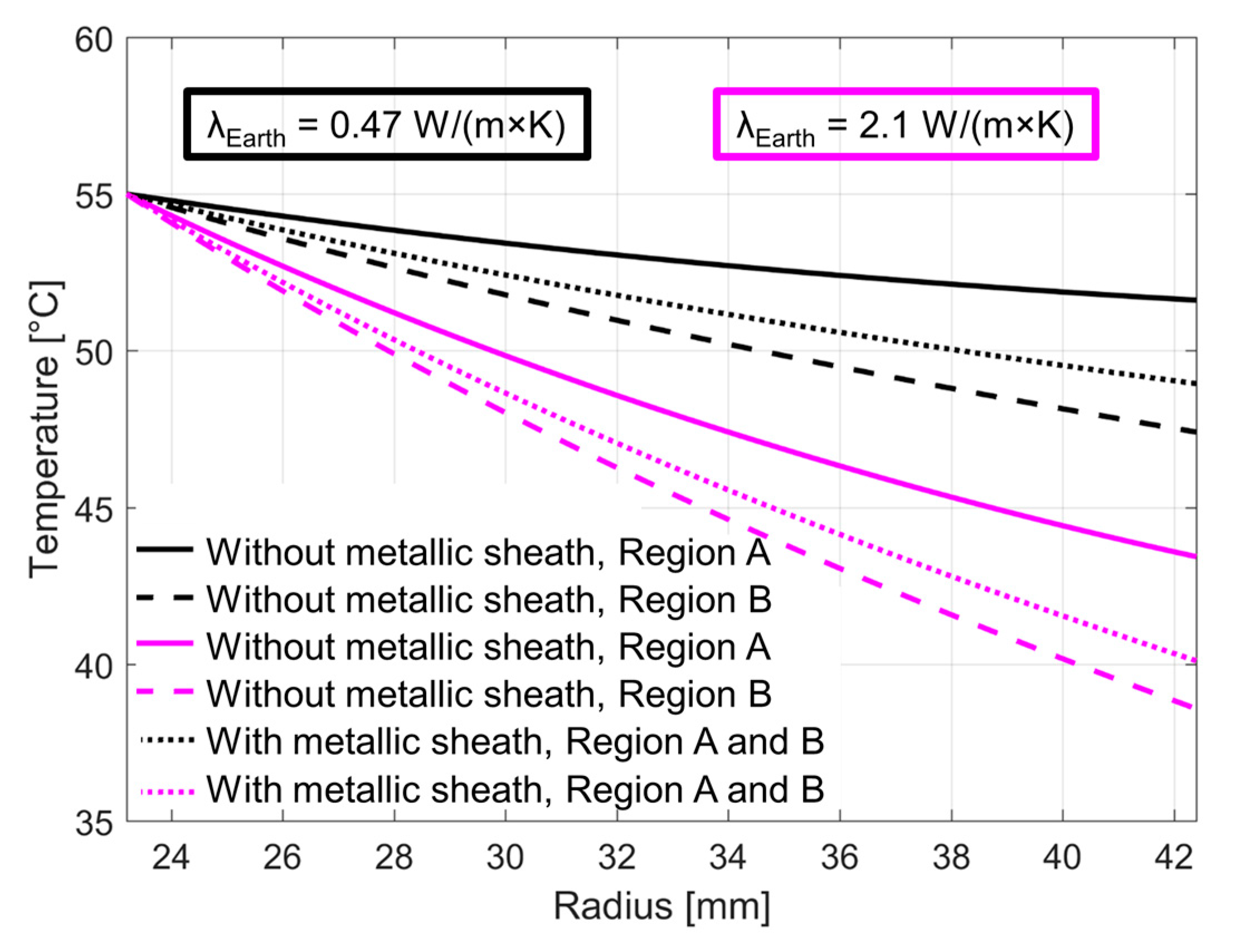
4. Simulation Results of the Temperature and the Electric Field
4.1. MI Cable Insulation
4.2. XLPE Cable Insulation
4.3. Comparison between the Temperature Calculation, Using Numerical Simulations and the Image Method
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| b | Vector of boundary conditions for the electric problem |
| bT | Vector of boundary conditions for the thermal problem |
| Electric field [V/m] | |
| Ea | Constant for the temperature dependency in (18) [eV] |
| G | Gradient matrix |
| GT | Discrete divergence matrix |
| hx | Buried depth of the cable [m] |
| I | Current within the conductor [A] |
| Current density [A/m2] | |
| j | Vector of current densities |
| J0 | Constant for the electric conductivity in (18) [A/m2] |
| k = 1.38×10−23 | Boltzmann constant [J/K] |
| Mε | Permittivity matrix |
| Mκ | Conductivity matrix |
| Mλ | Thermal conductivity matrix |
| m | Descrete time step |
| Q | Insulation losses [W/m3] |
| q | Vector of electric dual cell charges |
| Vector of insulation losses | |
| Heat current density [W/m2] | |
| RConductor | Electric resistivity of the conductor per length [Ω/m] |
| Rth,Earth | Thermal resistivity of the earth per length [m × K/W] |
| Rth,Insulation | Thermal resistivity of the insulation per length [m × K/W] |
| Rth,Sheath | Thermal resistivity of the outer sheath per length [m × K/W] |
| r | Radius [m] |
| ra | Radius of the insulation [m] |
| ri | Radius of the conductor [m] |
| rout | Radius of the outer sheath [m] |
| T | Temperature [°C] |
| Ti | Conductor temperature [°C] |
| T∞ | Environment temperature [°C] |
| t | Time [s] |
| tEND | Predefined end time for the numerical simulation [s] |
| U | Applied voltage [V] |
| Vector of nodal temperatures | |
| α | Constant for the temperature dependency in (17) [°C−1] |
| αth | Heat transfer coefficient [W/(m2 × K)] |
| β | Constant for the electric field dependency in (17) [m/V] |
| γ | Constant for the electric field dependency in (18) [m/V] |
| Δt | Time step [s] |
| ∆tCFL | Time step, determined by the Courant-Friedrich-Levy (CFL) criterion [s] |
| ε0 = 8.854 × 10−12 | Dielectric constant [As/(Vm)] |
| εr | Relative permittivity |
| η | Stop threshold |
| κ | Electric conductivity [S/m] |
| κ0 | Constant for the electric conductivity in (17) [S/m] |
| λ | Thermal conductivity [W/m × K] |
| ρ | Space charge density [C/m3] |
| τ | Time constant [s] |
| Φ | Vector of nodal scalar potentials |
| φ | Electric potential [V] |
References
- Mazzanti, G.; Marzinotto, M. Extruded Cables for High-Voltage Direct-Current Transmission: Advances in Research and Development; John Wiley & Sons Inc.: Hoboken, NJ, USA, 2013; pp. 49–75. ISBN 978-1-118-09666-6. [Google Scholar]
- Jeroense, M.J.P.; Morshuis, P.H.F. Electric fields in HVDC paper-insulated cables. IEEE Trans. Dielectr. Electr. Insul. 1998, 5, 225–236. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Thermal Breakdown in High Voltage Direct Current Cable Insulations due to Space Charges. COMPEL 2018, 37, 1689–1697. [Google Scholar] [CrossRef]
- Steinmetz, T.; Kurz, S.; Clemens, M. Domains of Validity of Quasistatic and Quasistationary Field Approximations. COMPEL 2011, 30, 1237–1247. [Google Scholar] [CrossRef]
- Steinmetz, T.; Helias, M.; Wimmer, G.; Fichte, L.O.; Clemens, M. Electro-Quasistatic Field Simulations Based on a Discrete Electromagnetism Formulation. IEEE Trans. Magn. 2006, 42, 755–758. [Google Scholar] [CrossRef]
- Clemens, M.; Wilke, M.; Benderskaya, G.; DeGersem, H.; Koch, W.; Weiland, T. Transient Electro-Quasistatic Adaptive Simulation Schemes. IEEE Trans. Magn. 2004, 40, 1294–1297. [Google Scholar] [CrossRef]
- Lupo, G.; Petrarca, C.; Egiziano, L.; Tucci, V.; Vitelli, M. Numerical Evaluation of the Field in Cable Terminations Equipped with nonlinear Grading Materials. Annual Report. In Proceedings of the Eletrical Insulation and Dielectric Phenomena (CEIDP), Atlanta, GA, USA, 25–28 October 1998; pp. 585–588. [Google Scholar] [CrossRef]
- Liu, Y.; Zhang, S.; Cao, X.; Zhang, C.; Li, W. Simulation of Electric Field Distribution in the XLPE Insulation of a 320 kV DC Cable under Steady and Time-Varying States. IEEE Trans. Dielectr. Electr. Insul. 2018, 25, 954–964. [Google Scholar] [CrossRef]
- Mauseth, F.; Haugdal, H. Electric Field Simulations of High Voltage DC Extruded Cable Systems. IEEE Electr. Insul. Mag. 2017, 33, 16–21. [Google Scholar] [CrossRef] [Green Version]
- Jörgens, C.; Clemens, M. Simulation of the Electric Field in High Voltage Direct Current Cables considering the Environment. Annual Report. In Proceedings of the 10th International Conference on Computational Electromagnetics (CEM), Edinburgh, UK, 19–20 June 2019. [Google Scholar] [CrossRef]
- Jörgens, C.; Clemens, M. Comparison of Two Electro-Quasistatic Field Formulations for the Computation of Electric Field and Space Charges in HVDC Cable Systems’. Annual Report. In Proceedings of the 22nd International Conference on the Computation of Electromagnetic Fields (COMPUMAG), Paris, France, 15–19 July 2019. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II: Stiff and Differential Algebraic Problems, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Hecht, F. New development in FreeFem++. J. Numer. Math. 2012, 20, 251–266. [Google Scholar] [CrossRef]
- Ebert, S.; Sill, F.; Diederichs, J. Extruded XLPE DC underground-cable technology and experiences up to 525 kV—A key building block for the German “Energiewende”. In VDE High Voltage Technology 2016; Annual Report; VDE: Berlin, Germany, 2016; pp. 8–13. [Google Scholar]
- Heinhold, L.; Stubbe, R. Kabel und Leitungen für Starkstrom; Publics MCD Verlag: Erlangen, Germany, 1999; pp. 271–295, 306–318. ISBN 3-89578-088-X. [Google Scholar]
- Peschke, E.; Olshausen, R.v. Kabelanlagen für Hoch- und Höchstspannung; Publics MCD Verlag: Erlangen, Germany, 1998; pp. 72–77. ISBN 3-89578-057-X. [Google Scholar]
- High Voltage Cable Systems–Cables and Accessories up to 550 kV nkt datasheet. Tech. Rep. 2012. Available online: https://www.cablejoints.co.uk/upload/NKT_Cables_Extra_High_Voltage_132kV_220kV_400kV_500kV___Brochure.pdf (accessed on 15 July 2021).
- Spitzner, M.H. VDI Wärmeatlas, 11th ed.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 196–198, 648, 686–687, 753–760. [Google Scholar] [CrossRef]
- Qi, X.; Boggs, S.A. Thermal and Mechanical Properties of EPR and XLPE Cable Components. IEEE Electr. Insul. Mag. 2006, 22, 19–24. [Google Scholar] [CrossRef]
- Eichhorn, R.M. A critical comparison of XLPE and EPR for use as electrical insulation on underground power cables. IEEE Trans. Electr. Insul. 1981, EI-6, 469–482. [Google Scholar] [CrossRef]
- Bodega, R.; Perego, G.; Morshuis, P.H.F.; Nilsson, U.H.; Smit, J.J. Space Charge and Electric Field Characteristics of Polymeric-type MV-size DC Cable Joint Models. Annual Report. In Proceedings of the Eletrical Insulation and Dielectric Phenomena (CEIDP), Nashville, TN, USA, 16–19 October 2005; pp. 507–510. [Google Scholar] [CrossRef]
- Eoll, C.K. Theory of Stress Distribution in Insulation of High-Voltage DC Cables: Part I. IEEE Trans. Dielectr. Electr. Insul. 1975, EI-10, 27–35. [Google Scholar] [CrossRef]
- Bodega. R. Space Charge Accumulation in Polymeric High Voltage Cable Systems. Ph.D. Thesis, Technical University of Delft, Delft, The Netherlands, 2006.
- Christen, T. Characterization and Robustness of HVDC Insulation.Annual Report. In Proceedings of the 13th International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; pp. 238–241. [Google Scholar] [CrossRef]
- Boggs, S.A.; Damon, D.H.; Hjerrild, J.; Holboll, J.T.; Henriksen, M. Effect of insulation properties on the field grading of solid dielectric DC cable. IEEE Trans. Power Del. 2001, 16, 456–461. [Google Scholar] [CrossRef]
- Küchler, A. High Voltage Engineering–Fundamentals Technology-Applications, 5th ed.; Springer Vieweg: Berlin/Heidelberg, Germany, 2018; pp. 310–317. [Google Scholar] [CrossRef]
- Allam, E.M.; McKean, A.L. Design of an Optimized ±600 kV DC Cable System. IEEE Trans. Power Appar. Syst. 1980, PAS-99, 1713–1721. [Google Scholar] [CrossRef]
- Huang. Z. Rating Methodology of High Voltage Mass Impregnated DC Cable Circuits. Ph.D. Thesis, University of Southampton, Southampton, UK, 2014.
- Frank, D.W.; Jos, V.R.; George, A.; Bruno, B.; Rusty, B.; James, P.; Marcio, C.; Georg, H.; Nikola, K.; Bo, M.; et al. A Guide for Rating Calculations of Insulated Cables. Cigré Tech. Broch. 2015, 640, 9–10, 30–45. [Google Scholar]
- De Wild, F.; Anders, G.J.; Bascom, E.C., III; Cray, S.; Joo, J.; Thyrvin, O. Overview of Cigré WG B1.56 regarding the verification of cable current ratings. In Proceedings of the 10th International Conference on Insulated Power Cables (JICABLE), Paris, France, 23–26 June 2019; pp. 1–6. [Google Scholar]





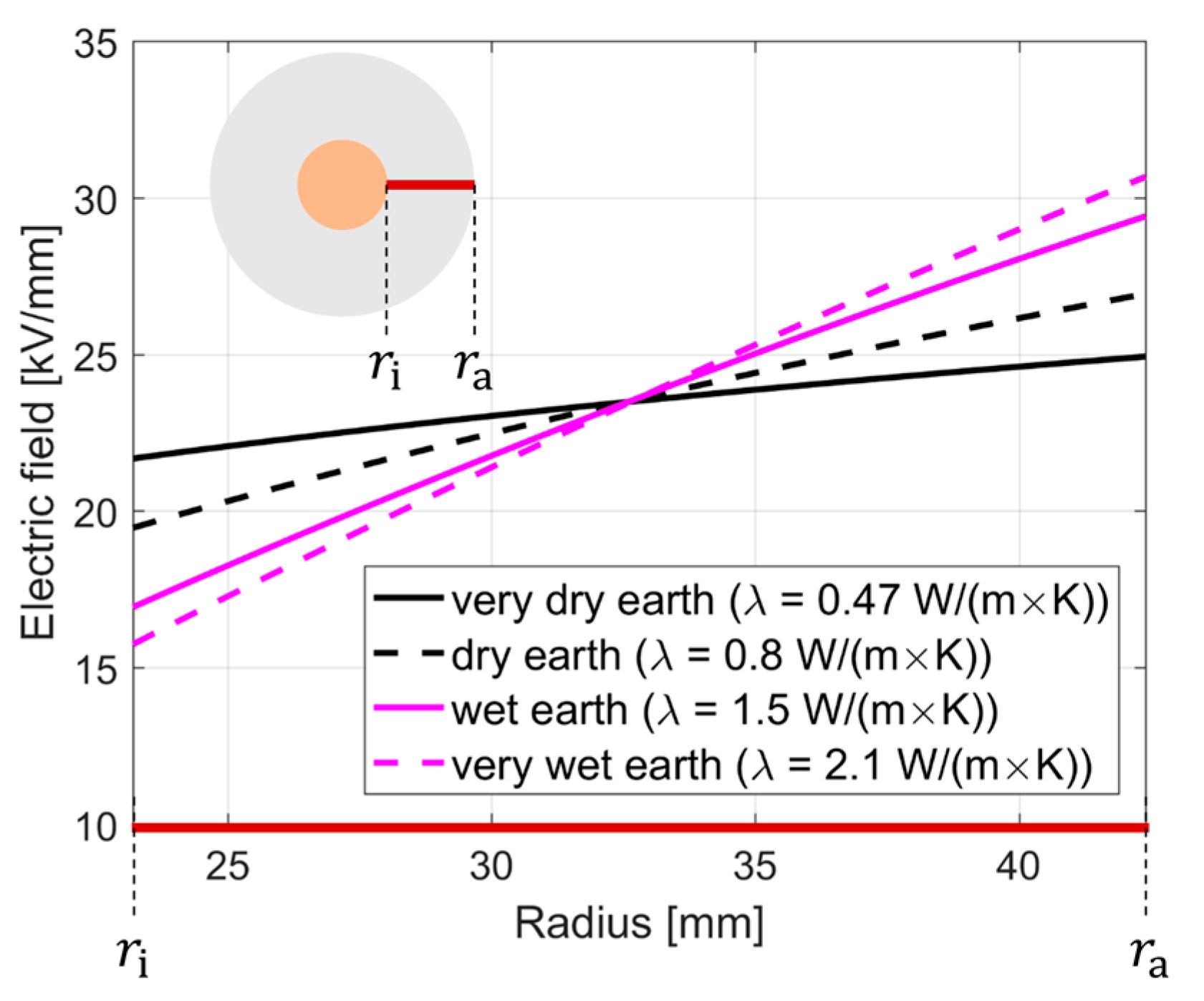
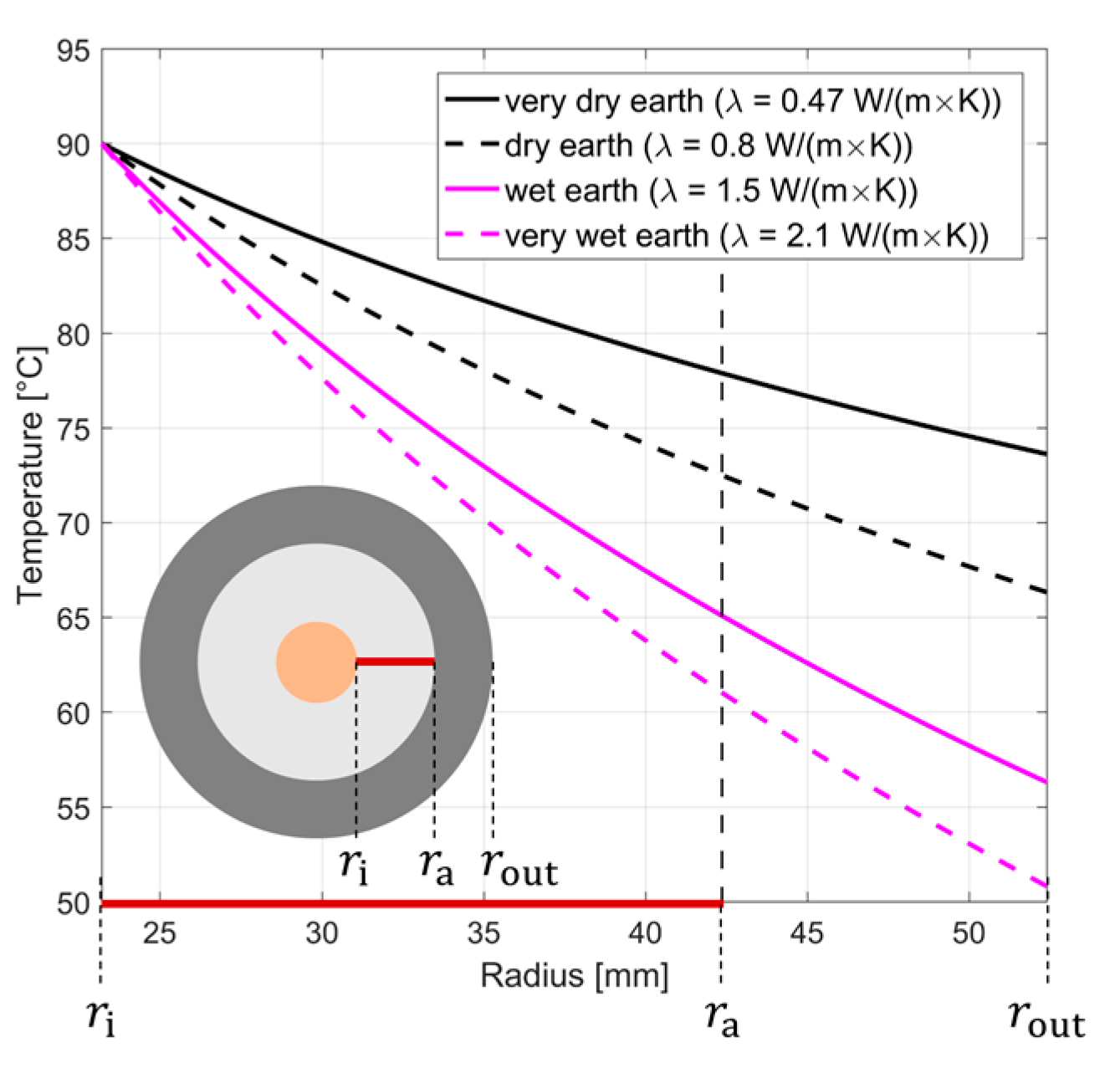
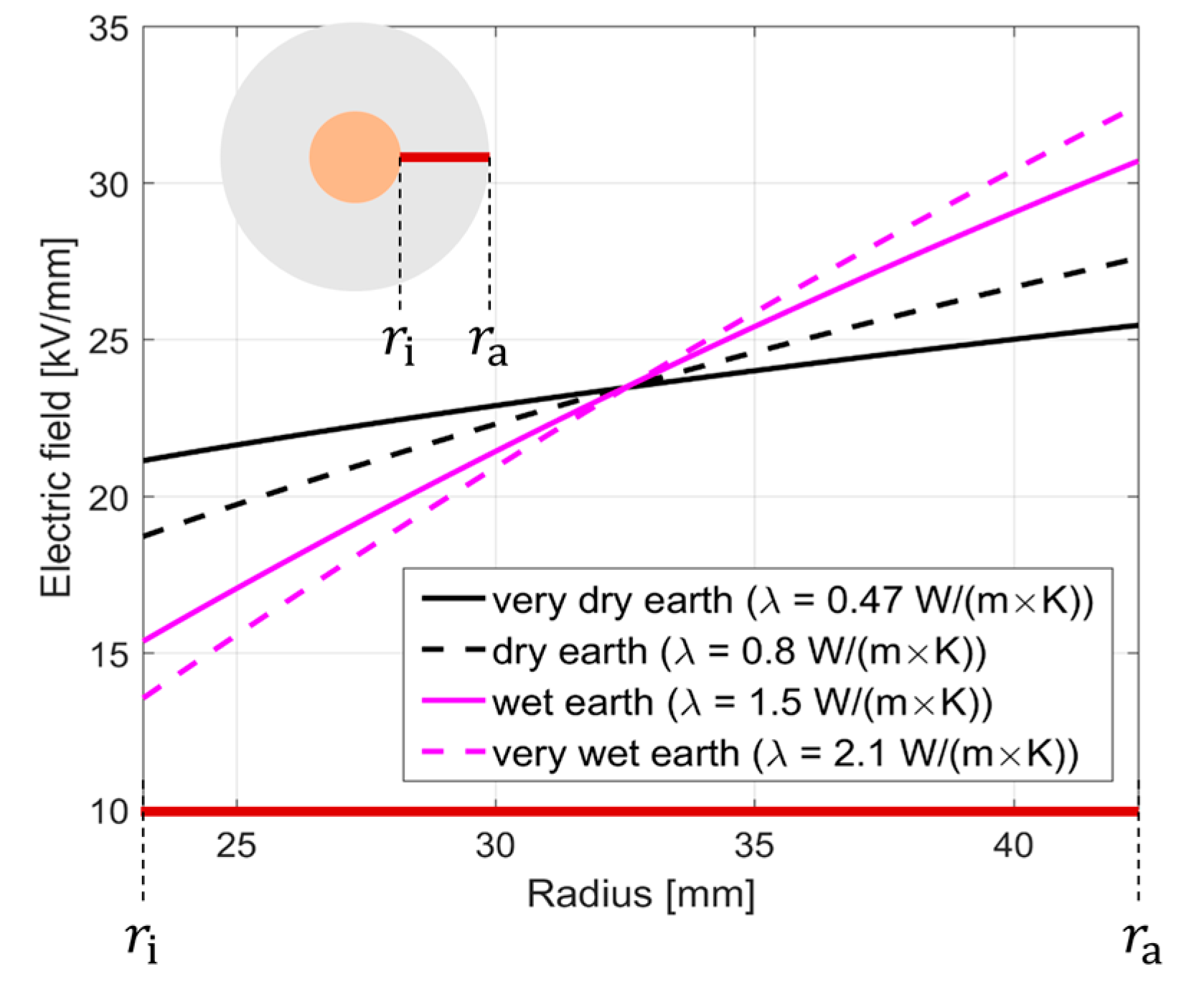
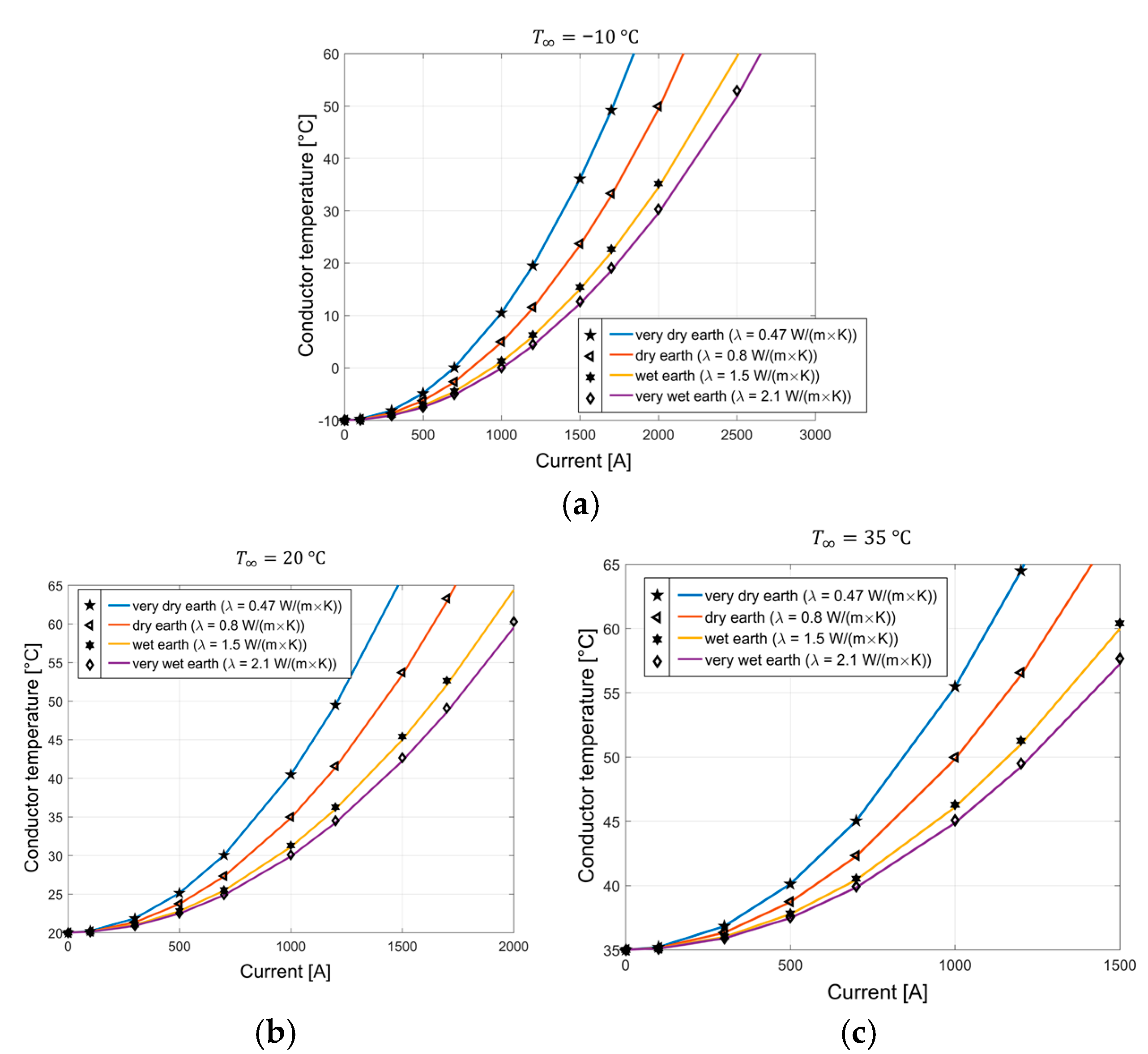

| Parameter | XLPE | MI |
|---|---|---|
| ri | 23.2 mm | 23.3 mm |
| ra | 42.4 mm | 42.4 mm |
| rout | 52.4 mm | 52.4 mm |
| λ | 0.3 W/(m×K) | 0.167 W/(m×K) |
| λPE | 0.3 W/(m×K) | 0.3 W/(m×K) |
| Ti | 90 °C | 55 °C |
| T∞ | 20 °C | 20 °C |
| εr | 2.3 | 3.5 |
| λEarth = 0.47 W/(m × K) | λEarth = 2.1 W/(m × K) | |
|---|---|---|
| T(ra) in XLPE | 77.9 °C | 61 °C |
| T(ra) in MI | 45.4 °C | 35.4 °C |
| T = T(ra) + (Ti − T(ra))/2in XLPE | 84 °C | 75.5 °C |
| T = T(ra) + (Ti − T(ra))/2in MI | 50.2 °C | 45.2 °C |
| E = U/(ra − ri)in XLPE | 23.4 kV/mm | 23.4 kV/mm |
| E = U/(ra − ri)in MI | 23.4 kV/mm | 23.4 kV/mm |
| (14) in XLPE | 0.3 W/m (83 W/m3) | 0.2 W/m (38 W/m3) |
| (15) in XLPE | 38 W/m (22∙103 W/m3) | 91 W/m (54∙103 W/m3) |
| (14) in MI | 0.2 W/m (46 W/m3) | 0.1 W/m (30 W/m3) |
| (15) in MI | 17 W/m (10∙103 W/m3) | 34 W/m (20∙103 W/m3) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jörgens, C.; Clemens, M. Electric Field and Temperature Simulations of High-Voltage Direct Current Cables Considering the Soil Environment. Energies 2021, 14, 4910. https://doi.org/10.3390/en14164910
Jörgens C, Clemens M. Electric Field and Temperature Simulations of High-Voltage Direct Current Cables Considering the Soil Environment. Energies. 2021; 14(16):4910. https://doi.org/10.3390/en14164910
Chicago/Turabian StyleJörgens, Christoph, and Markus Clemens. 2021. "Electric Field and Temperature Simulations of High-Voltage Direct Current Cables Considering the Soil Environment" Energies 14, no. 16: 4910. https://doi.org/10.3390/en14164910






