CFD-DEM Simulation of Fluidization of Polyhedral Particles in a Fluidized Bed
Abstract
:1. Introduction
2. Mathematical Model
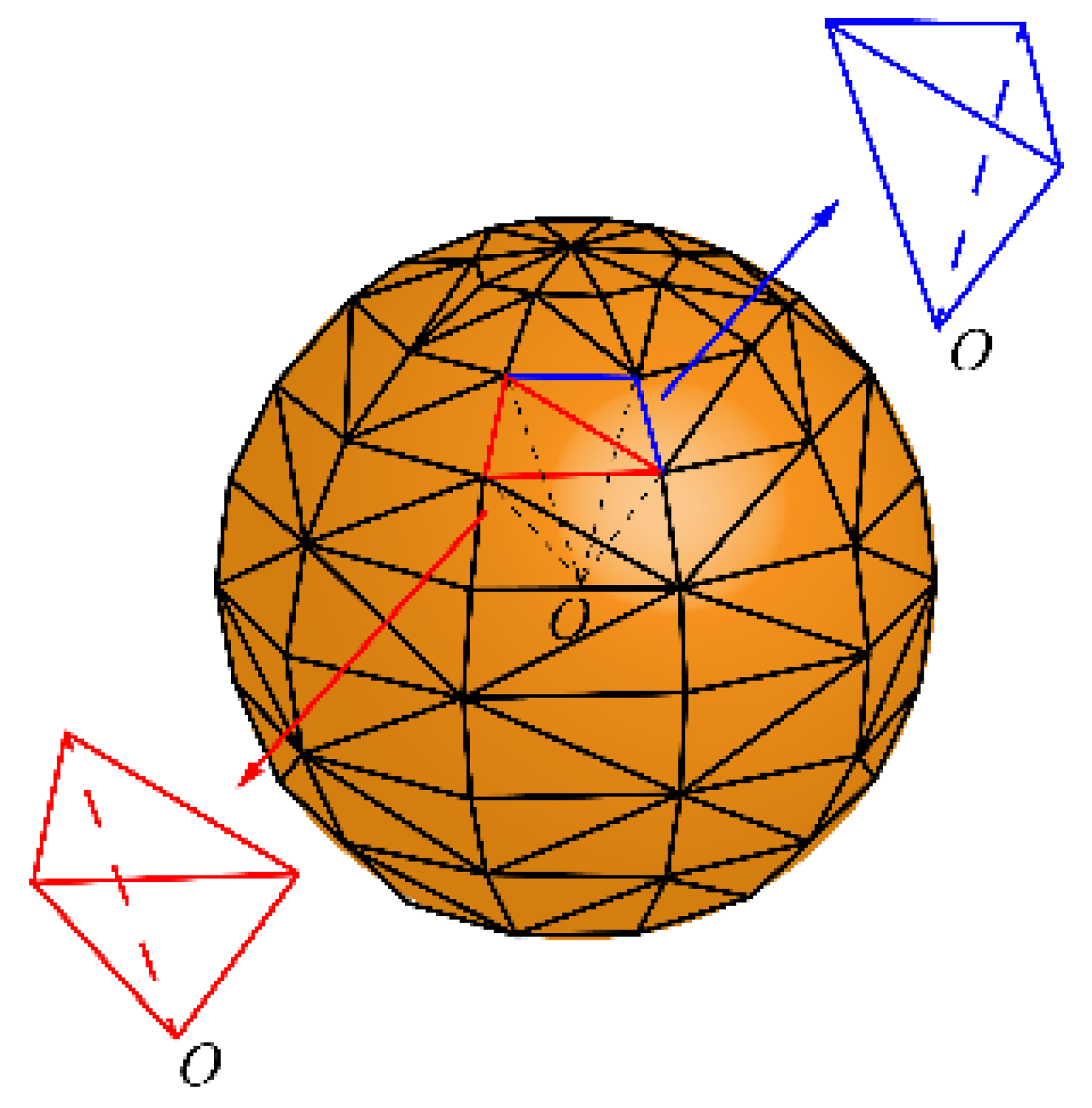
2.1. Particle Shape Representation Approach
2.2. Particle Motion Equations
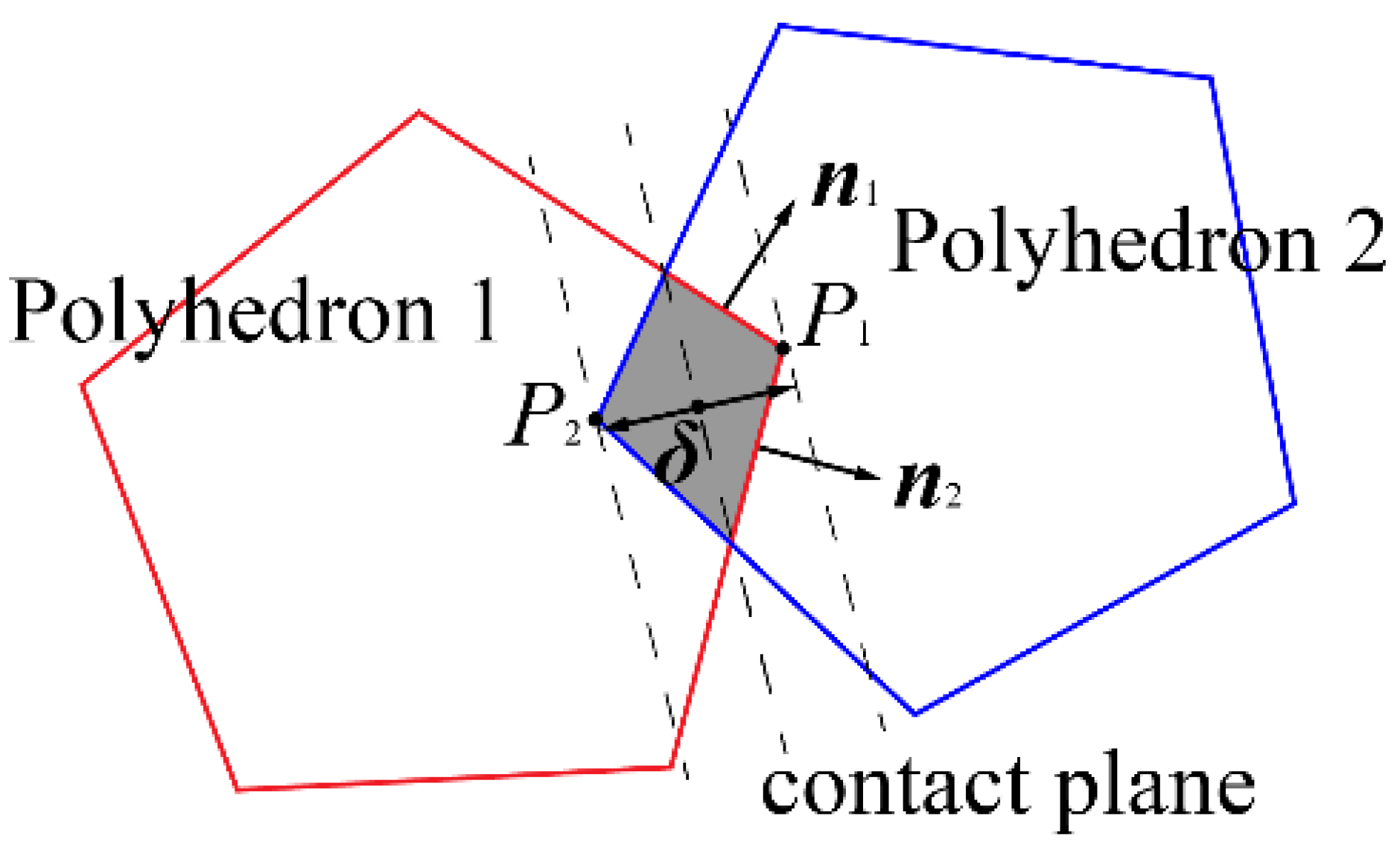
2.3. Contact Detection
2.4. Fluid Motion Equations
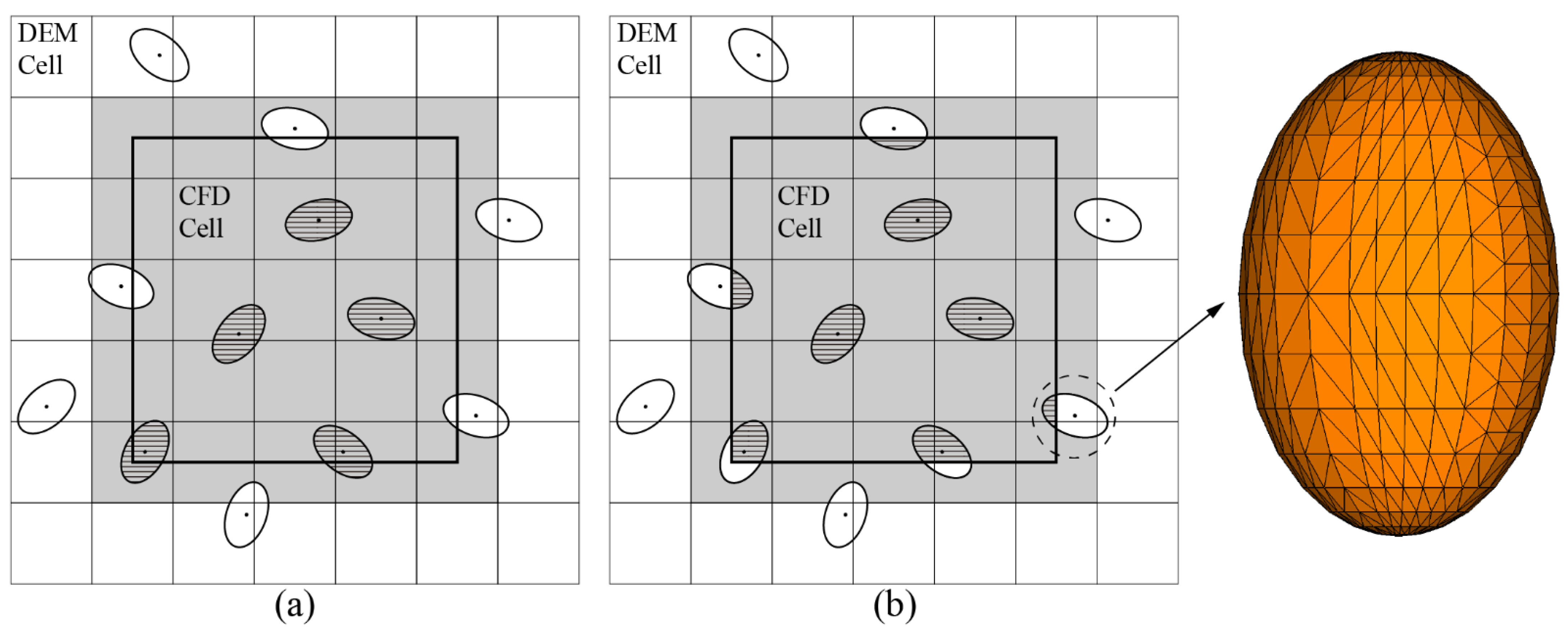
2.5. Gas-Particle Interaction Force
3. Solution and Simulation Conditions
4. Validation and Discussion
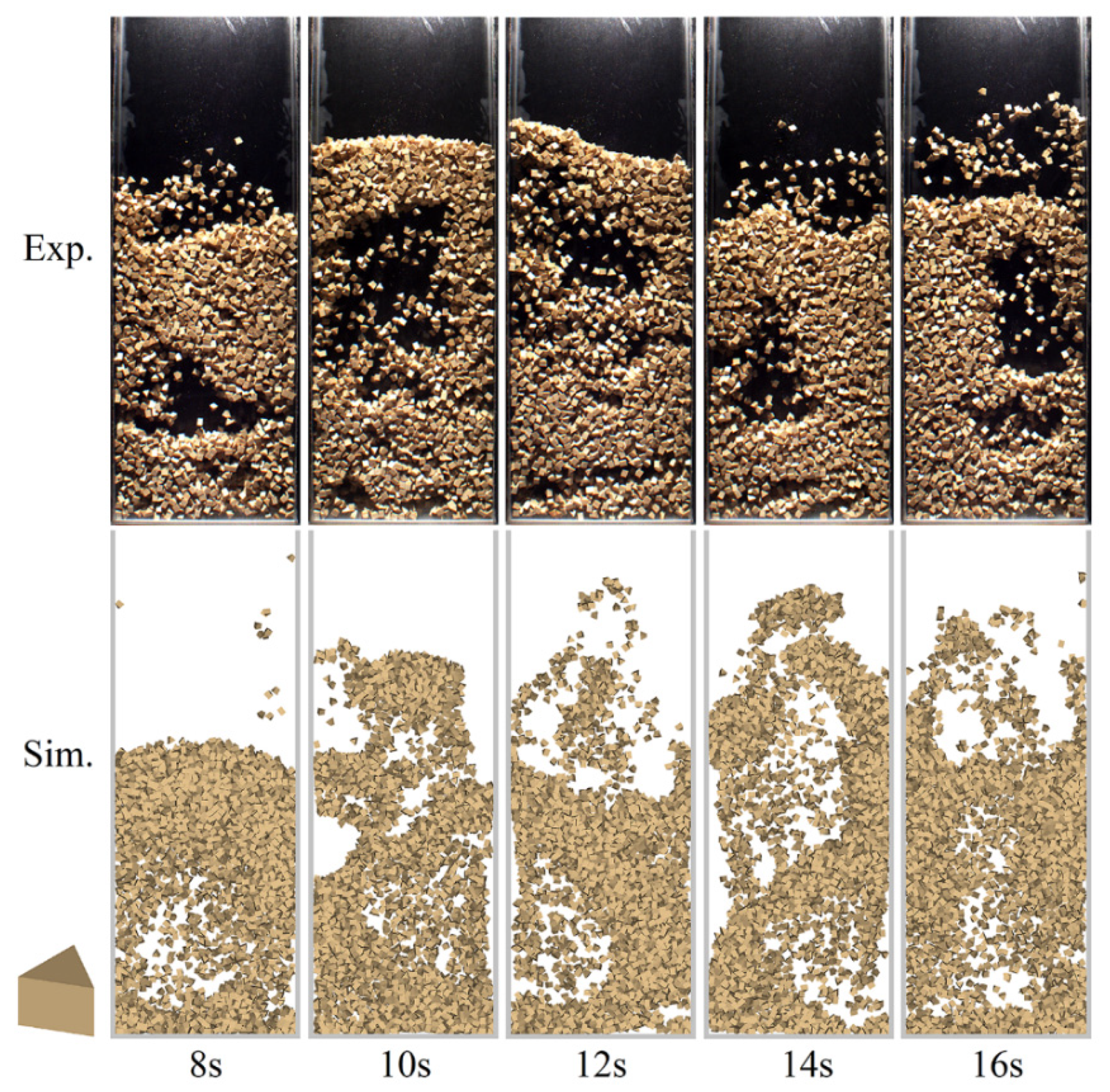
4.1. Validation of the CFD-DEM Model
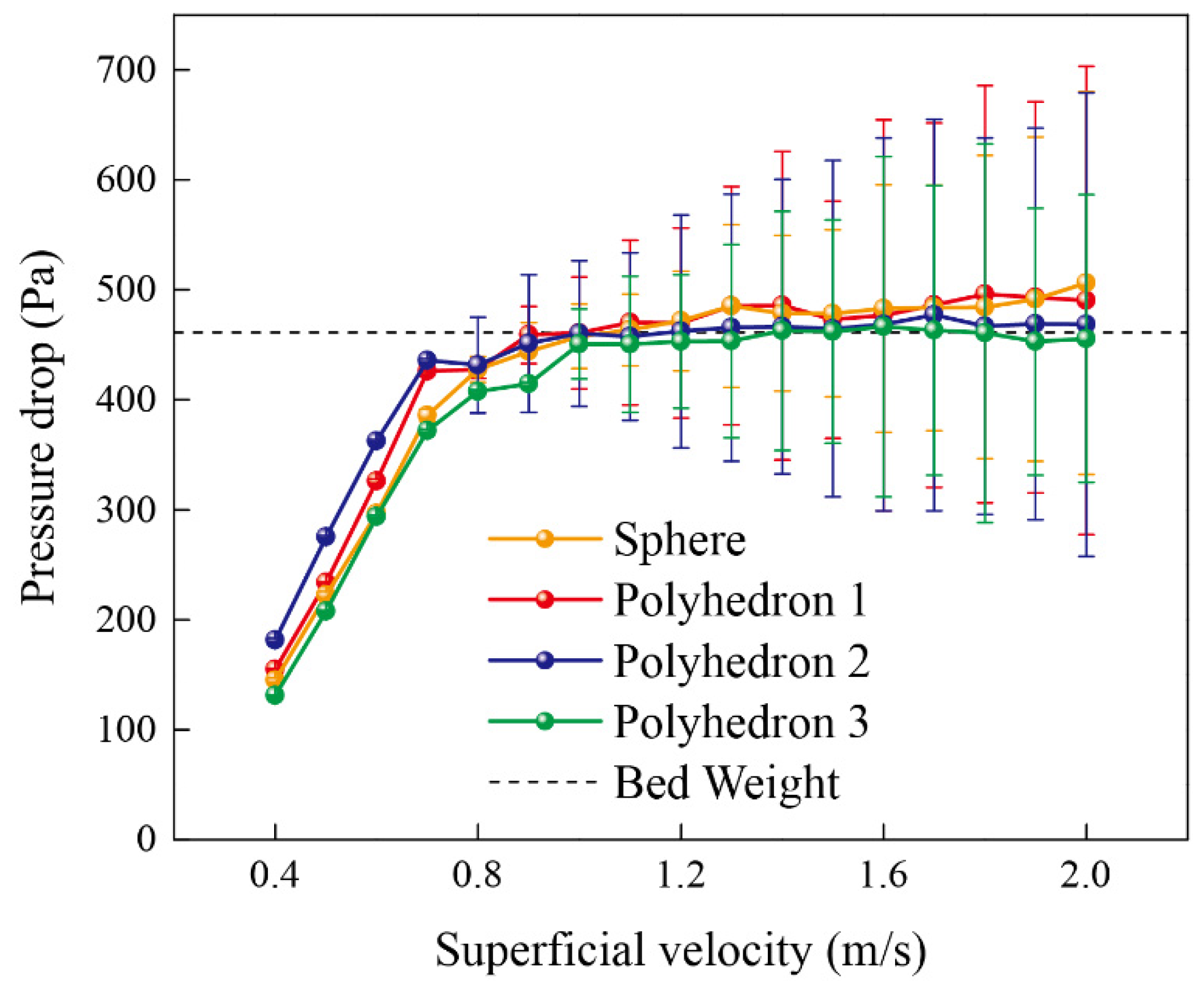
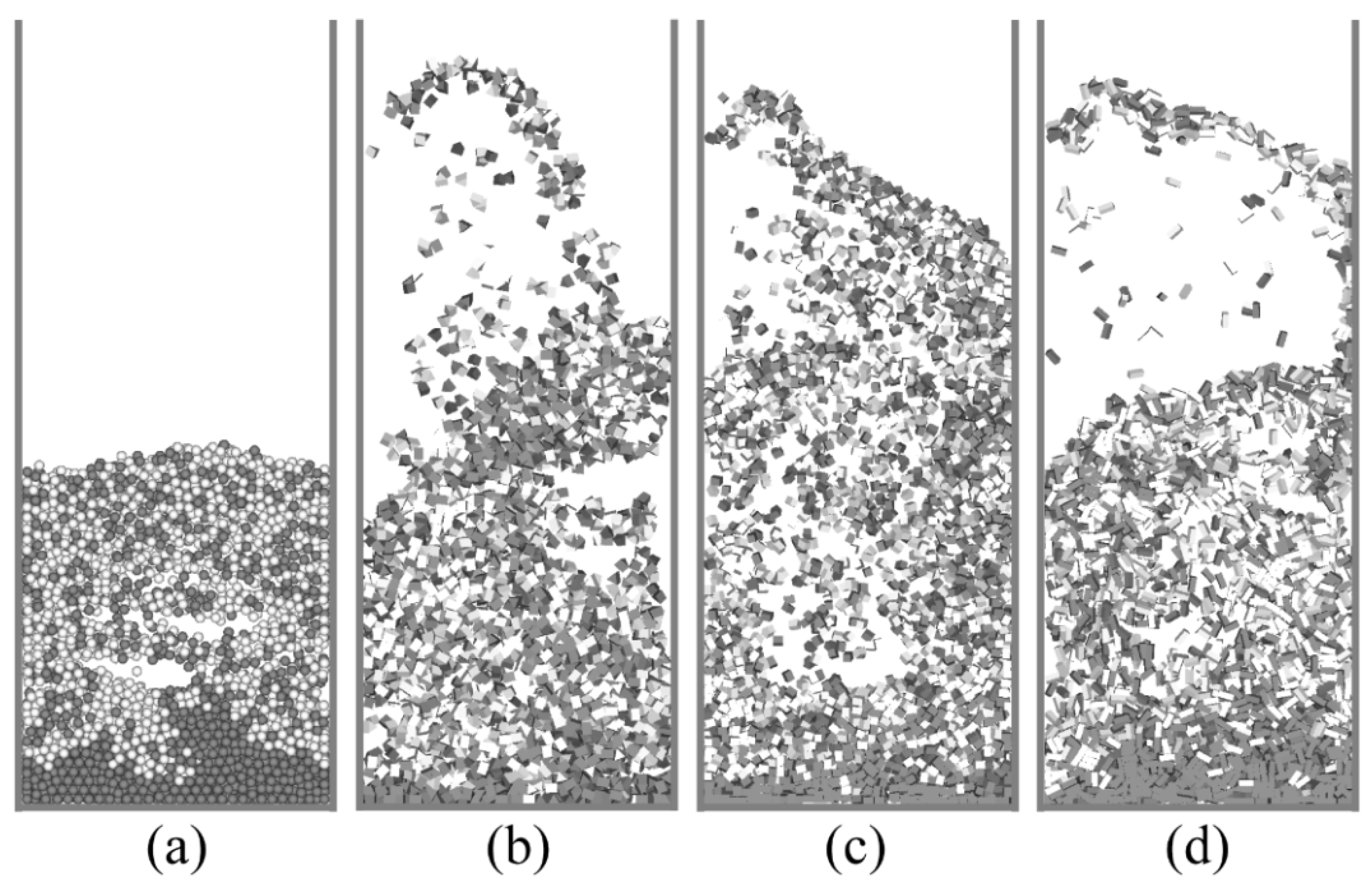
4.2. Fluidization Behaviors of Different Particles
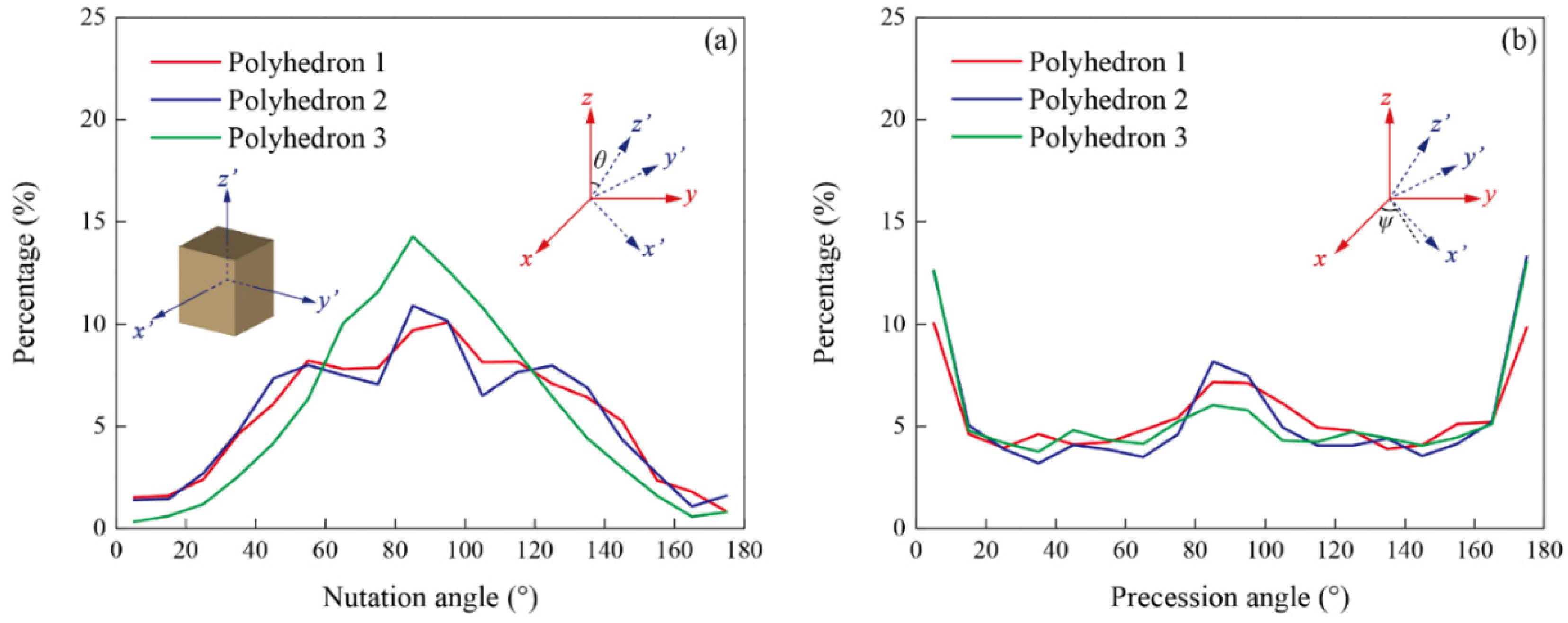
4.3. Particle Mixing in the Fluidized Bed
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Azmir, J.; Hou, Q.; Yu, A. CFD-DEM simulation of drying of food grains with particle shrinkage. Powder Technol. 2019, 343, 792–802. [Google Scholar] [CrossRef]
- Zhong, W.; Yu, A.; Liu, X.; Tong, Z.; Zhang, H. DEM/CFD-DEM Modelling of Non-spherical Particulate Systems: Theoretical Developments and Applications. Powder Technol. 2016, 302, 108–152. [Google Scholar] [CrossRef]
- Ma, H.; Xu, L.; Zhao, Y. CFD-DEM simulation of fluidization of rod-like particles in a fluidized bed. Powder Technol. 2017, 314, 355–366. [Google Scholar] [CrossRef]
- Höhner, D.; Wirtz, S.; Kruggel-Emden, H.; Scherer, V. Comparison of the multi-sphere and polyhedral approach to simulate non-spherical particles within the discrete element method: Influence on temporal force evolution for multiple contacts. Powder Technol. 2011, 208, 643–656. [Google Scholar] [CrossRef]
- Zhou, Y.; Zhou, B.; Li, J.; Wang, H. Study on the Multi-sphere Method Modeling the 3D Particle Morphology in DEM. Springer Proc. Phys. 2017, 188, 601–608. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Y.; Cheng, Y. CFD-DEM modeling of rod-like particles in a fluidized bed with complex geometry. Powder Technol. 2019, 344, 673–683. [Google Scholar] [CrossRef]
- Vollmari, K.; Oschmann, T.; Kruggel-Emden, H. Mixing quality in mono- and bidisperse systems under the influence of particle shape: A numerical and experimental study. Powder Technol. 2017, 308, 101–113. [Google Scholar] [CrossRef]
- Chang, J.; Wang, G.; Gao, J.; Zhang, K.; Chen, H.; Yang, Y. CFD modeling of particle–particle heat transfer in dense gas-solid fluidized beds of binary mixture. Powder Technol. 2012, 217, 50–60. [Google Scholar] [CrossRef]
- Lu, G.; Third, J.; Müller, C. Discrete element models for non-spherical particle systems: From theoretical developments to applications. Chem. Eng. Sci. 2015, 127, 425–465. [Google Scholar] [CrossRef]
- Cundall, P.A.; Strack, O.D.L. A discrete numerical model for granular assemblies. Géotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Tsuji, Y.; Kawaguchi, T.; Tanaka, T. Discrete particle simulation of two-dimensional fluidized bed. Powder Technol. 1993, 77, 79–87. [Google Scholar] [CrossRef]
- Kruggel-Emden, H.; Rickelt, S.; Wirtz, S.; Scherer, V. A study on the validity of the multi-sphere Discrete Element Method. Powder Technol. 2008, 188, 153–165. [Google Scholar] [CrossRef]
- Lin, X.; Ng, T.-T. Contact detection algorithms for three-dimensional ellipsoids in discrete element modelling. Int. J. Numer. Anal. Methods Géoméch. 1995, 19, 653–659. [Google Scholar] [CrossRef]
- Yan, B.; Regueiro, R.A.; Sture, S. Three-dimensional ellipsoidal discrete element modeling of granular materials and its coupling with finite element facets. Eng. Comput. 2010, 27, 519–550. [Google Scholar] [CrossRef]
- Mola, I.; Yu, A.; Zhou, Z. Particle scale modelling of mixing of ellipsoids and spheres in gas-fluidized beds by a modified drag correlation. Powder Technol. 2019, 343, 619–628. [Google Scholar] [CrossRef]
- You, Y.; Liu, M.; Ma, H.; Xu, L.; Liu, B.; Shao, Y.; Tang, Y.; Zhao, Y. Investigation of the vibration sorting of non-spherical particles based on DEM simulation. Powder Technol. 2018, 325, 316–332. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Y. Modelling of the flow of ellipsoidal particles in a horizontal rotating drum based on DEM simulation. Chem. Eng. Sci. 2017, 172, 636–651. [Google Scholar] [CrossRef]
- Zhao, Y.; Xu, L.; Umbanhowar, P.B.; Lueptow, R.M. Discrete element simulation of cylindrical particles using super-ellipsoids. Particuology 2019, 46, 55–66. [Google Scholar] [CrossRef]
- Govender, N.; Wilke, D.N.; Kok, S. Collision detection of convex polyhedra on the NVIDIA GPU architecture for the discrete element method. Appl. Math. Comput. 2015, 267, 810–829. [Google Scholar] [CrossRef]
- Govender, N.; Rajamani, R.; Wilke, D.; Wu, C.-Y.; Khinast, J.; Glasser, B.J. Effect of particle shape in grinding mills using a GPU based DEM code. Miner. Eng. 2018, 129, 71–84. [Google Scholar] [CrossRef] [Green Version]
- Höhner, D.; Wirtz, S.; Scherer, V. Experimental and numerical investigation on the influence of particle shape and shape approximation on hopper discharge using the discrete element method. Powder Technol. 2013, 235, 614–627. [Google Scholar] [CrossRef]
- Smeets, B.; Odenthal, T.; Vanmaercke, S.; Ramon, H. Polygon-based contact description for modeling arbitrary polyhedra in the Discrete Element Method. Comput. Methods Appl. Mech. Eng. 2015, 290, 277–289. [Google Scholar] [CrossRef] [Green Version]
- Xie, C.; Song, T.; Zhao, Y. Discrete element modeling and simulation of non-spherical particles using polyhedrons and super-ellipsoids. Powder Technol. 2020, 368, 253–267. [Google Scholar] [CrossRef]
- Freireich, B.; Kumar, R.; Ketterhagen, W.; Su, K.; Wassgren, C.; Zeitler, A. Comparisons of intra-tablet coating variability using DEM simulations, asymptotic limit models, and experiments. Chem. Eng. Sci. 2015, 131, 197–212. [Google Scholar] [CrossRef] [Green Version]
- Tao, H.; Jin, B.; Zhong, W.; Wang, X.; Ren, B.; Zhang, Y.; Xiao, R. Discrete element method modeling of non-spherical granular flow in rectangular hopper. Chem. Eng. Process. Process. Intensif. 2010, 49, 151–158. [Google Scholar] [CrossRef]
- Markauskas, D.; Kačianauskas, R.; Džiugys, A.; Navakas, R. Investigation of adequacy of multi-sphere approximation of elliptical particles for DEM simulations. Granul. Matter 2009, 12, 107–123. [Google Scholar] [CrossRef]
- Liu, Z.; Zhao, Y. Multi-super-ellipsoid model for non-spherical particles in DEM simulation. Powder Technol. 2020, 361, 190–202. [Google Scholar] [CrossRef]
- Liu, Z.; Ma, H.; Zhao, Y. Comparative study of discrete element modeling of tablets using multi-spheres, multi-super-ellipsoids, and polyhedrons. Powder Technol. 2021, 390, 34–49. [Google Scholar] [CrossRef]
- Hölzer, A.; Sommerfeld, M. New simple correlation formula for the drag coefficient of non-spherical particles. Powder Technol. 2008, 184, 361–365. [Google Scholar] [CrossRef]
- Haider, A.; Levenspiel, O. Drag coefficient and terminal velocity of spherical and nonspherical particles. Powder Technol. 1989, 58, 63–70. [Google Scholar] [CrossRef]
- Tran-Cong, S.; Gay, M.; Michaelides, E.E. Drag coefficients of irregularly shaped particles. Powder Technol. 2004, 139, 21–32. [Google Scholar] [CrossRef]
- Ganser, G.H. A rational approach to drag prediction of spherical and nonspherical particles. Powder Technol. 1993, 77, 143–152. [Google Scholar] [CrossRef]
- Ma, H.; Zhao, Y. Investigating the fluidization of disk-like particles in a fluidized bed using CFD-DEM simulation. Adv. Powder Technol. 2018, 29, 2380–2393. [Google Scholar] [CrossRef]
- Liu, X.; Gan, J.; Zhong, W.; Yu, A. Particle shape effects on dynamic behaviors in a spouted bed: CFD-DEM study. Powder Technol. 2020, 361, 349–362. [Google Scholar] [CrossRef]
- Farivar, F.; Zhang, H.; Tian, Z.F.; Gupte, A. CFD-DEM -DDM Model for Spray Coating Process in a Wurster Coater. J. Pharm. Sci. 2020, 109, 3678–3689. [Google Scholar] [CrossRef]
- Cundall, P. Formulation of a three-dimensional distinct element model—Part I. A scheme to detect and represent contacts in a system composed of many polyhedral blocks. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1988, 25, 107–116. [Google Scholar] [CrossRef]
- Nezami, E.G.; Hashash, Y.M.; Zhao, D.; Ghaboussi, J. A fast contact detection algorithm for 3-D discrete element method. Comput. Geotech. 2004, 31, 575–587. [Google Scholar] [CrossRef]
- Nezami, E.G.; Hashash, Y.M.A.; Zhao, D.; Ghaboussi, J. Shortest link method for contact detection in discrete element method. Int. J. Numer. Anal. Methods Géoméch. 2006, 30, 783–801. [Google Scholar] [CrossRef]
- Dong, K.; Wang, C.; Yu, A. A novel method based on orientation discretization for discrete element modeling of non-spherical particles. Chem. Eng. Sci. 2015, 126, 500–516. [Google Scholar] [CrossRef]
- Boon, C.; Houlsby, G.; Utili, S. A new algorithm for contact detection between convex polygonal and polyhedral particles in the discrete element method. Comput. Geotech. 2012, 44, 73–82. [Google Scholar] [CrossRef]
- Feng, Y.; Han, K.; Owen, D. Energy-conserving contact interaction models for arbitrarily shaped discrete elements. Comput. Methods Appl. Mech. Eng. 2012, 205–208, 169–177. [Google Scholar] [CrossRef]
- Fraige, F.Y.; Langston, P.A.; Chen, G. Distinct element modelling of cubic particle packing and flow. Powder Technol. 2008, 186, 224–240. [Google Scholar] [CrossRef]
- Mack, S.; Langston, P.; Webb, C.; York, T. Experimental validation of polyhedral discrete element model. Powder Technol. 2011, 214, 431–442. [Google Scholar] [CrossRef]
- Liu, L.; Ji, S. Bond and fracture model in dilated polyhedral DEM and its application to simulate breakage of brittle materials. Granul. Matter 2019, 21, 41. [Google Scholar] [CrossRef]
- Govender, N.; Wilke, D.; Pizette, P.; Abriak, N.-E. A study of shape non-uniformity and poly-dispersity in hopper discharge of spherical and polyhedral particle systems using the Blaze-DEM GPU code. Appl. Math. Comput. 2018, 319, 318–336. [Google Scholar] [CrossRef]
- Oschmann, T.; Hold, J.; Kruggel-Emden, H. Numerical investigation of mixing and orientation of non-spherical particles in a model type fluidized bed. Powder Technol. 2014, 258, 304–323. [Google Scholar] [CrossRef]
- Oschmann, T.; Vollmari, K.; Kruggel-Emden, H.; Wirtz, S. Numerical Investigation of the Mixing of Non-spherical Particles in Fluidized Beds and during Pneumatic Conveying. Procedia Eng. 2015, 102, 976–985. [Google Scholar] [CrossRef] [Green Version]
- Vollmari, K.; Jasevičius, R.; Kruggel-Emden, H. Experimental and numerical study of fluidization and pressure drop of spherical and non-spherical particles in a model scale fluidized bed. Powder Technol. 2016, 291, 506–521. [Google Scholar] [CrossRef]
- Xiong, H.; Wu, H.; Bao, X.; Fei, J. Investigating effect of particle shape on suffusion by CFD-DEM modeling. Constr. Build. Mater. 2021, 289, 123043. [Google Scholar] [CrossRef]
- Tang, C.; Yang, Y.-C.; Liu, P.-Z.; Kim, Y.-J. Prediction of Abrasive and Impact Wear Due to Multi-Shaped Particles in a Centrifugal Pump via CFD-DEM Coupling Method. Energies 2021, 14, 2391. [Google Scholar] [CrossRef]
- Zhou, J.W.; Liu, Y.; Liu, S.Y.; Du, C.L.; Li, J.P. Effects of particle shape and swirling intensity on elbow erosion in dilute-phase pneumatic conveying. Wear 2017, 380, 66–77. [Google Scholar] [CrossRef]
- Di Felice, R. The voidage function for fluid-particle interaction systems. Int. J. Multiph. Flow 1994, 20, 153–159. [Google Scholar] [CrossRef]
- Mahajan, V.V.; Padding, J.T.; Nijssen, T.M.J.; Buist, K.A.; Kuipers, J.A.M. Nonspherical particles in a pseudo-2D fluidized bed: Experimental study. Part. Technol. Fluid. 2018, 64, 1573–1590. [Google Scholar] [CrossRef] [PubMed]
- Lacey, P.M.C. Developments in the theory of particle mixing. J. Appl. Chem. 2007, 4, 257–268. [Google Scholar] [CrossRef]









| Shape | Diameter (mm) | Length (mm) | Width (mm) | Height (mm) | Number |
|---|---|---|---|---|---|
| Sphere | 6.8 | 3600 | |||
| Polyhedron 1 | 8 | 8 | 6 | 3600 | |
| Polyhedron 2 | 5 | 5 | 6.5 | 3600 | |
| Polyhedron 3 | 4 | 4 | 10 | 3600 |
| Parameters | Value |
|---|---|
| Particle number | 3600 |
| Particle density (kg/m3) | 480 |
| Fluidized bed dimensions (m) (width × thickness × height) | 0.2 × 0.03 × 1.0 |
| Restitution coefficient | 0.5 |
| Friction coefficient between particles | 0.5 |
| Friction coefficient between particle and wall | 0.4 |
| Gas density (kg/m3) | 1.225 |
| Gas viscosity (Pa·s) | 1.79 × 10−5 |
| DEM time step (s) | 8 × 10−6 |
| CFD time step (s) | 4 × 10−5 |
| Sphere | Polyhedron 1 | Polyhedron 2 | Polyhedron 3 | |
|---|---|---|---|---|
| Fill height (mm) | 171.74 | 189.76 | 176.19 | 182.93 |
| Voidage fraction | 0.425 | 0.474 | 0.447 | 0.475 |
| Surface area (mm2) | 145.27 | 199.43 | 147.5 | 152 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Z.; Ma, H.; Zhao, Y. CFD-DEM Simulation of Fluidization of Polyhedral Particles in a Fluidized Bed. Energies 2021, 14, 4939. https://doi.org/10.3390/en14164939
Liu Z, Ma H, Zhao Y. CFD-DEM Simulation of Fluidization of Polyhedral Particles in a Fluidized Bed. Energies. 2021; 14(16):4939. https://doi.org/10.3390/en14164939
Chicago/Turabian StyleLiu, Zihan, Huaqing Ma, and Yongzhi Zhao. 2021. "CFD-DEM Simulation of Fluidization of Polyhedral Particles in a Fluidized Bed" Energies 14, no. 16: 4939. https://doi.org/10.3390/en14164939
APA StyleLiu, Z., Ma, H., & Zhao, Y. (2021). CFD-DEM Simulation of Fluidization of Polyhedral Particles in a Fluidized Bed. Energies, 14(16), 4939. https://doi.org/10.3390/en14164939






