Influence of Different Sites on Impact Response of Steel-Plate Concrete Containment against a Large Commercial Aircraft
Abstract
:1. Introduction
2. Numerical Analysis Method and Models
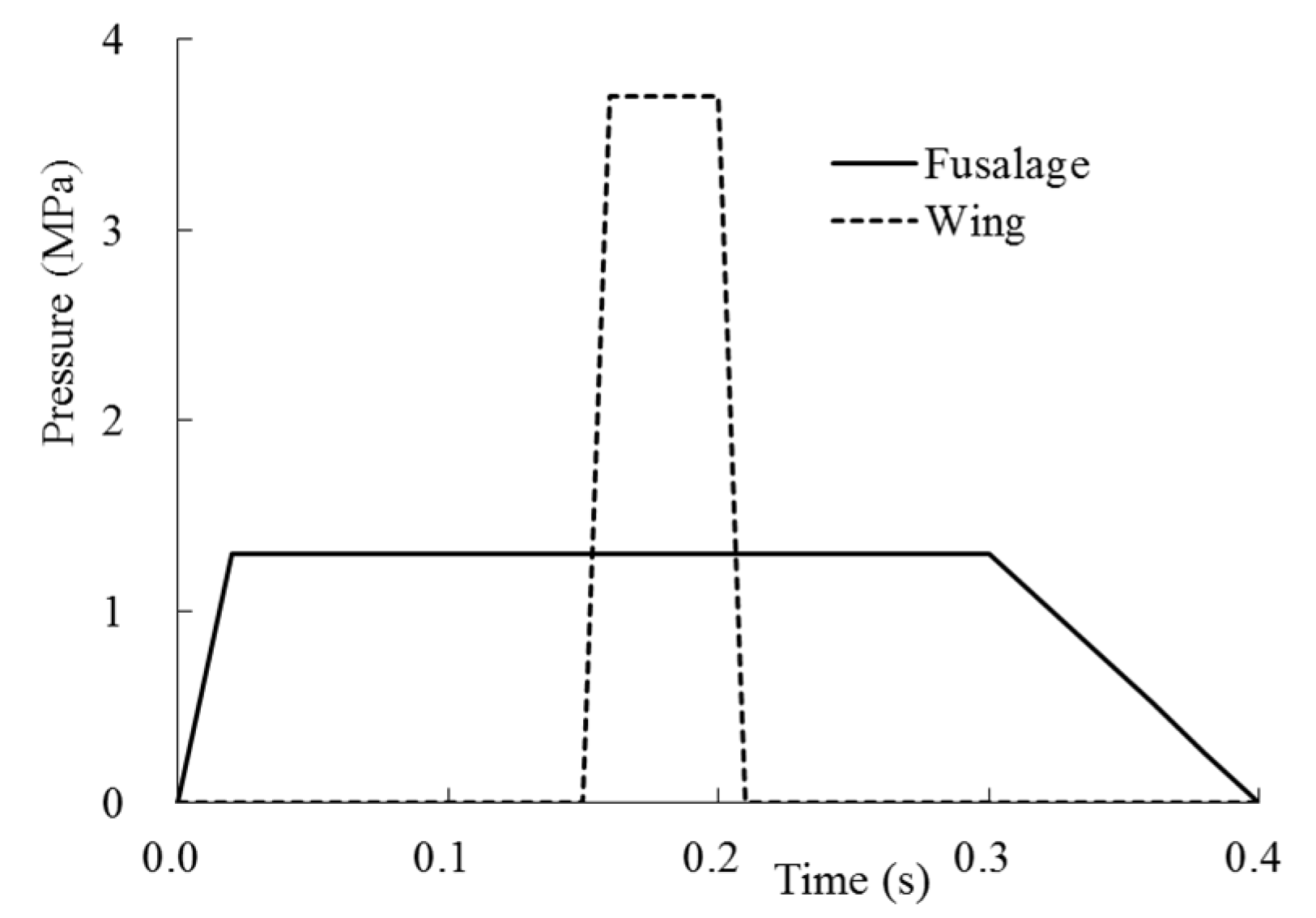
2.1. Impact Force Time-History Function
2.2. Numerical Model of Semi-Infinite Site
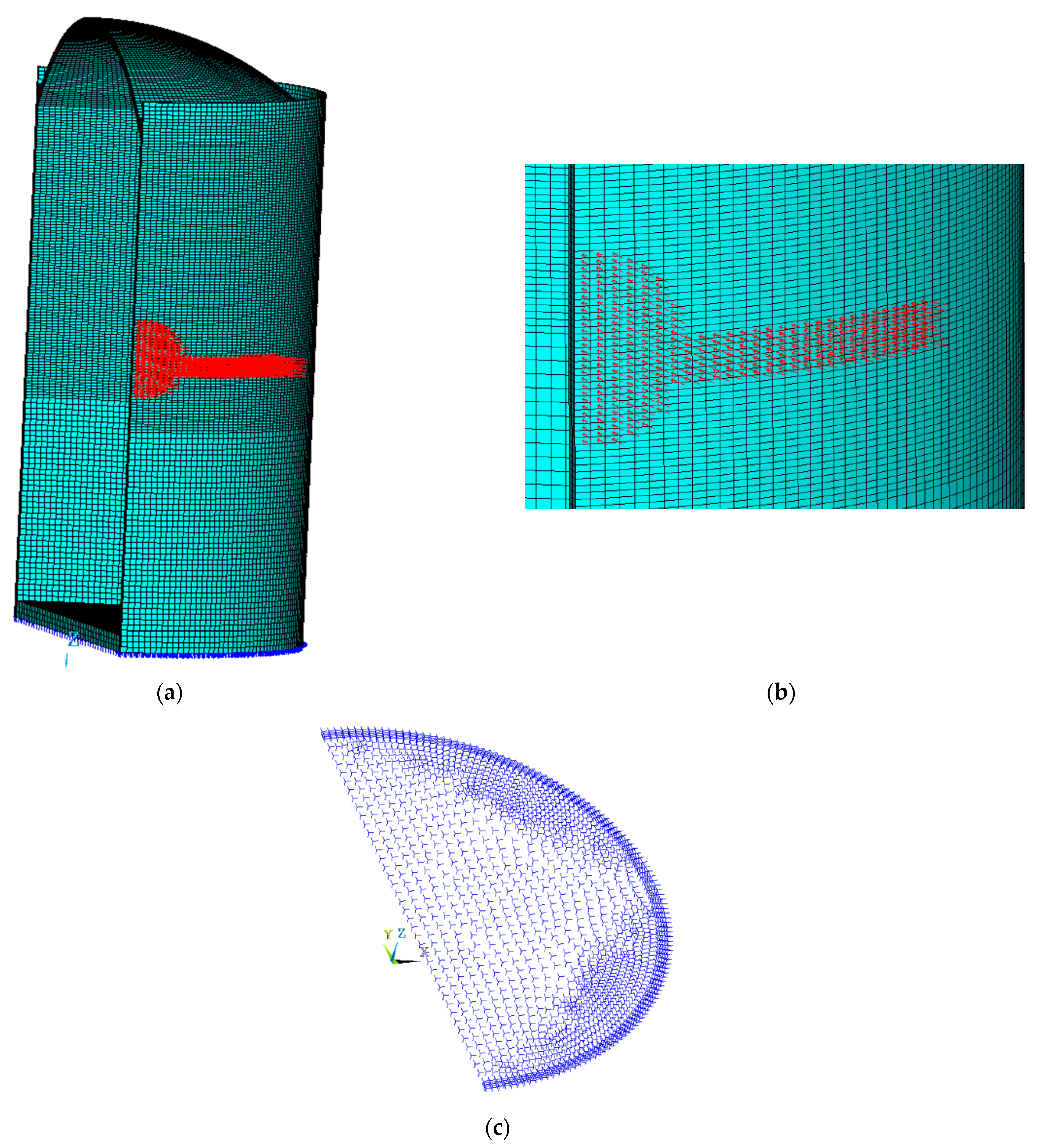
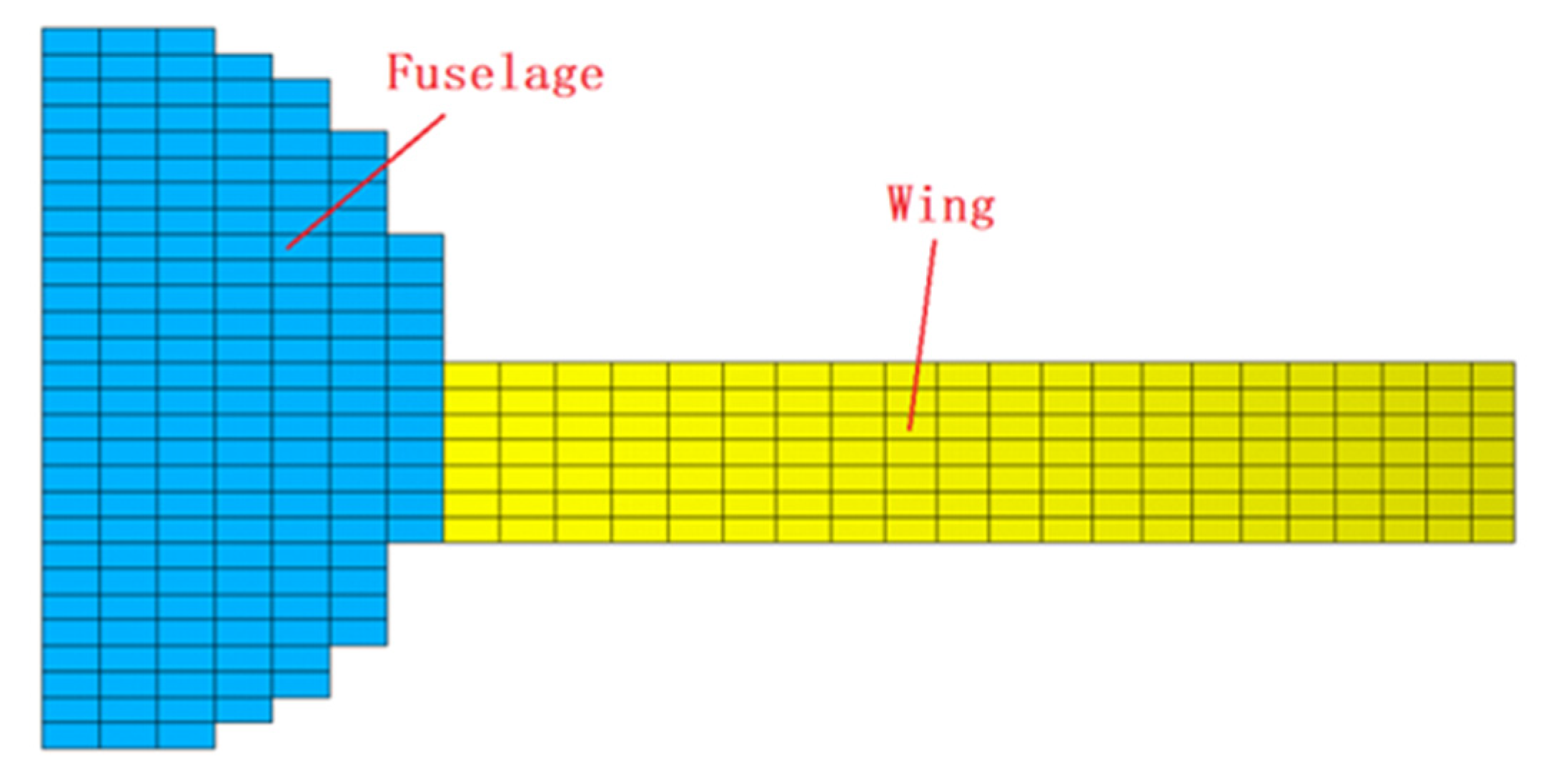
2.3. Finite Element Model
2.4. Numerical Material Models of Full SC Contaiment
2.4.1. Constitutive Model of Concrete and Steel Plate
2.4.2. Validation of Material Models
2.4.3. Material Properties of Full SC Containment
3. Results and Discussion
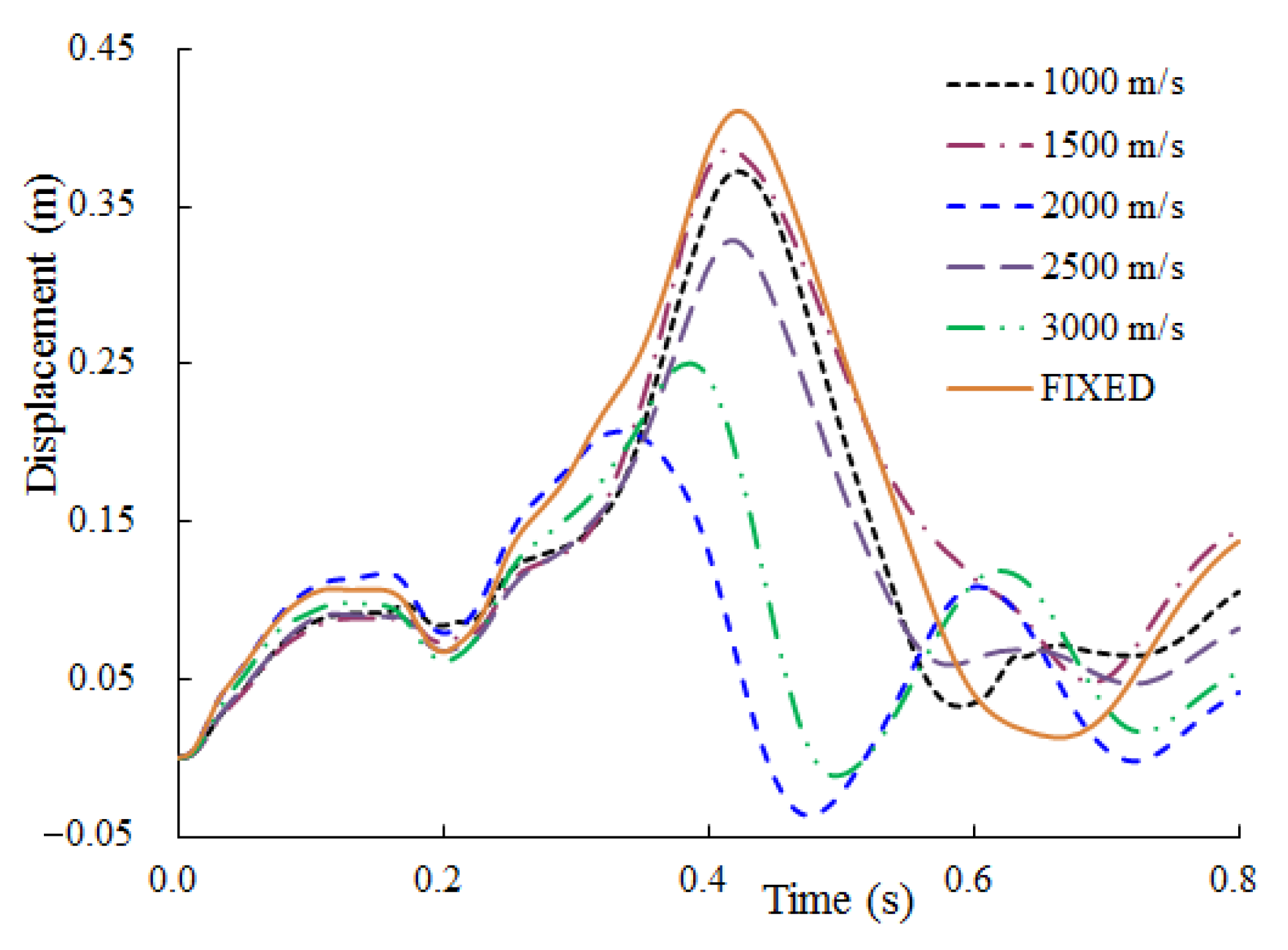
3.1. Comparison Analysis of Different Site Conditions
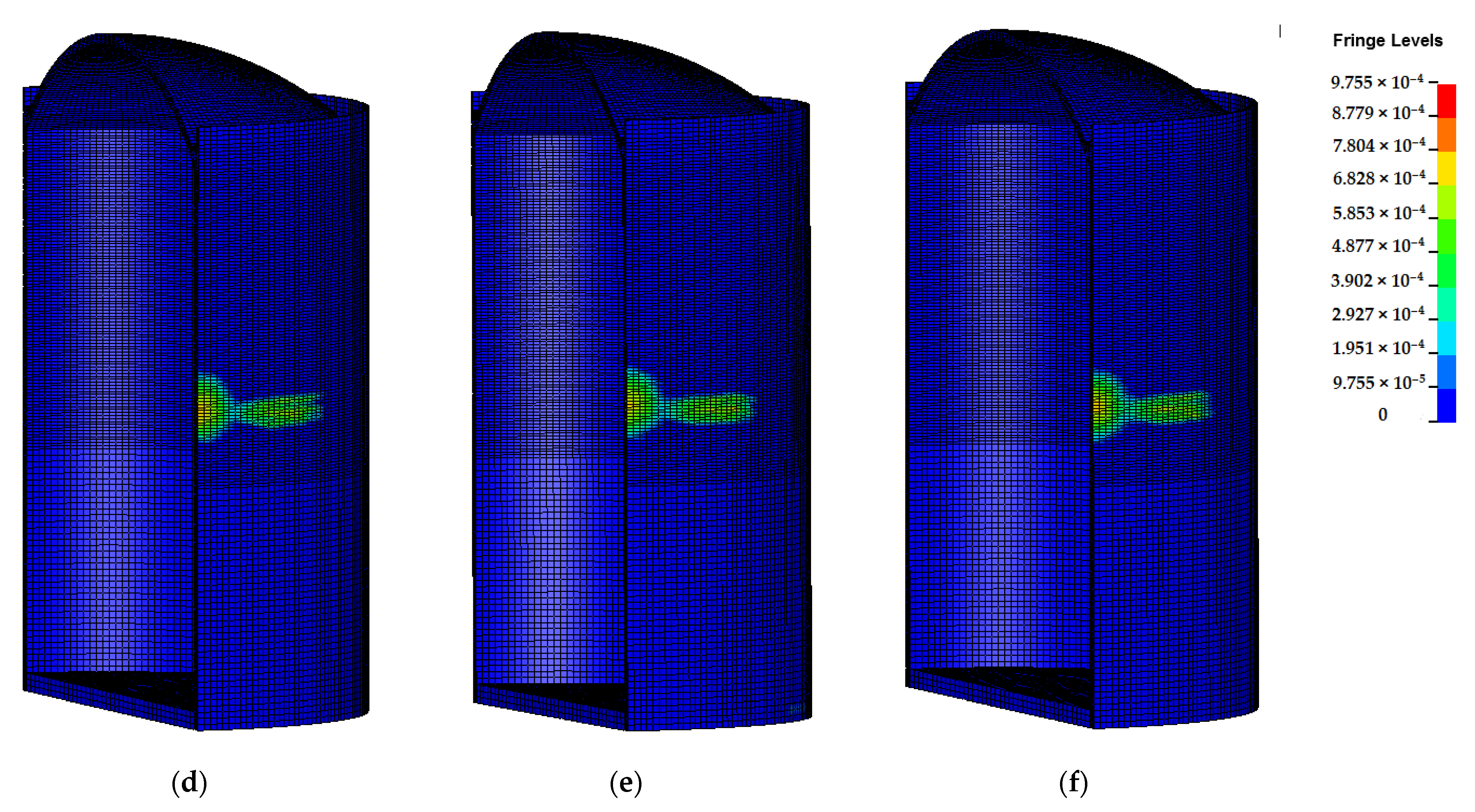
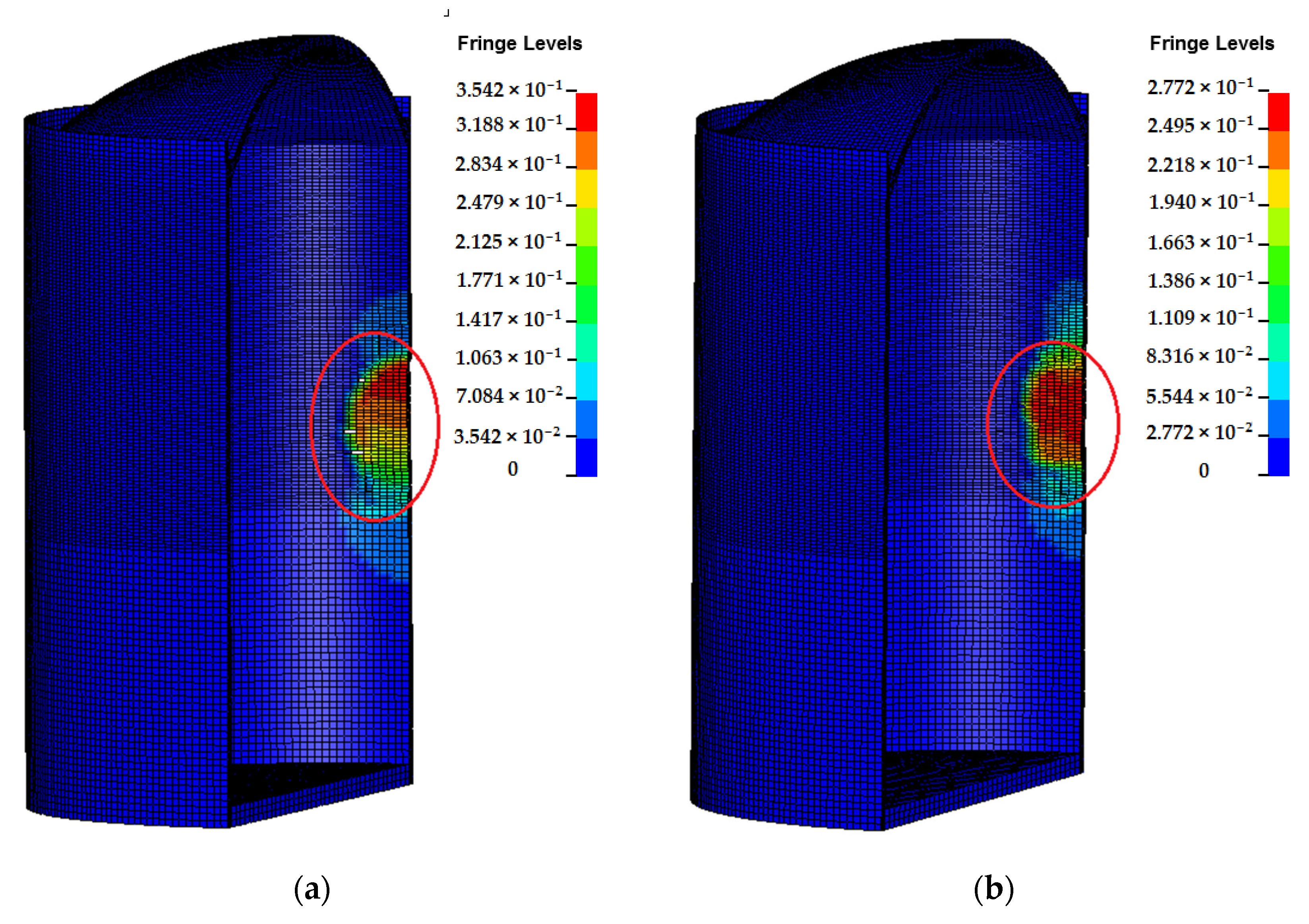
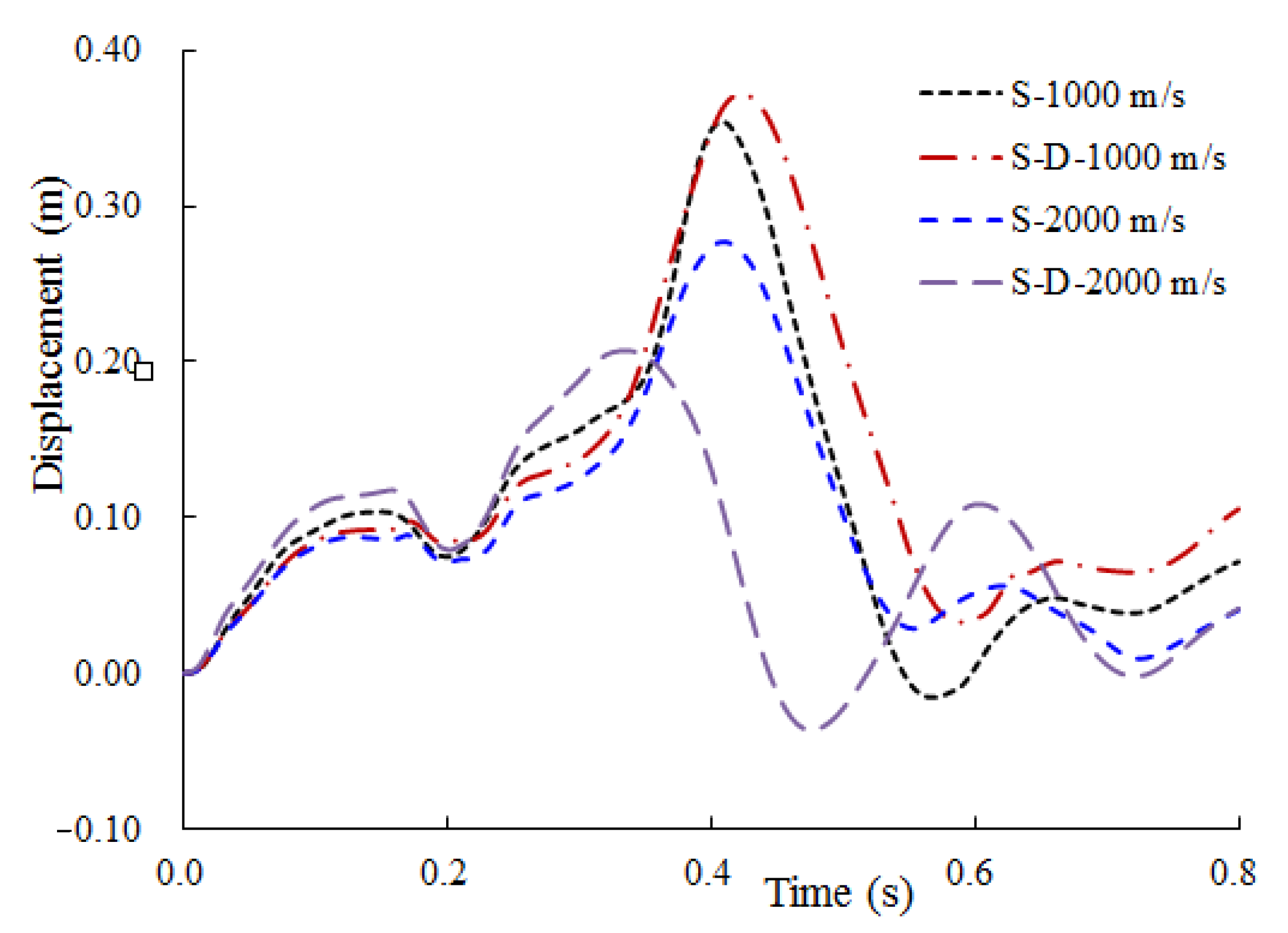
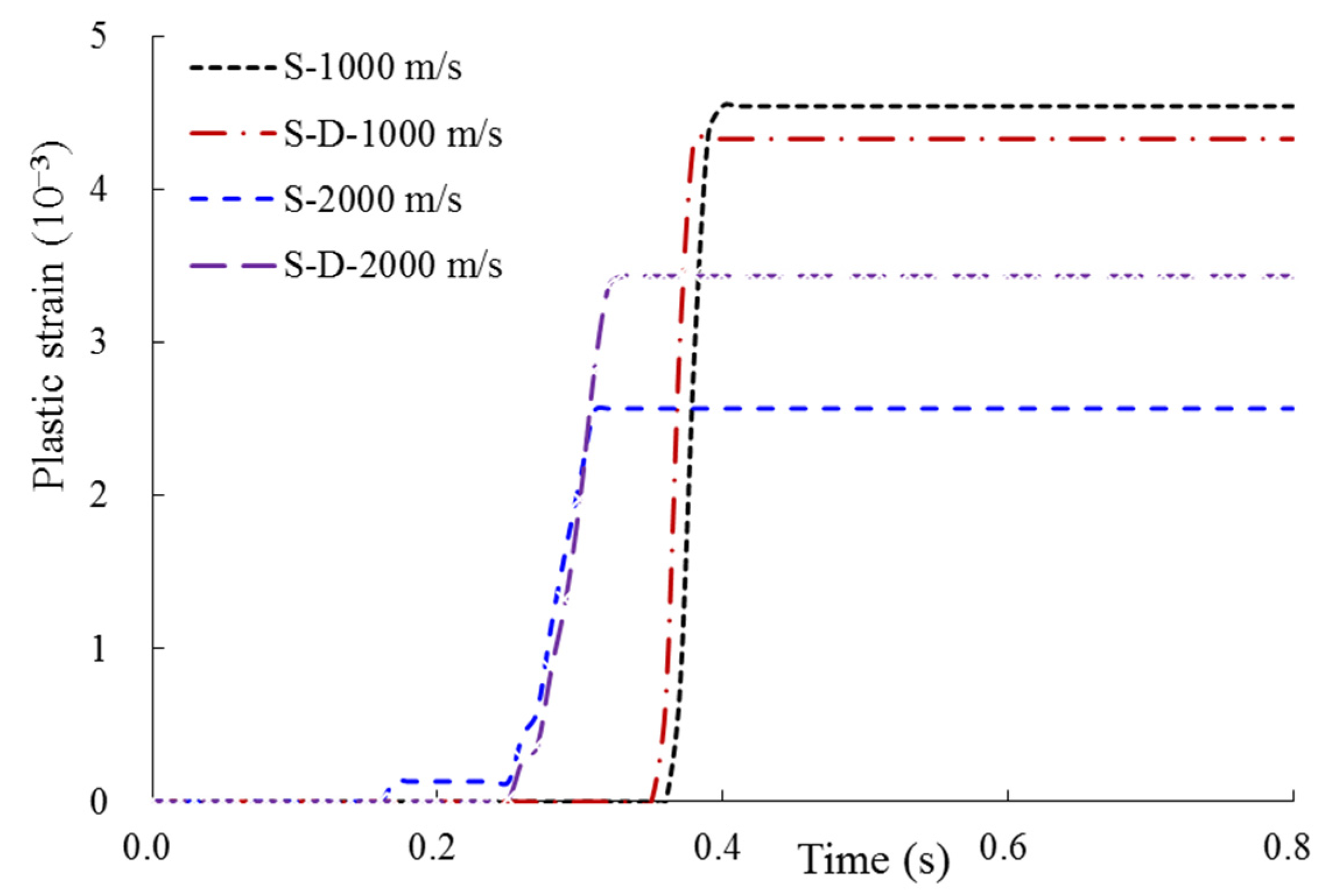
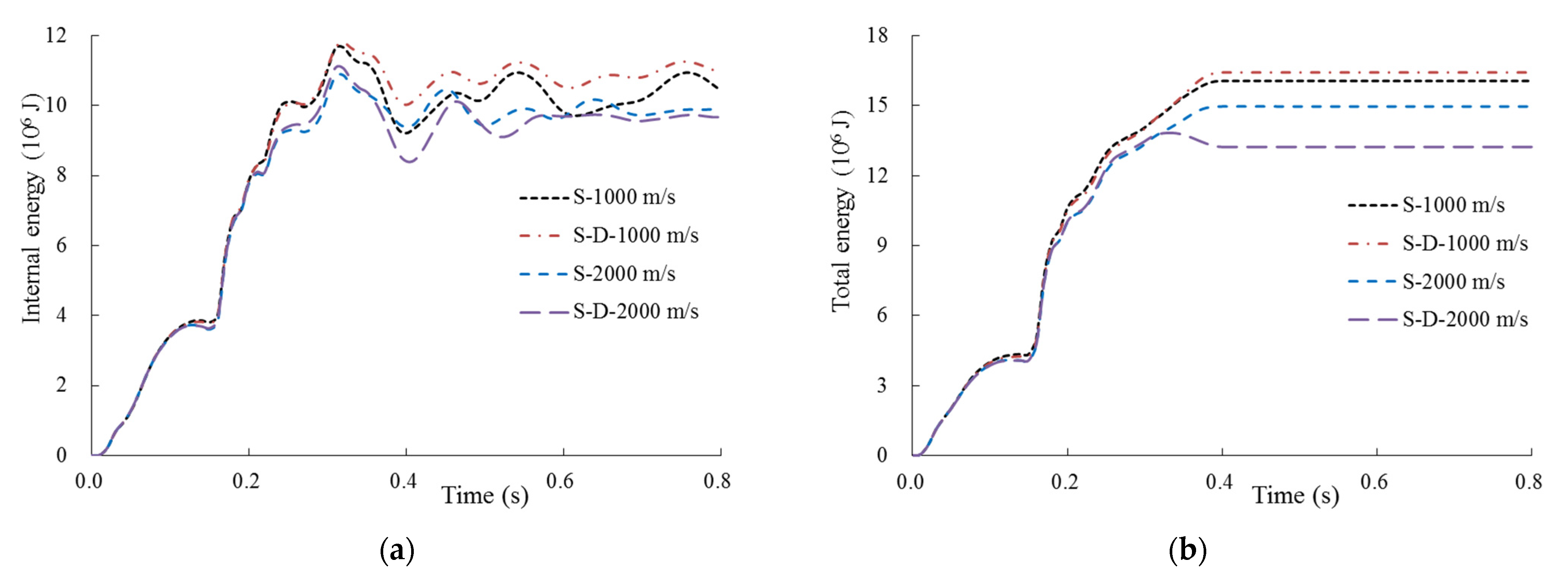
3.1.1. Full SC Containment with Thickness of 0.9 m
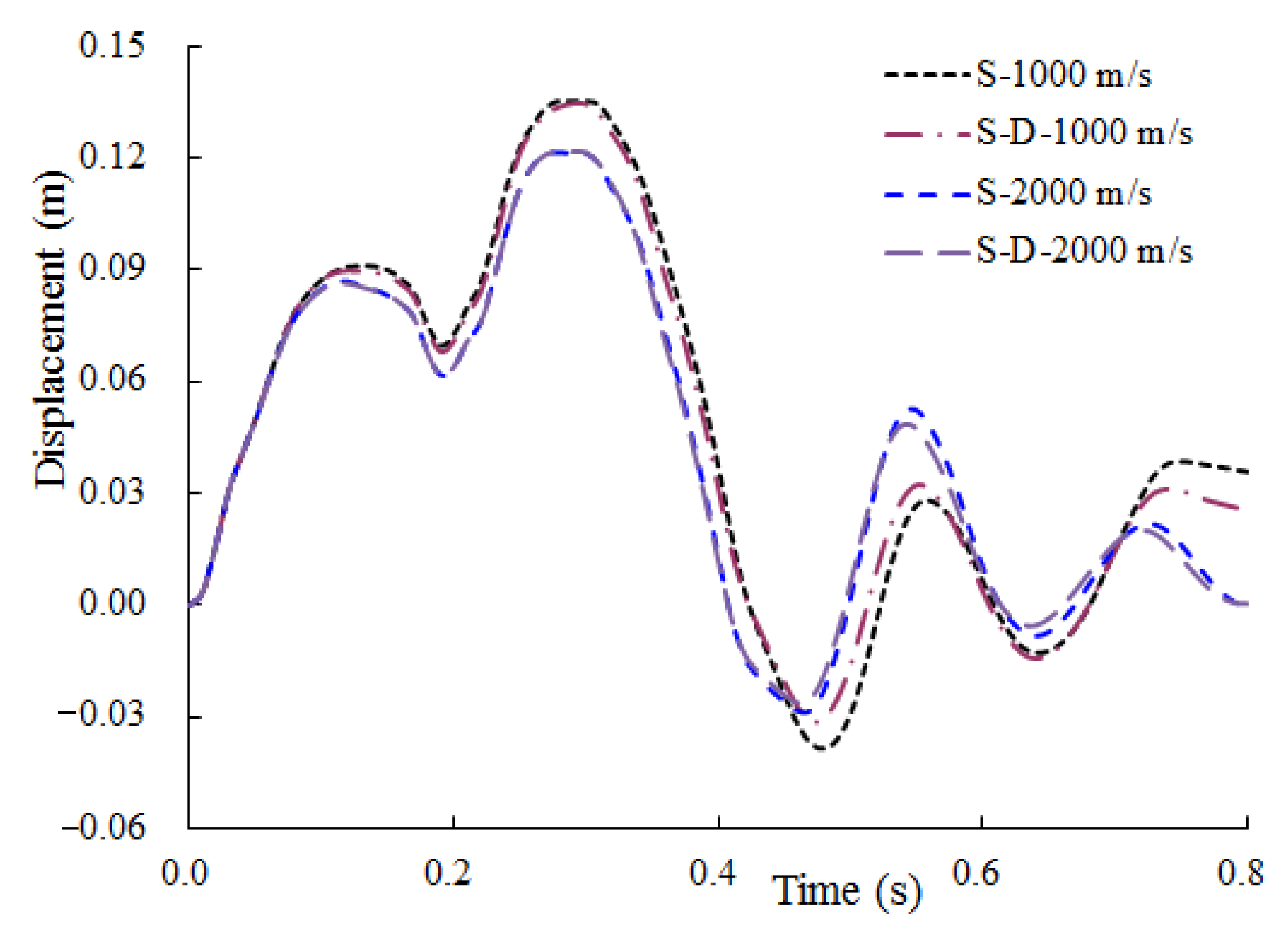
3.1.2. Full SC containment with Thickness of 1.0 m
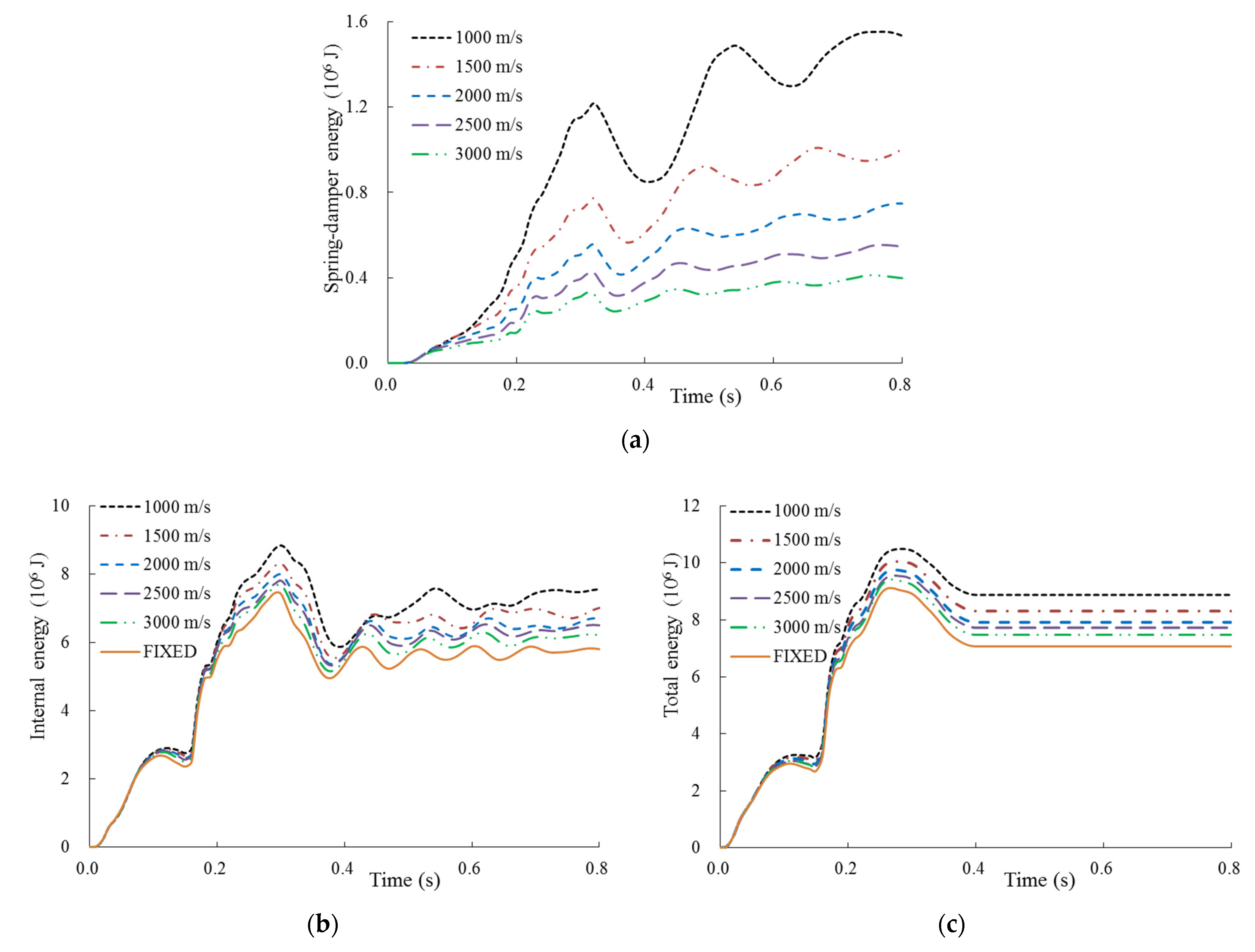
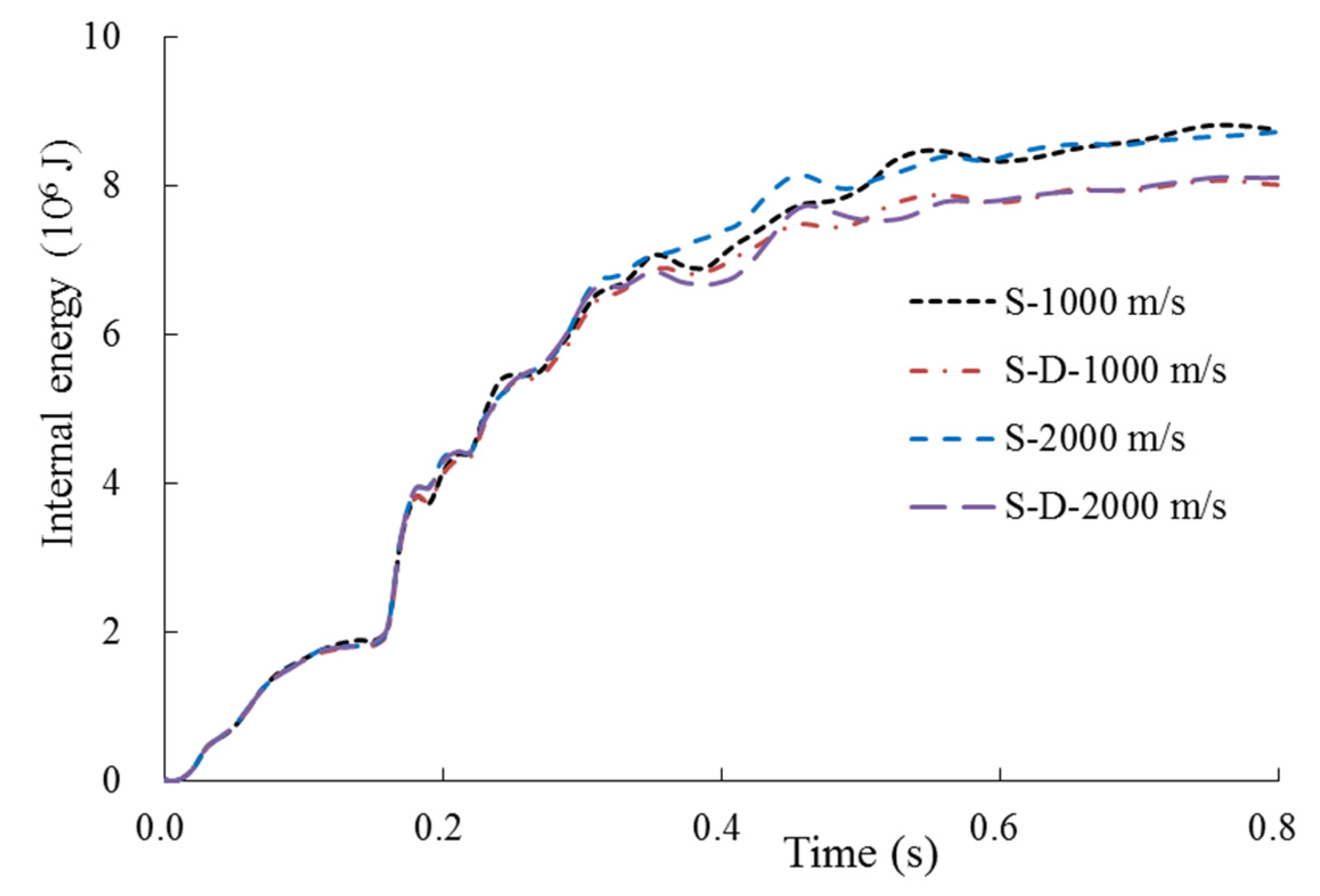
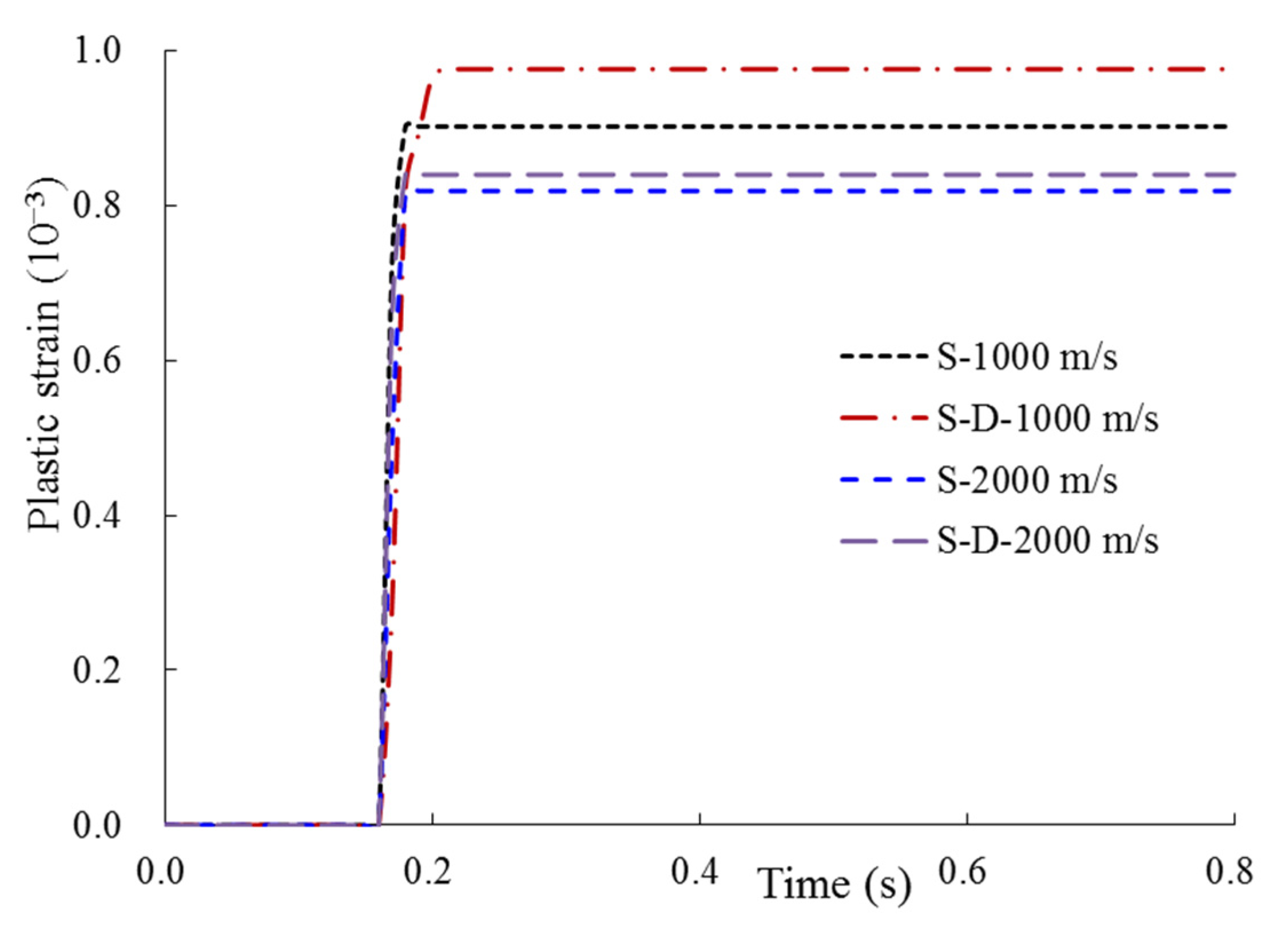
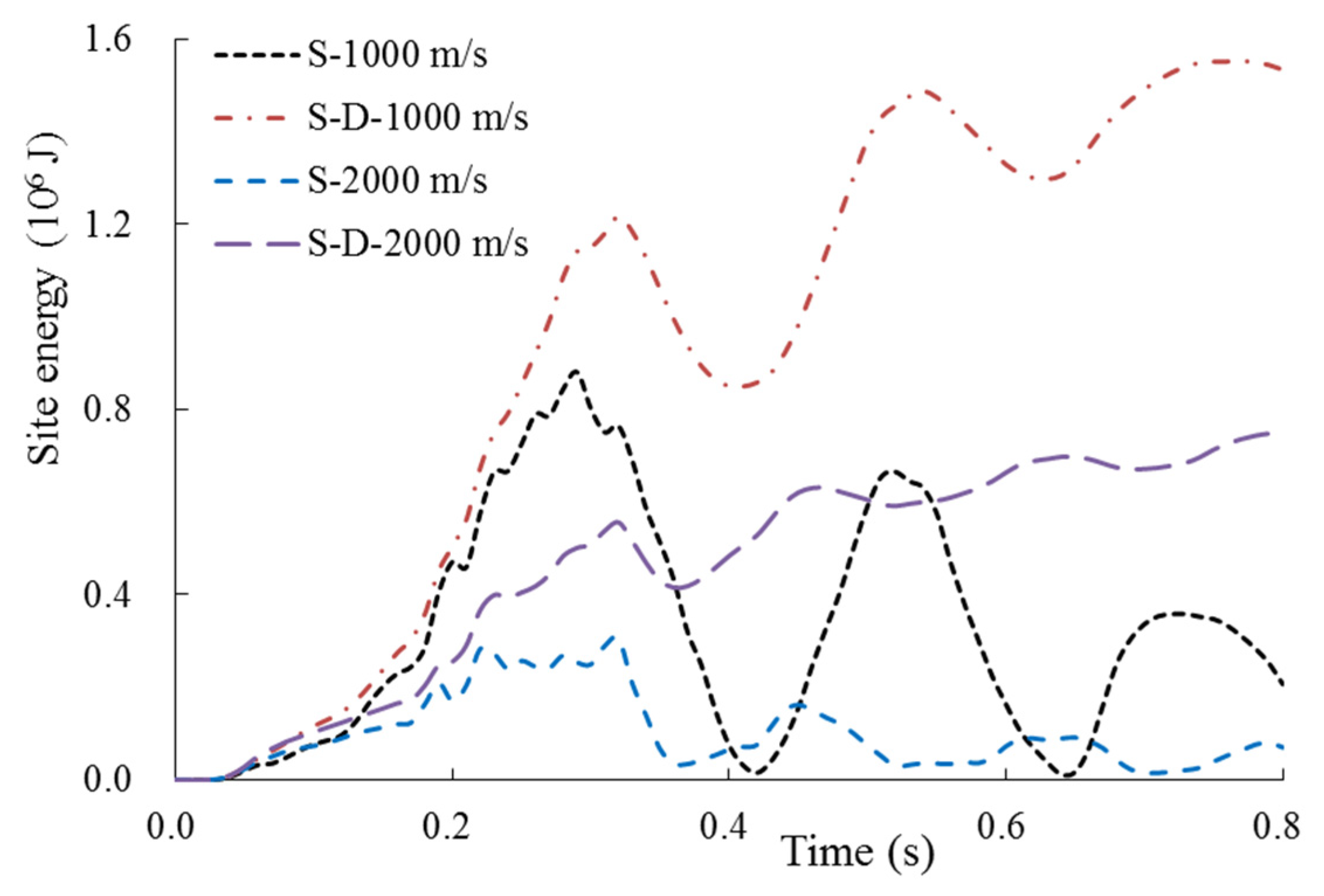
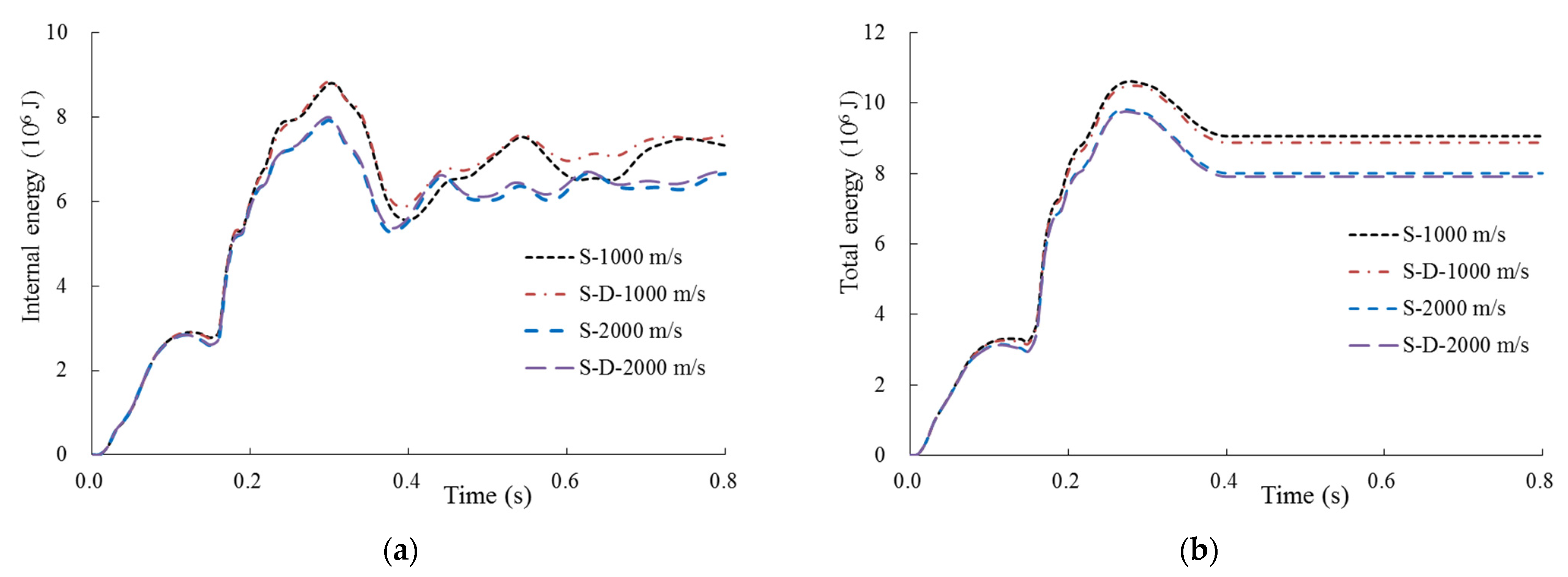
3.2. Analysis of Site Damping on the Impact Response
3.2.1. Full SC Containment with Thickness of 0.9 m
3.2.2. Full SC Containment with Thickness of 1.0 m
4. Conclusions
- (1)
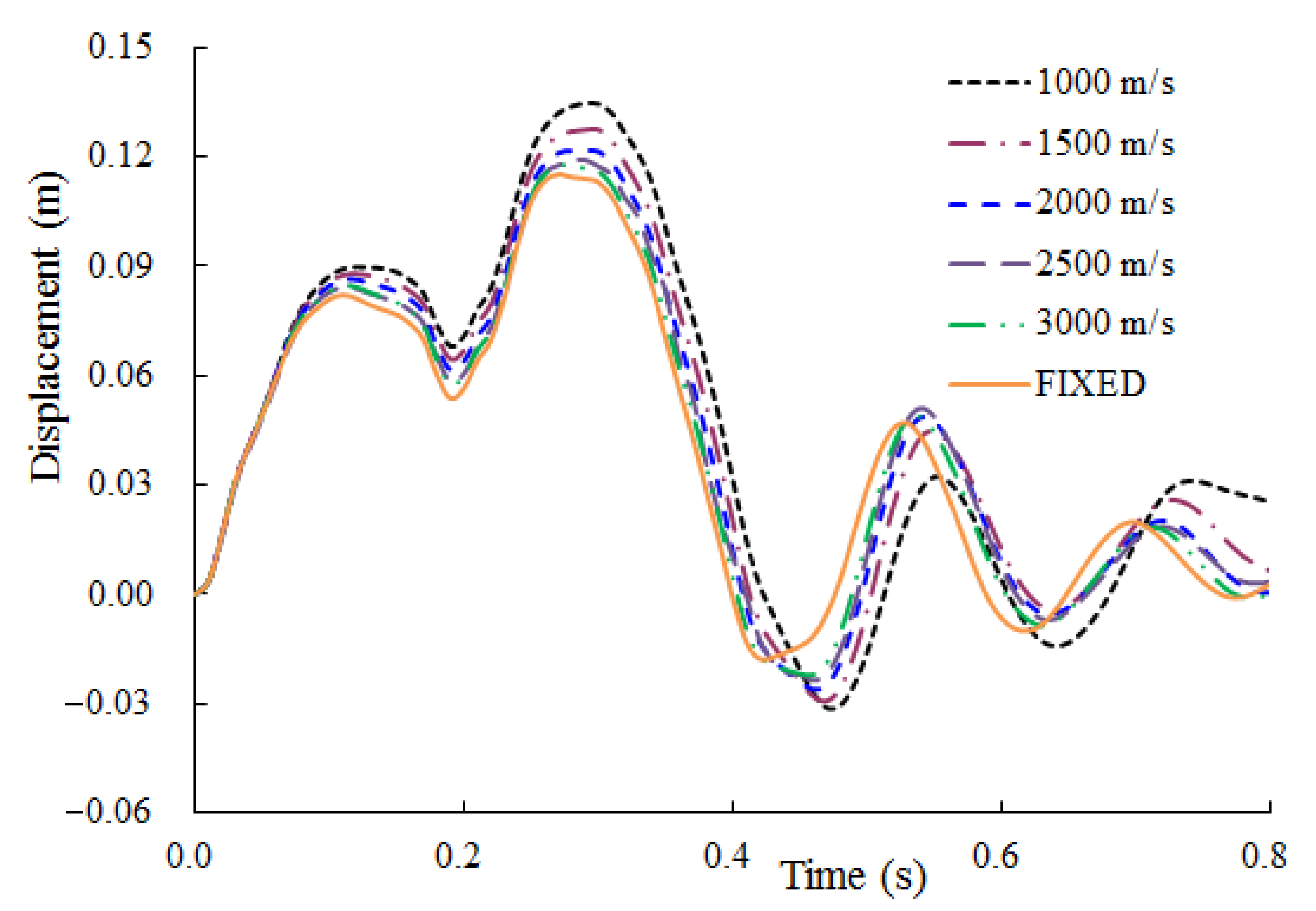
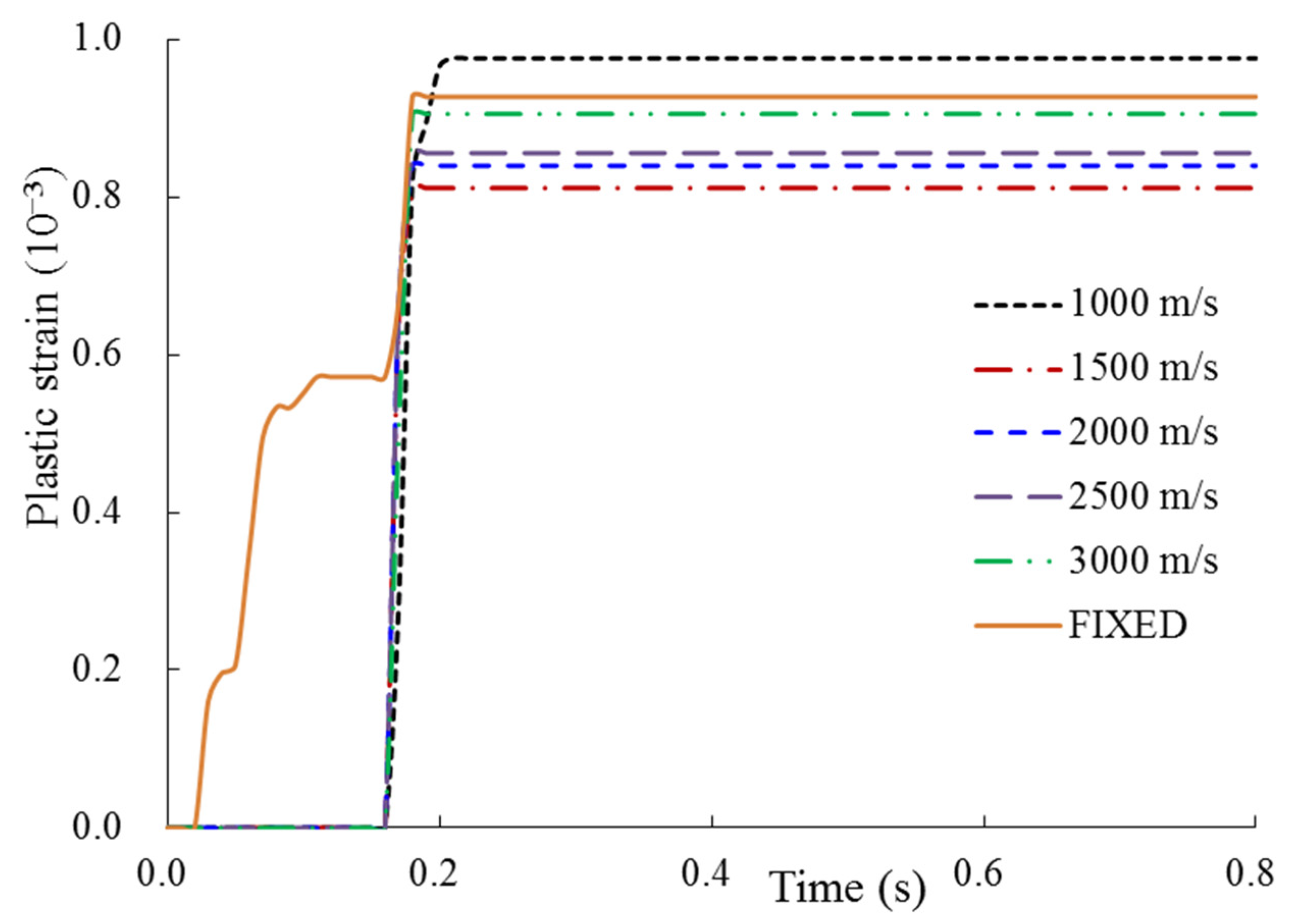
- For the relatively thin full SC containment, both the displacement and plastic strain under the fixed boundary are the largest, while the impact response calculated by other, different sites varies greatly, and there is no consistent rule. Overall, the boundary condition of this relatively thin containment, which is assumed to be fixed is relatively conservative.
- (2)
- For the thicker full SC containment, it is clear that the displacement response of containment decreased with the increasing of shear wave velocity, and that is the smallest when the fixed boundary is considered. The displacement and plastic strain of concrete calculated by the site of Vs = 3000 m/s is closest to that for the fixed boundary, only with 2.2% and 2.4% difference. Hence, when the shear wave velocity of the site is large enough, that is, the site is hard rock, its boundary condition which is assumed to be the fixed constraint is reasonable.
- (3)
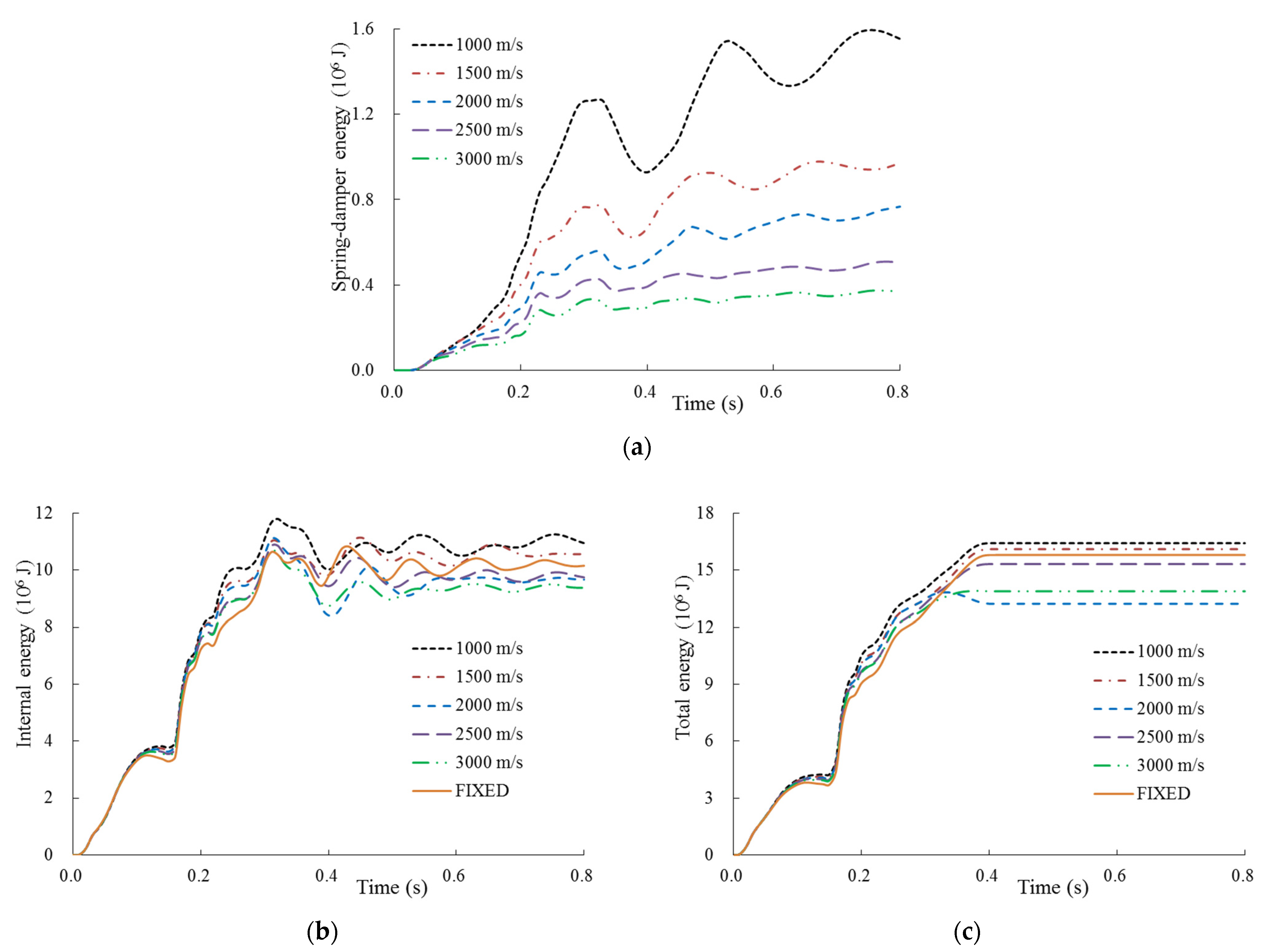
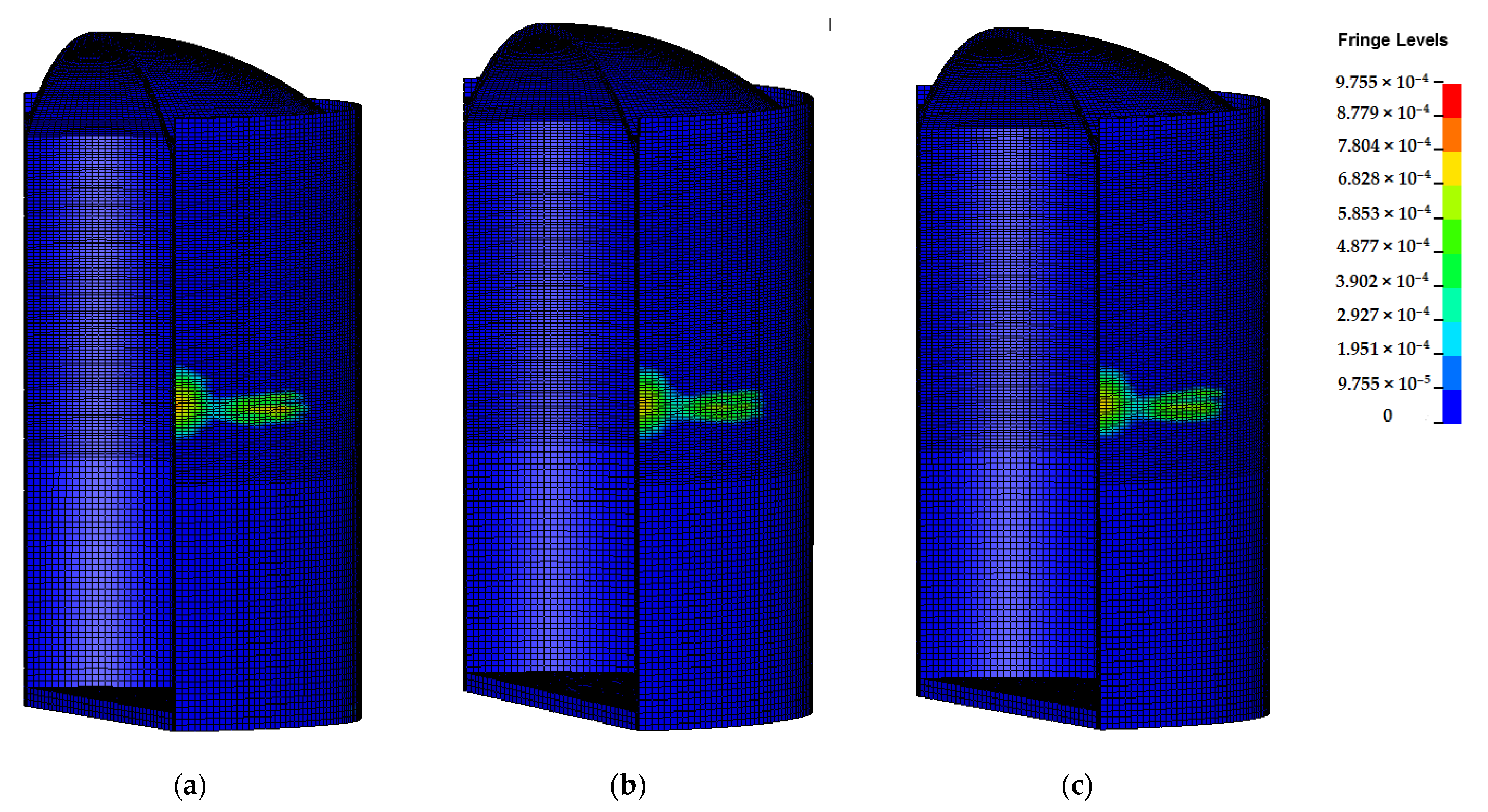
- For the relatively thin full SC containment, the damping effect of the site has a significant effect on the structural impact response (i.e., displacement, plastic strain, and local concrete damage). Nevertheless, the impact response of the thicker containment is slightly influenced by the site damping effect, especially for the impact displacement.
- (4)
- For the impact analysis of the structures of NPPs against a large commercial aircraft, it is suggested that both the specific site condition and fixed boundary should be considered. The reason is that for different site conditions, the impact response calculated by assuming the fixed constraint is not necessarily conservative.
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Conflicts of Interest
References
- 10CFR50.150. Aircraft Impact Assessment; Nuclear Regulatory Commission: Washington, DC, USA, 2009. [Google Scholar]
- ERIN Engineering & Research. Methodology for Performing Aircraft Impact Assessments for New Plant Designs; NEI 07-13, Revision 8P; Nuclear Energy Institute: Walnut Creek, CA, USA, 2011. [Google Scholar]
- HAF102. Design Safety Regulations for Nuclear Power Plants; National Nuclear Safety Administration: Beijing, China, 2016. [Google Scholar]
- Riera, J.D. On the stress analysis of structures subjected to aircraft impact forces. Nucl. Eng. Des. 1968, 8, 415–426. [Google Scholar] [CrossRef]
- Abbas, H.; Paul, D.K.; Godbole, P.N.; Nayak, G.C. Reaction-time response of aircraft crash. Comput. Struct. 1995, 55, 809–817. [Google Scholar] [CrossRef]
- Arros, J.; Doumbalski, N. Analysis of aircraft impact to concrete structures. Nucl. Eng. Des. 2007, 237, 1241–1249. [Google Scholar] [CrossRef]
- Sugano, T.; Tsubota, H.; Kasai, Y.; Koshika, N.; Orui, S.; Von Riesemann, W.A.; Bickel, D.C.; Parks, M.B. Full scale aircraft impact test for evaluation of impact force. Nucl. Eng. Des. 1993, 140, 373–385. [Google Scholar] [CrossRef]
- Tennant, D.; Levine, H.; Mould, J.; Vaughan, D. Rapid evaluation of buildings and infrastructure to accidental and deliberate aircraft impact. Nucl. Eng. Des. 2014, 269, 142–148. [Google Scholar] [CrossRef]
- Zhang, T.; Wu, H.; Fang, Q.; Gong, Z.M. Influences of nuclear containment radius on the aircraft impact force based on the Riera function. Nucl. Eng. Des. 2015, 293, 196–204. [Google Scholar] [CrossRef]
- Jiang, H.; Chorzepa, M.G. Aircraft impact analysis of nuclear safety-related concrete structures: A review. Eng. Fail. Anal. 2014, 46, 118–133. [Google Scholar] [CrossRef]
- Lee, K.; Hanb, S.E.; Hong, J.-W. Analysis of impact of large commercial aircraft on a prestressed containment building. Nucl. Eng. Des. 2013, 265, 431–449. [Google Scholar] [CrossRef]
- Frano, R.L.; Forasassi, G. Preliminary evaluation of aircraft impact on a near term nuclear power plant. Nucl. Eng. Des. 2011, 241, 5245–5250. [Google Scholar] [CrossRef]
- Thai, D.K.; Kim, S.E. Safety assessment of a nuclear power plant building subjected to an aircraft crash. Nucl. Eng. Des. 2015, 293, 38–52. [Google Scholar] [CrossRef]
- Shin, S.S.; Hahm, D.; Park, T. Shock vibration and damage responses of primary auxiliary buildings from aircraft impact. Nucl. Eng. Des. 2016, 310, 57–68. [Google Scholar] [CrossRef]
- Mizuno, J.; Koshika, N.; Sawamoto, Y.; Niwa, N.; Suzuki, A.; Yamashita, T. Investigations on impact resistance of steel plate reinforced concrete barriers against aircraft impact Part 1: Test program and results. In Proceedings of the Transactions of the 18th International Conference on Structural Mechanics in Reactor Technology, Beijing, China, 7–12 August 2005; pp. 2566–2579. [Google Scholar]
- Mullapudi, T.; Summers, P.; Moon, I.-H. Impact analysis of steel plated concrete wall. Struct. Congr. 2012, 1881–1893. [Google Scholar] [CrossRef] [Green Version]
- Liu, J.; Han, P. Numerical analysis of a shield building subjected to a large commercial aircraft impact. Shock. Vib. 2018, 2018, 7854969. [Google Scholar]
- Sadiq, M.; Khaliq, W.; Ilyas, M.; Khushnood, R.A.; Khan, S.A.; Rong, P. Analysis of full-scale aircraft impact to reinforced concrete and steel plate reinforced concrete multiple barriers protecting nuclear power plants. Structures 2020, 27, 732–746. [Google Scholar] [CrossRef]
- Zhu, X.; Li, J.; Lin, G.; Pan, R.; Li, L. Sensitivity analysis of steel-plate concrete containment against a large commercial aircraft. Energies 2021, 14, 2829. [Google Scholar] [CrossRef]
- Huang, T.; Zhang, T.; Dong, Z.; Wu, H.; Fang, H. An analysis of the dynamic response of nuclear containment under the impact of a large commercial aircraft. J. Vib. Shock. 2018, 37, 8–14. [Google Scholar]
- Clough, R.W. Non-linear mechanisms in the seismic response of arch dams. In Proceedings of the International Research Conference Earthquake Engineering, Skopje, Yugoslavia, 30 June–3 July 1980; pp. 669–684. [Google Scholar]
- Deeks, A.J.; Randolph, M.F. Axisymmetric time-domain transmitting boundaries. J. Eng. Mech. 1994, 120, 25–42. [Google Scholar] [CrossRef]
- Liu, J.; Lu, Y. A direct method for analysis of dynamic soil-structure interaction. China Civ. Eng. J. 1998, 31, 55–64. [Google Scholar]
- Jean, W.; Lin, T.; Penzien, J. System parameters of soil foundations for time domain dynamic analysis. Earthq. Eng. Struct. Dyn. 1990, 19, 541–553. [Google Scholar] [CrossRef]
- ASCE STANDARD, 4-98. Seismic Analysis of Safety-Related Nuclear Structures and Commentary; American Society of Civil Engineers: Reston, VA, USA, 1998. [Google Scholar]
- Ls-Dyna LSTC. LS-DYNA Keyword User’s Manual; Livermore Software Technology Corporation (LSTC): Livermore, CA, USA, 2010. [Google Scholar]
- Ottosen, N.S. Failure and Elasticity of Concrete; Danish Atomic Energy Commission; RISOE: Roskilde, Denmark, 1975; ISBN 8755003540. [Google Scholar]
- Sadiq, M.; Yun, Z.X.; Rong, P. Simulation analysis of impact tests of steel plate reinforced concrete and reinforced concrete slabs against aircraft impact and its validation with experimental results. Nucl. Eng. Des. 2014, 273, 653–667. [Google Scholar] [CrossRef]
- Tsubota, H.; Koshika, N.; Mizuno, J.; Sanai, M.; Peterson, B.; Saito, H.; Imamura, A. Scale model tests of multiple barriers against aircraft impact: Part 1. Experimental program and test results. In Proceedings of the Transactions of the 15th International Conference on Structural Mechanics in Reactor Technology (SMiRT-15), Seoul, Korea, 15–20 August 1999. [Google Scholar]




| Shear Wave Velocity (m/s) | Dynamic Shear Modulus (GPa) | Poisson’s Ratio | Density (kg/m3) | (N/m) | (N/m) | (N.s/m) | (N.s/m) |
|---|---|---|---|---|---|---|---|
| 1000 | 2.10 | 0.34 | 2100 | 2.653 × 1011 | 3.258 × 1011 | 3.912 × 109 | 7.090 × 109 |
| 1500 | 4.95 | 0.32 | 2200 | 6.210 × 1011 | 7.454 × 1011 | 6.105 × 109 | 1.081 × 1010 |
| 2000 | 9.60 | 0.31 | 2400 | 1.201 × 1012 | 1.425 × 1012 | 8.851 × 109 | 1.550 × 1010 |
| 2500 | 15.63 | 0.30 | 2500 | 1.948 × 1012 | 2.286 × 1012 | 1.149 × 1010 | 1.989 × 1010 |
| 3000 | 24.30 | 0.28 | 2700 | 3.011 × 1012 | 3.456 × 1012 | 1.480 × 1010 | 2.507 × 1010 |
| Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Compressive Strength (MPa) | Tensile Strength (MPa) | Aggregate Radius (mm) |
|---|---|---|---|---|---|
| 2400 | 35 | 0.2 | 46.7 | 3.8 | 15 |
| Density (kg/m3) | Young’s Modulus (GPa) | Poisson’s Ratio | Yield Strength (MPa) |
|---|---|---|---|
| 7800 | 206 | 0.3 | 430 |
| Sites | Displacement (cm) | Plastic Strain | Spring-Damper Energy (J) | Internal Energy (J) | Total Energy (J) |
|---|---|---|---|---|---|
| Vs = 1000 m/s | 37.21 | 4.328 × 10−3 | 1.594 × 106 | 11.799 × 106 | 16.420 × 106 |
| Vs = 1500 m/s | 38.53 | 8.861 × 10−3 | 0.978 × 106 | 11.143 × 106 | 16.105 × 106 |
| Vs = 2000 m/s | 20.70 | 3.433 × 10−3 | 0.767 × 106 | 11.081 × 106 | 13.227 × 106 |
| Vs = 2500 m/s | 32.83 | 4.967 × 10−3 | 0.509 × 106 | 10.865 × 106 | 15.319 × 106 |
| Vs = 3000 m/s | 24.96 | 9.553 × 10−3 | 0.374 × 106 | 10.680 × 106 | 13.885 × 106 |
| FIXED | 41.03 | 9.867 × 10−3 | / | 10.835 × 106 | 15.795 × 106 |
| Sites | Displacement (cm) | Plastic Strain | Spring-Damper Energy (J) | Internal Energy (J) | Total Energy (J) |
|---|---|---|---|---|---|
| Vs = 1000 m/s | 13.47 | 0.975 × 10−3 | 1.553 × 106 | 8.841 × 106 | 10.489 × 106 |
| Vs = 1500 m/s | 12.75 | 0.811 × 10−3 | 1.009 × 106 | 8.312 × 106 | 10.044 × 106 |
| Vs = 2000 m/s | 12.18 | 0.839 × 10−3 | 0.748 × 106 | 7.992 × 106 | 9.751 × 106 |
| Vs = 2500 m/s | 11.92 | 0.856 × 10−3 | 0.554 × 106 | 7.807 × 106 | 9.550 × 106 |
| Vs = 3000 m/s | 11.77 | 0.905 × 10−3 | 0.412 × 106 | 7.684 × 106 | 9.420 × 106 |
| FIXED | 11.52 | 0.927 × 10−3 | / | 5.806 × 106 | 9.109 × 106 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, X.; Li, J.; Lin, G.; Pan, R.; Li, L. Influence of Different Sites on Impact Response of Steel-Plate Concrete Containment against a Large Commercial Aircraft. Energies 2021, 14, 4957. https://doi.org/10.3390/en14164957
Zhu X, Li J, Lin G, Pan R, Li L. Influence of Different Sites on Impact Response of Steel-Plate Concrete Containment against a Large Commercial Aircraft. Energies. 2021; 14(16):4957. https://doi.org/10.3390/en14164957
Chicago/Turabian StyleZhu, Xiuyun, Jianbo Li, Gao Lin, Rong Pan, and Liang Li. 2021. "Influence of Different Sites on Impact Response of Steel-Plate Concrete Containment against a Large Commercial Aircraft" Energies 14, no. 16: 4957. https://doi.org/10.3390/en14164957
APA StyleZhu, X., Li, J., Lin, G., Pan, R., & Li, L. (2021). Influence of Different Sites on Impact Response of Steel-Plate Concrete Containment against a Large Commercial Aircraft. Energies, 14(16), 4957. https://doi.org/10.3390/en14164957





