A Statistical Assessment of Blending Hydrogen into Gas Networks
Abstract
:1. Introduction
1.1. Background
1.2. Literature Review
1.3. Motivation and Objectives
2. Methodology
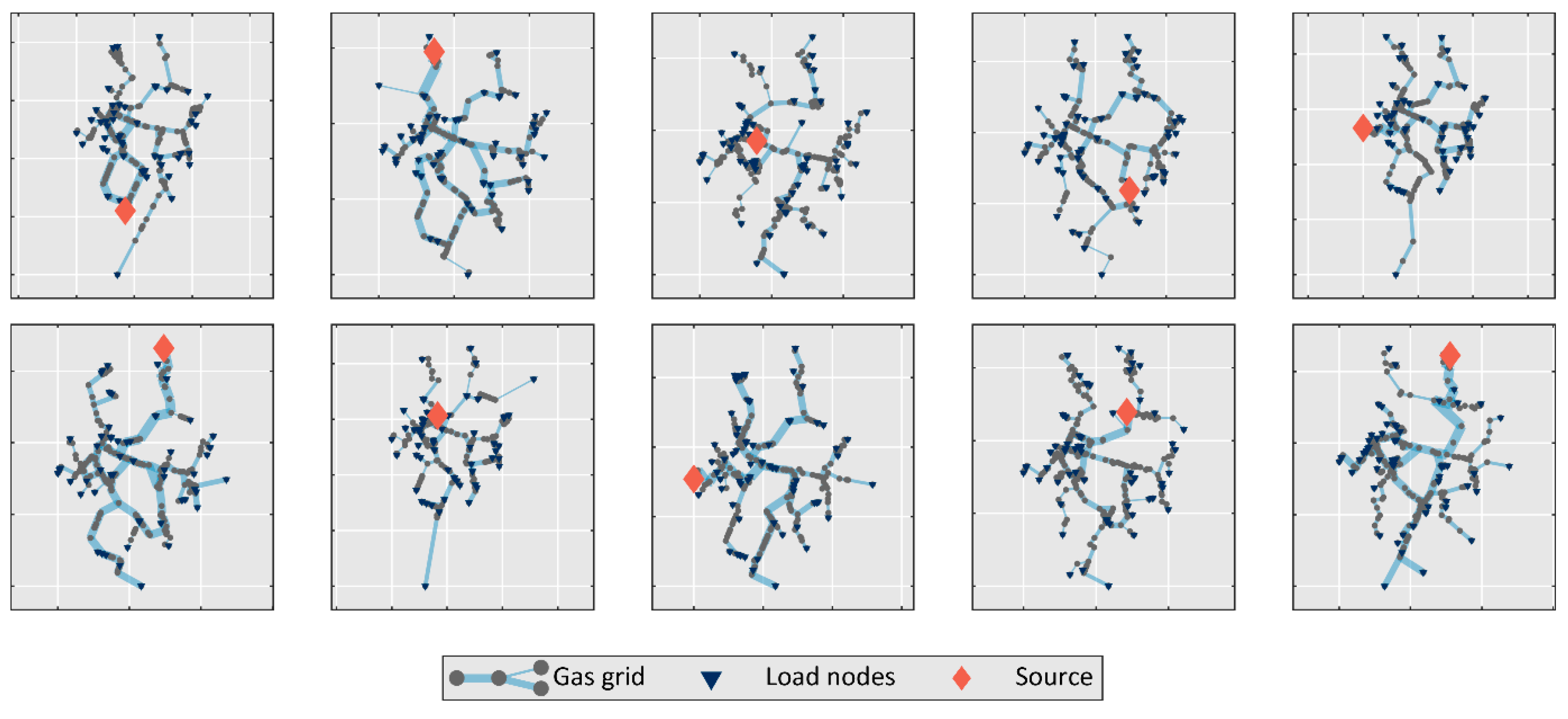
2.1. Synthetic Models of Distribution Gas Grids
2.1.1. Topology of the Synthetic Networks
- Fitting of a Gaussian Mixture Model (GMM): The spatial distribution of the reference grid is described with a statistical model fitted to the (x, y) coordinates of the nodes. Gaussian Mixture Models (GMM) are used for this purpose. A GMM is a simple, viable description of the probability that a given node of a network is located in a specific region of the plane. A weighted sum of bell-shaped (Gaussian) functions is adopted to describe the above probability, with parameters that are fitted from real data, i.e., from the (x, y) coordinates of a reference known network. Once the model parameters are computed, the GMM can be used (see item B) to generate randomly extracted nodes of a companion network that turns out to be coherent, even if different, with the initial reference network.In the above expressions, p is the probability, G is a Gaussian function, parameters and are the mean and the covariance matrix of the ith Gaussian component, is its weight and M is the number of components of the mixture. Vector x is for the planar coordinates of the network nodes. The resulting GMM is a statistical model fitted to the nodal coordinates of the reference grid, with an optimal selection of parameters (the Expectation–Maximization algorithm and the Bayesian Information Criterion are respectively used to fit M and θ to data);
- Creation of synthetic network nodes: A predefined number N of random points, constituting the nodes of the synthetic network, are generated in accordance with the fitted GMM. The coordinates of the synthetic nodes are determined by sampling N random points from the statistical model. As a result, the spatial distribution of the synthetic nodes is consistent with the original network. Since the nodes are randomly extracted from the GMM, their location is different for every synthetic network. In all the synthetic networks, N is set equal to 373 (the same network size as the reference grid is used);
- Establishment of basic network connectivity: Network connectivity is established by progressively adding connections among pairs of synthetic nodes. Node-to-node links are formed until all the nodes are included in the growing structure of the network. A probabilistic approach is followed, which favors links among close pairs of nodes to avoid unrealistic long-range connections. The resulting network is a connected graph with a tree structure featuring—by definition—N-1 edges;
- Network reinforcement: As gas networks are typically looped systems, additional pipelines are included in the tree-shaped network model to create loops. In medium-pressure networks, loops are established with the aim of improving the connectivity of the network. Therefore, the additional links are formed among those node pairs featuring the largest ratio between the topological distance (i.e., length of the network paths connecting the two nodes) and the physical distance (i.e., the Euclidean distance between the two nodes). The number of loops in a synthetic network is established in a random fashion, accounting for the variability of specific cycle numbers in real-world MP gas networks, which is observed to range between 0 and 0.124 loops/km.
2.1.2. Technical Parameters of the Synthetic Networks
- The maximum allowable operating pressure (MAOP): it represents the maximum pressure at which the system can be continuously operated at ordinary working conditions;
- The design minimum pressure (DMP): it is the minimum pressure level to be guaranteed across the system to ensure the safe and correct operation of customer appliances, service regulators and intermediate pressure reduction stations;
- The maximum gas flow velocity in pipelines: it constitutes a further constraint to prevent excessive mechanical stress, noise, dragging of impurities and corrosion of pipelines.
- Identification of the source node: the gas infeed point is identified in one node randomly selected among the end-nodes of the network—i.e., the nodes with a number of connections (or degree) equal to one. The selected node acts as the source of natural gas for the whole distribution system. Its pressure is assumed fixed and equal to the MAOP (i.e., 5 bar). The source node may represent a reduction and metering station fed by the upstream (high pressure) infrastructure or, in the case of islanded systems, a GNL storage tank and injection site;
- Identification of consumption nodes: loads are located in all the end nodes of the network, excluding the city gate. Being the network a medium-pressure infrastructure, load nodes may indiscriminately be large (e.g., industrial and commercial) gas users or MP/LP pressure regulators feeding downstream grid sections;
- Assignment of load values to consumption nodes: a total load of 30 MW is distributed among the consumption nodes, according to a suitable statistical model (Weibull distribution is adopted here);
- Technical sizing of the grid: having identified the location of the infeed site, the consuming nodes and their thermal loads, a rigorous system design is carried out respecting target operational restrictions (MAOP, DMP and maximum velocity).
2.2. Gas Network Analysis in the Presence of Hydrogen
2.2.1. Upstream Blending of Hydrogen with Natural Gas (Case A)
2.2.2. Distributed Injection of Hydrogen (Case B)
3. Effect of Blending Hydrogen in Distribution Gas Grids
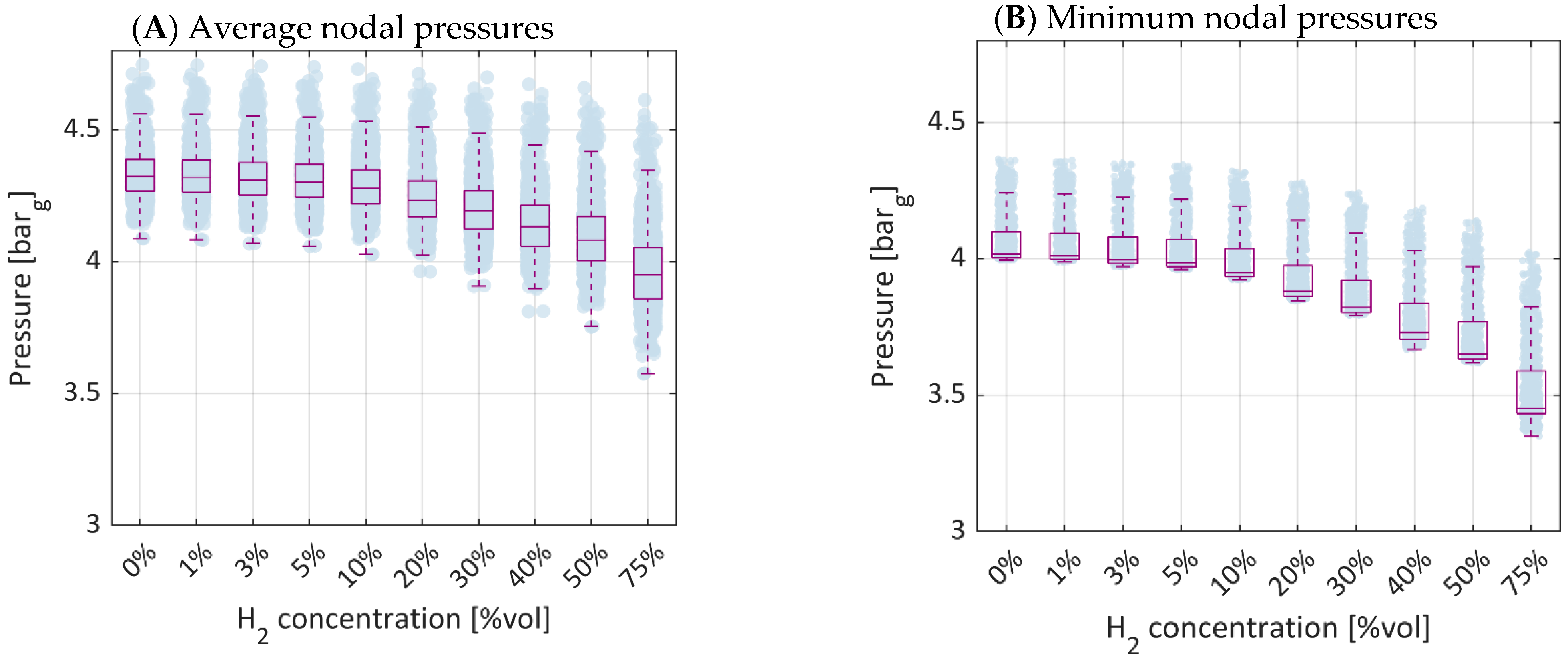
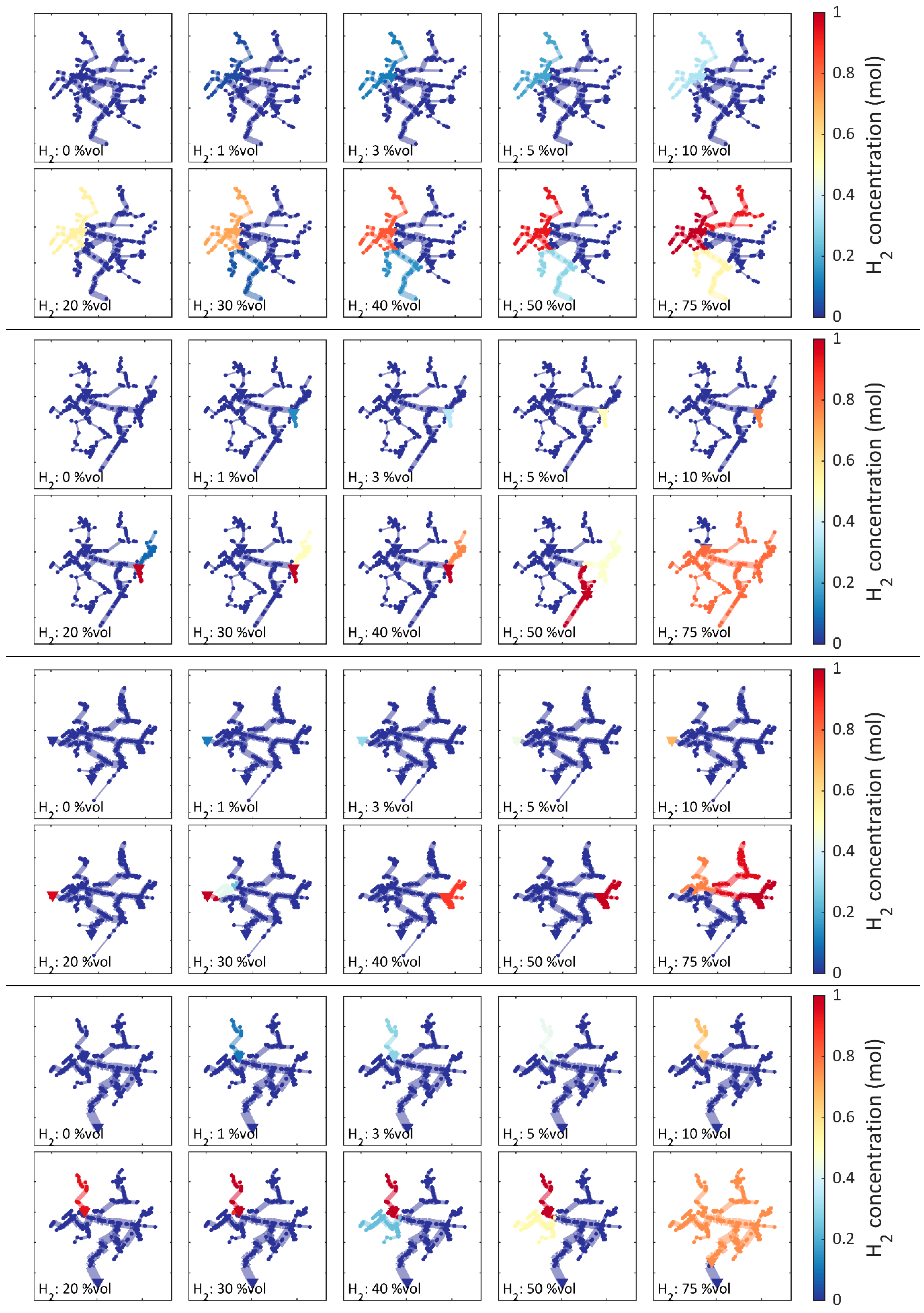
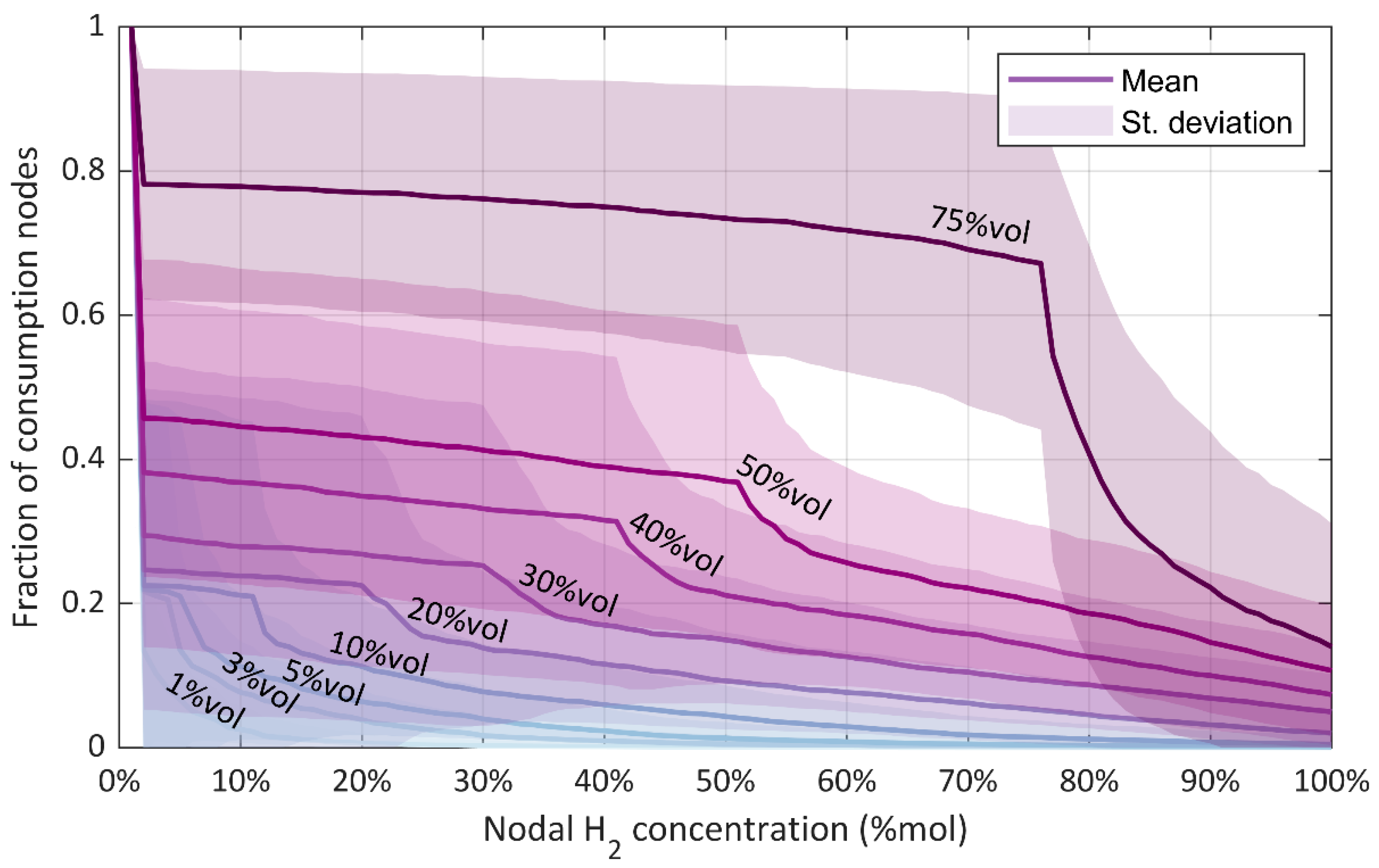
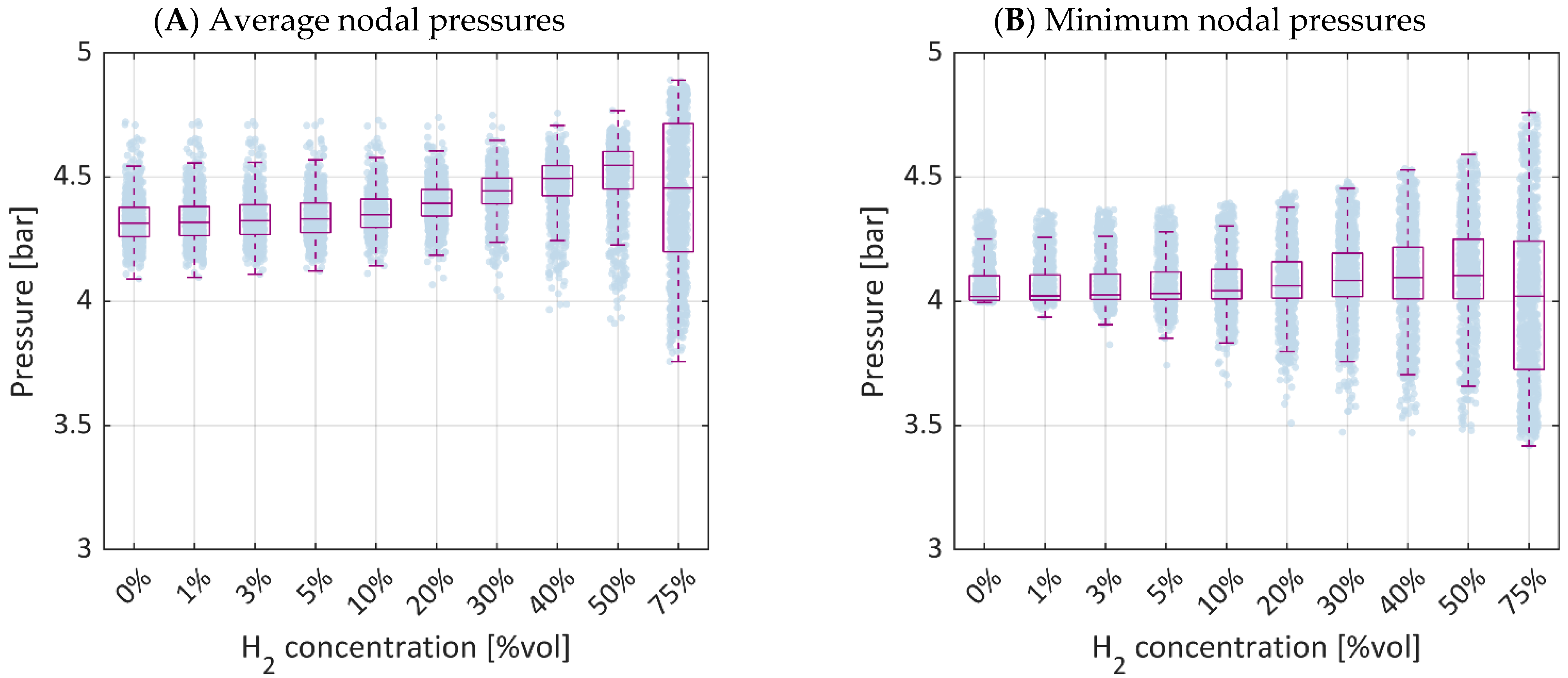
3.1. Case A: Effect of Injecting H2–NG Blends at the Network City Gate
3.2. Case B: Effect of Injecting Pure H2 in Random Network Locations
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- British Petroleum Statistical Review of World Energy 2020, 69th ed. 2020. Available online: https://www.bp.com/en/global/corporate/energy-economics/statistical-review-of-world-energy.html (accessed on 21 December 2020).
- Odyssee-Mure Project Sectorial Profile: Households. Available online: https://www.odyssee-mure.eu/publications/efficiency-by-sector/ (accessed on 15 June 2021).
- UNFCCC Secretariat. Paris Agreement. 2015, pp. 1–27. Available online: https://unfccc.int/sites/default/files/english_paris_agreement.pdf (accessed on 21 December 2020).
- European Commission. Stepping up Europe’s 2030 Climate Ambition; COM (2020) 562 Final; European Commission: Brussels, Belgium, 2020; pp. 1–23. [Google Scholar]
- Davis, S.J.; Lewis, N.S.; Shaner, M.; Aggarwal, S.; Arent, D.; Azevedo, I.L.; Benson, S.M.; Bradley, T.; Brouwer, J.; Chiang, Y.M.; et al. Net-zero emissions energy systems. Science 2018, 360, aas9793. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- International Energy Agency. World Energy Outlook 2020; International Energy Agency: Paris, France, 2020; pp. 1–461. Available online: https://www.iea.org/reports/world-energy-outlook-2020 (accessed on 21 December 2020).
- Memon, Z.A.; Trinchero, R.; Manfredi, P.; Canavero, F.; Stievano, I.S. Compressed Machine Learning Models for the Uncertainty Quantification of Power Distribution Networks. Energies 2020, 13, 4881. [Google Scholar] [CrossRef]
- Quarton, C.J.; Samsatli, S. Power-to-gas for injection into the gas grid: What can we learn from real-life projects, economic assessments and systems modelling? Renew. Sustain. Energy Rev. 2018, 98, 302–316. [Google Scholar] [CrossRef]
- Thema, M.; Bauer, F.; Sterner, M. Power-to-Gas: Electrolysis and methanation status review. Renew. Sustain. Energy Rev. 2019, 112, 775–787. [Google Scholar] [CrossRef]
- European Commission. A Hydrogen Strategy for a Climate-Neutral Europe; COM(2020) 301 Final; European Commission: Brussels, Belgium, 2020. [Google Scholar]
- Qadrdan, M.; Abeysekera, M.; Chaudry, M.; Wu, J.; Jenkins, N. Role of power-to-gas in an integrated gas and electricity system in Great Britain. Int. J. Hydrogen Energy 2015, 40, 5763–5775. [Google Scholar] [CrossRef]
- Guandalini, G.; Campanari, S.; Romano, M.C. Power-to-gas plants and gas turbines for improved wind energy dispatchability: Energy and economic assessment. Appl. Energy 2015, 147, 117–130. [Google Scholar] [CrossRef]
- European Commission. Powering a Climate-Neutral Economy: An EU Strategy for Energy System Integration; COM(2020) 299 Final; European Commission: Brussels, Belgium, 2020. [Google Scholar]
- Hydrogen Europe. Hydrogen in the EU’s Economic Recovery Plans; Hydrogen Europe. 2021. Available online: https://www.hydrogeneurope.eu/wp-content/uploads/2021/07/Hydrogen-Europe_EU-Recovery-Plan-Analysis_FINAL.pdf (accessed on 15 July 2021).
- International Energy Agency. Hydrogen Projects Database. Available online: https://www.iea.org/reports/hydrogen-projects-database (accessed on 11 January 2021).
- Abeysekera, M.; Wu, J.; Jenkins, N.; Rees, M. Steady state analysis of gas networks with distributed injection of alternative gas. Appl. Energy 2016, 164, 991–1002. [Google Scholar] [CrossRef] [Green Version]
- Sadler, D.; Cargill, A.; Crowther, M.; Rennie, A.; Watt, J.; Burton, S.; Haines, M. H21 Leeds City Gate Report. 2017, pp. 1–382. Available online: https://www.northerngasnetworks.co.uk/wp-content/uploads/2017/04/H21-Report-Interactive-PDF-July-2016.compressed.pdf (accessed on 21 December 2020).
- Pellegrino, S.; Lanzini, A.; Leone, P. Greening the gas network—The need for modelling the distributed injection of alternative fuels. Renew. Sustain. Energy Rev. 2017, 70, 266–286. [Google Scholar] [CrossRef]
- Gondal, I.A. Hydrogen integration in power-to-gas networks. Int. J. Hydrogen Energy 2019, 44, 1803–1815. [Google Scholar] [CrossRef]
- Osiadacz, A.J.; Chaczykowski, M. Modeling and Simulation of Gas Distribution Networks in a Multienergy System Environment. Proc. IEEE 2020, 108, 1580–1595. [Google Scholar] [CrossRef]
- Cavana, M.; Mazza, A.; Chicco, G.; Leone, P. Electrical and gas networks coupling through hydrogen blending under increasing distributed photovoltaic generation. Appl. Energy 2021, 290, 116764. [Google Scholar] [CrossRef]
- Cheli, L.; Guzzo, G.; Adolfo, D.; Carcasci, C. Steady-state analysis of a natural gas distribution network with hydrogen injection to absorb excess renewable electricity. Int. J. Hydrogen Energy 2021, 46, 25562–25577. [Google Scholar] [CrossRef]
- Elaoud, S.; Hafsi, Z.; Hadj-Taieb, L. Numerical modelling of hydrogen-natural gas mixtures flows in looped networks. J. Pet. Sci. Eng. 2017, 159, 532–541. [Google Scholar] [CrossRef]
- Vaccariello, E.; Trinchero, R.; Leone, P.; Stievano, I.S. Synthetic Gas Networks for the Statistical Assessment of Low-Carbon Distribution Systems. Available online: https://doi.org/10.31219/osf.io/tw9pa (accessed on 21 December 2020).
- Vaccariello, E.; Leone, P.; Canavero, F.G.; Stievano, I.S. Topological modelling of gas networks for co-simulation applications in multi-energy systems. Math. Comput. Simul. 2021, 183, 244–253. [Google Scholar] [CrossRef]
- Vaccariello, E.; Leone, P.; Stievano, I.S. Generation of synthetic models of gas distribution networks with spatial and multi-level features. Int. J. Electr. Power Energy Syst. 2020, 117, 105656. [Google Scholar] [CrossRef]
- Standard UNI 9165:2020, Gas Infrastructures—Pipelines for Maximum Operating Pressure up to and Including 0.5 MPa (5 bar)—Design, Construction, Testing, Operation, Maintenance and Rehabilitation 2020. Available online: https://www.uni.com/ (accessed on 21 December 2020).
- Autorità di Regolazione per Energia Reti e Ambiente (ARERA). Codice di Rete per il Servizio di Distribuzione Gas—CRDG. Available online: https://www.arera.it/it/gas/codicerete/crdg/crdg.htm# (accessed on 21 December 2020).
- Vaccariello, E. Synthetic Models of Distribution Gas Networks in Low-Carbon Energy Systems. Ph.D. Thesis, Politecnico di Torino, Turin, Italy, 2021. [Google Scholar]
- Ministero dello Sviluppo Economico (Italian Ministry of Economic Development) Decreto 16 Aprile 2008—Regola Tecnica per la Progettazione, Costruzione, Collaudo, Esercizio e Sorveglianza delle Opere e dei Sistemi di Distribuzione e di Linee Dirette del gas Naturale con Densità non Superiore a 0,8. Available online: https://www.mise.gov.it/images/stories/energia/di160408.pdf (accessed on 21 December 2020).
- Abeysinghe, S. A Statistical Assessment Tool for Electricity Distribution Networks. Ph.D. Thesis, Cardiff University, Cardiff, Wales, 2018. [Google Scholar]
- Standard ISO 6976:2016. Natural Gas—Calculation of Calorific Values, Density, Relative Density and Wobbe Indices From composition. Available online: https://www.uni.com/ (accessed on 21 December 2020).
- Segeler, C.G. Gas Engineers Handbook; Industrial Press, Inc.: New York, NY, USA, 1965; ISBN 10: 0831133872. [Google Scholar]
- Decreto Ministeriale 18 Maggio 2018—Gas Combustibile, Aggiornamento Regola Tecnica. Available online: https://www.mise.gov.it/index.php/it/normativa/decreti-ministeriali/2038129-decreto-ministeriale-18-maggio-2018-gas-combustibile-aggiornamento-regola-tecnica (accessed on 17 April 2021).





| Number of Nodes | 373 |
|---|---|
| Total peak load (design load) | 30 MW (50 MW) |
| MAOP | 5.0 bar |
| DMP | 1.5 bar |
| Maximum flow velocity vmax | 25 m/s |
| NG properties | |
| Higher heating value | 53.4 MJ/kg |
| Specific gravity | 0.608 |
| CH4 | C2H6 | C3H8 | iC4H10 | nC4H10 | iC5H12 | nC5H12 | C6H14 | N2 | CO2 |
|---|---|---|---|---|---|---|---|---|---|
| 92.90% | 4.60% | 0.68% | 0.09% | 0.10% | 0.02% | 0.01% | 0.02% | 0.90% | 0.65% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Vaccariello, E.; Trinchero, R.; Stievano, I.S.; Leone, P. A Statistical Assessment of Blending Hydrogen into Gas Networks. Energies 2021, 14, 5055. https://doi.org/10.3390/en14165055
Vaccariello E, Trinchero R, Stievano IS, Leone P. A Statistical Assessment of Blending Hydrogen into Gas Networks. Energies. 2021; 14(16):5055. https://doi.org/10.3390/en14165055
Chicago/Turabian StyleVaccariello, Enrico, Riccardo Trinchero, Igor S. Stievano, and Pierluigi Leone. 2021. "A Statistical Assessment of Blending Hydrogen into Gas Networks" Energies 14, no. 16: 5055. https://doi.org/10.3390/en14165055
APA StyleVaccariello, E., Trinchero, R., Stievano, I. S., & Leone, P. (2021). A Statistical Assessment of Blending Hydrogen into Gas Networks. Energies, 14(16), 5055. https://doi.org/10.3390/en14165055









