Optimization and Analysis of Multilayer Planar Spiral Coils for the Application of Magnetic Resonance Wireless Power Transfer to Wearable Devices
Abstract
:1. Introduction
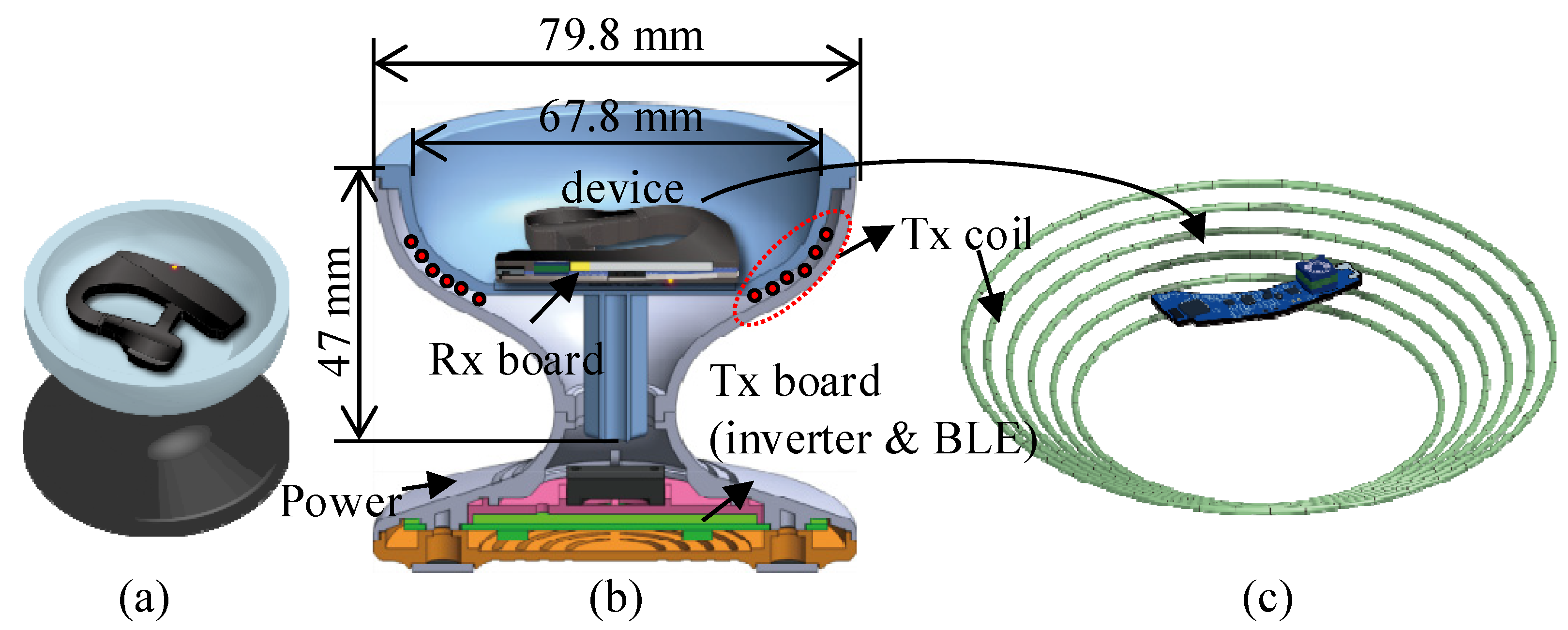
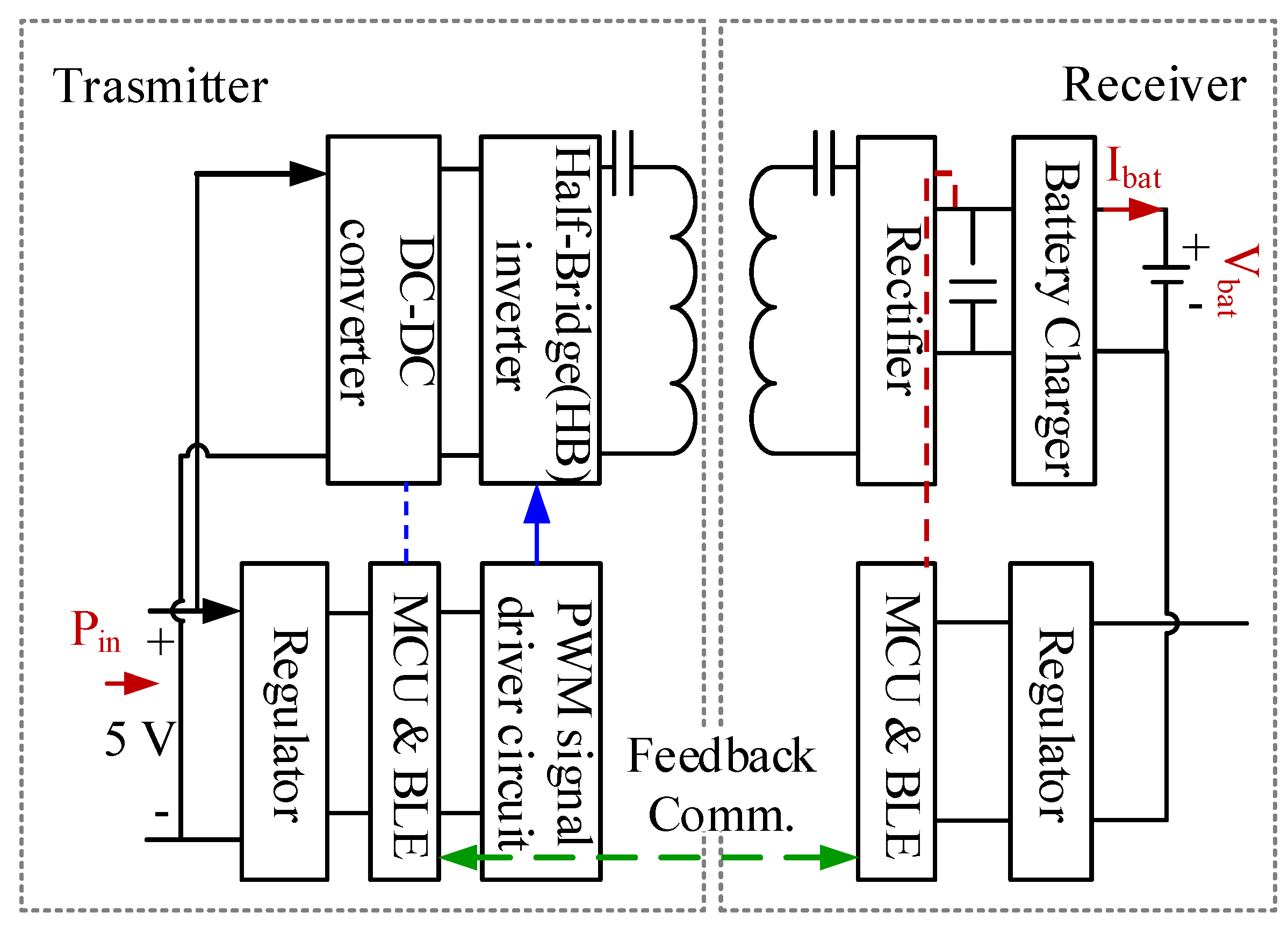
2. Proposed Wireless Power Transfer System for a Wearable Bio-Signal Monitoring Device
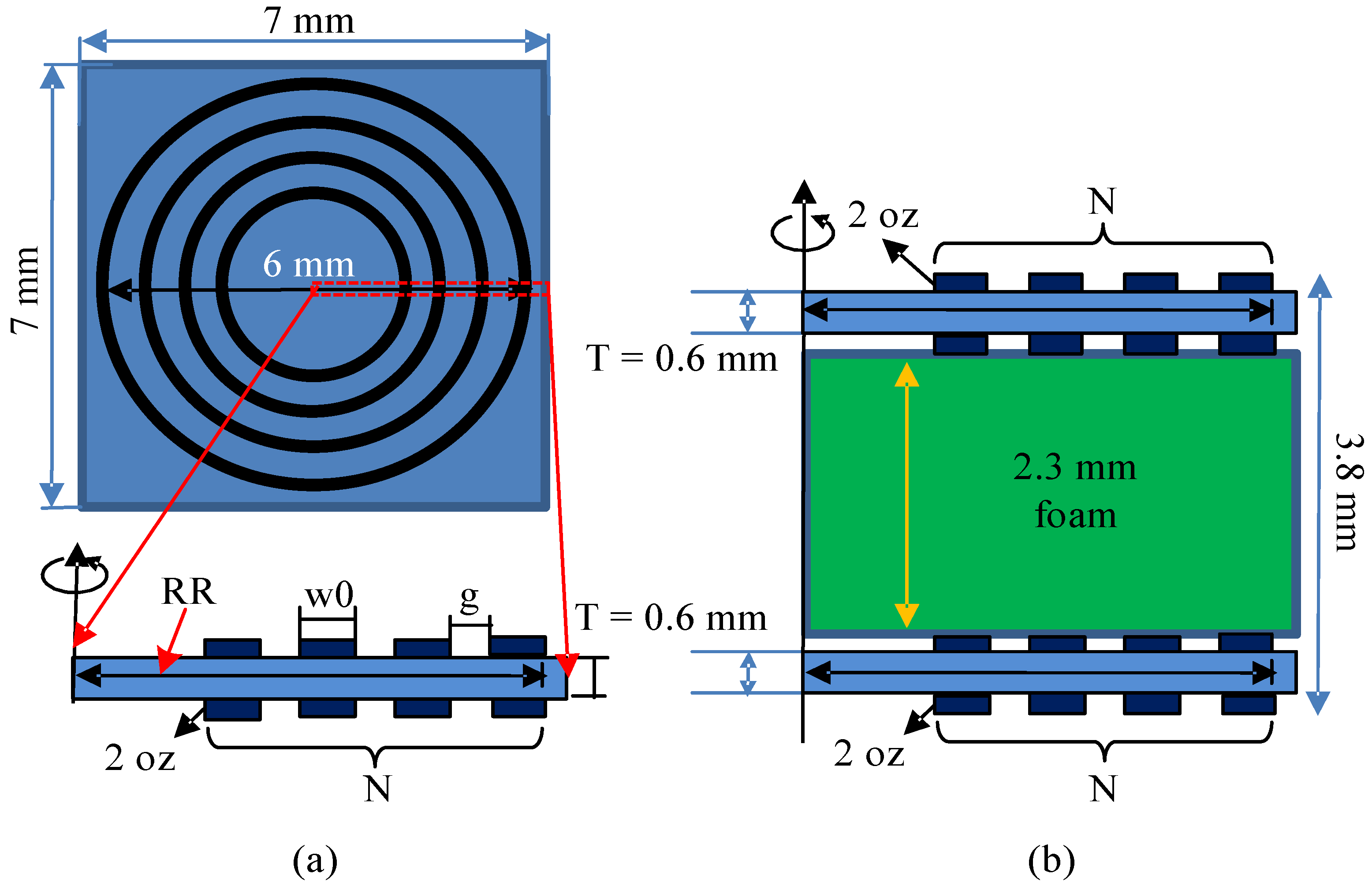
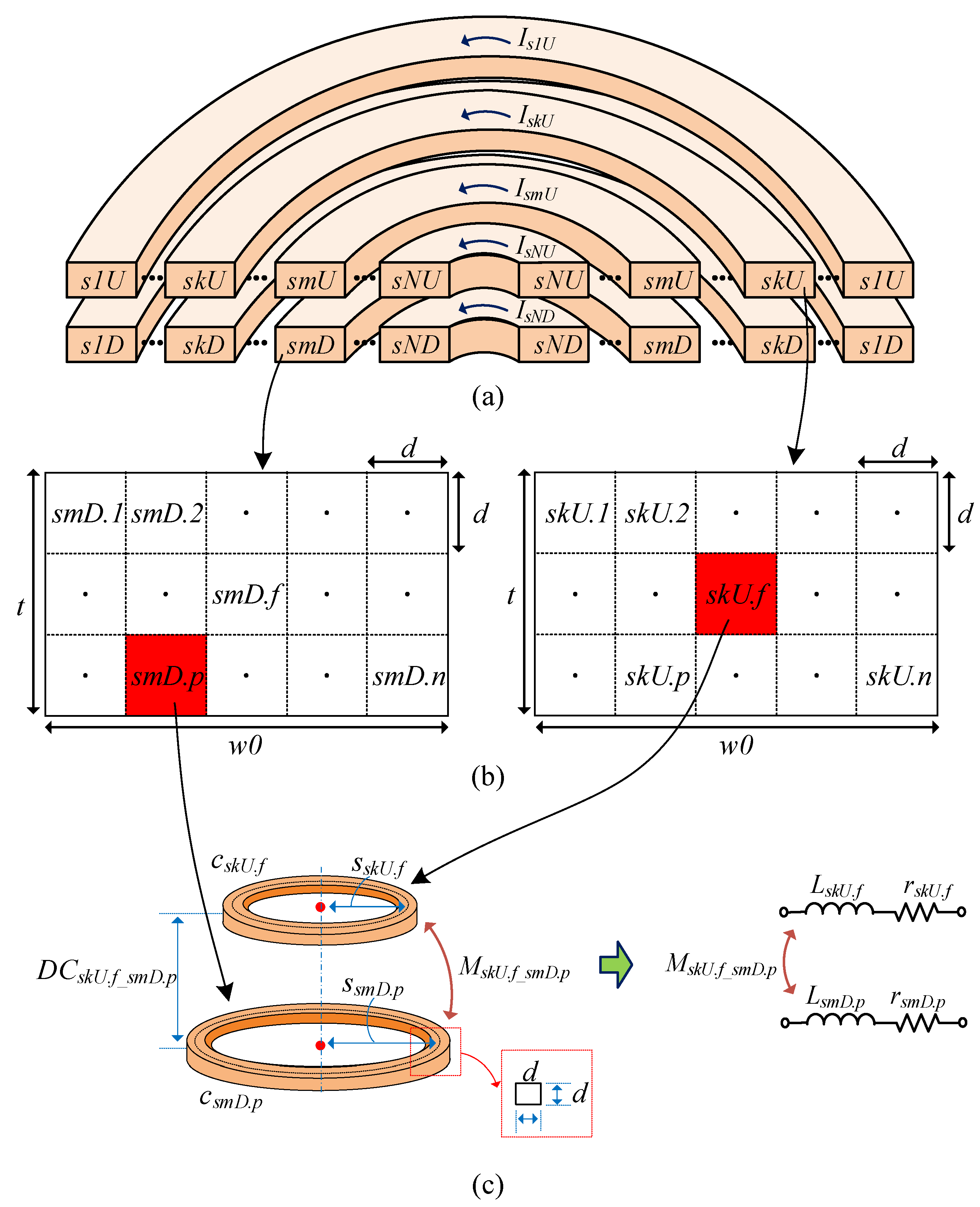
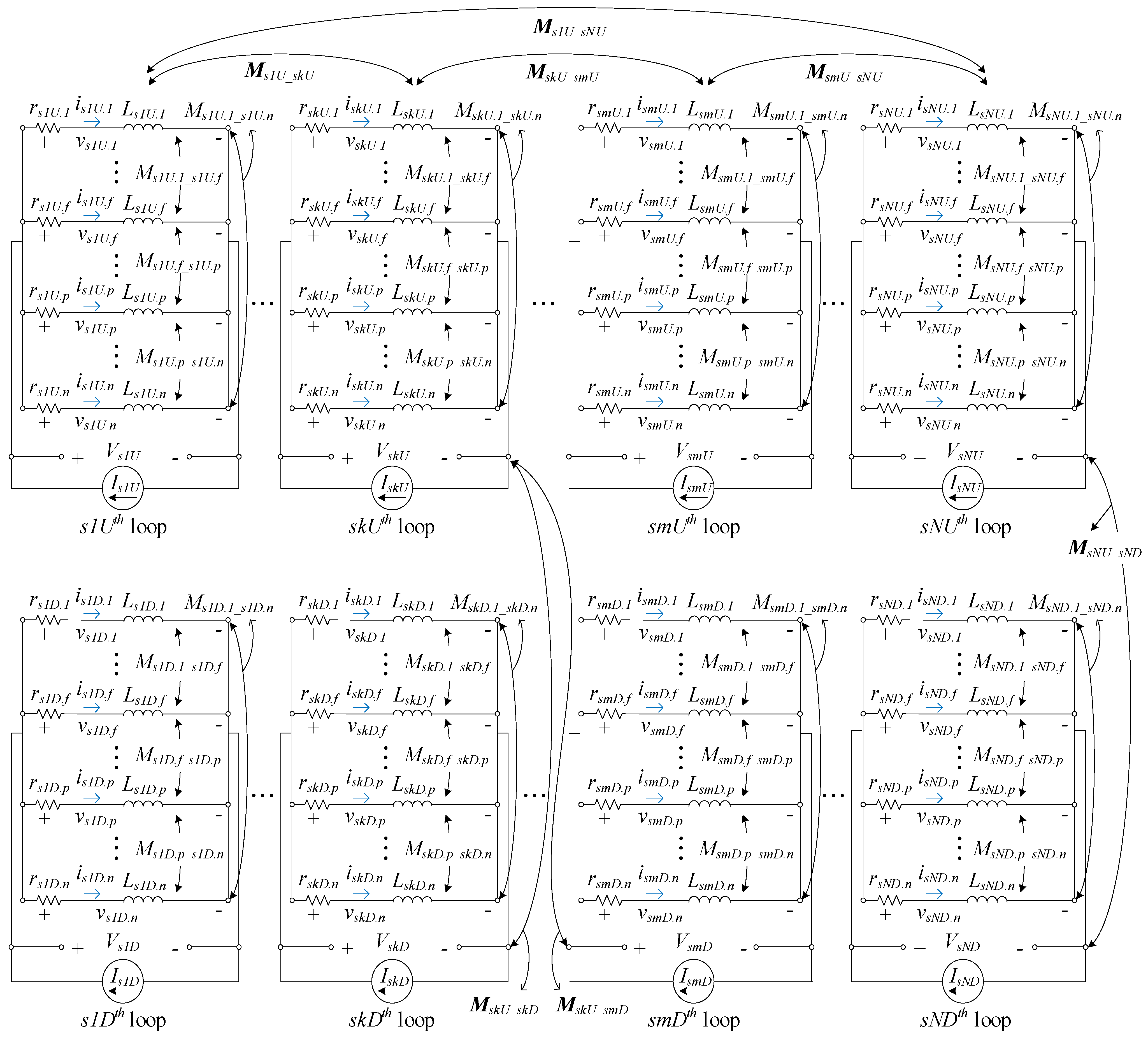
3. Calculation of Resistance and Inductance of the Multilayer Planar Spiral Coil
3.1. VFM and Equivalent Circuit Formulation for a Multilayer Planar Spiral Coil
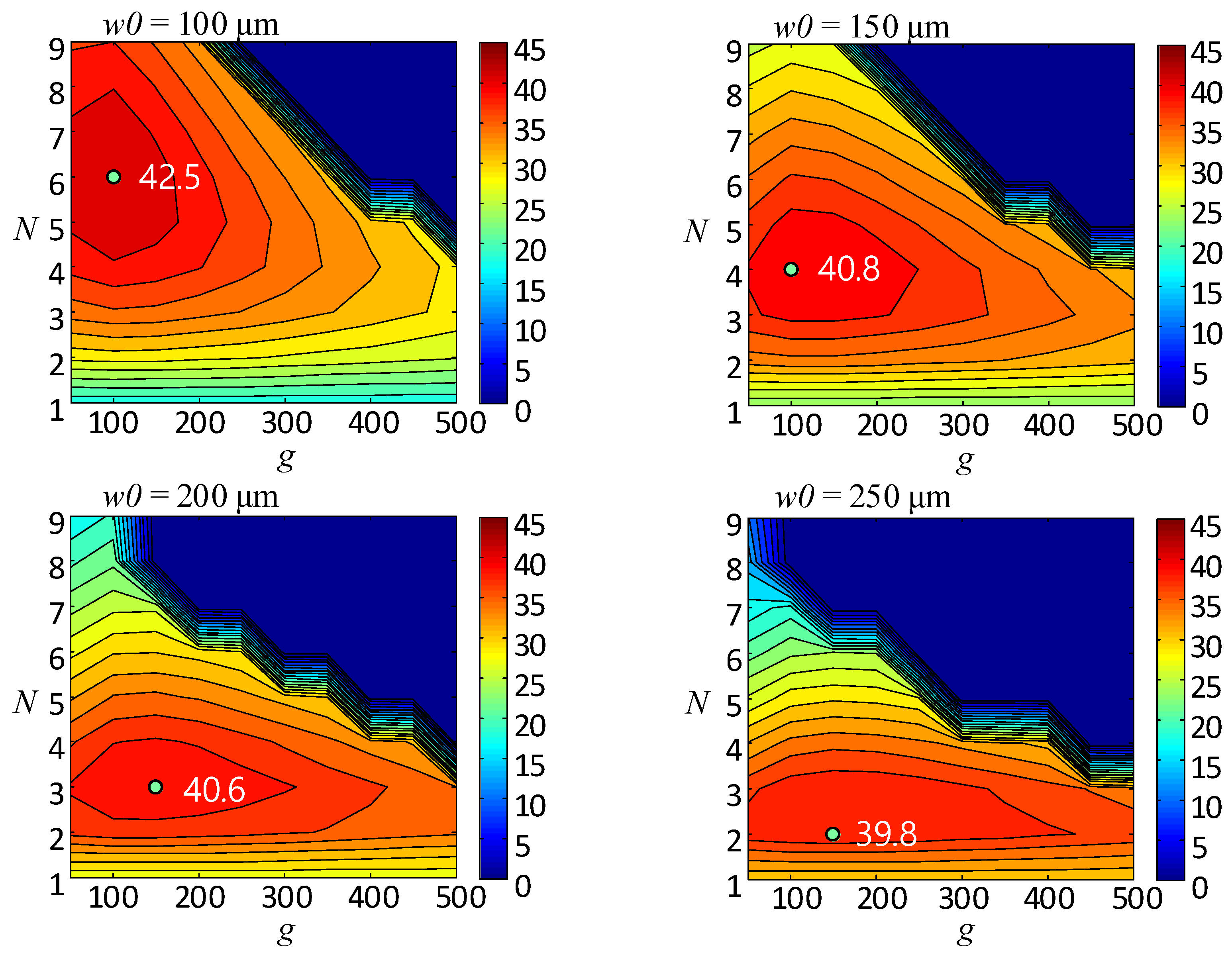
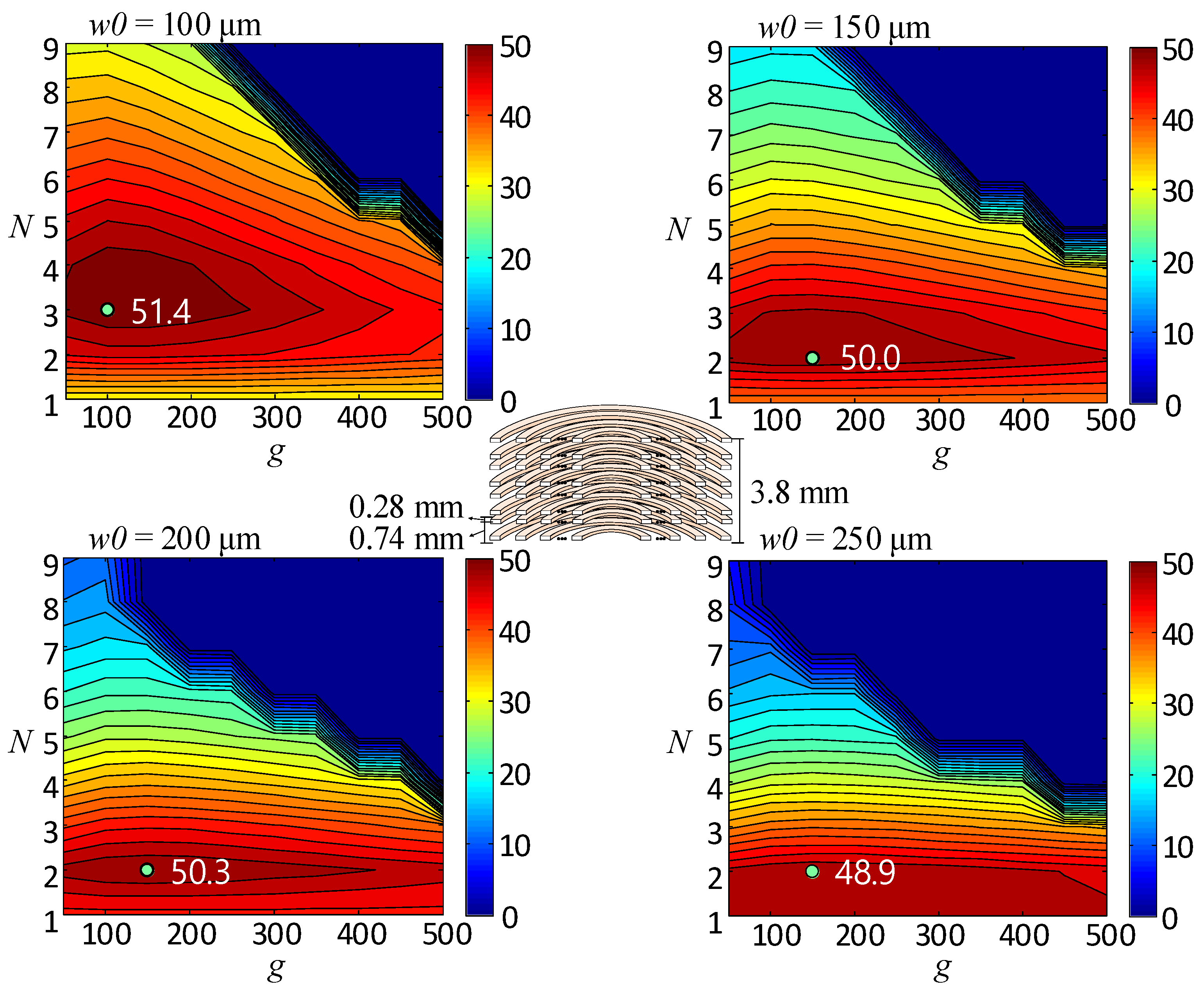
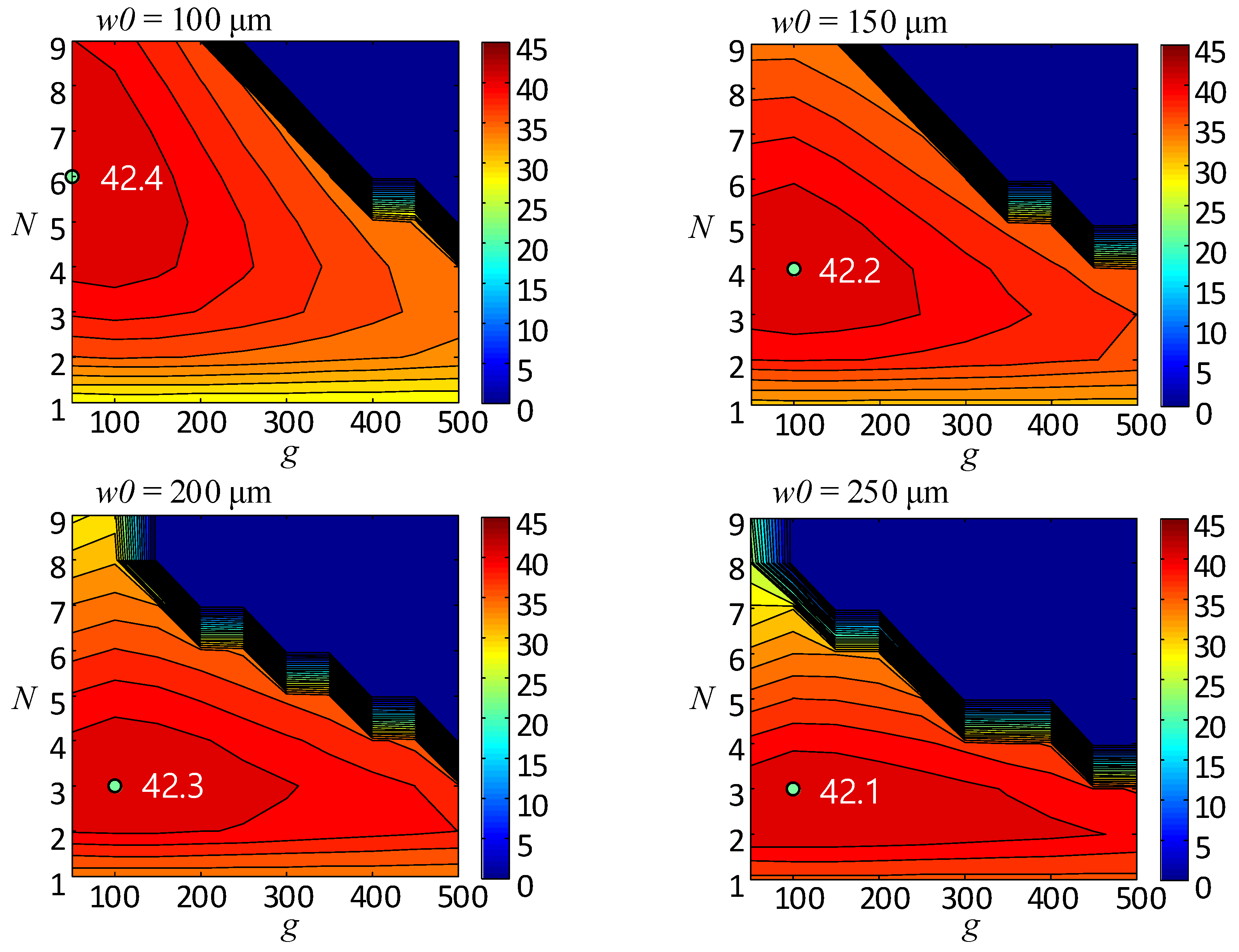
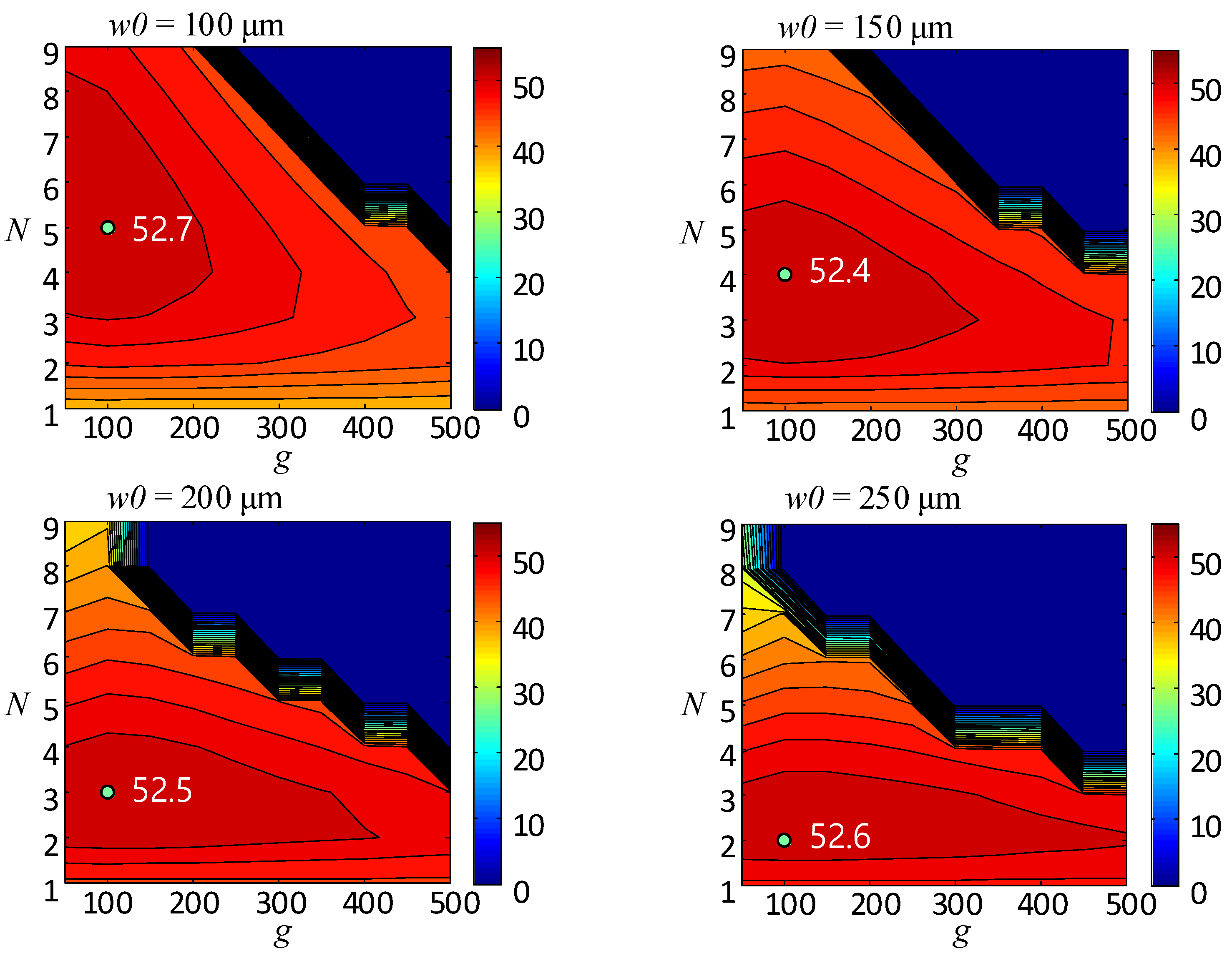
3.2. Calculation Results and Analysis
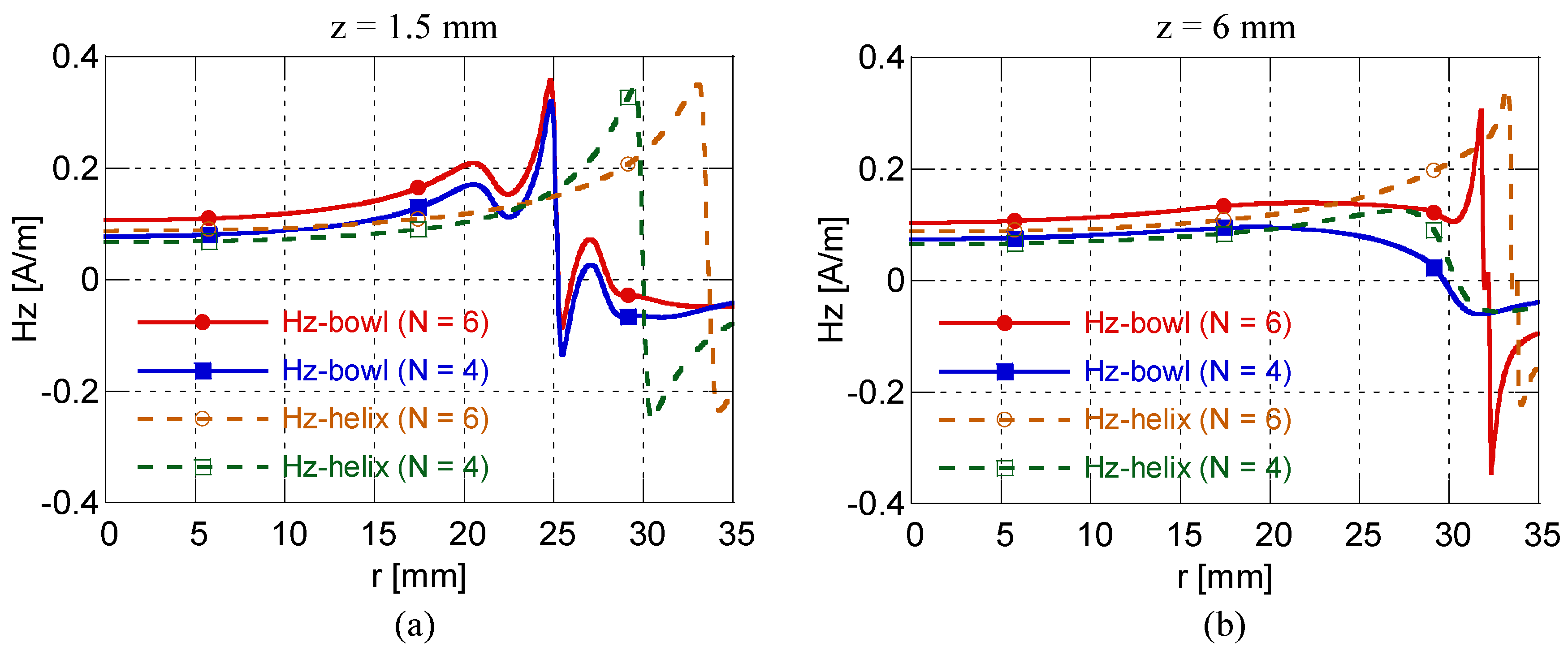
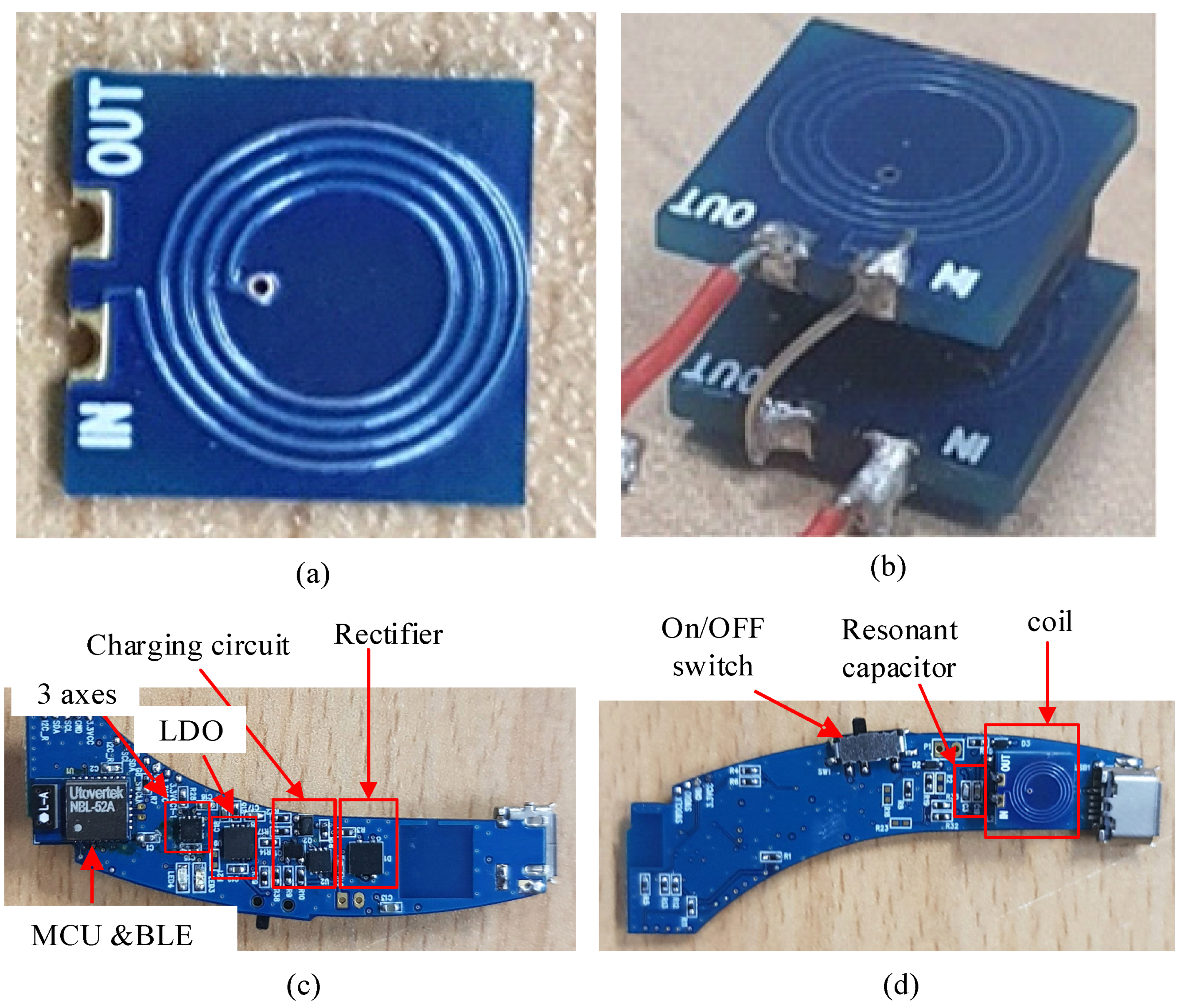
4. Coil Fabrication and Measurement
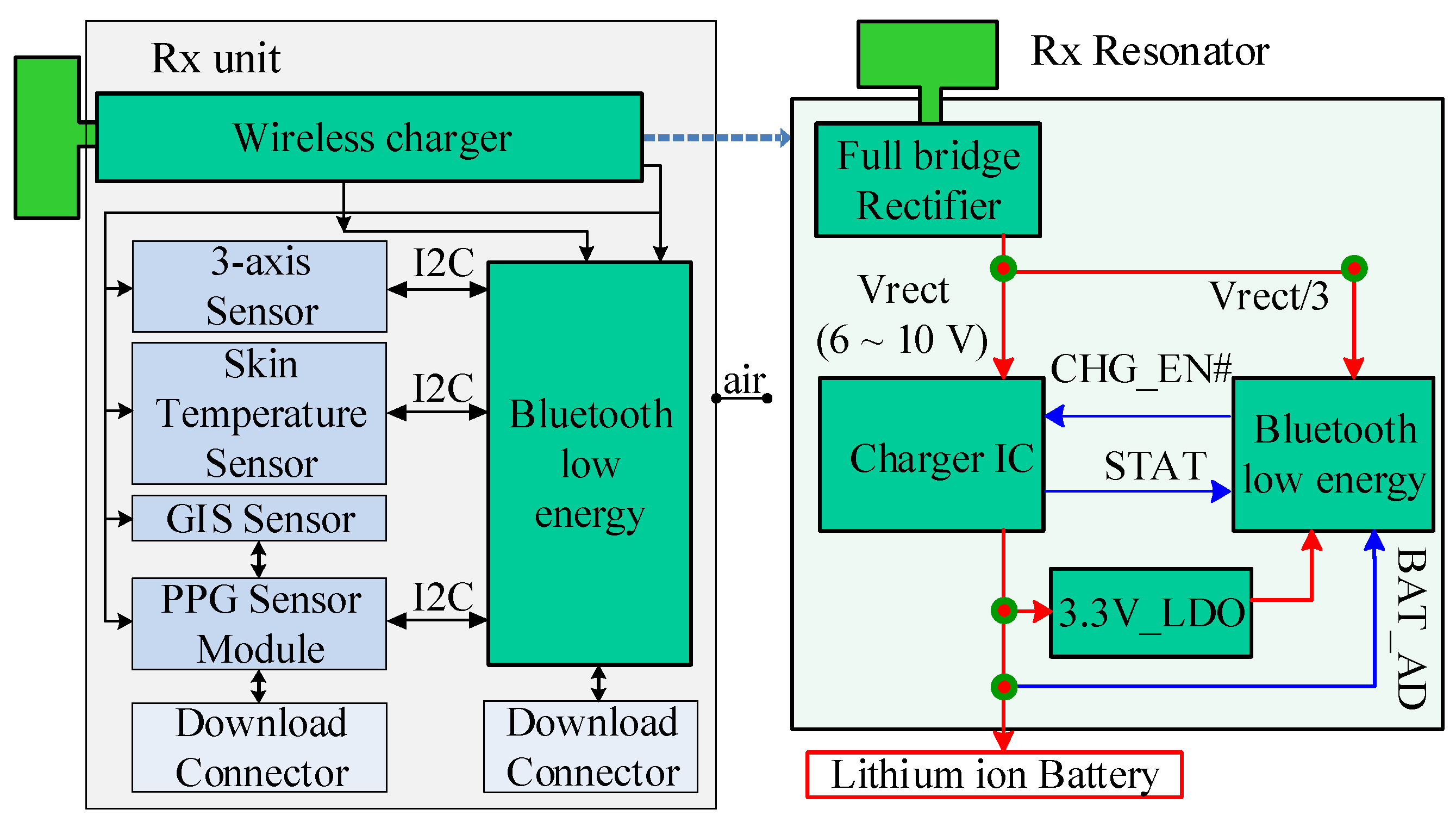
5. Wearable Bio-Signal Monitoring Device and Wireless Charging
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Won, S.M.; Song, E.; Reeder, E.T.; Rogers, J.A. Emerging Modalities and Implantable Technologies for Neuromodulation. Cell 2020, 181, 115–135. [Google Scholar] [CrossRef]
- Won, S.M.; Cai, L.; Gutruf, P.; Rogers, J.A. Wireless and battery-free technology for neuroengineering. Nat. Biomed. Eng. 2021, 1–19. [Google Scholar] [CrossRef]
- Jeong, S.; Kim, D.; Song, J.; Kim, H.; Lee, S.; Song, C.; Lee, J.; Song, J.; Kim, J. Smartwatch strap wireless power transfer system with flexible PCB coil and shielding material. IEEE Trans. Ind. Electron. 2019, 66, 4054–4064. [Google Scholar] [CrossRef]
- Wagih, M.; Komolafe, A.; Zaghari, B. Wearable Wireless Power Transfer using Direct-Write Dispenser Printed Flexible Coils. In Proceedings of the 2020 IEEE International Conference on Flexible and Printable Sensors and Systems (FLEPS), Manchester, UK, 16–19 August 2020; pp. 1–4. [Google Scholar] [CrossRef]
- Jow, U.-M.; Ghovanloo, M. Design and Optimization of Printed Spiral Coils for Efficient Transcutaneous Inductive Power Transmission. IEEE Trans. Biomed. Circuits Syst. 2007, 1, 193–202. [Google Scholar] [CrossRef] [PubMed]
- Kim, D.-H.; Park, Y.-J. Calculation of the inductance and AC resistance of planar rectangular coils. Electron. Lett. 2016, 52, 1321–1323. [Google Scholar] [CrossRef]
- Kim, C.Y.; Ku, M.J.; Qazi, R.; Nam, H.J.; Park, J.W.; Nam, K.S.; Oh, S.; Kang, I.; Jang, J.-H.; Kim, W.Y.; et al. Soft subdermal implant capable of wireless battery charging and programmable controls for applications in optogentics. Nat. Commun. 2021, 12, 535. [Google Scholar] [CrossRef] [PubMed]
- Lope, I.; Carretero, C.; Acero, J.; Alonso, R.; Burdio, J.M. AC Power Losses Model for Planar Windings With Rectangular Cross-Sectional Conductors. IEEE Trans. Pow. Electron. 2014, 29, 23–28. [Google Scholar] [CrossRef]
- Chen, K.; Zhao, Z. Analysis of the Double-Layer Printed Spiral Coil for Wireless Power Transfer. IEEE Trans. Emerg. Sel. Topics Power Electron. 2013, 1, 114–121. [Google Scholar] [CrossRef]
- Gong, F.; Cong, Y.; Wei, Z.; Yin, B.; Chi, H.; Luan, X. Analysis of the multi-layer Printed Spiral Coil for wireless power transfer system used in medical implants. 2016 Asia-Pacific Int. Symp. Electromag. Comp. (APEMC) 2016, 1, 460–462. [Google Scholar] [CrossRef]
- Bao, K.; Zekios, C.L.; Georgakopoulos, S.V. A wearable WPT system on flexible substrates. IEEE Antennas Wireless Propag. Lett. 2019, 18, 931–935. [Google Scholar] [CrossRef]
- Kim, D.-H.; Kim, J.; Park, Y.-J. Optimization and Design of Small Circular Coils in a Magnetically Coupled Wireless Power Transfer System in the Megahertz Frequency. IEEE Trans. Micro. Theory Tech. 2016, 64, 1–12. [Google Scholar] [CrossRef]
- Good, R.H. Elliptic integrals, the forgotten functions. Eur. J. Phys. 2001, 22, 119–126. [Google Scholar] [CrossRef]
- Kurs, A.; Karalis, A.; Moffatt, R.; Joannopoulos, J.D.; Fisher, P.; Soljacic, M. Wireless Power Transfer via Strongly Coupled Magnetic Resonances. Science 2007, 317, 83–86. [Google Scholar] [CrossRef] [Green Version]
- Kim, J.; Kim, D.-H.; Park, Y.-J. Free-Positioning Wireless Power Transfer to Multiple Devices Using a Planar Transmitting Coil and Switchable Impedance Matching Networks. IEEE Trans. Microw. Theory Tech. 2016, 64, 3714–3722. [Google Scholar] [CrossRef]
- Kim, J.; Kim, D.-H.; Choi, J.; Kim, K.-H.; Park, Y.-J. Free-Positioning Wireless Charging System for Small Electronic Devices Using a Bowl-Shaped Transmitting Coil. IEEE Trans. Microw. Theory Tech. 2015, 63, 791–800. [Google Scholar] [CrossRef]
- Na, K.; Kim, J.; Park, Y.-J. Free-Positioning Magnetic Resonance Wireless Power Transfer System for Biomedical Devices. In Proceedings of the 2019 IEEE Wireless Power Transfer Conference (WPTC), London, UK, 18–21 June 2019; pp. 497–501. [Google Scholar]







| Measurement | Calculation | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Position | L [nH] | R [mΩ] | M [nH] | FoM | Maximum Coupling Efficiency (%) | L [nH] | R [mΩ] | M [nH] | FoM | Maximum Coupling Efficiency (%) | |
| Rx1 | 1 | 307.31 | 444.29 | 21.5 | 2.10 | 39.9 | 323.20 | 372.03 | 19.9 | 2.18 | 41.1 |
| 2 | 307.31 | 444.29 | 32.7 | 3.19 | 54.0 | 323.20 | 372.03 | 27.4 | 3.01 | 52.1 | |
| Rx2 | 1 | 695.06 | 919.88 | 36.1 | 2.45 | 45.1 | 750.57 | 798.96 | 39.4 | 2.95 | 51.4 |
| 2 | 695.06 | 919.88 | 53.7 | 3.64 | 58.1 | 750.57 | 798.96 | 51.9 | 3.89 | 60.1 | |
| Rx3 | 1 | 693.02 | 929.24 | 43.0 | 2.90 | 50.8 | - | - | - | - | - |
| 2 | 693.02 | 929.24 | 61.5 | 4.15 | 62.0 | - | - | - | - | - | |
| Tx | 3032.2 | 429.15 | 2777.0 | 404.39 | |||||||
| [7] | [9] | [11] | This Work | |
|---|---|---|---|---|
| Rx coil size, metal thickness | 15 mm(W) × 10 mm(L), 1 oz | 288 mm × 288 mm, 3 oz | 64 mm(W) × 64 mm(L), 1 oz | 6 mm(W) × 6 mm(L), 2 oz (70 μm) |
| Number of layers | 2 (Rx coil) | 2 (Rx coil) | 12 (Tx coil) | 4 (Rx coil) |
| Frequency (MHz) | 6.78 | 4.03 | 80 | 6.78 |
| Coil-to-coil/ dc-dc efficiency | NA, less than 1% | NA, NA | 80%, NA | 58.1%, 16.1% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, Y.-J.; Kim, J.-E.; Na, K.-M.; Yang, K.-D.; Cho, K.-H. Optimization and Analysis of Multilayer Planar Spiral Coils for the Application of Magnetic Resonance Wireless Power Transfer to Wearable Devices. Energies 2021, 14, 5113. https://doi.org/10.3390/en14165113
Park Y-J, Kim J-E, Na K-M, Yang K-D, Cho K-H. Optimization and Analysis of Multilayer Planar Spiral Coils for the Application of Magnetic Resonance Wireless Power Transfer to Wearable Devices. Energies. 2021; 14(16):5113. https://doi.org/10.3390/en14165113
Chicago/Turabian StylePark, Young-Jin, Ji-Eun Kim, Kyung-Min Na, Ki-Dong Yang, and Kyung-Hwan Cho. 2021. "Optimization and Analysis of Multilayer Planar Spiral Coils for the Application of Magnetic Resonance Wireless Power Transfer to Wearable Devices" Energies 14, no. 16: 5113. https://doi.org/10.3390/en14165113






