Diagnostic Protocol for Thermal Performance of District Heating Pipes in Operation. Part 1: Estimation of Supply Pipe Temperature by Measuring Temperature at Valves after Shutdown
Abstract
:1. Introduction
2. Concept for Developing the Cooling Method
2.1. Requirements
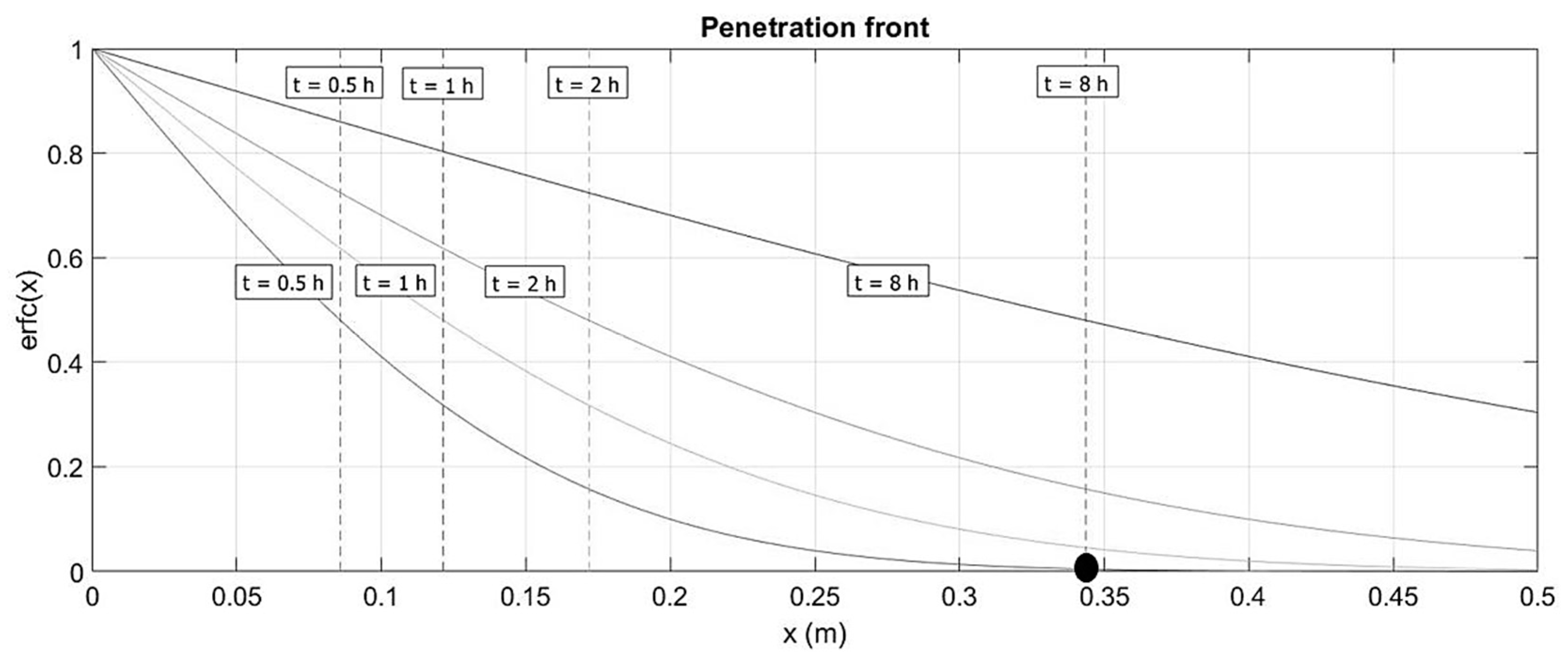
2.1.1. Influence of Seasonal Soil Temperature Variations on Estimating the Thermal Conductivity of the Pipe
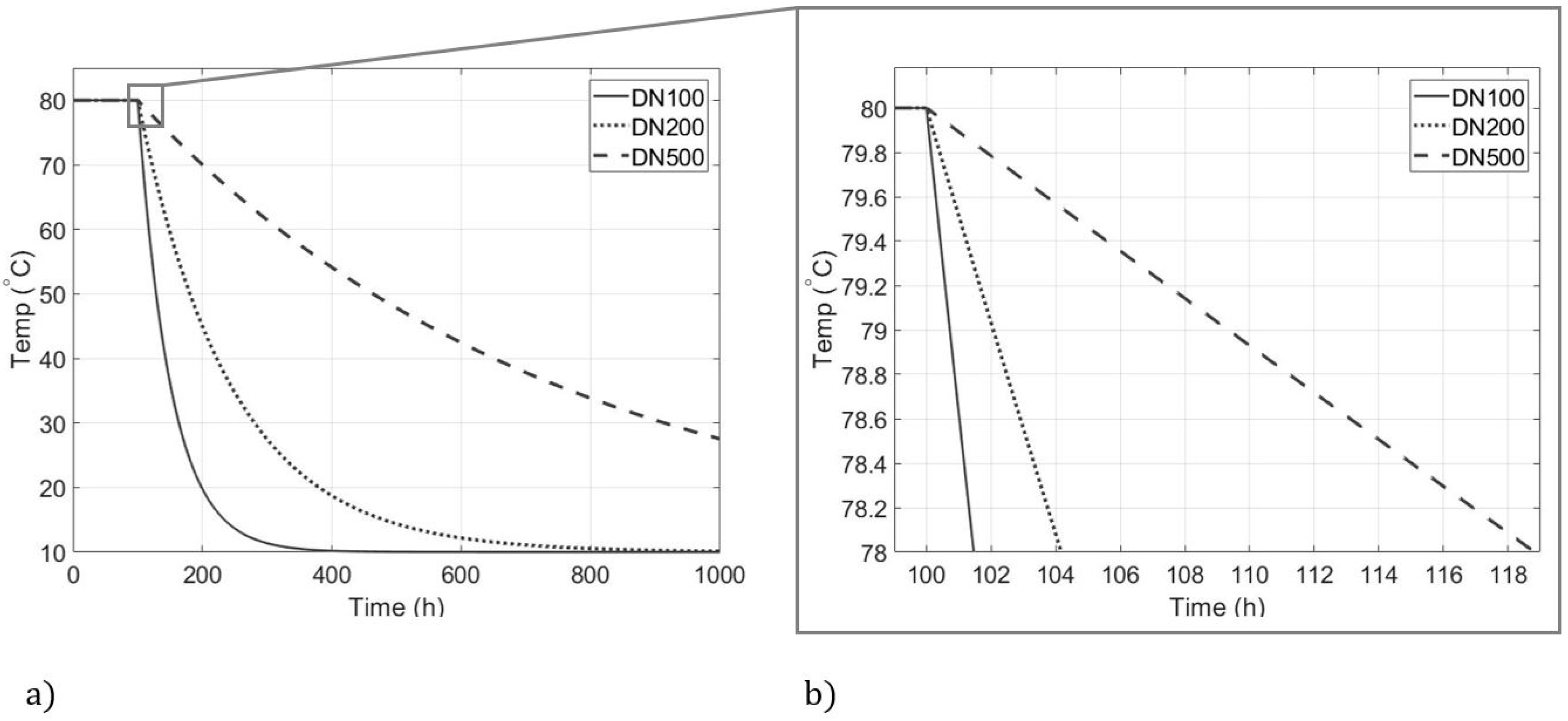
2.1.2. Shutdown Time
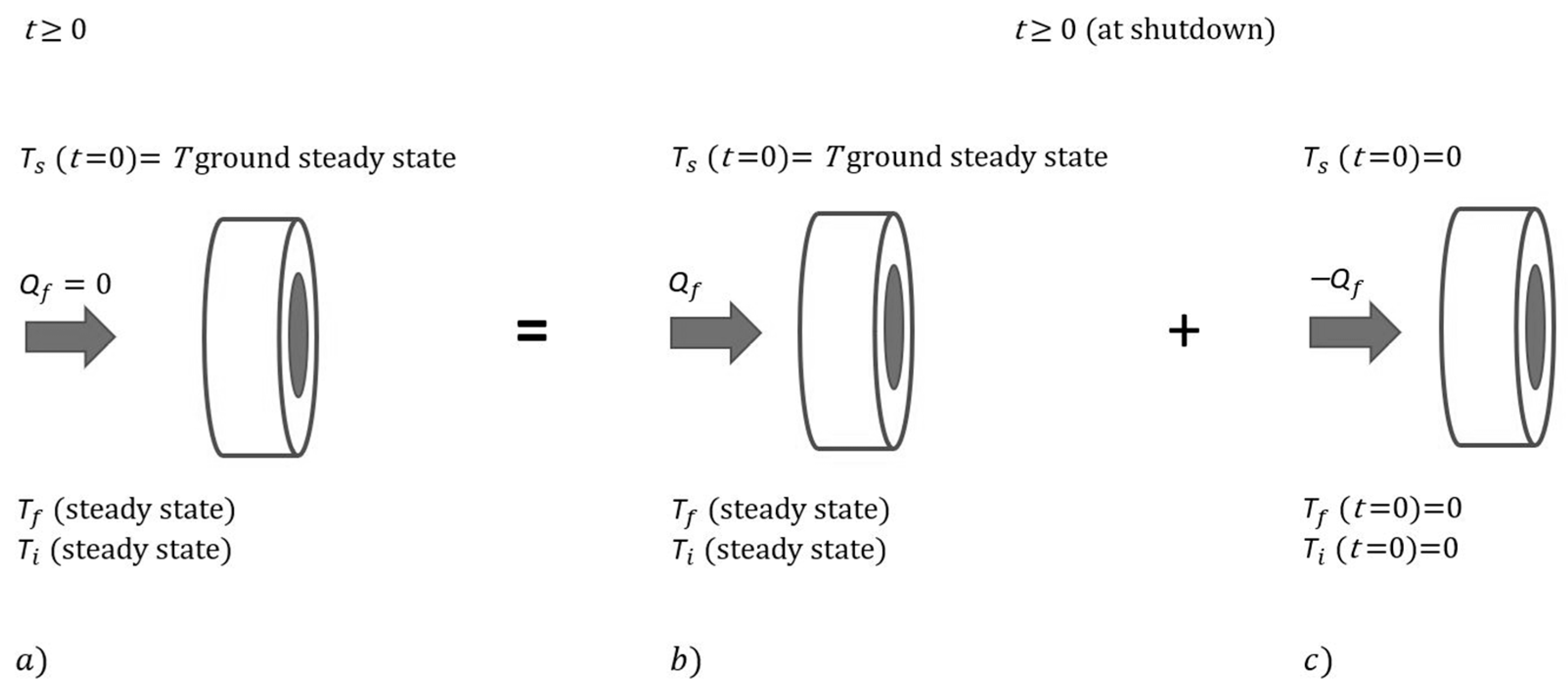
2.1.3. Influence of Thermal History of the Supply Pipe Temperature
2.2. Measuring Fluid Temperature through Valves
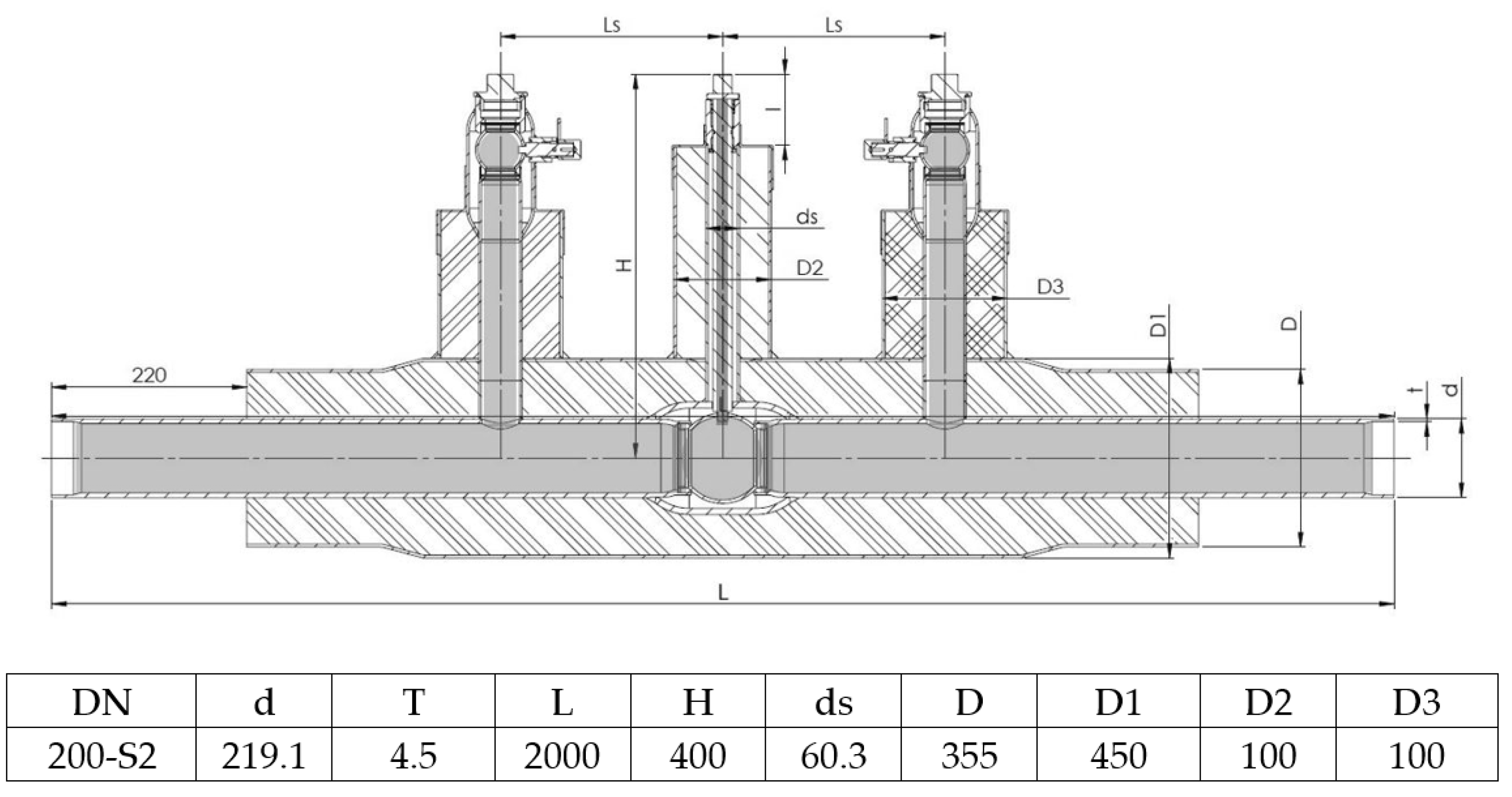
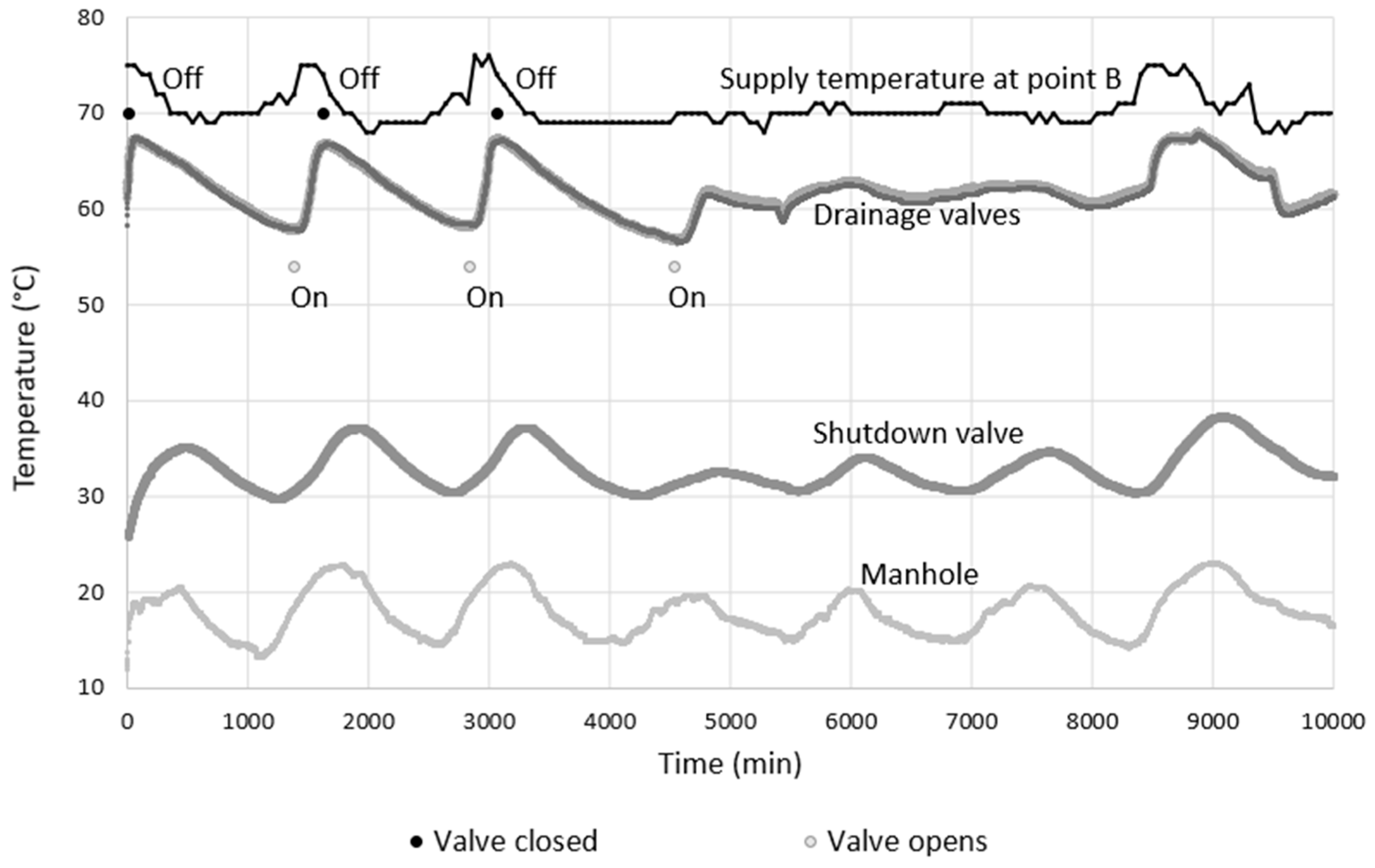
2.2.1. Shutdown Valve
2.2.2. Drainage Valve
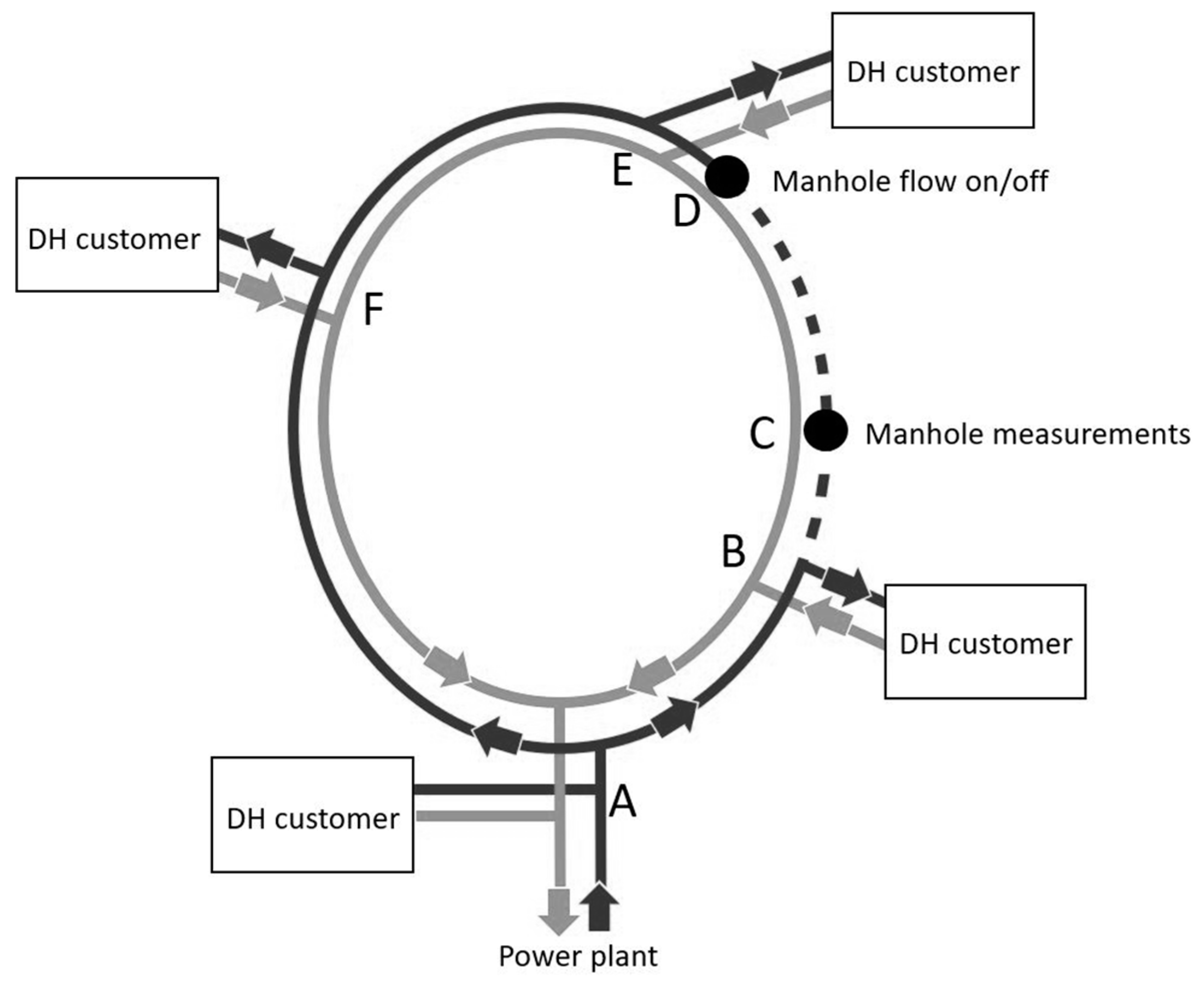
3. Field Measurement of a DH Network
4. Analysis of Valve Measurements
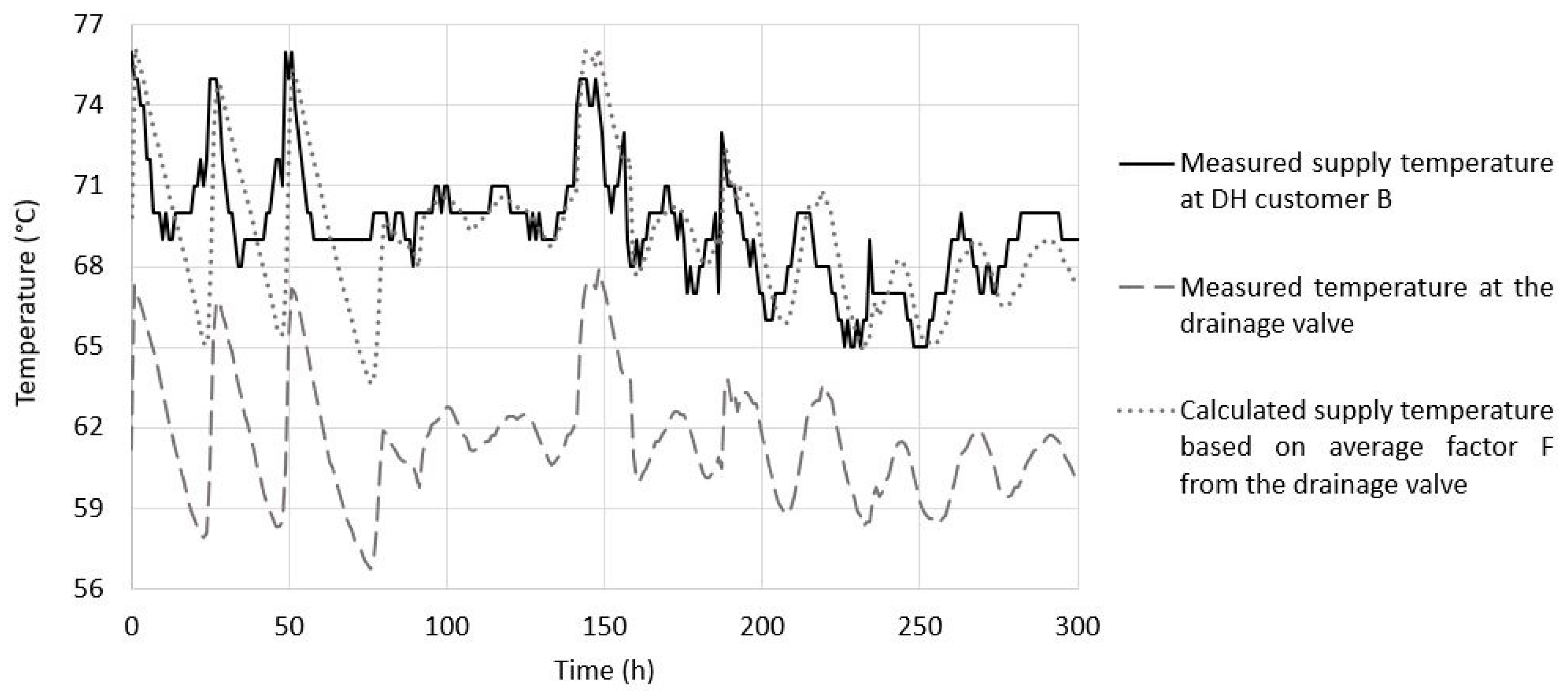
4.1. Absolute Temperature
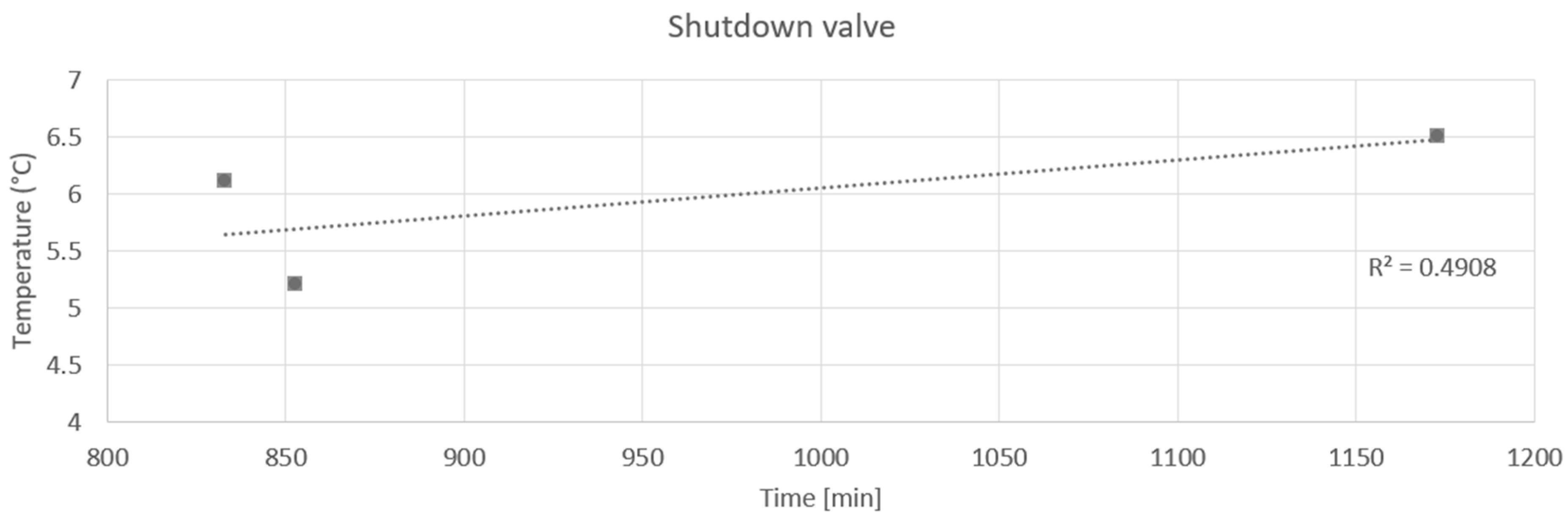
4.2. Thermal Response Time of Valve Material
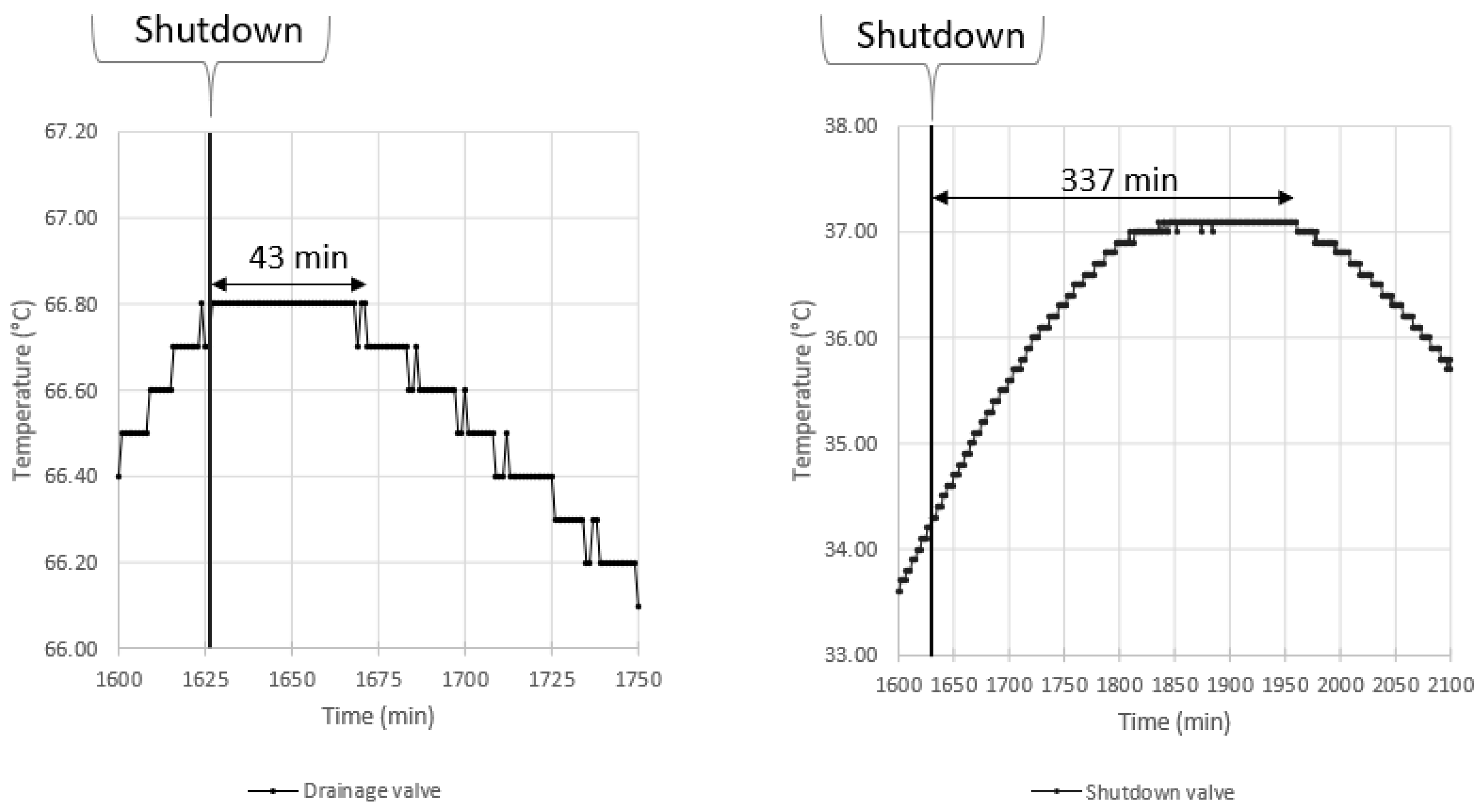
4.3. Temperature Decline during Shutdown
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Fredriksen, S.; Werner, S. District Heating and Cooling, 1st ed.; Studentliteratur AB: Lund, Sweden, 2013. [Google Scholar]
- Berge, A.; Adl-Zarrabi, B.; Hagentoft, C.-E. Assessing the Thermal Performance of District Heating Twin Pipes with Vacuum Insulation Panels. Energy Procedia 2015, 78, 382–387. [Google Scholar] [CrossRef] [Green Version]
- Kręcielewska, E.; Menard, D. Thermal conductivity coefficient of PUR insulation material from pre-insulated pipes after real operation on district heating networks and after artificial ageing process in heat chamber. In Proceedings of the 14th International Symposium on District Heating and Cooling, Stockholm, Sweden, 7–9 September 2014. [Google Scholar]
- Kakavand, A.; Adl-Zarrabi, B. Introduction of Possible Inspection Methods for Evaluating Thermal Aging Status of Existing Pre-Insulated District Heating Systems; Chalmers University of Technology: Gothenburg, Sweden, 2015. [Google Scholar]
- Lidén, H.P.; Adl-Zarrabi, B. Non destructive methods of district heating pipes. In Proceedings of the 12th European Conference on Non-Destructive Testing (ECNDT 2018), Gothenburg, Sweden, 11–15 June 2018. [Google Scholar]
- Lidén, H.P.; Adl-Zarrabi, B. Development of a Non-destructive Testing Method for Assessing Thermal Status of District Heating Pipes. J. Nondestruct. Eval. 2020, 39, 22. [Google Scholar] [CrossRef] [Green Version]
- Lidén, P.; Adl-Zarrabi, B. Non-destructive methods for assessment of district heating pipes: A pre study for selection of proper method. In Proceedings of the 15th International Symposium on District Heating and Cooling, Seoul, Korea, 4–7 September 2016. [Google Scholar]
- Lidén, P. Development of a Non-Destructive Testing Method for Thermal Assessment of a District Heating Network; Department of Architecture and Civil Engineering, Chalmers University of Technology: Gothenburg, Sweden, 2020. [Google Scholar]
- Hagentoft, C.E. Heat loss to the ground from a building. Slab on the ground and cellar, LTH/TVBH-1004. In Building Physics; Building Physics: Lund, Sweden, 1998. [Google Scholar]
- Bilskie, J. Dual Probe Methods for Determining Soil Thermal Properties, Numerical and Laboratory Study. Ph.D. Thesis, Iowa State University, Ames, IA, USA, 1994. [Google Scholar]
- Broen. District Heating Product Catalogue 2021. 2021. Available online: www.Broen.com (accessed on 5 May 2021).
- Powerpipe. Product Catalog. 2018. Available online: www.Powerpipe.se (accessed on 4 February 2021).
- Stadtwerke Leipzig. Zeitstandsverhalten von PUR-Schäumen in Praxisgealterten Kunststoffmantelrohren Hinsichtlich Wärmedämmung und Festigkeit (Verbundprojekt); Report; 2004; Available online: https://www.tib.eu/de/suchen/id/TIBKAT:477726356/Zeitstandsverhalten-von-PUR-Sch%C3%A4umen-in-praxisgealterten?cHash=87d46170aa884823417ce10077ab42bf (accessed on 4 February 2021). [CrossRef]
- Bing. Thermal Insulation Materials Made of Rigid Polyurethane foam (PUR/PIR) Properties—Manufacture; Federation of European Rigid Polyurethane Foam Assosiation: Brussels, Belgium, 2006. [Google Scholar]
- Matmatch. 2020. Available online: Matmatch.com (accessed on 5 January 2020).
- Fjellborg, F. Data Received from Energy Company; Borås Energy: Borås, Sweden, 2020. [Google Scholar]

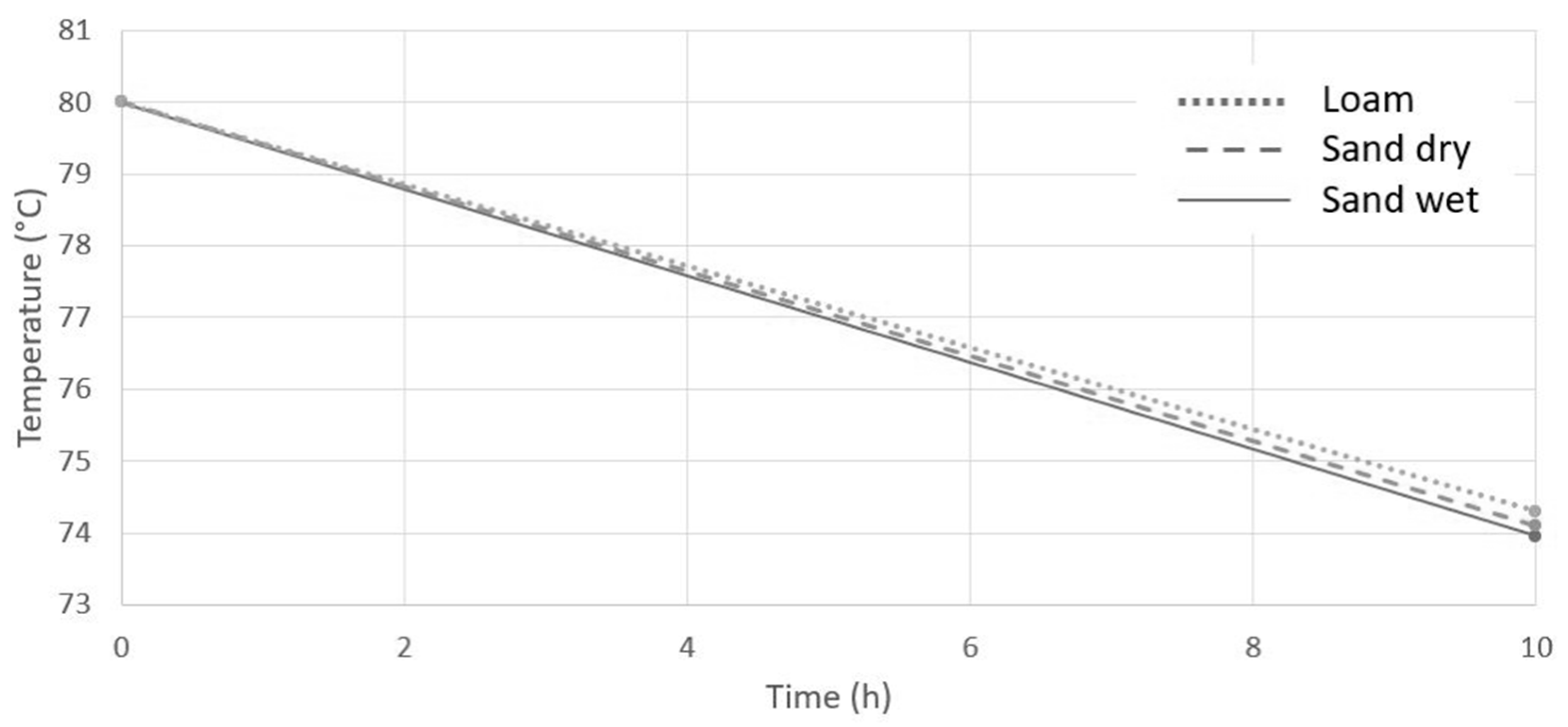




| Soil Type | Water Content (m3/m3) | Thermal Conductivity (W/mK) | Volumetric Heat Capacity (106 J/ m3K) |
|---|---|---|---|
| Loam | 0.295 | 1.01 | 2.16 |
| Sand dry | 0.022 | 1.53 | 1.36 |
| Sand wet | 0.351 | 3.08 | 2.68 |
| DH Component | Density (kg/m3) at 20 °C | Thermal Conductivity (W/mK) at 20 °C | Specific Heat Capacity (J/kgK) at 20 °C | Thermal Diffusivity (m2/s) at 20 °C |
|---|---|---|---|---|
| HDPE casing | 950 | 0.38–0.51 | 2100–2700 | 1.9710−7 |
| PUR insulation | 61 * | 0.026 * | 1400–1500 | 2.3110−7 |
| Mineral wool insulation | 130 | 0.36 | 840 | 0.2210−7 |
| DH water | 998 | 0.60 | 4200 | 1.4010−7 |
| P235GH ** | 7850 | 57.5 | 460 | 1.5910−5 |
| P235TR1/P235TR2 ** | 7850 | 56.9 | 460 | 1.5710−5 |
| AISI 304 *** | 7800 | 16.0 | 500 | 4.1010−6 |
| Drainage Valve | Shutdown Valve | |
|---|---|---|
| Factor (F) | 0.15 | 0.71 |
| Standard deviation | 0.02 | 0.28 |
| Coefficient of variation | 13.5% | 39.0% |
| Thermal Response Time (min) | Temperature Decline, Duration (min) | Temperature, MAX (°C) | Temperature, MIN (°C) | Temperature Difference (°C) | Temperature Decline (°C/h) | |
|---|---|---|---|---|---|---|
| First shutdown | 70 | 1316 | 67.4 | 58.0 | 9.4 | 0.43 |
| Second shutdown | 43 | 1075 | 66.8 | 58.4 | 8.0 | 0.45 |
| Third shutdown | 33 | 1461 | 67.2 | 56.5 | 10.6 | 0.44 |
| Thermal Response time(min) | Temperature Decline, Duration (min) | Temperature, MAX (°C) | Temperature, MIN (°C) | Temperature Difference (°C) | Temperature Decline (°C/h) | |
| First shutdown | 510 | 853 | 35.1 | 29.9 | 5.2 | 0.37 |
| Second shutdown | 337 | 833 | 36.7 | 30.6 | 6.1 | 0.44 |
| Third shutdown | 270 | 1173 | 36.7 | 30.2 | 6.5 | 0.33 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lidén, P.; Adl-Zarrabi, B.; Hagentoft, C.-E. Diagnostic Protocol for Thermal Performance of District Heating Pipes in Operation. Part 1: Estimation of Supply Pipe Temperature by Measuring Temperature at Valves after Shutdown. Energies 2021, 14, 5192. https://doi.org/10.3390/en14165192
Lidén P, Adl-Zarrabi B, Hagentoft C-E. Diagnostic Protocol for Thermal Performance of District Heating Pipes in Operation. Part 1: Estimation of Supply Pipe Temperature by Measuring Temperature at Valves after Shutdown. Energies. 2021; 14(16):5192. https://doi.org/10.3390/en14165192
Chicago/Turabian StyleLidén, Peter, Bijan Adl-Zarrabi, and Carl-Eric Hagentoft. 2021. "Diagnostic Protocol for Thermal Performance of District Heating Pipes in Operation. Part 1: Estimation of Supply Pipe Temperature by Measuring Temperature at Valves after Shutdown" Energies 14, no. 16: 5192. https://doi.org/10.3390/en14165192
APA StyleLidén, P., Adl-Zarrabi, B., & Hagentoft, C.-E. (2021). Diagnostic Protocol for Thermal Performance of District Heating Pipes in Operation. Part 1: Estimation of Supply Pipe Temperature by Measuring Temperature at Valves after Shutdown. Energies, 14(16), 5192. https://doi.org/10.3390/en14165192






