Optimal Sizing of Battery-Integrated Hybrid Renewable Energy Sources with Ramp Rate Limitations on a Grid Using ALA-QPSO
Abstract
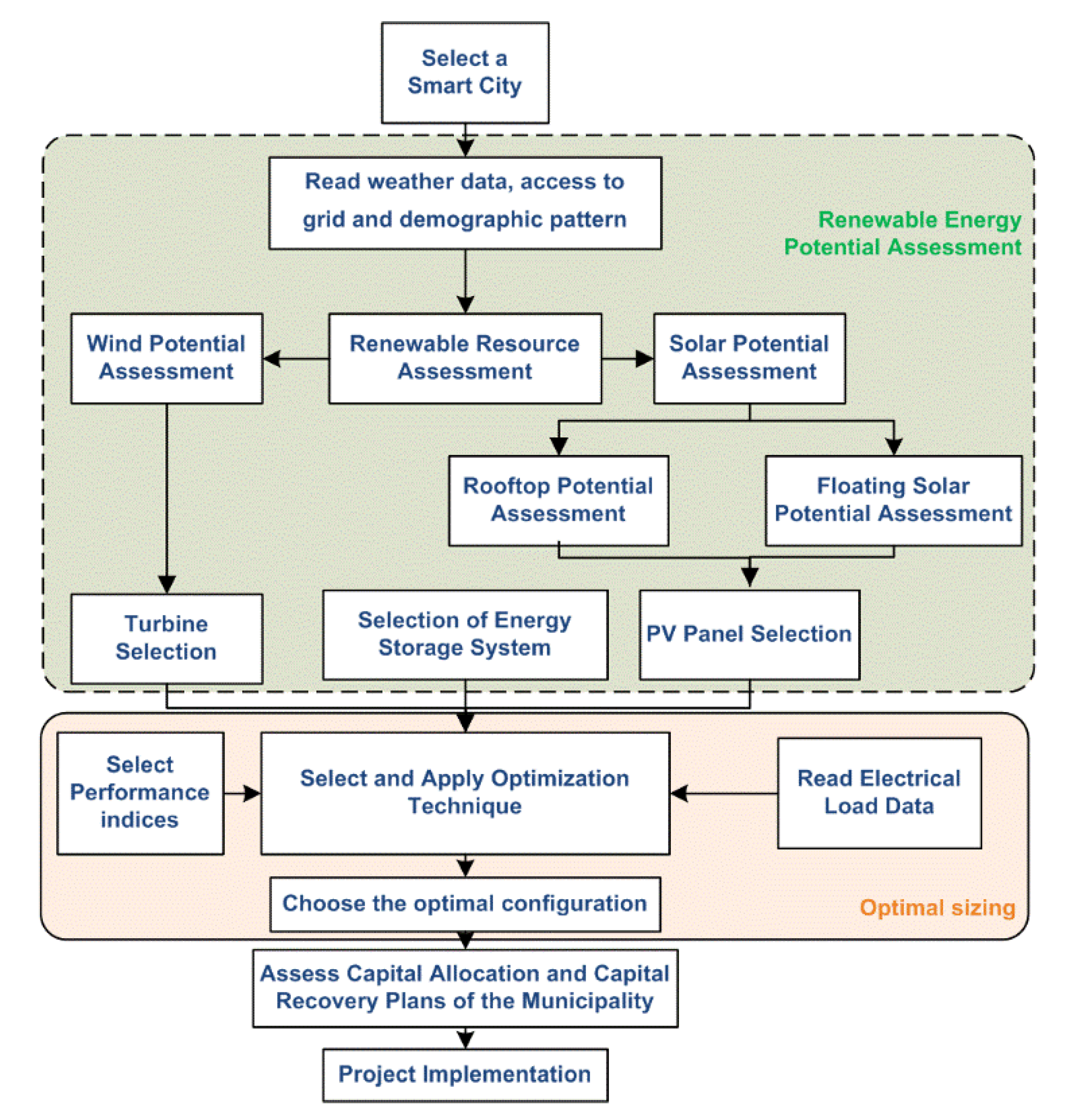
:1. Introduction
1.1. Current Electric Energy Scenario in India
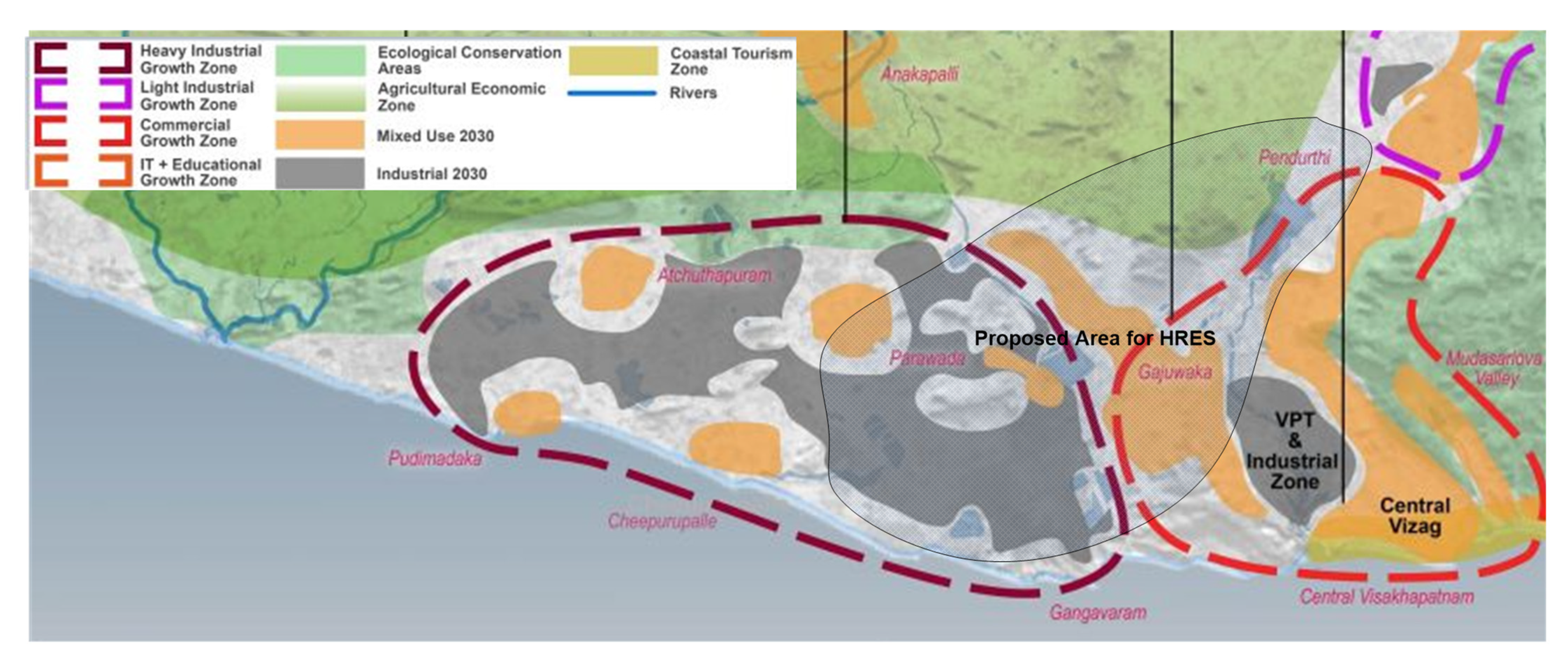
1.2. Electric Energy Scenario in the Proposed Location
2. Literature Review
2.1. Key Contributions
- i.
- A methodology for site selection, resource assessment, and energy management for large-scale renewable energy integration is developed.
- ii.
- Optimal sizing of potential renewable energy sources and a battery bank is assessed to minimize grid ramping, levelized cost of energy, and loss of load using various multi-objective optimization techniques.
2.2. Site Selection and Resource Assessment
2.3. Observations from the Load Profile of the Proposed Location
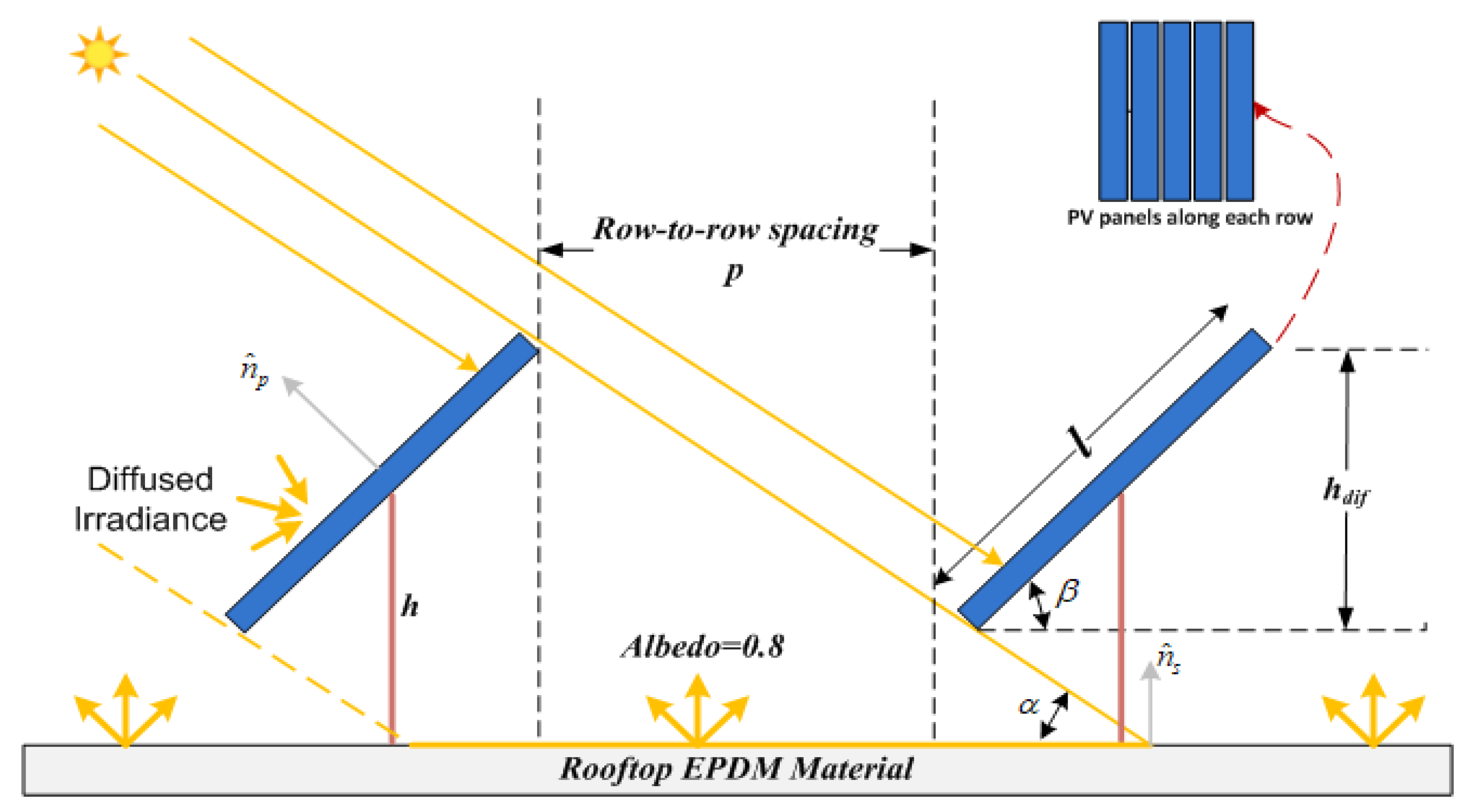
2.4. Land Cover and Shading Analysis
3. Mathematical Modeling
3.1. Solar PV System
- where ,—efficiencies of front and rear cells
- , —front &rear sides rating of panel
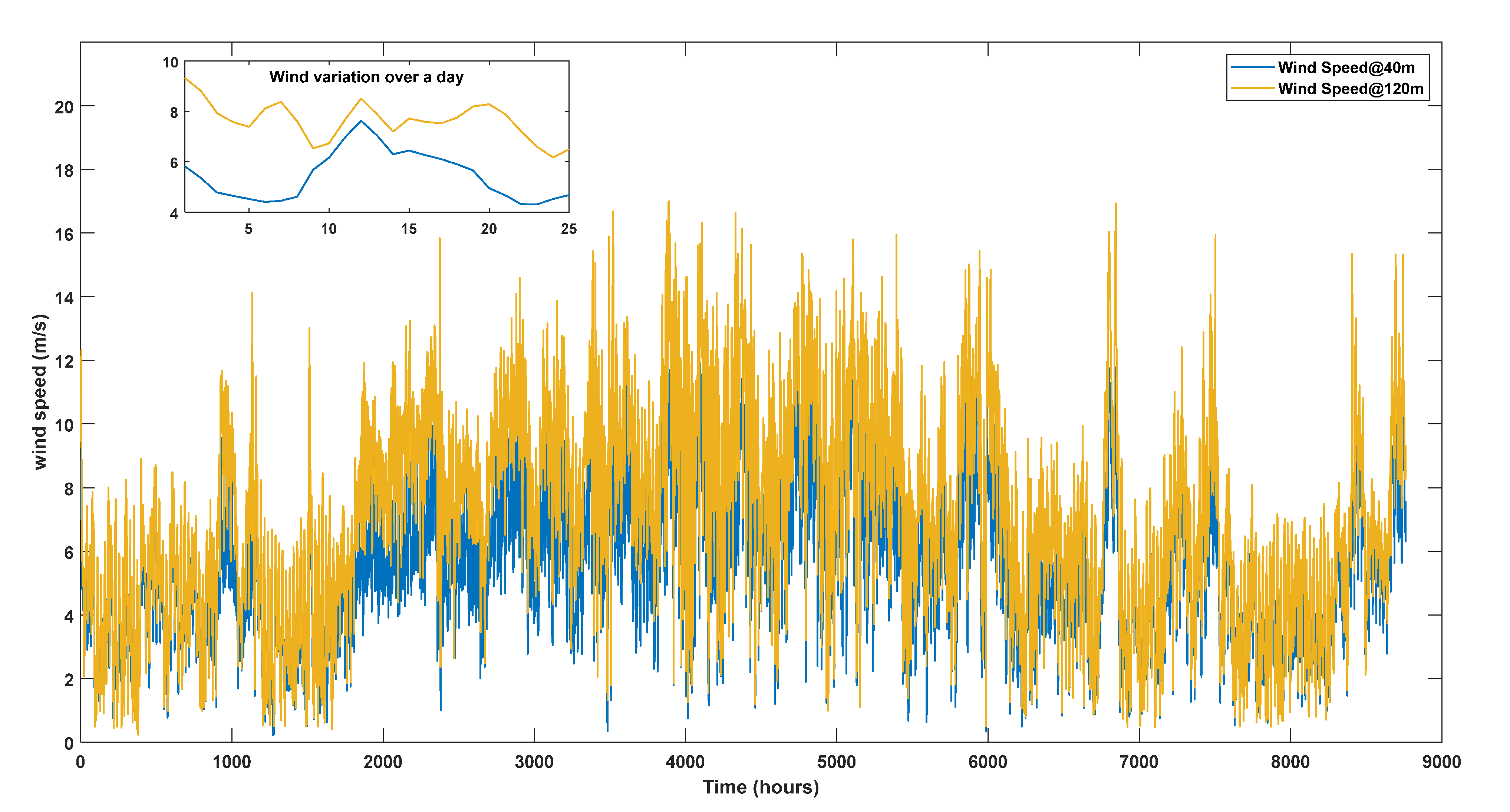
3.2. Wind Energy Conversion System (WECS)
3.3. Battery Energy Storage System
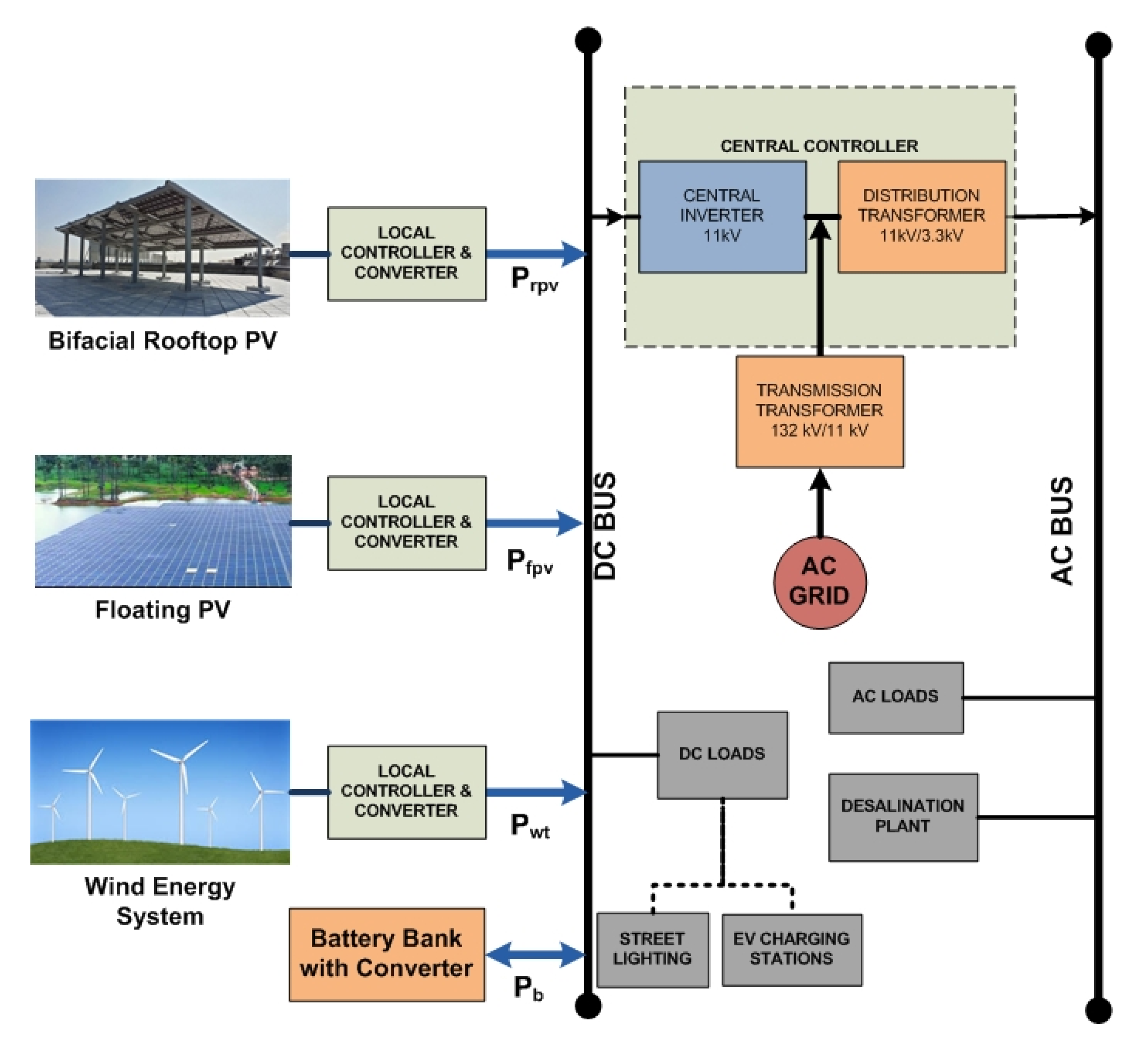
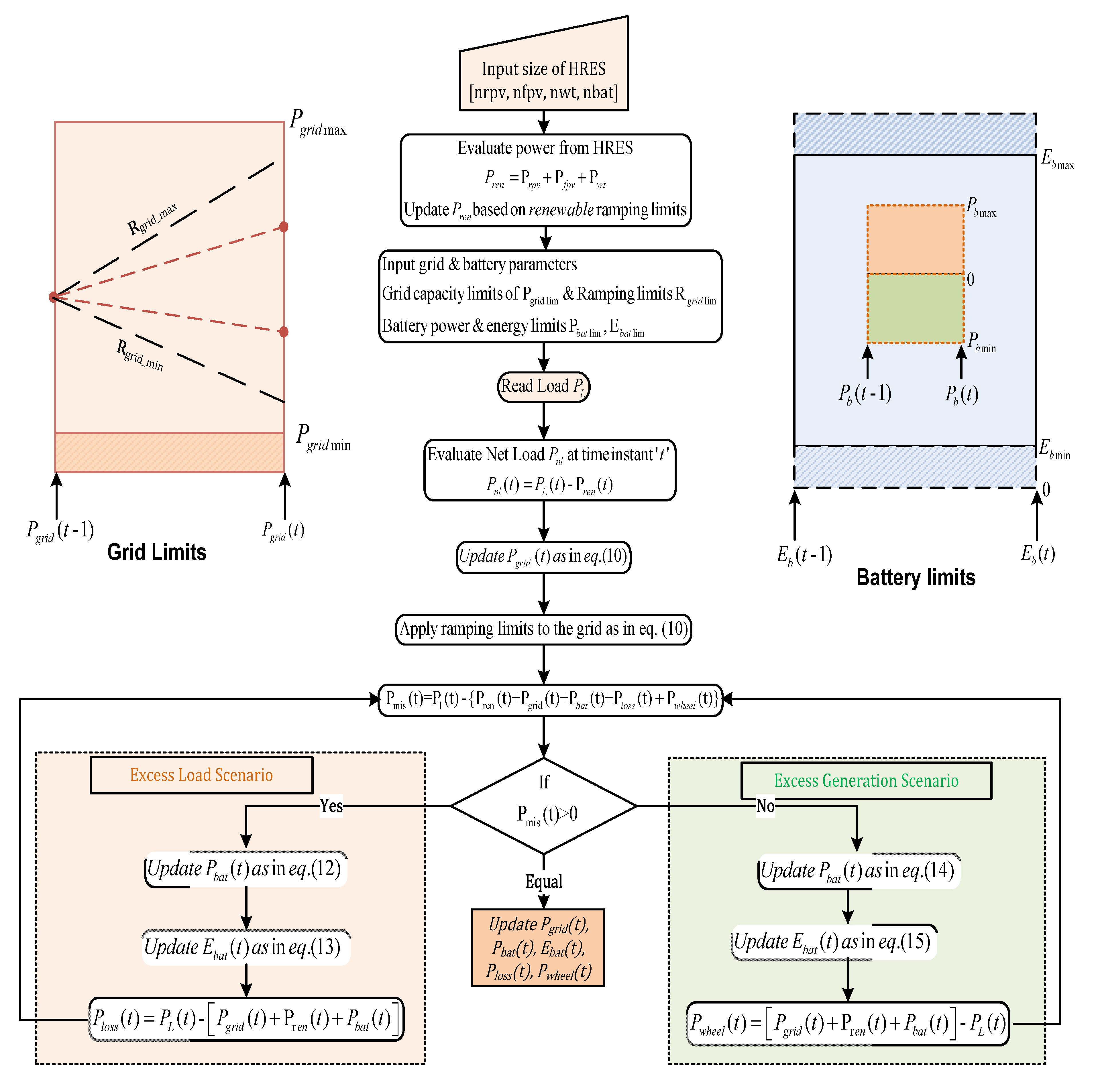
3.4. Energy Management Strategy
- i.
- The grid is never operated below the technical minimum of 55% of the load.
- ii.
- The grid is allowed to supply only 80% of the maximum load to accommodate future demand.
- iii.
- The ramp rates of the grid are restricted to ±0.5%/min of its capacity.
3.5. Excess Load Scenario
3.6. Excess Generation Scenario
4. Multi-Objective Adaptive-Local-Attractor-Based Quantum-Behaved Particle Swarm Optimization (ALA-QPSO)
| Algorithm 1 ALA-QPSO |
|
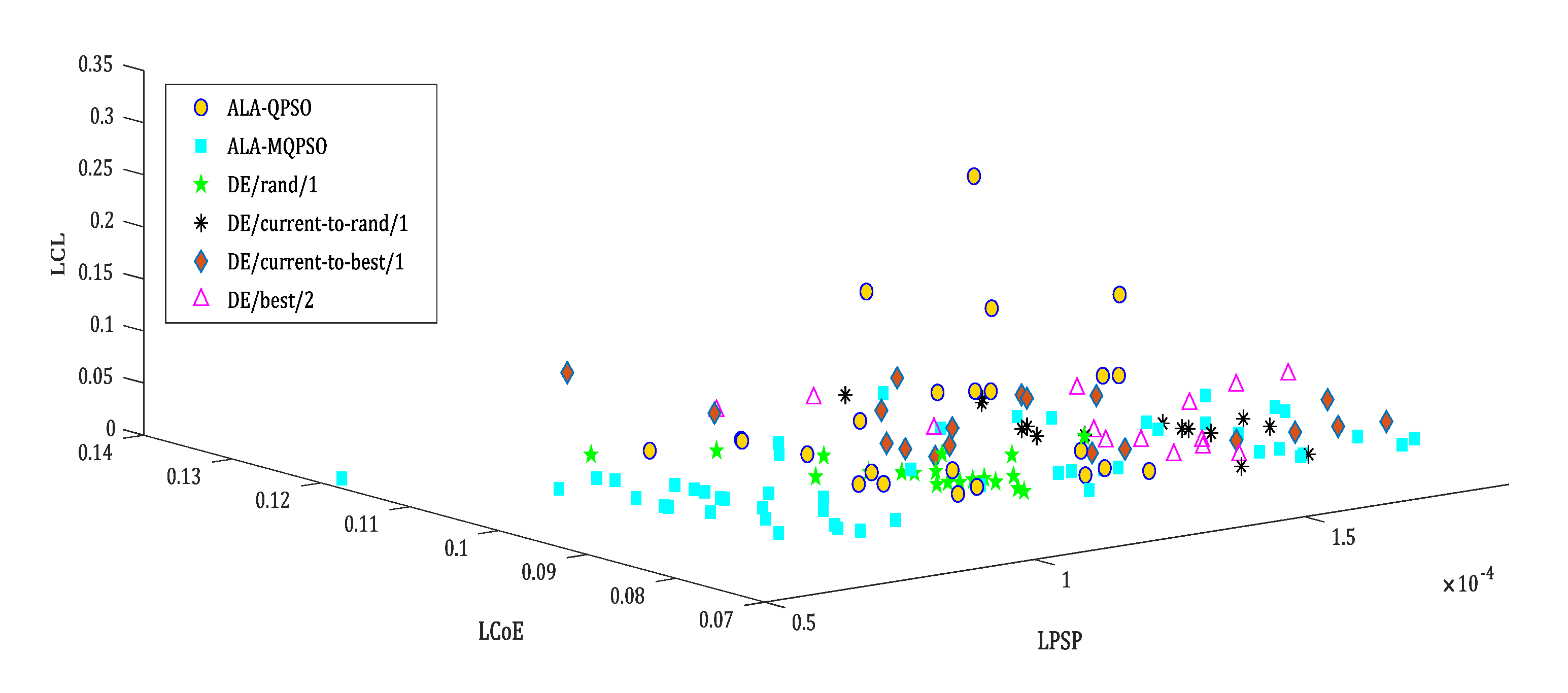
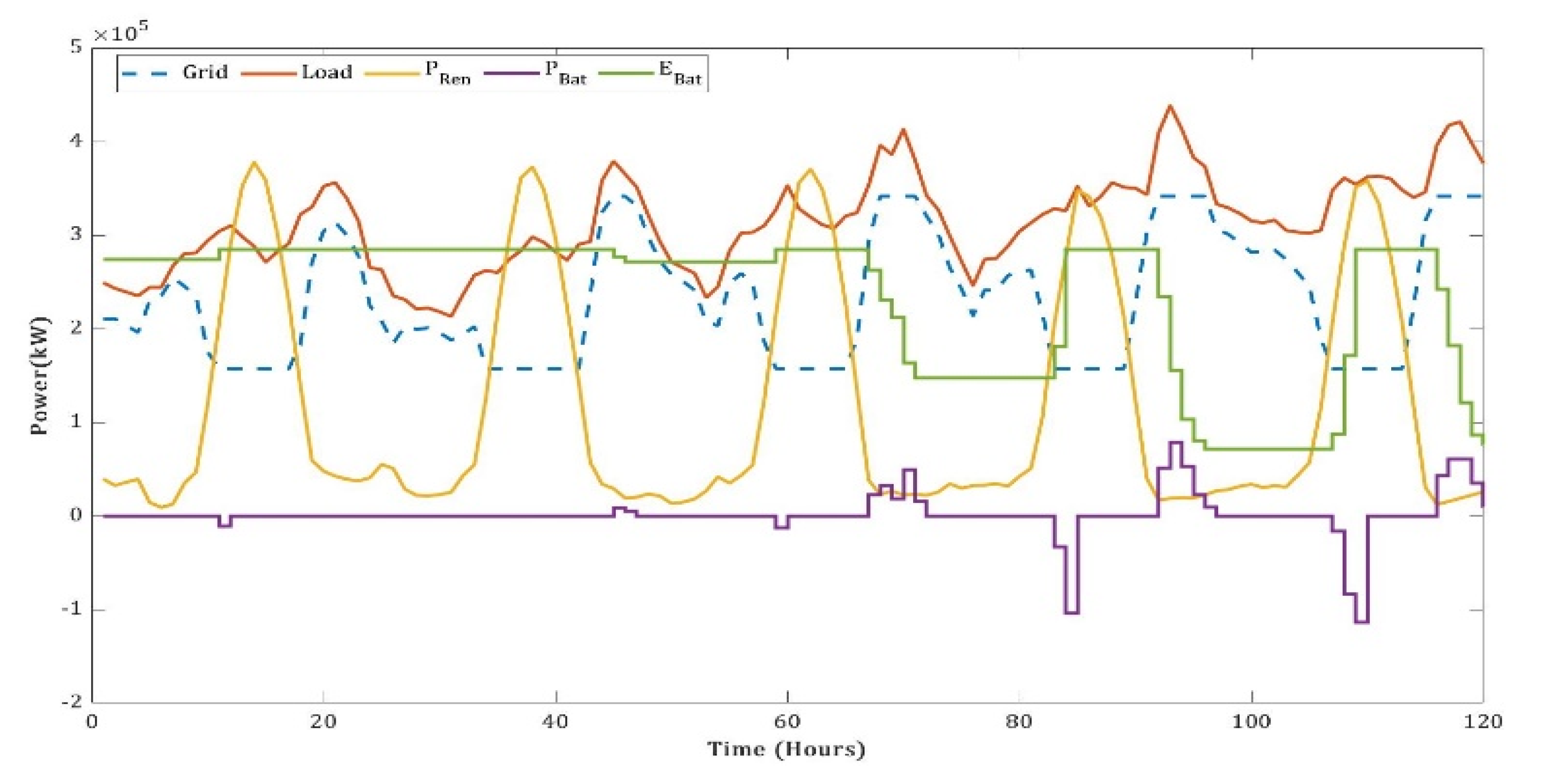
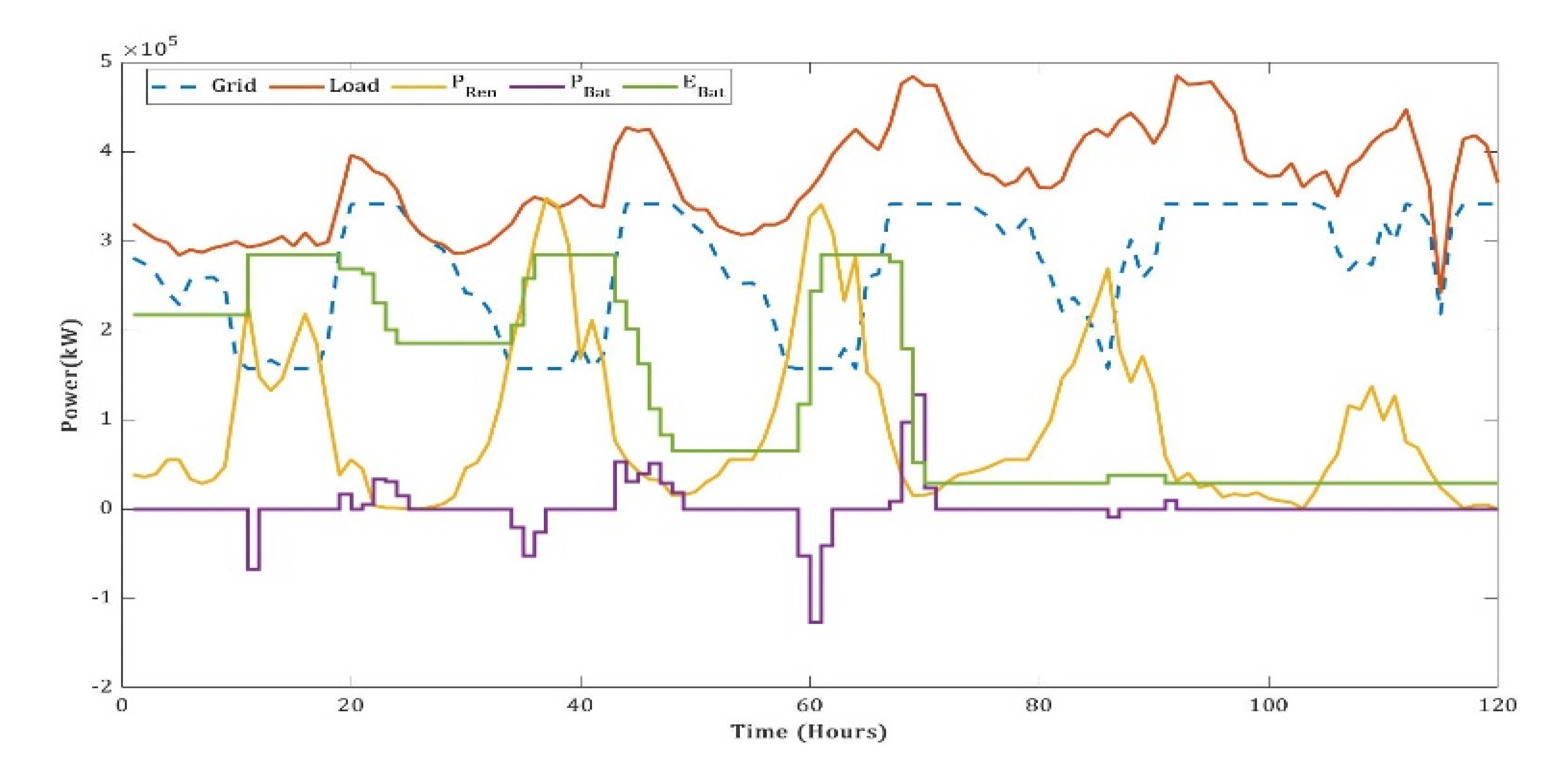
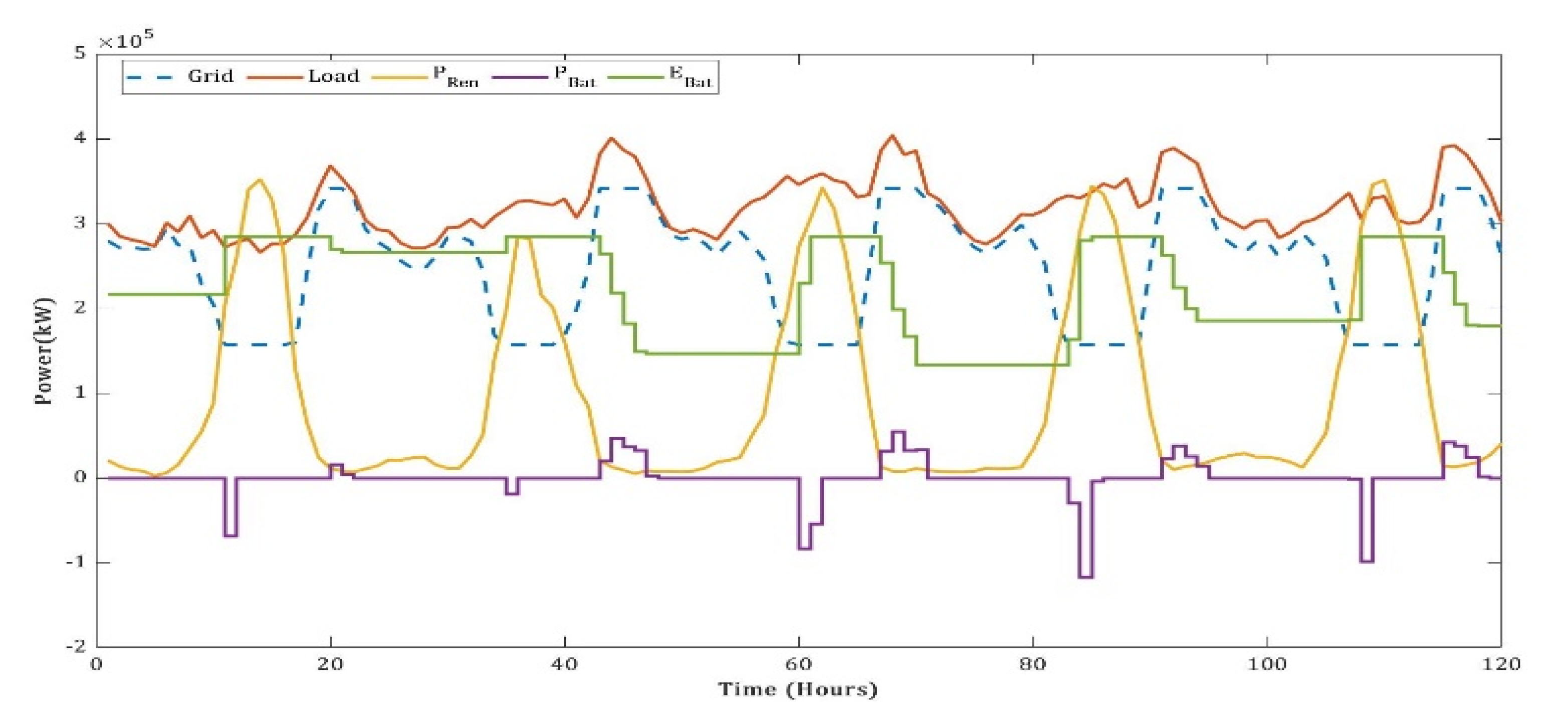
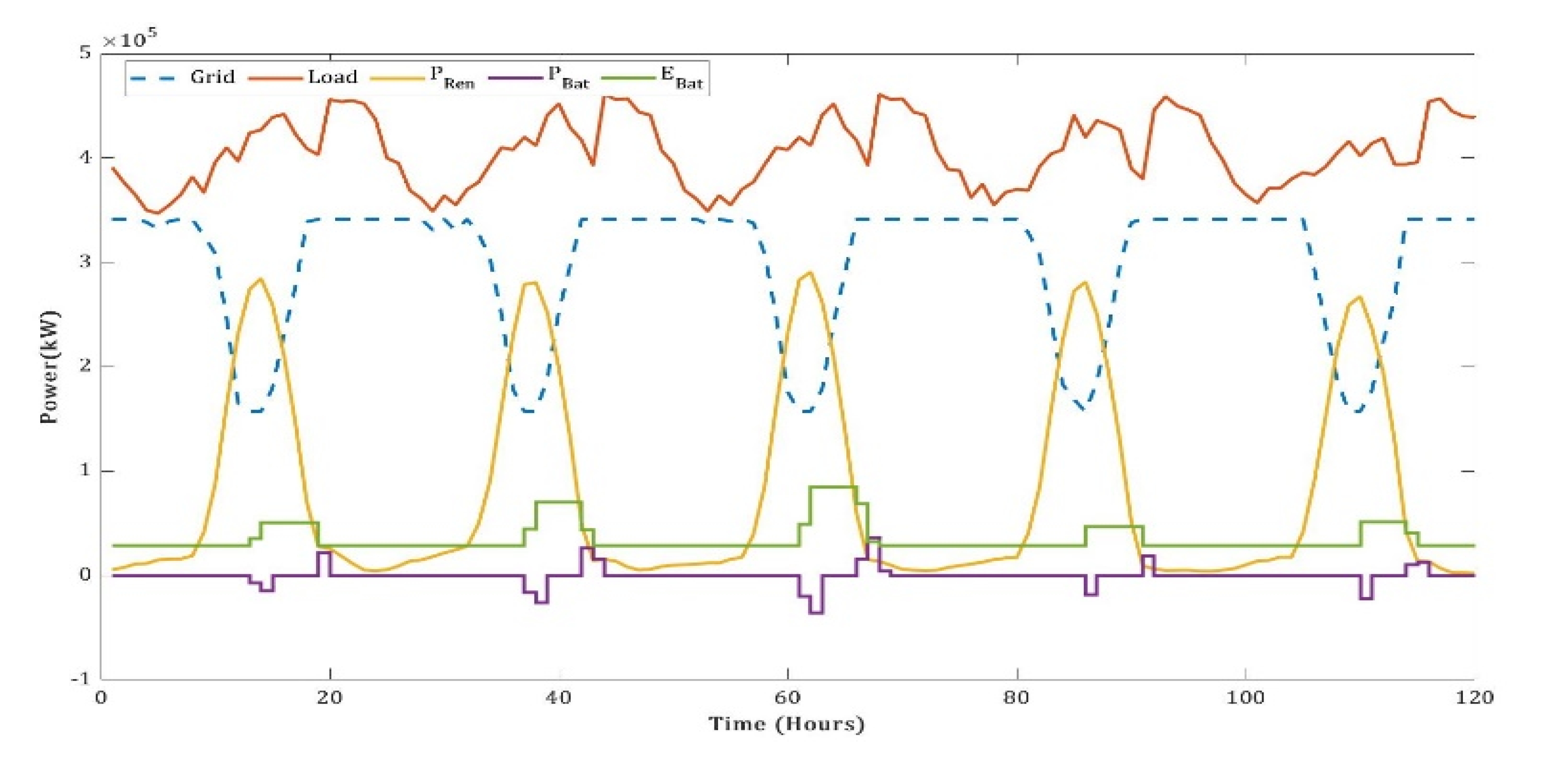
5. Simulation Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- International Renewable Energy Agency (IRENA). Renewable Power Generation Costs in 2017. Available online: https://www.irena.org/publications/2018/Jan/Renewable-power-generation-costs-in-2017 (accessed on 21 February 2021).
- Arto, I.; Capellán-Pérez, I.; Lago, R.; Bueno, G.; Bermejo, R. The energy requirements of a developed world. Energy Sustain. Dev. 2016, 33, 1–13. [Google Scholar] [CrossRef] [Green Version]
- Central Electricity Authority of India. Installed Capacity-February 2020. Available online: http://www.cea.nic.in/reports/monthly/installedcapacity/2020/installed_capacity-02.pdf (accessed on 21 February 2021).
- APERC. Andhra Pradesh Electricity Regulatory Commission 4th Floor; Singareni: Vijayawada, India, 2019. [Google Scholar]
- Tummala, A.S.; Inapakurthi, R.; Ramanarao, P.V. Observer based sliding mode frequency control for multi-machine power systems with high renewable energy. J. Mod. Power Syst. Clean Energy 2018, 6, 473–481. [Google Scholar] [CrossRef] [Green Version]
- Mongird, K. Energy Storage Technology and Cost Characterization Report, Department of Energy. Available online: https://www.energy.gov/eere/water/downloads/energy-storage-technology-and-cost-characterization-report (accessed on 18 August 2020).
- van der Stelt, S.; AlSkaif, T.; van Sark, W. Techno-economic analysis of household and community energy storage for residential prosumers with smart appliances. Appl. Energy 2018, 209, 266–276. [Google Scholar] [CrossRef]
- Jacob, A.S.; Banerjee, R.; Ghosh, P.C. Sizing of hybrid energy storage system for a PV based microgrid through design space approach. Appl. Energy 2018, 212, 640–653. [Google Scholar] [CrossRef]
- Raguraman, L.; Ravindran, M. MFLRS-RDF technique for optimal sizing and performance analysis of HRES. Int. J. Numer. Model. Electron. Netw. Devices Fields 2019, 33, e2675. [Google Scholar] [CrossRef]
- Ramli, M.A.; Bouchekara, H.; Alghamdi, A.S. Optimal sizing of PV/wind/diesel hybrid microgrid system using multi-objective self-adaptive differential evolution algorithm. Renew. Energy 2018, 121, 400–411. [Google Scholar] [CrossRef]
- Noura, N.; Boulon, L.; Jemeï, S. A Review of Battery State of Health Estimation Methods: Hybrid Electric Vehicle Challenges. World Electr. Veh. J. 2020, 11, 66. [Google Scholar] [CrossRef]
- Dong, C.; Wang, G.; Chen, Z.; Yu, Z. A method of self-adaptive inertia weight for PSO. In Proceedings of the International Conference on Computer Science and Software Engineering, Wuhan, China, 12–14 December 2008; Volume 1, pp. 1195–1198. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Suganthan, P.; Pan, Q.-K.; Tasgetiren, M.F. Differential evolution algorithm with ensemble of parameters and mutation strategies. Appl. Soft Comput. 2011, 11, 1679–1696. [Google Scholar] [CrossRef]
- Nagra, A.A.; Han, F.; Ling, Q.H. An improved hybrid self-inertia weight adaptive particle swarm optimization algorithm with local search. Eng. Optim. 2018, 51, 1115–1132. [Google Scholar] [CrossRef]
- Zhang, Q.; Ding, J.; Shen, W.; Ma, J.; Li, G. Multiobjective Particle Swarm Optimization for Microgrids Pareto Optimization Dispatch. Math. Probl. Eng. 2020, 2020, 1–13. [Google Scholar] [CrossRef] [PubMed]
- Ming, M.; Wang, R.; Zha, Y.; Zhang, T. Multi-Objective Optimization of Hybrid Renewable Energy System Using an Enhanced Multi-Objective Evolutionary Algorithm. Energies 2017, 10, 674. [Google Scholar] [CrossRef] [Green Version]
- Clerc, M.; Kennedy, J. The particle swarm-explosion, stability, and convergence in a multidimensional complex space. IEEE Trans. Evol. Comput. 2002, 6, 58–73. [Google Scholar] [CrossRef] [Green Version]
- Sun, J.; Feng, B.; Xu, W. Particle swarm optimization with particles having quantum behavior. In Proceedings of the 2004 Congress on Evolutionary Computation, Portland, OR, USA, 19–23 June 2004; Volume 1, pp. 325–331. [Google Scholar] [CrossRef]
- Han, F.; Sun, Y.-W.; Ling, Q.-H. An Improved Multiobjective Quantum-Behaved Particle Swarm Optimization Based on Double Search Strategy and Circular Transposon Mechanism. Complexity 2018, 2018, 1–22. [Google Scholar] [CrossRef]
- Sun, J.; Fang, W.; Palade, V.; Wu, X.; Xu, W. Quantum-behaved particle swarm optimization with Gaussian distributed local attractor point. Appl. Math. Comput. 2011, 218, 3763–3775. [Google Scholar] [CrossRef]
- Chen, S. Quantum-Behaved Particle Swarm Optimization with Weighted Mean Personal Best Position and Adaptive Local Attractor. Information 2019, 10, 22. [Google Scholar] [CrossRef] [Green Version]
- González, A.; Riba, J.-R.; Rius, A. Optimal Sizing of a Hybrid Grid-Connected Photovoltaic–Wind–Biomass Power System. Sustainability 2015, 7, 12787–12806. [Google Scholar] [CrossRef] [Green Version]
- Zhang, W.; Maleki, A.; Rosen, M.A.; Liu, J. Optimization with a simulated annealing algorithm of a hybrid system for renewable energy including battery and hydrogen storage. Energy 2018, 163, 191–207. [Google Scholar] [CrossRef]
- Jamshidi, M.; Askarzadeh, A. Techno-economic analysis and size optimization of an off-grid hybrid photovoltaic, fuel cell and diesel generator system. Sustain. Cities Soc. 2018, 44, 310–320. [Google Scholar] [CrossRef]
- Samy, M.; Barakat, S.; Ramadan, H. A flower pollination optimization algorithm for an off-grid PV-Fuel cell hybrid renewable system. Int. J. Hydrogen Energy 2019, 44, 2141–2152. [Google Scholar] [CrossRef]
- Kusakana, K. Optimal peer-to-peer energy management between grid-connected prosumers with battery storage and photovoltaic systems. J. Energy Storage 2020, 32, 101717. [Google Scholar] [CrossRef]
- Hakimi, S.M.; Hasankhani, A.; Shafie-Khah, M.; Catalão, J.P. Optimal sizing and siting of smart microgrid components under high renewables penetration considering demand response. IET Renew. Power Gener. 2019, 13, 1809–1822. [Google Scholar] [CrossRef] [Green Version]
- Bhatti, A.R.; Salam, Z.; Sultana, B.; Rasheed, N.; Awan, A.B.; Sultana, U.; Younas, M. Optimized sizing of photovoltaic grid-connected electric vehicle charging system using particle swarm optimization. Int. J. Energy Res. 2018, 43, 500–522. [Google Scholar] [CrossRef]
- Akram, U.; Khalid, M.; Shafiq, S. Optimal sizing of a wind/solar/battery hybrid grid-connected microgrid system. IET Renew. Power Gener. 2017, 12, 72–80. [Google Scholar] [CrossRef]
- Dominguez, O.D.M.; Kasmaei, M.P.; Lavorato, M.; Mantovani, J.R.S. Optimal siting and sizing of renewable energy sources, storage devices, and reactive support devices to obtain a sustainable electrical distribution systems. Energy Syst. 2017, 9, 529–550. [Google Scholar] [CrossRef] [Green Version]
- Miñambres-Marcos, V.M.; Guerrero-Martínez, M.; Barrero-González, F.; Milanés-Montero, M.I. A Grid Connected Photovoltaic Inverter with Battery-Supercapacitor Hybrid Energy Storage. Sensors 2017, 17, 1856. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chudinzow, D.; Haas, J.; Díaz-Ferrán, G.; Moreno-Leiva, S.; Eltrop, L. Simulating the energy yield of a bifacial photovoltaic power plant. Sol. Energy 2019, 183, 812–822. [Google Scholar] [CrossRef]
- Asgharzadeh, A.; Marion, B.; Deline, C.; Hansen, C.; Stein, J.S.; Toor, F. A Sensitivity Study of the Impact of Installation Parameters and System Configuration on the Performance of Bifacial PV Arrays. IEEE J. Photovolt. 2018, 8, 798–805. [Google Scholar] [CrossRef]
- Campana, P.E.; Wästhage, L.; Nookuea, W.; Tan, Y.; Yan, J. Optimization and assessment of floating and floating-tracking PV systems integrated in on- and off-grid hybrid energy systems. Sol. Energy 2018, 177, 782–795. [Google Scholar] [CrossRef]
- Energy Sector Management Assistance Program; Solar Energy Research Institute of Singapore. Where Sun Meets Water: Floating Solar Market Report; World Bank: Washington, DC, USA, 2019. [Google Scholar]
- Dizier, A. Techno-Economic Analysis of floating PV Solar Power Plants Using Active Cooling Technique A case Study for Taiwan; p. 68. Available online: http://www.diva-portal.org/smash/get/diva2:1290021/FULLTEXT01.pdf (accessed on 14 April 2020).
- Siratarnsophon, P.; Lao, K.W.; Rosewater, D.; Santoso, S. A Voltage Smoothing Algorithm Using Energy Storage PQ Control in PV-Integrated Power Grid. IEEE Trans. Power Deliv. 2019, 34, 2248–2250. [Google Scholar] [CrossRef]
- de la Parra, J.; Marcos, J.; García, M.; Marroyo, L. Control strategies to use the minimum energy storage requirement for PV power ramp-rate control. Sol. Energy 2015, 111, 332–343. [Google Scholar] [CrossRef]
- Ahmed, D.; Ebeed, M.; Ali, A.; Alghamdi, A.; Kamel, S. Multi-Objective Energy Management of a Micro-Grid Considering Stochastic Nature of Load and Renewable Energy Resources. Electronics 2021, 10, 403. [Google Scholar] [CrossRef]
- Oda, E.S.; El Hamed, A.M.A.; Ali, A.; Elbaset, A.A.; El Sattar, M.A.; Ebeed, M. Stochastic Optimal Planning of Distribution System Considering Integrated Photovoltaic-Based DG and DSTATCOM Under Uncertainties of Loads and Solar Irradiance. IEEE Access 2021, 9, 26541–26555. [Google Scholar] [CrossRef]
- Münderlein, J.; Ipers, G.; Steinhoff, M.; Zurmühlen, S.; Sauer, D.U. Optimization of a hybrid storage system and evaluation of operation strategies. Int. J. Electr. Power Energy Syst. 2020, 119, 105887. [Google Scholar] [CrossRef]
- Wang, S.; Guo, D.; Han, X.; Lu, L.; Sun, K.; Li, W.; Sauer, D.U.; Ouyang, M. Impact of battery degradation models on energy management of a grid-connected DC microgrid. Energy 2020, 207, 118228. [Google Scholar] [CrossRef]
- Figgener, J.; Stenzel, P.; Kairies, K.-P.; Linßen, J.; Haberschusz, D.; Wessels, O.; Angenendt, G.; Robinius, M.; Stolten, D.; Sauer, D.U. The development of stationary battery storage systems in Germany—A market review. J. Energy Storage 2020, 29, 101153. [Google Scholar] [CrossRef]
- Moseley, P.T.; Rand, D.A.; Davidson, A.; Monahov, B. Understanding the functions of carbon in the negative active-mass of the lead–acid battery: A review of progress. J. Energy Storage 2018, 19, 272–290. [Google Scholar] [CrossRef]
- Tran, M.-K.; Fowler, M. A Review of Lithium-Ion Battery Fault Diagnostic Algorithms: Current Progress and Future Challenges. Algorithms 2020, 13, 62. [Google Scholar] [CrossRef] [Green Version]
- Madlener, R.; Kirmas, A. Economic Viability of Second Use Electric Vehicle Batteries for Energy Storage in Residential Applications. Energy Procedia 2017, 105, 3806–3815. [Google Scholar] [CrossRef]
- Rehman, A.U.; Wadud, Z.; Elavarasan, R.M.; Hafeez, G.; Khan, I.; Shafiq, Z.; Alhelou, H.H. An Optimal Power Usage Scheduling in Smart Grid Integrated with Renewable Energy Sources for Energy Management. IEEE Access 2021, 9, 84619–84638. [Google Scholar] [CrossRef]
- Kiani, A.T.; Nadeem, M.F.; Ahmed, A.; Khan, I.; Elavarasan, R.M.; Das, N. Optimal PV Parameter Estimation via Double Exponential Function-Based Dynamic Inertia Weight Particle Swarm Optimization. Energies 2020, 13, 4037. [Google Scholar] [CrossRef]
- AECOM. Smart City Master Planning and Sector-Specific Smart City Infrastructure Projects for Visakhapatnam, Visakhapatnam. Available online: https://www.smartvizag.in/wp-content/uploads/2017/01/Green_Framework.pdf (accessed on 14 April 2020).
- Nuvvula, R.; Devaraj, E.; Srinivasa, K.T. A Comprehensive Assessment of Large-scale Battery Integrated Hybrid Renewable Energy System to Improve Sustainability of a Smart City. Energy Sources Part. A Recover. Util. Environ. Eff. 2021, 1–22. [Google Scholar] [CrossRef]
- Patel, M.T.; Khan, M.; Sun, X.; Alam, M.A. A worldwide cost-based design and optimization of tilted bifacial solar farms. Appl. Energy 2019, 247, 467–479. [Google Scholar] [CrossRef] [Green Version]
- Samsung, S.D.I. Datasheet: Battery-Spec-Samsung-P3-R101. 2018. Available online: https://www.samsungsdi.com/upload/ess_brochure/201804_SamsungSDI%20ESS_EN.PDF (accessed on 17 June 2020).
- Trina Solar, Datasheet: Duomax-Bi-facial Dual Glass 72-Cell Module. Available online: https://static.trinasolar.com/sites/ default/files/Datasheet%20DUOMAX%20Twin_DEG14C.07%28II%29_July_2017_B_web.pdf (accessed on 17 June 2020).
- Suzlon, “Technical Data S97-2.1 MW,” 2010. Available online: https://oakland.edu/Assets/upload/docs/Energy /Wind-Project/07-Suzlon-2.1-MW-S97---Technical-Data.pdf. (accessed on 17 June 2020).
- Ralon, P.; Taylor, M.; Ilas, A.; Diaz-Bone, H.; Kai-Philipp, K. Electricity Storage and Renewables: Costs and Markets To 2030, International Renewable Energy Agency (IRENA), Abu Dhabi UAE, October 2017. Available online: https://www.irena.org/-/media/Files/IRENA/Agency/Publication/2017/Oct/IRENA_Electricity_Storage_Costs_2017.pdf (accessed on 17 June 2020).
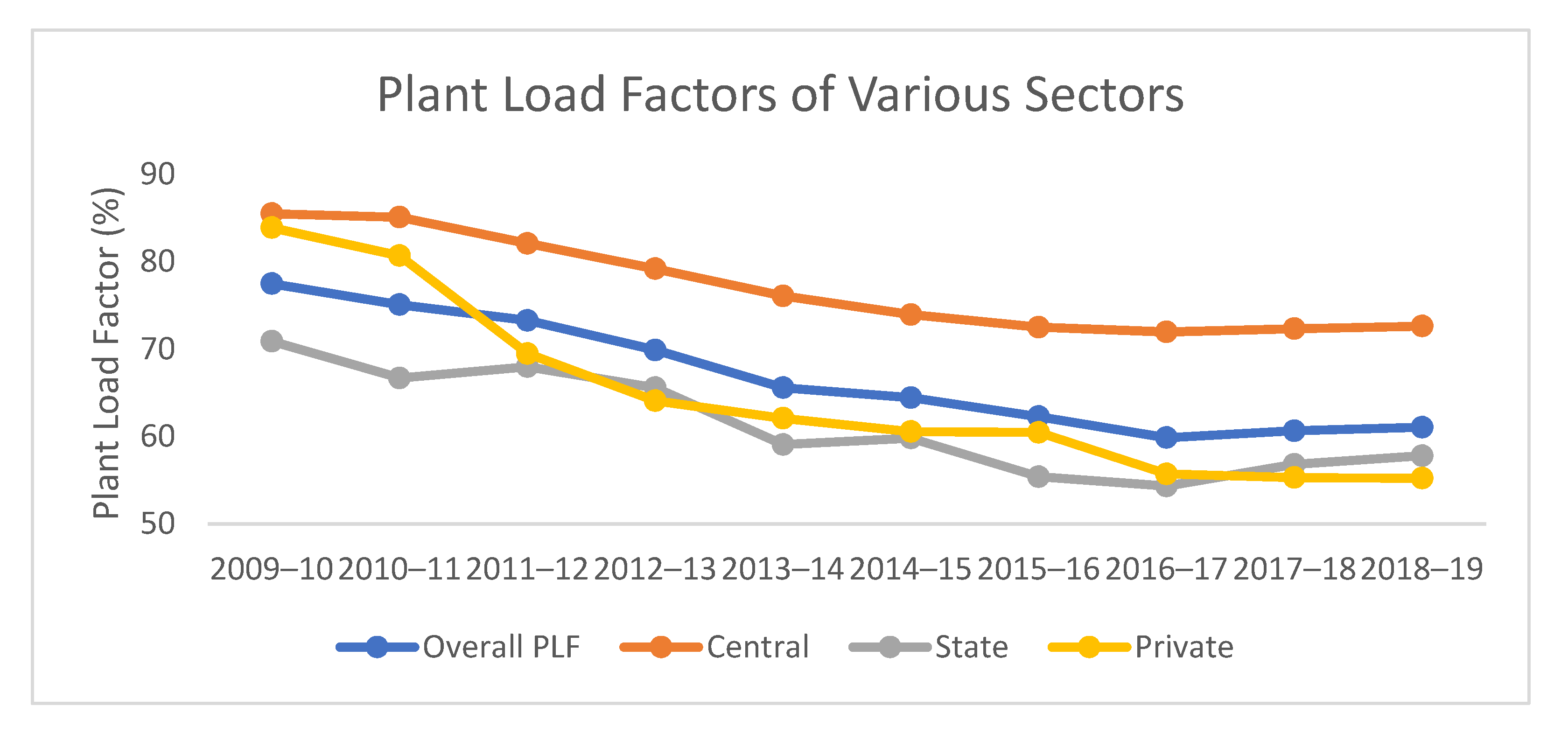
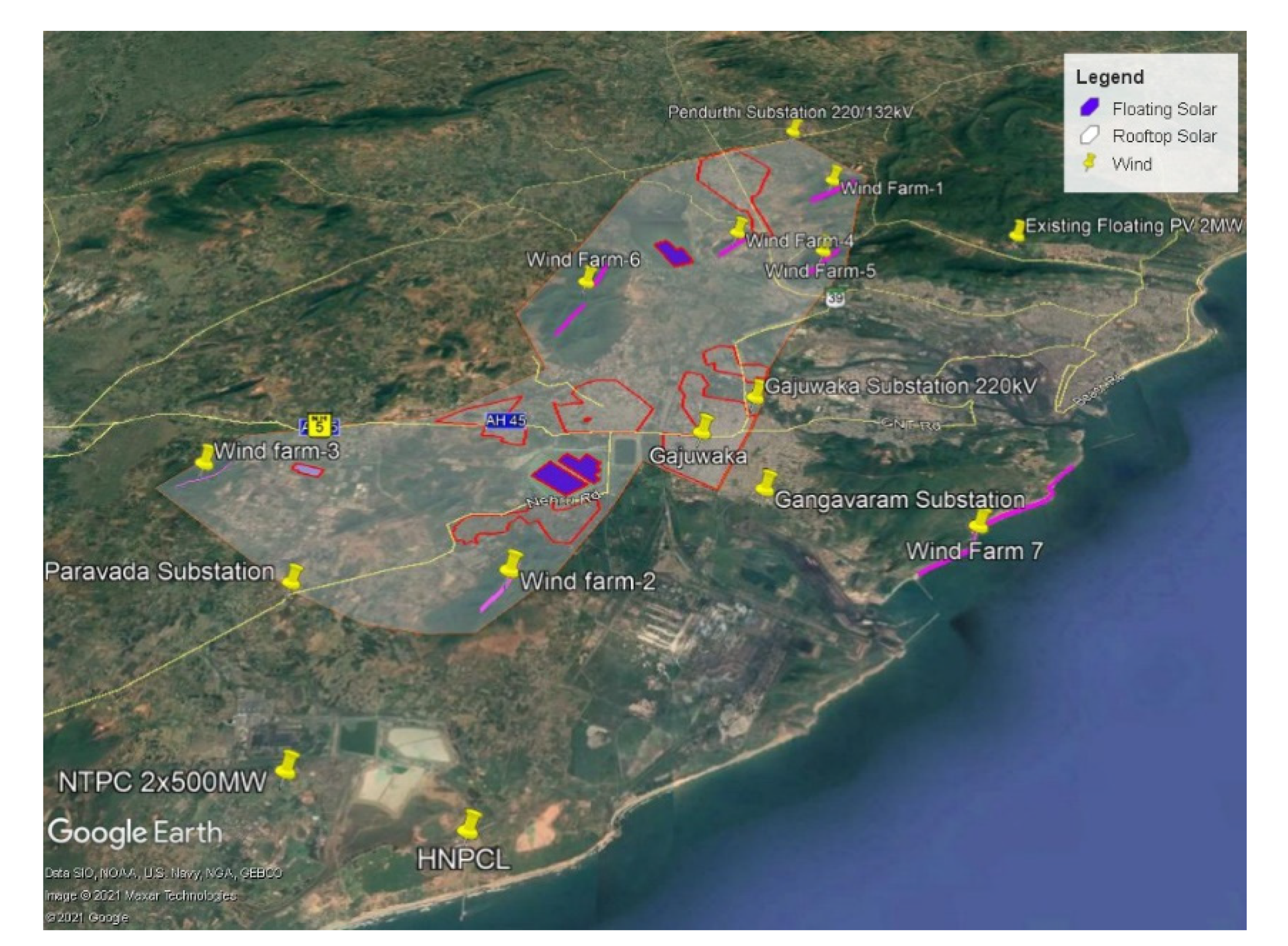
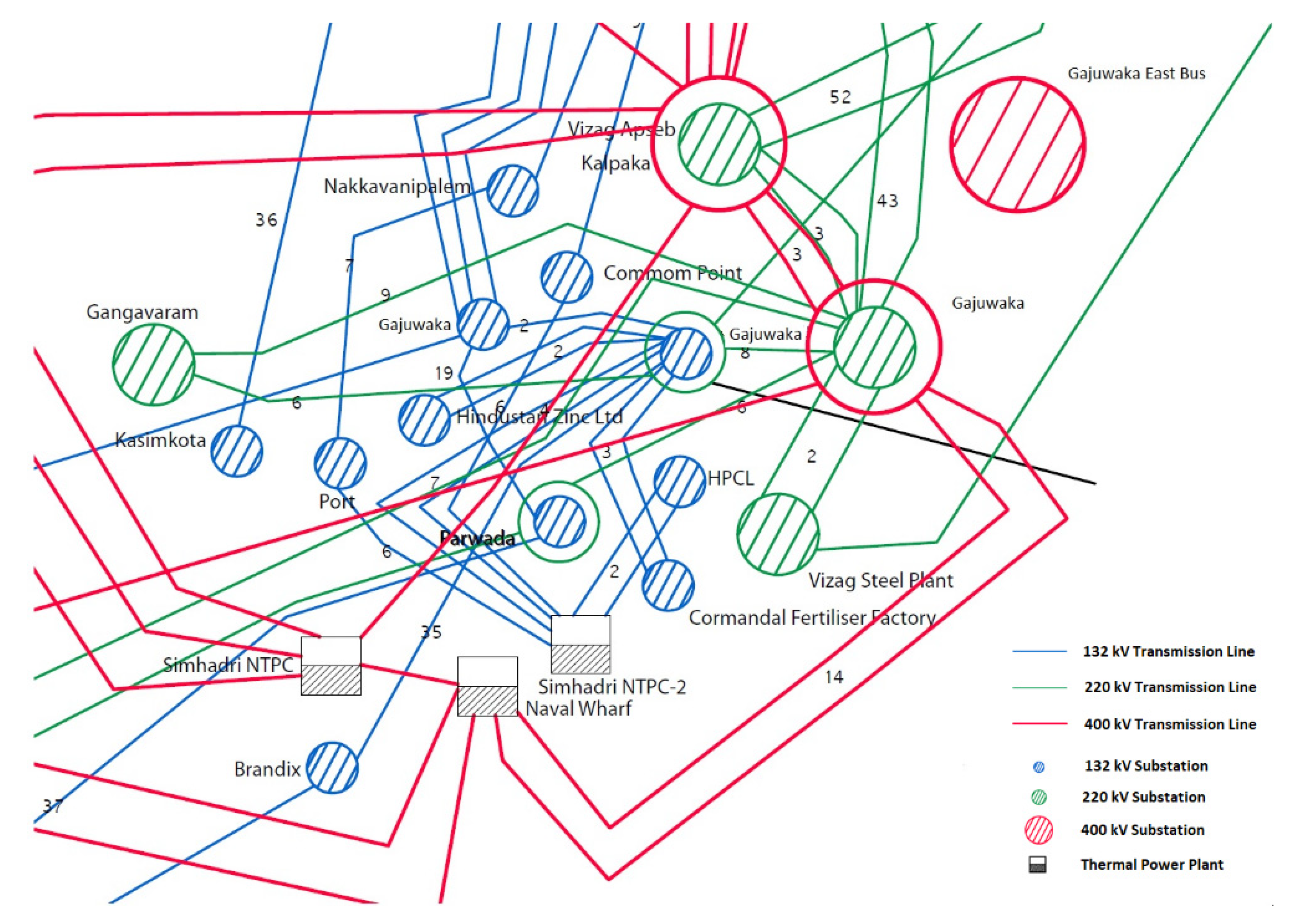
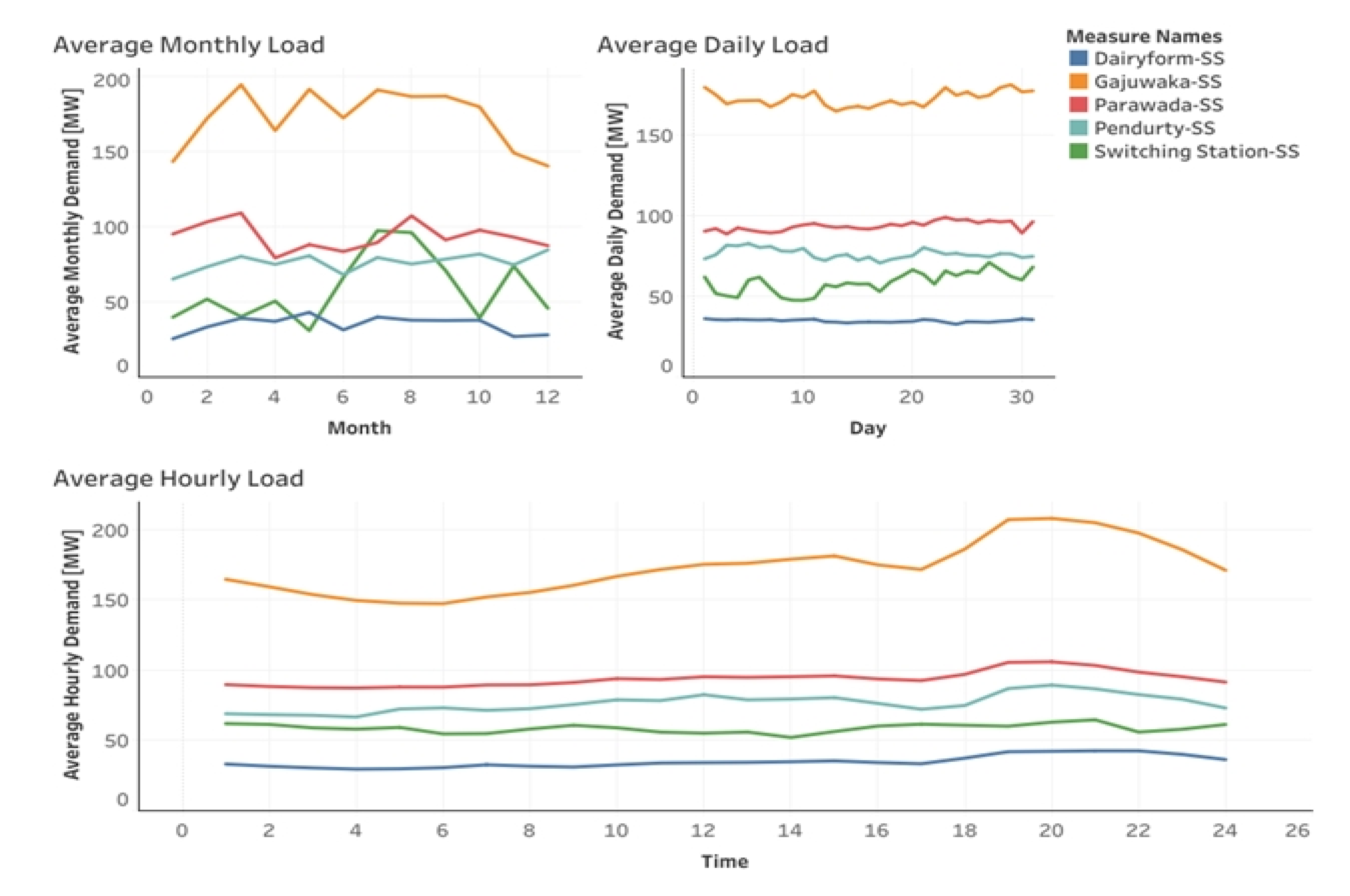
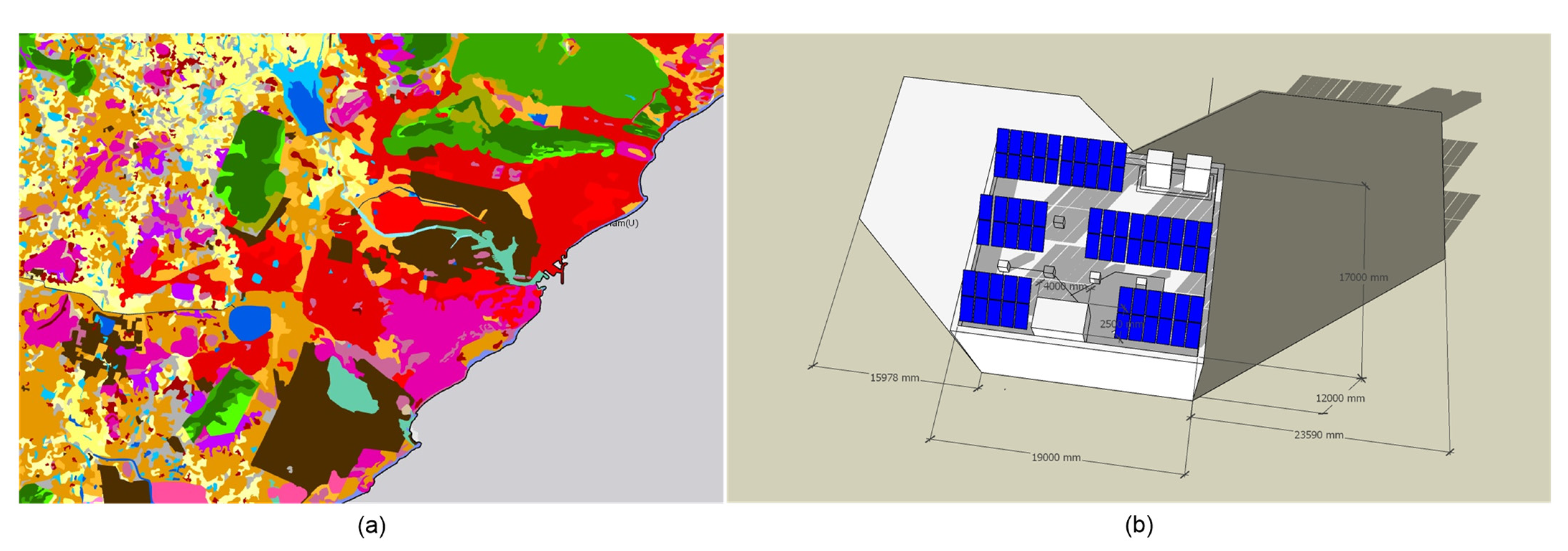
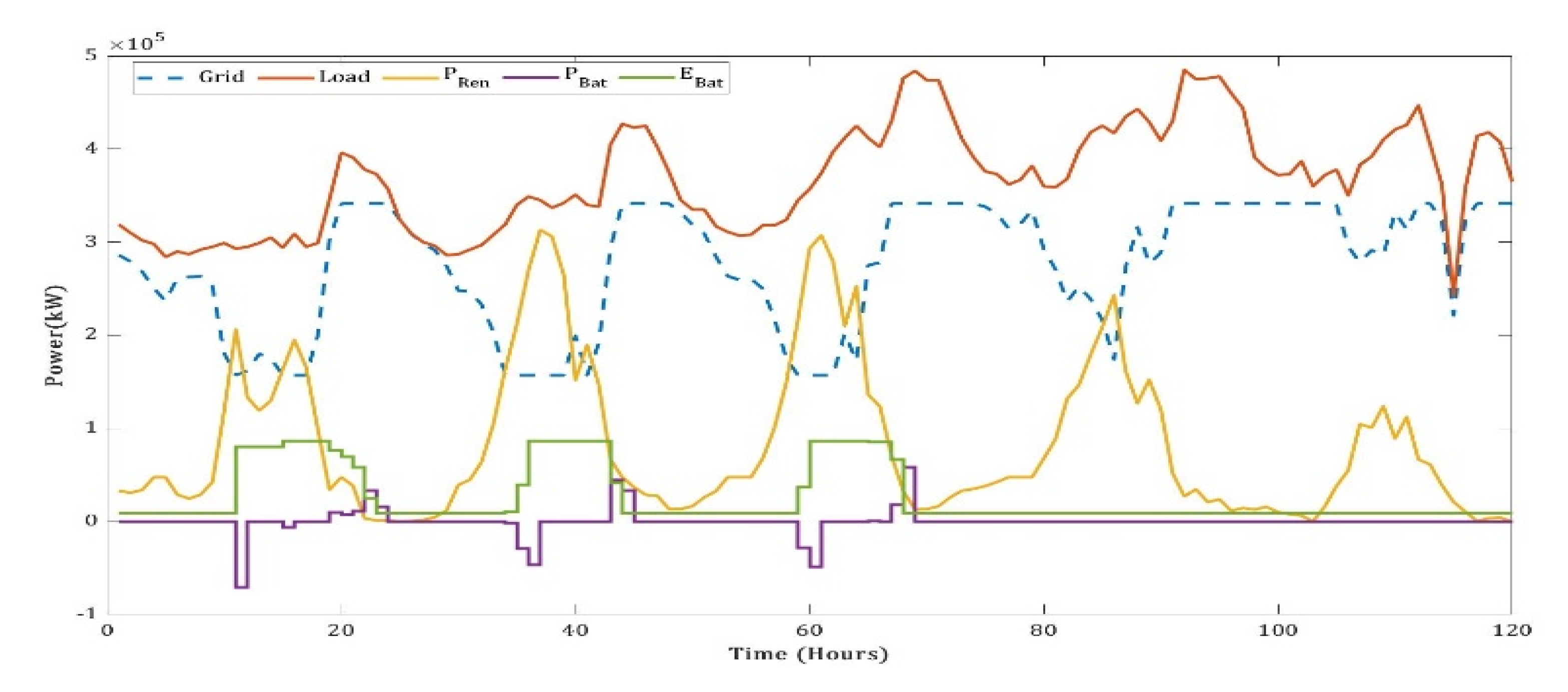
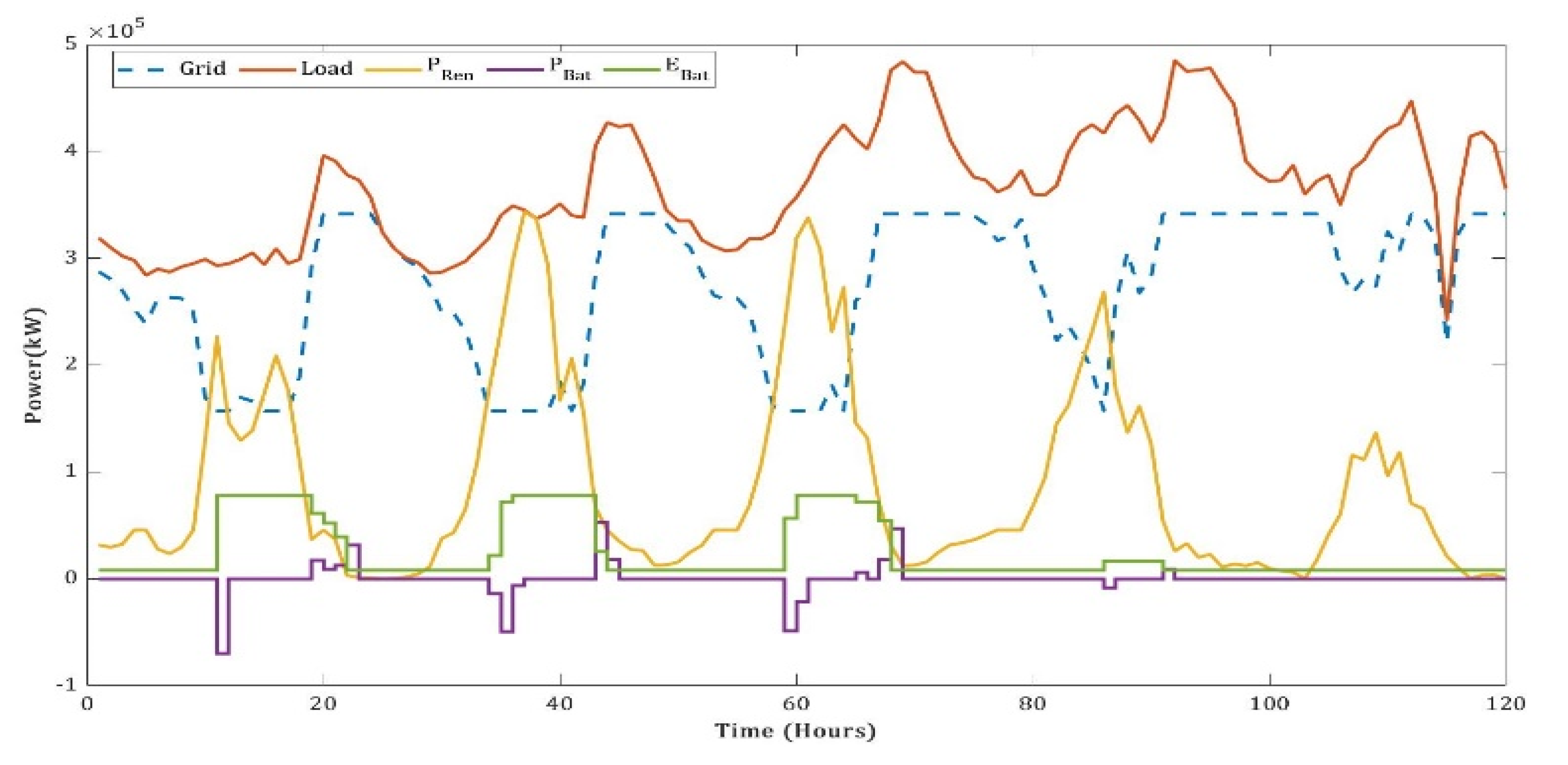


| Year | Required (MU) | Available (MU) | Deficit (%) | Peak Demand (MW) | Peak Met (MW) | Conventional Energy Generation(MU) | Year-on-Year Growth (%) |
|---|---|---|---|---|---|---|---|
| 2009–2010 | 8,30,594 | 7,46,644 | −10.1 | 1,19,166 | 1,04,009 | 771,551 | 6.6 |
| 2010–2011 | 8,61,591 | 7,88,355 | −8.5 | 1,22,287 | 1,10,256 | 811,143 | 5.56 |
| 2011–2012 | 9,37,199 | 8,57,886 | −8.5 | 1,30,006 | 1,16,191 | 876,887 | 8.11 |
| 2012–2013 | 9,95,557 | 9,08,652 | −8.7 | 1,35,453 | 1,23,294 | 912,056 | 4.01 |
| 2013–2014 | 10,02,257 | 9,59,829 | −4.2 | 1,35,918 | 1,29,815 | 967,150 | 6.04 |
| 2014–2015 | 10,68,923 | 10,30,785 | −3.6 | 1,48,166 | 1,41,160 | 1048,673 | 8.43 |
| 2015–2016 | 11,14,408 | 10,90,850 | −2.1 | 1,53,366 | 1,48,463 | 1107,822 | 5.64 |
| 2016–2017 | 11,42,929 | 11,35,334 | −0.7 | 1,59,542 | 1,56,934 | 1160,141 | 4.72 |
| 2017–2018 | 12,13,326 | 12,04,697 | −0.7 | 1,64,066 | 1,60,752 | 1206,306 | 3.98 |
| 2018–2019 | 12,74,595 | 12,67,526 | −0.6 | 1,77,022 | 1,75,528 | 1249,337 | 3.57 |
| S. no. | Technology | Potential of Renewable Resource | |
|---|---|---|---|
| 1 | Floating PV system | Identified number of areas | 4 |
| Total available area (km2) | 2.933 | ||
| Available area (m2) (assuming 20% use) | 586,630 | ||
| Potential for installed capacity (MW) (power density 180 W/m2) | 105 MW | ||
| Maximum-possible number of solar panels (360 Wp) | 293,315 | ||
| 2 | Rooftop bifacial PV system | Identified number of areas | 6 |
| Total available area (km2) | 24.46 | ||
| Available area (km2) (assuming 5% acceptance) | 1.223 | ||
| Potential for installed capacity (MW) (power density 215 W/m2) | 260 MW | ||
| Maximum-possible number of bifacial solar panels (430 Wp) | 611,500 | ||
| 3 | Wind energy system | Identified number of areas | 5 |
| Total length of hilltops and shoreline (m) | 11,140 | ||
| Available length (m) (assuming 100% use) | 11,140 | ||
| Potential for installed capacity (MW) | 62 MW | ||
| Maximum-possible number of wind turbines (2.1 MW) | 30 | ||
| S. no. | Type of Specification | Parameter | Bifacial Rooftop PV Panels [53] | Floating PV Panels [53] | Wind Turbines [54] | Batteries [52] | |
|---|---|---|---|---|---|---|---|
| 1 | Technology | Cell type | Polycrystalline | Mono c-Si | Tubular | Lithium ion | |
| 2 | Electrical | Voltage (VMPP) | 52.27 | 33.75 | 690 | 774–1004 V | |
| Current (A) | 9.31 | 9.78 | 1895 | 111 Ah | |||
| Power (energy) | 430 W | 360 W | 2.1 MW | (99 kWh) | |||
| Temperature coefficient | −0.42%/°C | −0.39%/°C | NA | NA | |||
| 3 | Mechanical | Dimensions | 1996 × 1310 × 40 (mm3) | 1640 × 992 × 35 (mm3) | 111 (m) | 442 × 702 × 2124 (mm3) | |
| Weight | 36.5 kg | 17.5 kg | NA | 670 kg | |||
| 4 | Financial [55] | Capital requirements | 796 USD | 1031 USD | 980 USD | 350 USD/kWh | |
| O&M costs | 12 USD | 16 USD | 25 USD | 35 USD | |||
| S. no. | Optimization Technique | Population | No of Iterations | Scaling Factor | Crossover Rate | Inertia | Personal Weight | Social Weight |
|---|---|---|---|---|---|---|---|---|
| 1 | ALA-mQPSO | 20 | 100 | - | - | 1 | 2 | 2 |
| 2 | ALA-QPSO | 20 | 100 | - | - | 1 | 2 | 2 |
| 3 | DE/best/1 | 100 | 100 | 0.8 | 0.9 | - | - | - |
| 4 | DE/rand/1 | 100 | 100 | 0.8 | 0.9 | - | - | - |
| 5 | DE/rand-to-best/1 | 100 | 100 | 0.8 | 0.9 | - | - | - |
| 6 | DE/best/2 | 100 | 100 | 0.8 | 0.9 | - | - | - |
| Optimization Technique | Technologies | Objectives | ||||||
|---|---|---|---|---|---|---|---|---|
| No of Bifacial Rooftop PV Panels | # Floating PV Panels | No of Wind Turbines | No of Batteries | LPSP (%) | LCoE | LCL | ||
| ALA-MQPSO | 611500 | 258756 | 30 | 3690 | 0.005 | 0.077 | 0.0087 | |
| ALA-QPSO | 596692 | 275716 | 29 | 3276 | 0.0098 | 0.0789 | 0.0096 | |
| Mode | DE/rand/1 | 607125 | 260731 | 29 | 3361 | 0.0089 | 0.077 | 0.0094 |
| DE/current-to-rand/1 | 418323 | 205534 | 29 | 2181 | 0.0144 | 0.0765 | 0.0091 | |
| DE/current-to-best/1 | 349610 | 288965 | 29 | 1130 | 0.0103 | 0.0786 | 0.0103 | |
| DE/best/2 | 559014 | 157921 | 29 | 9690 | 0.0123 | 0.0805 | 0.0091 | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nuvvula, R.S.S.; Elangovan, D.; Teegala, K.S.; Madurai Elavarasan, R.; Islam, M.R.; Inapakurthi, R. Optimal Sizing of Battery-Integrated Hybrid Renewable Energy Sources with Ramp Rate Limitations on a Grid Using ALA-QPSO. Energies 2021, 14, 5368. https://doi.org/10.3390/en14175368
Nuvvula RSS, Elangovan D, Teegala KS, Madurai Elavarasan R, Islam MR, Inapakurthi R. Optimal Sizing of Battery-Integrated Hybrid Renewable Energy Sources with Ramp Rate Limitations on a Grid Using ALA-QPSO. Energies. 2021; 14(17):5368. https://doi.org/10.3390/en14175368
Chicago/Turabian StyleNuvvula, Ramakrishna S. S., Devaraj Elangovan, Kishore Srinivasa Teegala, Rajvikram Madurai Elavarasan, Md. Rabiul Islam, and Ravikiran Inapakurthi. 2021. "Optimal Sizing of Battery-Integrated Hybrid Renewable Energy Sources with Ramp Rate Limitations on a Grid Using ALA-QPSO" Energies 14, no. 17: 5368. https://doi.org/10.3390/en14175368
APA StyleNuvvula, R. S. S., Elangovan, D., Teegala, K. S., Madurai Elavarasan, R., Islam, M. R., & Inapakurthi, R. (2021). Optimal Sizing of Battery-Integrated Hybrid Renewable Energy Sources with Ramp Rate Limitations on a Grid Using ALA-QPSO. Energies, 14(17), 5368. https://doi.org/10.3390/en14175368








