Applying Solar PV to Heat Pump and Storage Technologies in Australian Houses
Abstract
:1. Introduction
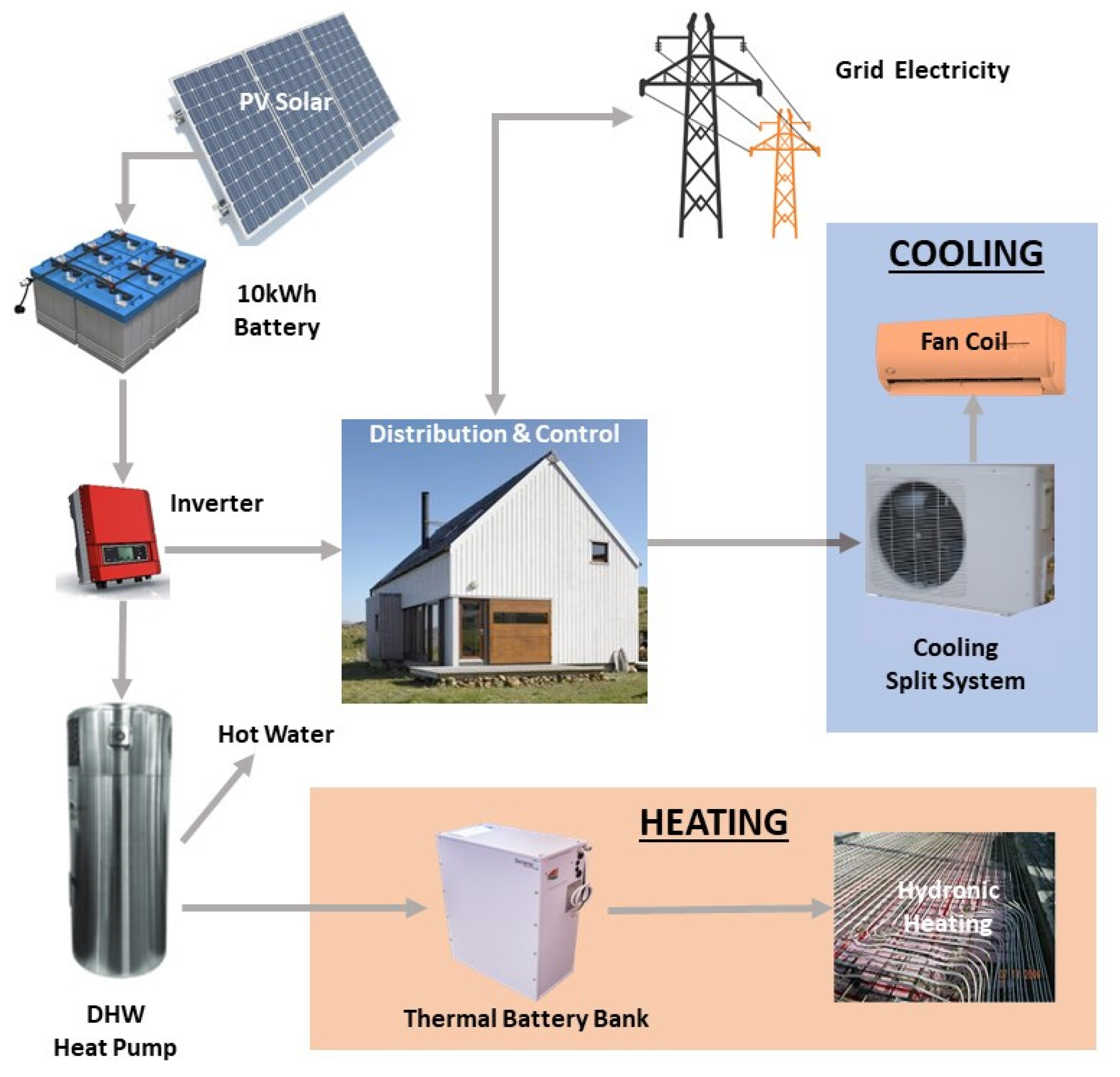
2. Description of the Mechanical System
2.1. System Components
2.2. Performance and Equations
3. Results and Analysis
3.1. Sizing of Heating System
3.2. Sizing of Cooling System
3.3. Economics
4. Discussion
5. Limitations
6. Conclusions
- A low input energy (less than 1.0 kW) service system design that can run off a solar PV, batteries and thermal storage.
- A design from readily available off-the-shelf components and appliances.
- A simplified method which takes into account the utility bills of peak daily consumption for winter and summer periods.
- A design constrained by the solar PV system size and the heat pump input power as distinct from designing for peak hourly loads to obtain a system size.
- An investigation of a real case medium sized average insulated house in Melbourne Australia demonstrates that it is possible for the service system to meet the target of above-mentioned constraints.
- Heating and DHW provided by a highly efficient HP that operates on 0.9 kW of power and uses CO2 a as the refrigerant;
- Cooling provided by a conventional split-system HP that operates on 0.8 kW and delivers 6 kW of cooling;
- A 6.5 kW solar PV system;
- Four thermal batteries (each of 10.5 kWh rated capacity); and
- Eight electrical batteries (each of 1.2 kWh capacity).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| AUD | Australian dollars |
| BT | buffer tank |
| C | capital cost |
| CO2 | carbon dioxide |
| COP | coefficient of performance |
| Cp | specific heat capacity |
| DCL | design cooling load |
| DHL | design heating load |
| DHW | domestic hot water |
| E | Energy |
| ε | Efficiency |
| EB | electrical battery |
| HP | heat pump |
| HVAC | heating ventilating and air conditioning |
| i | price inflation |
| kWh | kilowatt-hour |
| m | Mass |
| N | payback period |
| NZEB | net zero energy building |
| PCM | phase change material |
| PEB | positive energy building |
| PV | Photovoltaic |
| Q | thermal energy |
| Q’ | rate of heat transfer |
| S | Savings |
| T | Temperature |
| TB | thermal battery |
| USD | United States dollars |
| W’ | Power |
Appendix A. Calculation Method
- Solar System Size SettingsRated output: 6.5 kWAverage output in July: 13 kWh/dayAverage output in January: 31 kWh/dayBattery storage: 10 kWh
- Heating Analysis (Winter)
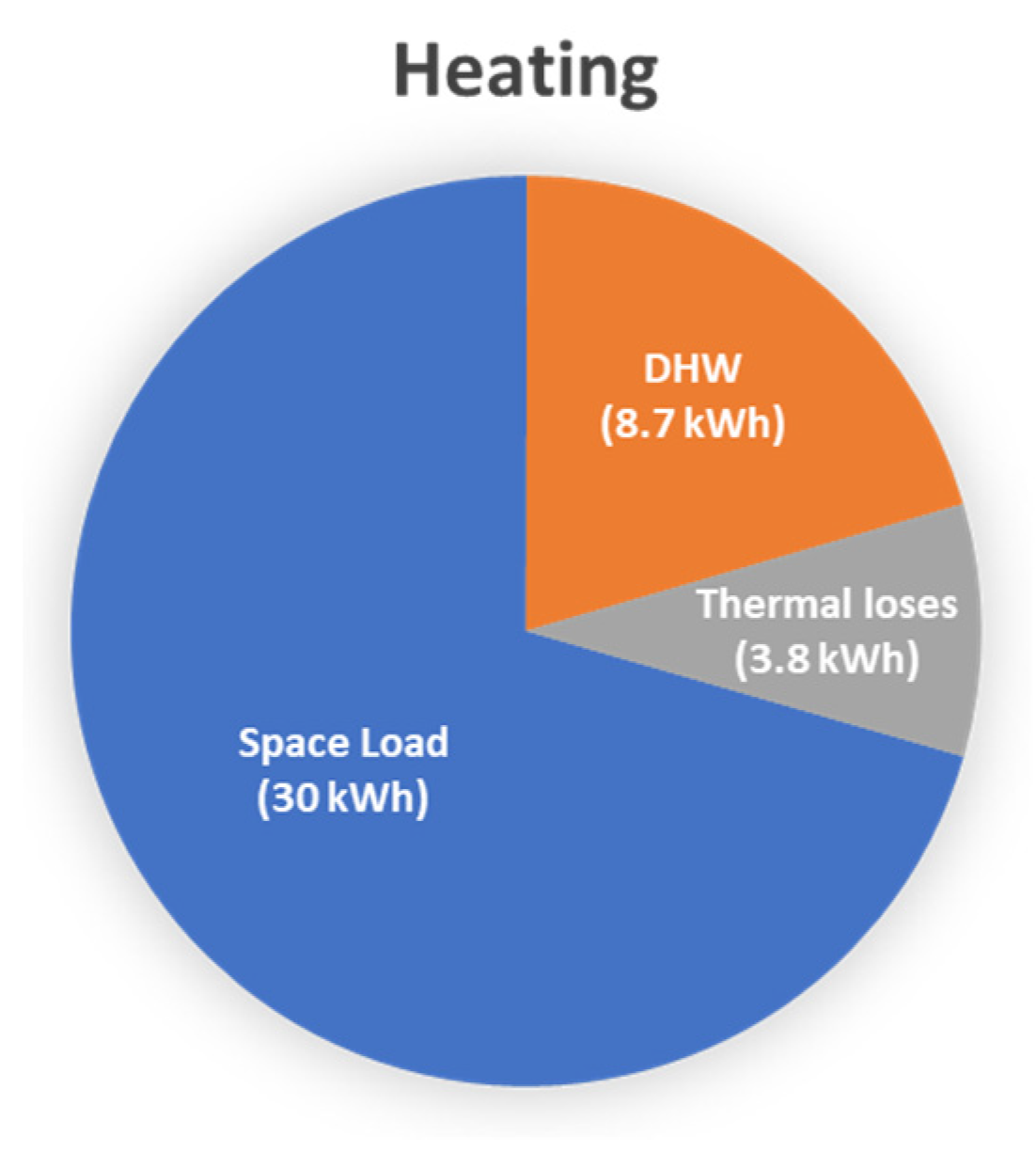
- Estimation of design heating loadAverage hourly heat loss, Q’loss = 5 kWHours per day space heating operated, theat = 6 hDHL = (Q’loss)(theat) = 30 kWh/day
- Heat pump settingsCOP of heat pump operating in heating mode (heat house), COPheat = 4.9COP of heat pump operating in cooling mode (cool house), COPcool = 6.0Maximum hot water temperature, THW,max = 65 °C
- Effective Thermal capacity of TBs for heating
- PCM componentMaximum temperature, Tmax,PCM = THW,max − 2 °C = 63 °C (accounts for thermal resistances)Minimum temperature, Tmin,PCM = 45 °CVolume, VPCM = 78 LHeat capacity of solid phase, Cp,s = 4 kJ/L·KLatent heat of fusion, hsl = 289 kJ/LHeat capacity of liquid phase, Cp,l = 4.5 kJ/L·KMelting temperature, Tmelt = 58 °CCapacity of PCM = (VPCM) [(Cp,s)(Tmelt − Tmin,PCM) + (hsl) + (Cp,l)(Tmax,PCM − Tmelt)]
- Water componentMaximum temperature, Tmax,water = THW,max = 65 °CMinimum temperature, Tmin,water = Tmin,PCM + 2 °C = 47 °C (accounts for thermal resistances)Volume, Vwater = 0.01 m3Density at mean temperature, pwater = 986 kg/m3Specific heat at mean temperature, Cp,water = 4.18 kJ/kg·KCapacity of Water = pwater (Vwater)Cp,water (Tmax,water -Tmin,water)Capacity of battery (in kWh), QTB = (Capacity of PCM + Capacity of water)/3600 = 8.1 kWhNumber of TBs required, NTB = DHLt/QTB = 4 TBs (rounded up)Extra capacity in TB bank, TBextra capacity = QTBNTB − Qheat = 2 kWh
The need to round up for the number of batteries builds in an overcapacity of 2 kWh. This will offset thermal losses from the TBs in the total thermal requirement calculation below. - DHW TankVolume of water in tank, VDHW = 0.16 m3Changes per day, B = 1Maximum temperature, Tmax,DHW = 60 °CMains water temperature in June, Tmains = 13 °CDensity at mean temperature, pDHW = 991 kg/m3Specific heat at mean temperature, Cp,DHW = 4.18 kJ/kg·KHeat required for DHW (in kWh), QDHW = pDHW(VDHW)Cp,waterB(Tmax,DHW − Tmains)/3600 = 8.7 kWh
- Losses and EfficiencyTB loss, LossTB = 0.7 kWh/day per TBDHW tank loss, LossDHW = 5% or 0.4 kWh/dayBuffer tank loss, Lossbuffer = 5% or 0.4 kWh/dayBattery Efficiency, εbatteries = 96%
- PumpsTB Supply Loop Pump (between DHW & TB) 0.012 kW for 18 h/day consumes Psupply= 0.216 kWh/dayDHW Loop Pump (between TB & DHW) 0.012 kW for 18 h/day consumes PDHW= 0.216 kWh/dayHydronic Heating Loop Pump (between TB & space) 0.12 kW for 6 h/day consumes Phydronic = 0.72 kWh/day
- Total heat requiredQtotal,winter = (QTB NTB) + (LossTB NTB − TBextra capacity) + QDHW + LossDHW + Lossbuffer = 43 kWh/day
- Total electricity required (winter peak)Etotal,winter = (Qtotal,winter/COPheat + Psupply + PDHW + Phydronic)(εbatteries × 0.01) = 10.3 kWh/daySolar PV system sufficient to meet this need as average output in June is 13 kWh/day10 kWh electrical battery sufficient as that 13 kWh/day from the solar PV is cycled through it
- Cooling Analysis (Summer)
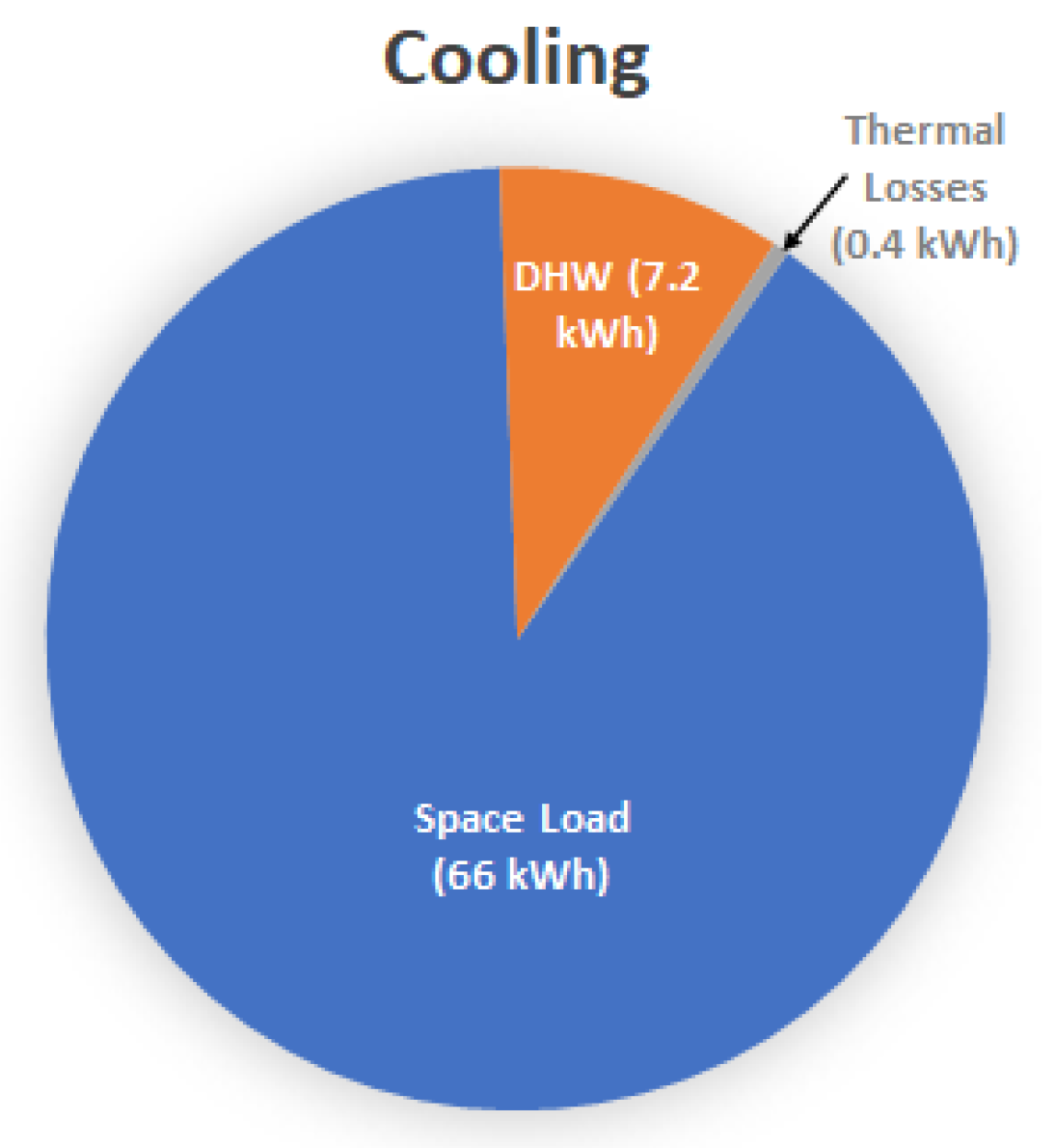
- Estimation of design cooling loadAverage rate of heat gain, Q’gain = 6 kWHours per day space cooling operated, tcool = 11 hDCL = (Q’gain)(tcool) = 66 kWh/day
- DHW TankSame procedure as above for heating but:Mains water temperature in January, Tmains = 21 °CDensity at mean temperature, pDHW = 992 kg/m3Heat required for DHW (in kWh), QDHW = pDHW(VDHW)Cp,waterB(Tmax,DHW − Tmains)/3600 = 7.2 kWhDHW tank loss, LossDHW = 5% or 0.4 kWh/dayIn the summer: TBs not used so no losses from there; and fluid circuit pumps not operated.
- Total electricity required (peak summer)Etotal,summer = [(DCL/COPcool) + (QDHW + LossDHW)/COPheat](εbatteries) = 13 kWh/daySolar PV system sufficient to meet this need as average output in January is 31 kWh/day10 kWh electrical battery sufficient to meet needs in evening.
References
- Stauffer, Y.; Koch, N.; Hutter, A.; Pflugradt, N.D. Quantifying the Potential of Smart Heat-Pump Control to Increase the Self-Consumption of Photovoltaic Electricity in Buildings. 2018. Available online: http://proceedings.ises.org/paper/eurosun2018/eurosun2018-0158-Stauffer.pdf (accessed on 27 August 2021).
- Sánchez, C.; Bloch, L.; Holweger, J.; Ballif, C.; Wyrsch, N. Optimised Heat Pump Management for Increasing Photovoltaic Penetration into the Electricity Grid. Energies 2019, 12, 1571. [Google Scholar] [CrossRef] [Green Version]
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Assessing the influence of the temporal resolution of electrical load and PV generation profiles on self-consumption and sizing of PV-battery systems. Appl. Energy 2016, 173, 331–342. [Google Scholar] [CrossRef]
- Beck, T.; Kondziella, H.; Huard, G.; Bruckner, T. Optimal operation, configuration and sizing of generation and storage technologies for residential heat pump systems in the spotlight of self-consumption of photovoltaic electricity. Appl. Energy 2017, 188, 604–619. [Google Scholar] [CrossRef]
- Luthander, R.; Widén, J.; Nilsson, D.; Palm, J. Photovoltaic self-consumption in buildings: A review. Appl. Energy 2015, 142, 80–94. [Google Scholar] [CrossRef] [Green Version]
- Torregrosa-Jaime, B.; Gonzalez, B.; Martínez, P.J.; Payá-Ballester, G. Analysis of the Operation of an Aerothermal Heat Pump in a Residential Building Using Building Information Modelling. Energies 2018, 11, 1642. [Google Scholar] [CrossRef] [Green Version]
- Xiao, B.; He, L.; Zhang, S.; Kong, T.; Hu, B.; Wang, R. Comparison and analysis on air-to-air and air-to-water heat pump heating systems. Renew. Energy 2020, 146, 1888–1896. [Google Scholar] [CrossRef]
- Maleki, A.; Rosen, M.A.; Pourfayaz, F. Optimal Operation of a Grid-Connected Hybrid Renewable Energy System for Residential Applications. Sustainability 2017, 9, 1314. [Google Scholar] [CrossRef] [Green Version]
- Heat Pump Association, UK, 2019 Delivering Net Zero: A Roadmap for The Role of Heat Pumps. Available online: https://www.heatpumps.org.uk/resources/ (accessed on 25 June 2021).
- Guertler, P. Getting on Track to Net Zero Ten Million Heat Pumps for Homes by 2030; E3G: London, UK, 2020. [Google Scholar]
- Vaishak, S.; Bhale, P.V. Photovoltaic/thermal-solar assisted heat pump system: Current status and future prospects. Sol. Energy 2019, 189, 268–284. [Google Scholar] [CrossRef]
- Energy Rating—Space Heating and Cooling. Available online: http://www.energyrating.gov.au/products/space-heating-and-cooling (accessed on 2 December 2020).
- Kolokotsa, D.; Rovas, D.; Kosmatopoulos, E.; Kalaitzakis, K. A roadmap towards intelligent net zero- and positive-energy buildings. Sol. Energy 2011, 85, 3067–3084. [Google Scholar] [CrossRef]
- Fabrizio, E.; Seguro, F.; Filippi, M. Integrated HVAC and DHW production systems for Zero Energy Buildings. Renew. Sustain. Energy Rev. 2014, 40, 515–541. [Google Scholar] [CrossRef]
- Bureau of Meteorology Climate Statistics for Australian Locations. Available online: http://www.bom.gov.au/climate/averages/tables/cw_086071.shtml (accessed on 2 December 2020).
- Sunamp—UNIQ Heat Batteries Reference Manual V2.3. Available online: http://www.sunamp.com/wp-content/uploads/2019/01/UniQ-Heat-batteries-reference-manual-ver_20180719_v2.3.pdf (accessed on 2 December 2020).
- Sunamp—Specialists in Thermal Energy Storage. Available online: https://www.sunamp.com/wp-content/uploads/2021/06/Sunamp-Brochure-May-2021-Artwork-LO-RES.pdf (accessed on 28 August 2021).
- Phase Change Products Pty Ltd.; West Perth, Australia. Personal communication with M.B. Luther, 2019.
- Bubleshop Sunamp UniQ E—Dual (Heating & Hot Water Storage). Available online: http://www.bublshop.co.uk/sunamp-uniq-e-dual-heating-hot-water-storage/p2040 (accessed on 3 June 2019).
- Sanden—Sanden Leading Hot Water Technology. Available online: http://www.newgensolar.com.au/heat-pump-hot-water/sanden-eco-heat-pump-hot-water-system.html (accessed on 2 December 2020).
- Pioneer_Aircon.pdf; Pioneer International Pty Ltd.: Minto, Australia, 2021.
- Moran, M.J.; Howard, N.; Shapiro, D.D.; Boettner, M.B.B. Fundamentals of Engineering Thermodynamics, 9th ed.; Wiley: Hoboken, NJ, USA, 2018. [Google Scholar]
- Standards Australia. AS/NZS 3823.2:2013 Performance of Electrical Appliances—Air Conditioners and Heat Pumps, Part 2 Energy Labelling and Minimum Energy Performance Standards (MEPS); Standards Australia: Sydney, Australia, 2013. [Google Scholar]
- Design Conditions for Melbourne, Australia. Available online: http://cms.ashrae.biz/weatherdata/STATIONS/948680_s.pdf (accessed on 2 December 2020).
- Sanden—Sanden SANCO2 Heat Pump Water Heater Technical Information. Available online: https://www.sandenwaterheater.com/sanden/assets/File/Sanden_sanc02_technical-info_10-2017_4.pdf (accessed on 3 June 2019).
- Sunamp—Sunamp and Trina Solar Sign MoU to Collaborate on Energy Saving Solution for Global Market. Available online: https://www.sunamp.com/sunamp-and-trina-solar-sign-mou/ (accessed on 2 December 2020).
- Enphase—Enphase AC Battery. Available online: https://www4.enphase.com/sites/default/files/downloads/support/ACBattery-DS-EN-UK.pdf (accessed on 28 August 2021).
- Bors, J.; Kenway, S. Water Temperature in Melbourne and Implications for Household Energy Use. Available online: https://www.waterportal.com.au/swf/images/swf-files/9tr1--001-water-energy-carbon-links_bors_2014_water_temperature_and_implications_for_household_energy_use.pdf (accessed on 29 August 2021).
- Solar Panel Payback Times. Available online: https://www.choice.com.au/home-improvement/energy-saving/solar/articles/solar-panel-payback-times (accessed on 2 December 2020).
- Solar Victoria—Solar Battery Rebate. Available online: https://www.solar.vic.gov.au/solar-battery-rebate (accessed on 2 December 2020).
- South Australia Government—Solar Photovoltaic Systems and Battery Storage. Available online: https://www.sa.gov.au/topics/energy-and-environment/energy-efficient-home-design/solar-photovoltaic-systems (accessed on 2 December 2020).
- Australian Building Codes Board—Climate Zone Map Australia. Available online: https://www.abcb.gov.au/resource/map/climate-zone-map-australia (accessed on 18 August 2021).
| Item | Heating Process | Cooling Process |
|---|---|---|
| Name | SU58-UniQ9 | SU11-UniQ9 |
| Volume of PCM (L) | 78 | 78 (assumed) |
| Tminimum (°C) | 45 | 6 |
| Tmelting (°C) | 58 | 11 |
| Tmaximum (°C) | 85 | 16 |
| Energy stored (kW·h) | 10.5 | 3.8 (calculated) |
| System | COP | At Test Temperatures | Adjusted for Design Operating Temperatures |
|---|---|---|---|
| Sanden Eco® plus | COPheating | 5.6 | 4.9 |
| Pioneer WB-18 5.1 kW | COPcooling | 6.1 | 6 |
| System | Test Temperatures | Operating Temperatures | ||
|---|---|---|---|---|
| TH | TC | TH | Tc | |
| Heating: Sanden Eco® plus | 65 | 24 | 65 | 6 |
| Cooling: Pioneer WB-18 | 35 | 27 | 32 | 25 |
| Item | Heating | Cooling |
|---|---|---|
| Space thermal energy load (kWh/day) | 30 | 66 |
| DHW energy required (kWh/day) | 8.7 | 7.2 |
| Thermal losses (kWh/day) | 3.8 | 0.4 |
| Thermal energy required (kWh/day) | 43 | 74 |
| Electrical energy required (kWh/day) | 10 | 13 |
| TB quantity | 4 | None |
| EB quantity | 8 | 8 |
| Solar PV system size (kW) | 6.5 | 6.5 |
| Sanden Eco® plus heating system | Yes | No |
| Pioneer cooling system (6 kW) | No | Yes |
| Item | Cost (AUD) |
|---|---|
| CO2 Heat pump & buffer tank (160 L) | 3000 |
| Thermal batteries for heating (4) | 8400 |
| Electrical batteries (8) | 11,800 |
| Domestic hot water tank (160 L) | 400 |
| Solar PV system (6.5 kW) | 4500 |
| Split system for cooling (5 kW) | 2000 |
| Total | 30,100 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Simko, T.; Luther, M.B.; Li, H.X.; Horan, P. Applying Solar PV to Heat Pump and Storage Technologies in Australian Houses. Energies 2021, 14, 5480. https://doi.org/10.3390/en14175480
Simko T, Luther MB, Li HX, Horan P. Applying Solar PV to Heat Pump and Storage Technologies in Australian Houses. Energies. 2021; 14(17):5480. https://doi.org/10.3390/en14175480
Chicago/Turabian StyleSimko, Tom, Mark B. Luther, Hong Xian Li, and Peter Horan. 2021. "Applying Solar PV to Heat Pump and Storage Technologies in Australian Houses" Energies 14, no. 17: 5480. https://doi.org/10.3390/en14175480
APA StyleSimko, T., Luther, M. B., Li, H. X., & Horan, P. (2021). Applying Solar PV to Heat Pump and Storage Technologies in Australian Houses. Energies, 14(17), 5480. https://doi.org/10.3390/en14175480







