Impact of Fracture Topology on the Fluid Flow Behavior of Naturally Fractured Reservoirs
Abstract
:1. Introduction
2. Mathematical Formulation
2.1. Topological Characterization of Fracture Network
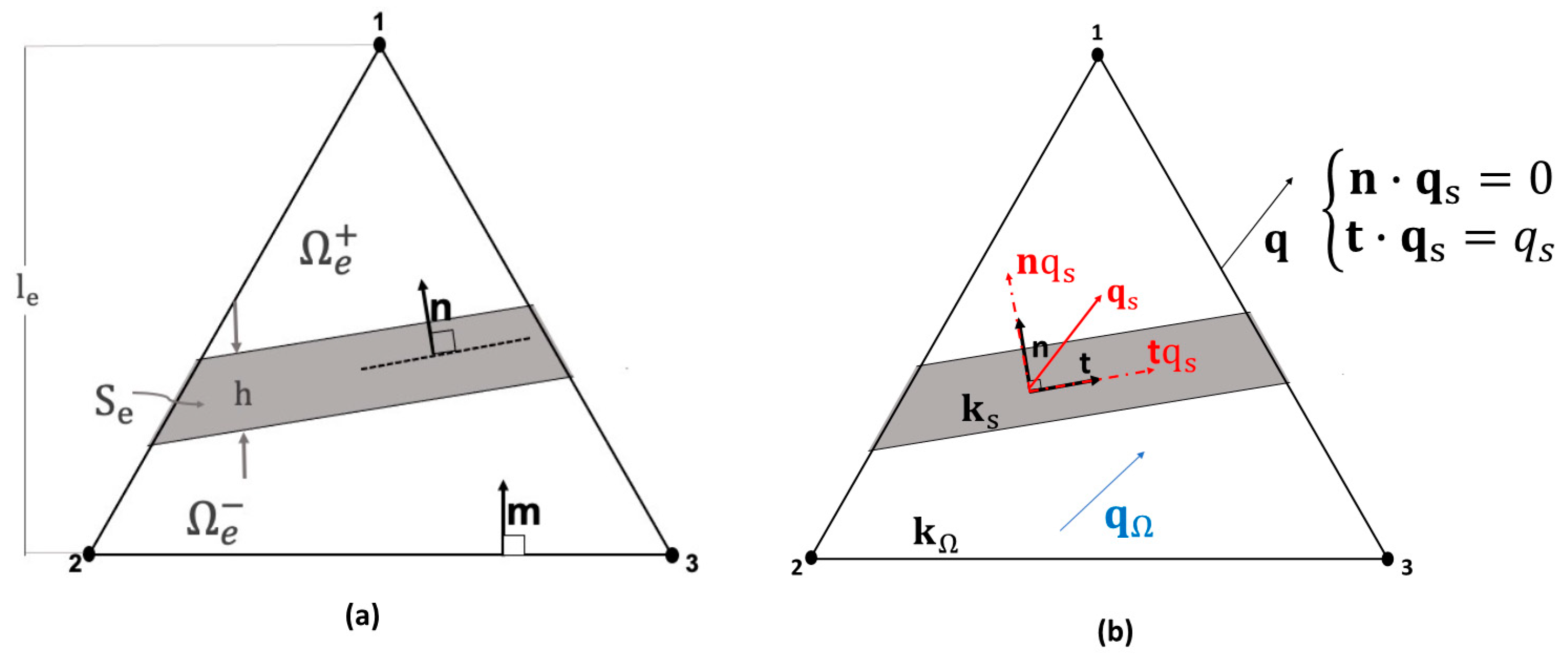
2.2. Discrete Fracture Model and Finite Element with Embedded Discontinuities
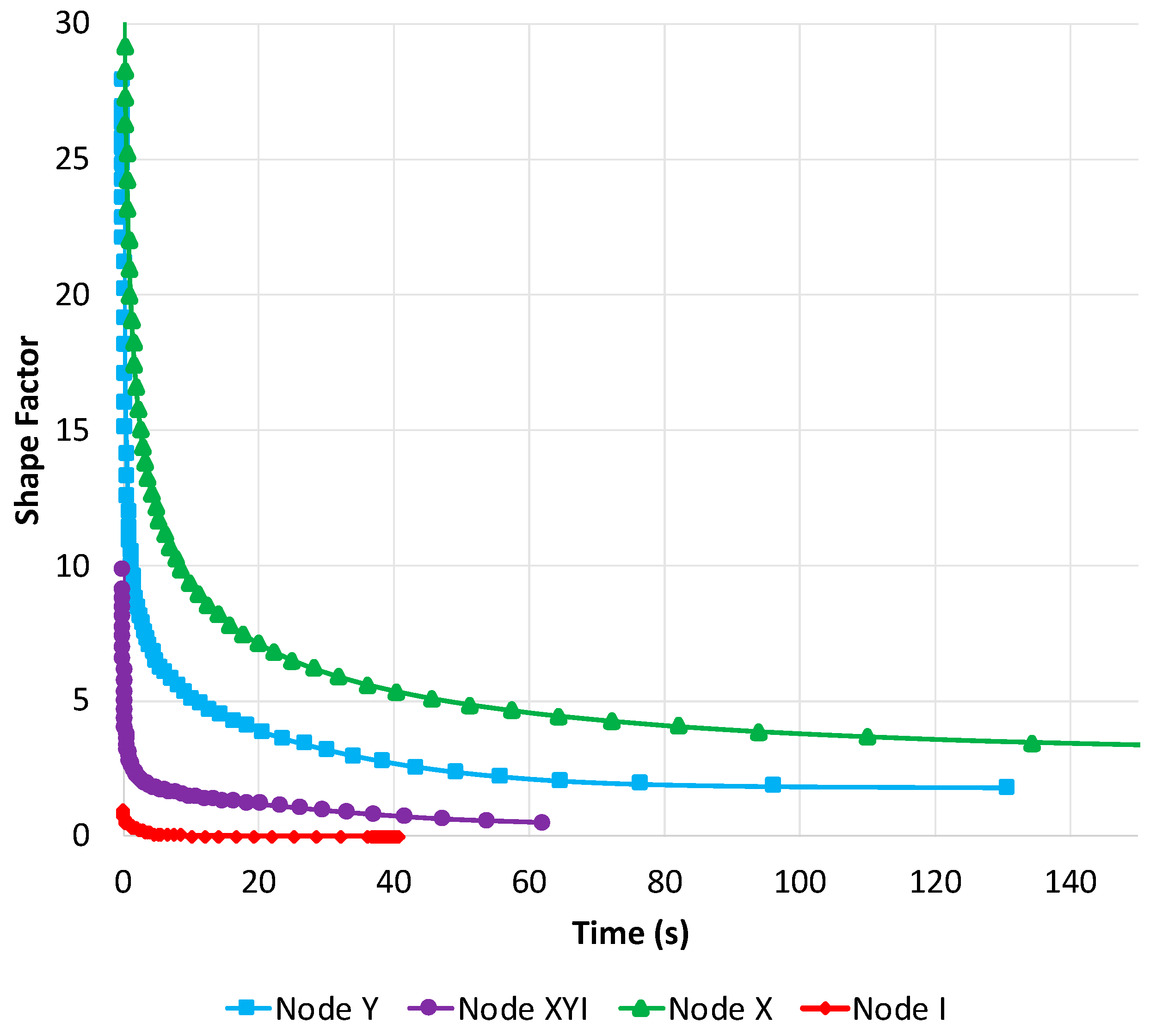
2.3. Calculation of Shape Factor for Dual-Porosity—Permeability Models
2.4. Oda Tensor Approach for Equivalent Permeability Estimation
3. Modeling of Studied Cases
3.1. Artificial Fractured Media
3.2. Real Fractured Reservoir Case: Brazilian Pre-Salt
4. Results
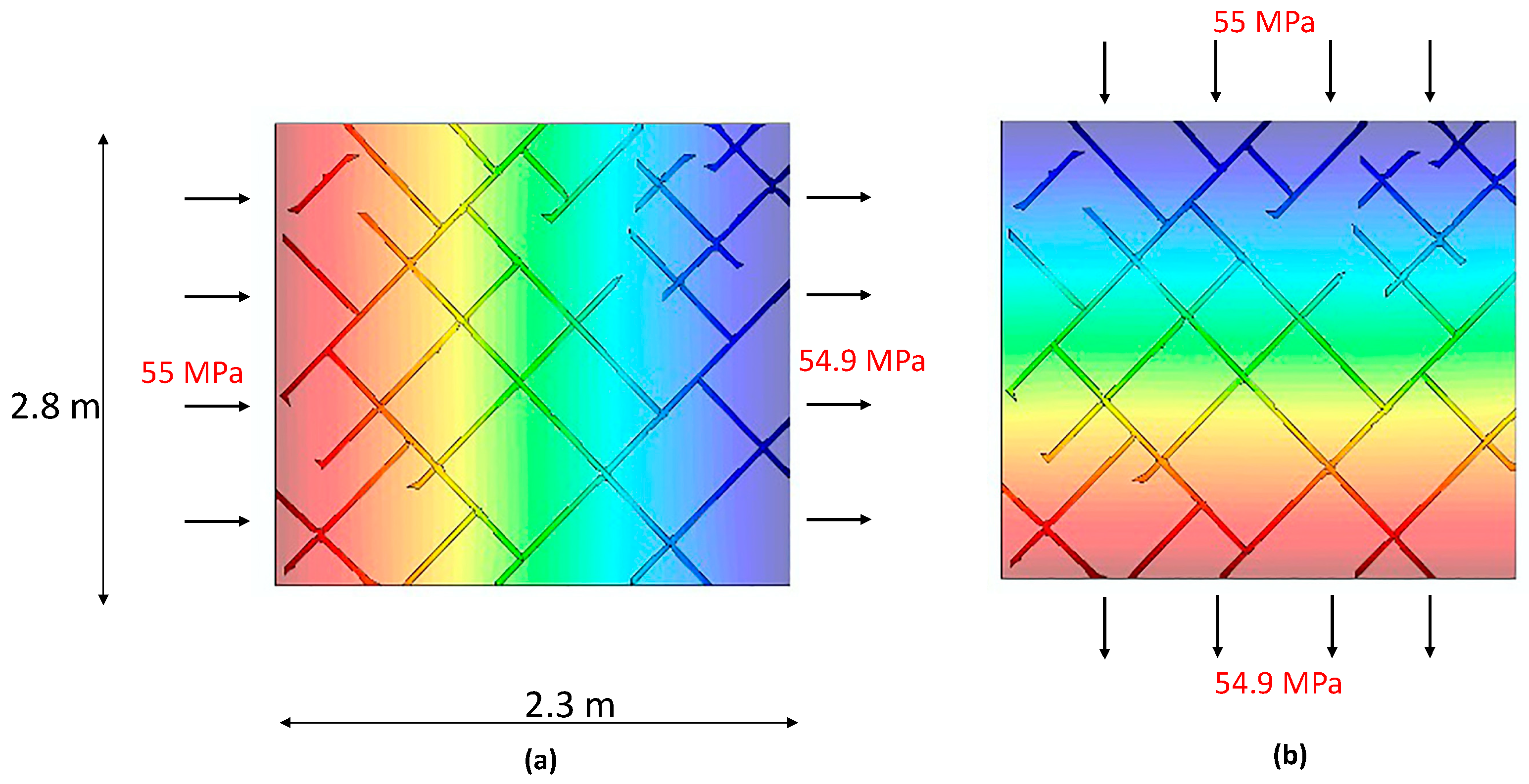
4.1. Artificial Scenarios
4.2. Numerical Simulation of Real Fractured Reservoir Scenarios of Brazilian Pre-Salt Interval
5. Discussion
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Jaffré, J.; Mnejja, M.; Roberts, J. A discrete fracture model for two-phase flow with matrix-fracture interaction. Procedia Comput. Sci. 2011, 4, 967–973. [Google Scholar] [CrossRef]
- Lima, B.E.M.; De Ros, L.F. Deposition, diagenetic and hydrothermal processes in the Aptian Pre-Salt lacustrine carbonate reservoirs of the northern Campos Basin, offshore Brazil. Sediment. Geol. 2019, 383, 55–81. [Google Scholar] [CrossRef]
- Lima, B.E.M.; Tedeschi, L.R.; Pestilho, A.L.S.; Santos, R.V.; Vazquez, J.C.; Guzzo, J.V.P.; De Ros, L.F. Deep-Burial Hydrothermal Alteration of the Pre-Salt Carbonate Reservoirs from Northern Campos Basin, Offshore Brazil: Evidence from Petrography, Fluid Inclu-sions, Sr, C and O Isotopes. Mar. Pet. Geol. 2020, 113, 104143. [Google Scholar] [CrossRef]
- Philip, Z.G.; Jennings, J.W.; Olson, J.E.; Laubach, S.E.; Holder, J. Modeling Coupled Frac-ture-Matrix Fluid Flow in Geomechanically Simulated Fracture Networks. SPE Reserv. Eval. Eng. 2005, 8, 300–308. [Google Scholar] [CrossRef]
- Bratton, T.; Canh, D.V.; Van Que, N.; Duc, N.V.; Gillespie, P.; Hunt, D.; Li, B.; Marcinew, R.; Ray, S.; Montaron, B.; et al. The Nature of Naturally Fractured Reservoirs. Oilfield Rev. 2006, 18, 4–23. [Google Scholar]
- Laubach, S.E.; Olson, J.E.; Gross, M.R. Mechanical and fracture stratigraphy. AAPG Bull. 2009, 93, 1413–1426. [Google Scholar] [CrossRef]
- Olson, J.E.; Laubach, S.E.; Lander, R.H. Natural fracture characterization in tight gas sandstones: Integrating mechanics and diagenesis. AAPG Bull. 2009, 93, 1535–1549. [Google Scholar] [CrossRef]
- Mohammed, I.; Olayiwola, T.O.; Alkathim, M.; Awotunde, A.A.; Alafnan, S.F. A review of pressure transient analysis in reservoirs with natural fractures, vugs and/or caves. Pet. Sci. 2021, 18, 154–172. [Google Scholar] [CrossRef]
- Bonnet, E.; Bour, O.; Odling, N.E.; Davy, P.; Main, I.; Cowie, P.; Berkowitz, B. Scaling of Fracture Systems in Geo-logical Media. Rev. Geophys. 2001, 39, 347–383. [Google Scholar] [CrossRef] [Green Version]
- Laubach, S.E.; Gale, J.F.W. Obtaining Fracture Information for Low-Permeability (Tight) Gas Sandstones from Sidewall Cores. J. Pet. Geol. 2006, 29, 147–158. [Google Scholar] [CrossRef]
- Laubach, S.E.; Lander, R.H.; Criscenti, L.J.; Anovitz, L.M.; Urai, J.L.; Pollyea, R.M.; Hooker, J.N.; Narr, W.; Evans, M.A.; Kerisit, S.N. The Role of Chemistry in Fracture Pattern Development and Opportunities to Advance Interpretations of Geological Materials. Rev. Geophys. 2019, 57, 1065–1111. [Google Scholar] [CrossRef] [Green Version]
- Nelson, R.A. Geologic Analysis of Naturally Fractured Reservoirs, 2nd ed.; Gulf Professional Publishing: Boston, MA, USA, 2001. [Google Scholar]
- Laubach, S.E. Fracture Networks in Selected Cretaceous Sandstones of the Green River and San Juan Basins: Wyoming, New Mexico, and Colorado. In Geological Studies Relevant to Horizontal Drilling: Examples from Western North America; Schmoker, J.W., Coalson, E.B., Brown, C.A., Eds.; Rocky Mountain Association of Geologists: Denver, CO, USA, 1992; pp. 115–127. [Google Scholar]
- Berkowitz, B.; Bour, O.; Davy, P.; Odling, N. Scaling of fracture connectivity in geological formations. Geophys. Res. Lett. 2000, 27, 2061–2064. [Google Scholar] [CrossRef]
- Roy, A.; Perfect, E.; Dunne, W.; Odling, N.; Kim, J.-W. Lacunarity analysis of fracture networks: Evidence for scale-dependent clustering. J. Struct. Geol. 2010, 32, 1444–1449. [Google Scholar] [CrossRef]
- Laubach, S.; Hundley, T.; Hooker, J.; Marrett, R. Spatial arrangement and size distribution of normal faults, Buckskin detachment upper plate, Western Arizona. J. Struct. Geol. 2018, 108, 230–242. [Google Scholar] [CrossRef]
- Sahu, A.K.; Ankur, R. Clustering, Connectivity and Flow Responses of Deterministic Fractal-Fracture Net-works. Adv. Geosci. 2020, 54, 149–156. [Google Scholar] [CrossRef]
- Silva, J.; Igor, G.; Rafael, S.; Tiago, M.; Ricardo, G.; Jose, B.; Leonardo, G.; Leila, B. Topological Analysis of Fracture Estimation Networks Integrated with Flow Simulation Models for Equivalent Fracture Permeability Estimation. J. Struct. Geol. 2021, 147, 104338. [Google Scholar] [CrossRef]
- Laubach, S.E. A Method to Detect Natural Fracture Strike in Sandstones. AAPG Bull. 1997, 81, 604–623. [Google Scholar] [CrossRef]
- Gong, J.; Rossen, W.R. Modeling Flow in Naturally Fractured Reservoirs: Effect of Fracture Aperture Distribu-tion on Dominant Sub-Network for Flow. Pet. Sci. 2017, 14, 138–154. [Google Scholar] [CrossRef] [Green Version]
- Sævik, P.N. Analytical Methods for Upscaling of Fractured Geological Reservoirs; University of Bergen: Bergen, Norway, 2015. [Google Scholar]
- Kumar, S.; Rey, A.; Dufour, G.; Ogunyomi, B. Understanding fluid flow behavior in fractured reservoir using dual porosity dual permeability and discretized frature model. In Proceedings of the SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar]
- Brenner, K.; Hennicker, J.; Masson, R.; Samier, P. Hybrid-dimensional modelling of two-phase flow through fractured porous media with enhanced matrix fracture transmission conditios. J. Comput. Phys. 2018, 357, 100–124. [Google Scholar] [CrossRef] [Green Version]
- Dershowitz, W.S.; Einstein, H.H. Characterizing rock joint geometry with joint system models. Rock Mech. Rock Eng. 1988, 21, 21–51. [Google Scholar] [CrossRef]
- Wong, D.L.Y.; Doster, F.; Geiger, S.; Francot, E.; Gouth, F. Fluid Flow Characterization Framework for Naturally Fractured Reservoirs Using Small-Scale Fully Explicit Models. Transp. Porous Med. 2020, 134, 399–434. [Google Scholar] [CrossRef]
- Berkowitz, B.; Balberg, I. Percolation theory and its application to groundwater hydrology. Water Resour. Res. 1993, 29, 775–794. [Google Scholar] [CrossRef]
- Niven, E.B.; Deutsch, C.V. A Sensitivity Analysis for Equivalent Permeability Tensors Calculated from 2D Discrete Fracture Networks. CCG Ann. Rep. 2009, 11, 1–8. [Google Scholar]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- van Harmelen, A.; Weijermars, R. Complex analytical solutions for flow in hydraulically fractured hydrocarbon reservoirs with and without natural fractures. Appl. Math. Model. 2018, 56, 137–157. [Google Scholar] [CrossRef]
- Hui, M.-H.R.; Karimi-Fard, M.; Mallison, B.; Durlofsky, L.J. A General Modeling Framework for Simulating Complex Recovery Processes in Fractured Reservoirs at Different Resolutions. SPE J. 2017, 23, 598–613. [Google Scholar] [CrossRef]
- Kasiri, N.; Bashiri, A. Status of Dual-Continuum Models for Naturally Fractured Reservoir Simulation. Pet. Sci. Technol. 2011, 29, 1236–1248. [Google Scholar] [CrossRef]
- Berre, I.; Doster, F.; Keilegavlen, E. Flow in Fractured Porous Media: A Review of Conceptual Models and Discretization Approaches. Transp. Porous Media 2019, 130, 215–236. [Google Scholar] [CrossRef] [Green Version]
- Parsons, R. Permeability of Idealized Fractured Rock. Soc. Pet. Eng. J. 1966, 6, 126–136. [Google Scholar] [CrossRef]
- Lang, P.S.; Paluszny, A.; Zimmerman, R.W. Permeability tensor of three-dimensional fractured porous rock and a comparison to trace map predictions. J. Geophys. Res. 2014, 119, 6288–6307. [Google Scholar] [CrossRef] [Green Version]
- Beserra, L.; Guimarães, L.; Manzoli, O.; Berrio, L. Finite Element with Embedded Discontinuities Analysis of Well Production Decline Due to Fracture Closure in Naturally Fr. In Proceedings of the ECMOR XVI—16th European Conference on the Mathematics of Oil Recovery; European Association of Geoscientists & Engineers, Barcelona, Spain, 3–6 September 2018. [Google Scholar]
- Falcao, F.; Barroso, J.; Murad, M.; Pereira, P.; Vargas, E.; Juvinao, A.; Muller, A.; Roehl, D.; Quevedo, R.; Mejia, C.; et al. Synthetic Benchmark for the Computation of Equivalent Properties in Coupled Flow and Geomechanics Conditions for a Fractured Carbonate Rock. In Proceedings of the 2nd International Discrete Fracture Network Engineering Conference, Seattle, DC, USA, 20–22 June 2018. [Google Scholar]
- Durlofsky, L.J. Upscaling of Geological Models for Reservoir Simulation: Issues and Approaches Introduction to the Special Issue. Comput. Geosci. 2002, 6, 1–4. [Google Scholar]
- Durlofsky, L.J. Upscaling and Gridding of Fine Scale Geological Models for Flow Simulation. In Proceedings of the 8th International Forum on Reservoir Simulation, Stresa, Italy, 20–24 June 2005; pp. 1–59. [Google Scholar]
- He, C.; Durlofsky, L. Structured flow-based gridding and upscaling for modeling subsurface flow. Adv. Water Resour. 2006, 29, 1876–1892. [Google Scholar] [CrossRef]
- Karimi-Fard, M.; Durlofsky, L.J.; Aziz, K. An Efficient Discrete-Fracture Model Applicable for General-Purpose Reservoir Simulators. SPE J. 2007, 9, 227–236. [Google Scholar] [CrossRef]
- Sævik, P.N.; Nixon, C.W. Inclusion of Topological Measurements into Analytic Estimates of Effective Permeability in Fractured Media. Water Resour. Res. 2017, 53, 9424–9443. [Google Scholar] [CrossRef]
- Sanderson, D.; Nixon, C.W. The use of topology in fracture network characterization. J. Struct. Geol. 2015, 72, 55–66. [Google Scholar] [CrossRef]
- Huseby, O.; Thovert, J.-F.; Adler, P.M. Geometry and topology of fracture systems. J. Phys. A Math. Gen. 1997, 30, 1415–1444. [Google Scholar] [CrossRef]
- Jing, L.; Stephansson, O. Network Topology and Homogenization of Fractured Rocks. In Fluid Flow and Transport in Rocks; Springer Science and Business Media LLC: Berlin/Heidelberg, Germany, 1997; pp. 191–202. [Google Scholar]
- Oda, M.; Saitoo, T.; Kamemura, K. Permeability of Rock Masses at Great Depth. Int. J. Rock Mech. Min. Sci. Geomech. Abstr. 1989, 27, 211. [Google Scholar]
- Warren, J.E.; Root, P.J. The Behavoir of Naturally Fractured Reservoirs. Soc. Pet. Eng. J. 1963, 3, 245–255. [Google Scholar] [CrossRef] [Green Version]
- Kazemi, H. Pressure Transient Analysis of Naturally Fractured Reservoirs with Uniform Fracture Distribution. Soc. Pet. Eng. J. 1969, 9, 451–462. [Google Scholar] [CrossRef]
- Coats, K. Implicit Compositional Simulation of Single-Porosity and Dual-Porosity Reservoirs (SPE-18427). In Proceedings of the SPE Symposium on Reservoir Simulation, Houston, TX, USA, 6–8 February 1989. [Google Scholar]
- Ueda, Y.; Murata, S.; Watanabe, Y.; Funatsu, K. Investigation of the Shape Factor Used in the Dual-Porosity Reservoir Simulator. In Proceedings of the SPE Asia-Pacific Conference, Sydney, Australia, 13 September 1989; pp. 35–44. [Google Scholar]
- Chang, M.-M. Deriving the shape factor of a fractured rock matrix. In Deriving the Shape Factor of a Fractured Rock Matrix; Office of Scientific and Technical Information (OSTI): Oak Ridge, TN, USA, 1993. [Google Scholar] [CrossRef] [Green Version]
- Lim, K.; Aziz, K. Matrix-fracture transfer shape factors for dual-porosity simulators. J. Pet. Sci. Eng. 1995, 13, 169–178. [Google Scholar] [CrossRef]
- Quintard, M.; Whitaker, S. Transport in chemically and mechanically heterogeneous porous media. II: Comparison with numerical experiments for slightly compressible single-phase flow. Adv. Water Resour. 1996, 19, 49–60. [Google Scholar] [CrossRef]
- Zendehboudi, S.; Chatzis, I.; Shafiei, A.; Dusseault, M. Empirical Modeling of Gravity Drainage in Fractured Porous Media. Energy Fuels 2011, 25, 1229–1241. [Google Scholar] [CrossRef]
- Lemonnier, P.; Bourbiaux, B. Simulation of Naturally Fractured Reservoirs. State of the Art Part 1. Oil Gas Sci. Technol. 2010, 65, 239–262. [Google Scholar] [CrossRef] [Green Version]
- If, F.; Frykman, P. Estimation of shape factors in fractured reservoirs. Geol. Soc. Lond. Pet. Geol. Conf. Ser. 2005, 6, 545–550. [Google Scholar] [CrossRef]
- Lewis, R.W.; Schrefler, B.A. Finite Element Method in the Deformation and Consolidation of Porous Media; John Wiley & Sons: Hoboken, NJ, USA, 1998. [Google Scholar]
- Olivella, S.; Gens, A.; Carrera, J.; Alonso, E.E. Numerical formulation for a simulator (CODE_BRIGHT) for the coupled analysis of saline media. Eng. Comput. 1996, 13, 87–112. [Google Scholar] [CrossRef] [Green Version]
- Guimarães, L.D.N.; Gens, A.; Olivella, S. Coupled Thermo-Hydro-Mechanical and Chemical Analysis of Expansive Clay Subjected to Heating and Hydration. Transp. Porous Media 2007, 66, 341–372. [Google Scholar] [CrossRef]
- Zimmerman, R.W.; Chen, G.; Hadgu, T.; Bodvarsson, G.S. A Numerical Dual-Porosity Model with Semi-Analytical Treatment of Fracture/Matrix Flow. Water Resour. Res. 1993, 29, 2127–2137. [Google Scholar] [CrossRef]
- Alvarez, L.L.; Beserra, L.; Guimarães, L.; Maciel, B.; Manzoli, O. Modeling of near—Wellbore Permeability Reduction Due to Depletion of a Naturally Fractured Reservoir. In Proceedings of the 54th U.S. Rock Mechanics/Geomechanics Symposium, Physical Event Cancelled, Golden, CO, USA, 28 June–1 July 2020. [Google Scholar]
- Cottereau, N.; Garcia, M.H.; Gosselin, O.R.; Vigier, L. Effective Fracture Network Permeability: Comparative Study of Calculation Methods. Presented at the SPE EUROPEC/EAGE Annual Conference and Exhibitio, Barcelona, Spain, 14–17 June 2010; pp. 1–31. [Google Scholar]
- Lei, Q.; Latham, J.-P.; Tsang, C.-F. The use of discrete fracture networks for modelling coupled geomechanical and hydrological behaviour of fractured rocks. Comput. Geotech. 2017, 85, 151–176. [Google Scholar] [CrossRef]
- Dershowitz William, S.; La Pointe, P.R.; Doe Thomas, W. Discrete Fracture Network Modeling: Current Status and Future Trends. In Proceedings of the US EPA/NGWA Fractured Rock Conference: State of the Science and Measuring Succes in Remediation, Portland, ME, USA, 13–15 September 2004; pp. 882–894. [Google Scholar]
- Ahmed Elfeel, M. Improved Upscaling and Reservoir Simulation of Enhanced Oil Recovery Process in Naturally Fractured Reservoirs. Ph.D. Thesis, Heriot-Watt University, Edinburgh, UK, 2014. [Google Scholar]
- da Costa Fraga, C.T.; Capeleiro Pinto, A.C.; Branco, C.C.M.; da Silva Paulo, C.A. Brazilian Pre-Alt: An Impressive Journey from Plans and Challenges to Concrete Results. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 7 May 2015. [Google Scholar]
- Madden, T.R. Random Networks and Mixing Laws. Geophysics 1976, 41, 1104–1125. [Google Scholar] [CrossRef]
- Katagiri, J.; Kimura, S.; Noda, S. Significance of shape factor on permeability anisotropy of sand: Representative elementary volume study for pore-scale analysis. Acta Geotech. 2020, 15, 2195–2203. [Google Scholar] [CrossRef]
- De Dreuzy, J.-R.; Méheust, Y.; Pichot, G. Influence of fracture scale heterogeneity on the flow properties of three-dimensional discrete fracture networks (DFN). J. Geophys. Res. Space Phys. 2012, 117, 1–21. [Google Scholar] [CrossRef] [Green Version]
- Haddad, A.S.; Hassanzadeh, H.; Abedi, J.; Chen, Z. Effect of Fracture Intensity and Longitudinal Dispersivity on Mass Transfer in Fractured Reservoirs. In Proceedings of the All Days; Society of Petroleum Engineers (SPE), Port-of-Spain, Trinidad, 11–13 June 2012; pp. 80–87. [Google Scholar]
- Oliver, J. Modelling Strong Discontinuities in Solid: Part 2. Int. J. Numer. Method in Eng. 1996, 39, 3601–3623. [Google Scholar] [CrossRef]
- Spencer, B.W. Finite Elements with Embedded Discontinuities for Modeling Reinforced Concrete Members By. Analysis (October). Ph.D. Thesis, University of Colorado at Boulder, Boulder, CO, USA, 2002. [Google Scholar]
- Manzoli, O.; Shing, P. A general technique to embed non-uniform discontinuities into standard solid finite elements. Comput. Struct. 2006, 84, 742–757. [Google Scholar] [CrossRef]
- Oliver, J.; Huespe, A.E.; Sánchez, P.J. A Comparative Study on Finite Elements for Capturing Strong Discontinuities: E-FEM vs X-FEM. Comput. Methods Appl. Mech. Eng. 2006, 195, 4732–4752. [Google Scholar] [CrossRef]
- Mejia, C.; Roehl, D.; Rueda, J.; Quevedo, R. A new approach for modeling three-dimensional fractured reservoirs with embedded complex fracture networks. Comput. Geotech. 2021, 130, 103928. [Google Scholar] [CrossRef]
- Fumagalli, A.; Scotti, A. A Reduced Model for Flow and Transport in Fractured Porous Media with Non-Matching Grids; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Zendehboudi, S.; Chatzis, I.; Mohsenipour, A.A.; Elkamel, A. Dimensional analysis ans scale-up of immiscible two-phase flow displacement in fractured porous media under controlled gravity drainage. Energy Fuels 2011, 25, 1731–1750. [Google Scholar] [CrossRef]
- Flemisch, B.; Berre, I.; Boon, W.; Fumagalli, A.; Schwenck, N.; Scotti, A.; Stefansson, I.; Tatomir, A. Benchmarks for single-phase flow in fractured porous media. Adv. Water Resour. 2018, 111, 239–258. [Google Scholar] [CrossRef] [Green Version]
- Fumagalli, A.; Keilegavlen, E.; Scialò, S. Conforming, Non-Conforming and Non-Matching Dis-cretization Couplings in Discrete Fracture Network Simulations. J. Comput. Phys. 2019, 376, 694–712. [Google Scholar] [CrossRef] [Green Version]
- Alghalandis, Y.F. ADFNE: Open Source Software for Discrete Fracture Network Engineering, Two and Three Dimensional Applications. Comput. Geosci. 2017, 102, 1–11. [Google Scholar] [CrossRef]
- Ghahfarokhi, P.K. The Structured Gridding Implications for Upscaling Model Discrete Fracture Net-works (DFN) Using Corrected Oda’s Method. J. Pet. Sci. Eng. 2017, 153, 70–80. [Google Scholar] [CrossRef]
- Haridy, M.G.; Sedighi, F.; Ghahri, P.; Ussenova, K.; Zhiyenkulov, M. Comprehensive Study of the ODA Corrected Permeability Upscaling Method. In Proceedings of the Society of Petroleum Engineers—SPE/IATMI Asia Pacific Oil and Gas Conference and Exhibition 2019, APOG 2019, Bali, Indonesia, 29–31 October 2019. [Google Scholar]
- Manzocchi, T. The connectivity of two-dimensional networks of spatially correlated fractures. Water Resour. Res. 2002, 38, 1. [Google Scholar] [CrossRef]
- Lahiri, S. Estimating effective permeability using connectivity and branch length distribution of fracture network. J. Struct. Geol. 2021, 146, 104314. [Google Scholar] [CrossRef]
- Barenblatt, G.; Zheltov, I.; Kochina, I. Basic concepts in the theory of seepage of homogeneous liquids in fissured rocks [strata]. J. Appl. Math. Mech. 1960, 24, 1286–1303. [Google Scholar] [CrossRef]
- Lemonnier, P.; Bourbiaux, B. Simulation of Naturally Fractured Reservoirs. State of the Art Part 2. Oil Gas Sci. Technol. 2010, 65, 263–286. [Google Scholar] [CrossRef] [Green Version]
- Thomas, L.K.; Dixon, T.N.; Pierson, R.G. Fractured Reservoir Simulation. Soc. Pet. Eng. J. 1983, 23, 42–54. [Google Scholar] [CrossRef]
- Landereau, P.; Noetinger, B.; Quintard, M. Quasi-Steady Two-Equation Models for Diffusive Transport in Fractured Porous Media: Large-Scale Properties for Densely Fractured Systems. Adv. Water Resour. 2001, 24, 863–876. [Google Scholar] [CrossRef]
- Penuela, G.; Civan, F.; Hughes, R.; Wiggins, M. Time-Dependent Shape Factors for Interporosity Flow in Naturally Fractured Gas-Condensate Reservoirs. In Proceedings of the All Days; Society of Petroleum Engineers (SPE), Calgary, AB, Canada, 29–30 April 2002; pp. 183–200. [Google Scholar]
- Sarda, S.; Jeannin, L.; Bourbiaux, B. Hydraulic Characterization of Fractured Reservoirs: Simulation on Discrete Fracture Models. SPE Reserv. Eval. Eng. 2002, 5, 154–162. [Google Scholar] [CrossRef]
- Al-Kobaisi, M.; Kazemi, H.; Ramirez, B.; Ozkan, E.; Atan, S. A Critical Review for Proper Use of Water-Oil-Gas Transfer Functions in Dual-Porosity Naturally Fractured Reservoirs—Part II. Presented at the International Petroleum Technology Conference, Dubai, United Arab Emirates, 4–6 December 2007. [Google Scholar] [CrossRef]
- Rostami, P.; Sharifi, M.; Dejam, M. Shape Factor for Regular and Irregular Matrix Blocks in Fractured Porous Me-dia. Pet. Sci. 2020, 17, 136–152. [Google Scholar] [CrossRef] [Green Version]
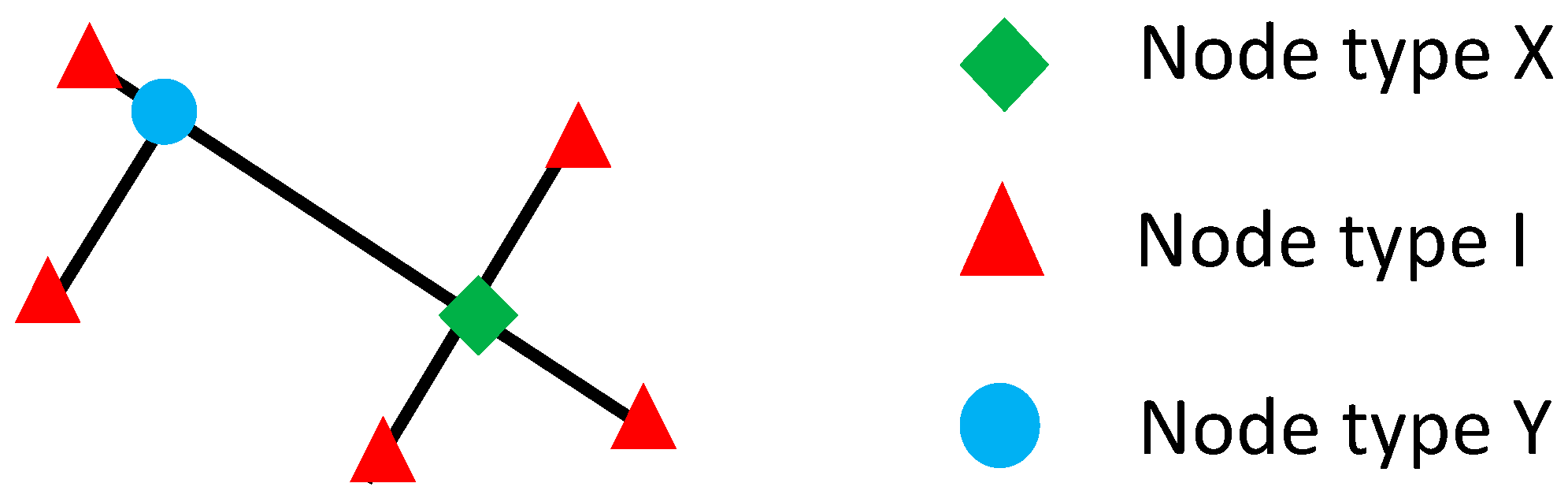
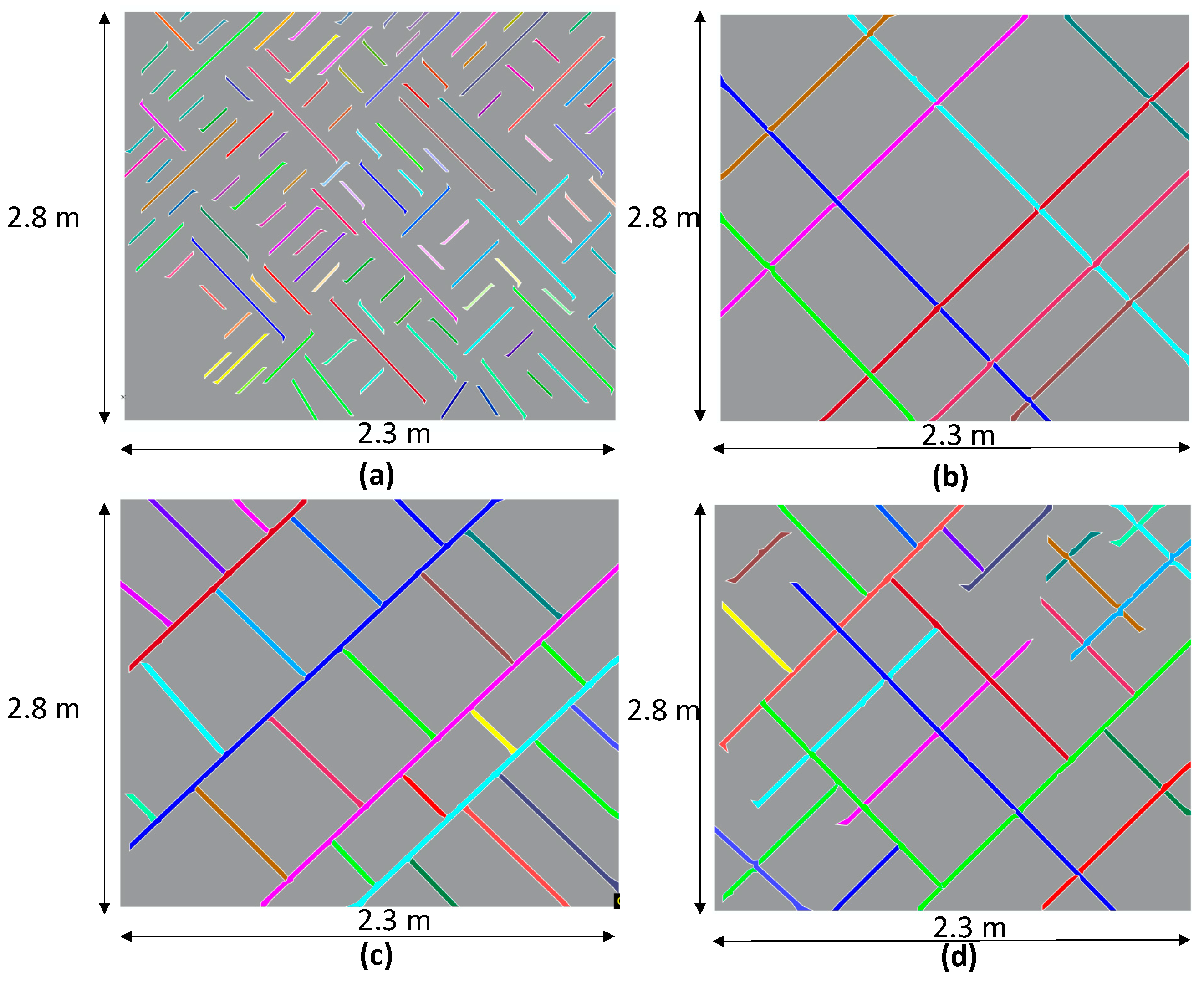

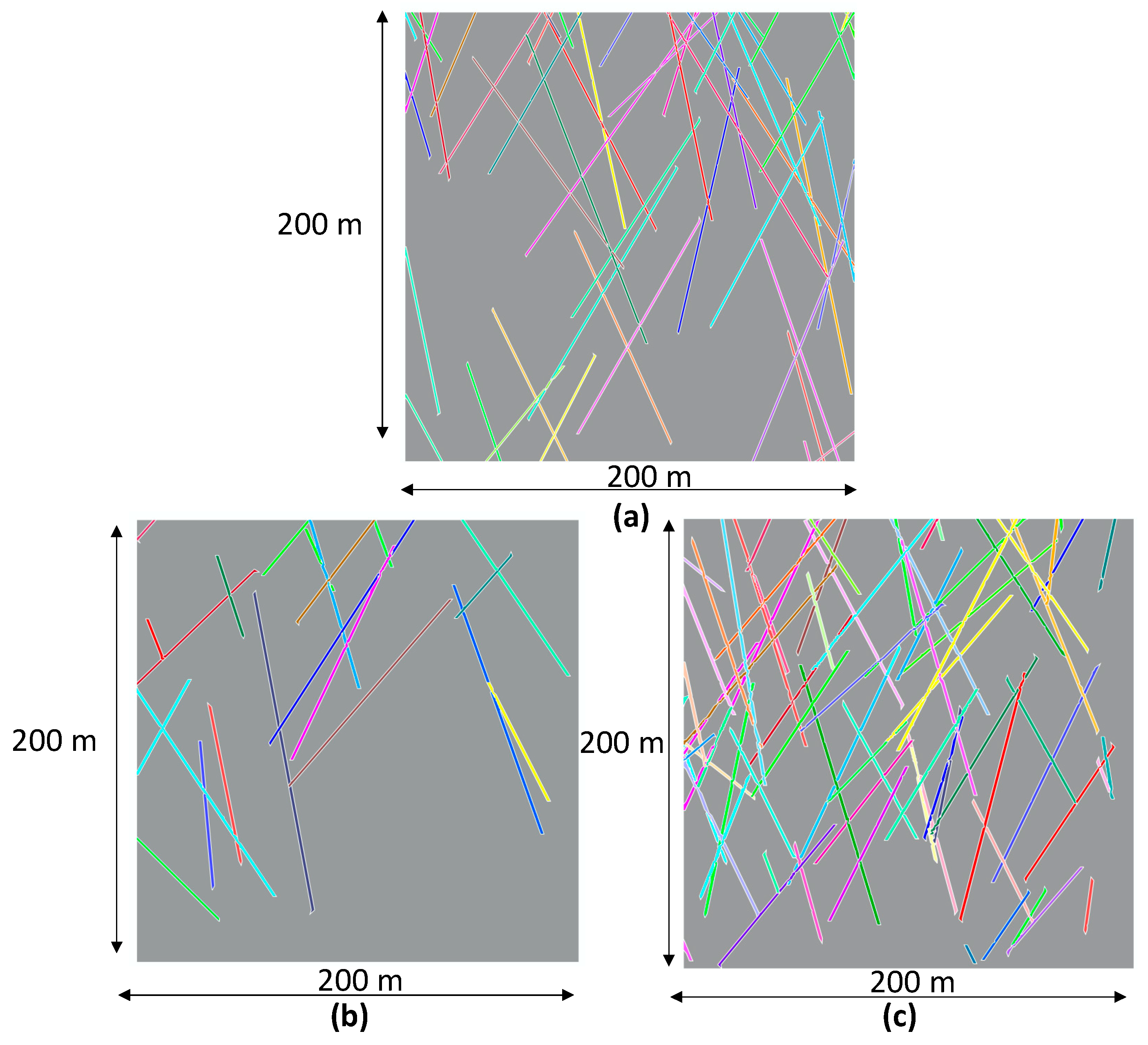




| Section | Node I | Node X | Node Y | Node XYI |
|---|---|---|---|---|
| Fractures | 115 | 9 | 26 | 24 |
| Pattern I | 230 | - | - | 11 |
| Pattern X | - | 13 | - | 14 |
| Pattern Y | - | - | 34 | 15 |
| Section 1 | Section 2 | Section 3 | |
|---|---|---|---|
| Fractures | 54 | 22 | 75 |
| Pattern I | 43 | 29 | 77 |
| Pattern X | 79 | 12 | 123 |
| Pattern Y | 12 | 3 | 23 |
| Section | Node I | Node X | Node Y | Node XYI |
|---|---|---|---|---|
| Fractures | 115 | 9 | 26 | 24 |
| Pattern I | 230 | - | - | 11 |
| Pattern X | - | 13 | - | 14 |
| Pattern Y | - | - | 34 | 15 |
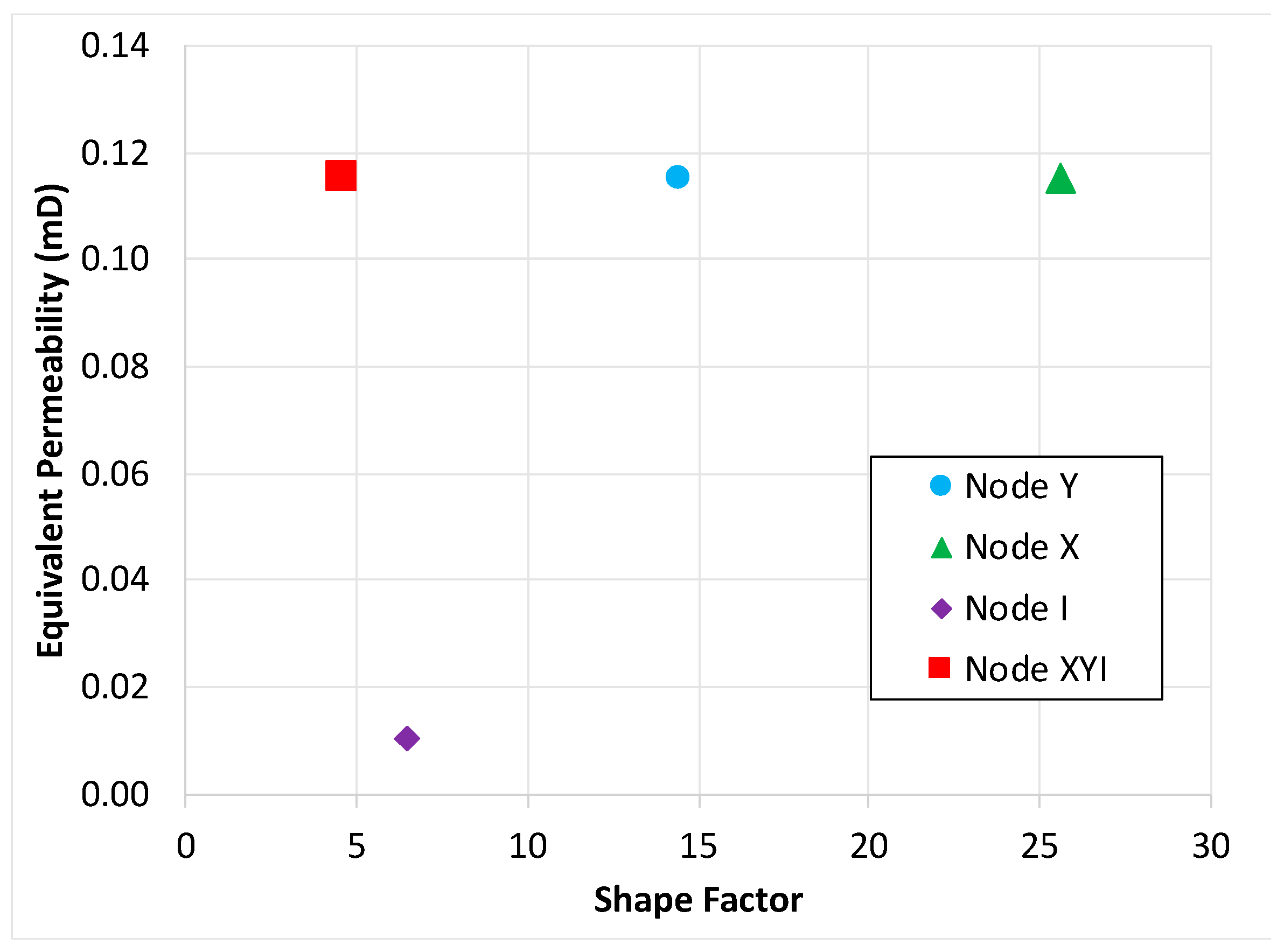
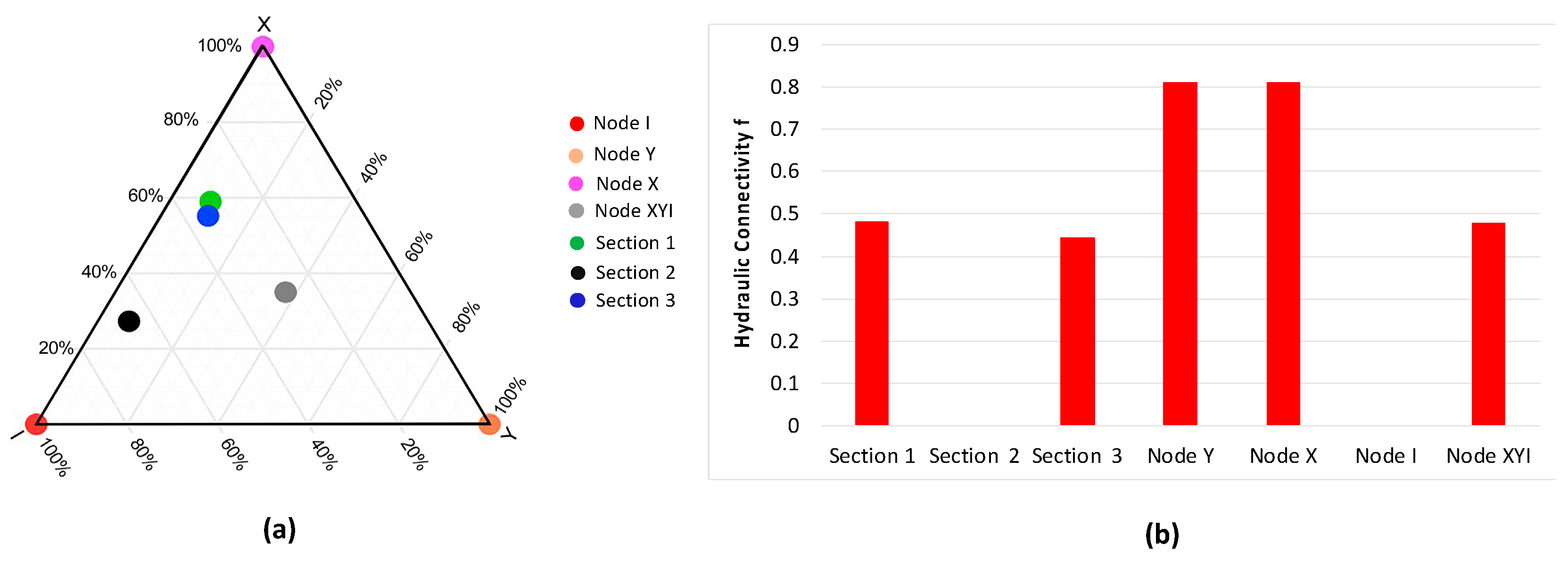
| Hydraulic Connectivity f | 0.0 | 0.81 | 0.81 | 0.48 |
| Matrix k (mD) | 0.1 | 0.1 | 0.1 | 0.1 |
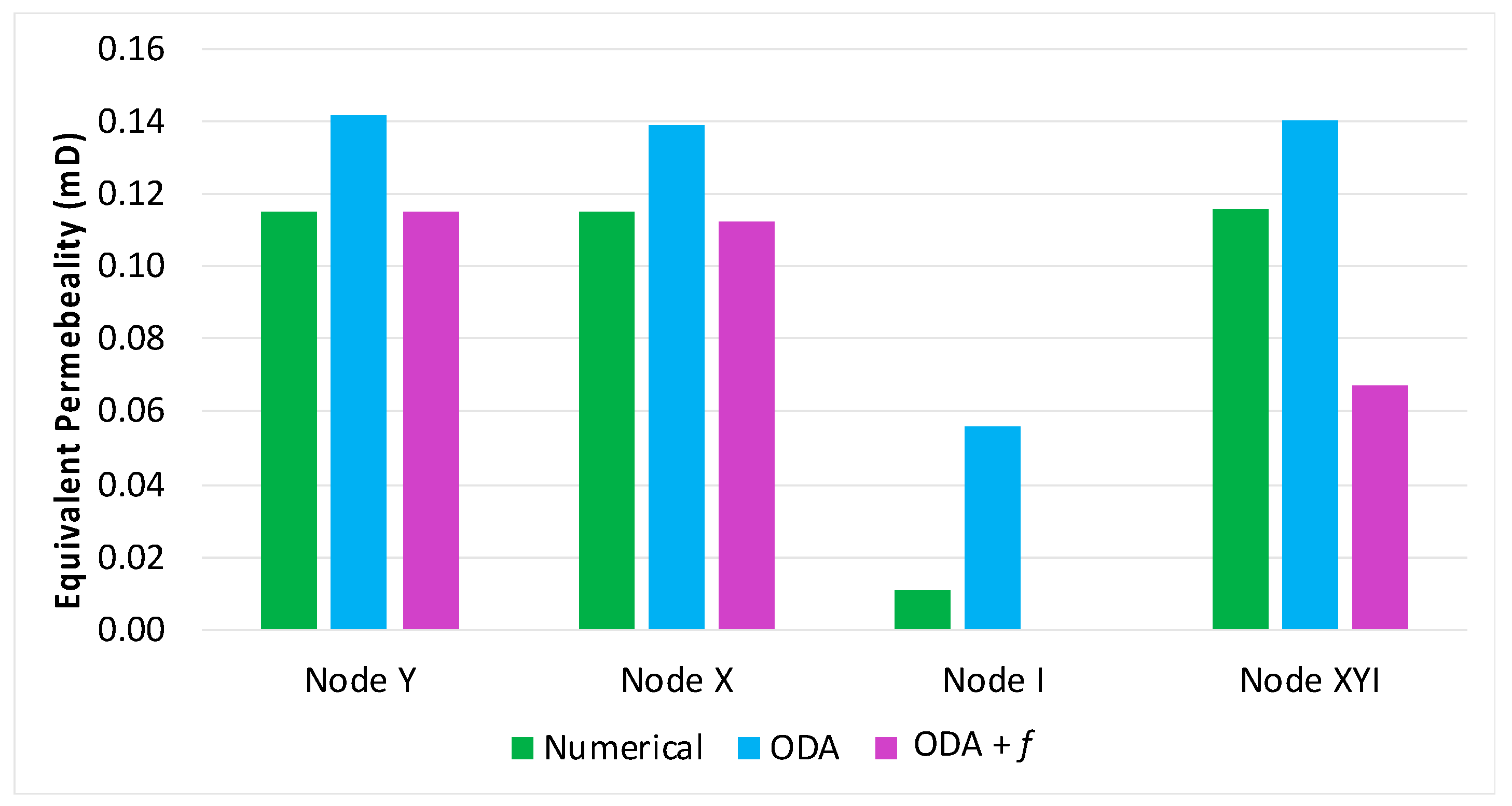
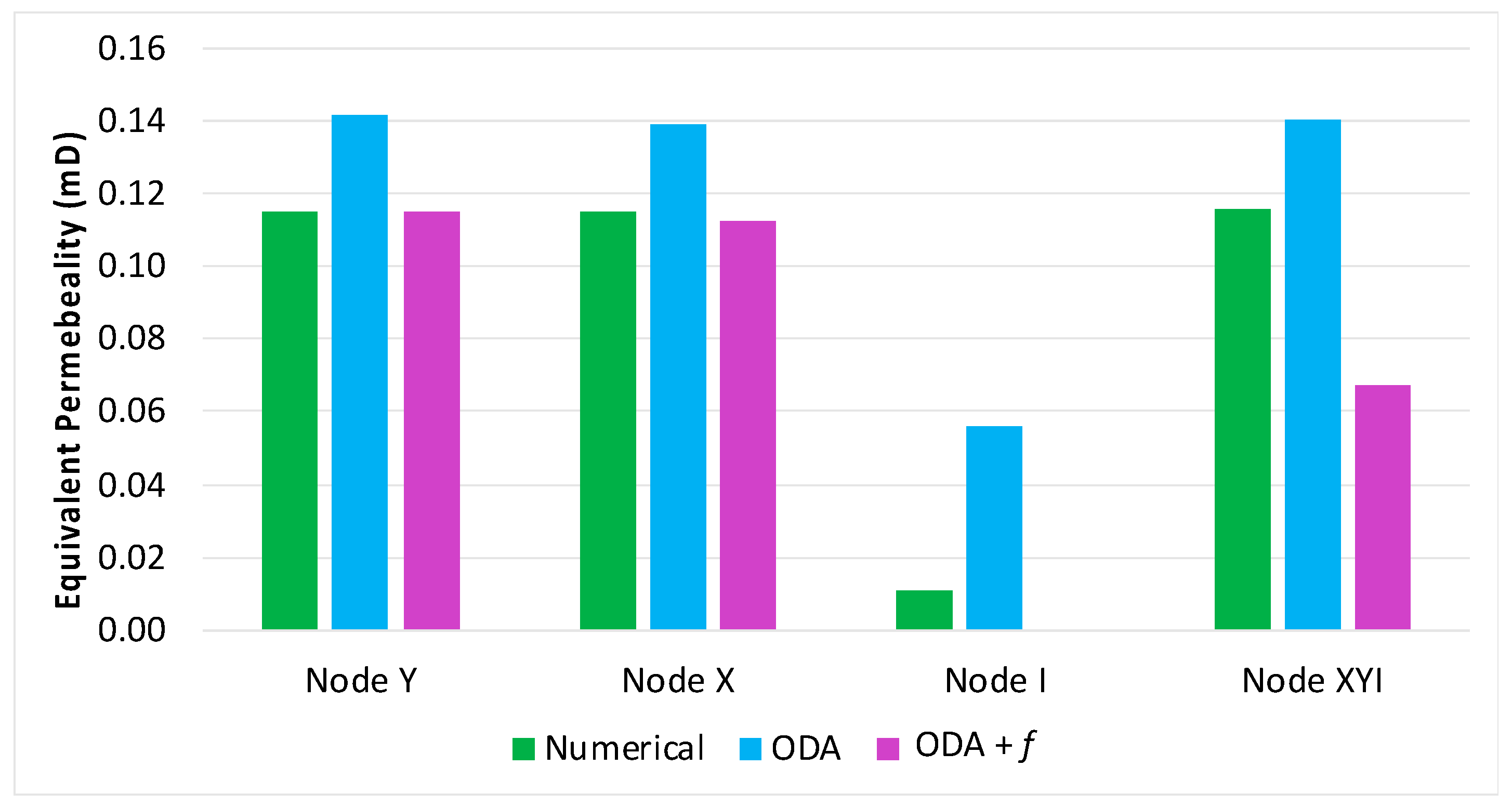
| Keq x–Numerical (mD) | 0.0107 | 0.1151 | 0.1153 | 0.1154 |
| Keq x–Oda’s (mD) | 0.0506 | 0.1390 | 0.1490 | 0.1406 |
| Keq x–f correction (mD) | 0.0 | 0.1126 | 0.1149 | 0.0670 |
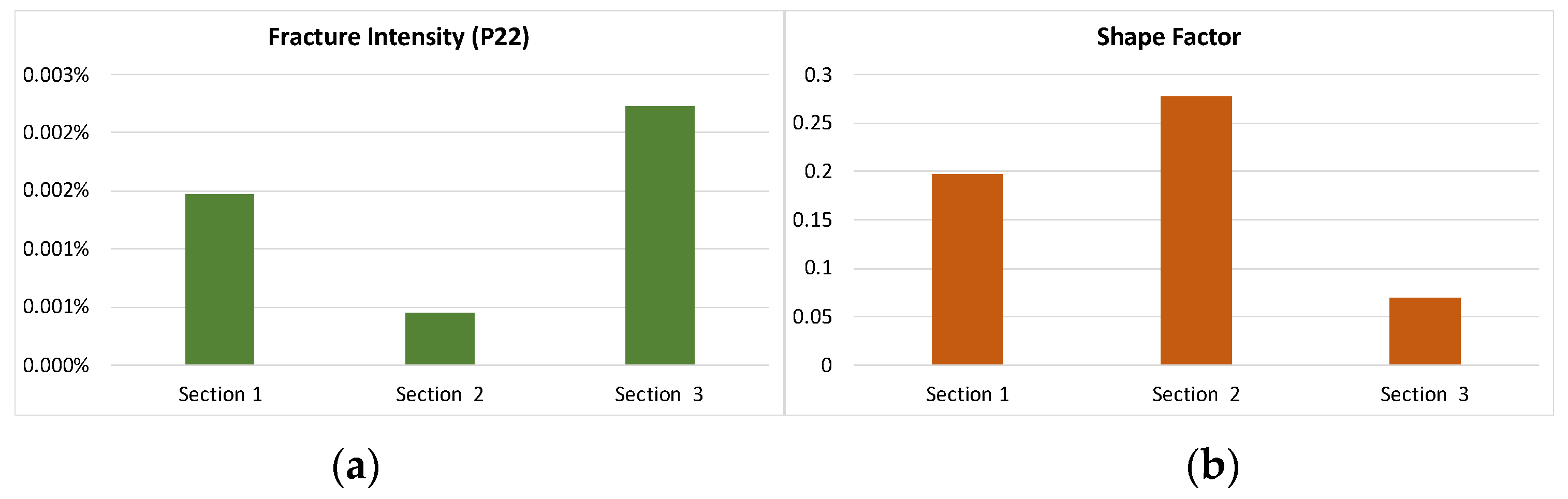
| Shape Factor | 6.54 | 25.6 | 14.5 | 4.64 |
| Section 1 | Section 2 | Section 3 | |
|---|---|---|---|
| Fractures | 54 | 22 | 75 |
| Pattern I | 43 | 29 | 77 |
| Pattern X | 79 | 12 | 123 |
| Pattern Y | 12 | 3 | 23 |
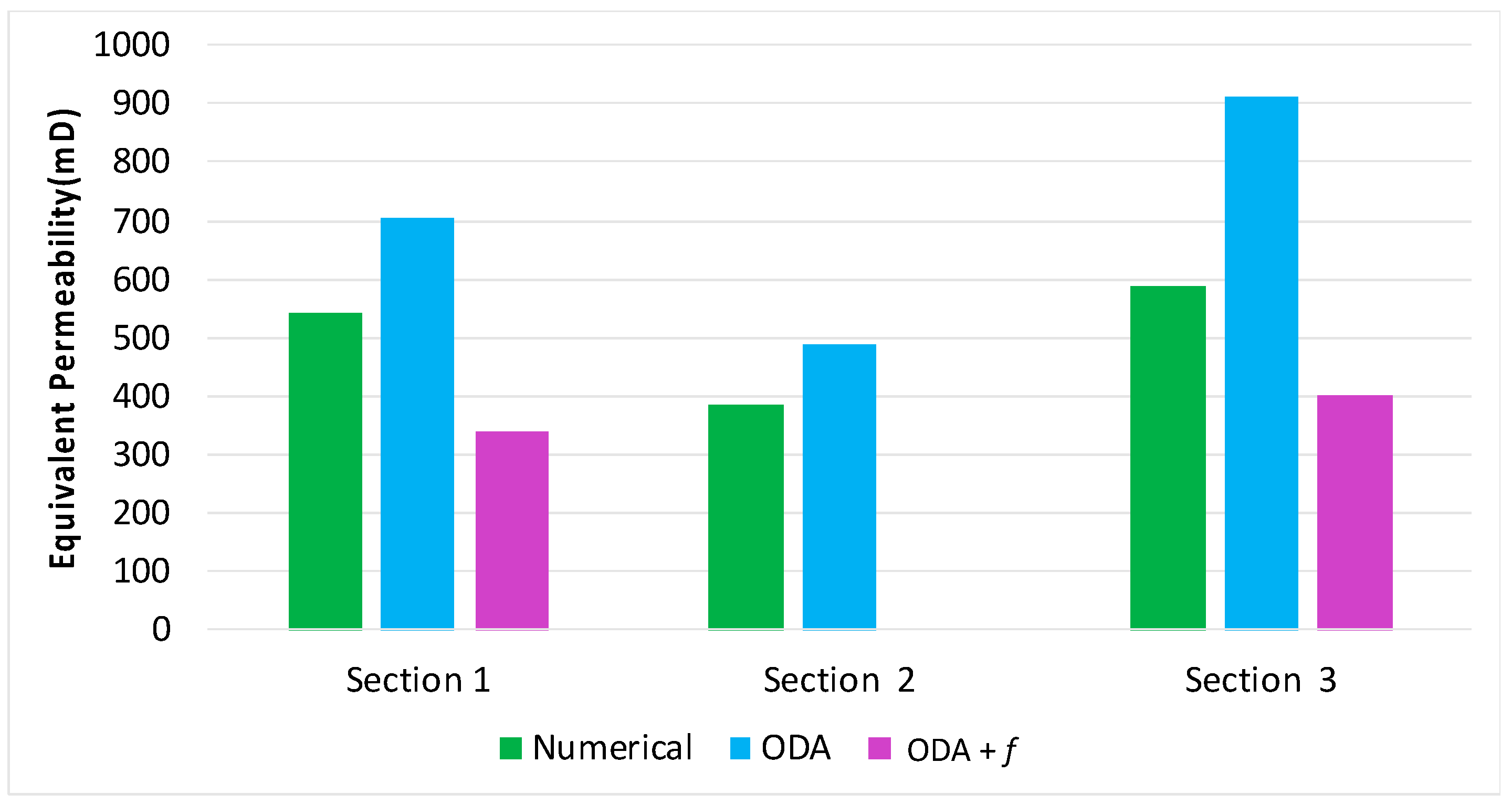
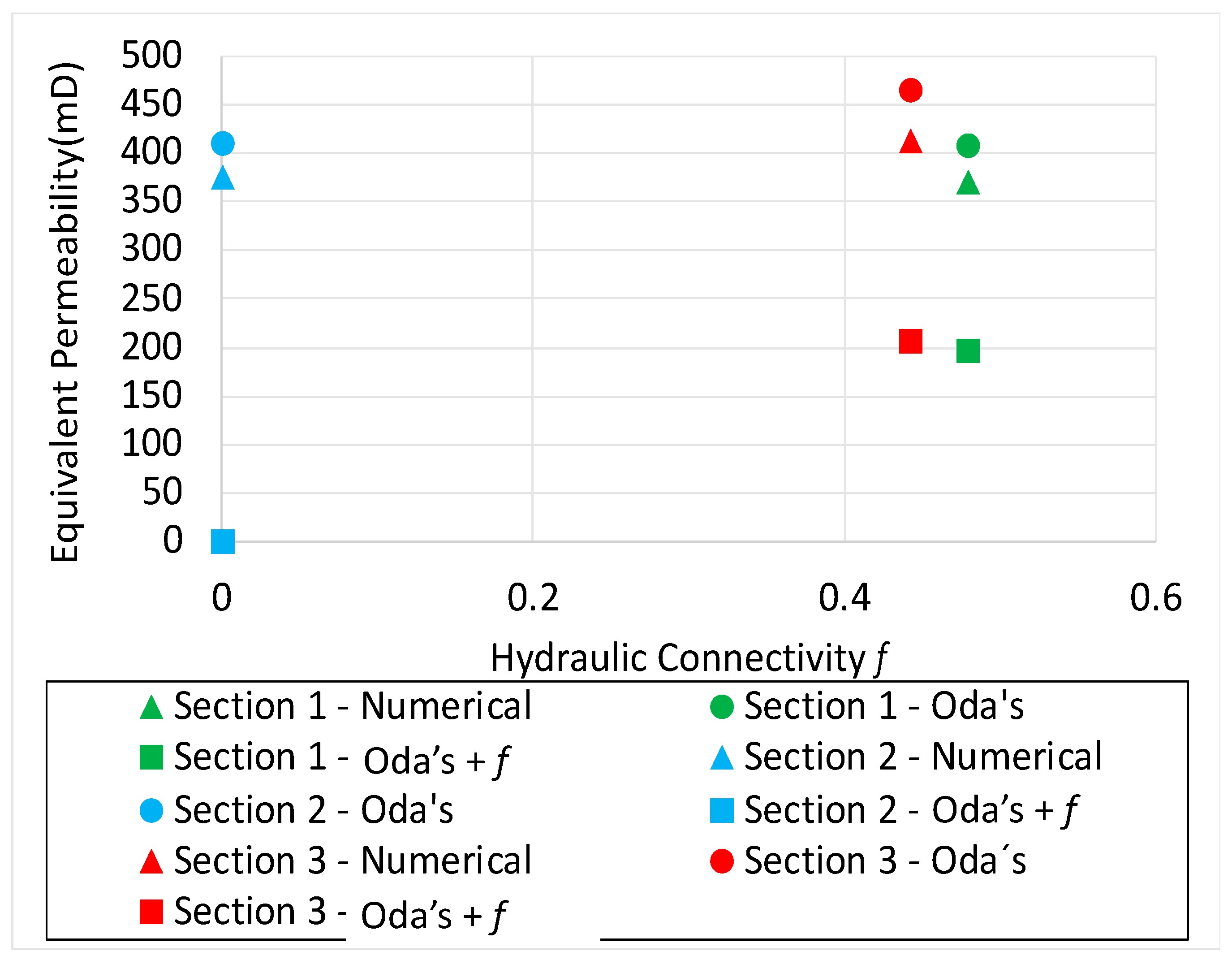
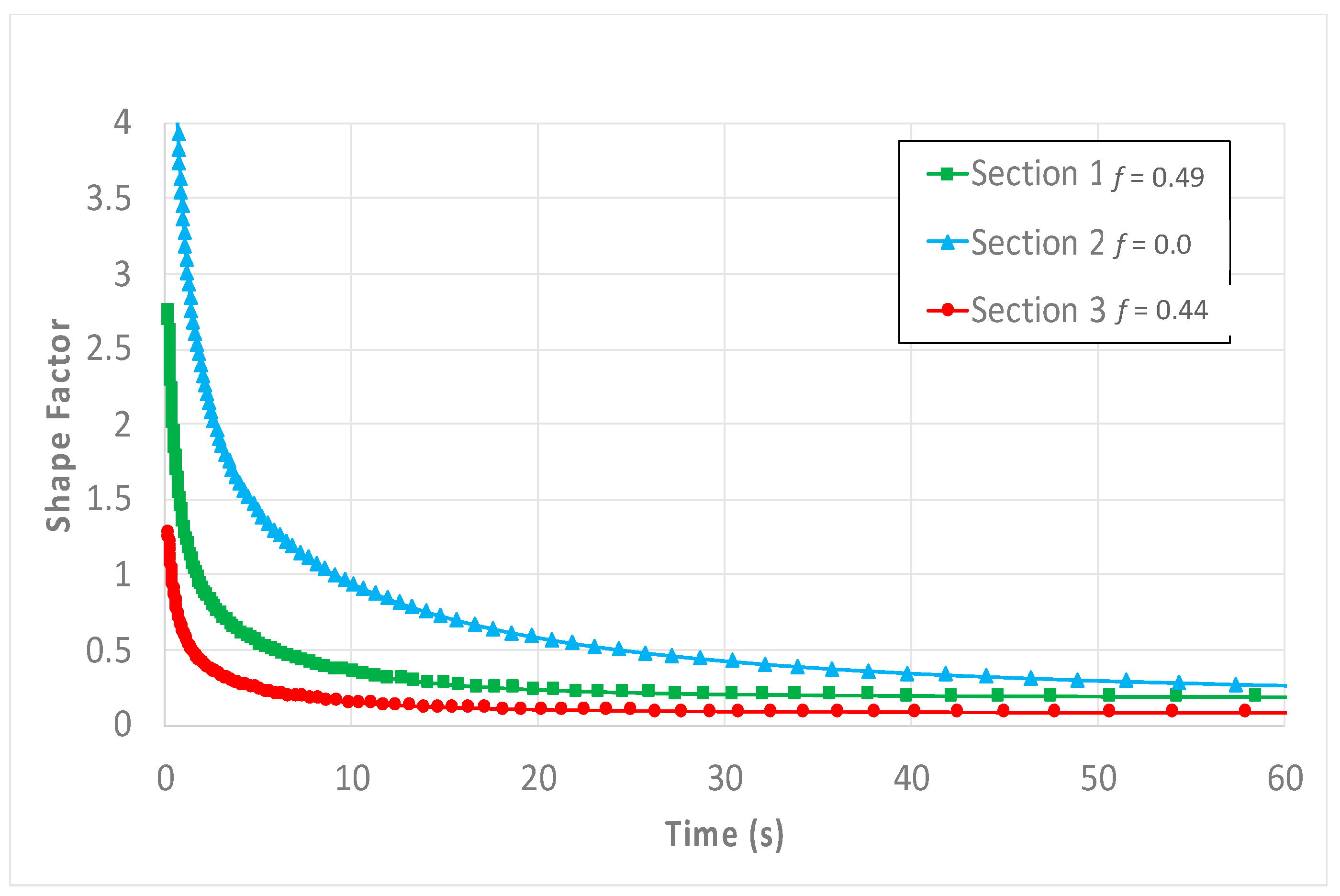
| Hydraulic Connectivity f | 0.48 | 0.0 | 0.44 |
| Matrix k (mD) | 343.28 | 343.28 | 343.28 |
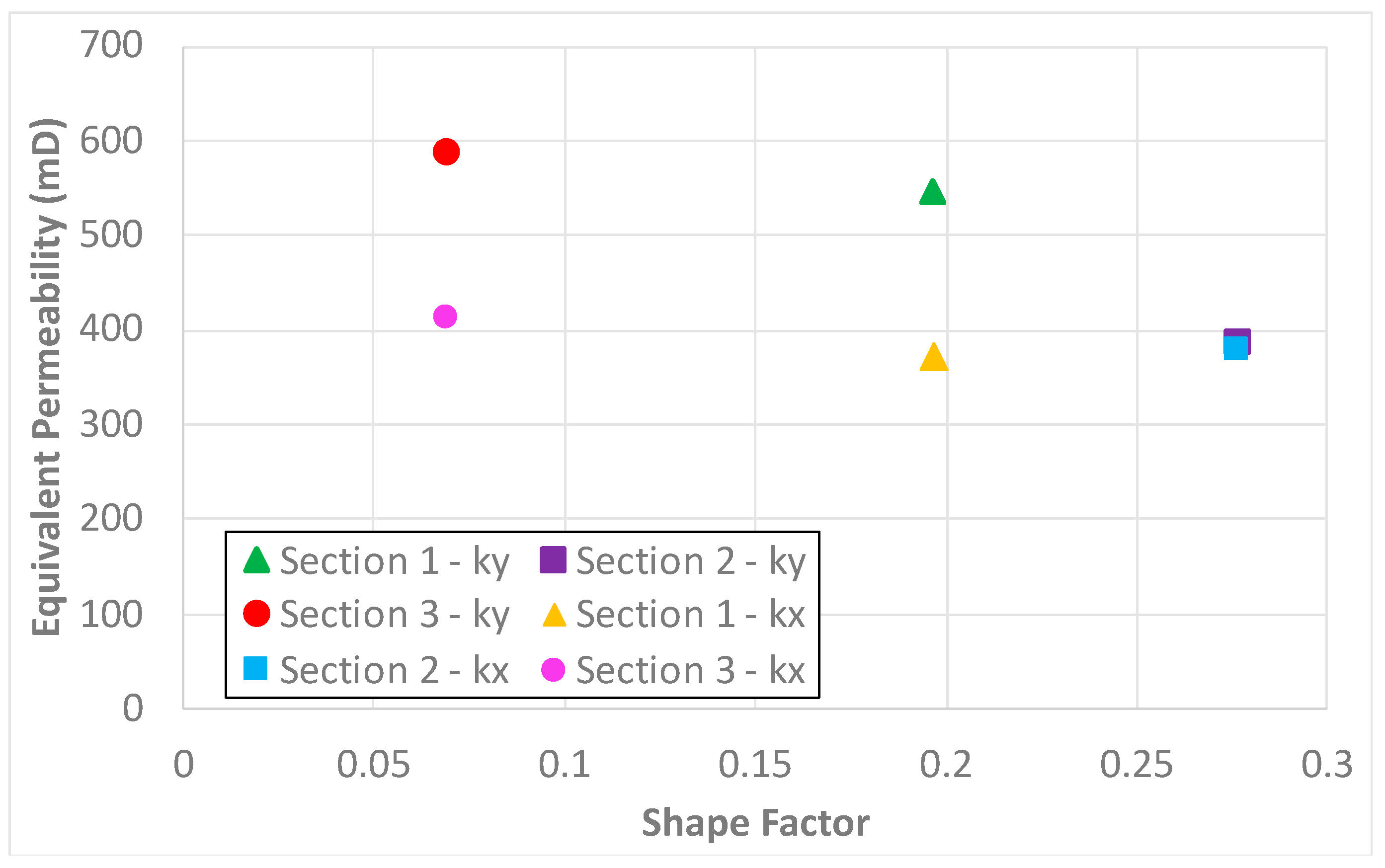
| Keq x–Numerical (mD) | 369.44 | 375.21 | 410.45 |
| Keq x–Oda’s (mD) | 407.37 | 409.56 | 464.52 |
| Keq x–f correction (mD) | 195.51 | 0.0 | 205.27 |
| Keq y–Numerical (mD) | 544.67 | 385.64 | 586.92 |
| Keq y–Oda’s (mD) | 705.02 | 488.73 | 913.90 |
| Keq y–f correction (mD) | 338.36 | 0.0 | 403.85 |
| Shape Factor | 0.1964 | 0.2766 | 0.0689 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alvarez, L.L.; Guimarães, L.J.d.N.; Gomes, I.F.; Beserra, L.; Pereira, L.C.; de Miranda, T.S.; Maciel, B.; Barbosa, J.A. Impact of Fracture Topology on the Fluid Flow Behavior of Naturally Fractured Reservoirs. Energies 2021, 14, 5488. https://doi.org/10.3390/en14175488
Alvarez LL, Guimarães LJdN, Gomes IF, Beserra L, Pereira LC, de Miranda TS, Maciel B, Barbosa JA. Impact of Fracture Topology on the Fluid Flow Behavior of Naturally Fractured Reservoirs. Energies. 2021; 14(17):5488. https://doi.org/10.3390/en14175488
Chicago/Turabian StyleAlvarez, Leidy Laura, Leonardo José do Nascimento Guimarães, Igor Fernandes Gomes, Leila Beserra, Leonardo Cabral Pereira, Tiago Siqueira de Miranda, Bruno Maciel, and José Antônio Barbosa. 2021. "Impact of Fracture Topology on the Fluid Flow Behavior of Naturally Fractured Reservoirs" Energies 14, no. 17: 5488. https://doi.org/10.3390/en14175488
APA StyleAlvarez, L. L., Guimarães, L. J. d. N., Gomes, I. F., Beserra, L., Pereira, L. C., de Miranda, T. S., Maciel, B., & Barbosa, J. A. (2021). Impact of Fracture Topology on the Fluid Flow Behavior of Naturally Fractured Reservoirs. Energies, 14(17), 5488. https://doi.org/10.3390/en14175488







