Abstract
All process industries involve the usage of heat exchanger equipment and understanding its performance during the design phase is very essential. The present research work specifies the performance of a pure cross flow heat exchanger in terms of dimensionless factors such as number of transfer units, capacity rate ratio, and heat exchanger effectiveness. Steady state sensible heat transfer was considered in the analysis. The matrix approach that was established in the earlier work was used in the study. The results were depicted in the form of charts, tables, and performance equations. It was observed that indeterminately increasing the number of transfer units past a threshold limit provided very marginal improvement in the performance of a pure cross flow heat exchanger. Likewise, flow pattern in a heat exchanger is usually assumed either as mixed or unmixed. However, due to various operating conditions, partially mixed conditions do exist. This work considers partially mixed conditions in the tube side of the heat exchanger. The correction factor for heat exchanger effectiveness was developed to accommodate partially mixed flow conditions in the pure cross flow heat exchanger.
1. Introduction
All process and manufacturing plants have a lot of heat exchanger equipment. Heat exchanger (HX) is an equipment used to transfer heat between two or more fluids, wherein the fluids are separated by a solid wall. Two fluid heat exchangers are quite common and are employed in several applications. There are several kinds of heat exchangers available in the market. Heat exchangers can be classified based on the construction and flow arrangement. Cross flow heat exchanger, shell and tube heat exchanger, double pipe heat exchanger, and plate heat exchanger are all commonly used in industries. The choice of heat exchanger depends on the application, operating conditions, etc.
In a cross flow heat exchanger, two fluids travel perpendicular to each other and thereby the name cross flow. Cross flow heat exchangers are popularly used for gas to liquid heat transfer applications where the gas is on the external side and the liquid is on the tube side of the heat exchanger. Most cross flow heat exchangers are finned tube heat exchangers. Fins enhance the surface area and these in turn enhance heat transfer. In most sensible heat transfer applications, the external fluid, which is usually gas, is treated as unmixed flow, while the tube side fluid, which is usually liquid, is treated as mixed flow. In unmixed flow, the fluid temperature varies in x- and y-directions, whereas in mixed flow, the fluid temperature varies only along the direction of flow, i.e., x-direction.
Researchers over time have come up with various methodologies for designing and analyzing the sensible performance of heat exchangers. The most common methodologies are effectiveness (ε) and number of transfer units (NTU) approach, log mean temperature difference (LMTD) approach, P-NTU approach, matrix approach, and many more. In this work, ε-NTU approach combined with a matrix approach shall be used. It must also be noted that, for steady state sensible heat transfer, the heat exchanger performance can be described through three major dimensionless factors, viz. capacity rate ratio (Cr), NTU, and heat exchanger effectiveness (ε). Most heat transfer operations do not occur at steady state, as they are often subjected to minute changes in temperature and mass flow rate. Analyzing unsteady performance of heat exchanger involves the use of numerical techniques, and this aspect is not considered in this analysis.
In this work, the concept of energy balance combined with the concept of effectiveness is applied to every row in a pure cross flow heat exchanger. The work initially focuses on developing performance equations for a given pure cross flow heat exchanger. The equations are simultaneous linear equations and can be expressed in a matrix form. Using the matrix inversion technique in MATLAB, the performance equations are solved. The results from MATLAB are used to generate design graphs, tables, and curve fit equations for a pure cross flow heat exchanger.
Design graphs, curve fit equations, and tables established in this work deliver the same information, i.e., the performance of heat exchanger in terms of dimensionless factors such as capacity rate ratio, NTU, and effectiveness. This information may help engineers to develop an optimal heat exchanger in terms of capital and operational cost. Curve fit equations are generated from design graphs and they aid in estimating heat exchanger effectiveness exclusively as a function of capacity rate ratio and NTU.
Design graphs are developed assuming that the external fluid is unmixed and while the tube side fluid is mixed. It must be recognized that an error shall be induced in the effectiveness estimation if the tube side fluid was partially mixed. Correction factors were developed for partially mixed conditions and such information is not yet published in the existing scientific literature. Partially mixed conditions can exist due to uneven flow distribution in the tube side of the heat exchanger. Understanding the impact of a partially mixed condition on the heat exchanger’s performance helps the engineers to develop a heat exchanger for the worst possible operating condition.
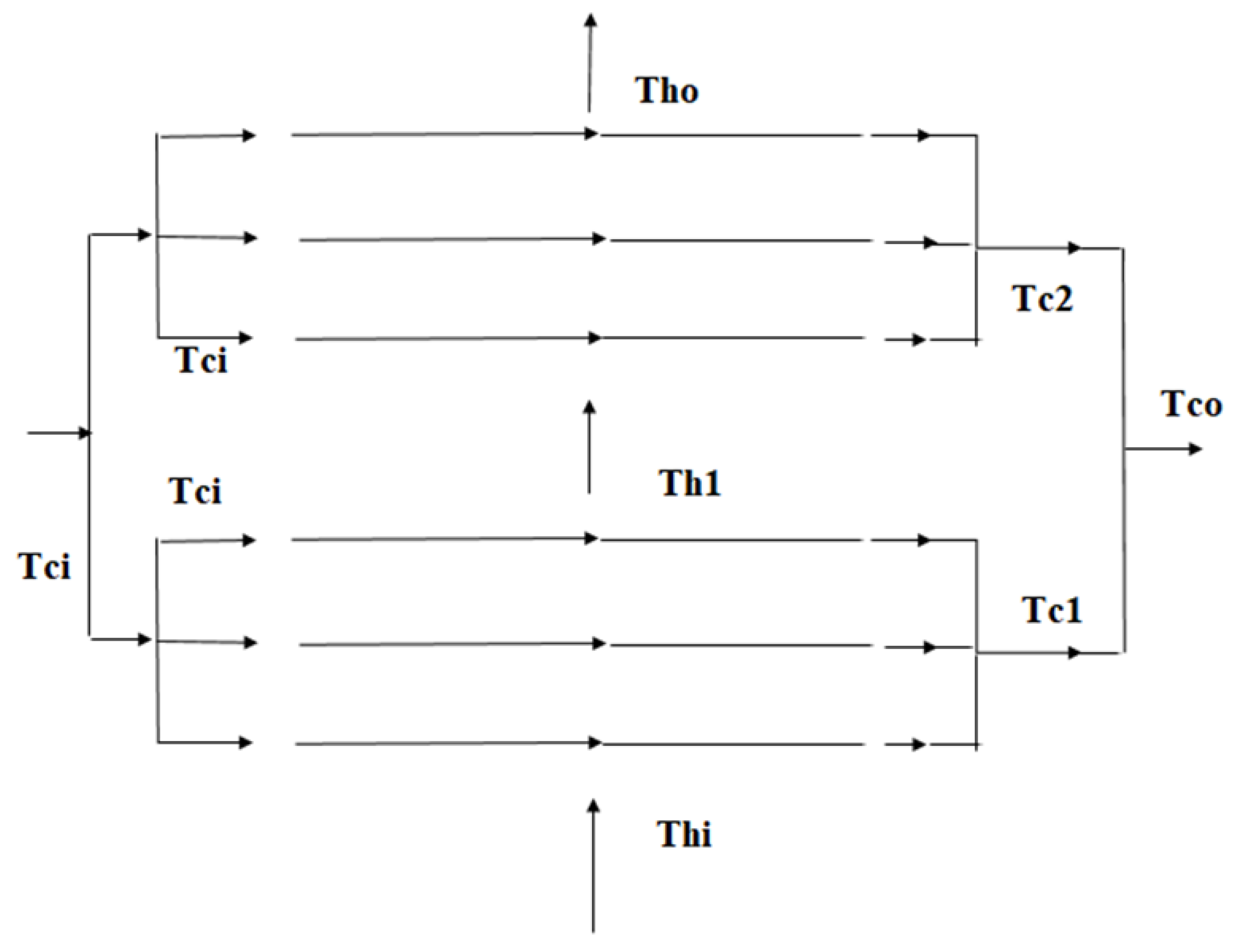
Consider Figure 1 describing the flow arrangement in a pure cross flow heat exchanger. The heat exchanger has two rows of tube banks, and each heat exchanger row has three tubes. Therefore, the above figure represents a three tube, 2-row pure cross flow heat exchanger. Some relevant papers related to the current work are described below.
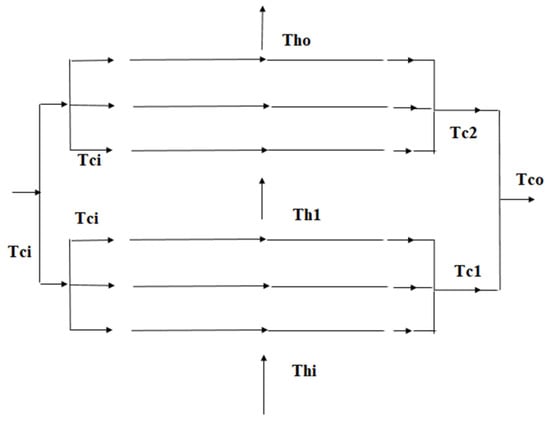
Figure 1.
Three tube, two row, pure cross flow heat exchanger.
Silaipillayarputhur and Idem [1] considered the sensible thermal performance of a heat exchanger and developed a matrix approach to study the intermediate and the overall performance of the heat exchanger. The matrix approach is used in this present research work to establish the performance of pure cross flow heat exchanger. Zhang et al. [2] considered the consequence of non-uniform flow on the thermal performance of heat exchanger. A graph was proposed to evaluate the thermal performance based on flow mal-distribution. Ishaque and Kim [3] considered the numerical modelling of finned tube heat exchanger that is used as an outdoor unit in heat pump applications. Therein, a non-uniform flow pattern of both air and refrigerant was considered. Herein, the numerical performance was compared with the experimental data. Hao et al. [4] derived a correction factor for a heat exchanger that represents the effect of flow arrangement on the heat transfer performance as a function of thermal resistance. Jouhara et al. [5] studied the performance of a multi pass, air to water heat pipe heat exchanger. The effect of Reynolds number on heat transfer rate was considered for a number of heat exchanger passes. Unger et al. [6] studied the effect of heat transfer coefficient on different kinds of fins in a finned tube heat exchanger. Based on experimentation, an empirical relationship for heat transfer coefficient was derived as a function of Nusselt number, Reynolds number, fin design, Prandtl number, and tube row number. Khan, Zou, and Yu [7] performed computational simulation of air side heat transfer and pressure drop performance in a twisted oval tube bundle cross flow heat exchanger. Therein, the air side heat transfer coefficient, the Nusselt number, and pressure drop were correlated with the Reynolds number. A generalized Nusselt number correlation was also developed in the research work. Geete et al. [8] fabricated a cross flow heat exchanger in a workshop and experimentally analyzed effectiveness, exergy, and entransy. Narkhede and Sur [9] considered the performance of a hollow compact micro-lattice-based cross flow heat exchanger. A numerical investigation was conducted to estimate the overall heat transfer coefficient. Choudhary et al. [10] experimentally examined the heat transfer and frictional losses of a tubular cross flow heat exchanger. Both solid and perforated splitter plates were used for the analyses. It was found that the heat exchanger experienced enhanced heat transfer while using perforated splitter plate. Bury and Hanuszkiewicz-Drapala [11] considered thermodynamic analysis of finned liquid to a gas cross flow heat exchanger. Therein, the heat transfer coefficient was computed using numerical simulation and empirical relationships. In the analysis, a non-uniform flow of gas at the heat exchanger inlet was considered. Zhao et al. [12] conducted a series of tests to study the thermal performance of air flow over a parallel cross flow heat exchanger used as a vehicle radiator. The performance of the heat exchanger was examined under representative irregular airflow. Gao et al. [13] studied the transient response of a cross flow heat exchanger subjected to a change in the inlet temperature and mass flow rate.
All references cited herein describe the thermal performance of a cross flow heat exchanger. A cross flow heat exchanger can operate in parallel flow configuration or counter flow configuration or can have pure cross flow circuiting as described in Figure 1. The performance of a pure cross flow heat exchanger is detailed in this work. In addition, correction factors were developed to describe partially mixed conditions in the tube side of a pure cross flow heat exchanger. It must be noted from [13] that a flow rate aberration at the heat exchanger’s inlet creates unsteady output, and the equipment requires a finite time to regain its steady state. In this work, it will be seen whether a partially mixed flow condition in the tube side will impact the steady state performance of the heat exchanger.
2. Governing Equations
The basic equations required for the modeling of a pure cross flow heat exchanger are presented in this section. These basic equations were then modeled in Matlab software to generate design graphs, tables, and curve fit equations. The assumptions for the project are as follows:
- ➢
- The heat exchanger undergoes steady state and a sensible heat transfer. The heat exchanger is symmetric; NTU is evenly distributed across the heat exchanger.
- ➢
- For the overall heat exchanger, external fluid (gas) is taken as the minimum capacity rate fluid, while the internal fluid (liquid) is taken as a maximum capacity rate fluid. This is a generally encountered condition for sensible heat transfer. However, there is a potential for these conditions to get reversed on a per row basis.
- ➢
- For prediction of a pure cross flow heat exchanger’s performance, the tube side fluid is assumed to be evenly distributed among the rows and individual tubes.
- ➢
- For the prediction of a pure cross flow heat exchanger’s performance, external fluid (gas) flow is assumed to be unmixed, while the tube side fluid (liquid) flow is assumed to be mixed.
The performance of the heat exchanger is evaluated at each heat exchanger tube row. At each tube row, the concept of energy balance and heat exchanger effectiveness is applied. Thus, for each tube row, two sets of equations are obtained. This procedure is carried out for all the tube rows in the heat exchanger. All the equations thus obtained are simultaneous linear equations and they are expressed in a matrix form. These equations are solved using a matrix inversion technique using MATLAB. The results from the MATLAB yield the unknown temperatures. The output temperatures can be used to compute the effectiveness of the heat exchanger. Capacity rate ratio and NTU are assumed dimensionless parameters in the analysis. Heat exchanger designers communicate through these dimensionless factors.
The capacity rate, C, of a heat exchanger is defined as follows [1]:
- for hot fluid:
- for cold fluid:
Obviously, either Ch or Cc will have a higher value. The one with a higher value is termed Cmax, and the one with lower value is termed Cmin. The capacity rate ratio is defined as the ratio between Cmin and Cmax. The capacity rate ratio is a dimensionless parameter, and it varies between 0 and 1:
Number of transfer units or NTU is a dimensionless parameter that accounts for heat exchanger area, material characteristics, fluid characteristics, flow rate, fouling, etc. Generally, the higher the NTU of the heat exchanger, the higher the rate of heat transfer would be. The NTU of the heat exchanger may be described as [1]
The effectiveness of the heat exchanger may be described as [1]:
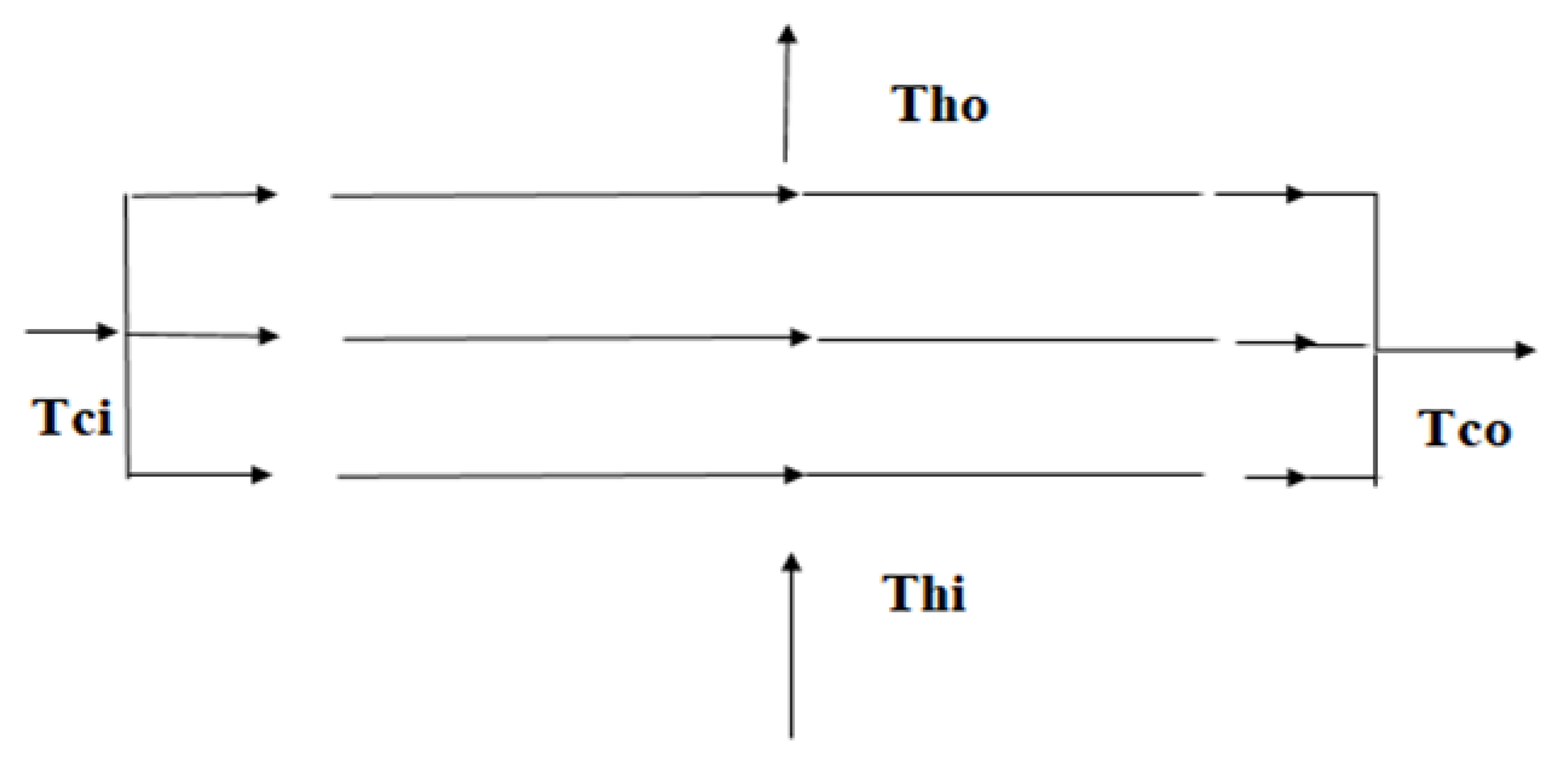
Consider a 1-row pure cross flow heat exchanger.
Applying energy balance to the heat exchanger yields:
q (heat lost by the hot fluid) = q (heat gained by cold fluid)
Recognize that external fluid is treated as the minimum capacity rate fluid. Likewise, it is arbitrarily considered that the external fluid is hot and the tube side fluid is cold. Reversing these conditions would still yield the same exact results:
Cmin [Th − Tho] = Cmax [Tco − Tci]
The effectiveness per row, ε’, is the same as overall effectiveness ε for a 1-row pure cross flow heat exchanger. Apply the effectiveness relationship [1]:
The effectiveness can also be determined directly if capacity rate ratio and the number of transfer units are known. Assuming the external fluid to be unmixed and the internal fluid to be mixed, effectiveness can be given as [1]
Note that, from Figure 2, there are two unknowns, namely Tho and Tco. Equations (7) and (8) can be used to solve for the unknown temperatures. These performance equations can be expressed in matrix form as follows:
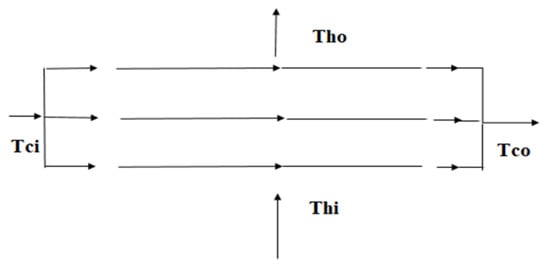
Figure 2.
1-row pure cross flow heat exchanger.
The unknown discharge temperatures can be determined by using the matrix inversion technique in MATLAB.
The same logic can be applied to a 2-row and a 3-row pure cross flow heat exchanger. For a 2-row pure cross flow heat exchanger, assuming external fluid as Cmin on per row basis, the performance equations can be given as follows:
In addition, for a 2-row pure cross flow heat exchanger, assuming external fluid as Cmax on a per row basis, performance equations can be given as follows:
Likewise, for a 3-row pure cross flow heat exchanger, assuming external fluid as Cmin on per row basis, the performance equations are given as:
Similarly, for a 3-row pure cross flow heat exchanger, assuming external fluid as Cmax on a per row basis, the performance equations are given as
Performance equations were derived for a pure cross flow heat exchanger for up to three tube rows. The performance equations can be developed for a pure cross flow heat exchanger having any number of tube rows. The resulting performance equations can be expressed in matrix form. Solving the matrix yields the unknown intermediary and outlet temperatures.
3. Performance Predictions
In this section, the performance of pure cross flow heat exchanger is expressed in terms of design graphs. Design graphs describe the performance of pure cross flow heat exchanger in terms of important dimensionless factors such as capacity rate ratio, NTU, and heat exchanger effectiveness. Curve fit equations were developed to understand the heat exchanger effectiveness in terms of capacity rate ratio and NTU.
In the development of design graphs, capacity ratio is varied between 0 and 1. The NTU of heat exchanger is arbitrarily varied between 0.1 and 10. This is the typical range observed in a commercial cross flow heat exchanger undergoing steady state sensible heat transfer. Once capacity rate ratio and NTU are known, the effectiveness per row can be estimated using Equation (9).
Appropriate inlet temperatures were assumed for the hot and cold fluid. A MATLAB model was established to solve the matrix and estimate the in-between and discharge temperatures. The overall effectiveness of the heat exchanger can be determined based on the inlet and discharge temperatures [1]:
It must be noted that the results obtained are independent of inlet temperatures assumed in the analysis. Figure 3, Figure 4 and Figure 5 and Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 describe the performance of a pure cross flow heat exchanger in terms of graphs, tables, and equations.
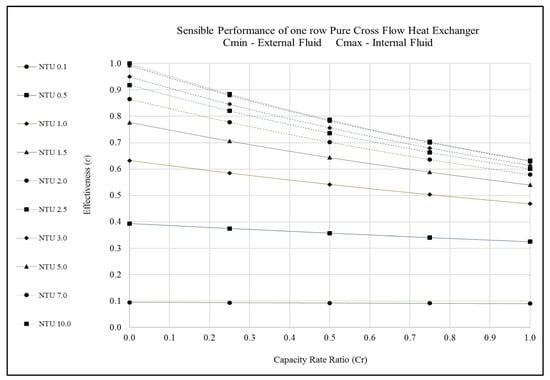
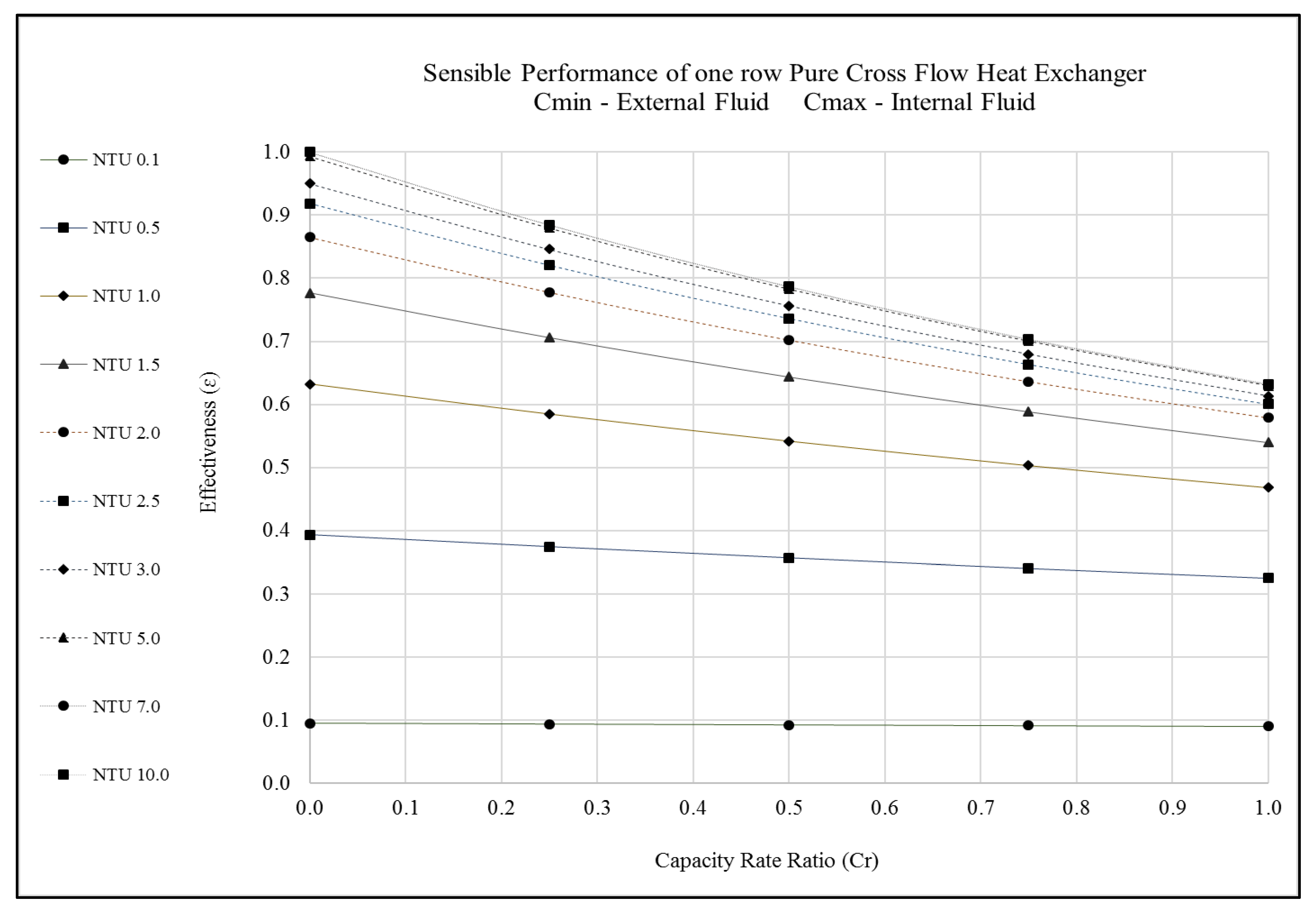
Figure 3.
Performance predictions of a 1-row pure cross flow heat exchanger.
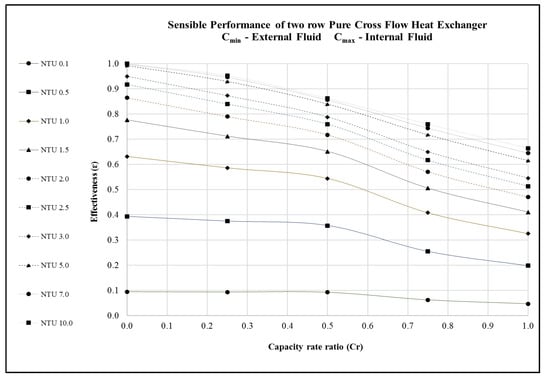
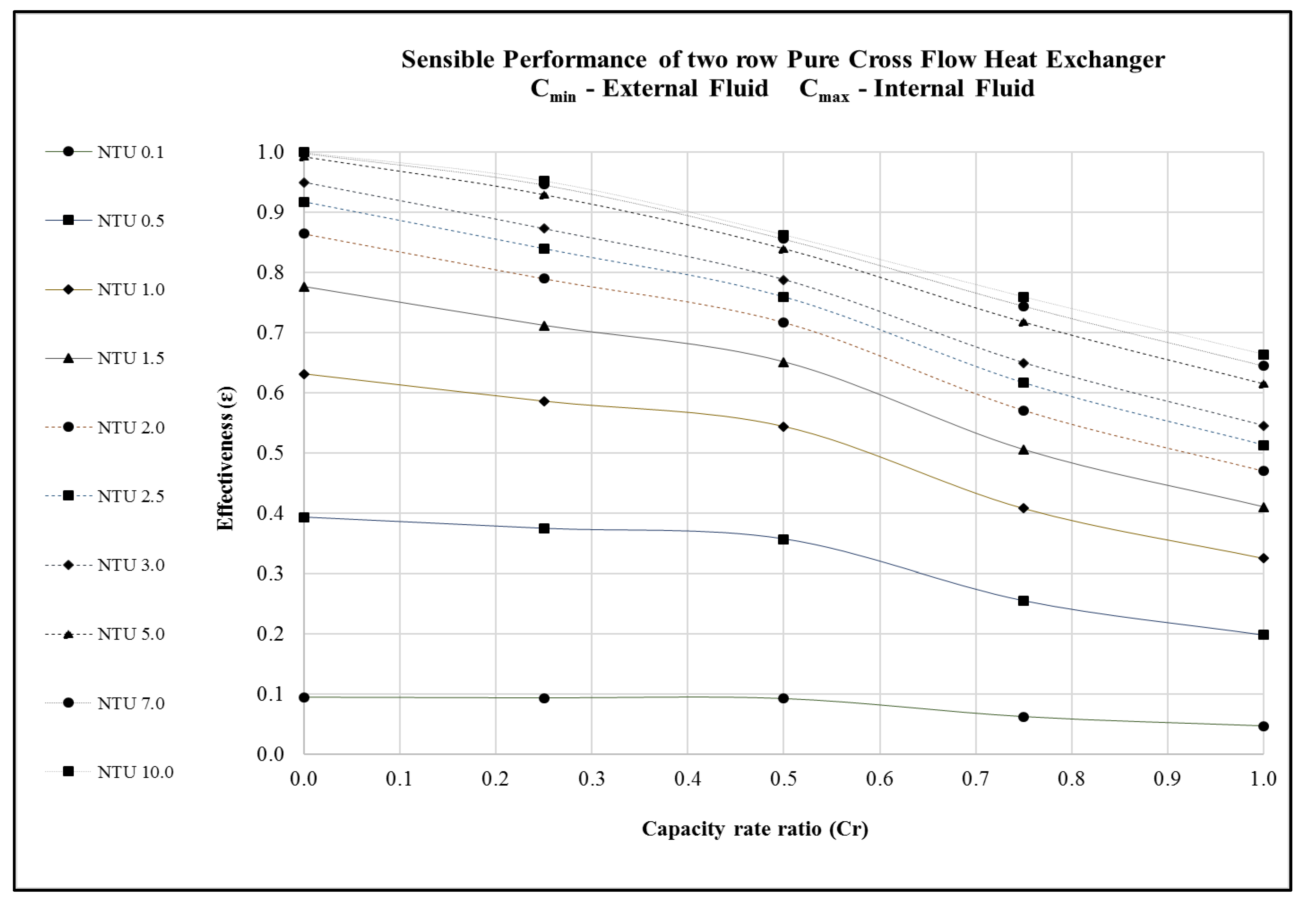
Figure 4.
Performance predictions of a 2-row pure cross flow heat exchanger undergoing sensible heat transfer.
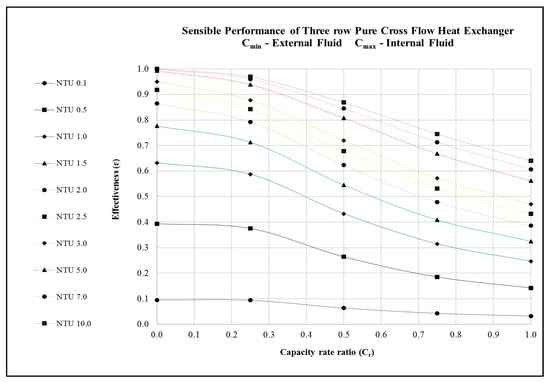
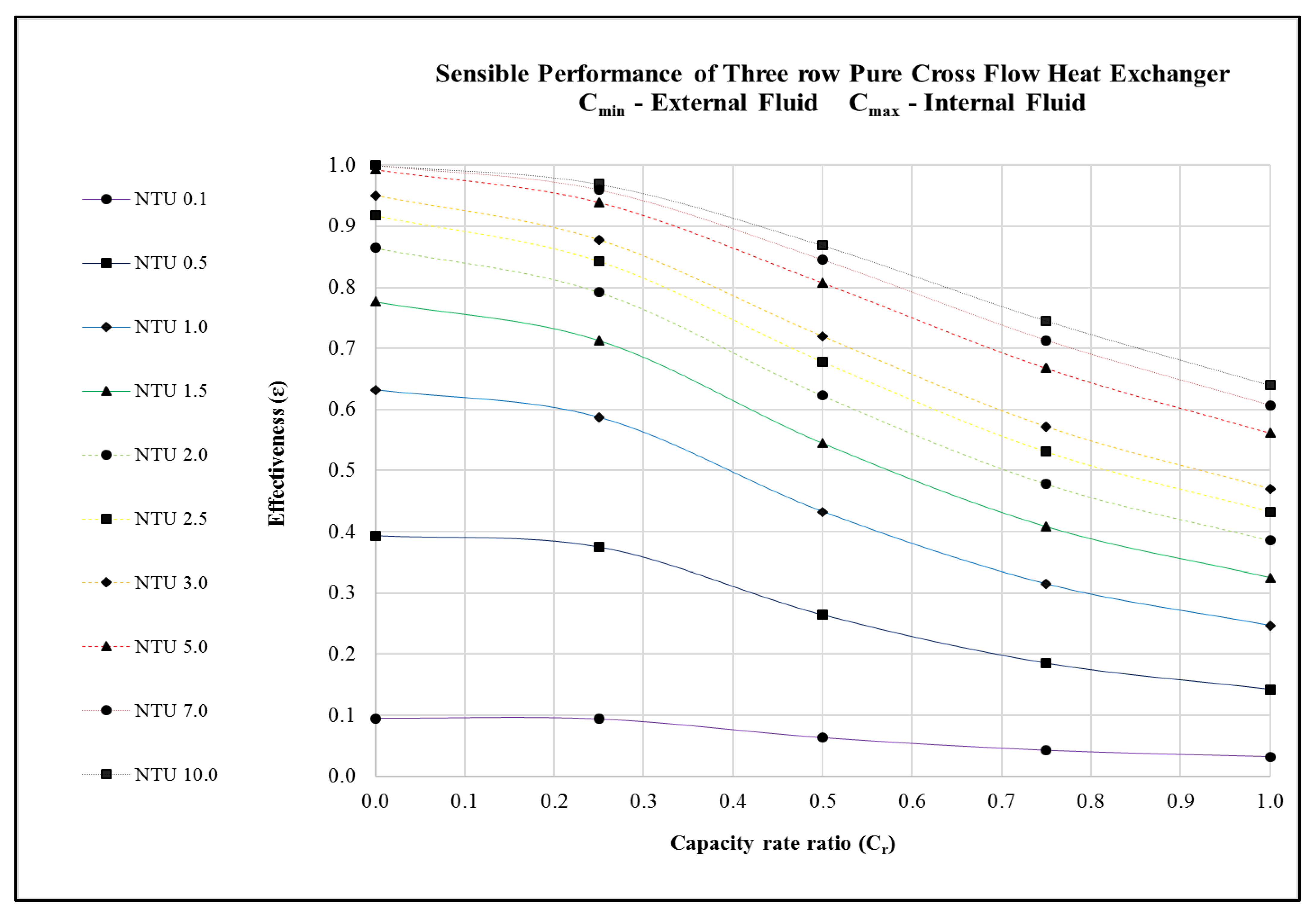
Figure 5.
Performance predictions of a 3-row pure cross flow heat exchanger undergoing sensible heat transfer.

Table 1.
Performance predictions of a 1-row pure cross flow heat exchanger in terms of dimensionless parameters. Cmin—External Fluid Cmax—Internal Fluid; sensible heat transfer.

Table 2.
Curve fit equations for effectiveness prediction—1-row pure cross flow heat exchanger. Cmin—External Fluid Cmax—Internal Fluid; sensible heat transfer.

Table 3.
Performance predictions of a 2-row pure cross flow heat exchanger in terms of dimensionless parameters. Cmin—External Fluid Cmax—Internal Fluid; sensible heat transfer.

Table 4.
Curve fit equations for effectiveness prediction—2-row pure cross flow heat exchanger. Cmin—External Fluid Cmax—Internal Fluid; sensible heat transfer.

Table 5.
Performance predictions of a 3-row pure cross flow heat exchanger in terms of dimensionless parameters. Cmin—External Fluid Cmax—Internal Fluid; sensible heat transfer.

Table 6.
Curve fit equations for effectiveness prediction—3-row pure cross flow heat exchanger. Cmin—External Fluid Cmax—Internal Fluid; sensible heat transfer.
In real life, since the inlet temperatures and the required discharge temperature are known, the engineers can compute the heat exchanger effectiveness (ε) using Equation (15). This means that, for a given application, number of transfer units (NTU) and capacity rate ratio (Cr) can be carefully chosen from the design graphs/tables. The detailed design of the heat exchanger may then be extrapolated from dimensionless parameters that govern the steady state sensible heat transfer.
NTU is a function of heat exchanger area (or) size. Therefore, selecting appropriate NTU will help the engineers to select a suitable heat exchanger surface area. In this context, it is very evident from Figure 3, Figure 4 and Figure 5 and Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 that for a given capacity rate ratio, increasing the NTU beyond 5.0, produces marginal improvement in the cross flow heat exchanger’s performance (effectiveness). This is against the common belief that larger surface area yields higher heat transfer. Choosing an ideal heat exchanger surface area (or NTU) may help to conserve material, weight, and price of the heat exchanger.
Likewise, capacity rate ratio accounts for the mass flow rate of fluids. Selecting an appropriate capacity rate ratio helps to conserve operating costs of the heat exchanger. The capacity rate ratio is directly linked with the pump power (required to move liquid through the tubes) and the fan power (required to push gases through the heat exchanger system). The information presented in Figure 3, Figure 4 and Figure 5 and Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 may help engineers in selecting a suitable capacity rate ratio that would minimize the operating cost of the heat exchanger.
Additionally, the production rate (throughput) in a plant will keep altering based on the demand. The operating set point of the heat exchanger will change when the production rate is altered. Figure 3, Figure 4 and Figure 5 and Table 1, Table 2, Table 3, Table 4, Table 5 and Table 6 can be used as a guide to understand whether the heat exchanger equipment can physically handle the new requirements. This piece of information can be critical in maintaining a steady production rate in the plant. Pushing the heat exchanger equipment beyond its capability will lead to unsteady heat exchanger output, fluctuating production, and monetary loss.
The design graphs, tables, and curve fit equations were obtained by assuming the external fluid as unmixed and the internal or tube side fluid as mixed. External fluid is treated as unmixed, as typically in a cross flow heat exchanger, there are fins in the external side that prevent mixing. However, due to geometry and various operating conditions, it is possible to have partially mixed conditions in the tube side. It is difficult to determine the fluid’s mixed condition as it requires spatial measurement of temperature.
The degree of mixedness or mixed fraction in the tube side may be given as
when
X = 0 the fluid flow is completely unmixed in the tube side;
X = 1 fluid flow is completely mixed in the tube side.
Table 1, Table 3, and Table 5 provide the effectiveness of pure cross flow heat exchanger where the external fluid is unmixed and the internal fluid is mixed (εu-m). The effectiveness of the heat exchanger assuming both external fluid and internal fluid as unmixed (εu-u) can be determined using Equation (17) [1]:
Considering Equation (16), the degree of mixedness in fluid flow is varied in steps between 0 and 1. For each instance, the effectiveness of the heat exchanger where the external fluid is completely unmixed and the internal fluid is partially mixed (εu-pm) is determined.
The error in heat exchanger effectiveness estimation may then be given as
The heat exchanger effectiveness correction factor can then be given as
For brevity, only the results from a 3-row pure cross flow heat exchanger are described in the Appendix A. Similar results have been observed for a pure cross flow heat exchanger subjected to multiple tube rows.
Understanding the impact of flow conditions in the heat exchanger’s output is important as the equipment’s performance strongly affects the performance of a heating/cooling system in process plants. It has been observed from the technical literature [13] that a flow rate deviation at the heat exchanger’s input initiates transient conditions, and the heat exchanger requires a finite time to regain back its steady state. This aspect is very significant as an unsteady heat exchanger output creates varying process conditions in the plant. The unsteady process condition affects the quality of the product and can lead to monetary loss. This aspect has been clearly seen in several nylon and polyester fiber manufacturing companies.
Laminar flow, fouling, uneven flow distribution, etc. can create partially mixed flow conditions on the tube side of the heat exchanger. As mentioned before, owing to the ease of analysis, it is a common practice to consider unmixed flow on the external side and mixed flow on the tube side of cross flow heat exchanger. This work analyzes the effect of partially mixed flow conditions on the steady state heat exchanger’s performance. The tables presented in the Appendix A, Table A1, Table A2, Table A3 and Table A4 describe the effectiveness of a heat exchanger at partially mixed conditions along with error and correction factors.
The results from this work clearly describe that mixed and partially mixed conditions on the tube side yield almost similar heat exchanger output. This finding is handy as the engineer can ignore this aspect while designing and operating a pure cross flow heat exchanger. It must be clearly noted that the finding is applicable only for pure cross flow heat exchanger configuration and that the results cannot be generalized for other heat exchanger types and configuration.
4. Conclusions
The work presented in this paper is comprised of two parts. The first part deals with expressing the performance of a pure cross flow heat exchanger in terms of dimensionless factors. Only sensible heat transfer at steady state conditions were considered for the performance analysis. The thermal performance of the heat exchanger was expressed in terms of graphs, tables, and curve fit equations.
In the performance analysis, it was observed that increasing the number of transfer units beyond a particular value does not significantly enhance the effectiveness of the heat exchanger. Likewise, for a given condition, it was observed that increasing the number of heat exchanger tube rows improves the performance (effectiveness) of the heat exchanger. Similarly, for a given condition, the best performance is obtained at a capacity rate ratio of zero.
In any finned-tube cross flow heat exchanger, it is normal to assume the external fluid flow as unmixed and tube side fluid flow as mixed. However, a partially mixed condition can occur in the tube side of the heat exchanger due to operating conditions, fouling, mal-distribution of flow, transient conditions, etc. The second part of this paper deals with the variation in the heat exchanger effectiveness due to partially mixed conditions in the tube side of the heat exchanger. It can be clearly seen that the error produced due to partially mixed conditions is very small and can be ignored for any practical purposes.
Author Contributions
Conceptualization, K.S.; formal analysis, K.S.; writing-original draft preparation, K.S.; writing-review and editing, K.S.; supervision, T.A.-M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Not Applicable.
Conflicts of Interest
The authors declare no conflict of interest.
Nomenclature
| Thi | The Inlet Temperature of the External Gas (K) |
| Th1 | The Discharged Temperature of the External Gas after 1st Row (K) |
| Th2 | The Discharged Temperature of the External Gas after 2nd Row (K) |
| Th3 | The Discharged Temperature of the External Gas after 3rd Row (K) |
| Tho | The Discharged Temperature of the External Gas after All Rows (K) |
| TCi | The Inlet Temperature of Chilled Water (K) |
| TC1 | Total Discharged of Chilled Water after the Three Tubes of the 1st Row (K) |
| TC2 | Total Discharged of Chilled Water after the Three Tubes of the 2nd Row (K) |
| TC3 | Total Discharged of Chilled Water after The Three Tubes of the 3rd Row (K) |
| TCo | The Discharged Temperature of Chilled Water after All Rows (K) |
| C | The Capacity Rate of the Heat Exchanger (W/K) |
| Ch | The Capacity Rate of the Heat Exchanger for Hot External Gas (W/K) |
| Cc | Capacity Rate of the Heat Exchanger for Cold Fluid (W/K) |
| Cr | Capacity Rate Ratio of the Heat Exchanger for The Chilled Water (Dimensionless) |
| The Capacity Rate Ratio Per Row (Dimensionless) | |
| Cmin | Minimum Capacity Rate of the Heat Exchanger Fluids (W/K) |
| Cmax | Maximum Capacity Rate of the Heat Exchanger Fluids (W/K) |
| NTU | Number of the Transmitted Units (Dimensionless) |
| The Number of the Transmitted Unit Per Row (Dimensionless) | |
| A | Cross Sectional Area of the Tube |
| U | Overall Heat Transfer Coefficients (W/K |
| q | Amount of Heat Transfer (W) |
| qmax | Maximum Amount of Heat Transfer (W) |
| The Effectiveness of the Heat Exchanger (Dimensionless) | |
| The Effectiveness of the Heat Exchanger Per Row (Dimensionless) | |
| The Effectiveness of heat exchanger unmixed (external side)—mixed (tube side) (Dimensionless) | |
| The Effectiveness of heat exchanger unmixed (external side)—unmixed (tube side) (Dimensionless) | |
| The Effectiveness of heat exchanger unmixed (external side)—partially mixed (tube side) (Dimensionless) | |
| F | Correction Factor (Dimensionless) |
| X | Degree of Mixedness (Dimensionless) |
Appendix A

Table A1.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid & mixed/partially mixed—tube side fluid; Cr = 0.25.
Table A1.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid & mixed/partially mixed—tube side fluid; Cr = 0.25.
| Cr | 0.25 | Cr | 0.25 | ||||
|---|---|---|---|---|---|---|---|
| NTU | 0.1 | NTU | 0.5 | ||||
| εu-m | 0.0940 | εu-m | 0.3750 | ||||
| εu-u | 0.0928 | εu-u | 0.3664 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.0928 | 0.987 | 1.3% | 0.0 | 0.3664 | 0.977 | 2.3% |
| 0.1 | 0.0929 | 0.988 | 1.2% | 0.1 | 0.3673 | 0.979 | 2.1% |
| 0.2 | 0.0931 | 0.990 | 1.0% | 0.2 | 0.3681 | 0.982 | 1.8% |
| 0.3 | 0.0932 | 0.991 | 0.9% | 0.3 | 0.3690 | 0.984 | 1.6% |
| 0.4 | 0.0933 | 0.992 | 0.8% | 0.4 | 0.3699 | 0.986 | 1.4% |
| 0.5 | 0.0934 | 0.993 | 0.7% | 0.5 | 0.3707 | 0.989 | 1.1% |
| 0.6 | 0.0935 | 0.995 | 0.5% | 0.6 | 0.3716 | 0.991 | 0.9% |
| 0.7 | 0.0937 | 0.996 | 0.4% | 0.7 | 0.3724 | 0.993 | 0.7% |
| 0.8 | 0.0938 | 0.997 | 0.3% | 0.8 | 0.3733 | 0.995 | 0.5% |
| 0.9 | 0.0939 | 0.999 | 0.1% | 0.9 | 0.3741 | 0.998 | 0.2% |
| 1.0 | 0.0940 | 1.000 | 0.0% | 1.0 | 0.3750 | 1.000 | 0.0% |
| NTU | 1.0 | NTU | 1.5 | ||||
| εu-m | 0.5871 | εu-m | 0.7135 | ||||
| εu-u | 0.5753 | εu-u | 0.7034 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.5753 | 0.980 | 2.0% | 0.0 | 0.7034 | 0.986 | 1.4% |
| 0.1 | 0.5765 | 0.982 | 1.8% | 0.1 | 0.7044 | 0.987 | 1.3% |
| 0.2 | 0.5777 | 0.984 | 1.6% | 0.2 | 0.7054 | 0.989 | 1.1% |
| 0.3 | 0.5789 | 0.986 | 1.4% | 0.3 | 0.7064 | 0.990 | 1.0% |
| 0.4 | 0.5800 | 0.988 | 1.2% | 0.4 | 0.7074 | 0.992 | 0.8% |
| 0.5 | 0.5812 | 0.990 | 1.0% | 0.5 | 0.7084 | 0.993 | 0.7% |
| 0.6 | 0.5824 | 0.992 | 0.8% | 0.6 | 0.7094 | 0.994 | 0.6% |
| 0.7 | 0.5836 | 0.994 | 0.6% | 0.7 | 0.7104 | 0.996 | 0.4% |
| 0.8 | 0.5848 | 0.996 | 0.4% | 0.8 | 0.7114 | 0.997 | 0.3% |
| 0.9 | 0.5859 | 0.998 | 0.2% | 0.9 | 0.7124 | 0.999 | 0.1% |
| 1.0 | 0.5871 | 1.000 | 0.0% | 1.0 | 0.7135 | 1.000 | 0.0% |
| NTU | 2.0 | NTU | 2.5 | ||||
| εu-m | 0.7922 | εu-m | 0.8432 | ||||
| εu-u | 0.7858 | εu-u | 0.8408 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.7858 | 0.992 | 0.8% | 0.0 | 0.8408 | 0.997 | 0.3% |
| 0.1 | 0.7864 | 0.993 | 0.7% | 0.1 | 0.8411 | 0.997 | 0.3% |
| 0.2 | 0.7871 | 0.994 | 0.6% | 0.2 | 0.8413 | 0.998 | 0.2% |
| 0.3 | 0.7877 | 0.994 | 0.6% | 0.3 | 0.8416 | 0.998 | 0.2% |
| 0.4 | 0.7883 | 0.995 | 0.5% | 0.4 | 0.8418 | 0.998 | 0.2% |
| 0.5 | 0.7890 | 0.996 | 0.4% | 0.5 | 0.8420 | 0.999 | 0.1% |
| 0.6 | 0.7896 | 0.997 | 0.3% | 0.6 | 0.8423 | 0.999 | 0.1% |
| 0.7 | 0.7903 | 0.998 | 0.2% | 0.7 | 0.8425 | 0.999 | 0.1% |
| 0.8 | 0.7909 | 0.998 | 0.2% | 0.8 | 0.8428 | 0.999 | 0.1% |
| 0.9 | 0.7915 | 0.999 | 0.1% | 0.9 | 0.8430 | 1.000 | 0.0% |
| 1.0 | 0.7922 | 1.000 | 0.0% | 1.0 | 0.8432 | 1.000 | 0.0% |
| NTU | 3.0 | NTU | 5.0 | ||||
| εu-m | 0.8775 | εu-m | 0.9396 | ||||
| εu-u | 0.8788 | εu-u | 0.9508 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.8788 | 1.001 | 0.1% | 0.0 | 0.9508 | 1.012 | 1.2% |
| 0.1 | 0.8787 | 1.001 | 0.1% | 0.1 | 0.9497 | 1.011 | 1.1% |
| 0.2 | 0.8786 | 1.001 | 0.1% | 0.2 | 0.9485 | 1.010 | 1.0% |
| 0.3 | 0.8784 | 1.001 | 0.1% | 0.3 | 0.9474 | 1.008 | 0.8% |
| 0.4 | 0.8783 | 1.001 | 0.1% | 0.4 | 0.9463 | 1.007 | 0.7% |
| 0.5 | 0.8782 | 1.001 | 0.1% | 0.5 | 0.9452 | 1.006 | 0.6% |
| 0.6 | 0.8780 | 1.001 | 0.1% | 0.6 | 0.9441 | 1.005 | 0.5% |
| 0.7 | 0.8779 | 1.000 | 0.0% | 0.7 | 0.9430 | 1.004 | 0.4% |
| 0.8 | 0.8778 | 1.000 | 0.0% | 0.8 | 0.9418 | 1.002 | 0.2% |
| 0.9 | 0.8777 | 1.000 | 0.0% | 0.9 | 0.9407 | 1.001 | 0.1% |
| 1.0 | 0.8775 | 1.000 | 0.0% | 1.0 | 0.9396 | 1.000 | 0.0% |
| NTU | 7.0 | NTU | 10.0 | ||||
| εu-m | 0.9593 | εu-m | 0.9692 | ||||
| εu-u | 0.9751 | εu-u | 0.9883 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.9751 | 1.016 | 1.6% | 0.0 | 0.9883 | 1.020 | 2.0% |
| 0.1 | 0.9735 | 1.015 | 1.5% | 0.1 | 0.9864 | 1.018 | 1.8% |
| 0.2 | 0.9719 | 1.013 | 1.3% | 0.2 | 0.9845 | 1.016 | 1.6% |
| 0.3 | 0.9703 | 1.012 | 1.2% | 0.3 | 0.9826 | 1.014 | 1.4% |
| 0.4 | 0.9688 | 1.010 | 1.0% | 0.4 | 0.9806 | 1.012 | 1.2% |
| 0.5 | 0.9672 | 1.008 | 0.8% | 0.5 | 0.9787 | 1.010 | 1.0% |
| 0.6 | 0.9656 | 1.007 | 0.7% | 0.6 | 0.9768 | 1.008 | 0.8% |
| 0.7 | 0.9640 | 1.005 | 0.5% | 0.7 | 0.9749 | 1.006 | 0.6% |
| 0.8 | 0.9624 | 1.003 | 0.3% | 0.8 | 0.9730 | 1.004 | 0.4% |
| 0.9 | 0.9609 | 1.002 | 0.2% | 0.9 | 0.9711 | 1.002 | 0.2% |
| 1.0 | 0.9593 | 1.000 | 0.0% | 1.0 | 0.9692 | 1.000 | 0.0% |

Table A2.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid and mixed/partially mixed—tube side fluid; Cr = 0.5.
Table A2.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid and mixed/partially mixed—tube side fluid; Cr = 0.5.
| Cr | 0.5 | Cr | 0.5 | ||||
|---|---|---|---|---|---|---|---|
| NTU | 0.1 | NTU | 0.5 | ||||
| εu-m | 0.0635 | εu-m | 0.2644 | ||||
| εu-u | 0.0627 | εu-u | 0.2587 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.0627 | 0.988 | 1.2% | 0.0 | 0.2587 | 0.978 | 2.2% |
| 0.1 | 0.0628 | 0.989 | 1.1% | 0.1 | 0.2592 | 0.981 | 1.9% |
| 0.2 | 0.0629 | 0.991 | 0.9% | 0.2 | 0.2598 | 0.983 | 1.7% |
| 0.3 | 0.0629 | 0.992 | 0.8% | 0.3 | 0.2604 | 0.985 | 1.5% |
| 0.4 | 0.0630 | 0.993 | 0.7% | 0.4 | 0.2610 | 0.987 | 1.3% |
| 0.5 | 0.0631 | 0.994 | 0.6% | 0.5 | 0.2615 | 0.989 | 1.1% |
| 0.6 | 0.0632 | 0.995 | 0.5% | 0.6 | 0.2621 | 0.991 | 0.9% |
| 0.7 | 0.0632 | 0.996 | 0.4% | 0.7 | 0.2627 | 0.994 | 0.6% |
| 0.8 | 0.0633 | 0.998 | 0.2% | 0.8 | 0.2632 | 0.996 | 0.4% |
| 0.9 | 0.0634 | 0.999 | 0.1% | 0.9 | 0.2638 | 0.998 | 0.2% |
| 1.0 | 0.0635 | 1.000 | 0.0% | 1.0 | 0.2644 | 1.000 | 0.0% |
| NTU | 1.0 | NTU | 1.5 | ||||
| εu-m | 0.4328 | εu-m | 0.5451 | ||||
| εu-u | 0.4240 | εu-u | 0.5366 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.4240 | 0.980 | 2.0% | 0.0 | 0.5366 | 0.984 | 1.6% |
| 0.1 | 0.4249 | 0.982 | 1.8% | 0.1 | 0.5375 | 0.986 | 1.4% |
| 0.2 | 0.4258 | 0.984 | 1.6% | 0.2 | 0.5383 | 0.988 | 1.2% |
| 0.3 | 0.4267 | 0.986 | 1.4% | 0.3 | 0.5391 | 0.989 | 1.1% |
| 0.4 | 0.4276 | 0.988 | 1.2% | 0.4 | 0.5400 | 0.991 | 0.9% |
| 0.5 | 0.4284 | 0.990 | 1.0% | 0.5 | 0.5408 | 0.992 | 0.8% |
| 0.6 | 0.4293 | 0.992 | 0.8% | 0.6 | 0.5417 | 0.994 | 0.6% |
| 0.7 | 0.4302 | 0.994 | 0.6% | 0.7 | 0.5425 | 0.995 | 0.5% |
| 0.8 | 0.4311 | 0.996 | 0.4% | 0.8 | 0.5434 | 0.997 | 0.3% |
| 0.9 | 0.4320 | 0.998 | 0.2% | 0.9 | 0.5442 | 0.998 | 0.2% |
| 1.0 | 0.4328 | 1.000 | 0.0% | 1.0 | 0.5451 | 1.000 | 0.0% |
| NTU | 2.0 | NTU | 2.5 | ||||
| εu-m | 0.6228 | εu-m | 0.6785 | ||||
| εu-u | 0.6165 | εu-u | 0.6752 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.6165 | 0.990 | 1.0% | 0.0 | 0.6752 | 0.995 | 0.5% |
| 0.1 | 0.6172 | 0.991 | 0.9% | 0.1 | 0.6755 | 0.996 | 0.4% |
| 0.2 | 0.6178 | 0.992 | 0.8% | 0.2 | 0.6759 | 0.996 | 0.4% |
| 0.3 | 0.6184 | 0.993 | 0.7% | 0.3 | 0.6762 | 0.997 | 0.3% |
| 0.4 | 0.6190 | 0.994 | 0.6% | 0.4 | 0.6765 | 0.997 | 0.3% |
| 0.5 | 0.6197 | 0.995 | 0.5% | 0.5 | 0.6768 | 0.998 | 0.2% |
| 0.6 | 0.6203 | 0.996 | 0.4% | 0.6 | 0.6772 | 0.998 | 0.2% |
| 0.7 | 0.6209 | 0.997 | 0.3% | 0.7 | 0.6775 | 0.999 | 0.1% |
| 0.8 | 0.6216 | 0.998 | 0.2% | 0.8 | 0.6778 | 0.999 | 0.1% |
| 0.9 | 0.6222 | 0.999 | 0.1% | 0.9 | 0.6781 | 1.000 | 0.0% |
| 1.0 | 0.6228 | 1.000 | 0.0% | 1.0 | 0.6785 | 1.000 | 0.0% |
| NTU | 3.0 | NTU | 5.0 | ||||
| εu-m | 0.7194 | εu-m | 0.8078 | ||||
| εu-u | 0.7194 | εu-u | 0.8196 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.7194 | 1.000 | 0.0% | 0.0 | 0.8196 | 1.015 | 1.5% |
| 0.1 | 0.7194 | 1.000 | 0.0% | 0.1 | 0.8184 | 1.013 | 1.3% |
| 0.2 | 0.7194 | 1.000 | 0.0% | 0.2 | 0.8172 | 1.012 | 1.2% |
| 0.3 | 0.7194 | 1.000 | 0.0% | 0.3 | 0.8160 | 1.010 | 1.0% |
| 0.4 | 0.7194 | 1.000 | 0.0% | 0.4 | 0.8149 | 1.009 | 0.9% |
| 0.5 | 0.7194 | 1.000 | 0.0% | 0.5 | 0.8137 | 1.007 | 0.7% |
| 0.6 | 0.7194 | 1.000 | 0.0% | 0.6 | 0.8125 | 1.006 | 0.6% |
| 0.7 | 0.7194 | 1.000 | 0.0% | 0.7 | 0.8113 | 1.004 | 0.4% |
| 0.8 | 0.7194 | 1.000 | 0.0% | 0.8 | 0.8102 | 1.003 | 0.3% |
| 0.9 | 0.7194 | 1.000 | 0.0% | 0.9 | 0.8090 | 1.001 | 0.1% |
| 1.0 | 0.7194 | 1.000 | 0.0% | 1.0 | 0.8078 | 1.000 | 0.0% |
| NTU | 7.0 | NTU | 10.0 | ||||
| εu-m | 0.8447 | εu-m | 0.8686 | ||||
| εu-u | 0.8649 | εu-u | 0.8975 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.8649 | 1.024 | 2.4% | 0.0 | 0.8975 | 1.033 | 3.3% |
| 0.1 | 0.8629 | 1.021 | 2.1% | 0.1 | 0.8946 | 1.030 | 3.0% |
| 0.2 | 0.8608 | 1.019 | 1.9% | 0.2 | 0.8917 | 1.027 | 2.7% |
| 0.3 | 0.8588 | 1.017 | 1.7% | 0.3 | 0.8888 | 1.023 | 2.3% |
| 0.4 | 0.8568 | 1.014 | 1.4% | 0.4 | 0.8860 | 1.020 | 2.0% |
| 0.5 | 0.8548 | 1.012 | 1.2% | 0.5 | 0.8831 | 1.017 | 1.7% |
| 0.6 | 0.8528 | 1.010 | 1.0% | 0.6 | 0.8802 | 1.013 | 1.3% |
| 0.7 | 0.8508 | 1.007 | 0.7% | 0.7 | 0.8773 | 1.010 | 1.0% |
| 0.8 | 0.8488 | 1.005 | 0.5% | 0.8 | 0.8744 | 1.007 | 0.7% |
| 0.9 | 0.8467 | 1.002 | 0.2% | 0.9 | 0.8715 | 1.003 | 0.3% |
| 1.0 | 0.8447 | 1.000 | 0.0% | 1.0 | 0.8686 | 1.000 | 0.0% |

Table A3.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid and mixed/partially mixed—tube side fluid; Cr = 0.75.
Table A3.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid and mixed/partially mixed—tube side fluid; Cr = 0.75.
| Cr | 0.75 | Cr | 0.75 | ||||
|---|---|---|---|---|---|---|---|
| NTU | 0.1 | NTU | 0.5 | ||||
| εu-m | 0.0428 | εu-m | 0.1851 | ||||
| εu-u | 0.0424 | εu-u | 0.1823 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.0424 | 0.992 | 0.0% | 0.0 | 0.1823 | 0.985 | 0.0% |
| 0.1 | 0.0425 | 0.993 | 0.1% | 0.1 | 0.1826 | 0.986 | 0.2% |
| 0.2 | 0.0425 | 0.994 | 0.2% | 0.2 | 0.1829 | 0.988 | 0.3% |
| 0.3 | 0.0425 | 0.994 | 0.2% | 0.3 | 0.1832 | 0.989 | 0.5% |
| 0.4 | 0.0426 | 0.995 | 0.3% | 0.4 | 0.1834 | 0.991 | 0.6% |
| 0.5 | 0.0426 | 0.996 | 0.4% | 0.5 | 0.1837 | 0.992 | 0.8% |
| 0.6 | 0.0426 | 0.997 | 0.5% | 0.6 | 0.1840 | 0.994 | 0.9% |
| 0.7 | 0.0427 | 0.998 | 0.6% | 0.7 | 0.1843 | 0.995 | 1.1% |
| 0.8 | 0.0427 | 0.998 | 0.6% | 0.8 | 0.1846 | 0.997 | 1.2% |
| 0.9 | 0.0427 | 0.999 | 0.7% | 0.9 | 0.1848 | 0.998 | 1.4% |
| 1.0 | 0.0428 | 1.000 | 0.8% | 1.0 | 0.1851 | 1.000 | 1.5% |
| NTU | 1.0 | NTU | 1.5 | ||||
| εu-m | 0.3148 | εu-m | 0.4085 | ||||
| εu-u | 0.3102 | εu-u | 0.4038 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.3102 | 0.985 | 0.0% | 0.0 | 0.4038 | 0.988 | 0.0% |
| 0.1 | 0.3107 | 0.987 | 0.1% | 0.1 | 0.4043 | 0.990 | 0.1% |
| 0.2 | 0.3111 | 0.988 | 0.3% | 0.2 | 0.4048 | 0.991 | 0.2% |
| 0.3 | 0.3116 | 0.990 | 0.4% | 0.3 | 0.4052 | 0.992 | 0.4% |
| 0.4 | 0.3121 | 0.991 | 0.6% | 0.4 | 0.4057 | 0.993 | 0.5% |
| 0.5 | 0.3125 | 0.993 | 0.7% | 0.5 | 0.4062 | 0.994 | 0.6% |
| 0.6 | 0.3130 | 0.994 | 0.9% | 0.6 | 0.4066 | 0.995 | 0.7% |
| 0.7 | 0.3134 | 0.996 | 1.0% | 0.7 | 0.4071 | 0.997 | 0.8% |
| 0.8 | 0.3139 | 0.997 | 1.2% | 0.8 | 0.4076 | 0.998 | 0.9% |
| 0.9 | 0.3144 | 0.999 | 1.3% | 0.9 | 0.4081 | 0.999 | 1.1% |
| 1.0 | 0.3148 | 1.000 | 1.5% | 1.0 | 0.4085 | 1.000 | 1.2% |
| NTU | 2.0 | NTU | 2.5 | ||||
| εu-m | 0.4780 | εu-m | 0.5308 | ||||
| εu-u | 0.4744 | εu-u | 0.5288 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.4744 | 0.992 | 0.0% | 0.0 | 0.5288 | 0.996 | 0.0% |
| 0.1 | 0.4747 | 0.993 | 0.1% | 0.1 | 0.5290 | 0.997 | 0.0% |
| 0.2 | 0.4751 | 0.994 | 0.2% | 0.2 | 0.5292 | 0.997 | 0.1% |
| 0.3 | 0.4755 | 0.995 | 0.2% | 0.3 | 0.5294 | 0.997 | 0.1% |
| 0.4 | 0.4758 | 0.995 | 0.3% | 0.4 | 0.5296 | 0.998 | 0.2% |
| 0.5 | 0.4762 | 0.996 | 0.4% | 0.5 | 0.5298 | 0.998 | 0.2% |
| 0.6 | 0.4766 | 0.997 | 0.5% | 0.6 | 0.5300 | 0.999 | 0.2% |
| 0.7 | 0.4769 | 0.998 | 0.5% | 0.7 | 0.5302 | 0.999 | 0.3% |
| 0.8 | 0.4773 | 0.998 | 0.6% | 0.8 | 0.5304 | 0.999 | 0.3% |
| 0.9 | 0.4777 | 0.999 | 0.7% | 0.9 | 0.5306 | 1.000 | 0.3% |
| 1.0 | 0.4780 | 1.000 | 0.8% | 1.0 | 0.5308 | 1.000 | 0.4% |
| NTU | 3.0 | NTU | 5.0 | ||||
| εu-m | 0.5717 | εu-m | 0.6679 | ||||
| εu-u | 0.5717 | εu-u | 0.6759 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.5717 | 1.000 | 0.0% | 0.0 | 0.6759 | 1.012 | 0.0% |
| 0.1 | 0.5717 | 1.000 | 0.0% | 0.1 | 0.6751 | 1.011 | 0.1% |
| 0.2 | 0.5717 | 1.000 | 0.0% | 0.2 | 0.6743 | 1.010 | 0.2% |
| 0.3 | 0.5717 | 1.000 | 0.0% | 0.3 | 0.6735 | 1.008 | 0.4% |
| 0.4 | 0.5717 | 1.000 | 0.0% | 0.4 | 0.6727 | 1.007 | 0.5% |
| 0.5 | 0.5717 | 1.000 | 0.0% | 0.5 | 0.6719 | 1.006 | 0.6% |
| 0.6 | 0.5717 | 1.000 | 0.0% | 0.6 | 0.6711 | 1.005 | 0.7% |
| 0.7 | 0.5717 | 1.000 | 0.0% | 0.7 | 0.6703 | 1.004 | 0.8% |
| 0.8 | 0.5717 | 1.000 | 0.0% | 0.8 | 0.6695 | 1.002 | 0.9% |
| 0.9 | 0.5717 | 1.000 | 0.0% | 0.9 | 0.6687 | 1.001 | 1.1% |
| 1.0 | 0.5717 | 1.000 | 0.0% | 1.0 | 0.6679 | 1.000 | 1.2% |
| NTU | 7.0 | NTU | 10.0 | ||||
| εu-m | 0.7131 | εu-m | 0.7456 | ||||
| εu-u | 0.7272 | εu-u | 0.7660 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.7272 | 1.020 | 0.0% | 0.0 | 0.7660 | 1.027 | 0.0% |
| 0.1 | 0.7258 | 1.018 | 0.2% | 0.1 | 0.7640 | 1.025 | 0.3% |
| 0.2 | 0.7244 | 1.016 | 0.4% | 0.2 | 0.7619 | 1.022 | 0.5% |
| 0.3 | 0.7230 | 1.014 | 0.6% | 0.3 | 0.7599 | 1.019 | 0.8% |
| 0.4 | 0.7216 | 1.012 | 0.8% | 0.4 | 0.7578 | 1.016 | 1.1% |
| 0.5 | 0.7202 | 1.010 | 1.0% | 0.5 | 0.7558 | 1.014 | 1.3% |
| 0.6 | 0.7187 | 1.008 | 1.2% | 0.6 | 0.7537 | 1.011 | 1.6% |
| 0.7 | 0.7173 | 1.006 | 1.4% | 0.7 | 0.7517 | 1.008 | 1.9% |
| 0.8 | 0.7159 | 1.004 | 1.6% | 0.8 | 0.7496 | 1.005 | 2.1% |
| 0.9 | 0.7145 | 1.002 | 1.8% | 0.9 | 0.7476 | 1.003 | 2.4% |
| 1.0 | 0.7131 | 1.000 | 1.9% | 1.0 | 0.7456 | 1.000 | 2.7% |

Table A4.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid and mixed/partially mixed—tube side fluid; Cr = 1.0.
Table A4.
Effectiveness correction factor “F” and Error in effectiveness estimation—3-row pure cross flow heat exchanger. Unmixed—external fluid and mixed/partially mixed—tube side fluid; Cr = 1.0.
| Cr | 1.0 | Cr | 1.0 | ||||
|---|---|---|---|---|---|---|---|
| NTU | 0.1 | NTU | 0.5 | ||||
| εu-m | 0.0323 | εu-m | 0.1423 | ||||
| εu-u | 0.0321 | εu-u | 0.1407 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.0321 | 0.994 | 0.6% | 0.0 | 0.1407 | 0.988 | 1.2% |
| 0.1 | 0.0321 | 0.995 | 0.5% | 0.1 | 0.1408 | 0.990 | 1.0% |
| 0.2 | 0.0321 | 0.995 | 0.5% | 0.2 | 0.1410 | 0.991 | 0.9% |
| 0.3 | 0.0321 | 0.996 | 0.4% | 0.3 | 0.1412 | 0.992 | 0.8% |
| 0.4 | 0.0321 | 0.996 | 0.4% | 0.4 | 0.1413 | 0.993 | 0.7% |
| 0.5 | 0.0322 | 0.997 | 0.3% | 0.5 | 0.1415 | 0.994 | 0.6% |
| 0.6 | 0.0322 | 0.998 | 0.2% | 0.6 | 0.1417 | 0.995 | 0.5% |
| 0.7 | 0.0322 | 0.998 | 0.2% | 0.7 | 0.1418 | 0.997 | 0.3% |
| 0.8 | 0.0322 | 0.999 | 0.1% | 0.8 | 0.1420 | 0.998 | 0.2% |
| 0.9 | 0.0322 | 0.999 | 0.1% | 0.9 | 0.1422 | 0.999 | 0.1% |
| 1.0 | 0.0323 | 1.000 | 0.0% | 1.0 | 0.1423 | 1.000 | 0.0% |
| NTU | 1.0 | NTU | 1.5 | ||||
| εu-m | 0.2469 | εu-m | 0.3255 | ||||
| εu-u | 0.2441 | εu-u | 0.3226 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.2441 | 0.989 | 1.1% | 0.0 | 0.3226 | 0.991 | 0.9% |
| 0.1 | 0.2444 | 0.990 | 1.0% | 0.1 | 0.3229 | 0.992 | 0.8% |
| 0.2 | 0.2446 | 0.991 | 0.9% | 0.2 | 0.3231 | 0.993 | 0.7% |
| 0.3 | 0.2449 | 0.992 | 0.8% | 0.3 | 0.3234 | 0.994 | 0.6% |
| 0.4 | 0.2452 | 0.993 | 0.7% | 0.4 | 0.3237 | 0.995 | 0.5% |
| 0.5 | 0.2455 | 0.994 | 0.6% | 0.5 | 0.3240 | 0.995 | 0.5% |
| 0.6 | 0.2458 | 0.995 | 0.5% | 0.6 | 0.3243 | 0.996 | 0.4% |
| 0.7 | 0.2460 | 0.997 | 0.3% | 0.7 | 0.3246 | 0.997 | 0.3% |
| 0.8 | 0.2463 | 0.998 | 0.2% | 0.8 | 0.3249 | 0.998 | 0.2% |
| 0.9 | 0.2466 | 0.999 | 0.1% | 0.9 | 0.3252 | 0.999 | 0.1% |
| 1.0 | 0.2469 | 1.000 | 0.0% | 1.0 | 0.3255 | 1.000 | 0.0% |
| NTU | 2.0 | NTU | 2.5 | ||||
| εu-m | 0.3859 | εu-m | 0.4330 | ||||
| εu-u | 0.3835 | εu-u | 0.4317 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.3835 | 0.994 | 0.6% | 0.0 | 0.4317 | 0.997 | 0.3% |
| 0.1 | 0.3837 | 0.994 | 0.6% | 0.1 | 0.4318 | 0.997 | 0.3% |
| 0.2 | 0.3840 | 0.995 | 0.5% | 0.2 | 0.4319 | 0.998 | 0.2% |
| 0.3 | 0.3842 | 0.996 | 0.4% | 0.3 | 0.4321 | 0.998 | 0.2% |
| 0.4 | 0.3844 | 0.996 | 0.4% | 0.4 | 0.4322 | 0.998 | 0.2% |
| 0.5 | 0.3847 | 0.997 | 0.3% | 0.5 | 0.4323 | 0.998 | 0.2% |
| 0.6 | 0.3849 | 0.998 | 0.2% | 0.6 | 0.4325 | 0.999 | 0.1% |
| 0.7 | 0.3851 | 0.998 | 0.2% | 0.7 | 0.4326 | 0.999 | 0.1% |
| 0.8 | 0.3854 | 0.999 | 0.1% | 0.8 | 0.4327 | 0.999 | 0.1% |
| 0.9 | 0.3856 | 0.999 | 0.1% | 0.9 | 0.4328 | 1.000 | 0.0% |
| 1.0 | 0.3859 | 1.000 | 0.0% | 1.0 | 0.4330 | 1.000 | 0.0% |
| NTU | 7.0 | NTU | 10.0 | ||||
| εu-m | 0.6069 | εu-m | 0.6402 | ||||
| εu-u | 0.6167 | εu-u | 0.6540 | ||||
| X | εu-pm | F | Error | X | εu-pm | F | Error |
| 0.0 | 0.6167 | 1.016 | 1.6% | 0.0 | 0.6540 | 1.021 | 2.1% |
| 0.1 | 0.6157 | 1.014 | 1.4% | 0.1 | 0.6526 | 1.019 | 1.9% |
| 0.2 | 0.6148 | 1.013 | 1.3% | 0.2 | 0.6512 | 1.017 | 1.7% |
| 0.3 | 0.6138 | 1.011 | 1.1% | 0.3 | 0.6499 | 1.015 | 1.5% |
| 0.4 | 0.6128 | 1.010 | 1.0% | 0.4 | 0.6485 | 1.013 | 1.3% |
| 0.5 | 0.6118 | 1.008 | 0.8% | 0.5 | 0.6471 | 1.011 | 1.1% |
| 0.6 | 0.6108 | 1.006 | 0.6% | 0.6 | 0.6457 | 1.009 | 0.9% |
| 0.7 | 0.6099 | 1.005 | 0.5% | 0.7 | 0.6444 | 1.006 | 0.6% |
| 0.8 | 0.6089 | 1.003 | 0.3% | 0.8 | 0.6430 | 1.004 | 0.4% |
| 0.9 | 0.6079 | 1.002 | 0.2% | 0.9 | 0.6416 | 1.002 | 0.2% |
| 1.0 | 0.6069 | 1.000 | 0.0% | 1.0 | 0.6402 | 1.000 | 0.0% |
References
- Silaipillayarputhur, K.; Idem, S. A general Matrix Approach to model steady state performance of cross flow heat exchangers. Heat Transf. Eng. 2013, 34, 338–348. [Google Scholar] [CrossRef]
- Zhang, K.; Li, M.J.; Liu, H.; Xiong, J.G.; He, Y.L. A general and rapid method to evaluate the effect of flow mal-distribution on the performance of heat exchangers. Int. J. Therm. Sci. 2021, 170, 107152. [Google Scholar] [CrossRef]
- Ishaque, S.; Kim, M.H. Numerical modeling of an outdoor unit heat exchanger for residential heat pump systems with non-uniform air flow and refrigerant distribution. Int. J. Heat Mass Transf. 2021, 175, 121323. [Google Scholar] [CrossRef]
- Hao, J.; Chen, Q.; Li, X.; Zhao, T. A correction factor based general resistance formula for heat exchanger design and performance analysis. J. Therm. Sci. 2021, 30, 892–901. [Google Scholar] [CrossRef]
- Jouhara, H.; Almahmoud, S.; Brough, D.; Delpech, B.; Chauhan, A.; Ahmad, L.; Serey, N. Experimental and theoretical investigation of the performance of an air to water multi pass heat pipe based heat exchanger. Energy 2021, 219, 119624. [Google Scholar] [CrossRef]
- Unger, S.; Beyer, M.; Pietruske, H.; Szalinski, L.; Hampel, U. Air side heat transfer and flow characteristics of additively manufactured finned tubes in staggered arrangement. Int. J. Therm. Sci. 2021, 161, 106752. [Google Scholar] [CrossRef]
- Khan, M.S.; Zou, R.; Yu, A. Computational simulation of air-side heat transfer and pressure drop performance in staggered mannered twisted oval tube bundle operating in crossflow. Int. J. Therm. Sci. 2021, 161, 106748. [Google Scholar] [CrossRef]
- Geete, A.; Mahajan, A.; Shinde, A.; Modak, D. Experimental exergy and entransy analyses on designed and fabricated crossflow heat exchanger. Heat Transf. 2021, 50, 1758–1775. [Google Scholar] [CrossRef]
- Narkhede, S.; Sur, A. Performance prediction of hollow micro-lattice cross flow heat exchanger using a numerical approach. Int. J. Ambient. Energy 2021, 1–18. [Google Scholar] [CrossRef]
- Choudhary, A.; Kumar, M.; Patil, A.K.; Chamoli, S. Enhanced thermal and fluid flow performance of cross flow tube bank with perforated splitter plate. Exp. Heat Transf. 2021, 34, 329–341. [Google Scholar] [CrossRef]
- Bury, T.; Hanuszkiewicz-Drapala, M. Impact of the heat transfer coefficient determination method on the simulation of the operation of fin and tube cross flow heat exchangers at a non-uniform inflow of mediums. Heat Transf. Eng. 2021, 42, 191–204. [Google Scholar] [CrossRef]
- Zhao, L.; Wang, B.; Wang, J.; Zhu, Z.; Li, T.; Guo, B.; Zhang, J.; Zhang, H.; Yang, Z. Effect of non-uniform airflow on the performance of a parallel-flow heat exchanger considering internal fluid distribution—Simulation studies and its experimental validation. Appl. Therm. Eng. 2020, 180, 115685. [Google Scholar] [CrossRef]
- Gao, T.; Geer, J.; Sammakia, B. Review and analysis of cross flow heat exchanger transient modeling for flow rate and temperature variations. J. Therm. Sci. Eng. Appl. 2015, 7, 041017. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).