Design of Gerotor Pump and Influence on Oil Supply System for Hybrid Transmission
Abstract
:1. Introduction
- (1)
- Hydraulic system in Prius hybrid system
- (2)
- Hydraulic system in Malibu hybrid system
- (3)
- Hydraulic system in Lexus hybrid system
- (4)
- Hydraulic system in Trumpchi hybrid system
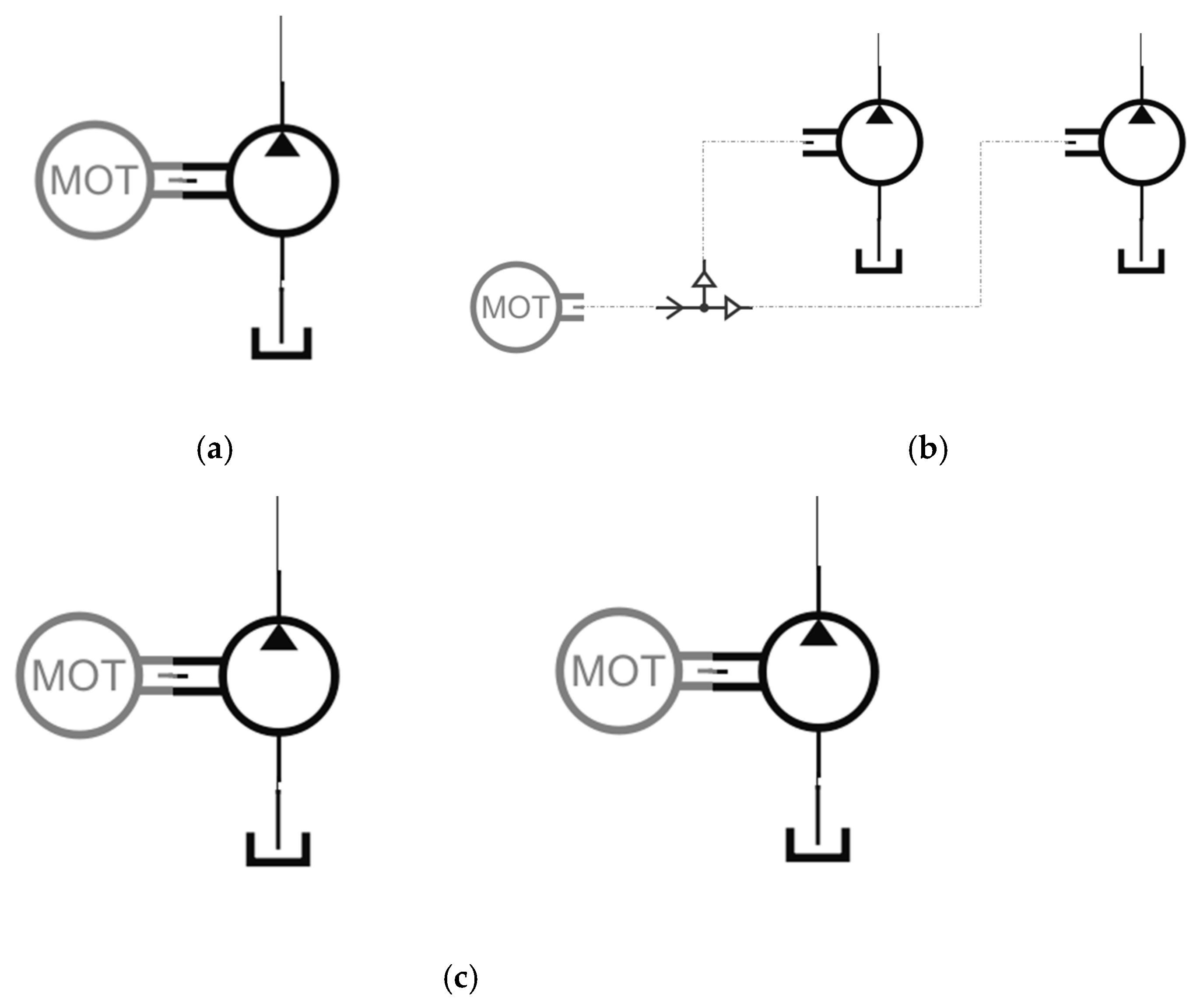
2. Design of Gerotor Pump Oil Supply System for Hybrid Transmission
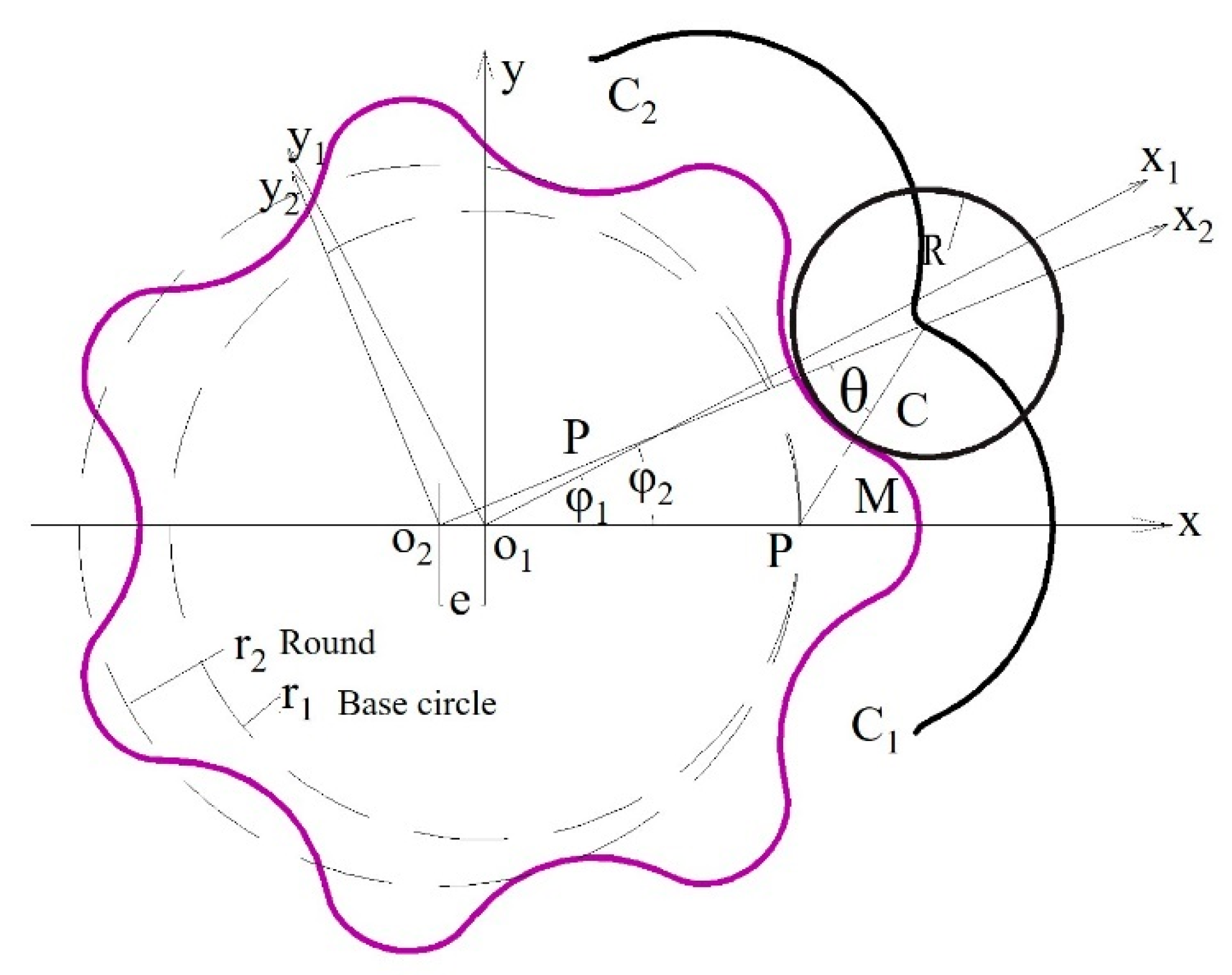
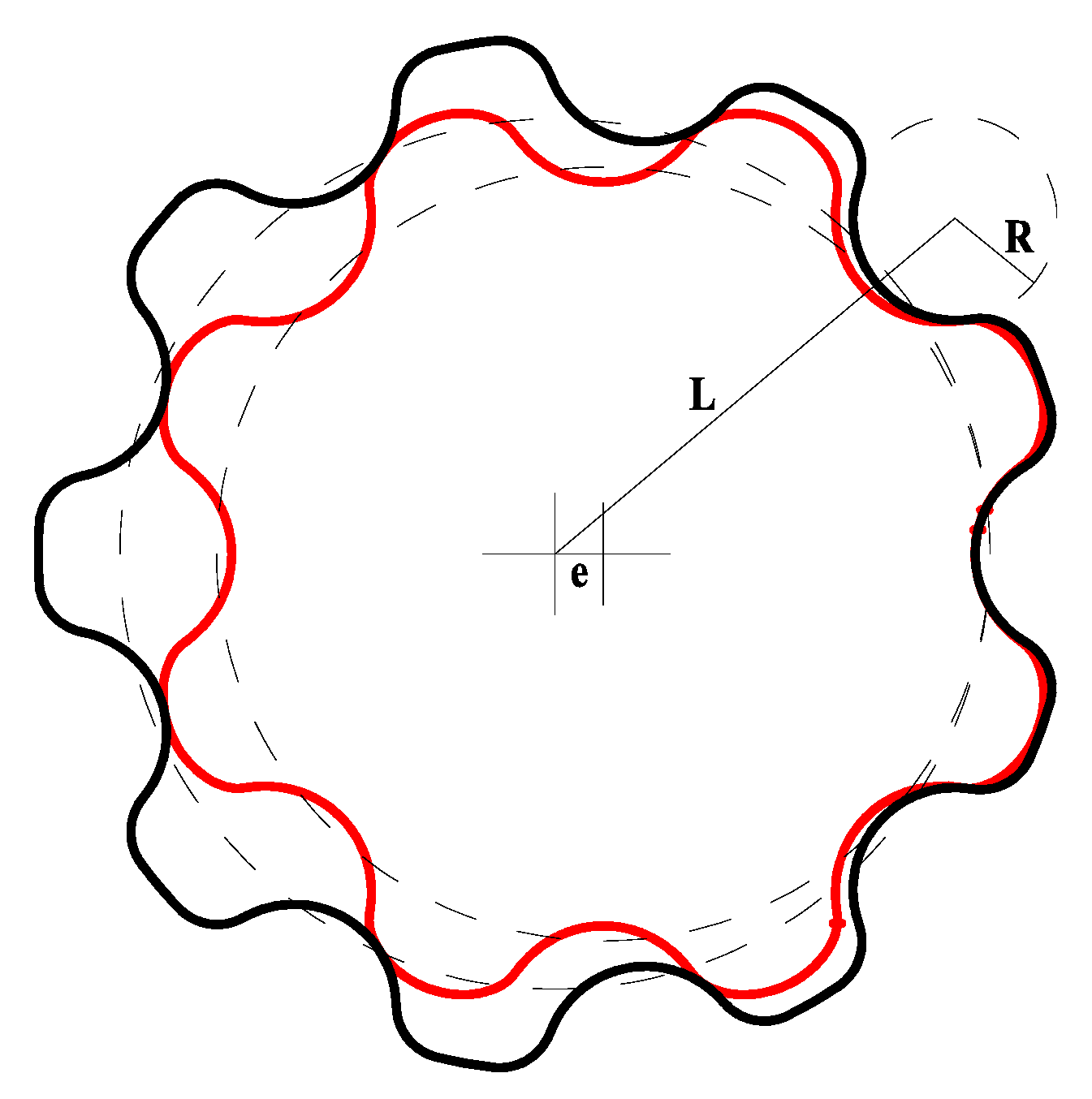
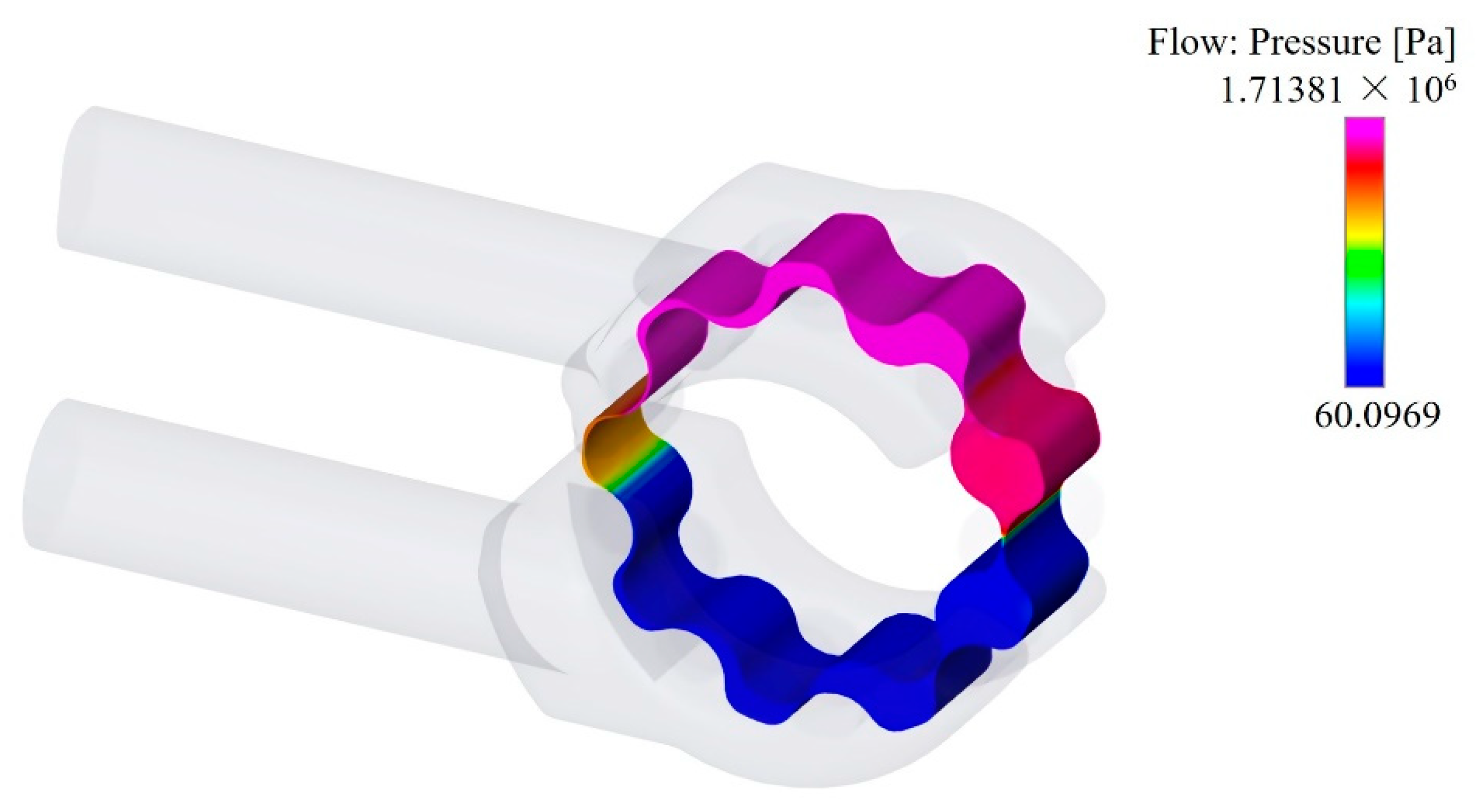
3. Influence of Gerotor Pump Parameters on Oil Supply System
4. Conclusions
- (1)
- A gerotor pump was designed. The tooth profile was analyzed and designed in line with the requirements of the hydraulic system for hybrid transmission;
- (2)
- NSGA-II algorithm was employed to optimize the design of tooth profile parameters according to the mathematical model of instantaneous flow. The parameters of the gerotor pump can be determined;
- (3)
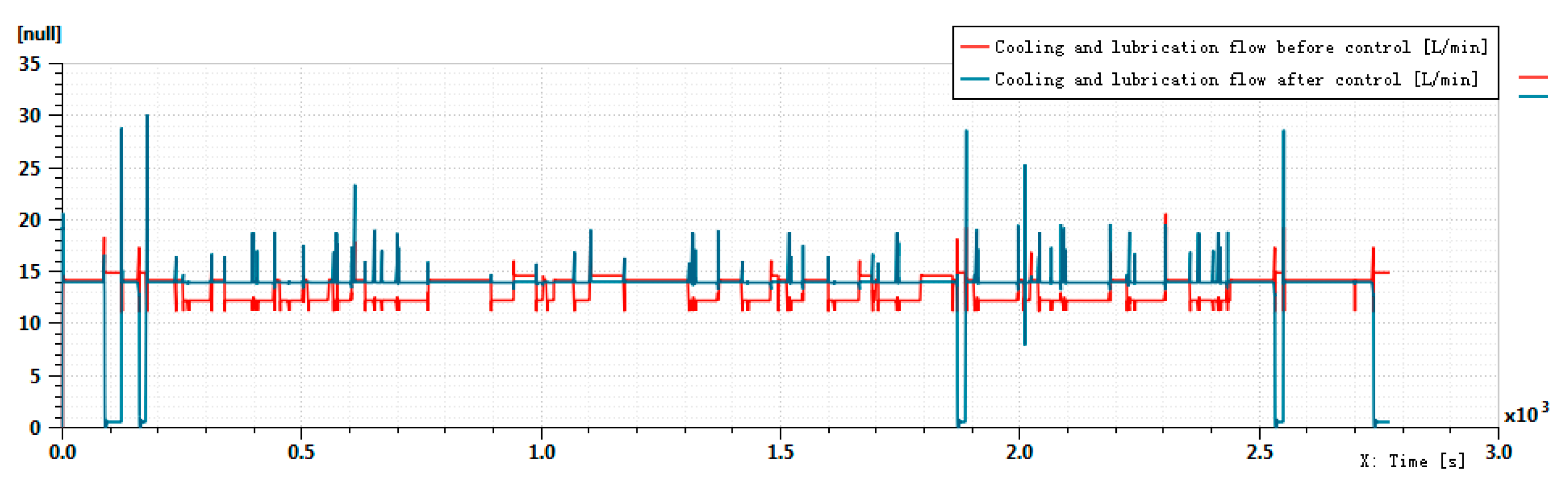
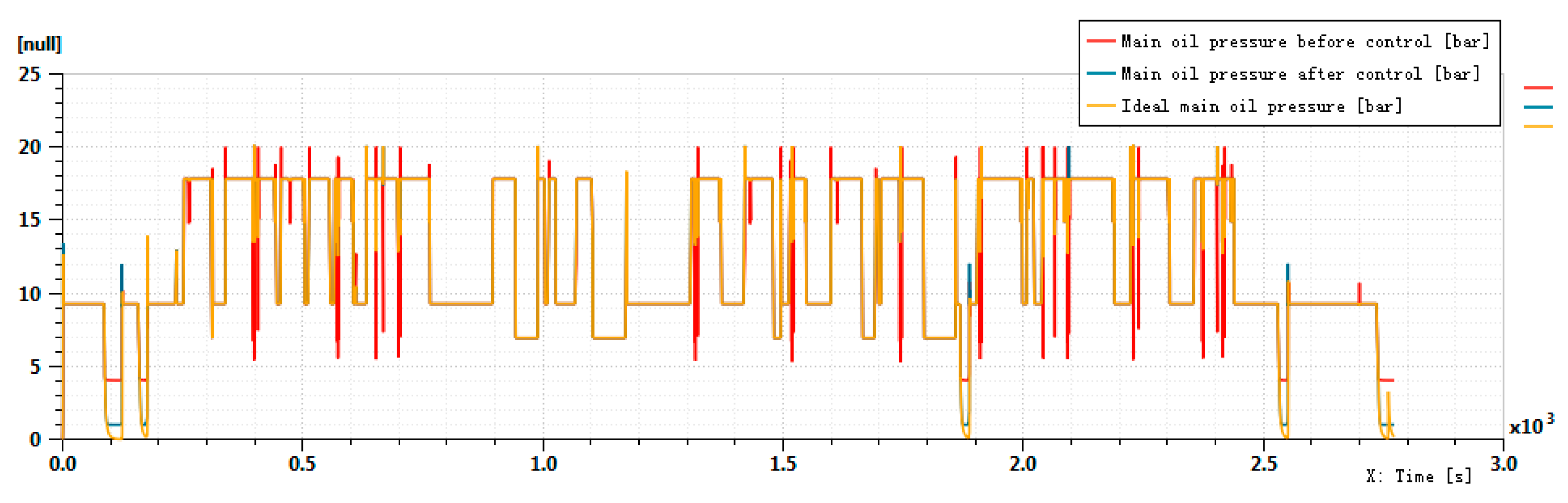
- Based on the AMESim platform, a PD control strategy was employed to develop the oil pump speed control model of the oil supply system. In addition, the influence of the designed gerotor pump on the performance of the oil supply system was simulated;
- (4)
- Prototypes were made, an oil pump test platform was built, and oil pump unit tests were conducted to confirm the rationality of the oil pump design and simulation reliability. Besides, the designed oil pump can meet the functional requirements of a hybrid transmission.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Tang, X.; Zhang, D.; Liu, T.; Khajepour, A.; Yu, H.; Wang, H. Research on the energy control of a dual-motor hybrid vehicle during engine start-stop process. Energy 2019, 166, 1181–1193. [Google Scholar] [CrossRef]
- Fletcher, T.; Thring, R.; Watkinson, M. An Energy Management Strategy to concurrently optimise fuel consumption & PEM fuel cell lifetime in a hybrid vehicle. Int. J. Hydrog. Energy 2016, 41, 21503–21515. [Google Scholar]
- Xu, X.; Dong, P.; Liu, Y.; Zhang, H. Progress in automotive transmission technology. Automot. Innov. 2018, 1, 187–210. [Google Scholar] [CrossRef] [Green Version]
- Chung, C.T.; Wu, C.H.; Hung, Y.H. Effects of electric circulation on the energy efficiency of the power split e-CVT hybrid systems. Energies 2018, 11, 2342. [Google Scholar] [CrossRef] [Green Version]
- Guo, W.; Xu, X.; Liu, X. Cooperative control of P2 hybrid system. J. China Highw. 2018, 31, 308–316. [Google Scholar]
- Zhang, Y.; Yang, Y.; Li, L. Brake energy recovery strategy for hybrid vehicles with dual-motor hybrid configuration. China Mech. Eng. 2019, 30, 1631–1637. [Google Scholar]
- Kanayama, T.; Yanagida, E.; Kano, S. Development of New Hybrid System for Mid-Size SUV. SAE Int. J. Adv. Curr. Pract. Mobil. 2020, 2, 3356–3363. [Google Scholar]
- Mayet, C.; Welles, J.; Bouscayrol, A.; Hofman, T.; Lemaire-Semail, B. Influence of a CVT on the fuel consumption of a parallel medium-duty electric hybrid truck. Math. Comput. Simulat. 2019, 158, 120–129. [Google Scholar] [CrossRef]
- Taniguchi, M.; Yashiro, T.; Takizawa, K. Development of New Hybrid Transaxle for Compact-Class Vehicles; SAE Technical Papers 2016-01-1163; SAE: Warrendale, PA, USA, 2016. [Google Scholar]
- Du, A.; Liu, K.; Zhu, Z. Structural optimization of single-mode composite power split hybrid power system. China Mech. Eng. 2015, 26, 2976–2981. [Google Scholar]
- Lian, J.; Han, H.; Li, L. Research on control strategy of hybrid electric vehicle based on optimal transmission system efficiency. J. Dalian Univ. Technol. 2013, 53, 666–670. [Google Scholar]
- Miyachi, E.; Ishiguro, M.; Mizumoto, K. Development of Electric Oil Pump; SAE Technical Papers 2006-01-1595; SAE: Warrendale, PA, USA, 2006. [Google Scholar]
- Ma, K.; Sun, D.; Sun, G.; Kan, Y.; Shi, J. Design and efficiency analysis of wet dual clutch transmission decentralised pump-controlled hydraulic system. Mech. Mach. Theory 2020, 154, 104003. [Google Scholar] [CrossRef]
- Liu, Y.; Zhou, Y.; Qu, D.; Zhang, F.; Bao, X. Electric oil pump design of hybrid continuously variable transmission. IET Electr. Power App. 2019, 13, 1089–1096. [Google Scholar] [CrossRef]
- Suzuki, Y.; Nishimine, A.; Baba, S.; Miyasaka, K.; Tsuchida, M.; Endo, H.; Yamamura, N.; Miyazaki, T. Development of New Plug-in Hybrid Transaxle Forcompact-Class Vehicles; SAE Technical Papers 2017-01-1151; SAE: Warrendale, PA, USA, 2017. [Google Scholar]
- Nozawa, N.; Maekawa, T.; Nozawa, S.; Asakura, K. Development of power control unit for compact-class vehicle. SAE Int. J. Passeng. Cars-Electron. Electr. 2009, 2, 376–382. [Google Scholar] [CrossRef]
- Fushiki, S. The new generation front wheel drive hybrid system. SAE Int. J. Altern. Powertrains 2016, 5, 109–114. [Google Scholar] [CrossRef]
- Furukawa, T.; Lbaraki, R.; Kimura, H.; Baba, S.; Tsuchida, M.; Mizutani, T.; Endo, H.; Kimura, H. Development of New Hybrid Transaxle for Subcompact-Class Vehicles; SAE Technical Papers 2012-01-0623; SAE: Warrendale, PA, USA, 2012. [Google Scholar]
- Ichikawa, S.; Takeuchi, H.; Fukuda, S.; Tomita, Y.; Suzuki, Y.; Hirasawa, T. Development of new plug-in hybrid system for compact-class vehicle. SAE Int. J. Altern. Powertrains 2017, 6, 95–102. [Google Scholar] [CrossRef]
- Xu, Q.; Sun, J.; Ye, X.; Wang, Z.; Liu, X.; Wang, H. Optimized parameters sizing between EVT and THS used for hybrid electric vehicles. In Proceedings of the 2017 IEEE Transportation Electrification Conference and Expo, Asia-Pacific (ITEC Asia-Pacific), Harbin, China, 7–10 August 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 1–5. [Google Scholar]
- Zhang, X.; Li, S.E.; Peng, H.; Sun, J. Design of multimode power-split hybrid vehicles—A case study on the voltec powertrain system. IEEE Trans. Veh. Technol. 2016, 65, 4790–4801. [Google Scholar] [CrossRef]
- Kim, N.; Choi, S.; Jeong, J.; Vijayagopal, R.; Stutenberg, K.; Rousseau, A. Vehicle level control analysis for Voltec powertrain. World Electr. Veh. J. 2018, 9, 29. [Google Scholar] [CrossRef] [Green Version]
- Okuda, K.; Yasuda, Y.; Adachi, M.; Tabata, A.; Suzuki, H.; Takagi, K.; Atarashi, T.; Horie, R. Development of multi stage hybrid transmission. SAE Int. J. Altern. Powertrains 2017, 6, 77–83. [Google Scholar] [CrossRef]
- Zhang, X.; Zhang, A.; Duan, X. Development and Application of Guangqi Electric and Mechanical Coupled System (G-MC). J. Chongqing Univ. Technol. 2019, 33, 50–55. [Google Scholar]
- Ni, J.; Han, B. Design and dynamic simulation of hydraulic system of hybrid transmission. J. Adv. Mech. Des. Syst. 2011, 8, 121–123. [Google Scholar]
- Schweiger, W.; Schoefmann, W.; Vacca, A. Gerotor pumps for automotive drivetrain applications: A multi domain simulation approach. SAE Int. J. Passeng. Cars-Mech. Syst. 2011, 4, 1358–1376. [Google Scholar] [CrossRef]
- Qu, D.; Luo, W.; Liu, Y.; Fu, B.; Zhou, Y.; Zhang, F. Simulation and experimental study on the pump efficiency improvement of continuously variable transmission. Mech. Mach. 2019, 131, 137–151. [Google Scholar] [CrossRef]
- Qi, F.; Dhar, S.; Nichani, V.H. A CFD study of an electronic hydraulic power steering helical external gear pump: Model development, validation and application. SAE Int. J. Passeng. Cars-Mech. Syst. 2016, 9, 346–352. [Google Scholar] [CrossRef]
- Zhang, D.; Perng, C.Y.; Laverty, M. Gerotor oil pump performance and flow/pressure ripple study. SAE Trans. 2006, 115, 204–209. [Google Scholar]
- Esfe, M.H.; Hajmohammad, H.; Moradi, R.; Arani, A.A.A. Multi-objective optimization of cost and thermal performance of double walled carbon nanotubes/water nanofluids by NSGA-II using response surface method. Appl. Eng. 2017, 112, 1648–1657. [Google Scholar]
- Vo-Duy, T.; Duong-Gia, D.; Ho-Huu, V. Multi-objective optimization of laminated composite beam structures using NSGA-II algorithm. Compos. Struct. 2017, 168, 498–509. [Google Scholar] [CrossRef] [Green Version]
- Elarbi, M.; Bechikh, S.; Gupta, A. A new decomposition-based NSGA-II for many-objective optimization. IEEE Trans. Syst. Man Cybern. Syst. 2017, 48, 1191–1210. [Google Scholar] [CrossRef]
- Ni, H.; Zhang, J.; Zhao, N.; Wang, C.; Lv, S.; Ren, F.; Wang, X. Design on the Winter Jujubes Harvesting and Sorting Device. Appl. Sci. 2019, 9, 5546. [Google Scholar] [CrossRef] [Green Version]
- Ni, H.; Zhang, J.; Lv, S.; Wang, X.; Pei, Y.; Li, F. Coating Process Parameters and Structural Properties of the Tubular Electrodes of Fuel Cells Based on a Self-Made Coating Device. Coatings 2020, 10, 830. [Google Scholar] [CrossRef]
- Sun, N.; Yang, T.; Fang, Y. Transportation Control of Double-Pendulum Cranes with a Nonlinear Quasi-PID Scheme: Design and Experiments. IEEE Trans. Syst. Man Cybern. Syst. 2018, 49, 1408–1418. [Google Scholar] [CrossRef]
- Vasiliu, N.; Vasiliu, D.; Călinoiu, C.; Puhalschi, R. Simulation of Fluid Power Systems with Simcenter Amesim; CRC Press: Boca Raton, FL, USA, 2018; pp. 10–15. [Google Scholar]


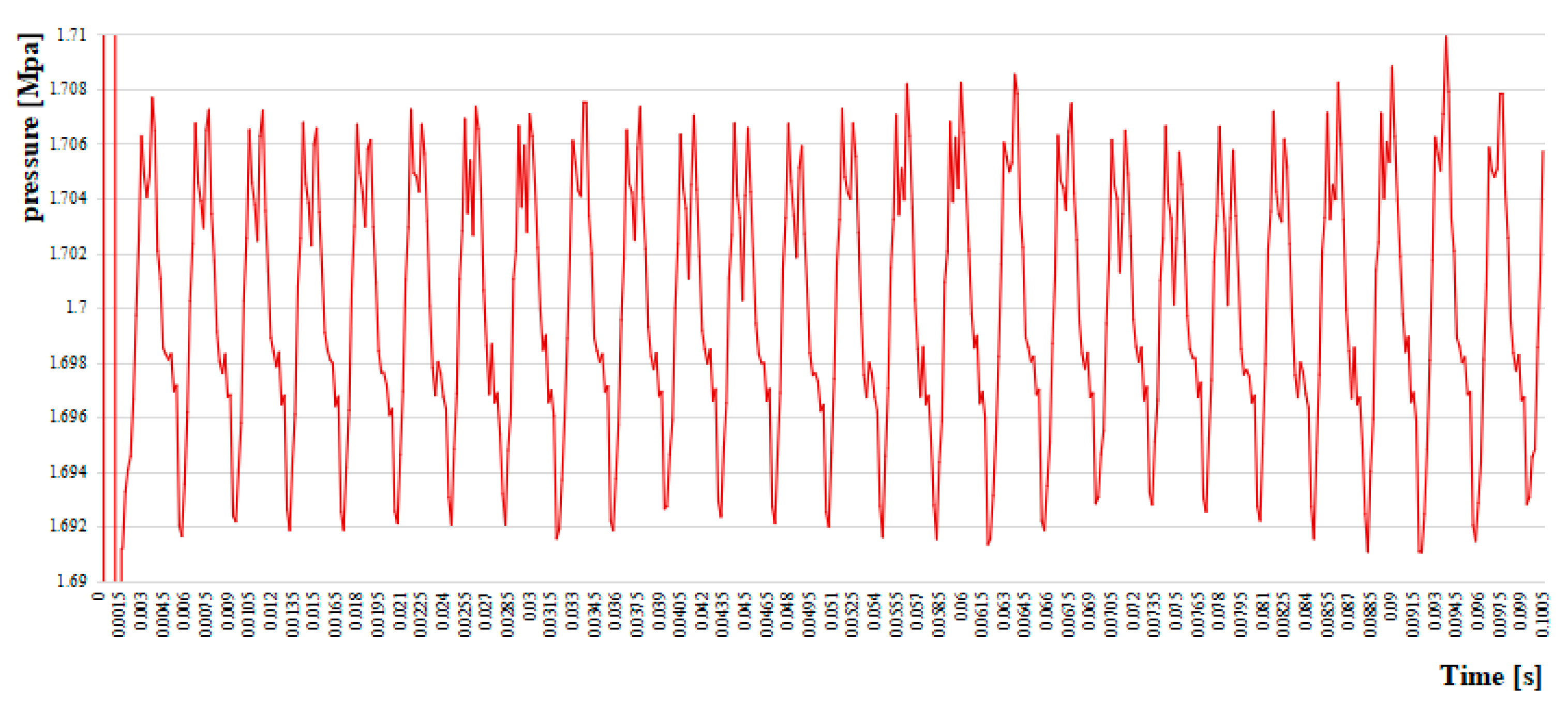

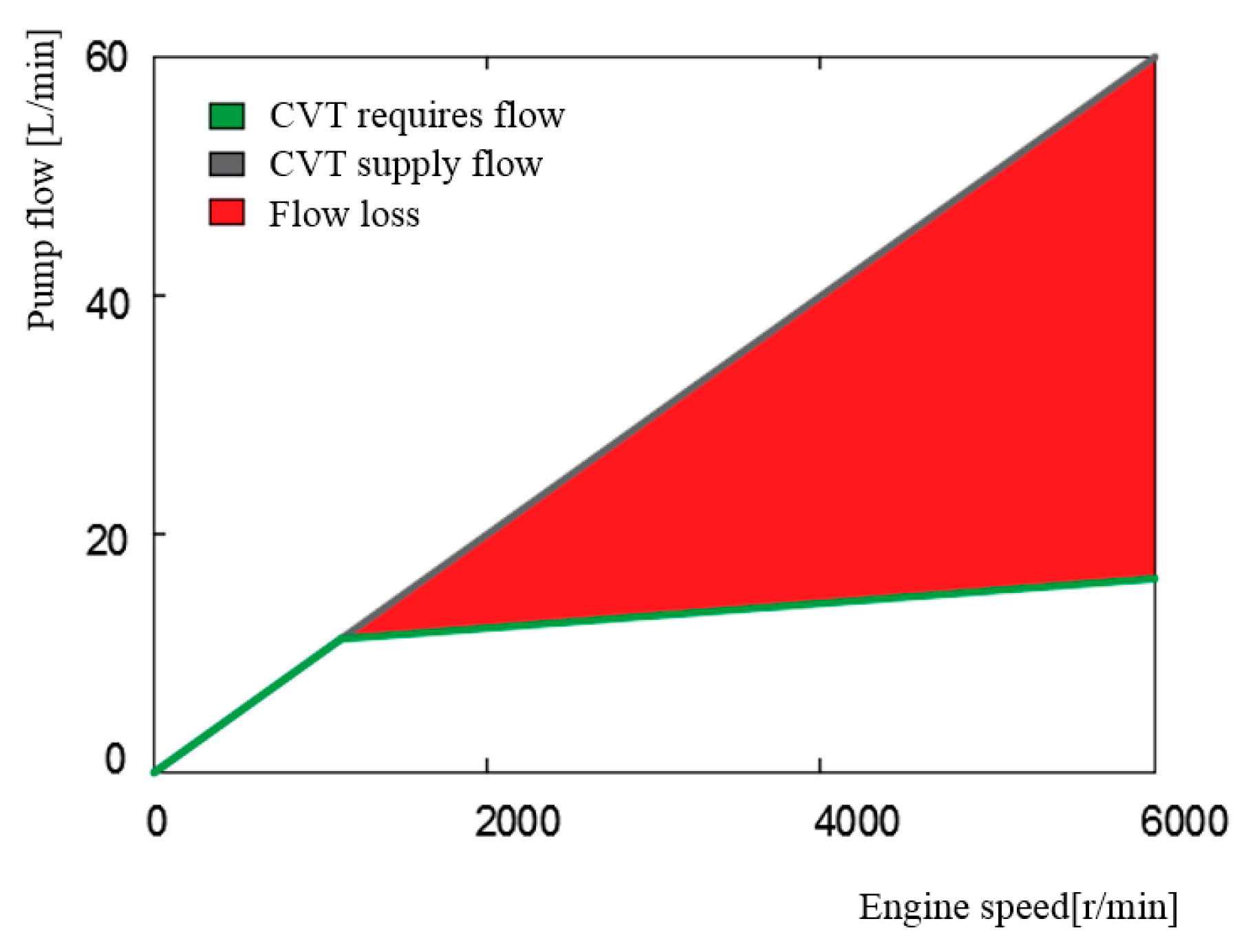
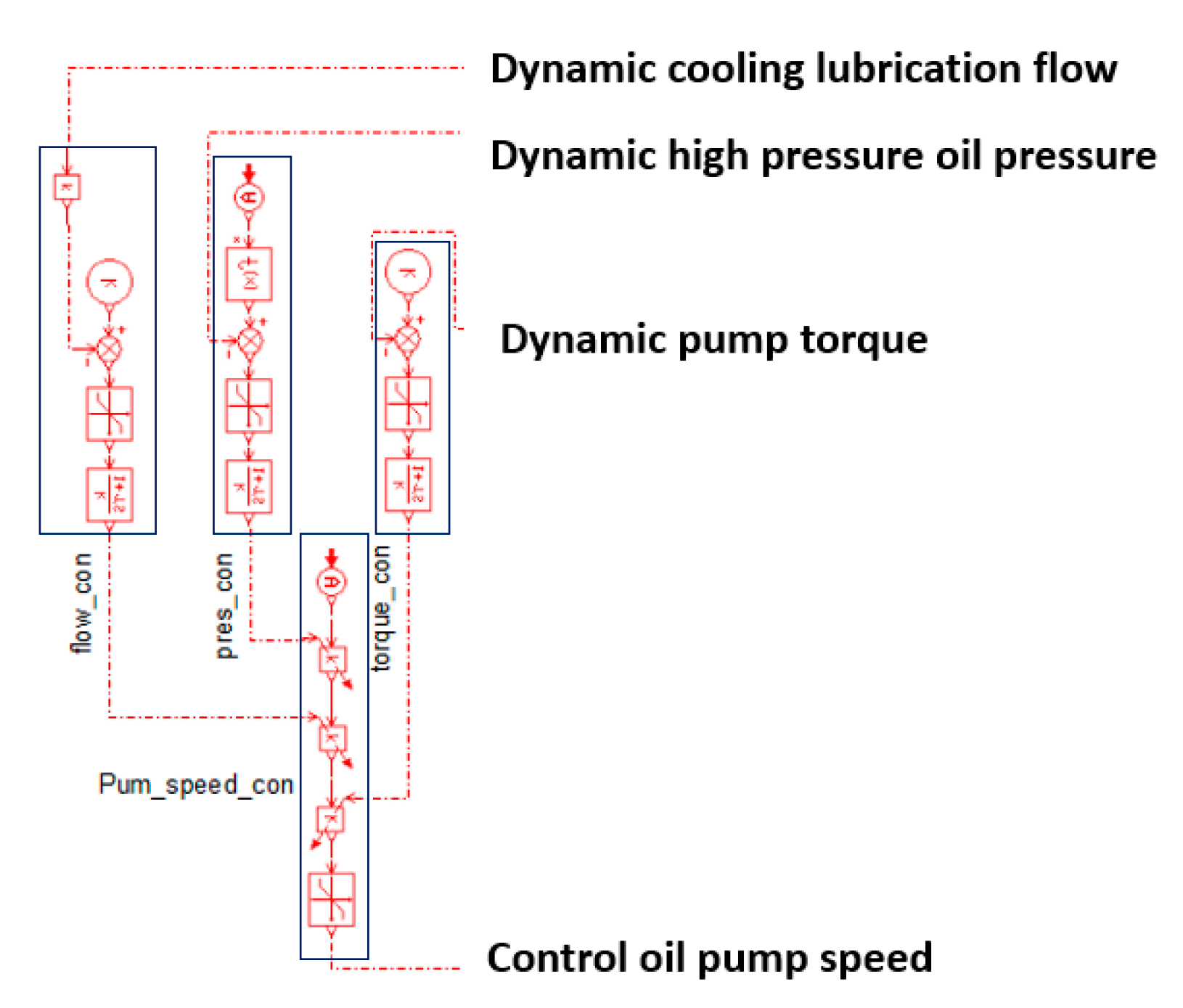
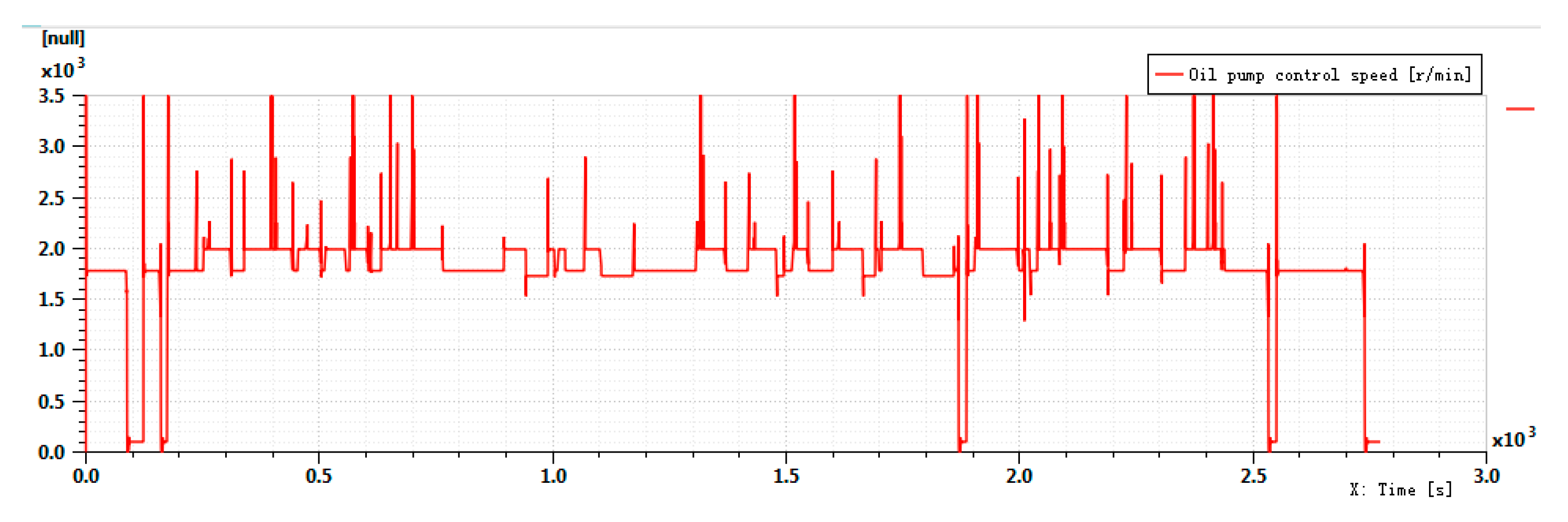
| Test Conditions | Pressure: 0 Bar Theoretical Displacement: 4 mL/r | |||
|---|---|---|---|---|
| Oil Pump Number | Rotating Speed (r/min) | Flow (L/min) | Calculated Displacement (mL/min) | Deviation (%) |
| 1# | 1000 | 3.85 | 3.85 | 3.75% |
| 1500 | 5.8 | 3.87 | 3.25% | |
| 2# | 1000 | 3.84 | 3.84 | 4% |
| 1500 | 5.8 | 3.87 | 3.25% | |
| Test Conditions | Pressure: 0 Bar Theoretical Displacement: 8 mL/r | |||
|---|---|---|---|---|
| Oil Pump Number | Rotating Speed (r/min) | Flow (L/min) | Calculated Displacement (mL/min) | Deviation (%) |
| 1# | 1000 | 7.9 | 7.90 | 1.25% |
| 1500 | 11.8 | 7.87 | 1.63% | |
| 2# | 1000 | 7.9 | 7.90 | 1.25% |
| 1500 | 11.8 | 7.87 | 1.63% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, M.; Shi, C.; Zhu, Y.; Zhang, J.; Zhang, F. Design of Gerotor Pump and Influence on Oil Supply System for Hybrid Transmission. Energies 2021, 14, 5649. https://doi.org/10.3390/en14185649
Huang M, Shi C, Zhu Y, Zhang J, Zhang F. Design of Gerotor Pump and Influence on Oil Supply System for Hybrid Transmission. Energies. 2021; 14(18):5649. https://doi.org/10.3390/en14185649
Chicago/Turabian StyleHuang, Mingyu, Chongshi Shi, Yu Zhu, Jiaqiao Zhang, and Fubao Zhang. 2021. "Design of Gerotor Pump and Influence on Oil Supply System for Hybrid Transmission" Energies 14, no. 18: 5649. https://doi.org/10.3390/en14185649
APA StyleHuang, M., Shi, C., Zhu, Y., Zhang, J., & Zhang, F. (2021). Design of Gerotor Pump and Influence on Oil Supply System for Hybrid Transmission. Energies, 14(18), 5649. https://doi.org/10.3390/en14185649






