An Overview of Probabilistic Dimensioning of Frequency Restoration Reserves with a Focus on the Greek Electricity Market
Abstract
:1. Introduction
1.1. Context
1.2. Reserve Dimensioning Methods
1.2.1. Heuristic Reserve Sizing
1.2.2. Probabilistic Methods
1.2.3. Bottom-Up Unit Commitment/Economic Dispatch Models
1.3. The Taxonomy of Reserve Dimensioning
- Sizing methodology: The sizing methodology refers to how the decision-making problem of sizing reserves is quantified. The three predominant approaches in this respect that were listed in Section 1.2 are heuristic methods, probabilistic methods, and bottom-up unit commitment and economic dispatch models.
- Adaptiveness: Adaptiveness refers to whether the sizing methodology is adaptive to the forecast conditions of the system or not. Two options in this respect are static sizing and dynamic sizing.
- Stochastic models: This dimension refers to the way in which uncertainty is modeled. Two options are possible among stochastic models: parametric or non-parametric.
1.4. Contributions and Outline of the Paper
2. Sizing Methodology in the Greek Electricity Market
2.1. Sizing before the Target Model
2.2. Target Model Methodology
- The minimum FRR requirement (which in itself is a function of maximum load in the system);
- A constant corresponding to the technical minimum of a typical thermal unit (meant to capture the possibility that a unit is asked to turn on but fails to do so);
- The scheduled interchange;
- The scheduled demand.
- Upward/downward aFRR;
- Renewable forecasts;
- Demand ramps;
- Scheduled interchanges;
- An indicator for extreme conditions (indicatively, unfavorable weather, large renewable forecast deviations, reduced adequacy, contingencies, strikes, reduced fuel reserves for thermal units, low hydro energy levels, or a combination of the above).
3. Model of Imbalances in the Greek System
3.1. Modeling Imbalances
- Load data with hourly resolution from 1 January 2018 until 31 October 2020, thereby spanning 2 years and 10 months (namely, 1035 days).
- Renewable energy supply data with the same characteristics.
- Import/export data with the same characteristics.
- Imbalances are driven by both contingencies and “normal” imbalance drivers, such as forecast errors.
- Imbalances can be explained by a number of factors in the system, such as renewable energy forecasts, load forecasts, and scheduled imports. These factors are referred to as imbalance drivers. Other imbalance drivers may include the change of the hour (due to market ramps), temperature, and so on. Higher forecasts tend to result in higher imbalances.
- On the other hand, a significant portion of the system imbalance signal may not be possible to explain based on imbalance drivers. Past analyses of the Belgian system [2] have shown that approximately half of the imbalance signal may not be attributable to imbalance drivers. It is assumed that this portion of the imbalances can be represented by white noise.
- Imbalance drivers do not have symmetric distributions in the upward and downward directions. For example, high renewable supply forecasts are more likely to lead to significant negative imbalances (under-supply) and low positive imbalances (over-supply) since the renewable supply will mostly decrease during periods of high output.
- Use representative “day types” to model contingency risk in the system. The idea is presented in Section 3.2.
- Use imbalance drivers (load, RES and imports) to model factors that contribute to the system imbalance based on skewed distributions, the variance of which depends on the imbalance drivers. The idea is presented in Section 3.3.
- Use “white noise” to model the part of the imbalance signal that cannot be explained by imbalance drivers. The idea is presented in Section 3.4.
- Tune the parameters of the model so that the resulting imbalance is consistent with the reliability achieved by the reserve dimensioning that is employed in the Greek market. The idea is presented in Section 3.5.
- The baseline dimensioning methodology is then compared to the probabilistic dimensioning methods that are described in Section 4.
3.2. Contingencies
- Winter weekday: 15 January 2018
- Winter weekend: 7 January 2018
- Spring weekday: 8 March 2018
- Spring weekend: 11 March 2018
- Summer weekday: 7 June 2018
- Summer weekend: 10 June 2018
- Fall weekday: 6 September 2018
- Fall weekend: 9 September 2018
3.3. Imbalance Drivers
- The minimum load in the dataset is 2840 MW; the maximum load is 9529 MW.
- The minimum renewable supply within the dataset is 103 MW; the maximum renewable supply is 4245 MW.
- The minimum amount imported was −1428 MW (i.e., the maximum amount that has been exported historically is 1428 MW); the maximum amount imported was 2041 MW (i.e., the maximum amount that has been imported historically is 2041 MW).
3.4. Idiosyncratic Noise
3.5. Matching the Model to a Static Sizing Methodology
4. Probabilistic Dimensioning Methodology
4.1. Overview of k-Means Clustering Applied to Probabilistic Dimensioning
4.2. Implementation of Probabilistic Dimensioning Based on k-Means
- Step 1: Cluster imbalance drivers in order to determine the day types.
- Step 2: Approximate imbalances, e.g., using kernel density estimation or the empirical distribution of the data.
- Step 3: Determine the reserve requirement of each day type from the appropriate quantile of the distribution computed in step 2.
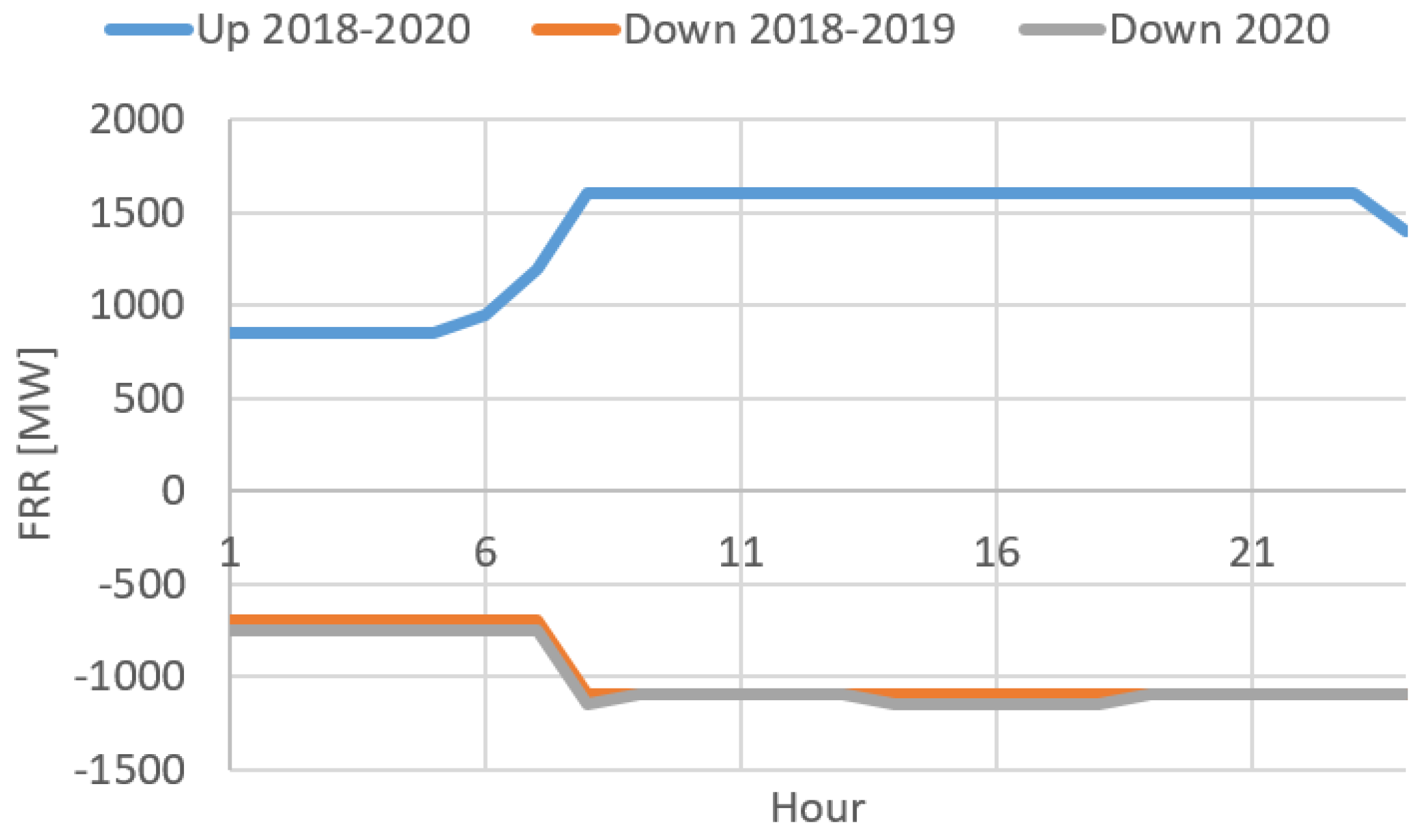
- The upward capacity requirement of Figure 1 served all but 4/99,360 incidents, as noted in Section 3.5.
- The downward capacity requirement of Figure 1 served all but 30/99,360 incidents, as noted in Section 3.5.
5. Case Study of Probabilistic Dimensioning
5.1. Case Study Description
- Load data with hourly resolution from 1 January 2018 until 31 October 2020, thus spanning 2 years and 10 months (namely, 1035 days).
- Renewable energy supply data with the same characteristics.
- Import/export data with the same characteristics.
- Average reserves committed, measured in MW.
- Unreliability: a measure of how many incidents of oversupply or undersupply occur per year, measured in hours per year. This corresponds to the loss of load expectation (LOLE) measure in reliability studies, but is here measured in both the case of upward and downward imbalances.
- Shortage or oversupply, measured in MWh/year. This corresponds to expected energy not served in adequacy studies, but is also measured in the downward direction (in the sense of quantity of energy oversupplied).
5.2. Reserve Requirements
5.3. Risk Profile
5.4. Integration with System Operations
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- Papavasiliou, A.; Oren, S.S.; O’Neill, R.P. Reserve requirements for wind power integration: A scenario-based stochastic programming framework. IEEE Trans. Power Syst. 2011, 26, 2197–2206. [Google Scholar] [CrossRef] [Green Version]
- De-Vos, K.; Stevens, N.; Devolder, O.; Papavasiliou, A.; Hebb, B.; Matthys-Donnadieu, J. Dynamic Dimensioning Approach for Operating Reserves: Proof of Concept in Belgium. Energy Policy 2019, 124, 272–285. [Google Scholar] [CrossRef]
- ENTSO-E. Load-Frequency Control and Performance. In Continental Europe Operation Handbook; Technical Report; ENTSO-E: Brussels, Belgium, 2009. [Google Scholar]
- Holttinen, H.; Milligan, M.; Kirby, B.; Acker, T.; Neimane, V.; Molinski, T. Using standard deviation as a measure of increased operational reserve requirement for wind power. Wind Eng. 2008, 32, 355–377. [Google Scholar] [CrossRef]
- Ohsenbruegge, A.; Klingenberg, T.; Lehnhoff, S. Dynamic Data Driven Dimensioning of Balancing Power with k-Nearest Neighbors. In Proceedings of the Power and Energy Student Summit (PESS) 2015, Dortmund, Germany, 13–14 January 2015. [Google Scholar]
- Ohsenbrugge, A.; Lehnhoff, S. Dynamic Dimensioning of Balancing Power with Flexible Feature Selection. In Proceedings of the 23rd International Conference on Electricity Distribution, Lyon, France, 15–18 June 2015. [Google Scholar]
- Dvorkin, Y.; Ortega-Vazuqez, M.A.; Kirschen, D.S. Wind generation as a reserve provider. IET Gener. Transm. Distrib. 2015, 9, 779–787. [Google Scholar] [CrossRef] [Green Version]
- Papavasiliou, A.; Oren, S.S. Multi-Area Stochastic Unit Commitment for High Wind Penetration in a Transmission Constrained Network. Oper. Res. 2013, 61, 578–592. [Google Scholar] [CrossRef]
- European Commission. Commission Regulation (EU) 2017/2195 of 23 November 2017 Establishing a Guideline on Electricity Balancing; Technical Report; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- European Commission. Commission Regulation (EU) 2017/1485 of 2 August 2017 Establishing a Guideline on Electricity Transmission System Operation; Technical Report; European Commission: Brussels, Belgium, 2017. [Google Scholar]
- Jost, D.; Speckmann, M.; Sandau, F.; Schwinn, R. A new method for day-ahead sizing of control reserve in Germany under a 100% renewable energy sources scenario. Electr. Power Syst. Res. 2015, 119, 485–491. [Google Scholar] [CrossRef]
- Breuer, C.; Engelhardt, C.; Moser, A. Expectation-based reserve capacity dimensioning in power systems with an increasing intermittent feed-in. In Proceedings of the 2013 10th International Conference on the European Energy Market (EEM), Stockholm, Sweden, 27–31 May 2013. [Google Scholar]
- Maurer, C.; Krahl, S.; Weber, H. Dimensioning of secondary and tertiary control reserve by probabilistic methods. Eur. Trans. Electr. Power 2009, 19, 544–552. [Google Scholar] [CrossRef]
- Kays, J.; Schwippe, J.; Rehtanz, C. Dimensioning of reserve capacity by means of a multidimensional method considering uncertainties. In Proceedings of the IEEE PSCC Stockholm Conference, Stockholm, Sweden, 22–26 August 2011. [Google Scholar]
- Kippelt, S.; Schlüter, T.; Rehtanz, C. Flexible dimensioning of control reserve for future energy scenarios. In Proceedings of the 2013 IEEE Grenoble Conference, Grenoble, France, 16–20 June 2013. [Google Scholar]
- Dvorkin, Y.; Pandžić, H.; Ortega-Vazquez, M.A.; Kirschen, D.S. A hybrid stochastic/interval approach to transmission-constrained unit commitment. IEEE Trans. Power Syst. 2014, 30, 621–631. [Google Scholar] [CrossRef]
- Meibom, P.; Barth, R.; Hasche, B.; Brand, H.; Weber, C.; O’Malley, M. Stochastic optimization model to study the operational impacts of high wind penetrations in Ireland. IEEE Trans. Power Syst. 2010, 26, 1367–1379. [Google Scholar] [CrossRef]
- Dietrich, K.; Latorre, J.; Olmos, L.; Ramos, A.; Perez-Arriaga, I. Stochastic unit commitment considering uncertain wind production in an isolated system. In Proceedings of the 4th Conference on Energy Economics and Technology, Dresden, Germany, 3–6 April 2009. [Google Scholar]
- Bertsimas, D.; Litvinov, E.; Sun, X.A.; Zhao, J.; Zheng, T. Adaptive Robust Optimization for the Security Constrained Unit Commitment Problem. IEEE Trans. Power Syst. 2013, 28, 52–63. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M.A.; Kirschen, D.S. Estimating the spinning reserve requirements in systems with significant wind power generation penetration. IEEE Trans. Power Syst. 2008, 24, 114–124. [Google Scholar] [CrossRef]
- Zhou, Z.; Botterud, A.; Wang, J.; Bessa, R.J.; Keko, H.; Sumaili, J.; Miranda, V. Application of probabilistic wind power forecasting in electricity markets. Wind Energy 2013, 16, 321–338. [Google Scholar] [CrossRef]
- Tuohy, A.; Meibom, P.; Denny, E.; O’Malley, M. Unit Commitment for Systems with High Wind Penetration. IEEE Trans. Power Syst. 2009, 24, 592–601. [Google Scholar] [CrossRef] [Green Version]
- Gooi, H.; Mendes, D.; Bell, K.; Kirschen, D. Optimal scheduling of spinning reserve. IEEE Trans. Power Syst. 1999, 14, 1485–1492. [Google Scholar] [CrossRef]
- Bessa, R.J.; Mendes, J.; Miranda, V.; Botterud, A.; Wang, J.; Zhou, Z. Quantile-copula density forecast for wind power uncertainty modeling. In Proceedings of the 2011 IEEE Trondheim PowerTech, Trondheim, Norway, 19–23 June 2011. [Google Scholar]
- Bessa, R.J.; Miranda, V.; Botterud, A.; Zhou, Z.; Wang, J. Time-adaptive quantile-copula for wind power probabilistic forecasting. Renew. Energy 2012, 40, 29–39. [Google Scholar] [CrossRef]
- Bruninx, K.; Delarue, E. A statistical description of the error on wind power forecasts for probabilistic reserve sizing. IEEE Trans. Sustain. Energy 2014, 5, 995–1002. [Google Scholar] [CrossRef]
- Elia. Evolution of Ancillary Services Needs to Balance the Belgian Control Area towards 2018; Technical Report; Elia: Brussels, Belgium, 2013. [Google Scholar]
- Jost, D.; Braun, A.; Fritz, R. Dynamic Dimensioning of Frequency Restoration Reserve Capacity based on Quantile Regression. In Proceedings of the 12th International Conference on the European Energy Market (EEM), Lisbon, Portugal, 19–22 May 2015. [Google Scholar]
- Jost, D.; Braun, A.; Fritz, R.; Otterson, S. Dynamic sizing of automatic and manual frequency restoration reserves for different product lengths. In Proceedings of the 2016 13th International Conference on the European Energy Market (EEM), Porto, Portugal, 6–9 June 2016. [Google Scholar]
- Juban, J.; Siebert, N.; Kariniotakis, G.N. Probabilistic short-term wind power forecasting for the optimal management of wind generation. In Proceedings of the 2007 IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 683–688. [Google Scholar]
- Kim, S.K.; Park, J.H.; Yoon, Y.T. Determination of Secondary Reserve Requirement Through Interaction-dependent Clearance Between Ex-ante and Ex-post. J. Electr. Eng. Technol. 2014, 9, 71–79. [Google Scholar] [CrossRef]
- Menemenlis, N.; Huneault, M.; Robitaille, A. Computation of dynamic operating balancing reserve for wind power integration for the time-horizon 1–48 h. IEEE Trans. Sustain. Energy 2012, 3, 692–702. [Google Scholar] [CrossRef]
- Nielsen, H.A.; Madsen, H.; Nielsen, T.S. Using quantile regression to extend an existing wind power forecasting system with probabilistic forecasts. Wind Energy 2006, 9, 95–108. [Google Scholar] [CrossRef]
- De Vos, K.; Morbee, J.; Driesen, J.; Belmans, R. Impact of wind power on sizing and allocation of reserve requirements. IET Renew. Power Gener. 2013, 7, 1–9. [Google Scholar] [CrossRef]
- Zhou, Z.; Botterud, A. Dynamic Scheduling of Operating Reserves in Co-Optimized Electricity Markets with Wind Power. IEEE Trans. Power Syst. 2014, 29, 160–171. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Wang, X. Review on probabilistic forecasting of wind power generation. Renew. Sustain. Energy Rev. 2014, 32, 255–270. [Google Scholar] [CrossRef]
- Ren, Z.; Yan, W.; Zhao, X.; Li, W.; Yu, J. Chronological Probability Model of Photovoltaic Generation. IEEE Trans. Power Syst. 2014, 29, 1077–1088. [Google Scholar] [CrossRef]
- Bucksteeg, M.; Niesen, L.; Weber, C. Impacts of Dynamic Probabilistic Reserve Sizing Techniques on Reserve Requirements and System Costs. IEEE Trans. Sustain. Energy 2016, 7, 1408–1420. [Google Scholar] [CrossRef]
- ADMIE. Methodology for the Determination of Zonal/System Needs for Balancing Power; Technical Report; ADMIE: Athina, Greece, 2020. [Google Scholar]
- Lloyd, S. Least squares quantization in PCM. IEEE Trans. Inf. Theory 1982, 28, 129–137. [Google Scholar] [CrossRef]
- Arthur, D.; Vassilvitskii, S. k-Means++: The Advantages of Careful Seeding; Technical Report; Stanford InfoLab Publication Server: Stanford, UK, 2006. [Google Scholar]
- Zheng, T.; Litvinov, E. Contingency-based zonal reserve modeling and pricing in a co-optimized energy and reserve market. IEEE Trans. Power Syst. 2008, 23, 277–286. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Bouso, A.; Apelfröjd, S.; Wik, E.; Gueuning, T.; Langer, Y. Multi-Area Reserve Dimensioning Using Chance-Constrained Optimization; Technical Report; IEEE: Piscataway, NJ, USA, 2021. [Google Scholar]
- European Commission. EU Reference Scenario 2016; Technical Report; European Commission: Brussels, Belgium, 2016. [Google Scholar]



| Heuristic | Probabilistic | UC/ED | Static | Dynamic | Parametric pdfs | Non-Parametric pdfs | |
|---|---|---|---|---|---|---|---|
| [24] | X | ||||||
| [25] | X | ||||||
| [19] | X | X | |||||
| [26] | X | X | |||||
| [12] | X | X | |||||
| [18] | X | X | |||||
| [16] | X | X | |||||
| [7] | X | X | X | ||||
| [3] | X | X | |||||
| [27] | X | X | |||||
| [23] | X | X | X | X | |||
| [4] | X | X | |||||
| [28] | X | X | |||||
| [11] | X | X | X | ||||
| [29] | X | X | X | ||||
| [30] | X | ||||||
| [15] | X | X | |||||
| [14] | X | X | X | ||||
| [31] | X | X | X | ||||
| [32] | X | X | X | ||||
| [13] | X | X | X | ||||
| [17] | X | X | |||||
| [33] | X | ||||||
| [20] | X | X | X | X | |||
| [5] | X | X | |||||
| [6] | X | X | |||||
| [1] | X | X | |||||
| [22] | X | X | |||||
| [34] | X | X | |||||
| [2] | X | X | X | ||||
| [35] | X | X | |||||
| [36] | X | X | |||||
| [21] | X | X | X | ||||
| [37] | X |
| Load | Renewables | Imports | Reserve Up | Reserve Down |
|---|---|---|---|---|
| 6810 (H) | 2091 (H) | 1331 (H) | 1383 | 1085 |
| 6810 (H) | 2091 (H) | 471 (L) | 1282 | 1043 |
| 6810 (H) | 782 (L) | 1331 (H) | 1119 | 1028 |
| 6810 (H) | 782 (L) | 471 (L) | 1187 | 919 |
| 4886 (L) | 2091 (H) | 1331 (H) | 981 | 855 |
| 4886 (L) | 2091 (H) | 471 (L) | 912 | 845 |
| 4886 (L) | 782 (L) | 1331 (H) | 991 | 802 |
| 4886 (L) | 782 (L) | 471 (L) | 970 | 737 |
| Figure 1 | Probabilistic | |
|---|---|---|
| Res-Up (MW) | 1392 | 1111 |
| Unrel.-Up (hours/y) | 0.3 | 0.4 |
| Shortage (MWh/y) | 40.2 | 21.5 |
| Res-Down (MW) | 993 | 950 |
| Unrel.-Down (hours/y) | 2.8 | 1.9 |
| Oversupply (MWh/y) | 208.4 | 159.1 |
| Interval Type | No. Occurrences | Fails Prob. (h/yr) | Fails Figure 1 (h/yr) |
|---|---|---|---|
| LoH-ReH-ImH | 13,292 (13.4%) | 0.44 (18.5%) | 0.44 (14.3%) |
| LoH-ReH-ImL | 9644 (9.7%) | 0.09 (3.7%) | 0.09 (2.9%) |
| LoH-ReL-ImH | 12,144 (12.2%) | 0.09 (3.7%) | 0.26 (8.6%) |
| LoH-ReL-ImL | 10,812 (10.9%) | 0.53 (22.2%) | 0.09 (2.9%) |
| LoL-ReH-ImH | 7960 (8.0%) | 0.26 (11.1%) | 0.18 (5.7%) |
| LoL-ReH-ImL | 6952 (7.0%) | 0.09 (3.7%) | 0.09 (2.9%) |
| LoL-ReL-ImH | 26,296 (26.5%) | 0.53 (22.2%) | 1.59 (51.4%) |
| LoL-ReL-ImL | 12,260 (12.3%) | 0.35 (14.8%) | 0.35 (11.4%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Papavasiliou, A. An Overview of Probabilistic Dimensioning of Frequency Restoration Reserves with a Focus on the Greek Electricity Market. Energies 2021, 14, 5719. https://doi.org/10.3390/en14185719
Papavasiliou A. An Overview of Probabilistic Dimensioning of Frequency Restoration Reserves with a Focus on the Greek Electricity Market. Energies. 2021; 14(18):5719. https://doi.org/10.3390/en14185719
Chicago/Turabian StylePapavasiliou, Anthony. 2021. "An Overview of Probabilistic Dimensioning of Frequency Restoration Reserves with a Focus on the Greek Electricity Market" Energies 14, no. 18: 5719. https://doi.org/10.3390/en14185719
APA StylePapavasiliou, A. (2021). An Overview of Probabilistic Dimensioning of Frequency Restoration Reserves with a Focus on the Greek Electricity Market. Energies, 14(18), 5719. https://doi.org/10.3390/en14185719






