Evaporator Frosting in Refrigerating Appliances: Fundamentals and Applications
Abstract
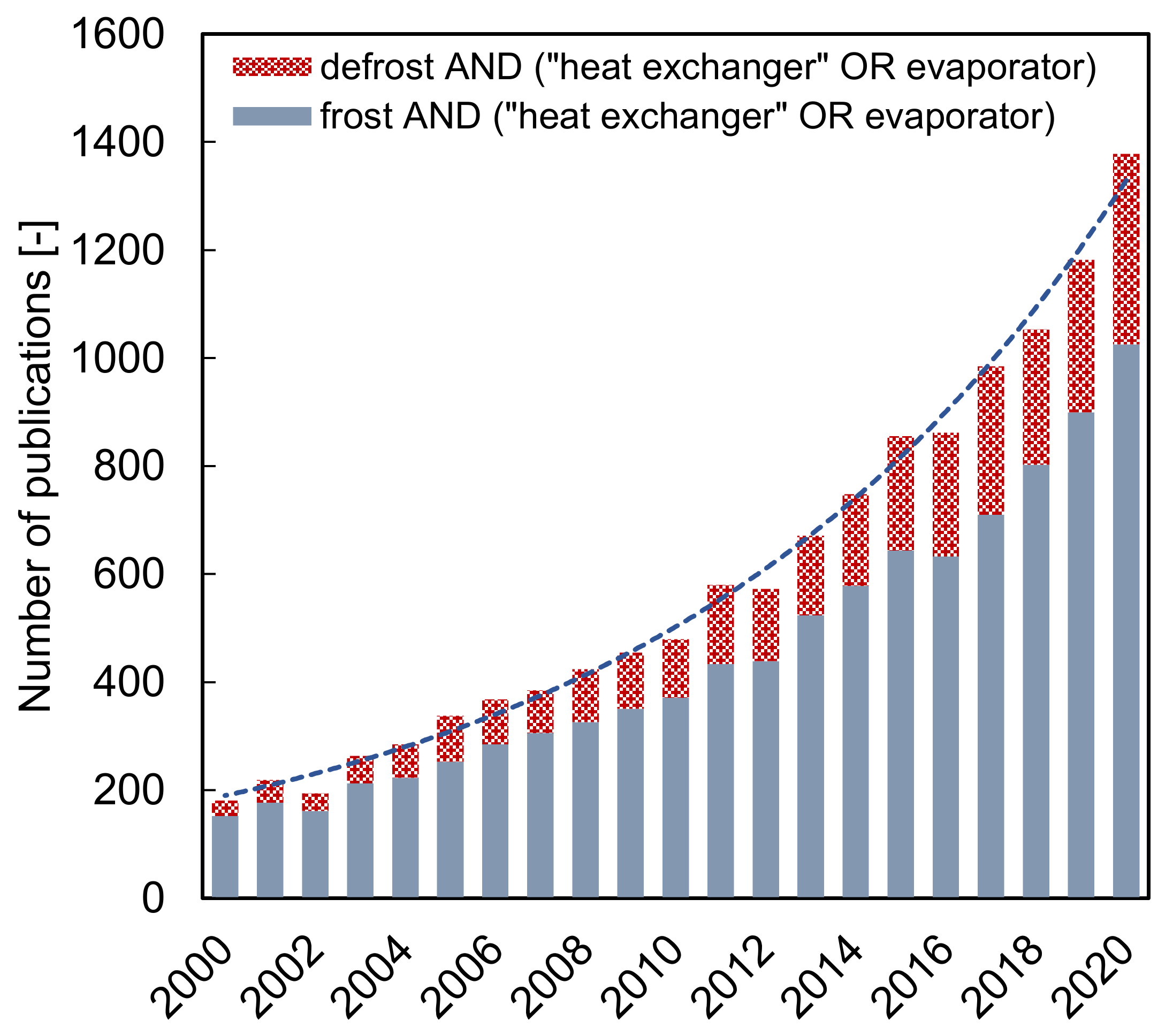
:1. Introduction
2. Frost Fundamentals
2.1. Background
2.2. Crystal Nucleation
2.3. Frost Build-Up
2.4. Thermophysical Properties
3. Evaporator Frosting
4. Optimal Defrosting
5. Final Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bejan, A.; Vargas, J.; Lim, J.S. When to defrost a refrigerator, and when to remove the scale from the heat exchanger of a power plant. Int. J. Heat Mass Transf. 1994, 37, 523–532. [Google Scholar] [CrossRef]
- Dupont, J.L.; Domanski, P.; Lebrum, P.; Ziegler, F. The role of refrigeration in the global economy. In Proceedings of the 38th Informatory Note on Refrigeration Technologies, Paris, France, 1 June 2019. [Google Scholar]
- Borges, B.N.; Melo, C.; Hermes, C.J. Transient simulation of a two-door frost-free refrigerator subjected to periodic door opening and evaporator frosting. Appl. Energy 2015, 147, 386–395. [Google Scholar] [CrossRef]
- Da Silva, D.L.; Hermes, C.J. Optimal defrost cycle for air coolers revisited: A study of fan-supplied tube-fin evaporators. Int. J. Refrig. 2018, 89, 142–148. [Google Scholar] [CrossRef]
- Iragorry, J.; Tao, Y.-X.; Jia, S. Review Article: A Critical Review of Properties and Models for Frost Formation Analysis. HVAC&R Res. 2004, 10, 393–420. [Google Scholar] [CrossRef]
- Song, M.; Dang, C. Review on the measurement and calculation of frost characteristics. Int. J. Heat Mass Transf. 2018, 124, 586–614. [Google Scholar] [CrossRef]
- Lock, G.S.H. The Growth and Decay of Ice; Cambridge University Press: Cambridge, UK, 1990. [Google Scholar]
- Piucco, R.O.; Hermes, C.J.L.; Melo, C.; Barbosa, J.R., Jr. A study of frost nucleation on flat surfaces. Exp. Therm. Flud. Sci. 2008, 32, 1710–1715. [Google Scholar] [CrossRef]
- Becker, R.; Doring, W. Kinetische Behandlung der Keimbildung in übersättigten Dämpfen. Ann. Phys. Lpz. 1935, 24, 719. [Google Scholar] [CrossRef]
- Fletcher, N.H. The Chemical Physics of Ice; Cambridge University Press: Cambridge, UK, 1970. [Google Scholar]
- Volmer, M.; Flood, H. Tropfchenbildung in Dampfen. Z. Phys. Chem. A 1934, 170, 273–285. [Google Scholar] [CrossRef]
- Hermes, C.J.L.; Nascimento, V.S.; Loyola, F.R.; Cardoso, R.P.; Sommers, A.D. A study of frost build-up on hydrophilic and hydrophobic surfaces under forced convection conditions. Exp. Therm. Fluid Sci. 2019, 100, 76–88. [Google Scholar] [CrossRef]
- Wang, Z.-J.; Kwon, D.-J.; deVries, K.L.; Park, J.-M. Frost formation and anti-icing performance of a hydrophobic coating on aluminum. Exp. Therm. Fluid Sci. 2015, 60, 132–137. [Google Scholar] [CrossRef]
- Cai, L.; Wang, R.; Hou, P.; Zhang, X. Study on restraining frost growth at initial stage by hydrophobic coating and hygro-scopic coating. Energy Build. 2011, 43, 1159–1163. [Google Scholar] [CrossRef]
- Liu, Z.; Gou, Y.; Wang, J.; Cheng, S. Frost formation on a super-hydrophobic surface under natural convection conditions. Int. J. Heat Mass Transf. 2008, 51, 5975–5982. [Google Scholar] [CrossRef]
- Na, B.; Webb, R.L. A fundamental understanding of factors affecting frost nucleation. Int. J. Heat Mass Transf. 2003, 46, 3797–3808. [Google Scholar] [CrossRef]
- Hermes, C.J.L.; Piucco, R.O.; Barbosa, J.R., Jr.; Melo, C. A study of frost growth and densification on flat surfaces. Exp. Therm. Fluid Sci. 2009, 33, 371–379. [Google Scholar] [CrossRef]
- Nakaya, U. Snow Crystals: Natural and Artificial; Harvard University Press: Cambridge, MA, USA, 1954. [Google Scholar]
- Libbrecht, K. The physics of snow crystals. Rep. Prog. Phys. 2005, 68, 855–895. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T. On the Habit of Snow Crystals Artificially Produced at Low Pressures. J. Meteorol. Soc. Jpn. 1958, 36, 193–208. [Google Scholar] [CrossRef] [Green Version]
- Kobayashi, T. The growth of snow crystals at low supersaturations. Philos. Mag. 1961, 6, 1363–1370. [Google Scholar] [CrossRef]
- Kobayashi, T. On the variation of ice crystal habit with temperature. In Proceedings of the Conference on Physics of Snow and Ice, Sapporo, Japan, 14–19 August 1966. [Google Scholar]
- Magono, C.; Lee, C.W. Meteorological classification of natural snow crystals. J. Fac. Sci. 1966, 2, 321–335. [Google Scholar]
- Kuroda, T.; Lacmann, R. Growth kinetics of ice from the vapour phase and its growth forms. J. Cryst. Growth 1982, 56, 189–205. [Google Scholar] [CrossRef]
- Libbrecht, K.G.; Yu, H. Crystal Growth in the presence of surface melting: Supersaturation dependence of the growth of co-lumnar ice crystals. J. Cryst. Growth 2001, 222, 822–831. [Google Scholar] [CrossRef] [Green Version]
- Hermes, C.J.L.; Sommers, A.D.; Barbosa, J.R., Jr. Time scaling of frost accretion and the square-root-of-time rule. Int. Comm. Heat Mass Transf. 2019, 108, 104281. [Google Scholar] [CrossRef]
- O’Neal, D.L. The Effect of Frost Formation on the Performance of a Parallel Plate Heat Exchanger. Ph.D. Thesis, Purdue University, West Lafayette, IN, USA, 1982. [Google Scholar]
- Wu, X.; Dai, W.; Shan, X.; Wang, W.; Tang, L. Visual and Theoretical Analyses of the Early Stage of Frost Formation on Cold Surfaces. J. Enhanc. Heat Transf. 2007, 14, 257–268. [Google Scholar] [CrossRef]
- Brian, P.L.T.; Reid, R.C.; Brazinsky, L. Cryogenic frost properties. Cryog. Technol. 1969, 5, 205–212. [Google Scholar]
- Schneider, H. Equation of the growth rate of frost forming on cooled surfaces. Int. J. Heat Mass Transf. 1978, 21, 1019–1024. [Google Scholar] [CrossRef]
- Sanders, C.T.H. The Influence of Frost Formation and Defrosting on the Performance of Air Coolers. Ph.D. Thesis, Technische Hogeschool, Delft, The Netherlands, 1974. [Google Scholar]
- Sami, S.M.; Duong, T. Numerical prediction of frost formation on cooled beat exchangers. Int. Comm. Heat Mass Transf. 1988, 15, 81–84. [Google Scholar] [CrossRef]
- Yonko, J.D.; Sepsy, C.F. An investigation of the thermal conductivity of frost while forming on a horizontal plate. ASHRAE Trans. 1967, 73, 1. [Google Scholar]
- Sherif, S.; Raju, S.; Padki, M.; Chan, A. A semi-empirical transient method for modelling frost formation on a flat plate. Int. J. Refrig. 1993, 16, 321–329. [Google Scholar] [CrossRef]
- Hayashi, Y.; Aoki, A.; Adachi, S.; Hori, K. Study of Frost Properties Correlating with Frost Formation Types. J. Heat Transf. 1977, 99, 239–245. [Google Scholar] [CrossRef]
- Tao, Y.X.; Besant, R.W.; Mao, Y. Characteristics of frost growth on a flat plate during the early growth period. ASHRAE Trans. 1993, 93, 746–753. [Google Scholar]
- Le Gall, R.; Grillot, J.M. Modelling of frost growth and densification. Int. J. Heat Mass Transf. 1997, 40, 3177–3187. [Google Scholar] [CrossRef]
- Auracher, H. Effective Thermal Conductivity of Frost. In Proceedings of the International Symposium on Heat and Mass Transfer in Refrigeration and Cryogenics, Dubrovnik, Croatia, 1–5 September 1986. [Google Scholar]
- Lee, K.-S.; Kim, W.-S.; Lee, T.-H. A one-dimensional model for frost formation on a cold flat surface. Int. J. Heat Mass Transf. 1997, 40, 4359–4365. [Google Scholar] [CrossRef]
- Ismail, K.; Salinas, C. Modeling of frost formation over parallel cold plates. Int. J. Refrig. 1999, 22, 425–441. [Google Scholar] [CrossRef]
- Mao, Y.; Besant, R.W.; Rezkallah, K.S. Measurement and correlations of frost properties with airflow over a flat plate. ASHRAE Trans. 1992, 98, 65–77. [Google Scholar]
- Lüer, A.; Beer, H. Frost deposition in a parallel plate channel under laminar flow conditions. Int. J. Therm. Sci. 2000, 39, 85–95. [Google Scholar] [CrossRef]
- Cheng, C.-H.; Cheng, Y.-C. Predictions of frost growth on a cold plate in atmospheric air. Int. Commun. Heat Mass Transf. 2001, 28, 953–962. [Google Scholar] [CrossRef]
- Yang, D.-K.; Lee, K.-S. Dimensionless correlations of frost properties on a cold plate. Int. J. Refrig. 2004, 27, 89–96. [Google Scholar] [CrossRef]
- Na, B.; Webb, R.L. New model for frost growth rate. Int. J. Heat Mass Transf. 2004, 47, 925–936. [Google Scholar] [CrossRef]
- Lee, Y.; Ro, S. Analysis of the frost growth on a flat plate by simple models of saturation and supersaturation. Exp. Therm. Fluid Sci. 2005, 29, 685–696. [Google Scholar] [CrossRef]
- Kandula, M. Frost growth and densification in laminar flow over flat surfaces. Int. J. Heat Mass Transf. 2011, 54, 3719–3731. [Google Scholar] [CrossRef]
- Hermes, C.J. An analytical solution to the problem of frost growth and densification on flat surfaces. Int. J. Heat Mass Transf. 2012, 55, 7346–7351. [Google Scholar] [CrossRef]
- Loyola, F.R.; Nascimento, V.S.; Hermes, C.J. Modeling of frost build-up on parallel-plate channels under supersaturated air-frost interface conditions. Int. J. Heat Mass Transf. 2014, 79, 790–795. [Google Scholar] [CrossRef]
- Nascimento, V.S.; Loyola, F.R.; Hermes, C.J. A study of frost build-up on parallel plate channels. Exp. Therm. Fluid Sci. 2015, 60, 328–336. [Google Scholar] [CrossRef]
- El Cheikh, A.; Jacobi, A. A mathematical model for frost growth and densification on flat surfaces. Int. J. Heat Mass Transf. 2014, 77, 604–611. [Google Scholar] [CrossRef]
- O’Neal, D.L.; Tree, D.L. Measurements of frost growth and density in a parallel plate geometry. ASHRAE Trans. 1984, 90, 278–290. [Google Scholar]
- Hermes, C.J.; Sommers, A.D.; Gebhart, C.W.; Nascimento, V.S. A semi-empirical model for predicting frost accretion on hydrophilic and hydrophobic surfaces. Int. J. Refrig. 2018, 87, 164–171. [Google Scholar] [CrossRef]
- Sommers, A.D.; Napora, A.C.; Truster, N.L.; Caraballo, E.J.; Hermes, C.J. A semi-empirical correlation for predicting the frost density on hydrophilic and hydrophobic substrates. Int. J. Refrig. 2017, 74, 313–323. [Google Scholar] [CrossRef]
- Baehr, H.D.; Stephan, K. Heat and Mass Transfer, 2nd ed.; Springer: Berlin, Germany, 2006. [Google Scholar]
- Na, B.; Webb, R.L. Mass transfer on and within a frost layer. Int. J. Heat Mass Trans. 2004, 47, 899–911. [Google Scholar] [CrossRef]
- Negrelli, S.; Hermes, C.J. A semi-empirical correlation for the thermal conductivity of frost. Int. J. Refrig. 2015, 58, 243–252. [Google Scholar] [CrossRef]
- Negrelli, S.; Cardoso, R.P.; Hermes, C.J. A finite-volume diffusion-limited aggregation model for predicting the effective thermal conductivity of frost. Int. J. Heat Mass Transf. 2016, 101, 1263–1272. [Google Scholar] [CrossRef]
- Negrelli, S.; Nascimento, V.S.; Hermes, C.J. A study of the effective thermal conductivity of frost formed on parallel plate channels. Exp. Therm. Fluid Sci. 2016, 78, 301–308. [Google Scholar] [CrossRef]
- Hosseini, S.H.; Valizadeh, M.; Zendehboudi, A.; Song, M. General correlation for frost thermal conductivity on parallel sur-face channels. Energy Build. 2020, 225, 110282. [Google Scholar] [CrossRef]
- Hermes, C.J.; Loyola, F.R.; Nascimento, V.S. A semi-empirical correlation for the frost density. Int. J. Refrig. 2014, 46, 100–104. [Google Scholar] [CrossRef]
- Kim, M.-H.; Kim, H.; Lee, K.-S.; Kim, D.R. Frosting characteristics on hydrophobic and superhydrophobic surfaces: A review. Energy Convers. Manag. 2017, 138, 1–11. [Google Scholar] [CrossRef]
- Kim, K.; Lee, K.-S. Frosting and defrosting characteristics of a fin according to surface contact angle. Int. J. Heat Mass Transf. 2011, 54, 2758–2764. [Google Scholar] [CrossRef]
- Antonini, C.; Innocenti, M.; Horn, T.; Marengo, M.; Amirfazli, A. Understanding the effect of superhydrophobic coatings on energy reduction in anti-icing systems. Cold Reg. Sci. Technol. 2011, 67, 58–67. [Google Scholar] [CrossRef]
- Rahimi, M.; Afshari, A.; Fojan, P.; Gurevich, L. The effect of surface modification on initial ice formation on aluminum sur-faces. Appl. Surf. Sci. 2015, 355, 327–333. [Google Scholar] [CrossRef]
- Rahman, M.A.; Jacobi, A.M. Effects of microgroove geometry on the early stages of frost formation and frost properties. Appl. Therm. Eng. 2015, 56, 91–100. [Google Scholar] [CrossRef]
- Yang, W.; Zeng, B.; Zhang, Y.; He, S.; Zhao, X. Frosting performance of a nanoporous hydrophilic aluminium surface. Energies 2018, 11, 3483. [Google Scholar] [CrossRef] [Green Version]
- Mahvi, A.J.; Boyna, K.; Musser, A.; Elbel, S.; Miljkovic, N. Superhydrophobic heat exchangers delay frost formation and enhance efficiency of electric vehicle heat pumps. Int. J. Heat Mass Transf. 2021, 172, 121162. [Google Scholar] [CrossRef]
- Bergman, T.L.; Lavine, A.S.; Incropera, F.P.; DeWitt, D.P. Fundamentals of Heat and Mass Transfer, 7th ed.; John Wiley & Sons: Hoboken, NJ, USA, 2011. [Google Scholar]
- Chatterjee, A.; Derby, M.M.; Peles, Y.; Jensen, M.K. Enhancement of condensation heat transfer with patterned surfaces. Int. J. Heat Mass Transf. 2014, 71, 675–681. [Google Scholar] [CrossRef] [Green Version]
- Seo, D.; Lee, C.; Nam, Y. Influence of geometric patterns of microstructured superhydrophobic surfaces on water-harvesting performance dewing. Langmuir 2014, 30, 15468–15476. [Google Scholar] [CrossRef]
- Peng, B.; Ma, X.; Lan, Z.; Xu, W.; Wen, R. Experimental investigation on steam condensation heat transfer enhancement with vertically patterned hydrophobic-hydrophilic hybrid surfaces. Int. J. Heat Mass Transf. 2015, 83, 27–38. [Google Scholar] [CrossRef]
- Alwazzan, M.; Egab, K.; Peng, B.; Khan, J.; Li, C. Condensation on hybrid-patterned copper tubes (I): Characterization of con-densation heat transfer. Int. J. Heat Mass Transf. 2017, 112, 991–1004. [Google Scholar] [CrossRef]
- Sommers, A.D.; Brest, T.J.; Eid, K.F. Topography-Based Surface Tension Gradients to Facilitate Water Droplet Movement on Laser-Etched Copper Substrates. Langmuir 2013, 29, 12043–12050. [Google Scholar] [CrossRef] [PubMed]
- Liu, C.; Sun, J.; Li, J.; Xiang, C.; Chenghao, X.; Wang, Z.; Zhou, X. Long-range spontaneous droplet self-propulsion on wettability gradient surfaces. Sci. Rep. 2017, 7, 1–8. [Google Scholar] [CrossRef]
- Sommers, A.D.; Panth, M.; Eid, K.F. Self-propelled water droplet movement on a laser-etched radial gradient copper surface. Appl. Therm. Eng. 2020, 173, 115226. [Google Scholar] [CrossRef]
- Storey, B.; Jacobi, A. The effect of streamwise vortices on the frost growth rate in developing laminar channel flows. Int. J. Heat Mass Transf. 1999, 42, 3787–3802. [Google Scholar] [CrossRef]
- Sommers, A.; Jacobi, A. Air-side heat transfer enhancement of a refrigerator evaporator using vortex generation. Int. J. Refrig. 2005, 28, 1006–1017. [Google Scholar] [CrossRef]
- Stoecker, W.F. How frost formation on coils affects refrigeration systems. Refrig. Eng. 1957, 65, 42–46. [Google Scholar]
- Da Silva, D.L.; Hermes, C.J.; Melo, C. Experimental study of frost accumulation on fan-supplied tube-fin evaporators. Appl. Therm. Eng. 2011, 31, 1013–1020. [Google Scholar] [CrossRef] [Green Version]
- Kondepudi, S.N.; O’Neal, D.L. The effect of frost growth on extended surface heat exchanger performance: A review. ASHRAE Trans. 1987, 93, 258–274. [Google Scholar]
- Rite, R.W.; Crawford, R.R. The effect of frost accumulation on the performance of domestic refrigerator-freezer finned-tube evaporator coils. ASHRAE Trans. 1991, 97, 428–437. [Google Scholar]
- Ogawa, K.; Tanaka, N.; Takeshita, M. Performance improvement of plate fin-and-tube heat exchangers under frosting condi-tions. ASHRAE Trans. 1993, 99, 762–771. [Google Scholar]
- Carlson, D.M.; Hrnjak, P.S.; Bullard, C.W. Deposition, Distribution, and Effects of Frost on a Multi-Row Heat Exchanger Performance; Technical Report; University of Illinois at Urbana-Champaign: Champaign, IL, USA, 2001. [Google Scholar]
- Jhee, S.; Lee, K.-S.; Kim, W.-S. Effect of surface treatments on the frosting/defrosting behavior of a fin-tube heat exchanger. Int. J. Refrig. 2002, 25, 1047–1053. [Google Scholar] [CrossRef]
- Inan, C.; Karatas, H.; Egrican, N.; Lale, C. Real time upright freezer evaporator performance under frosted conditions. In Proceedings of the International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 16–19 July 2002. [Google Scholar]
- Deng, D.-Q.; Xu, L.; Xu, S.-Q. Experimental investigation on the performance of air cooler under frosting conditions. Appl. Therm. Eng. 2003, 23, 905–912. [Google Scholar] [CrossRef]
- Chen, H.; Thomas, L.; Besant, R.W. Fan supplied heat exchanger fin performance under frosting conditions. Int. J. Refrig. 2002, 26, 140–149. [Google Scholar] [CrossRef]
- Seker, D.; Karatas, H.; Egrican, N. Frost formation on fin-and-tube heat exchangers. Part I—Modeling of frost formation on fin-and-tube heat exchangers. Int. J. Refrig. 2004, 27, 367–374. [Google Scholar] [CrossRef]
- Liu, Z.; Zhu, H.; Wang, H. Study on Transient Distributed Model of Frost on Heat Pump Evaporator. J. Asian Arch. Build. Eng. 2005, 4, 265–270. [Google Scholar] [CrossRef] [Green Version]
- Tso, C.; Cheng, Y.; Lai, A.; Lai, C.K.A. Dynamic behavior of a direct expansion evaporator under frosting condition. Part, I. Distributed model. Int. J. Refrig. 2006, 29, 611–623. [Google Scholar] [CrossRef]
- Xia, Y.; Zhong, Y.; Hrnjak, P.; Jacobi, A. Frost, defrost, and refrost and its impact on the air-side thermal-hydraulic performance of louvered-fin, flat-tube heat exchangers. Int. J. Refrig. 2006, 29, 1066–1079. [Google Scholar] [CrossRef]
- Aljuwayhel, N.F. Numerical and Experimental Study of the Influence of Frost Formation and Defrosting on the Performance of Industrial Evaporator Coils. Ph.D. Thesis, University of Wisconsin-Madison, Madison, WI, USA, 2006. [Google Scholar]
- Yang, D.-K.; Lee, K.-S.; Song, S. Fin spacing optimization of a fin-tube heat exchanger under frosting conditions. Int. J. Heat Mass Transf. 2006, 49, 2619–2625. [Google Scholar] [CrossRef]
- Özkan, D.B.; Ozil, E. Experimental study on the effect of frost parameters on domestic refrigerator finned tube evaporator coils. Appl. Therm. Eng. 2006, 26, 2490–2493. [Google Scholar] [CrossRef]
- Ngonda, T.N.; Sheer, T.J. Frost formation on cooling coil in supersaturated supply air. In Proceedings of the International Con-gress of Refrigeration, Beijing, China, 21–26 August 2007. [Google Scholar]
- Albert, M.; Sahinagic, R.; Gasser, L.; Wellig, B.; Hilfiker, K. Prediction of ice and frost formation in the fin tube evaporators for air/water heat pumps. In Proceedings of the 9th IEA Heat Pump Conference, Zurich, Switzerland, 20–22 May 2008. [Google Scholar]
- Huang, J.M.; Hsieh, W.C.; Ke, X.J.; Wang, C.C. The effects of frost thickness on the heat transfer of finned tube heat ex-changer subject to the combined influence of fan types. Appl. Therm. Eng. 2008, 28, 728–737. [Google Scholar] [CrossRef]
- Zhang, P.; Hrnjak, P. Air-side performance evaluation of three types of heat exchangers in dry, wet and periodic frosting conditions. Int. J. Refrig. 2009, 32, 911–921. [Google Scholar] [CrossRef] [Green Version]
- Lenic, K.; Trp, A.; Frankovic, B. Prediction of an effective cooling output of the fin-and-tube heat exchanger under frosting conditions. Appl. Therm. Eng. 2009, 29, 2534–2543. [Google Scholar] [CrossRef]
- Moallem, E.; Cremaschi, L.; Fischer, D.E. Experimental investigation of frost growth on microchannel heat exchangers. In Proceedings of the 13th International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 12–15 August 2010. [Google Scholar]
- Knabben, F.T.; Hermes, C.J.; Melo, C. In-situ study of frosting and defrosting processes in tube-fin evaporators of household refrigerating appliances. Int. J. Refrig. 2011, 34, 2031–2041. [Google Scholar] [CrossRef]
- Da Silva, D.L.; Hermes, C.J.; Melo, C. First-principles modeling of frost accumulation on fan-supplied tube-fin evaporators. Appl. Therm. Eng. 2011, 31, 2616–2621. [Google Scholar] [CrossRef]
- Wu, J.; Ouyang, G.; Hou, P.; Xiao, H. Experimental investigation of frost formation on a parallel flow evaporator. Appl. Energy 2011, 88, 1549–1556. [Google Scholar] [CrossRef]
- Jopollo, C.M.; Molinaroli, L.; Antonellis, S.D.; Merlo, U. Experimental analysis of frost formation with presence of an electric field on fin and tube evaporator. Int. J. Refrig. 2012, 35, 468–474. [Google Scholar] [CrossRef]
- Kim, K.; Kim, D.R.; Lee, K.-S. Local frosting behavior of a plated-fin and tube heat exchanger according to the refrigerant flow direction and surface treatment. Int. J. Heat Mass Transf. 2013, 64, 751–758. [Google Scholar] [CrossRef]
- Ribeiro, R.S.; Hermes, C.J. Algebraic modeling and thermodynamic design of fan-supplied tube-fin evaporators running under frosting conditions. Appl. Therm. Eng. 2014, 70, 552–559. [Google Scholar] [CrossRef]
- Da Silva, D.L.; Melo, C.; Hermes, C.J. Effect of frost morphology on the thermal-hydraulic performance of fan-supplied tube-fin evaporators. Appl. Therm. Eng. 2017, 111, 1060–1068. [Google Scholar] [CrossRef]
- Timmermann, M.A.S.; Kaviany, M.; Barbosa, J.R., Jr. Thermal performance of peripheral-finned tube evaporators under frost-ing. Int. J. Heat Mass Trans. 2018, 116, 194–207. [Google Scholar] [CrossRef]
- Popovac, M.; Seichter, S.; Benovsky, P.; Fleckl, T.; Reichl, C. Numerical analysis of the frosting performance of the air side of a heat pump. In Proceedings of the 24th International Congress of Refrigeration, Yokohama, Japan, 16–22 August 2015. [Google Scholar]
- Amer, M.; Wang, C.-C. Experimental investigation on defrosting of a cold flat plate via ultrasonic vibration under natural convection. Appl. Therm. Eng. 2020, 179, 115729. [Google Scholar] [CrossRef]
- Amer, M.; Wang, C.-C. Review of defrosting methods. Renew. Sustain. Energy Rev. 2017, 73, 53–74. [Google Scholar] [CrossRef]
- Dong, J.; Deng, S.S.; Jiang, Y.; Xia, L.; Yao, Y. An experimental study on defrosting heat supplies and energy consumptions during a reverse cycle defrost operation for an air source heat pump. Appl. Therm. Eng. 2012, 37, 380–387. [Google Scholar] [CrossRef]
- Kim, Y.-S.; Tikhonov, A.N.; Shin, Y.; Lee, J. Experimental study on high performance defrosting heater for household refrigerator. In Proceedings of the 13th International Heat Transfer Conference, Sydney, Australia, 13–18 August 2006. [Google Scholar]
- Stoecker, W. Selecting the size of pipes carrying hot gas to defrost evaporators. Int. J. Refrig. 1984, 7, 225–228. [Google Scholar] [CrossRef]
- Niederer, D.H. Frosting and defrosting effects on coil heat transfer. ASHRAE Trans. 1986, 82, 467–473. [Google Scholar]
- Cho, H.; Kim, Y.; Jang, I. Performance of a showcase refrigeration system with multi-evaporator during on–off cycling and hot-gas bypass defrost. Energy 2005, 30, 1915–1930. [Google Scholar] [CrossRef]
- Byun, J.-S.; Lee, J.; Jeon, C.-D. Frost retardation of an air-source heat pump by the hot gas bypass method. Int. J. Refrig. 2008, 31, 328–334. [Google Scholar] [CrossRef]
- Minglu, Q.; Liang, X.; Deng, S.; Yiqiang, J. Improved indoor thermal comfort during defrost with a novel reverse-cycle de-frosting method for air source heat pumps. Build. Environ. 2010, 45, 2354–2361. [Google Scholar] [CrossRef]
- Zakrzewski, B. Optimal defrost cycle for the air cooler. Int. J. Refrig. 1984, 7, 41–45. [Google Scholar] [CrossRef]
- Bansal, P.; Fothergill, D.; Fernandes, R. Thermal analysis of the defrost cycle in a domestic freezer. Int. J. Refrig. 2010, 33, 589–599. [Google Scholar] [CrossRef]
- Özkan, D.B.; Ozil, E.; Inan, C. Experimental Investigation of the Defrosting Process on Domestic Refrigerator Finned Tube Evaporators. Heat Transf. Eng. 2012, 33, 548–557. [Google Scholar] [CrossRef]
- Melo, C.; Knabben, F.T.; Pereira, P.V. An experimental study on defrost heaters applied to frost-free household refrigerators. Appl. Therm. Eng. 2013, 51, 239–245. [Google Scholar] [CrossRef]
- Knabben, F.T.; Melo, C. An experimental study on the effect of a new defrosting strategy on the energy consumption of household refrigerator. In Proceedings of the 16th International Refrigeration and Air Conditioning Conference at Purdue, West Lafayette, IN, USA, 11–14 July 2016. [Google Scholar]
- Malik, A.N.; Khan, S.A.; Lazoglu, I. A novel hybrid frost detection and defrosting system for domestic refrigerators. Int. J. Refrig. 2020, 117, 256–268. [Google Scholar] [CrossRef]













| Author | Year | Origin | Porous Medium | Geometry | Density | Thermal Conductivity | Air-Frost Interface |
|---|---|---|---|---|---|---|---|
| Brian et al. [29] | 1969 | USA | No | Flat plate | Their own | Various | Saturated |
| Schneider [30] | 1978 | Germany | No | Flat plate | Their own | Their own | Saturated |
| O’Neal [27] | 1982 | USA | Yes | Channel | Prescribed | Sanders [31] | Saturated |
| Sami and Duong [32] | 1988 | Canada | Yes | Flat plate | - | Yonko and Sepsy [33] | Saturated |
| Sherif et al. [34] | 1993 | USA | Yes | Flat plate | Hayashi et al. [35] | Various | Saturated |
| Tao et al. [36] | 1993 | Canada | No | Flat plate | Prescribed | Their own | Saturated |
| Le gall et al. [37] | 1997 | France | Yes | Flat plate | Prescribed | Auracher [38] | Saturated |
| Lee et al. [39] | 1997 | S. Korea | No | Flat plate | - | Their own | Saturated |
| Ismael and Salinas [40] | 1999 | Brazil | Yes | Channel | Mao et al. [41] | Yonko and Sepsy [33] | Saturated |
| Lüer and Beer [42] | 2000 | Germany | Yes | Channel | Various | Auracher [38] | Saturated |
| Cheng and Cheng [43] | 2001 | China | No | Flat plate | Hayashi et al. [35] | Brian et al. [29] | Saturated |
| Yang and Lee [44] | 2004 | S. Korea | No | Flat plate | Their own | Their own | Saturated |
| Na and Webb [45] | 2004 | USA | Yes | Flat plate | Prescribed | Sanders [31] | Supersaturated |
| Lee and Ro [46] | 2005 | S. Korea | Yes | Flat plate | Prescribed | Auracher [38] | Supersaturated |
| Hermes et al. [17] | 2009 | Brazil | Yes | Flat plate | Their own | Lee et al. [39] | Saturated |
| Cai et al. [14] | 2011 | USA | Yes | Flat plate | Their own | Their own | Saturated |
| Kandula [47] | 2011 | USA | Yes | Flat plate | His own | His own | Saturated |
| Hermes [48] | 2012 | Brazil | Yes | Flat plate | His own | His own | Saturated |
| Loyola et al. [49] | 2014 | Brazil | Yes | Channel | Nascimento et al. [50] | Hermes [48] | Supersaturated |
| El Cheikh and Jacobi [51] | 2014 | USA | Yes | Flat plate | Prescribed | O’Neal and Tree [52] | Supersaturated |
| Hermes et al. [53] | 2018 | USA/Brazil | No | Flat plate | Sommers et al. [54] | - | Saturated |
| Author | Year | Origin | Technology | Approach | Fan |
|---|---|---|---|---|---|
| Stoecker [79] | 1957 | USA | Tube-fin | Experimental | No |
| Kondepudi and O’Neil [81] | 1987 | USA | Tube-fin | Numerical (lumped) | No |
| Rite and Crawford [82] | 1991 | USA | Tube-fin | Experimental | No |
| Ogawa et al. [83] | 1993 | Japan | No-frost | Experimental | No |
| Bejan et al. [1] | 1994 | USA | No-frost | Theoretical | No |
| Carlson et al. [84] | 2001 | USA | Microchannel | Experimental | No |
| Jhee et al. [85] | 2002 | S. Korea | Tube-fin | Experimental | No |
| Inan et al. [86] | 2002 | Turkey | Tube-fin | Experimental | Yes |
| Deng et al. [87] | 2003 | China | Tube-fin | Experimental | No |
| Chen et al. [88] | 2003 | Canada | Heat sink | Numerical (lumped) | Yes |
| Seker et al. [89] | 2004 | Turkey | No-frost | Numerical (lumped) | No |
| Liu et al. [90] | 2005 | China | Tube-fin | Numerical (distributed) | No |
| Tso et al. [91] | 2006 | Singapore | Tube-fin | Numerical (distributed) | No |
| Xia et al. [92] | 2006 | USA | Microchannel | Numerical (lumped) | No |
| Aljuwayhel [93] | 2006 | USA | Industrial | Numerical (distributed) | Yes |
| Yang et al. [94] | 2006 | S. Korea | Tube-fin | Numerical (distributed) | No |
| Özkan and Ozil [95] | 2006 | Turkey | Tube-fin | Experimental | Yes |
| Ngonda and Sheer [96] | 2007 | S. Africa | Tube-fin | Numerical (distributed) | No |
| Albert et al. [97] | 2008 | Switzerland | Tube-fin | Numerical (distributed) | No |
| Huang et al. [98] | 2008 | Taiwan | Tube-fin | CFD | Yes |
| Zhang and Hrnjak [99] | 2009 | USA | Tube-fin | Experimental | No |
| Lenic et al. [100] | 2009 | Croatia | Tube-fin | Numerical (distributed) | No |
| Moallem et al. [101] | 2010 | USA | Microchannel | Experimental | No |
| Knabben et al. [102] | 2011 | Brazil | Tube-fin | Numerical (distributed) | Yes |
| Da Silva et al. [80] | 2011 | Brazil | Tube-fin | Experimental | Yes |
| Da Silva et al. [103] | 2011 | Brazil | Tube-fin | Numerical (distributed) | Yes |
| Wu et al. [104] | 2011 | China | Microchannel | Experimental | No |
| Jopollo et al. [105] | 2012 | Italy | Tube-fin | Experimental | No |
| Kim et al. [106] | 2013 | S. Korea | Tube-fin | Experimental | No |
| Ribeiro and Hermes [107] | 2014 | Brazil | Tube-fin | Numerical (lumped) | Yes |
| Borges et al. [3] | 2015 | Brazil | Tube-fin | Numerical (distributed) | Yes |
| Da Silva et al. [108] | 2017 | Brazil | Tube-fin | Numerical (distributed) | Yes |
| Timmermann et al. [109] | 2018 | Brazil | Peripheral | Numerical (distributed) | Yes |
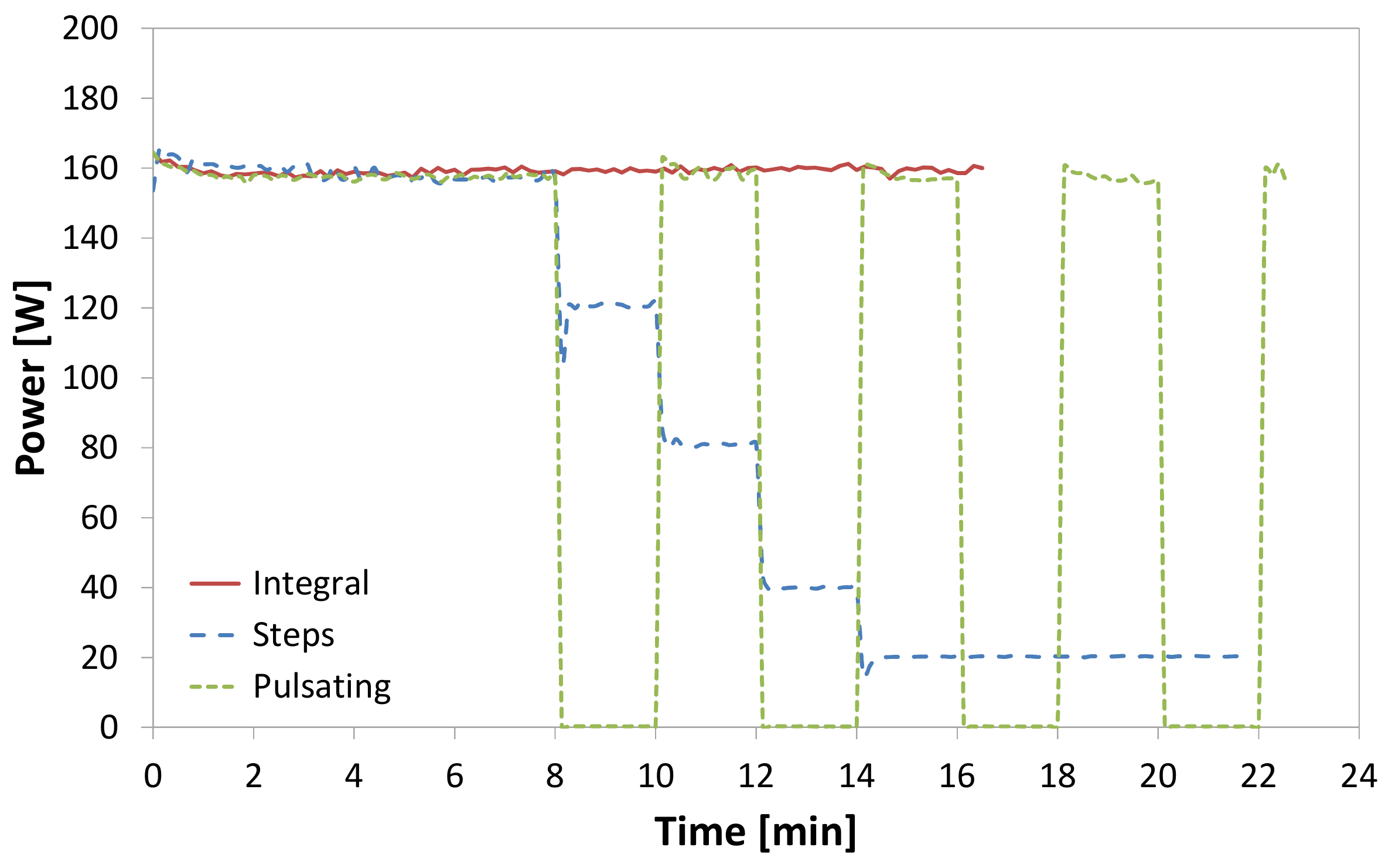
| Test | Heater Type | Mode | Defrost Time [min] | Defrost Power [W] | Defrost Efficiency [%] |
|---|---|---|---|---|---|
| 1 | Distributed | Integral | 19.6 | 160 | 31.1 ± 2.0 |
| 2 | Distributed | Integral | 15.2 | 160 | 38.6 ± 2.6 |
| 3 | Calrod | Integral | 11.9 | 300 | 27.5 ± 1.8 |
| 4 | Calrod | Integral | 19.3 | 160 | 34.0 ± 2.0 |
| 5 | Glass tube | Integral | 16.8 | 160 | 36.0 ± 2.0 |
| 6 | Distributed | Steps | 28.5 | 160 to 20 | 45.7 ± 2.6 |
| 7 | Calrod | Steps | 22.3 | 160 to 20 | 43.4 ± 2.8 |
| 8 | Glass tube | Steps | 21.9 | 160 to 20 | 48.0 ± 2.9 |
| 9 | Distributed | Pulsating | 22.9 | 160 to 0 | 39.9 ± 2.3 |
| 10 | Calrod | Pulsating | 23.2 | 160 to 0 | 42.7 ± 2.4 |
| 11 | Glass tube | Pulsating | 22.6 | 160 to 0 | 39.8 ± 2.4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hermes, C.J.L.; Boeng, J.; da Silva, D.L.; Knabben, F.T.; Sommers, A.D. Evaporator Frosting in Refrigerating Appliances: Fundamentals and Applications. Energies 2021, 14, 5991. https://doi.org/10.3390/en14185991
Hermes CJL, Boeng J, da Silva DL, Knabben FT, Sommers AD. Evaporator Frosting in Refrigerating Appliances: Fundamentals and Applications. Energies. 2021; 14(18):5991. https://doi.org/10.3390/en14185991
Chicago/Turabian StyleHermes, Christian J. L., Joel Boeng, Diogo L. da Silva, Fernando T. Knabben, and Andrew D. Sommers. 2021. "Evaporator Frosting in Refrigerating Appliances: Fundamentals and Applications" Energies 14, no. 18: 5991. https://doi.org/10.3390/en14185991
APA StyleHermes, C. J. L., Boeng, J., da Silva, D. L., Knabben, F. T., & Sommers, A. D. (2021). Evaporator Frosting in Refrigerating Appliances: Fundamentals and Applications. Energies, 14(18), 5991. https://doi.org/10.3390/en14185991





