Experimental Analysis of the R744/R404A Cascade Refrigeration System with Internal Heat Exchanger. Part 1: Coefficient of Performance Characteristics
Abstract
:1. Introduction
2. Experimental Apparatus and Data Reduction
2.1. Experimental Apparatus
2.2. Experimental Procedure
- Adjust the temperature of the heat source water by a constant-temperature bath to the set temperature and operate the heat source water.
- Turn on the power of the R404A compressor and adjust the required R404A evaporation temperature and mass flow rate by adjusting the high-temperature expansion valve and inverter frequency for the R404A compressor.
- After operating the R404A refrigeration cycle, when the R744 condensation pressure drops to a certain pressure, the R744 compressor is turned on, and the low-temperature expansion valve and inverter frequency are adjusted for the R744 compressor to control the evaporation temperature and mass flow rate of the CRS.
- The flow rate of the heat source water and R744 mass flow are adjusted to control the subcooling and superheating of the high- and low-temperature cycles, respectively.
- When the system reaches a steady state (temperature variation within ±0.5 °C, pressure variation within ±5 kPa, and mass flow rate within ±0.05 kg/min over a 15-min measurement period), the measurement equipment is operated, and the temperature, pressure, and mass flow data are sent to the computer using GPIB communication. The temperature of the refrigerant, pressure mass flow rate, and power consumption of the compressor are measured three times at 5-min intervals. The operating conditions are shown in Table 3.
2.3. Data Reduction
2.4. Uncertainties
3. Results and Discussion
3.1. Effect of the Degree of Subcooling and Superheating
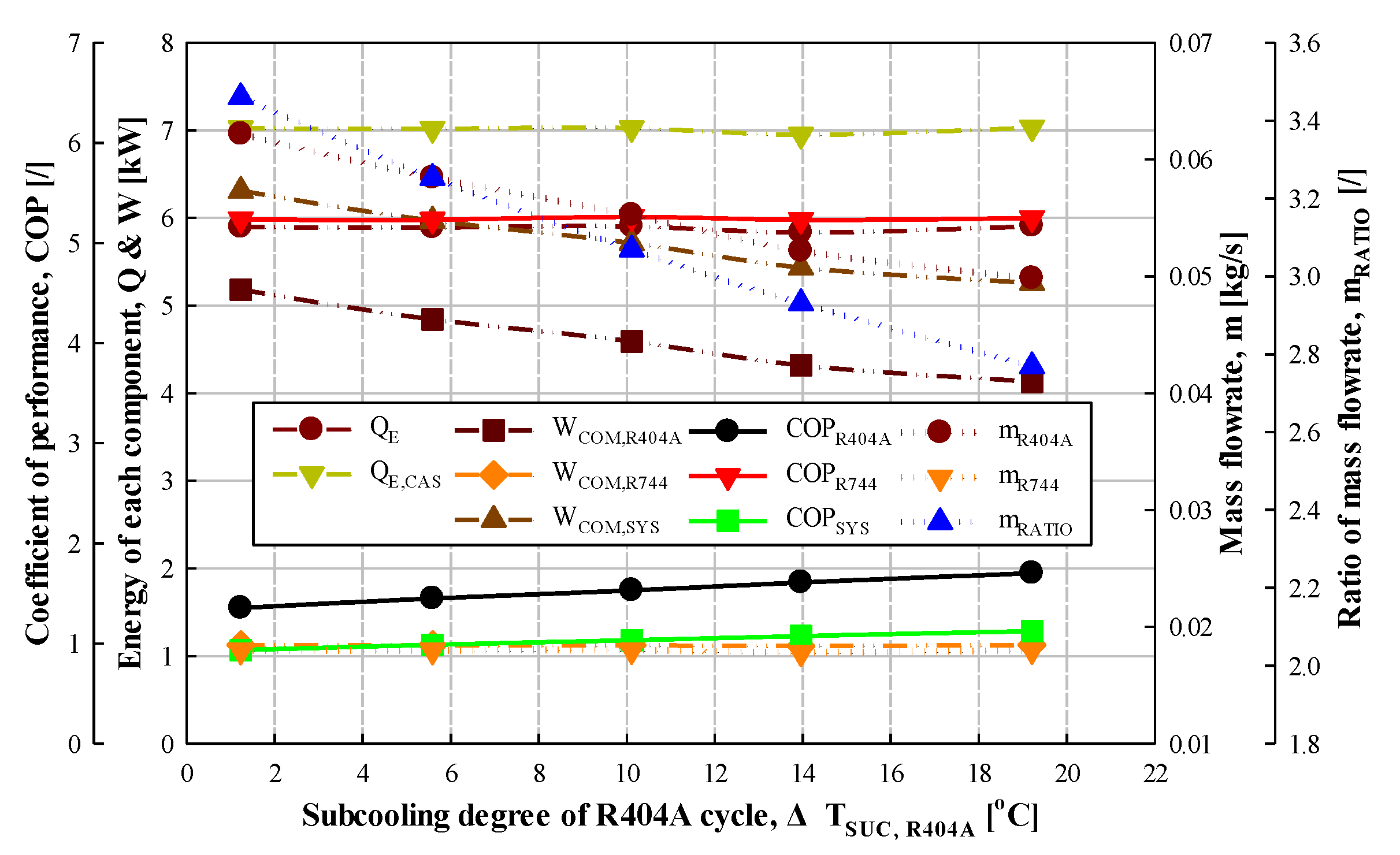
3.1.1. Effect of the Degree of Subcooling
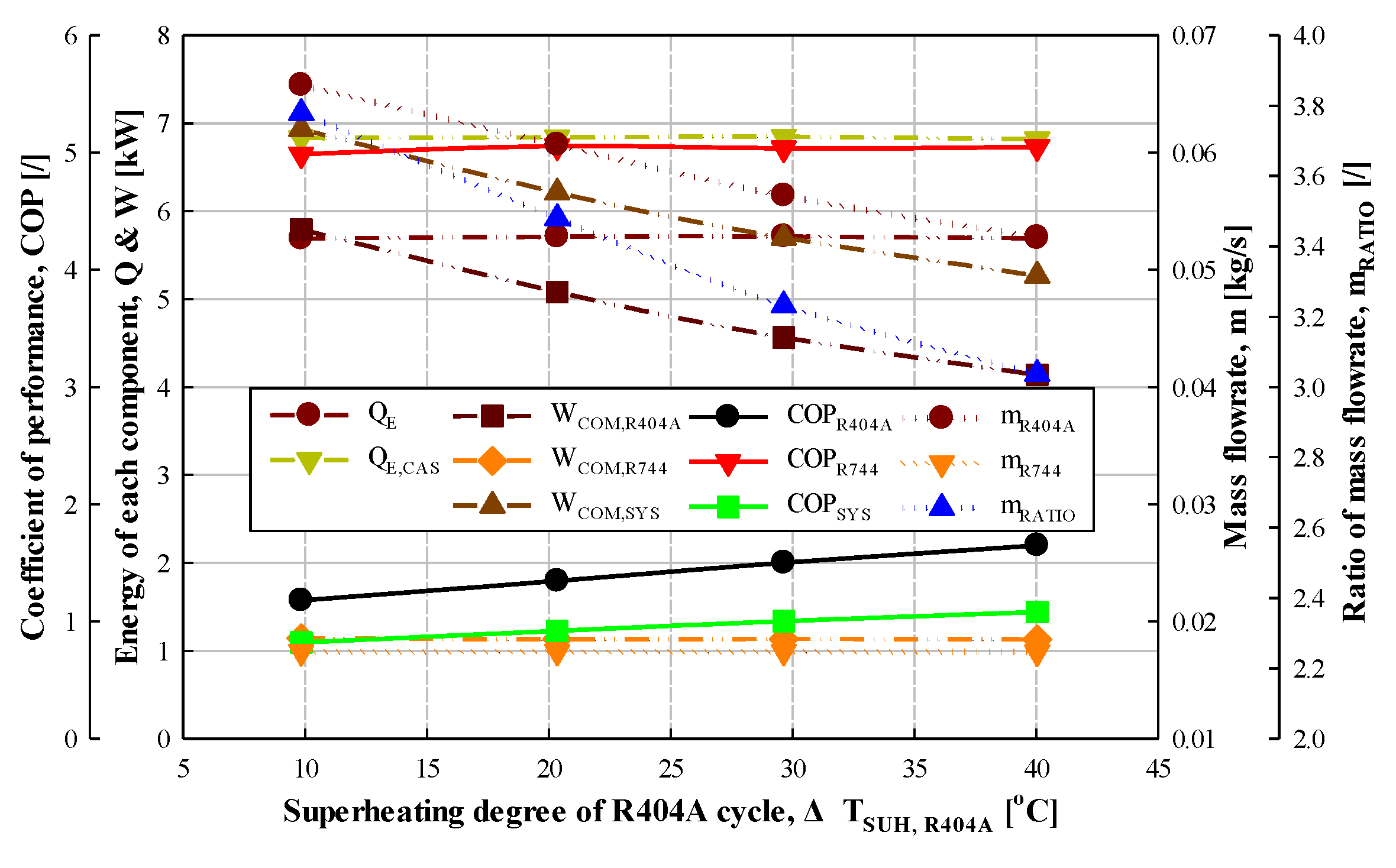
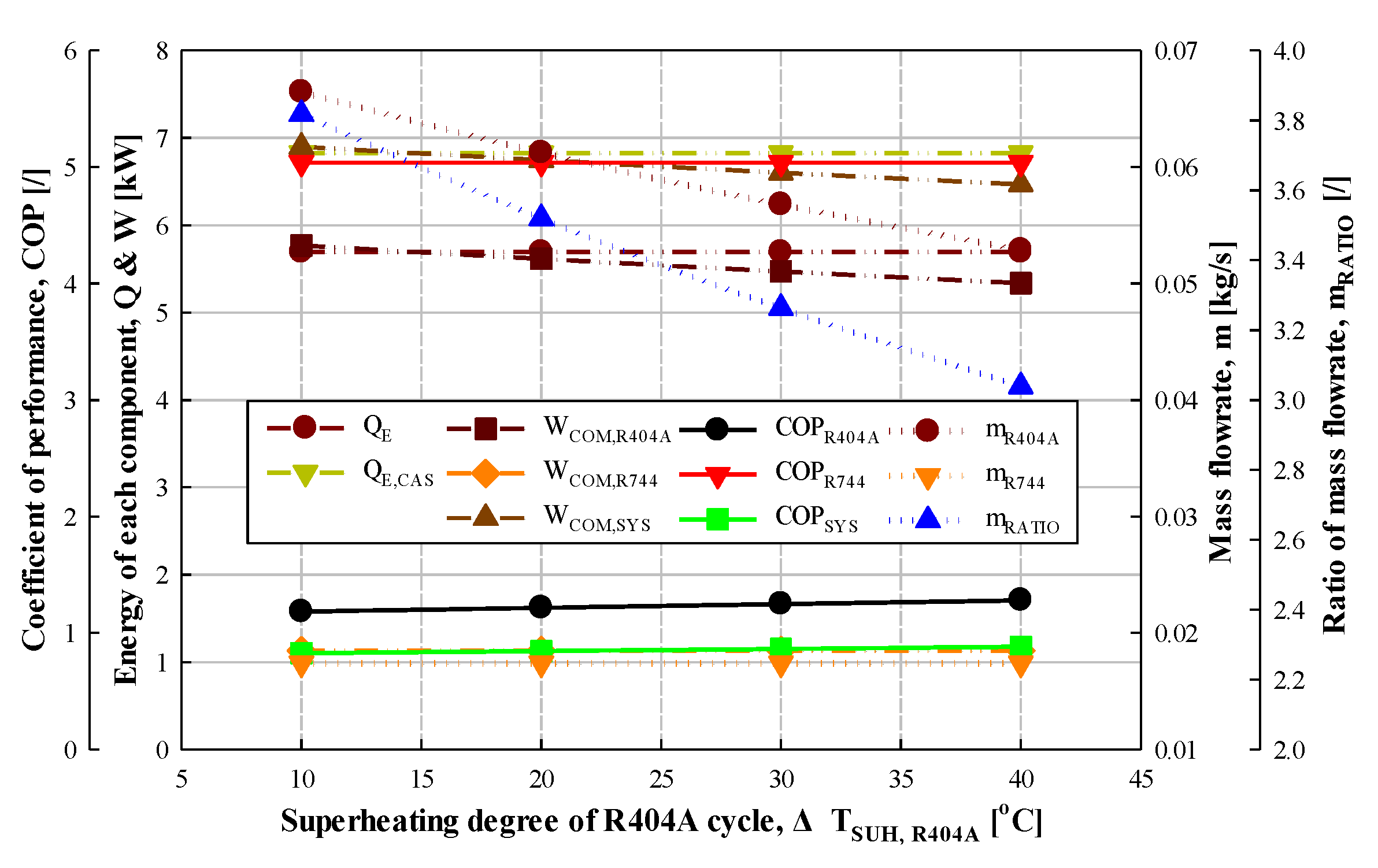
3.1.2. Effect of Degree of Superheating
3.2. Effect of Condensation and Evaporation Temperature
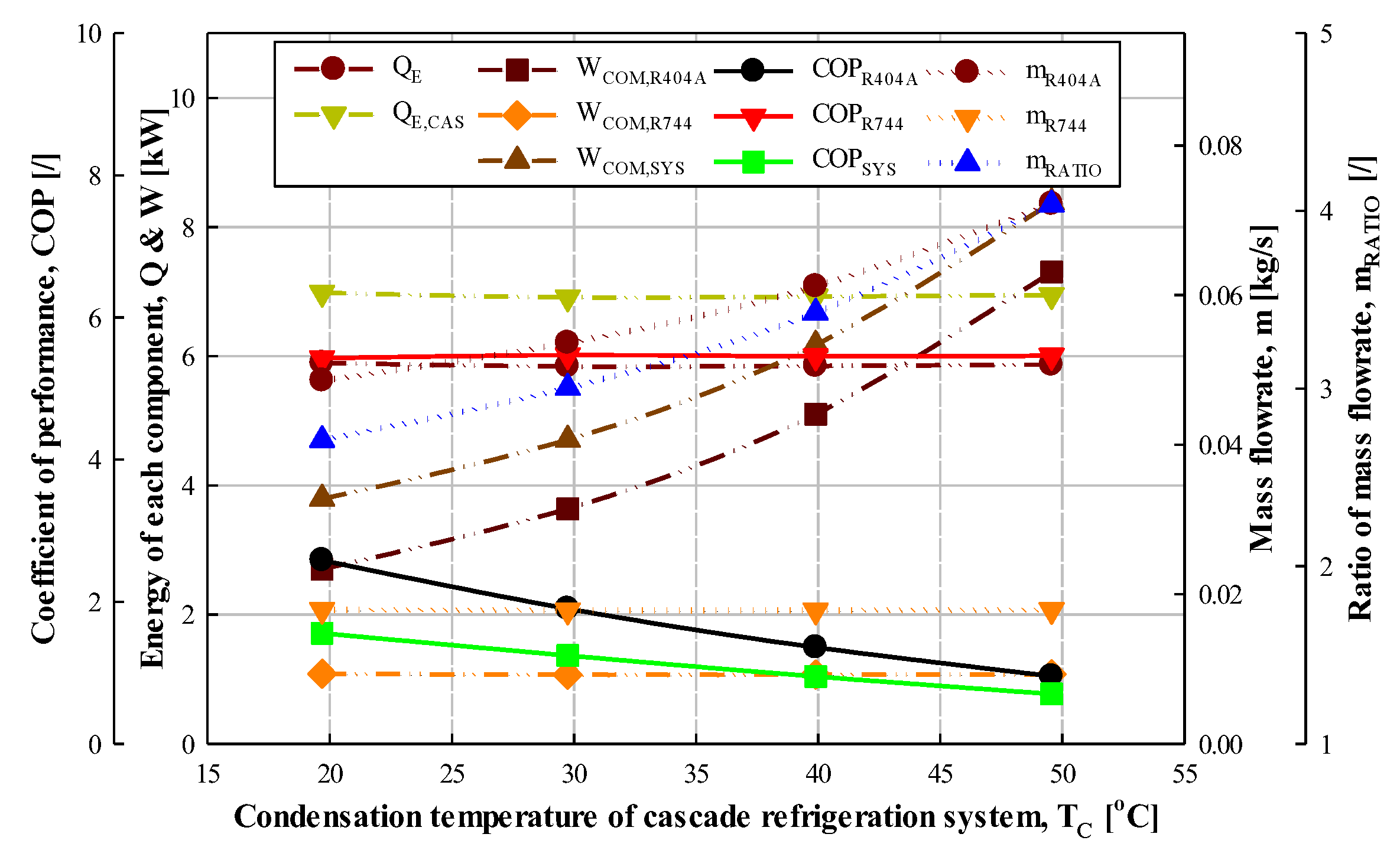
3.2.1. Effect of Condensation Temperature
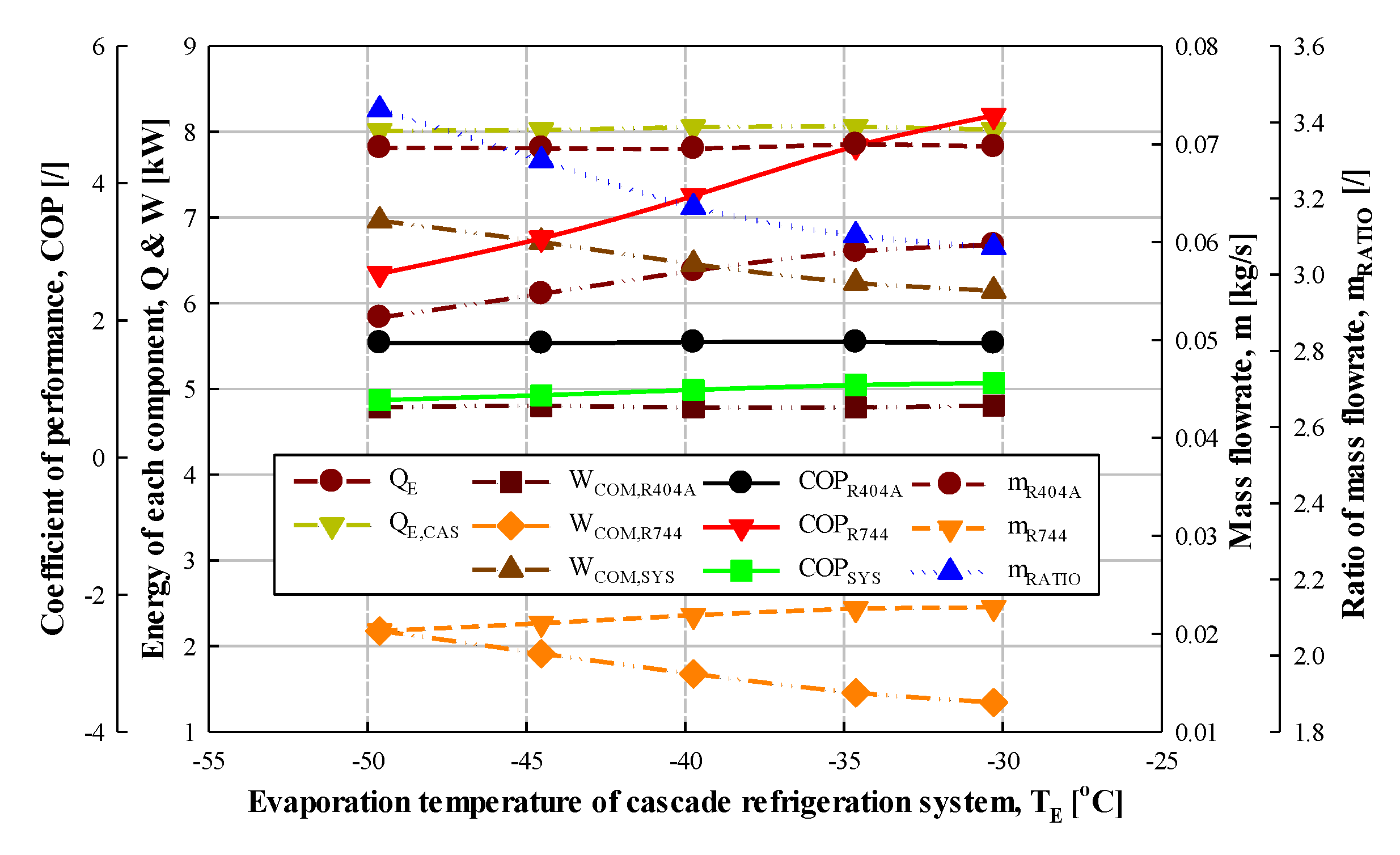
3.2.2. Effect of Evaporation Temperature
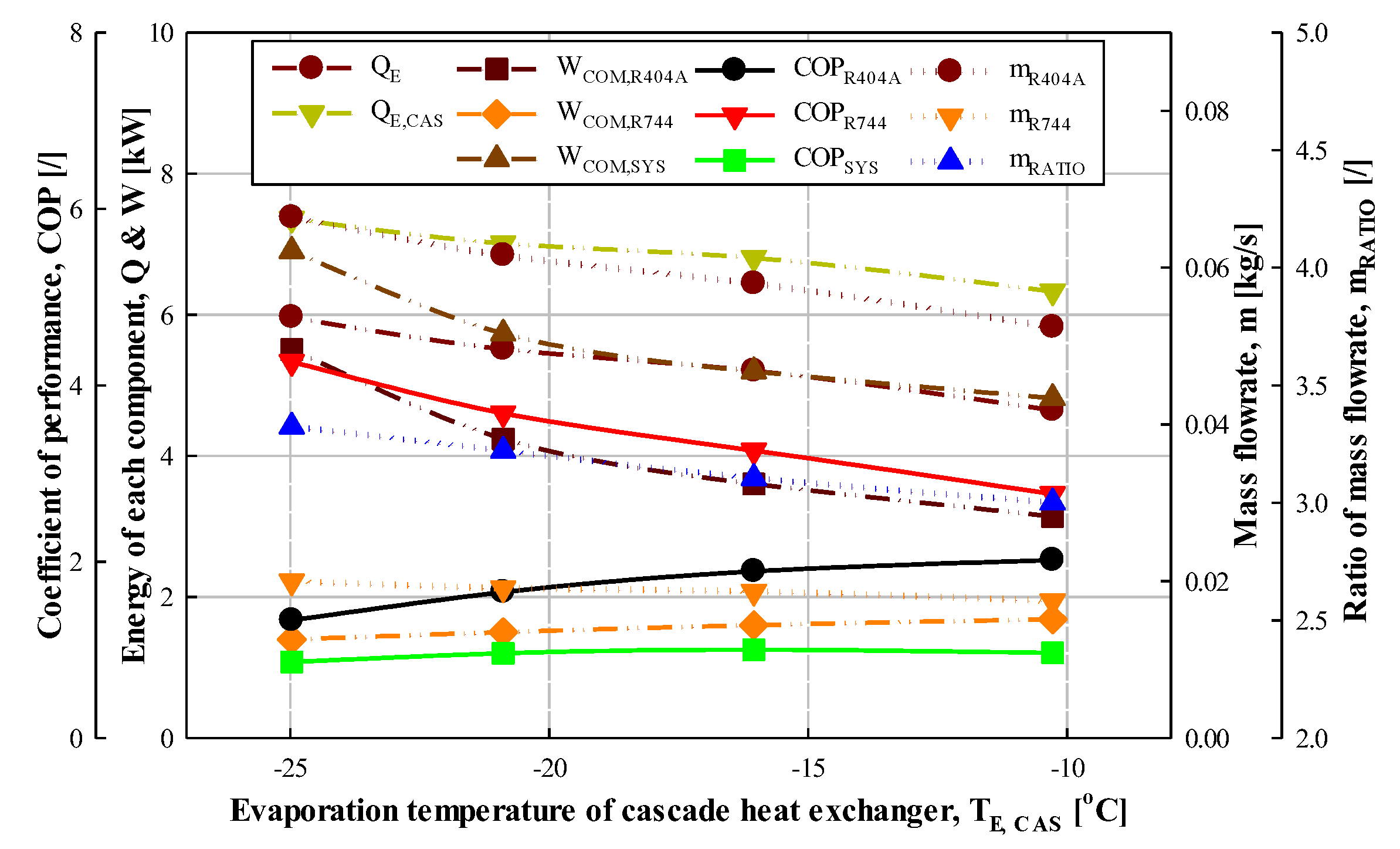
3.3. Effect of Evaporation Temperature of Cascade Heat Exchanger
3.4. Effect of Internal Heat Exchanger Efficiency
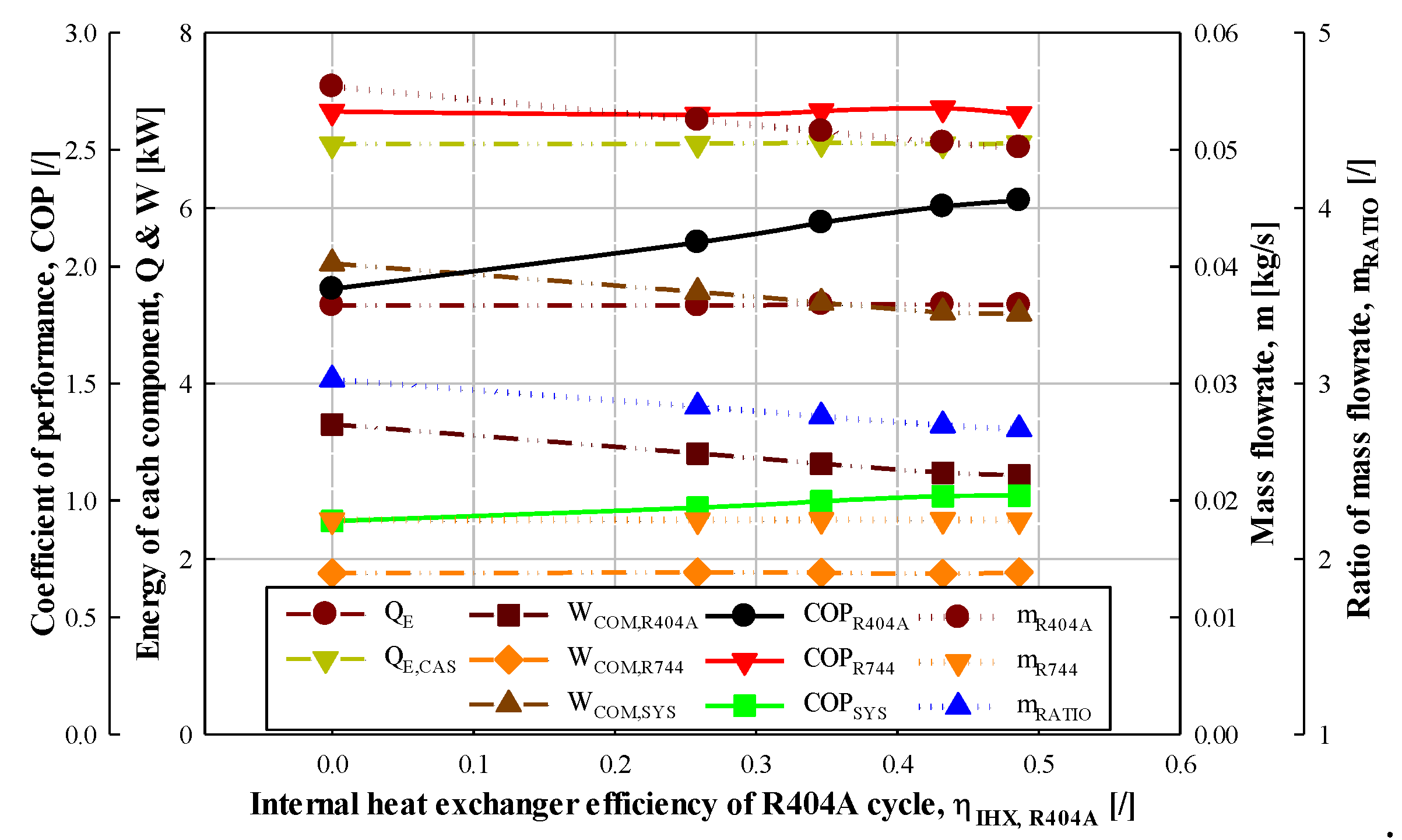
3.4.1. Effect of Internal Heat Exchanger Efficiency at R404A Cycle
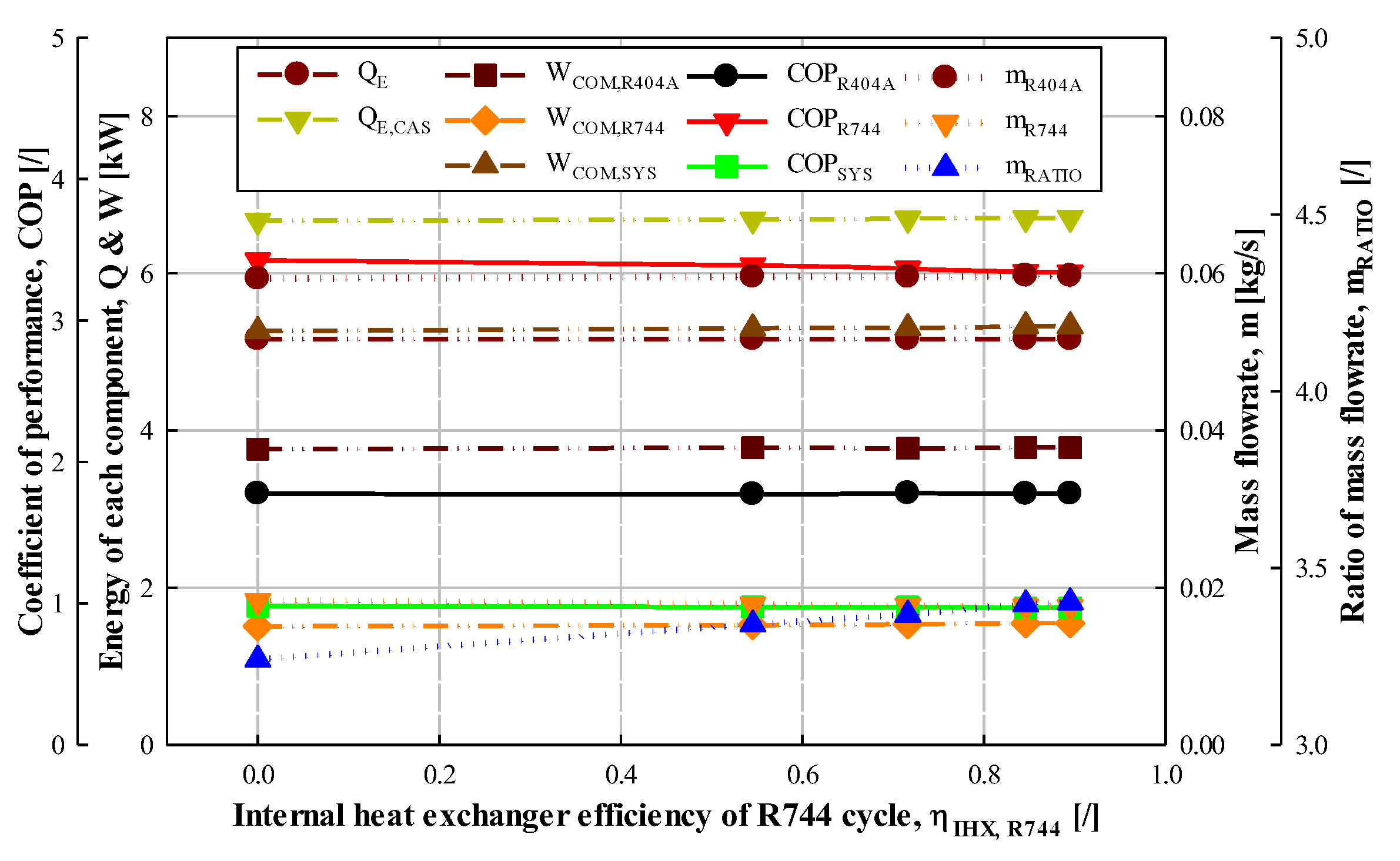
3.4.2. Effect of Internal Heat Exchanger Efficiency at R744 Cycle
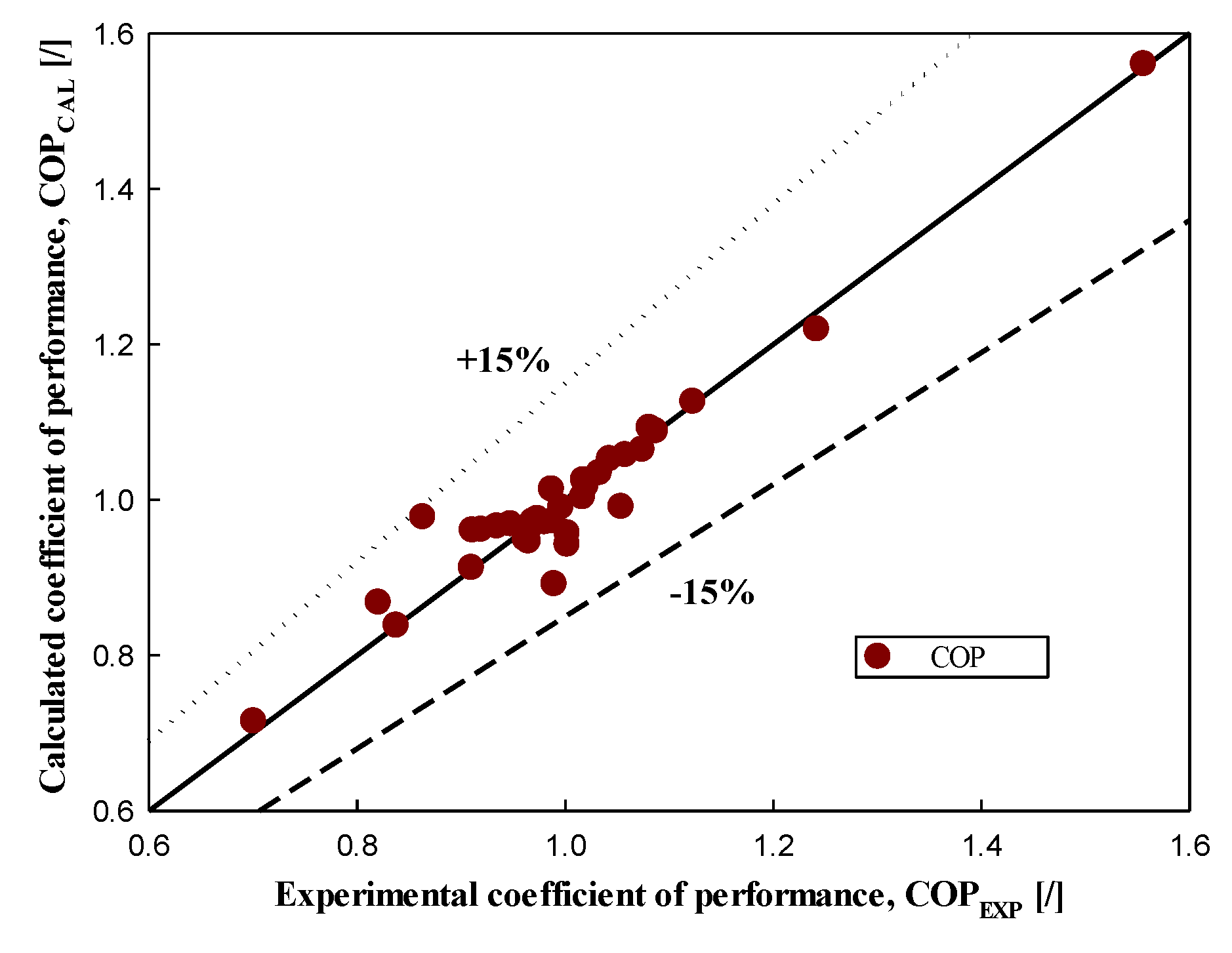
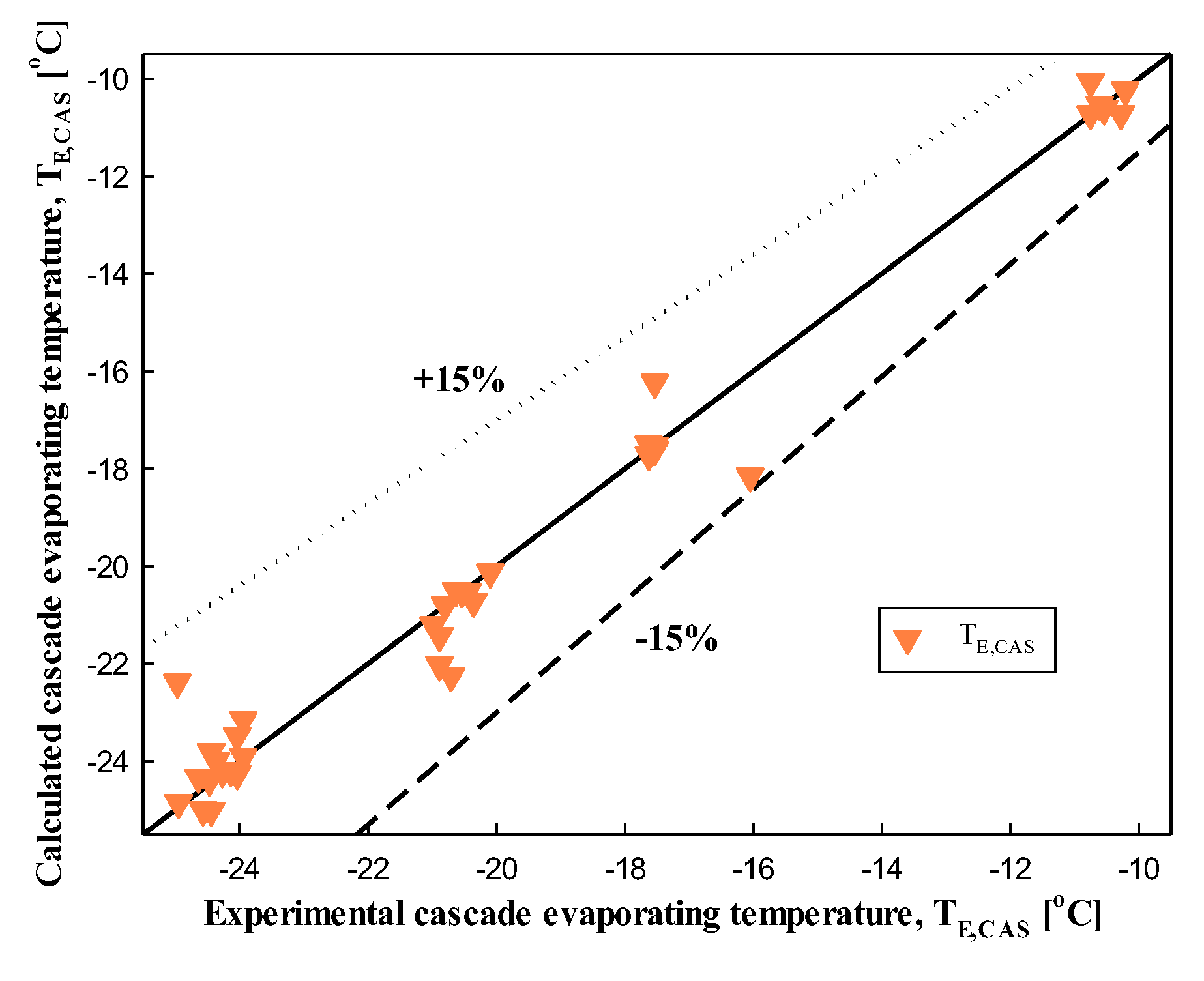
3.5. Comparison of Experimental and Performance Analysis Data
3.6. Multilinear Regression Analysis
4. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
Nomenclature
| SYMBOLS | SUBSCRIPTS | |||
| COP | Coefficients of performance | - | C | Condensation, Condenser |
| Exergy rate | kW | cal | Calculated | |
| i | Enthalpy | kJ/kg | CAS | Cascade heat exchanger |
| Mass flow rate | kg/s | COM | Compression | |
| P | Pressure | kPa | D | Destruction |
| Q | Heat capacity | kW | E | Evaporation, Evaporator |
| s | Entropy | kJ/(kg·K) | Exergy | |
| T | Temperature | °C | exp | Experimental |
| W | Power consumption | kW | F | Fuel |
| IHX | Internal heat exchanger | |||
| GREEK SYMBOLS | k | kth component | ||
| Difference | P | Product | ||
| η | Efficiency | Ratio | Ratio | |
| R404A | R404A refrigeration cycle | |||
| SUPERSCRIPTS | R744 | R744 refrigeration cycle | ||
| M | Mechanical | SUC | Subcooling | |
| T | Thermal | SUH | Superheating | |
| SYS | Cascade refrigeration system | |||
References
- Bitzer Refrigerant Report. Available online: https://www.bitzer-refrigerantreport.com/refrigerants/substitutes-for-r22-in-refrigeration-systems/ (accessed on 19 September 2021).
- Da Silva, A.; Filho, E.P.B.; Antunes, A.H.P. Comparison of a R744 cascade refrigeration system with R404A and R22 conventional systems for supermarkets. Appl. Therm. Eng. 2012, 41, 30–35. [Google Scholar] [CrossRef]
- Sawalha, S. Using CO2 in supermarket refrigeration. ASHRAE 2005, 47, 26–30. [Google Scholar]
- Nekså, P. CO2 as Refrigerant for Systems in Transcritical Operation Principles and Technology. Available online: http://www.ammonia21.com/files/pdf_310.pdf (accessed on 19 September 2021).
- Queiroz, M.V.A.; Panato, V.H.; Antunes, A.H.P.; Parise, J.A.R.; Filho, E.P.B. Experimental comparison of a cascade refrigeration system operating with R744/R134a and R744/R404A. In Proceedings of the International Refrigeration and Air-Conditioning Conference, West Lafayette, IN, USA, 11–13 July 2016; Paper 1785. pp. 1–10. Available online: http://docs.lib.purdue.edu/iracc/1785 (accessed on 19 September 2020).
- Wikipedia. Available online: https://en.wikipedia.org/wiki/List_of_refrigerants#cite_note-ASHRAE2007-34m-v-10 (accessed on 25 July 2021).
- Di Nicola, G.; Giuliani, G.; Polonara, F.; Stryjek, R. Blends of carbon dioxide and HFCs as working fluids for the low-temperature circuit in cascade refrigerating systems. Int. J. Refrig. 2005, 28, 130–140. [Google Scholar] [CrossRef]
- Dopazo, J.A.; Fernández-Seara, J.; Sieres, J.; Uhía, F.J. Theoretical analysis of a CO2–NH3 cascade refrigeration system for cooling applications at low temperatures. Appl. Therm. Eng. 2009, 29, 1577–1583. [Google Scholar] [CrossRef] [Green Version]
- Lee, T.-S.; Liu, C.-H.; Chen, T.-W. Thermodynamic analysis of optimal condensing temperature of cascade-condenser in CO2/NH3 cascade refrigeration systems. Int. J. Refrig. 2006, 29, 1100–1108. [Google Scholar] [CrossRef]
- Bingming, W.; Huagen, W.; Jianfeng, L.; Ziwen, X. Experimental investigation on the performance of NH3/CO2 cascade refrigeration system with twin-screw compressor. Int. J. Refrig. 2009, 32, 1358–1365. [Google Scholar] [CrossRef]
- Getu, H.; Bansal, P. Thermodynamic analysis of an R744–R717 cascade refrigeration system. Int. J. Refrig. 2008, 31, 45–54. [Google Scholar] [CrossRef]
- Yun, R.; Cho, Y. Evaluation of the performance for the CO2-NH3 cascade system and the two stage CO2 systems. In Proceedings of the 2010 SAREK Summer Annual Conference, Pyeongchang-gun, Korea, 23–25 June 2010; pp. 824–829. [Google Scholar]
- Abubakar, N.; Fitri, S.P. Thermodynamic analysis of cascade refrigeration system using CO2-NH3 refrigerant for fish cold storage application. In Proceedings of the 3rd International Conference on Marine Technology (SENTA 2018), Surabaya, Indonesia, 5–6 December 2020; pp. 170–175. [Google Scholar]
- Bresolin, C.S. A cascade R134a/R744 refrigeration cycle thermal analysis: Evaluation of the intermediate heat-exchanger parameters. In Proceedings of the 24th ABCM International Congress of Mechanical Engineering, Curitiba, Brazil, 3–8 December 2017; pp. 1–6. [Google Scholar]
- Kumar, S.; Ranga, V. Work study on low temperature (cascade) refrigeration system. Int. Res. J. Eng. Tech. 2018, 5, 2300–2305. [Google Scholar]
- Victorin, C.K.; Louis, A.O.; Alain, A.; Clotilde, G.T. Parametric study of NH3/CO2 cascade refrigeration cycles for hot climates. Int. J. Res. Rev. 2020, 7, 219–229. [Google Scholar]
- Islam, M.U.; Singh, S.K. Analysis of thermodynamic performance of a cascade refrigeration system for refrigerant couples of R22/R404a, and R744/R404a. Int. J. Sci. Res. Eng. Trends 2019, 5, 1530–1537. [Google Scholar]
- Kumar, R.; Randa, R. Comparison of thermodynamics analysis of CRS for refrigerant pairs R23/R404A and R41/R404A. Int. J. Innov. Res. Tech. 2020, 7, 324–328. [Google Scholar]
- Shakya, A.; Faisal, N.; Chauhan, T. Performance analysis of vapour compression cascade refrigeration system using refrigerants R404A and R134a. Int. J. Sci. Dev. Res. 2019, 4, 319–325. [Google Scholar]
- Winkler, J.M.; Aute, V.; Radermacher, R.; Shapiro, D. Simulation and validation of a R404A/CO2 cascade refrigeration system. In Proceedings of the International Refrigeration and Air-Conditioning Conference, Purdue, IN, USA, 14–17 July 2008. [Google Scholar]
- Bai, T.; Yu, J.; Yan, G. Advanced exergy analysis on a modified auto-cascade freezer cycle with an ejector. Energy 2016, 113, 385–398. [Google Scholar] [CrossRef]
- Sun, Z.; Liang, Y.; Liu, S.; Ji, W.; Zang, R.; Liang, R.; Guo, Z. Comparative analysis of thermodynamic performance of a cascade refrigeration system for refrigerant couples R41/R404A and R23/R404A. Appl. Energy 2016, 184, 19–25. [Google Scholar] [CrossRef]
- Morosuk, T.; Tsatsaronis, G. Advanced exergetic evaluation of refrigeration machines using different working fluids. Energy 2009, 34, 2248–2258. [Google Scholar] [CrossRef]
- Kline, S.J.; McClintock, F.A. Describing Uncertainties in Single Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- Moffat, R.J. Describing the uncertainties in experimental results. Exp. Therm. Fluid Sci. 1988, 1, 3–17. [Google Scholar] [CrossRef] [Green Version]
- Kumar, S.S.; Sivaram, A.R.; Rajavel, R. Thermodynamic Analysis of a Cascade Refrigeration System with R744/R290 Mixtures. Indian J. Sci. Technol. 2015, 8, 1–9. [Google Scholar] [CrossRef]
- Son, C.-H.; Moon, C.-G. Performance Analysis of the Cascade Refrigeration System using R744 with the low temperature cycle. J. Korean Soc. Power Syst. Eng. 2019, 23, 5–11. [Google Scholar] [CrossRef]
- Yılmaz, D.; Sınar, Ü.; Özyurt, A.; Yılmaz, B.; Mancuhan, E. Ultra Düşük Sıcaklıklarda Çalışan İki Kademeli Bir Soğutma Sisteminde Aşırı Soğutma ve Isıtmanın Performansa Etkilerinin Sayısal İncelenmesi. Afyon Kocatepe Univ. J. Sci. Eng. 2017, 17, 1172–1180. [Google Scholar] [CrossRef]
- Mosaffa, A.; Farshi, L.G.; Ferreira, C.I.; Rosen, M. Exergoeconomic and environmental analyses of CO2/NH3 cascade refrigeration systems equipped with different types of flash tank intercoolers. Energy Convers. Manag. 2016, 117, 442–453. [Google Scholar] [CrossRef] [Green Version]
- Parmar, G.G.; Kapadia, R.G. Thermodynamic Analysis of Cascade Refrigeration System using a Natural Refrigerants for Supermarket Application. Int. J. Innov. Res. Sci. Eng. Technol. 2015, 4, 1839–1846. [Google Scholar]
- Hendri; Nurhasanah, R.; Prayudi; Suhengki. Energy and Exergy Analysis of Cascade Refrigeration System Using MC22 and MC134 on HTC, R404A and R502 on LTC. J. Adv. Res. Fluid Mech. Therm. Sci. 2021, 80, 73–83. [Google Scholar] [CrossRef]
- Messineo, A.; Panno, D. Performance evaluation of cascade refrigeration systems using different refrigerants. Int. J. Air-Conditioning Refrig. 2012, 20, 1–8. [Google Scholar] [CrossRef]
- Parekh, A.D.; Tailor, P.R. Thermodynamic analysis of cascade refrigeration, system using R12-R13, 290-R23 and R404A-R23, World Academy of Science, Engineering and Technology. Int. J. Mech. Mechatron. Eng. 2014, 8, 1351–1356. [Google Scholar]
- Kilicarslan, A.; Hosoz, M. Energy and irreversibility analysis of a cascade refrigeration system for various refrigerant couples. Energy Convers. Manag. 2010, 51, 2947–2954. [Google Scholar] [CrossRef]
- Yilmaz, F.; Selbaş, R. Comparative thermodynamic performance analysis of a cascade system for cooling and heating applications. Int. J. Green Energy 2019, 16, 674–686. [Google Scholar] [CrossRef]
- Dokandari, D.A.; Hagh, A.S.; Mahmoudi, S.M.S. Thermodynamic investigation and optimization of novel ejector-expansion CO2/NH3 cascade refrigeration cycles (novel CO2/NH3 cycle). Int. J. Refrig. 2014, 46, 26–36. [Google Scholar] [CrossRef]
- Oruç, V.; Devecioğlu, A.G. Experimental assessment of the retrofit of an internal heat exchanger in refrigeration systems: The effect on energy performance and system operation. Appl. Therm. Eng. 2020, 180, 115843. [Google Scholar] [CrossRef]
- Jin, L.; Cao, F.; Yang, D.; Wang, X. Performance investigations of an R404A air-source heat pump with an internal heat exchanger for residential heating in northern China. Int. J. Refrig. 2016, 67, 239–248. [Google Scholar] [CrossRef]
- Llopis, R.; Sanz-Kock, C.; Cabello, R.; Sánchez, D.; Nebot-Andrés, L.; Catalán-Gil, J. Effects caused by the internal heat exchanger at the low temperature cycle in a cascade refrigeration plant. Appl. Therm. Eng. 2016, 103, 1077–1086. [Google Scholar] [CrossRef] [Green Version]
- Zhang, F.; Jiang, P.; Lin, Y.; Zhang, Y. Efficiencies of subcritical and transcritical CO2 inverse cycles with and without an internal heat exchanger. Appl. Therm. Eng. 2011, 31, 432–438. [Google Scholar] [CrossRef]


| Component | Characteristics |
|---|---|
| R744 compressor | Bock, model: HGX12P/40-4. Displacement with 1450 min−1: 4.4 m3h−1, No. of cylinders: 2, weight: 53 kg, max. power consumption: 2.1 kW |
| Evaporator | Hand-made, type: Horizontal double tube, material: copper tube, Internal diameter of inner tube: 11.46 mm, Internal diameter of outer tube: 33.27 mm, length of the evaporator: 8000 mm |
| Cascade heat exchanger | Alfa Laval, model: ACH-70X-50H-F, Heat exchanged: 10.86 kW, Heat transfer area: 2.45 m2 |
| R404A compressor | Bock, model: HGX34P/380-4S. Displacement with 1450 min−1:33.1 m3h−1, No. of cylinders: 4, weight: 96 kg, max. power consumption: 11.1 kW |
| Condenser | Alfa Laval, model: ACH-70X-50H-F, Heat exchanged: 38.44 kW, Heat transfer area: 2.45 m2 |
| Measuring Equipment | Detail |
|---|---|
| Mass flow rate of R404A cycle | Oval Ultra mass MKII Flow meter, model: CT9401-CN10, Range: 0–24 kg min−1 |
| Mass flow rate of R744 cycle | Oval Ultra mass MKII Flow meter, model: CT9401-CN06, Range: 0–12 kg min−1 |
| Power meter | YOKOGAWA Digital power meter, model: WT230, Range: 15–600 V, 0.5–20 A, 0.5–100 kHz |
| Pressure transmitter | WIKA, model: S-10, Range: 0–160 bar abs, 0–5 V |
| Temperature | ONDI, model: TT-TE(T-type), Range: -270–400 °C |
| Water flow rate | Corea Flow, model: TBN-II-AD(Turbine flowmeter), Range: 0.6~6 m3hr |
| Cycle | Component | Range | Unit |
|---|---|---|---|
| High-temperature refrigeration cycle (R404A) | Condensation temperature | 20, 30, 40 *, 50 | °C |
| Internal heat exchanger efficiency | 0 *, 1, 2, 3, 4 | stage | |
| Subcooling degree | 0 *, 5, 10, 15, 20 | °C | |
| Superheating degree | 10, 20 *, 30, 40 | °C | |
| Cascade evaporation temperature | −30, −25 *, −20, −15, −10 | °C | |
| Temperature difference of cascade heat exchanger | 5 | °C | |
| Low-temperature refrigeration cycle (R744) | |||
| Cascade condensation temperature | −25, −20 *, −15, −10, −5 | °C | |
| Evaporation temperature | −50, −45, −40 *, −35, −30 | °C | |
| Internal heat exchanger efficiency | 0 *, 1, 2, 3, 4 | stage | |
| Subcooling degree | 2* | °C | |
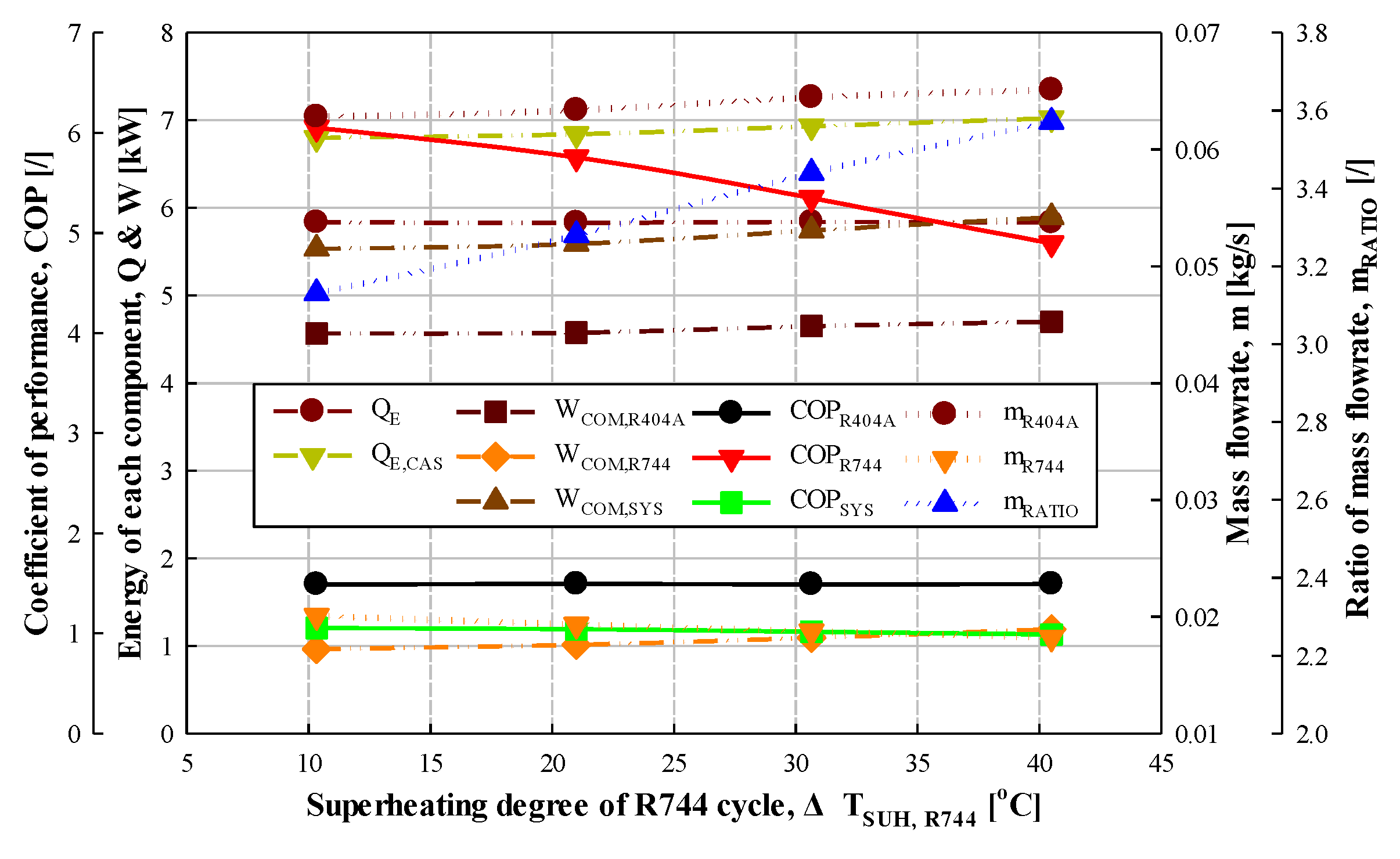
| Superheating degree | 10, 20, 30, 40* | °C |
| Cycle | Component | Energy | Mass |
|---|---|---|---|
| High-temperature refrigeration cycle (R404A) | Compressor (1→2) | | |
| Condenser (2→4) | |||
| Subcooling degree (3→4) | |||
| Internal heat exchanger (4→5 and 8→1) | |||
| Expansion valve (5→6) | |||
| Evaporator (6→8) | |||
| Superheating degree (7→8) | |||
| Low-temperature refrigeration cycle(R744) | Compressor(11→12) | ||
| Condenser (12→14) | |||
| Subcooling degree (13→14) | |||
| Internal heat exchanger (14→15 and 18→11) | |||
| Expansion valve (15→16) | |||
| Evaporator (16→18) | |||
| Superheating degree (17→18) |
| Parameters | Unit | Uncertainty |
|---|---|---|
| Mass flow rate | [kg/min] | 0.0100 |
| Power consumption of compressor | [kW] | 0.0350 |
| COP of R404A refrigeration system | [/] | 0.0128 |
| COP of R744 refrigeration system | [/] | 0.0128 |
| COP of CRS | [/] | 0.0135 |
| Temperature | [°C] | 0.2000 |
| [°C] | 0.4000 | |
| Pressure | [kPa] | 5.2700 |
| (Pressure drop) | [kPa] | 0.0100 |
| Mass flow rate of coolant | [kg/h] | 7.5300 |
| Linear Regression Coefficients for COPMAX | Linear Regression Coefficients for (TE,CAS)OPT | Linear Regression Coefficients for (mR404A/mR744)OPT | ||||
|---|---|---|---|---|---|---|
| Value | Standard Error | Value | Standard Error | Value | Standard Error | |
| a0 | 1.869 | 18.501 | −2.5873 | 3.9672 | −1.57 | 1.91 |
| a1 | 1.706 | 1.558 | −2.3562 | 3.340 | −9.93−1 | 1.61 |
| a2 | 4.227−2 | 0.039 | −6.181 | 8.430−1 | −1.98−2 | 4.06−2 |
| a3 | 3.484−4 | 0.000 | −5.334−2 | 7.037−3 | −1.26−4 | 3.39−4 |
| a4 | 3.111−2 | 0.049 | −1.923 | 1.047 | 4.66−2 | 5.04−2 |
| a5 | −1.103−3 | 0.002 | 1.150−1 | 4.512−2 | −1.90−3 | 2.17−3 |
| a6 | 9.719−6 | 0.000 | −1.785−3 | 5.881−4 | 3.06−5 | 2.83−5 |
| a7 | −1.015 | 1.211 | 1.3432 | 2.597 | 5.00−1 | 1.25 |
| a8 | 6.801−1 | 0.694 | −8.824 | 1.488 | −3.37−1 | 7.17−1 |
| a9 | −1.328−1 | 0.123 | 1.689 | 2.637 | 6.88−2 | 1.27−1 |
| a10 | 1.229−1 | 1.060 | −1.071 | 2.272 | 2.38−1 | 1.09 |
| a11 | −2.695−1 | 2.945 | 1.244 | 6.315 | 1.10−1 | 3.04 |
| a12 | 1.447−1 | 2.007 | 1.351 | 4.304 | −2.29−1 | 2.07 |
| a13 | 6.347 | 4.952 | −3.6742 | 1.0622 | −1.29 | 5.12 |
| a14 | −2.128 | 1.615 | 1.4162 | 3.464 | 4.00 | 1.67 |
| a15 | 2.376−1 | 0.178 | −1.827 | 3.811 | −3.98−1 | 1.84−1 |
| a16 | 8.977−2 | 0.039 | −4.703 | 8.455−1 | 1.93−2 | 4.07−2 |
| a17 | −3.977−3 | 0.002 | 2.211−1 | 3.844−2 | −2.14−3 | 1.85−3 |
| a18 | 5.570−5 | 0.000 | −3.012−3 | 5.217−4 | 2.93−5 | 2.51−5 |
| a19 | 1.803−2 | 0.026 | 1.980−1 | 5.519−1 | −5.40−2 | 2.66−2 |
| a20 | −1.563−3 | 0.003 | −2.023−2 | 6.779−2 | 1.93−3 | 3.27−3 |
| a21 | 5.853−5 | 0.000 | 5.123−4 | 2.222−3 | −5.62−5 | 1.07−4 |
| a22 | −7.559−2 | 1.502 | 1.722 | 3.220 | −1.19 | 1.55 |
| a23 | 5.192−1 | 8.106 | −1.2562 | 1.7382 | 4.89 | 8.38 |
| a24 | 3.280−2 | 10.898 | 1.8532 | 2.3372 | −7.74 | 1.13 |
| a25 | −6.086−2 | 0.093 | −6.747 | 1.985 | 5.13−2 | 9.57−2 |
| a26 | 8.071−4 | 0.003 | 1.862−1 | 5.831−2 | −7.17−4 | 2.81−3 |
| a27 | −6.180−6 | 0.000 | −1.608−3 | 5.436−4 | 1.12−5 | 2.62−5 |
| Number of points (n) = 1560 rms = 0.03462 R2 = 97.4% | Number of points (n) = 1560 rms = 0.74232 R2 = 97.69% | Number of points (n) = 1560 rms = 0.03577 R2 = 98.47% | ||||
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, M.-J. Experimental Analysis of the R744/R404A Cascade Refrigeration System with Internal Heat Exchanger. Part 1: Coefficient of Performance Characteristics. Energies 2021, 14, 6003. https://doi.org/10.3390/en14186003
Jeon M-J. Experimental Analysis of the R744/R404A Cascade Refrigeration System with Internal Heat Exchanger. Part 1: Coefficient of Performance Characteristics. Energies. 2021; 14(18):6003. https://doi.org/10.3390/en14186003
Chicago/Turabian StyleJeon, Min-Ju. 2021. "Experimental Analysis of the R744/R404A Cascade Refrigeration System with Internal Heat Exchanger. Part 1: Coefficient of Performance Characteristics" Energies 14, no. 18: 6003. https://doi.org/10.3390/en14186003
APA StyleJeon, M.-J. (2021). Experimental Analysis of the R744/R404A Cascade Refrigeration System with Internal Heat Exchanger. Part 1: Coefficient of Performance Characteristics. Energies, 14(18), 6003. https://doi.org/10.3390/en14186003






