Sensitivity of Reservoir and Operational Parameters on the Energy Extraction Performance of Combined CO2-EGR–CPG Systems
Abstract
:1. Introduction
- (i)
- The combined system exhibits less pore-water influence (due to the presence of residual natural gas), potentially reducing the resistance to flow of the CO2 in the reservoir. It may also reduce the extent of unwanted geochemical CO2-rock-brine interaction, such as salt precipitation;
- (ii)
- Additional natural gas and geothermal energy are extracted for power generation, which leads to an increase in the gas field’s total amount of producible energy;
- (iii)
- The natural gas-based power generation would likely be operated with CCS, providing the CO2 for the EGR and CPG operations;
- (iv)
- Economic (cost-saving) benefits are achieved by using/sharing already-existing multidisciplinary datasets (on reservoir parameters) and infrastructure (surface facilities, wells etc.). Hence, investment costs are significantly reduced;
- (v)
- The combined system extends the useful lifetime of the gas reservoir, recovering otherwise stranded assets, such as wells, offshore platforms etc., thereby postponing the expensive decommissioning phase of the wells and abandonment stages of the gas field.
- (i)
- Accommodate lessons learned from ref. [54], including that the bottom-hole production flowrate directly influences how much water enters the production well and that the two-phase (water/CO2) flow regime in the production well is an important design parameter;
- (ii)
- Determine the effect of the residual CH4 content of the reservoir and the effect of the CO2-plume-establishment stage on the performance of the combined system, as quantified by the amount of natural gas recovery, fluid-pressure buildup, and electric power generation;
- (iii)
- Determine the sensitivity of the performance metrics mentioned in (i) and (ii) to various important reservoir and operational (non-reservoir) parameters.
2. Methodology
2.1. Reservoir Modeling and Simulation
2.1.1. Reservoir Model
2.1.2. Reservoir Simulation Schemes
- The CNGR stage with a base-case duration of 25 years at a production flowrate of 4 kg/s/well;
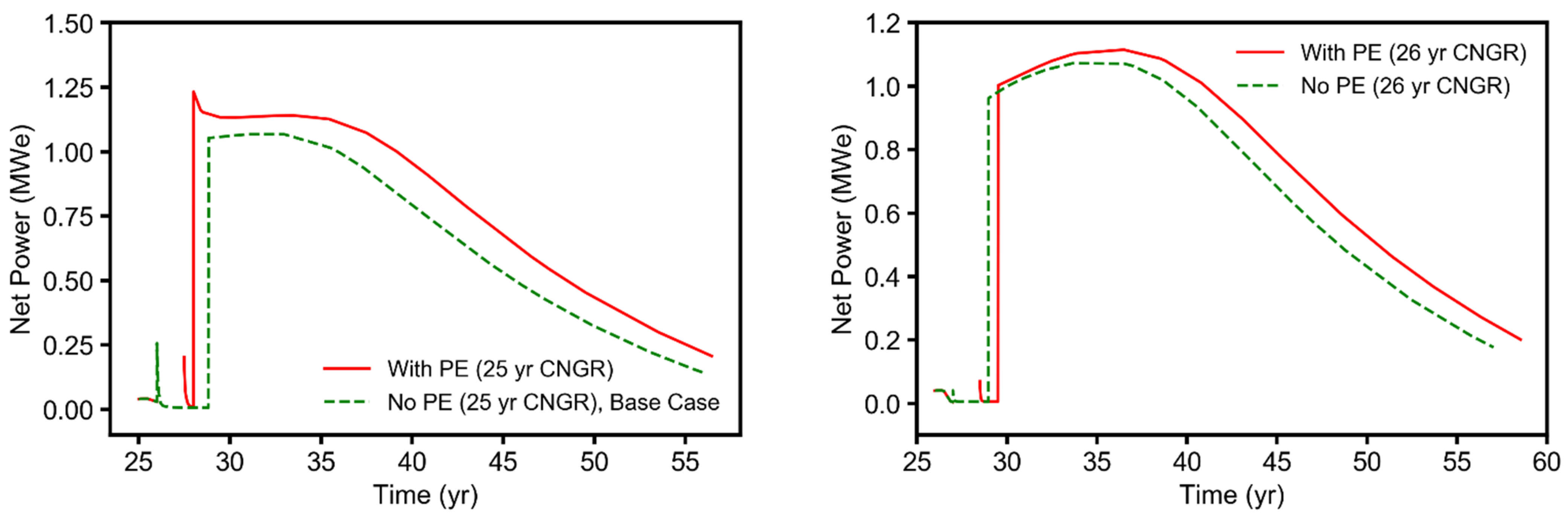
- The CO2-EGR stage with all simulated cases lasting for 1 year with a high injection-production flowrate ratio [45,51] (i.e., injection flowrate of 30 kg/s/well and production flowrate of 4 kg/s/well). The high injection-production flowrate ratio is beneficial for achieving a good CO2-EGR performance as well as a short duration for establishing an adequate CO2-plume reservoir [51]. After the 1 year period of high injection-production flow-rate ratio, the production rate was increased to 30 kg/s/well (equal to the injection flowrate). The CO2-EGR stage ended when the mass fraction of CO2 (XCO2) at the production-well region reached 90%. In this study, we considered some cases that were associated with 1.5 years of the CO2-plume establishment (PE) stage after the 1 year CO2-EGR stage. After the PE stage, the transition period, which involves CO2-CH4 separation, continued till 90% CO2 mass fraction (in the gas phase) was reached at the production well region;
- Finally, the CPG stage, where the base-case CPG-stage duration was 30 years at a circulation flowrate of 30 kg/s/well.
2.2. Performance Metrics
- (a)
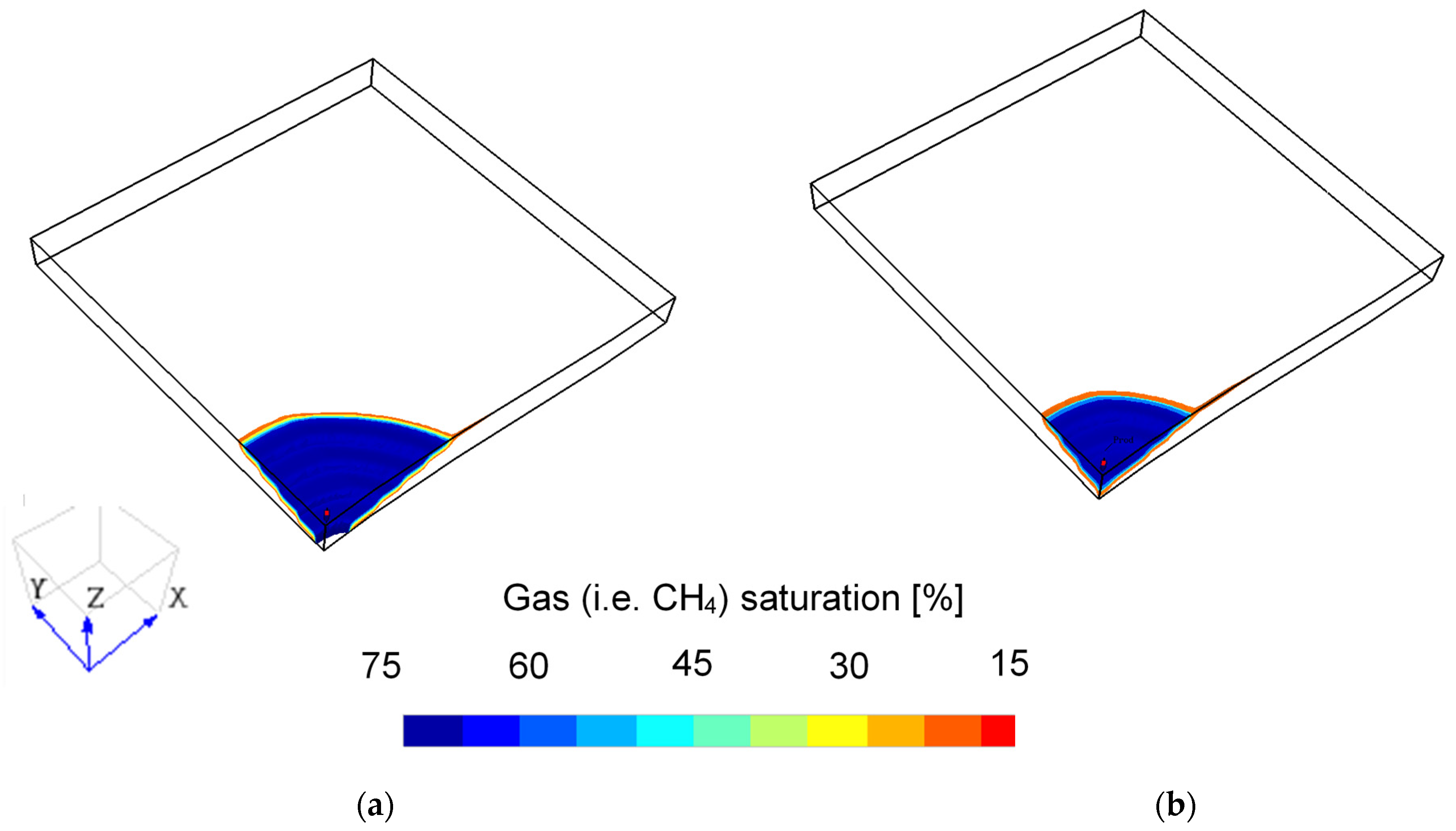
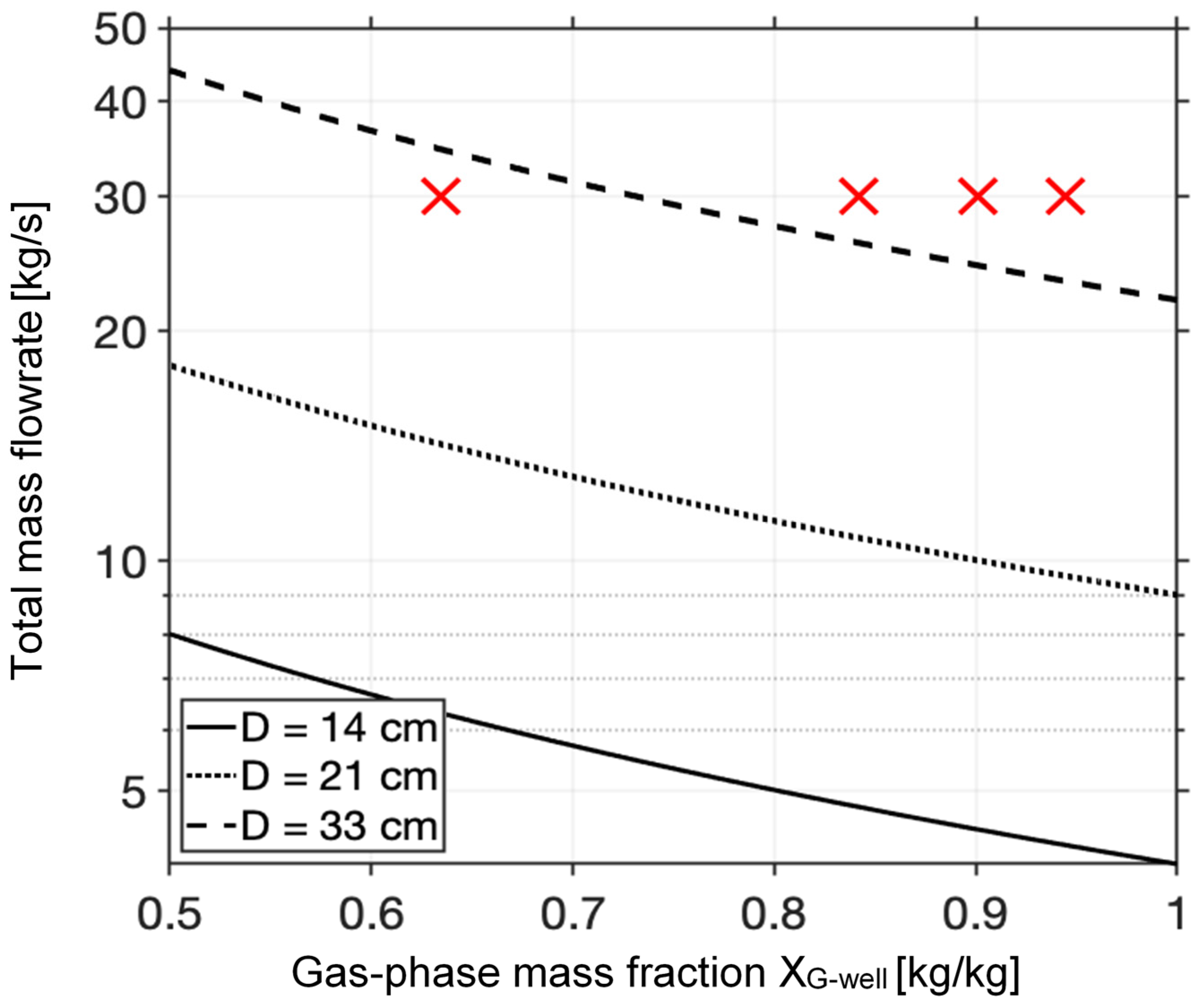
- The CO2 saturation (in the reservoir and in the production well), and the corresponding flow regime established (at the bottom-hole section of the production well) at the time of the highest water saturation around the production-well inlet region of the reservoir (ref. [45]). This performance metric was only applicable for the reservoir parameters, and it can be used to determine the importance of the PE stage for the combined system to achieve an annular flow regime (dominant CO2 flow) in the production well. The method to calculate this metric, using the gas saturation in the well and flowrate, can be found in ref. [54];
- (b)
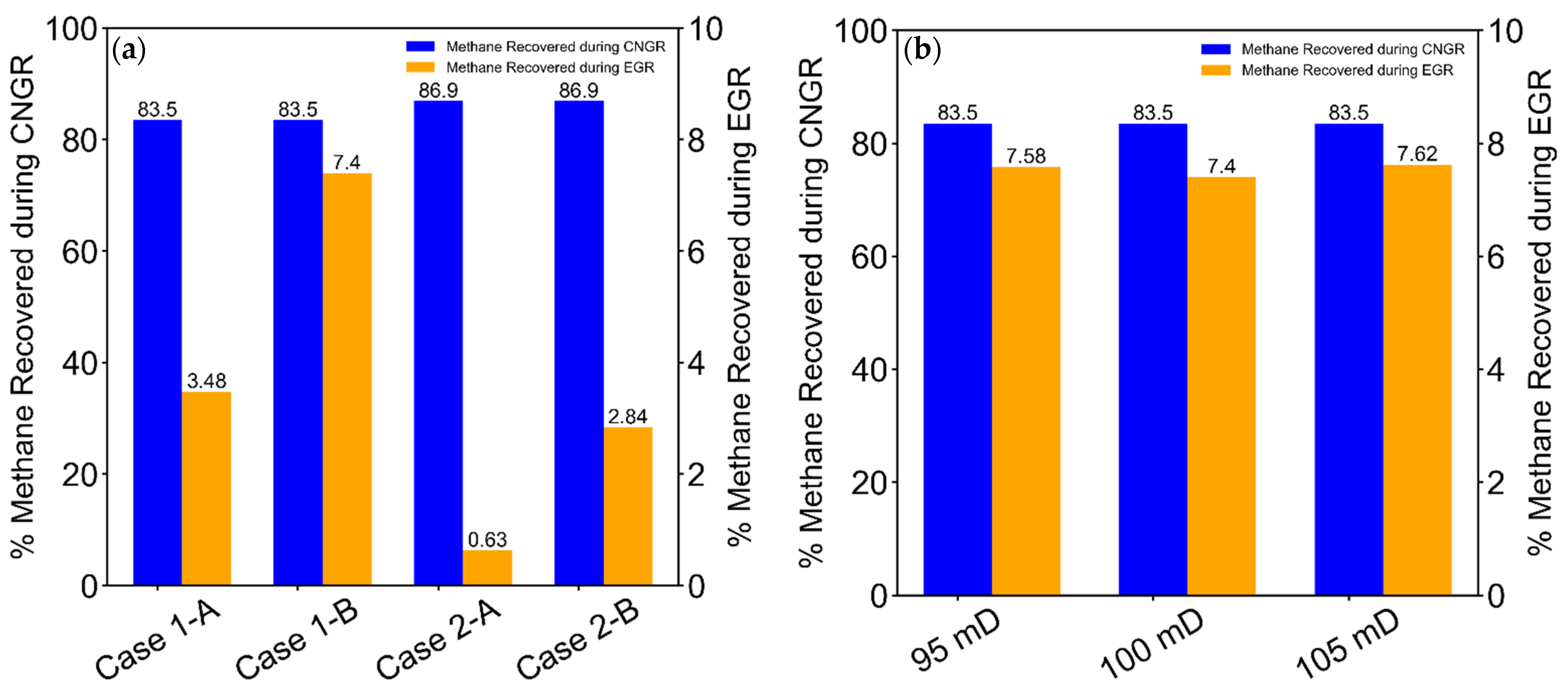
- The natural gas recovery performance (NGRP), which incorporates the amount of natural gas recovered (in terms of natural gas recovery factor) and the duration of the CNGR and CO2-EGR stages (including the transition period, TP). This implies that the duration of natural gas recovery also includes the time of CH4-CO2 separation at the land surface. The natural gas recovery factor during the CNGR and CO2-EGR stages can be measured as a percentage of the original gas in place (OGIP). These respective factors are calculated as:where is the volume of gas produced during the CNGR stage, and is the volume of gas initially in place,where is the volume of gas produced during the CO2-EGR stage,The volumes of the produced gas during the CNGR and CO2-EGR stages can be obtained from the TOUGH2 simulation output files.The natural gas recovery performance was measured using a natural gas recovery index (RI), which is calculated as the ultimate recovery factor [%] divided by the sum of the durations of the CNGR stage, [year] and CO2-EGR+TP stage, [year] (Equation (4)).The recovery index provides a way to select the best reservoir parameters and strategies that favor natural gas recovery and a shorter duration of the CO2-CH4 separation. The shorter this transition period is, the higher the energy efficiency of the combined system. Hence, a high value of RI is favorable;
- (c)
- The pressure buildup at the injection wells was one of the performance metrics considered for the combined system. It can compromise the integrity of the caprock overlying the natural gas reservoir. The non-dimensional pressure buildup (PBU) metric, used in this study, compares the maximum pressure in the injection well, , to the initial reservoir pressure, , as shown in Equation (5).can be calculated by using Equation (6) from ref. [52].where is the injectivity index, calculated asis the average of the maximum pressures in the injection grid cells of the two injection wells. The perforation layer thickness, , is 20 m, the well radius, , is 0.07 m, and the effective gridblock radius, . Here, A is the grid block area, which is 100 m2. The is the CO2 mass flowrate [kg/s], is the relative permeability [-], and and are the density [kg/m3] and the dynamic viscosity [Pa·s] of the gas (i.e., CO2) phase, respectively;
- (d)
- The average net geothermal electricity (measured in gigawatt-hours [GWeh]) generated using the produced natural gas (via the organic/CO2-based Rankine cycle) during the CNGR, , and EGR, , stages and from the produced CO2 (via the direct CO2 turbomachinery) during the direct-CPG stage, . The average net power generated was calculated using the output wellhead temperature and pressure results obtained from the wellbore heat transfer model described in ref. [45]. The power system models applied in this study for the indirect and direct CO2 turbomachinery power systems were extensively described in ref. [43] and ref. [45].
2.3. Sensitivity Analysis of the Performance Metrics
2.3.1. Residual Methane Content and CO2-Plume Establishment Stage
2.3.2. Reservoir and Operational Parameters
3. Results and Discussions
3.1. Effects of Residual CH4 Content and CO2-Plume Establishment Stage on the Performance Metrics
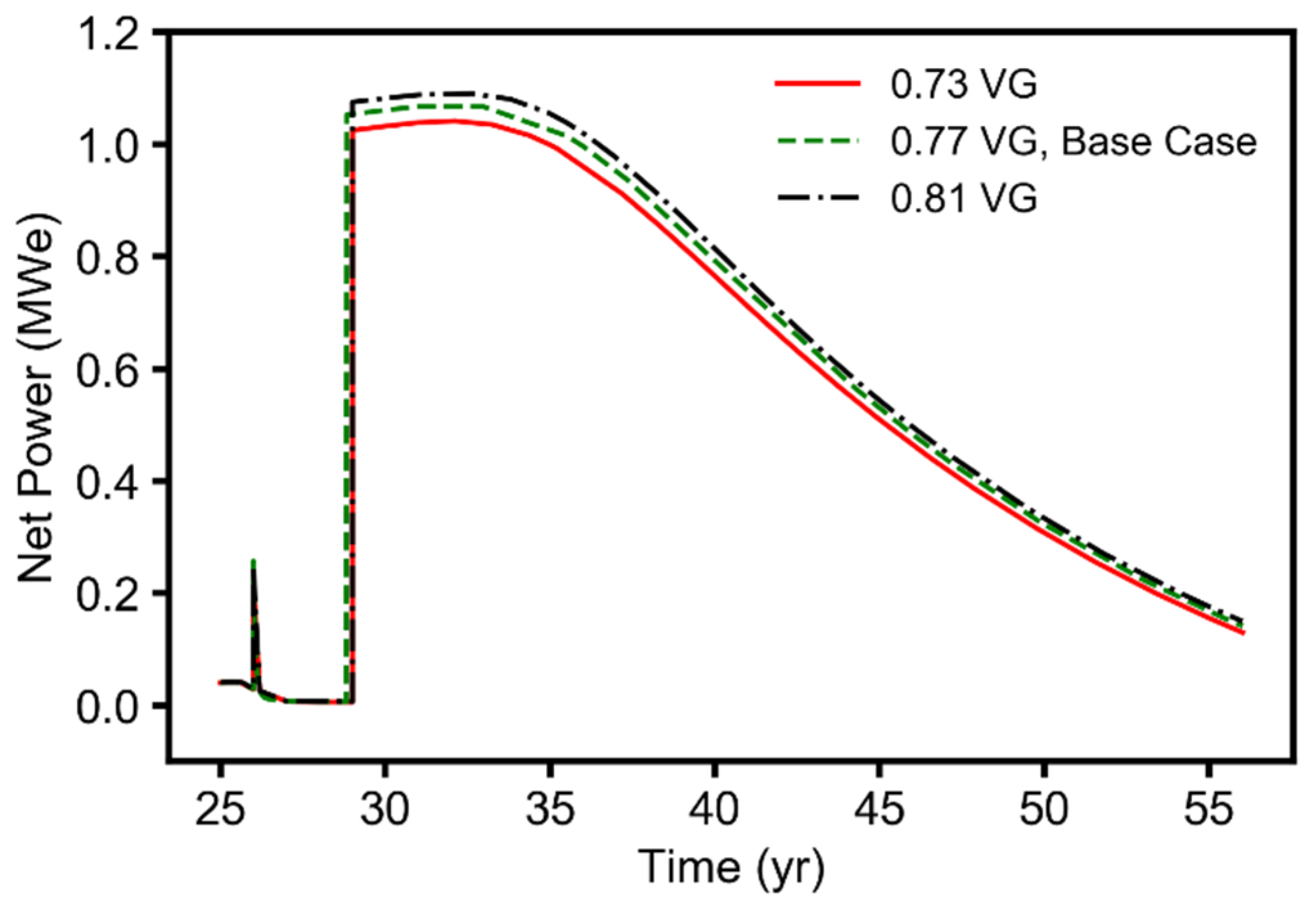
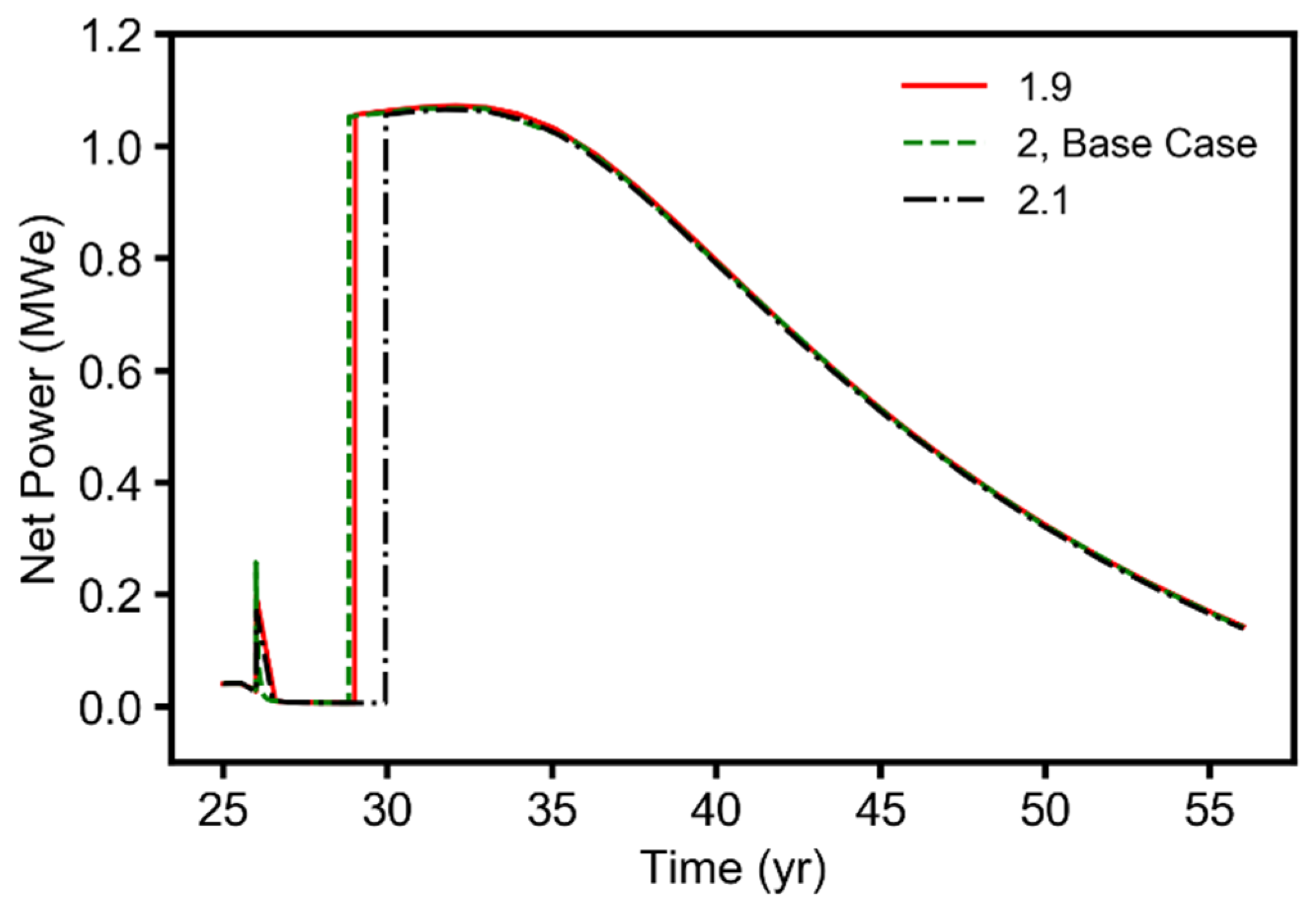
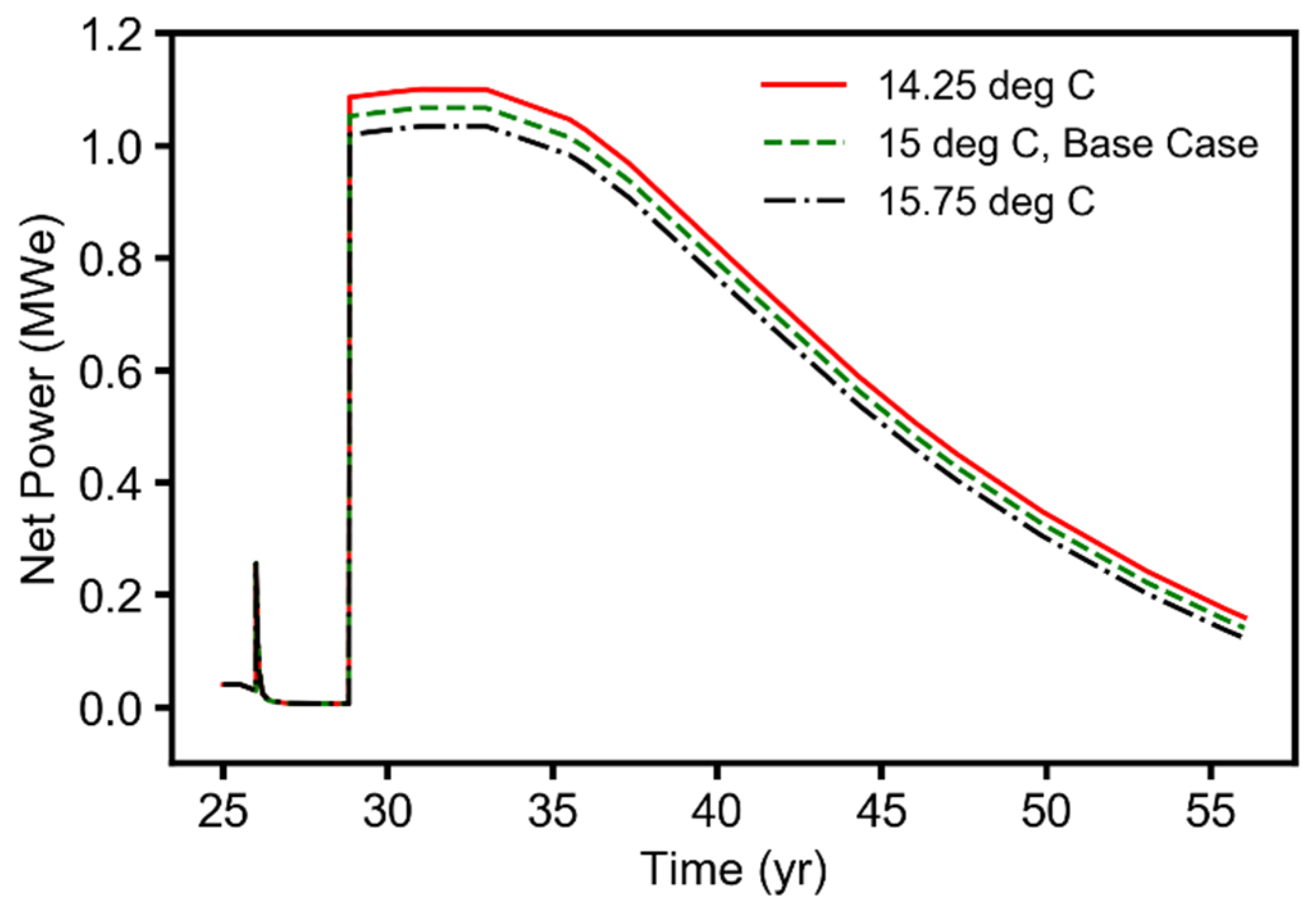
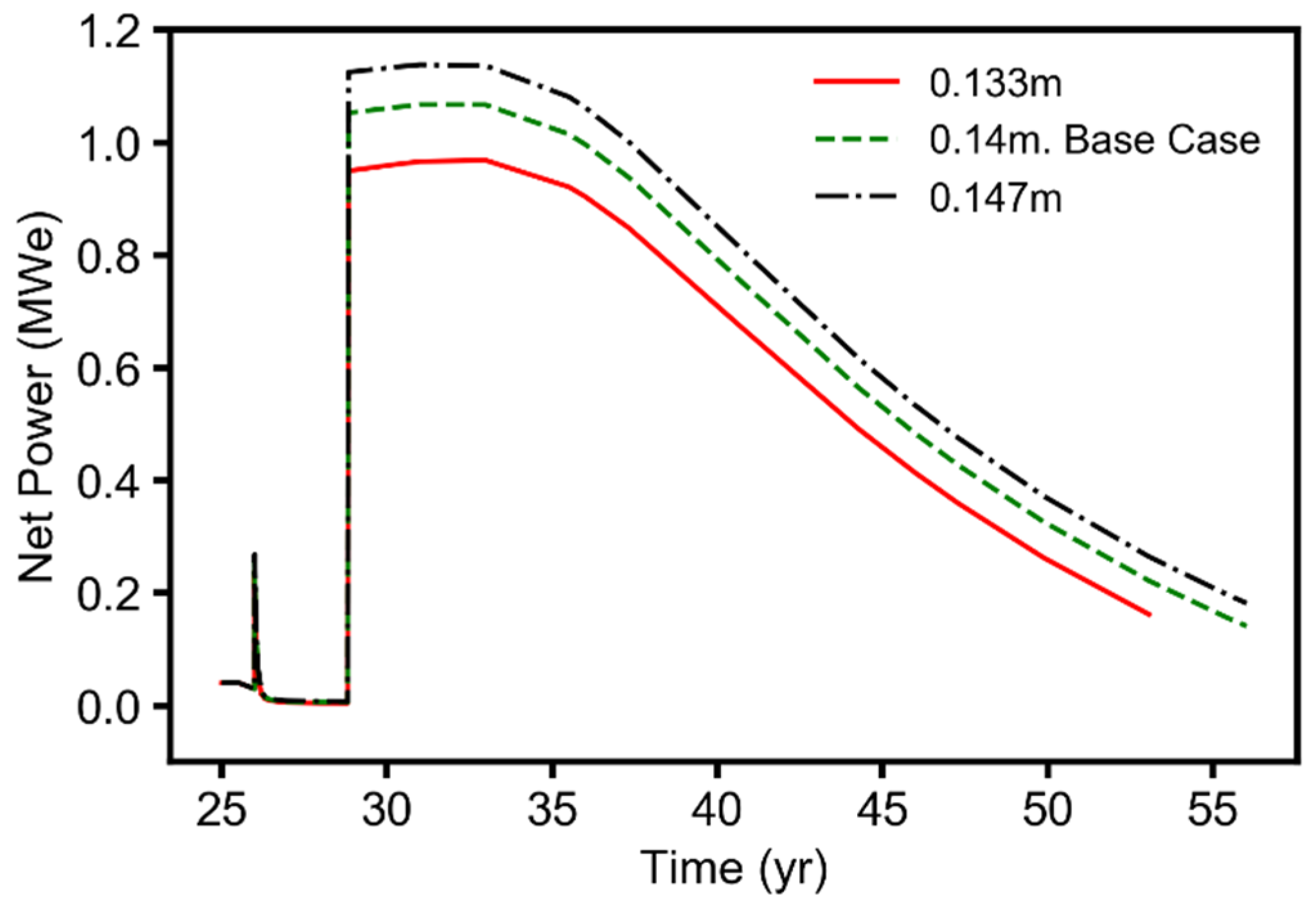
3.2. Effects of Reservoir and Operational Parameters on the Performance Metrics
3.2.1. Natural Gas Recovery Performance and Maximum Fluid-Pressure Buildup
3.2.2. Geothermal Energy (Electricity) Generation Performance during the CNGR, CO2-EGR+TP, and CPG Stages
4. Conclusions
- The PE stage was important to establish the desired annular flow regime near the bottom of the production well, especially when large-diameter wells were used. However, it was possible to achieve an annular flow regime by using wells with smaller diameters;
- Commencing with the injection of CO2 into the natural gas reservoir before it was completely depleted and including the PE stage increased the natural gas recovery performance of the combined CO2-EGR-CPG system;
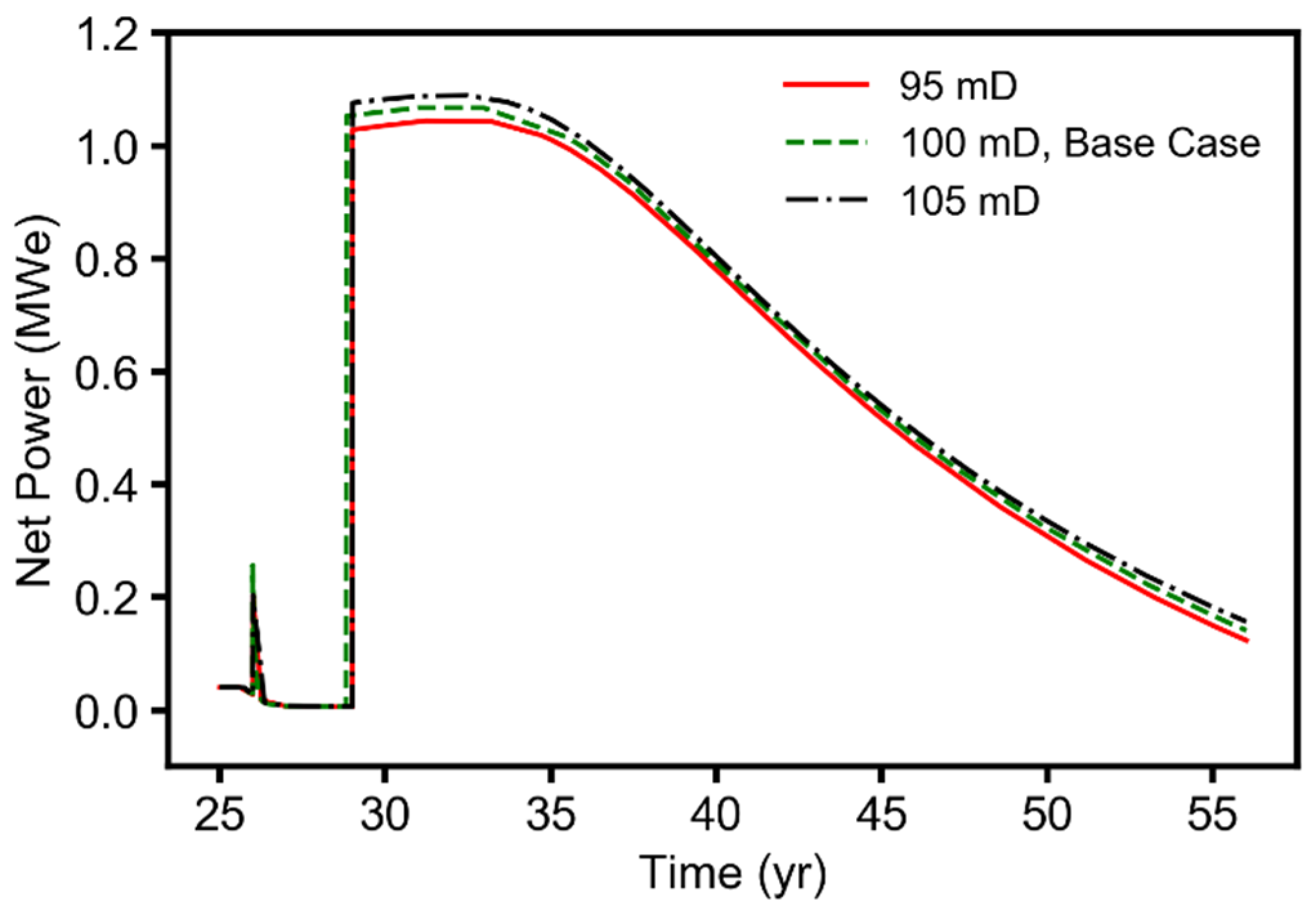
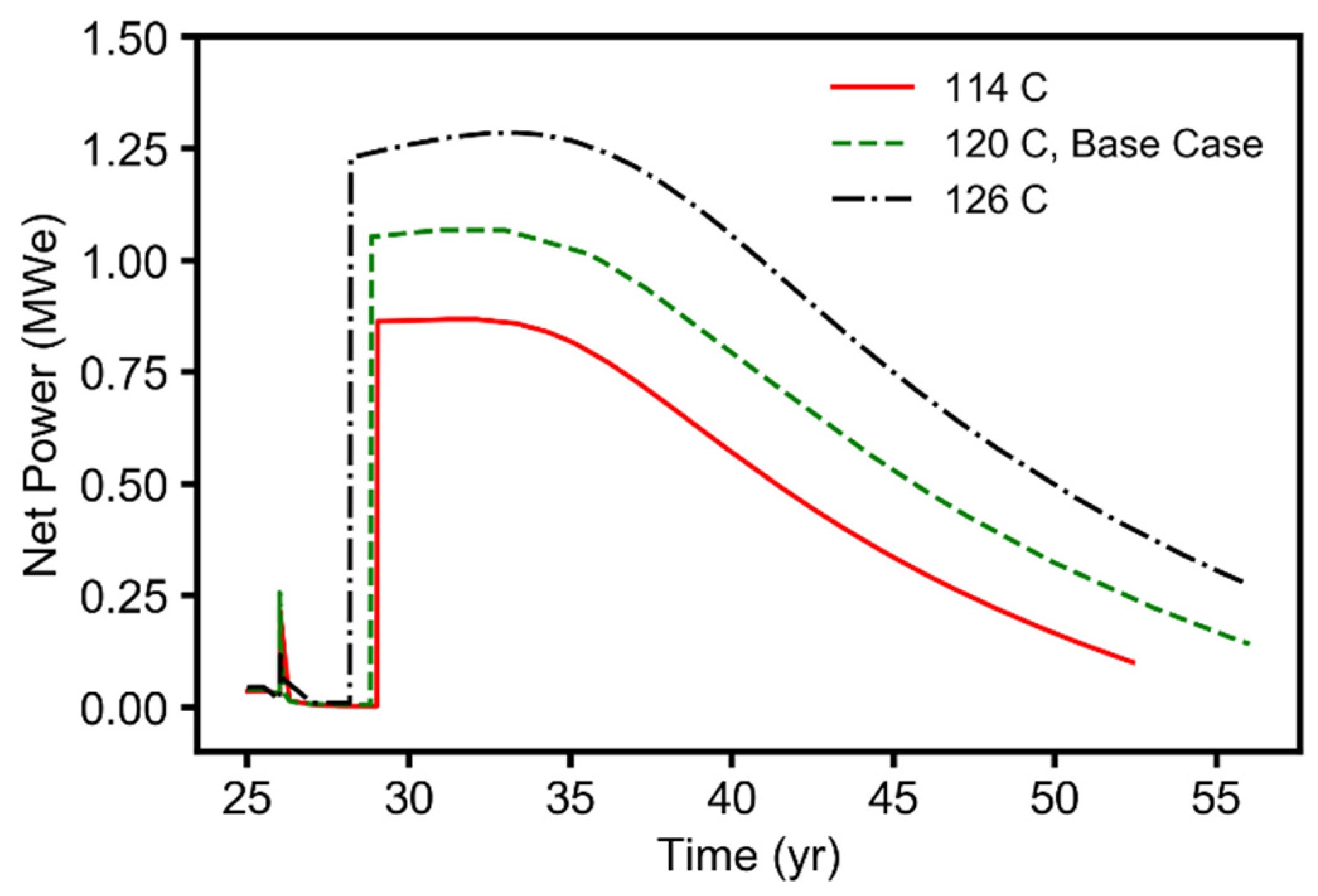
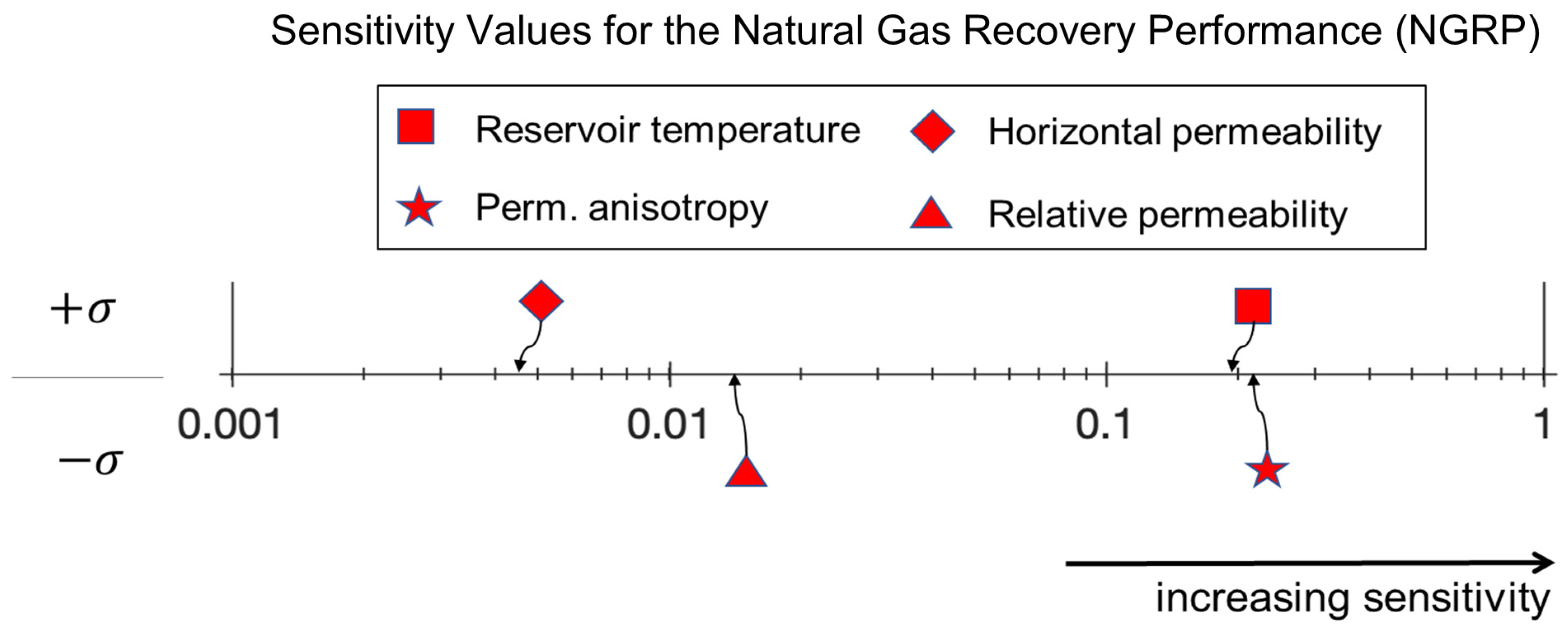
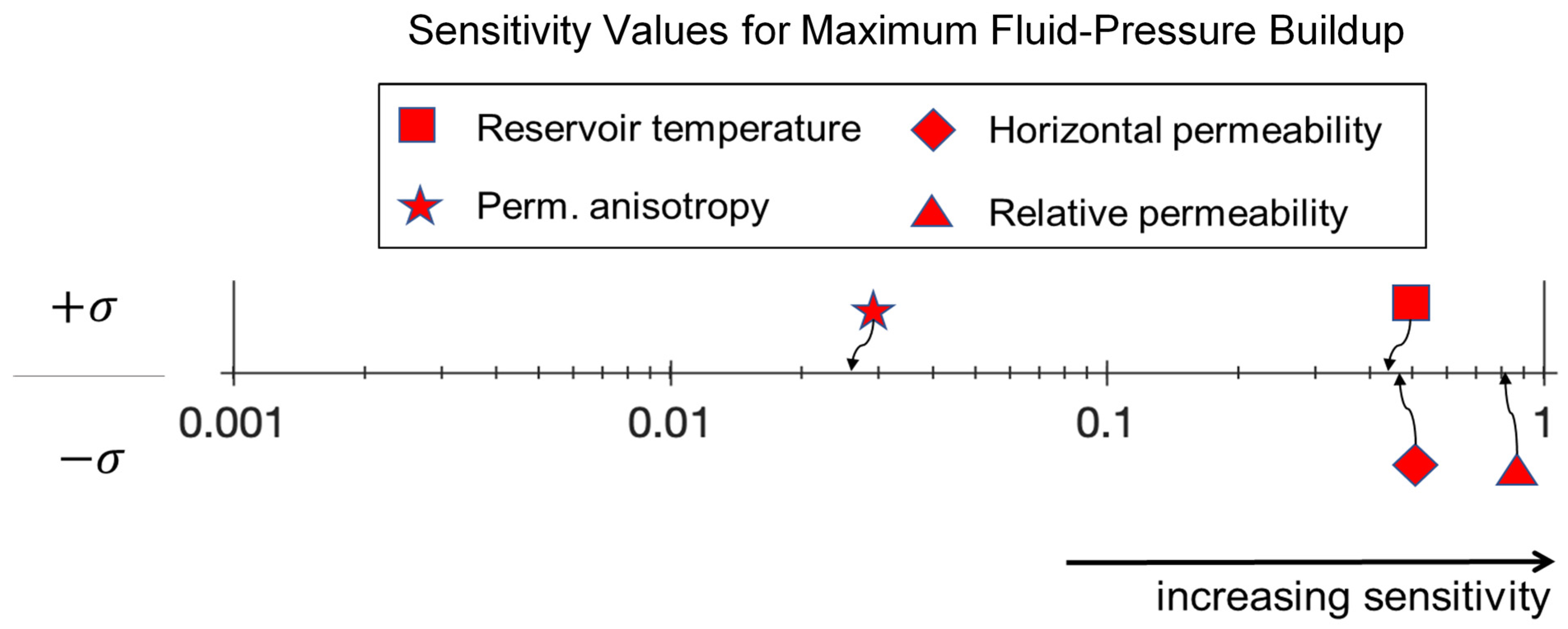
- Of the four reservoir parameters (permeability anisotropy, horizontal permeability, relative permeability, and reservoir temperature) considered in this study, permeability anisotropy and reservoir temperature were the parameters that most strongly affected the natural gas recovery performance. The fluid pressure buildup at the injection wells was most sensitive to changes in the van Genuchten relative permeability and horizontal-permeability parameters;
- The sensitivity results revealed that, for a given CO2 flowrate, the reservoir temperature was the parameter the geothermal power generation performance was most sensitive to. The production wellbore diameter was the second most sensitive parameter. Changes in the van Genuchten relative permeability parameter for pore-size distribution did not have a significant influence on the geothermal power generation performance of the combined CO2-EGR-CPG system.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A

References
- Rubin, E.; De Coninck, H. IPCC Special Report on Carbon Dioxide Capture and Storage; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Global Status of CCS: Targeting Climate Change; Global CCS Institute: Docklands, Australia, 2019.
- Townsend, A.; Raji, N.; Zapantis, A. The Value of Carbon Capture and Storage (CCS); Global CCS Institute: Docklands, Australia, 2020. [Google Scholar]
- Oldenburg, C.M.; Pruess, K.; Benson, S.M. Process modeling of CO2 injection into natural gas reservoirs for carbon sequestration and enhanced gas recovery. Energy Fuels 2001, 15, 293–298. [Google Scholar] [CrossRef]
- Oldenburg, C.; Stevens, S.; Benson, S. Economic feasibility of carbon sequestration with enhanced gas recovery (CSEGR). Energy 2004, 29, 1413–1422. [Google Scholar] [CrossRef] [Green Version]
- Polak, S.; Grimstad, A.A. Reservoir simulation study of CO2 storage and CO2-EGR in the Atzbach–Schwanenstadt gas field in Austria. In Energy Procedia; Elsevier: Amsterdam, The Netherlands, 2009; Volume 1, pp. 2961–2968. [Google Scholar]
- Leeuwenburgh, O.; Neele, F.; Hofstee, C.; Weijermans, P.-J.; de Boer, H.; Oosthoek, P.; Lefebvre, A.; Godderij, R.; Gutierrez-Neri, M. Enhanced Gas Recovery—A Potential ‘U’ for CCUS in The Netherlands. In Energy Procedia; Elsevier: Amsterdam, The Netherlands, 2014; Volume 63, pp. 7809–7820. [Google Scholar]
- Koide, H.; Tazaki, Y.; Noguchi, Y.; Iijima, M.; Ito, K.; Shindo, Y. Underground storage of carbon dioxide in depleted natural gas reservoirs and in useless aquifers. Eng. Geol. 1993, 34, 175–179. [Google Scholar] [CrossRef]
- Van der Burgt, M.J.; Cantle, J.; Boutkan, V.K. Carbon dioxide disposal from coal-based IGCC’s in depleted gas fields. Energy Convers. Manag. 1992, 33, 603–610. [Google Scholar] [CrossRef]
- Papay, J. Improved recovery of conventional natural gas. Part I: Theortical discussion of recovery methods. Erdoel Erdgas Kohle 1999, 6, 302–308. [Google Scholar]
- Papay, J. Improved recovery of conventional natural gas. Part II: Results of a pilot test. Erdoel Erdgas Kohle 1999, 115, 354–356. [Google Scholar]
- Van Der Meer, L.G.; Kreft, E.; Geel, C.; Hartman, J. K12-B A Test site for CO2 storage and enhanced gas recovery. In Proceedings of the SPE Europec/EAGE Annual Conference and Exhibition, Madrid, Spain, 13–16 June 2005; pp. 1–9. [Google Scholar]
- Van Der Meer, B.L.G.H.; Arts, R.J.; Geel, C.R.; Hofstee, C.; Winthaegen, P.; Hartman, J.; D’Hoore, D. K12-B: Carbon Dioxide Injection in a Nearly Depleted Gas Field Offshore the Netherlands. In Carbon Dioxide Sequestration in Geological Media—State of the Science; Grobe, M., Pashin, J.C., Dodge, R.L., Eds.; American Association of Petroleum Geologists: Tulsa, OK, USA, 2009; Volume 59, pp. 379–390. [Google Scholar]
- Denney, D. Technical and economic challenge of mature gas fields: The Giant Altmark Field, Germany. J. Pet. Technol. 2006, 58, 38–39. [Google Scholar] [CrossRef]
- Kühn, M.; Förster, A.; Großmann, J.; Meyer, R.; Reinicke, K.; Schäfer, D.; Wendel, H. CLEAN: Preparing for a CO2-based enhanced gas recovery in a depleted gas field in Germany. In Energy Procedia; Elsevier: Amsterdam, The Netherlands, 2011; Volume 4, pp. 5520–5526. [Google Scholar]
- Kühn, M.; Tesmer, M.; Pilz, P.; Meyer, R.; Reinicke, K.; Förster, A.; Kolditz, O.; Schäfer, D. CLEAN Partners CLEAN: Project overview on CO2 large-scale enhanced gas recovery in the Altmark natural gas field (Germany). Environ. Earth Sci. 2012, 67, 311–321. [Google Scholar] [CrossRef]
- Oldenburg, C.M.; Benson, S.M. CO2 injection for enhanced gas production and carbon sequestration. In Proceedings of the SPE International Petroleum Conference and Exhibition in Mexico, Villahermosa, Mexico, 10–12 February 2002; Society of Petroleum Engineers: Richardson, TX, USA, 2002; pp. 1–10. [Google Scholar]
- Oldenburg, C.M. Carbon dioxide as cushion gas for natural gas storage. Energy Fuels 2003, 17, 240–246. [Google Scholar] [CrossRef] [Green Version]
- Jikich, S.A.; Smith, D.H.; Sams, W.N.; Bromhal, G.S. Enhanced Gas Recovery (EGR) with Carbon Dioxide Sequestration: A Simulation Study of Effects of Injection Strategy and Operational Parameters. In Proceedings of the SPE Eastern Regional Meeting, Pittsburgh, PA, USA, 6–10 September 2003; Society of Petroleum Engineers: Richardson, TX, USA, 2003; pp. 1–9. [Google Scholar]
- Rückheim, J.; Voigtlaender, G.; Stein-Khokhlov, M. The Technical and Economic Challenge of “Mature Gas Fields”: The Giant Altmark Field, a German Example. In Proceedings of the SPE Europec/EAGE Annual Conference, Madrid, Spain, 13–16 June 2005; Society of Petroleum Engineers: Richardson, TX, USA, 2005; pp. 1–4. [Google Scholar]
- Gou, Y.; Hou, Z.; Liu, H.; Zhou, L.; Were, P. Numerical simulation of carbon dioxide injection for enhanced gas recovery (CO2-EGR) in Altmark natural gas field. Acta Geotech. 2014, 9, 49–58. [Google Scholar] [CrossRef]
- Procesi, M.; Cantucci, B.; Buttinelli, M.; Armezzani, G.; Quattrocchi, F.; Boschi, E. Strategic use of the underground in an energy mix plan: Synergies among CO2, methane geological storage and geothermal energy. Latium Region case study (Central Italy). Appl. Energy 2013, 110, 104–131. [Google Scholar] [CrossRef]
- Clemens, T.; Secklehner, S.; Mantatzis, K.; Jacobs, B. Enhanced gas recovery, challenges shown at the example of three gas fields. In Proceedings of the SPE EUROPEC/EAGE Annual Conference and Exhibition, Barcelona, Spain, 14–17 June 2010; pp. 1–17. [Google Scholar]
- Polak, S.; Zweigel, J.; Lindeberg, E.; Pannetier-Lescoffit, S.; Schulz, H.-M.; Faber, E.; Teschner, M.; Poggenburg, J.; May, F.; Krooss, B.; et al. The Atzbach-Schwanenstadt gas field—A potential site for onshore CO2 storage and EGR. Geophysics 2006, 25, 1272–1275. [Google Scholar] [CrossRef]
- Khan, C.; Amin, R.; Madden, G. Carbon dioxide injection for enhanced gas recovery and storage (reservoir simulation). Egypt. J. Pet. 2013, 22, 225–240. [Google Scholar] [CrossRef] [Green Version]
- Regan, M.L.M. A Numerical Investigation into the Potential to Enhance Natural Gas Recovery in Water-Drive Gas Reservoirs through the Injection of CO2. Ph.D. Dissertation, The University of Adelaide, Adelaide, Australia, 2010. [Google Scholar]
- Xie, H.; Li, X.; Fang, Z.; Wang, Y.; Li, Q.; Shi, L.; Bai, B.; Wei, N.; Hou, Z. Carbon geological utilization and storage in China: Current status and perspectives. Acta Geotech. 2014, 9, 7–27. [Google Scholar] [CrossRef]
- Shi, Y.; Jia, Y.; Pan, W.; Huang, L.; Yan, J.; Zheng, R. Potential evaluation on CO2-EGR in tight and low-permeability reservoirs. Nat. Gas Ind. B 2017, 4, 311–318. [Google Scholar] [CrossRef]
- Rybach, L. Geothermal energy: Sustainability and the environment. Geothermics 2003, 32, 463–470. [Google Scholar] [CrossRef]
- Axelsson, G.; Stefánsson, V.; Björnsson, G.; Liu, J. Sustainable management of geothermal resources and utilization for 100–300 years. In Proceedings of the World Geothermal Congress, Antalya, Turkey, 24–29 April 2005; International Geothermal Association: Bonn, Germany, 2005; pp. 1–8. [Google Scholar]
- Lund, J.W.; Boyd, T.L. Direct utilization of geothermal energy 2015 worldwide review. Geothermics 2016, 60, 66–93. [Google Scholar] [CrossRef]
- Brown, D.W. A hot dry rock geothermal energy concept utilizing supercritical CO2 instead of water. In Proceedings of the Twenty-Fifth Workshop on Geothermal Reservoir Engineering, Stanford, CA, USA, 24–26 January 2000; pp. 1–6. [Google Scholar]
- Pruess, K. Enhanced Geothermal Systems (EGS) comparing water with CO2 as heat transmission fluids. In New Zealand Geothermal Workshop; University of Auckland: Auckland, New Zealand, 2007; pp. 1–13. [Google Scholar]
- Pruess, K. Enhanced geothermal systems (EGS) using CO2 as working fluid-A novel approach for generating renewable energy with simultaneous sequestration of carbon. Geothermics 2006, 35, 351–367. [Google Scholar] [CrossRef] [Green Version]
- Randolph, J.B.; Saar, M.O. Combining geothermal energy capture with geologic carbon dioxide sequestration. Geophys. Res. Lett. 2011, 38, 1–7. [Google Scholar] [CrossRef] [Green Version]
- Pruess, K. On production behavior of enhanced geothermal systems with CO2 as working fluid. Energy Convers. Manag. 2008, 49, 1446–1454. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.L.; Cheng, W.L.; Nian, Y.L.; Yang, L.; Han, B.B.; Liu, M.H. Simulation of heat extraction from CO2-based enhanced geothermal systems considering CO2 sequestration. Energy 2018, 142, 157–167. [Google Scholar] [CrossRef]
- Majer, E.L.; Baria, R.; Stark, M.; Oates, S.; Bommer, J.; Smith, B.; Asanuma, H. Induced seismicity associated with Enhanced Geothermal Systems. Geothermics 2007, 36, 185–222. [Google Scholar] [CrossRef]
- Amann, F.; Gischig, V.; Evans, K.; Doetsch, J.; Jalali, R.; Valley, B.; Krietsch, H.; Dutler, N.; Villiger, L.; Brixel, B.; et al. The seismo-hydromechanical behavior during deep geothermal reservoir stimulations: Open questions tackled in a decameter-scale in situ stimulation experiment. Solid Earth 2018, 9, 115–137. [Google Scholar] [CrossRef] [Green Version]
- Randolph, J.B.; Saar, M.O. Coupling Carbon Dioxide Sequestration with Geothermal Energy Capture in Naturally Permeable, Porous Geologic Formations: Implications for CO2. In Energy Procedia; Elsevier: Amsterdam, The Netherlands, 2011; Volume 4, pp. 2206–2213. [Google Scholar]
- Garapati, N.; Randolph, J.B.; Saar, M.O. Brine displacement by CO2, energy extraction rates, and lifespan of a CO2-limited CO2-Plume Geothermal (CPG) system with a horizontal production well. Geothermics 2015, 55, 182–194. [Google Scholar] [CrossRef] [Green Version]
- Adams, B.M.; Kuehn, T.H.; Bielicki, J.M.; Randolph, J.B.; Saar, M.O. On the importance of the thermosiphon effect in CPG (CO2 plume geothermal) power systems. Energy 2014, 69, 409–418. [Google Scholar] [CrossRef]
- Adams, B.M.; Kuehn, T.H.; Bielicki, J.M.; Randolph, J.B.; Saar, M.O. A comparison of electric power output of CO2 Plume Geothermal (CPG) and brine geothermal systems for varying reservoir conditions. Appl. Energy 2015, 140, 365–377. [Google Scholar] [CrossRef]
- Adams, B.M.; Vogler, D.; Kuehn, T.H.; Bielicki, J.M.; Garapati, N.; Saar, M.O. Heat Depletion in Sedimentary Basins and its Effect on the Design and Electric Power Output of CO2 Plume Geothermal (CPG) Systems. Renew. Energy 2021, 172, 1393–1403. [Google Scholar] [CrossRef]
- Ezekiel, J.; Ebigbo, A.; Adams, B.M.; Saar, M.O. Combining natural gas recovery and CO2-based geothermal energy extraction for electric power generation. Appl. Energy 2020, 269, 1–21. [Google Scholar] [CrossRef]
- Fleming, M.R.; Adams, B.M.; Kuehn, T.H.; Bielicki, J.M.; Saar, M.O. Increased Power Generation due to Exothermic Water Exsolution in CO2 Plume Geothermal (CPG) Power Plants. Geothermics 2020, 88, 101865. [Google Scholar] [CrossRef]
- Norouzi, A.M.; Babaei, M.; Han, W.S.; Kim, K.-Y.; Niasar, V. CO2-plume geothermal processes: A parametric study of salt precipitation influenced by capillary-driven backflow. Chem. Eng. J. 2021, 425, 130031. [Google Scholar] [CrossRef]
- Cui, G.; Ren, S.; Rui, Z.; Ezekiel, J.; Zhang, L.; Wang, H. The influence of complicated fluid-rock interactions on the geothermal exploitation in the CO2 plume geothermal system. Appl. Energy 2017, 227, 49–63. [Google Scholar] [CrossRef]
- McDonnell, K.; Molnár, L.; Harty, M.; Murphy, F. Feasibility Study of Carbon Dioxide Plume Geothermal Systems in Germany−Utilising Carbon Dioxide for Energy. Energies 2020, 13, 2416. [Google Scholar] [CrossRef]
- Cui, G.; Zhang, L.; Ren, S. Assessment of Heat Mining Rate for Geothermal Exploitation from Depleted High-Temperature Gas Reservoirs via Recycling Supercritical CO2. In Energy Procedia; Elsevier: Amsterdam, The Netherlands, 2017; Volume 105, pp. 875–880. [Google Scholar]
- Zhang, L.; Li, X.; Zhang, Y.; Cui, G.; Tan, C.; Ren, S. CO2 injection for geothermal development associated with EGR and geological storage in depleted high-temperature gas reservoirs. Energy 2017, 123, 139–148. [Google Scholar] [CrossRef]
- Pruess, K.; Oldenburg, C.; Moridis, G. TOUGH2 User’s Guide, Version 2 (Revised); Lawrence Berkeley National Laboratory (LBNL): Berkeley, CA, USA, 2012. [Google Scholar]
- Oldenburg, C.M.; Moridis, G.J.; Spycher, N.; Pruess, K. EOS7C Version 1.0: TOUGH2 Module for Cambon Dioxide or Nitrogen in Natural Gas (Methane) Reservoirs; Ernest Orlando Lawrence Berkeley NationalLaboratory: Berkeley, CA, USA, 2004. [Google Scholar]
- Ezekiel, J.; Adams, B.M.; Saar, M.O.; Ebigbo, A. Numerical analysis and optimization of the performance of CO2-plume geothermal (CPG) production wells and implications for electric power generation. Geothermics 2021. under review. [Google Scholar]


| Parameter | Value |
|---|---|
| Reservoir size, x (km), y (km), z (km) | 4.5 × 4.5 × 0.1 |
| Depth (km) | 3.0 |
| Porosity (-) | 0.20 |
| Horizontal permeability, kh (m2) | 10−13 (100 mD) |
| Anisotropy kh/kv (-) | 2.0 |
| Thickness (m) | 100 |
| Reservoir initial pressure | Hydrostatic (30 MPa at the reservoir top) |
| Reservoir initial temperature (°C) | 120 |
| Initial CO2 mass fraction in gas phase | 0.025 (dissolved in brine) |
| Residual gas saturation (-) | 0.05 |
| Residual brine saturation (-) | 0.25 |
| van Genuchten parameters α (Pa), m (-) | 3 × 103, 0.77 |
| Native brine NaCl saturation (ppm) | 150,000 |
| Mol. diffusivity in gas; in water (m2/s) | 10−5; 10−10 |
| Rock grain density (kg/m3) | 2650 |
| Thermal conductivity λwet, λdry (W/m °C) | 2.51, 1.6 |
| Rock specific heat capacity (J/kg °C) | 1000 |
| Geothermal gradient (°C/km) | 35 |
| Rock compressibility (1/Pa) | 10−10 |
| CO2 injection enthalpy (J/kg) | 2.8 × 105 |
| Well diameter (m) | 0.14 |
| Lateral boundary conditions of the reservoir | Hydrostatic pressure; 120 °C (Dirichlet boundary conditions) |
| Top and bottom boundary conditions of the reservoir | No fluid flow and no heat flux |
| Cases | Case 1-A | Case 1-B | Case 2-A | Case 2-B |
|---|---|---|---|---|
| CNGR period (years) | 25 | 25 | 26 | 26 |
| Reservoir type | Partially depleted natural gas reservoir | Partially depleted natural gas reservoir | Depleted natural gas reservoir | Depleted natural gas reservoir |
| PE stage considered | Yes | No | Yes | No |
| Cases | %OGIP Recovered at CNGR Stage | %OGIP Recovered at EGR+TP Stage | Total %OGIP Recovered, FUR | Duration of CO2-EGR+TP Stage (Year) | Total Duration of NG Recovery (Year) | RI (%/Year) |
|---|---|---|---|---|---|---|
| Case 1-A: 25 years w/PE | 83.51 | 3.48 | 86.99 | 1.50 | 28.50 | 3.28 |
| Case 1-B: 25 years no PE | 83.51 | 7.43 | 90.94 | 3.82 | 28.82 | 3.16 |
| Case 2-A: 26 years w/PE | 86.85 | 0.63 | 87.48 | 2.00 | 28.00 | 3.12 |
| Case 2-B: 26 years no PE | 86.85 | 2.84 | 89.69 | 2.97 | 28.97 | 3.10 |
| Cases | Net Electricity Generated at CNGR Stage [GWeh] | Net Electricity Generated at CO2-EGR+TP Stage [GWeh] * | Net Electricity Generated at CPG Stage [GWeh] ** | Total Net Electricity Generated during the Project [GWeh] |
|---|---|---|---|---|
| Case 1-A: 25 years w/PE | 9.163 | 0.676 | 232.048 | 241.887 |
| Case 1-B: 25 years no PE | 9.163 | 1.767 | 173.443 | 184.373 |
| Case 2-A: 26 years w/PE | 9.246 | 0.484 | 214.514 | 224.244 |
| Case 2-B: 26 years no PE | 9.246 | 0.599 | 199.342 | 209.184 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ezekiel, J.; Kumbhat, D.; Ebigbo, A.; Adams, B.M.; Saar, M.O. Sensitivity of Reservoir and Operational Parameters on the Energy Extraction Performance of Combined CO2-EGR–CPG Systems. Energies 2021, 14, 6122. https://doi.org/10.3390/en14196122
Ezekiel J, Kumbhat D, Ebigbo A, Adams BM, Saar MO. Sensitivity of Reservoir and Operational Parameters on the Energy Extraction Performance of Combined CO2-EGR–CPG Systems. Energies. 2021; 14(19):6122. https://doi.org/10.3390/en14196122
Chicago/Turabian StyleEzekiel, Justin, Diya Kumbhat, Anozie Ebigbo, Benjamin M. Adams, and Martin O. Saar. 2021. "Sensitivity of Reservoir and Operational Parameters on the Energy Extraction Performance of Combined CO2-EGR–CPG Systems" Energies 14, no. 19: 6122. https://doi.org/10.3390/en14196122
APA StyleEzekiel, J., Kumbhat, D., Ebigbo, A., Adams, B. M., & Saar, M. O. (2021). Sensitivity of Reservoir and Operational Parameters on the Energy Extraction Performance of Combined CO2-EGR–CPG Systems. Energies, 14(19), 6122. https://doi.org/10.3390/en14196122






