Analytical, Experimental, and Numerical Investigation of Energy in Hydraulic Cylinder Dynamics of Agriculture Scale Excavators
Abstract
:1. Introduction
2. Nonlinear Nominal Model
3. Physical Parameter Identification
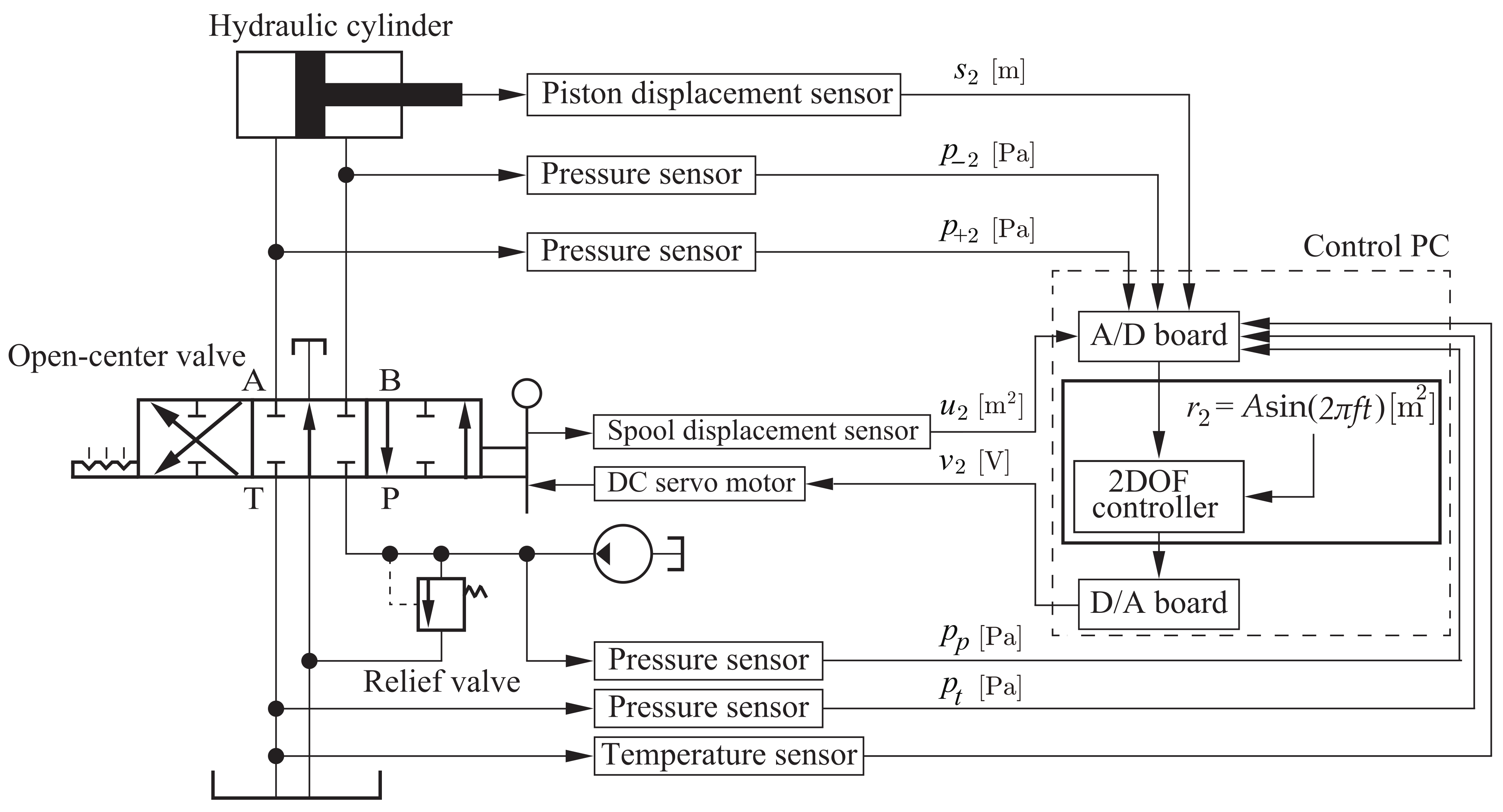
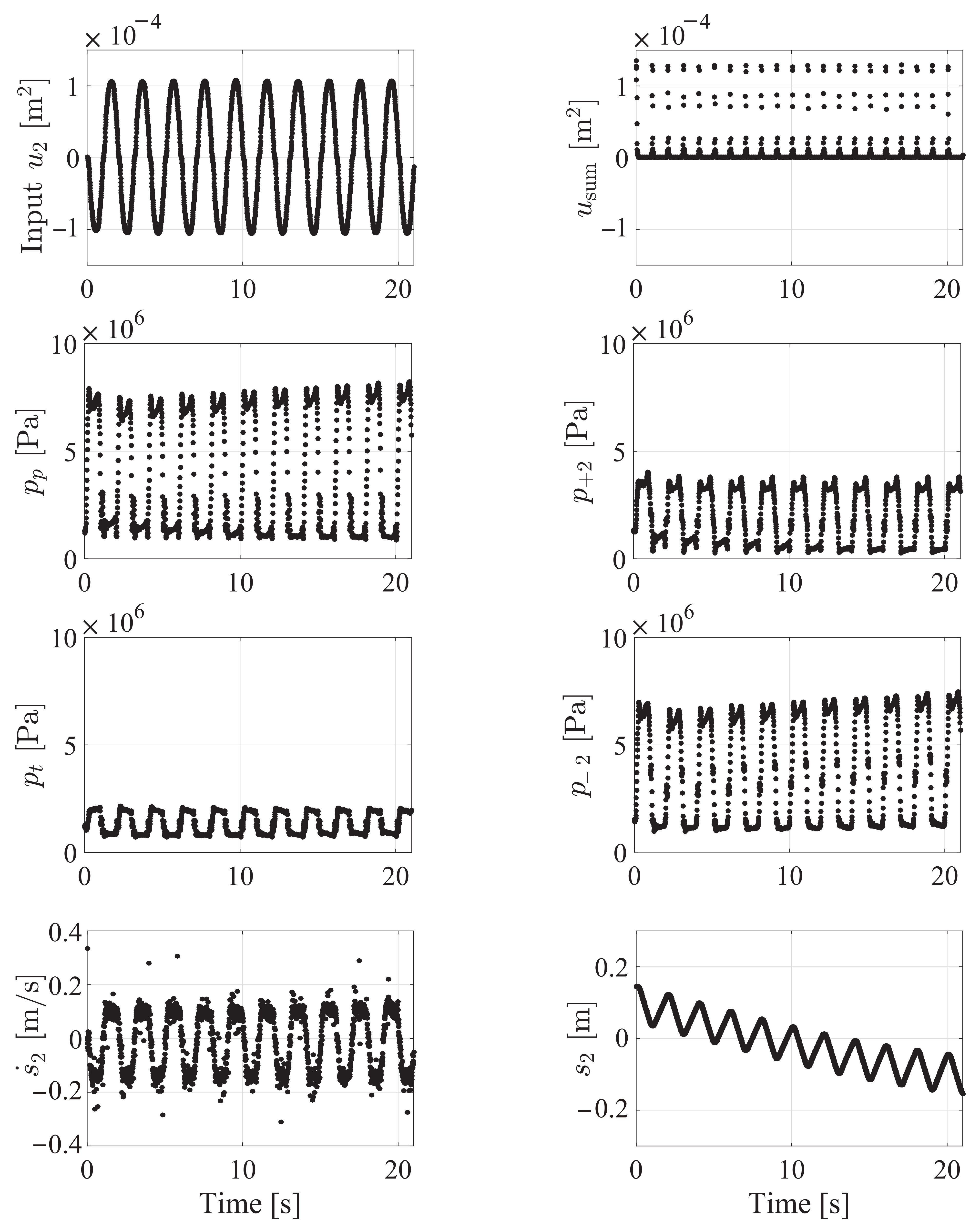
3.1. Experimental Condition (Identification)
3.2. Experimental Results and Discussion (Identification)
4. Cross Validation
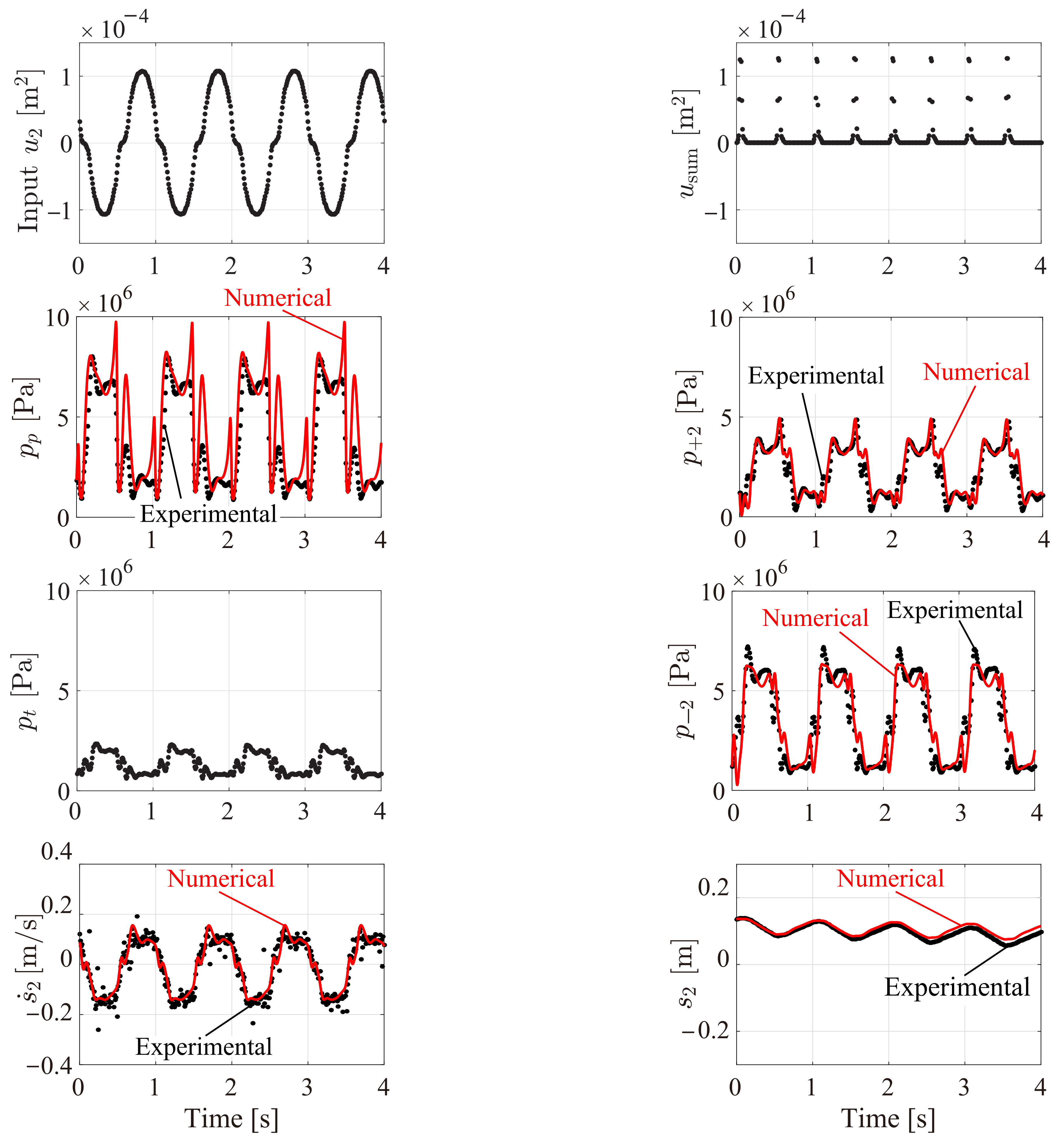
4.1. Experimental and Numerical Condition (Cross Validation)
4.2. Experimental and Numerical Results and Discussion (Cross Validation)
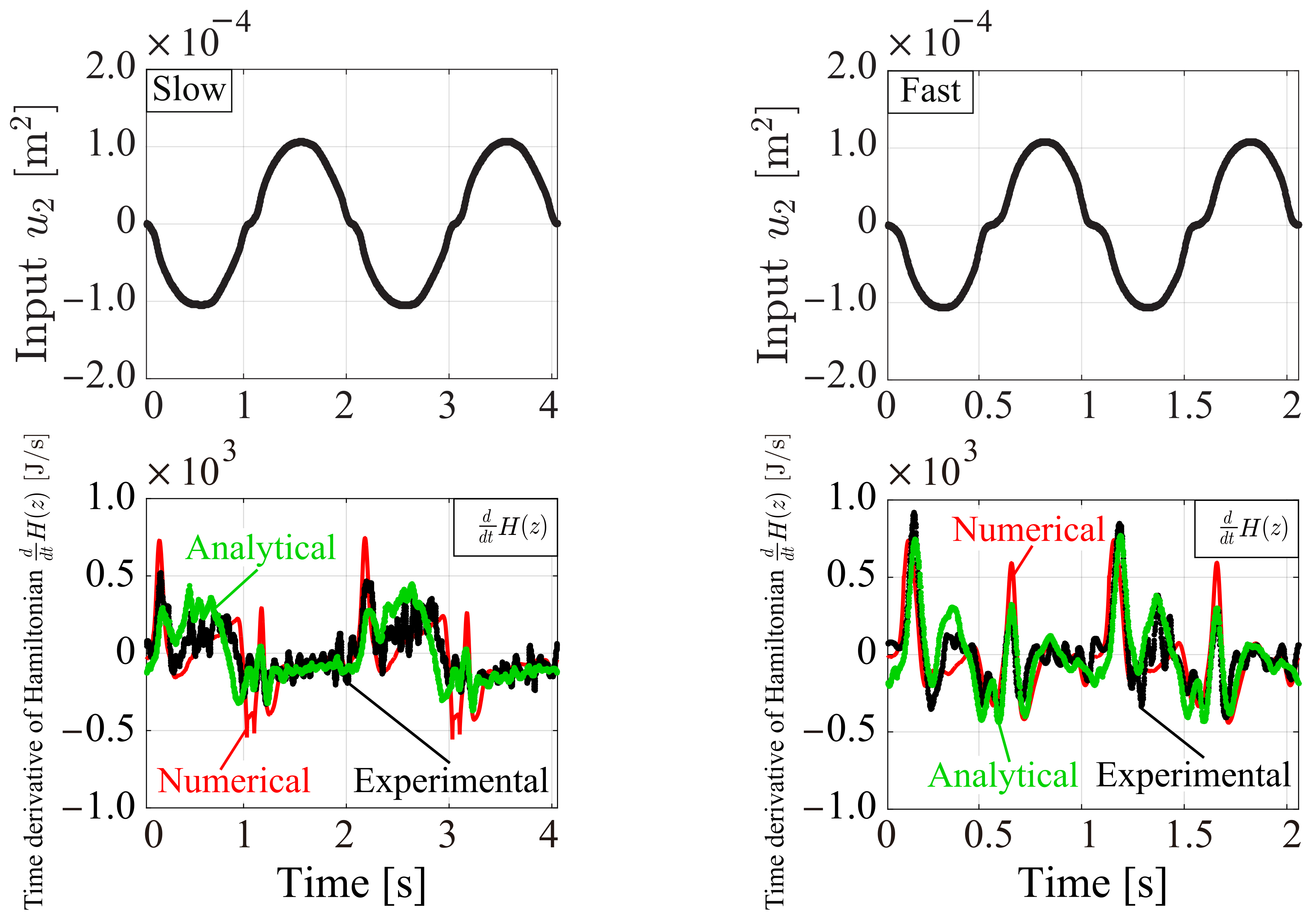
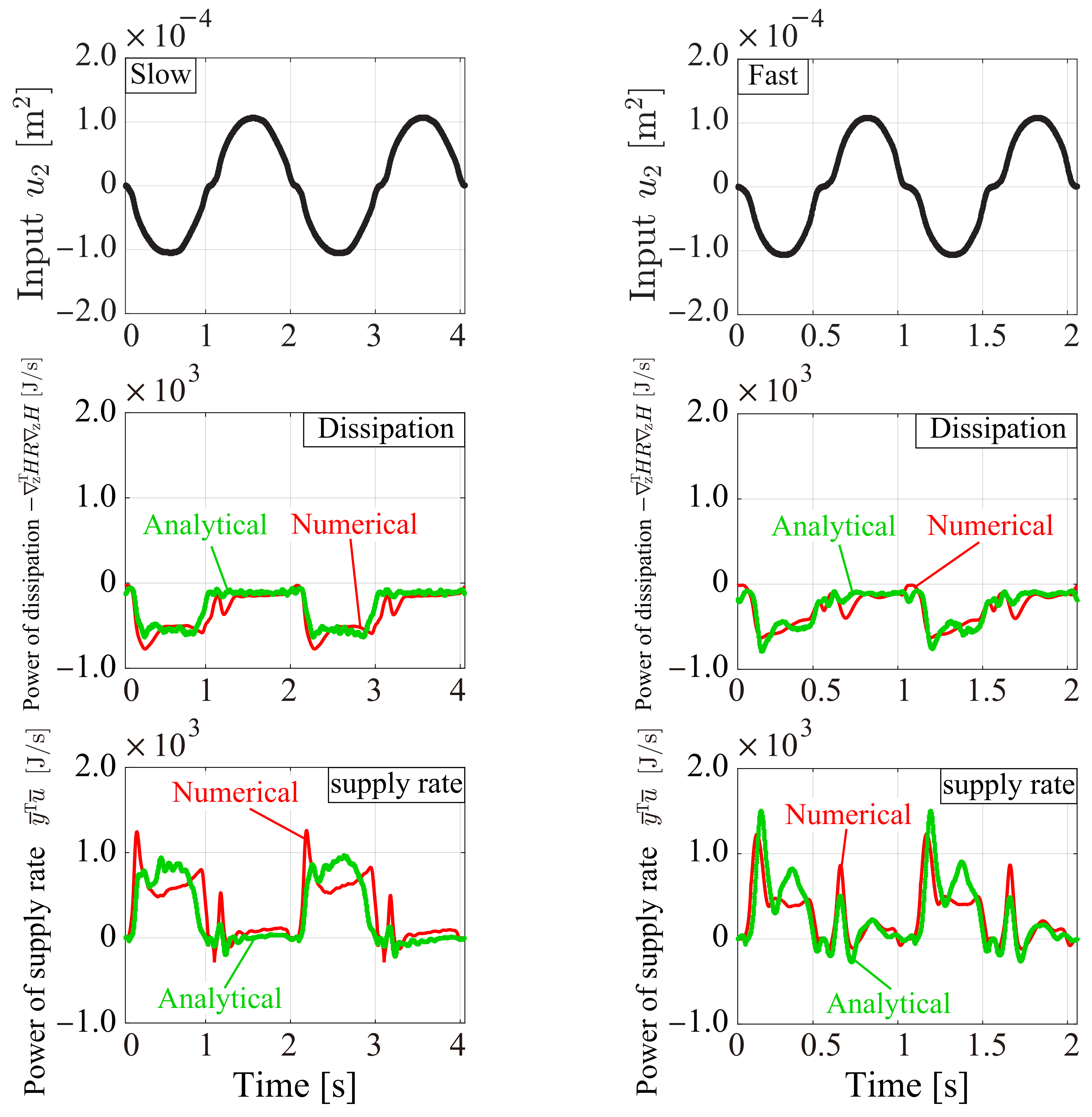
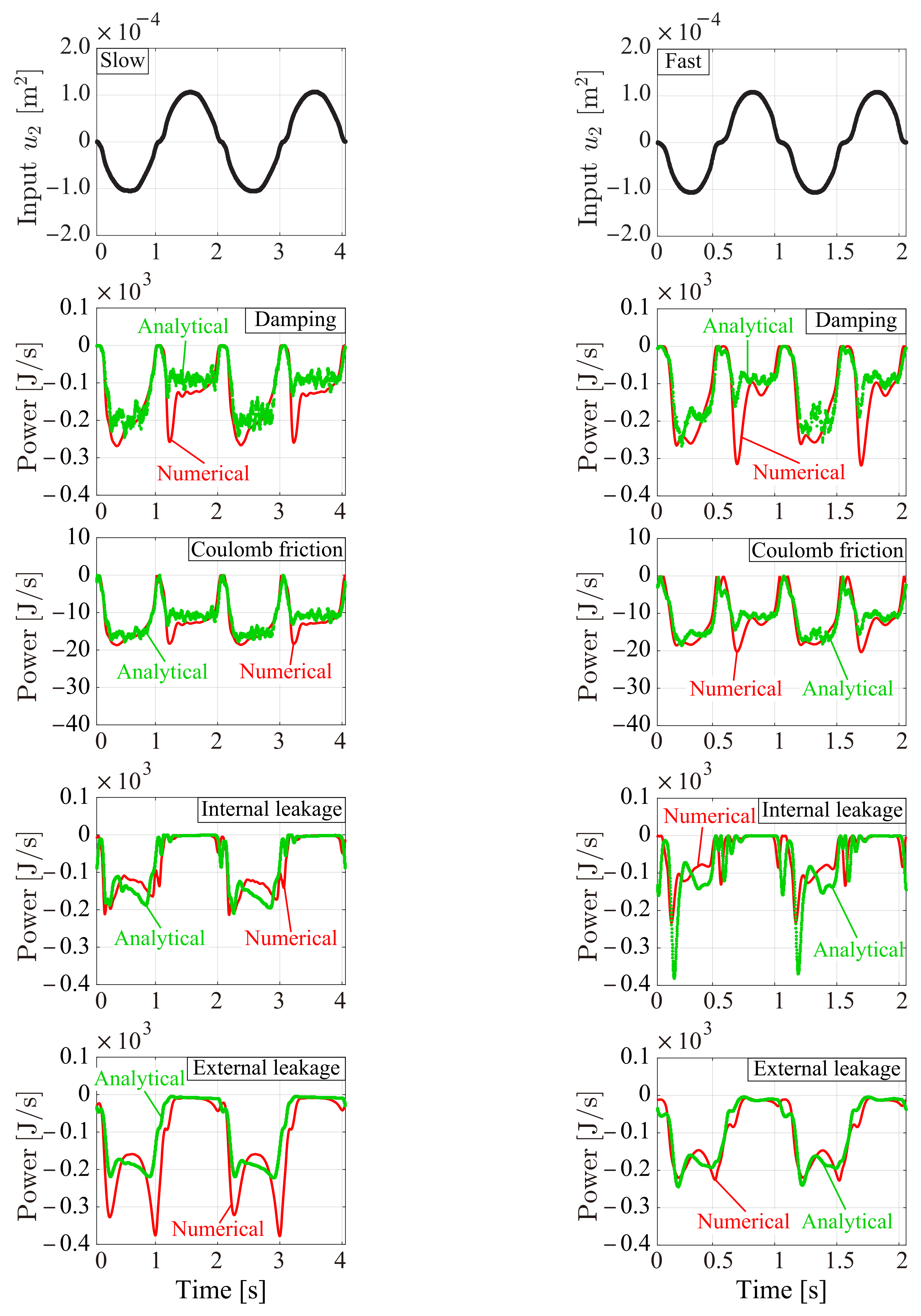
5. Energy Behavior Analysis
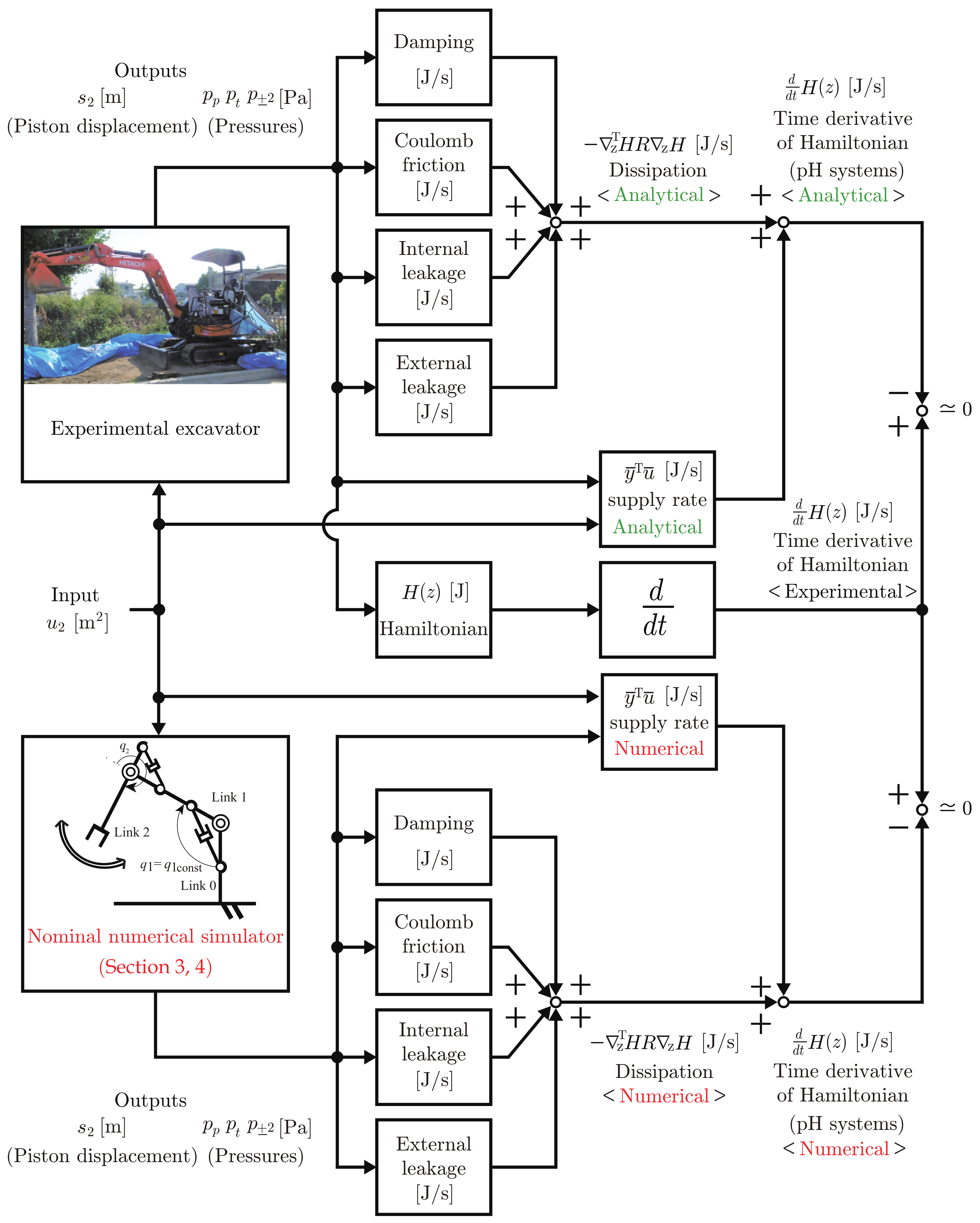
5.1. Analytical, Experimental, and Numerical Condition (Energy Behavior Analysis)
5.2. Analytical, Experimental, and Numerical Results and Discussion (Energy Behavior Analysis)
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
References
- Zhang, Q. Basics of HYDRAULIC SYSTEMS; Taylor & Francis: Abingdon, UK, 2008. [Google Scholar]
- Huang, Y.; Zhang, Q. Agricultural Cybernetics; Springer: Berlin/Heidelberg, Germany, 2021. [Google Scholar]
- Sakai, S.; Iida, M.; Osuka, K.; Umeda, M. Design and Control of a Heavy Material Handling Manipulator for Agricultural Robots. Auton. Robot. 2008, 25, 189–204. [Google Scholar] [CrossRef] [Green Version]
- Mattila, J.; Koivumaki, D.; Caldwell, D.G.; Semini, C. A survey on control of hydraulic robotic manipulators with projection to future trends. IEEE/ASME Trans. Mechatron. 2017, 22, 669–680. [Google Scholar] [CrossRef]
- Raibert, M.; Blankespoor, K.; Nelson, G.; Playter, R. BigDog, the Rough-Terrain Quadruped Robot. In Proceedings of the IFAC World Congress, Seul, Korea, 6–11 June 2008; pp. 10822–10825. [Google Scholar]
- Merritt, H. Hydraulic Control Systems; John Willey & Sons: Hoboken, NJ, USA, 1967. [Google Scholar]
- Watton, J. Fluid Power Systems; Springer: Englewood Cliffs, NJ, USA, 1989. [Google Scholar]
- Mohieddine, J.; Andreas, K. Hydraulic Servo-Systems; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Duindam, V.; Macchelli, A.; Stramigioli, S.; Bruyninckx, H. Modeling and Control of Complex Physical Systems: The Port-Hamiltonian Approach; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Van der Schaft, A.J. L2-Gain and Passivity Techniques in Nonlinear Control; Springer: Berlin/Heidelberg, Germany, 2000. [Google Scholar]
- Khalil, H. Nonlinear Systems; Prentice Hall: Hoboken, NJ, USA, 2002. [Google Scholar]
- Sakai, S. Fast Computation by Simplifications of a Class of Hydro-Mechanical Systems. In Proceedings of the IFAC Workshop on Lagrangian and Hamiltonian Methods for Nonlinear Control, Bertinoro, Italy, 29–31 August 2012; pp. 7–12. [Google Scholar]
- Kugi, A.; Kemmetmuller, W. New Energy-based Nonlinear Controller for Hydraulic Piston Actuators. Eur. J. Control 2004, 10, 163–173. [Google Scholar] [CrossRef]
- Nurmi, J.; Mattila, J. Global Energy-Optimal Redundancy Resolution of Hydraulic Manipulators: Experimental Results for a Forestry Manipulator. Energies 2017, 10, 647. [Google Scholar] [CrossRef] [Green Version]
- Vukovic, M.; Leifeld, R.; Murrenhoff, H. Reducing Fuel Consumption in Hydraulic Excavators—A Comprehensive Analysis. Energies 2017, 10, 687. [Google Scholar] [CrossRef] [Green Version]
- Lu, L.; Yao, B. Energy-Saving Adaptive Robust Control of a Hydraulic Manipulator Using Five Cartridge Valves With an Accumulator. IEEE Trans. Ind. Electron. 2014, 61, 7046–70548. [Google Scholar] [CrossRef]
- Abdel-Baqi, O.; Miller, P.; Nasiri, A. Energy Management for an 8000 hp Hybrid Hydraulic Mining Shovel. IEEE Trans. Ind. Appl. 2015, 1–8. [Google Scholar] [CrossRef]
- Sakai, S.; Stramigioli, S. Visualization of Hydraulic Cylinder Dynamics by a Structure Preserving Nondimensionalization. IEEE/Asme Int. Trans. Mechatron. 2018, 23, 2196–2206. [Google Scholar] [CrossRef]
- Morselli, R.; Zanasi, R.; Ferracin, P. Dynamic Model of an Electro-hydraulic Three Point Hitch. In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006. [Google Scholar] [CrossRef]
- Maeshima, Y.; Sakai, S.; Nakanishi, M.; Osuga, K. A Base Parameter Identification Method and Model Validation for Hydraulic Arms. J. JFPS 2012, 43, 16–21. [Google Scholar]
- Sakai, S.; Maeshima, Y. A New Method for Parameter Identification for N-DOF Hydraulic Robot. In Proceedings of the IEEE International Conference on Robotics and Automation (ICRA), Hong Kong, China, 31 May–5 June 2014; pp. 5983–5989. [Google Scholar]
- Saleem, A.; Kim, M.H. CFD Analysis on the Air-Side Thermal-Hydraulic Performance of Multi-Louvered Fin Heat Exchangers at Low Reynolds Numbers. Energies 2017, 10, 823. [Google Scholar] [CrossRef] [Green Version]
- Castilla, R.; Alemany, I.; Alger, A.; Javier Gamez-Montero, P.; Roquet, P.; Codina, E. Pressure-Drop Coefficients for Cushioning System of Hydraulic Cylinder With Grooved Piston: A Computational Fluid Dynamic Simulation. Energies 2017, 10, 1704. [Google Scholar] [CrossRef] [Green Version]
- Zardin, B.; Cillo, G.; Borghi, M.; D’Adamo, A.; Fontanesi, S. Pressure Losses in Multiple-Elbow Paths and in V-Bends of Hydraulic Manifolds. Energies 2017, 10, 788. [Google Scholar] [CrossRef] [Green Version]
- Li, Y.; Wang, Q. Pump-Pressure-Compensation-Based Adaptive Neural Torque Control of a Hydraulic Excavator with open-center Valves. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM), Auckland, NZ, USA, 9–12 July 2018; pp. 610–615. [Google Scholar]
- Tatsuoka, A.; Sakai, S.; Zhang, Q. Modeling of Hydraulic Robots with an Open-Center Dynamics. In Proceedings of the SICE ISCS, Kumamoto, Japan, 7–9 March 2019. [Google Scholar]
- Luenberger, D. Optimization by Vector Space Method; Wiley Interscience: Chichester, NY, USA, 1968. [Google Scholar]
- Sakai, S.; Osuka, K.; Umeda, M.; Maekawa, T.; Umeda, M. Robust Control Systems of a Heavy Material Handling Agricultural Robot: A Case Study for Initial Cost Problem. IEEE Trans. Control Syst. Technol. 2007, 15, 1038–1048. [Google Scholar] [CrossRef]
- Ljung, L. System Identification: Theory for the User; Prentice Hall: Hoboken, NJ, USA, 1999. [Google Scholar]
- Sakai, S. A Direct Teaching Control via Casimir of Force Sensorless Hydraulic Arms. In Proceedings of the IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Hong Kong, China, 8–12 July 2019; pp. 211–216. [Google Scholar]
- Arai, R.; Sakai, S. A Verification Method of the Impedance Control Based on the Conserved Quantity for Symmetrical Hydraulic Arms. In Proceedings of the Conference of Japan Fluid Power System Society (JFPS), Okayama, Japan, 8–9 September 2020; pp. 54–56. (In Japanese). [Google Scholar]
- Richard, E.; Vivalda, J. Mathematical Analysis of Stability and Drift Behavior of Hydraulic Cylinders Driven by a Servovalve. ASME J. Dyn. Syst. Meas. Control 2002, 124, 206–213. [Google Scholar] [CrossRef]
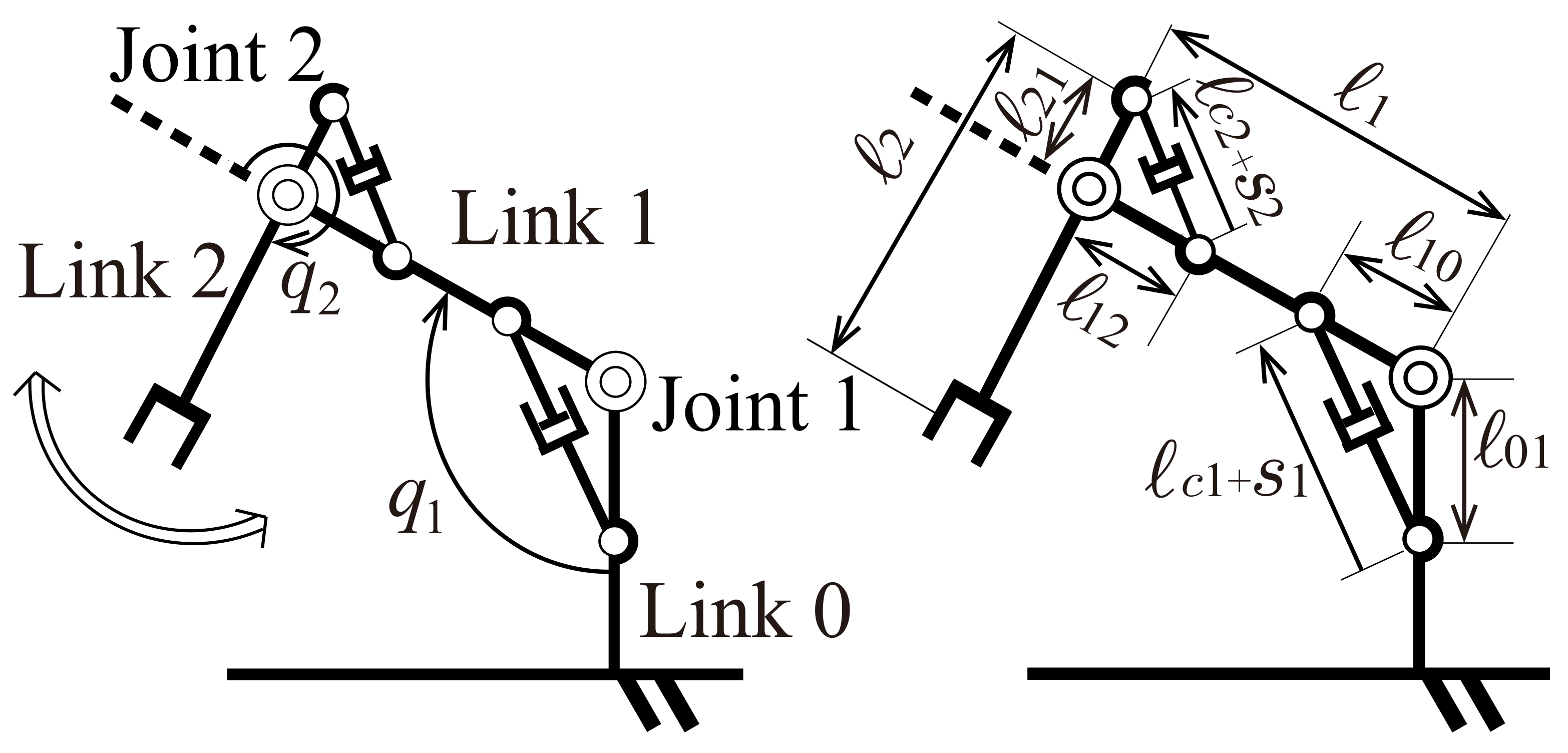
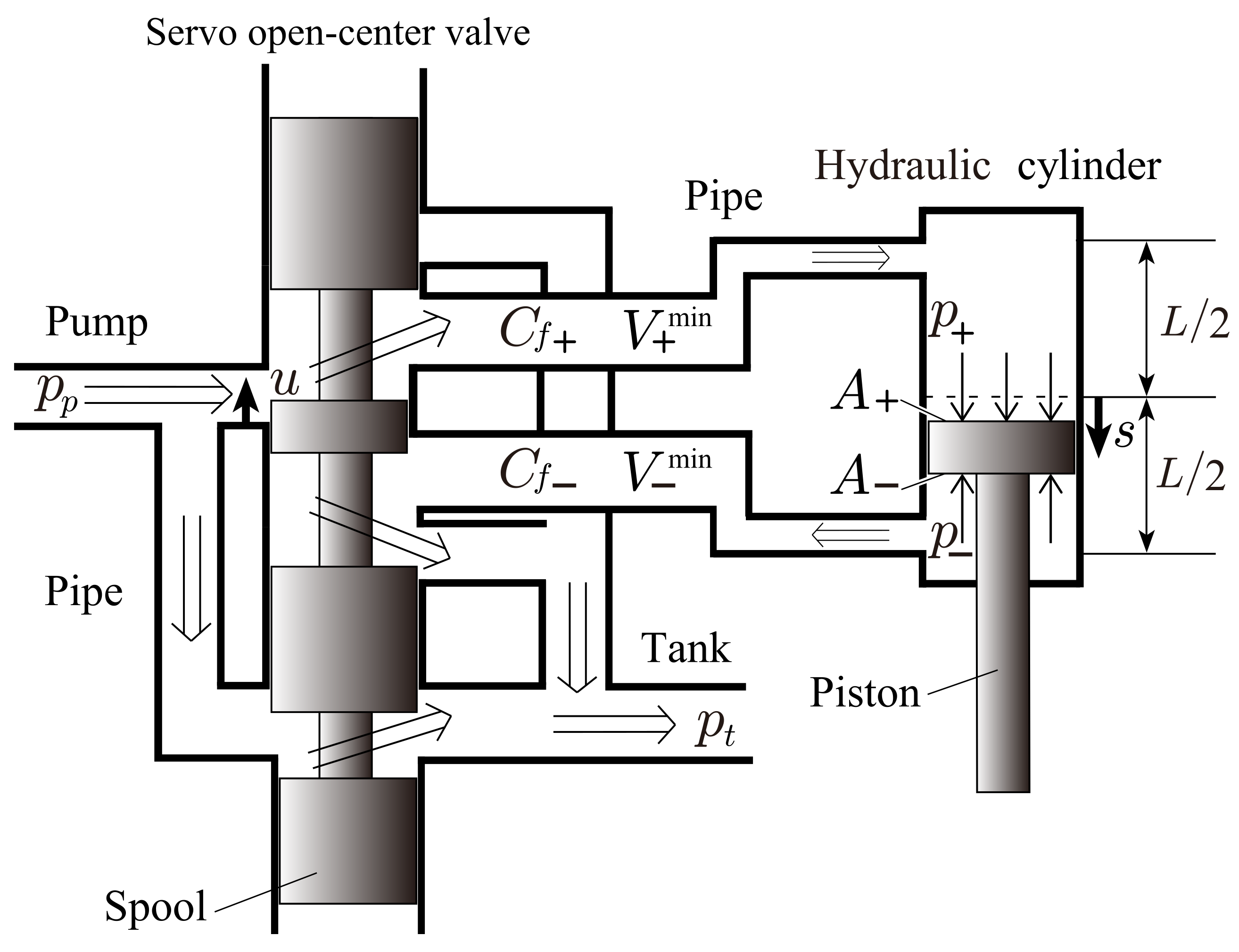
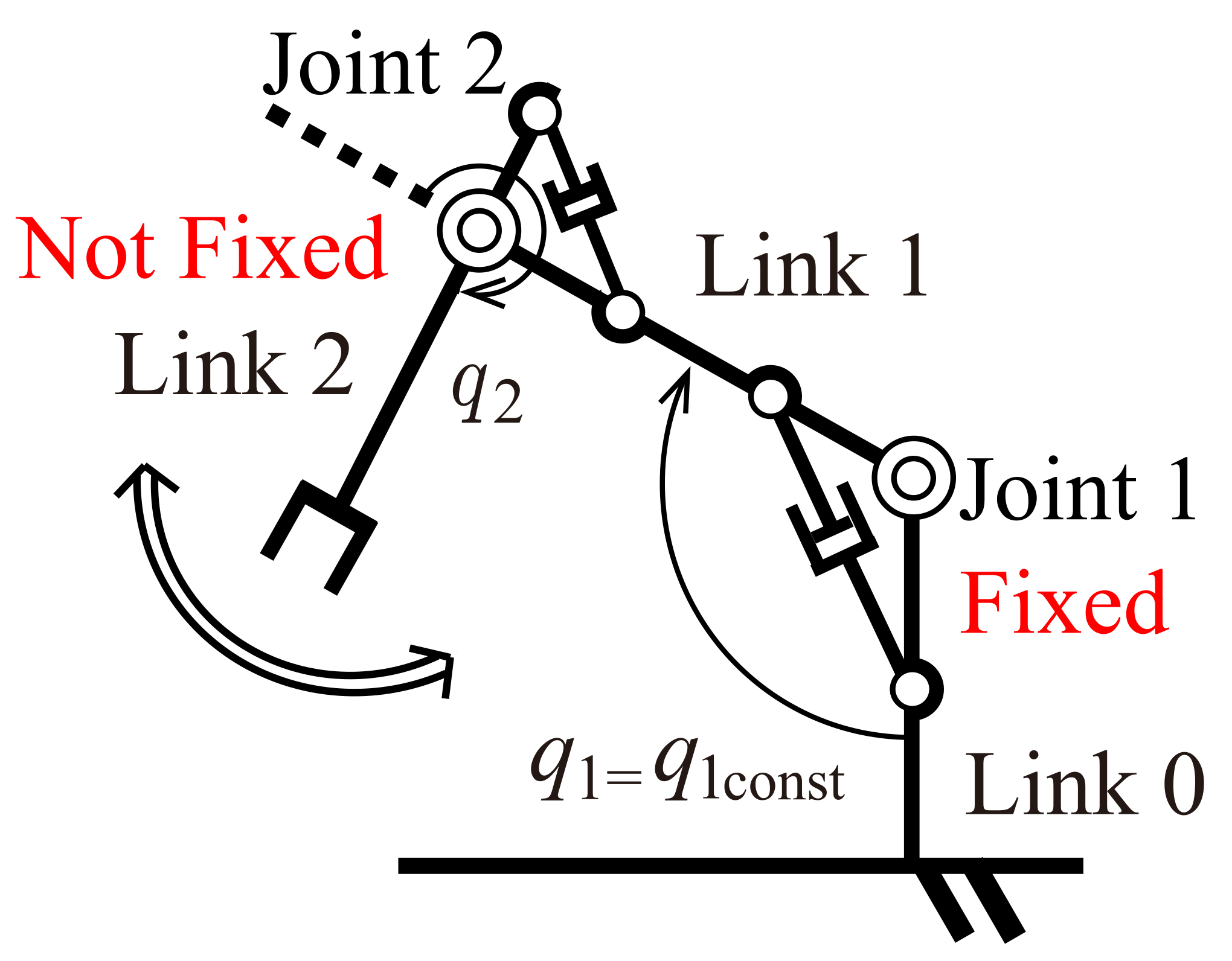

| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| Moment of inertia | Unknown | ||
| Damping coefficient | Unknown | ||
| Coulomb friction coefficient | Unknown | ||
| Gravity coefficient | Unknown | ||
| Gravity acceleration | |||
| Standard length of piston | |||
| Standard length of piston | |||
| Piston attachment position | |||
| Piston attachment position | |||
| Stroke | |||
| Cap area | |||
| Rod area | |||
| Bulk modulus | Unknown | ||
| Pump bulk modulus | Unknown | ||
| Flow gain | Unknown | ||
| Internal leakage coefficient | Unknown | ||
| External leakage coefficient | Unknown | ||
| Tank flow gain | Unknown | ||
| Cap pipe volume | |||
| Rod pipe volume | |||
| Pump pipe volume | |||
| Pump flow rate |
| Symbol | Parameter | Value | Unit |
|---|---|---|---|
| Moment of inertia | |||
| Damping coefficient | |||
| Coulomb friction coefficient | |||
| Gravity coefficient | |||
| Bulk modulus | |||
| Pump bulk modulus | |||
| Flow gain | |||
| Flow gain | |||
| Internal leakage coefficient | |||
| External leakage coefficient | |||
| External leakage coefficient | |||
| Tank flow gain |
| Pump pressure | 33 > 0 |
| Cap pressure | 56 > 0 |
| Rod pressure | 53 > 0 |
| Piston velocity | 67 > 0 |
| Piston displacement | 48 > 0 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Arai, R.; Sakai, S.; Tatsuoka, A.; Zhang, Q. Analytical, Experimental, and Numerical Investigation of Energy in Hydraulic Cylinder Dynamics of Agriculture Scale Excavators. Energies 2021, 14, 6210. https://doi.org/10.3390/en14196210
Arai R, Sakai S, Tatsuoka A, Zhang Q. Analytical, Experimental, and Numerical Investigation of Energy in Hydraulic Cylinder Dynamics of Agriculture Scale Excavators. Energies. 2021; 14(19):6210. https://doi.org/10.3390/en14196210
Chicago/Turabian StyleArai, Ryo, Satoru Sakai, Akihiro Tatsuoka, and Qin Zhang. 2021. "Analytical, Experimental, and Numerical Investigation of Energy in Hydraulic Cylinder Dynamics of Agriculture Scale Excavators" Energies 14, no. 19: 6210. https://doi.org/10.3390/en14196210
APA StyleArai, R., Sakai, S., Tatsuoka, A., & Zhang, Q. (2021). Analytical, Experimental, and Numerical Investigation of Energy in Hydraulic Cylinder Dynamics of Agriculture Scale Excavators. Energies, 14(19), 6210. https://doi.org/10.3390/en14196210







