Three-Phase and Single-Phase Measurement of Overhead Power Line Impedance Evaluation

Abstract

Calculation and measurement of the overhead power lines electrical parameters is common practice in today’s electrical engineering industry; however, there is very little data to actually compare these two approaches because measured data in such detail are mostly unavailable for academic purposes. Based on the very detailed model of an overhead power line in MATLAB Simulink environment and conducted experimental measurement, this article specifically covers the exact evaluation of the impedance of the investigated overhead power line. Differences between calculation and experimental measurement are shown and discussed accordingly, where, surprisingly, the biggest deviation was observed in the positive resistance parameter. The connection between different measurement techniques (multiple single-phase and three-phase methods), as well as the power line asymmetry reflection in the impedance matrix is explained as well as compared to expected values from the computations. The complete mathematical approach for electrical parameters evaluation from different measurement methods is explained step-by-step, and the final equations are introduced for each method. Proposed methods of obtaining the electrical parameters of the power line are then concluded as the ones with great accuracy and wide usage in practical applications. It shows the great importance of correct input data for the electrical parameters’ theoretical computations and the need to know the measurement methodology and apparatus perfectly to process the measured data and interpret them correctly.

1. Introduction

Currently, most power system applications use system impedances as a mathematical definition of particular equipment. Among such can be included applications as data analysis and digital relay data analysis, protection settings, planning models for load flow and dynamic calculations, short-circuit and post-event analyses, real-time and offline models, etc. [1,2,3]. In this respect, accuracy is an important requirement. Accurate knowledge of impedance parameters helps to improve accuracy in many areas of electrical power engineering. In the field electrical protection, there is a great importance on the improvement of post-event fault location, which leads to a quicker restoration of the systems relay settings. Accuracy is also important in the area of simulation calculation due to improvement of power line modeling, such as state estimation or operation planning calculations [4,5,6,7].

Typical elements with impedance and significant representation in the power system are overhead power lines. The overhead power line is an element whose impedance is characterized by parameters based mostly on its length (many km, number of towers), construction (variations due to landscape impacting the sag and therefore also final length), environment (soil resistivity, temperature or generally weather) and mutual impedance with other lines [8,9,10,11,12]. Impedance of the line is generally magnetic field dependent, and, therefore, it is not as predisposed to being impacted by the external factors as the admittance because permeability of the environment in the vicinity of the line is rarely changed to be distinguished from the permeability of vacuum [13].

Today, power line parameters are estimated based on the tower geometries, conductor dimensions and structure (stranding, materials, etc.), estimates of actual line length, conductor sag, and other factors and assumptions [14,15,16]. Well-known methodologies for calculating power line impedance are used, mainly based on line schedule [17]. The calculation is often considered to be an exact and final impedance value. However, this reasoning may not always be true, as it is necessary to distinguish between the symmetrical component value and the phase values.

Therefore, the article focuses on the evaluation of transmission power line impedance, especially positive-sequence and zero-sequence impedance, using the offline method measurement. Offline measurement requires a transmission line that is out of service, and several approaches can be applied to evaluate the impedance value [18]. Attention is paid to the comparison of the exact impedance evaluation of the investigated transmission power line by calculation (with an exhaustive summary of theory), simulation and measurement methods focusing on differences identification.

Nowadays, the synchronized phasor measurement technology (PMU) opens a new path to parameter identification and estimation [18,19,20,21,22,23]. In addition, the demands of today’s modern power systems, traditional methods for power line impedance determination are often marked as not accurate enough. On the other hand, this approach undoubtedly brings new possibilities, but it is still characterized by several uncertainties that we point out in the article.

Literature Review

Modern trends of overhead power line measurement are mostly oriented towards synchronous PMU measurement on both sides of the line [19,20,21,22,23]. Using this methodology, it is possible to obtain the electrical parameters of the power line in time, limited only with the sampling frequency of the devices. However, this approach is not applicable on all of the power lines because of absence of the PMU devices on many profiles and the results are not always very precise with the percentual error reaching up to single digit numbers. This topic is also discussed further and in more detail in the article. The more conservative, but more consistent testing methods for impedance measurement of AC transmission lines and calculating methods for the resistance and inductance of the tested line are provided by the IEEE Std 1870™-2019 [18]. The 1-phase and 3-phase voltage and current measurements on the tested line are basic inputs needed for the estimation of the series impedance matrix of the line. Academic articles with this IEEE measurement methodology are nearly non-existent, while the engineering practice shows otherwise, when the measurement apparatus for this purpose has also been available for quite some time [24]. It is therefore not possible to include any relevant articles about comparisons of the measured serial impedances of the line with the detailed calculations, because there are none to be found (to the authors’ best knowledge). On the other hand, calculations of the serial impedances of the overhead power lines are a quite common and well-known topic. Every computational method is based on the Carson’s integral expression in 1926 [25], with its latest closed-form expression made in 2005 by Noda [26]. Other additions to the impedance calculations is the multilayer earth component [27] or temperature correction on conductor resistance. Further details about the impedance calculation methods and principles are provided in the following section.

2. Calculation of Overhead Power Line Impedances

The actual theory of overhead power lines impedance calculation is known from the time of Carson’s first equations introduced in the article “Wave propagation in overhead wires with ground return” [25] (independently solved the same way in the same year also by Pollaczek [28], but solution applied to buried power cables). His findings were essential to understand the principles of the real earth modelling with connection to overhead lines’ electrical parameters. The prerequisites for these formulas were that the power is distributed through the power line as a wave, and the ground has one definable uniform value of resistivity.

2.1. Integral-Form Expressions for Series Impedance Matrix

The universal equation for obtaining the series impedance matrix of overhead power line can be written as following integral expression with nomenclature as in [26]:

$${\overline{Z}}_{Carson}=\frac{j\omega {\mu }_0}{2\pi }\left(ln\frac{D_2}{D_1}+I\right)$$

(1)

$$I={{\displaystyle \int }}_0^{\infty }\frac{2e^{-H\xi }}{\xi +\sqrt{{\xi }^2+j\omega \mu \sigma }}cos\left(x\xi \right)d\xi$$

(2)

where generally:

• D₁—distance from the center of the origin to the destination
• D₂—distance from the center of the origin to the mirrored destination in the ground
• H—vertical distance between the origin and the mirrored destination
• x—horizontal distance between the centers of origin and destination
• ω—angular frequency; ω = 2πf
• µ—uniform permeability of the ground
• σ—uniform conductivity of the ground

To calculate the self-impedance of the conductor “i” as pictured in Figure 1, following substitutions have to be made:

$$\begin{gathered} D_1=r_i \\ {D}_2=2h_i \\ H=2h_i \\ x=0 \end{gathered}$$

(3)

Resulting in:

$${\overline{Z}}_{ii,Carson}=\frac{j\omega \mu }{2\pi }ln\left(\frac{2h_i}{r_i}\right)+{\overline{Z}}_{gii}$$

(4)

$${\overline{Z}}_{gii}=R_{gii}+j{X}_{gii}=\frac{j\omega \mu }{\pi }{{\displaystyle \int }}_0^{\infty }\frac{e^{-2h_i\xi }}{{\xi }^2+\sqrt{{\xi }^2+j\omega \mu \sigma }}d\xi$$

(5)

To calculate the mutual impedance between the conductors “i” and “k” as pictured in the Figure 1, following substitutions have to be made:

$$\begin{gathered} D_1=r_i \\ {D}_2=2h_i \\ H=2h_i \\ x=0 \end{gathered}$$

(6)

Resulting in:

$${\overline{Z}}_{ik,Carson}=\frac{j\omega \mu }{2\pi }ln\left(\frac{D_{i{k}^{\prime }}}{D_{ik}}\right)+{\overline{Z}}_{gik}$$

(7)

$${\overline{Z}}_{gik}=R_{gik}+j{X}_{gik}=\frac{j\omega \mu }{\pi }{{\displaystyle \int }}_0^{\infty }\frac{e^{-\left(h_i+h_k\right)\xi }}{\xi +\sqrt{{\xi }^2+j\omega \mu \sigma }}cos\left(d_{ik}\xi \right)d\xi$$

(8)

Final form of the series impedance matrix (simple N-phase system without a ground wire) is as follows:

$$\left[{\overline{Z}}_{ABC-NN}\right]=\left[\begin{array}{ccc}{\overline{Z}}_{ik}& \cdots & {\overline{Z}}_{iN}\\ ⋮& \ddots & ⋮\\ {\overline{Z}}_{Nk}& \cdots & {\overline{Z}}_{NN}\end{array}\right]$$

(9)

If there are any ground wires present, the series impedance matrix will take following form:

$$\left[{\overline{Z}}_{ABC-MN}\right]=\left[\begin{array}{ccc}{\overline{Z}}_{ik}& \cdots & {\overline{Z}}_{iN}\\ ⋮& \ddots & ⋮\\ {\overline{Z}}_{Mk}& \cdots & {\overline{Z}}_{MN}\end{array}\right]$$

(10)

where “N” index is the number of phase wires, and “M” index is the sum of the phase wires and ground wires.

2.2. Closed-Form Expressions for Series Impedance Matrix

However, the coefficients used in these formulas cannot be solved analytically because they are expressed in the form of infinite series [29] which is not very practical for engineering purposes. The closed forms (approximations) of the original equations simplify the computations of the overhead line impedances with as little inaccuracy as possible. The most common were obtained by:

• Carson-Clem [30]
  • Introduced unified fictional earth return depth;
• Sunde [31]
  • Introduced complex propagation constant in earth;
• Dubanton, Gary and Deri [32,33,34]
  • Introduced fictional complex earth return depth;
• Alvarado–Betancourt [35]
  • Increased numerical accuracy of Sunde and Dubanton’s closed-form expressions;
• Noda [26]
  • Further extended the Dubanton’s complex earth return depth concept.

Their exact mathematical notation can be found summarized here [36,37,38], since it is not the main aim of this article. The resulting series impedance matrix is applicable for transposed as well as for untransposed overhead power lines, which is granting the universal application of all beforementioned expressions.

2.3. Positive and Zero-Sequence Impedance

The most useful format for the practical purposes is the symmetrical components transformation of the series impedance matrix [39]. A general procedure to obtain the positive and zero-sequence impedance is by using the transformation matrix and its inverse matrix as follows:

$$\left[\overline{T}\right]=\left[\begin{array}{ccc}1& 1& 1\\ 1& a^2& a\\ 1& a& a^2\end{array}\right]$$

(11)

$${\left[\overline{T}\right]}^{-1}=\frac{1}{3}\left[\begin{array}{ccc}1& 1& 1\\ 1& a& a^2\\ 1& a^2& a\end{array}\right]$$

(12)

where:

• $a=1\angle 120°$
• $a^2=1\angle 240°$

If the series impedance matrix is not the N × N size, the Kron reduction needs to be implemented before the next step [40,41]. Then, the transformation into the symmetrical components for the square N × N series impedance matrix will be as follows:

$$\left[{\overline{Z}}_{012}\right]={\left[\overline{T}\right]}^{-1}\left[{\overline{Z}}_{ABC-NN}\right] \left[\overline{T}\right]$$

(13)

$$\left[{\overline{Z}}_{012}\right]=\left[\begin{array}{ccc}{\overline{Z}}_{00}& {\overline{Z}}_{01}& {\overline{Z}}_{02}\\ {\overline{Z}}_{10}& {\overline{Z}}_{11}& {\overline{Z}}_{12}\\ {\overline{Z}}_{20}& {\overline{Z}}_{21}& {\overline{Z}}_{22}\end{array}\right]$$

(14)

where:

• $\left[{\overline{Z}}_{ABC-NN}\right]$ is the N × N series impedance matrix
• $\left[{\overline{Z}}_{012}\right]$—symmetrical components of the series impedance matrix
• ${\overline{Z}}_{00}={\overline{Z}}_0$—zero-sequence impedance
• ${\overline{Z}}_{11}={\overline{Z}}_1$—positive-sequence impedance
• ${\overline{Z}}_{22}={\overline{Z}}_2$—negative-sequence impedance

2.4. Positive Sequence Impedance per Phase

Overhead power line (OPL) protection setting often requires positive sequence impedance per phase value ${\overline{Z}}_{1-A}, {\overline{Z}}_{1-B}, {\overline{Z}}_{1-C}$. N × N matrix $\left[{\overline{Z}}_{ABC-MN}\right]$ for 3-phase system is:

$$\left[{\overline{Z}}_{ABC-MN}]=[{\overline{Z}}_{ABC}\right]=\left[\begin{array}{ccc}{\overline{Z}}_{aa}& {\overline{Z}}_{ab}& {\overline{Z}}_{ac}\\ {\overline{Z}}_{ba}& {\overline{Z}}_{bb}& {\overline{Z}}_{bc}\\ {\overline{Z}}_{ca}& {\overline{Z}}_{cb}& {\overline{Z}}_{cc}\end{array}\right]$$

(15)

Positive sequence impedance per phase are then calculated using classical approach (EMTP methodology) [40]:

$$\begin{gathered} {\overline{Z}}_{1-A}=\left({\overline{Z}}_{aa}+a^2{\overline{Z}}_{ab}+a{\overline{Z}}_{ac}\right) \\ {\overline{Z}}_{1-B}=\left({\overline{Z}}_{bb}+a{\overline{Z}}_{ab}+a^2{\overline{Z}}_{bc}\right) \\ {\overline{Z}}_{1-C}=\left({\overline{Z}}_{cc}+a^2{\overline{Z}}_{ac}+a{\overline{Z}}_{bc}\right) \end{gathered}$$

(16)

Alternatively, they can be acquired by calculating phase-phase loop impedances ${\overline{Z}}_{AB}$, ${\overline{Z}}_{AC}, {\overline{Z}}_{BC}$

$$\begin{gathered} {\overline{Z}}_{AB}=\left({\overline{Z}}_{aa}+{\overline{Z}}_{bb}\right)-\left({\overline{Z}}_{ab}+{\overline{Z}}_{ba}\right) \\ {\overline{Z}}_{AC}=\left({\overline{Z}}_{aa}+{\overline{Z}}_{cc}\right)-\left({\overline{Z}}_{ac}+{\overline{Z}}_{ca}\right) \\ {\overline{Z}}_{BC}=\left({\overline{Z}}_{bb}+{\overline{Z}}_{cc}\right)-\left({\overline{Z}}_{bc}+{\overline{Z}}_{cb}\right) \end{gathered}$$

(17)

Positive sequence impedance per phase from phase loop ${\overline{Z}}_{1-A}^P , {\overline{ Z}}_{1-B}^P , {\overline{Z}}_{1-C}^P$ are calculated as follows:

$$\begin{gathered} {\overline{Z}}_{1-A}^P=\frac{1}{2} \left({\overline{Z}}_{AB}+{\overline{Z}}_{AC }-{\overline{Z}}_{BC}\right) \\ {\overline{Z}}_{1-B}^P=\frac{1}{2} \left({\overline{Z}}_{AB}+{\overline{Z}}_{BC }-{\overline{Z}}_{AC}\right) \\ {\overline{Z}}_{1-C}^P=\frac{1}{2} \left({\overline{Z}}_{AC}+{\overline{Z}}_{BC }-{\overline{Z}}_{AB}\right) \end{gathered}$$

(18)

For transposed and untransposed lines OPL equals:

$$\left({\overline{Z}}_{1-A}^P+{\overline{Z}}_{1-B}^P+{\overline{ Z}}_{1-C}^P\right)\frac{1}{3}=\left({\overline{Z}}_{1-A}+{\overline{Z}}_{1-B}+{\overline{Z}}_{1-C}\right) \frac{1}{3}={\overline{Z}}_1$$

(19)

For transposed OPL equals:

$${\overline{Z}}_{1-A}^P={\overline{Z}}_{1-A} {\overline{Z}}_{1-B}^P={\overline{Z}}_{1-B} {\overline{ Z}}_{1-C}^P={\overline{Z}}_{1-C}$$

(20)

Equation (20) is not equal for untransposed lines. Above statements can be easily proved by following the example of a 160 km 500 kV line from [39]. Matrix $\left[{\overline{Z}}_{tran}\right]$ represents transposed line and matrix ${\overline{[Z}}_{nontran}]$ represents untransposed line. Both matrices are in per unit vales (Ω/mile). In the example, conductors are in horizontal configuration. Result may vary based on other conductor configurations, however inequality between positive sequence impedances calculation approaches per phase is preserved.

$$\left[{\overline{Z}}_{tran}\right]=\left[\begin{array}{ccc}0.048+j0.432& 0.036+j0.17& 0.036+j0.17\\ 0.036+j0.17& 0.048+j0.432& 0.036+j0.17\\ 0.036+j0.17& 0.036+j0.17& 0.048+j0.432\end{array}\right]$$

(21)

$$\left[{\overline{Z}}_{untran}\right]=\left[\begin{array}{ccc}0.048+j0.432& 0.036+j0.181& 0.036+j0.147\\ 0.036+j0.181& 0.048+j0.432& 0.036+j0.17\\ 0.036+j0.147& 0.036+j0.181& 0.048+j0.432\end{array}\right]$$

(22)

The results in

Table 1. Results of positive sequence impedances per phase calculated by two different approaches for transposed and untransposed OPL.

		Transposed OPL		Untransposed OPL
		$\mathit{R} \left(\Omega k{m}^{-1}\right)$	$\mathit{X} \left(\Omega k{m}^{-1}\right)$	$\mathit{R} \left(\Omega k{m}^{-1}\right)$	$\mathit{X} \left(\Omega k{m}^{-1}\right)$
EMTP methodology	${\overline{Z}}_{1-A}$	0.012	0.262	0.041	0.268
	${\overline{Z}}_{1-B}$	0.012	0.262	0.012	0.251
	${\overline{Z}}_{1-C}$	0.012	0.262	−0.017	0.268
	${\overline{Z}}_1$	0.012	0.262	0.012	0.262
Phase-phase loop	${\overline{Z}}_{1-A}^P$	0.012	0.262	0.012	0.285
	${\overline{Z}}_{1-B}^P$	0.012	0.262	0.012	0.217
	${\overline{Z}}_{1-C}^P$	0.012	0.262	0.012	0.285
	${\overline{Z}}_1$	0.012	0.262	0.012	0.262

show values of calculated positive-sequence impedances per phase which gives the following conclusions:

• For transposed OPL

  ○

  ${\overline{Z}}_{1-A} \mathrm{equals} {\overline{Z}}_{1-A}^P$ (similar for other phases);

  ○

  Average values of positive sequence impedance per phase equals ${\overline{Z}}_1$.

• For untransposed OPL

  ○

  ${\overline{Z}}_{1-A} \mathrm{not} \mathrm{equals} {\overline{Z}}_{1-A}^P$ (similar for other phases);

  ○

  ${\overline{Z}}_{1-A}$ can result into negative values of resistance (similar for other phases);

  ○

  Average values of positive sequence impedance per phase over equals ${\overline{Z}}_1$;

  ○

  Both positive sequence impedance per phase calculated by emtp methodology and by phase loop can be measured as it will be shown in Section 3.1.

3. Measurement of Overhead Power Line Impedances

The following section describes in great detail the general methodology and actual measurement apparatus for single system OPL measurement. The section also provides methodology for calculation of ${\overline{Z}}_0$, ${\overline{Z}}_1$ and positive sequence impedance per phase (EMTP methodology, phase-phase loop) from measured voltages and currents. This methodology is mainly based on IEEE recommendations [18], except for measurements M3b and M4 which are the authors’ contribution. In general, presented measurements can be characterized by:

• Off-frequency measurement—frequencies at which impedances are measured differs from power frequency 50 Hz. This is for suppressing the interference with power frequency $f_{50}$ voltages and current induced by surrounding lines, traction lines, etc. In all measurements, frequency range $f_{range}$ of power source was used. Power frequency, 50 Hz, is omitted because OPLs already have naturally induced voltages from other parallel OPLs in their close vicinity and measured superposed signal is hard to distinguish.

  $$f_{range}=\left(43;47;49;51;53;57\right) \left(\mathrm{Hz}\right)$$

  (23)
• Off-line measurement—power line is disconnected from the power grid.

Equipment required for OPL measurement consist of:

• Power source (single-phase and three-phase);
• Inverter capable of generating sinusoidal waveforms in range 50 ± 10 Hz;
• Voltage and current measurement equipment.

A detailed description of the measuring apparatus is stated in Section 3.2.

3.1. Measurement Methodology

Based on connection of circuit and used power source there are several ways how to measure and then calculate from measured data impedances ${\overline{Z}}_0$ and ${\overline{Z}}_1$.

In all measured cases, positive sequence resistance $R_1={ℛ}_e\left\{{\overline{Z}}_{1_f}\right\}$ is a function of OPL temperature. It is standard nowadays to calculate and measure resistance at a temperature of 20 °C. In simple form, the resistance of ACSR conductor at $T_{20°\mathrm{C}}$ can be expressed as follows [10]:

$$R_{T_{20°\mathrm{C}}}=\frac{R_T}{\left(1+{\alpha }_R\left(T-20\right)+{\beta }_R\left(T-20\right){ }^2\right)}$$

(24)

where:

• $R_{T_{20°\mathrm{C}}}$—is resistance at 20 °C
• $T$—T is conductor temperature
• $R_T$—is resistance at temperature $T$
• ${\alpha }_R$—linear temperature coefficient $\left(K^{-1}\right)$
• ${\beta }_R$—quadratic linear coefficient $\left(K^{-2}\right)$

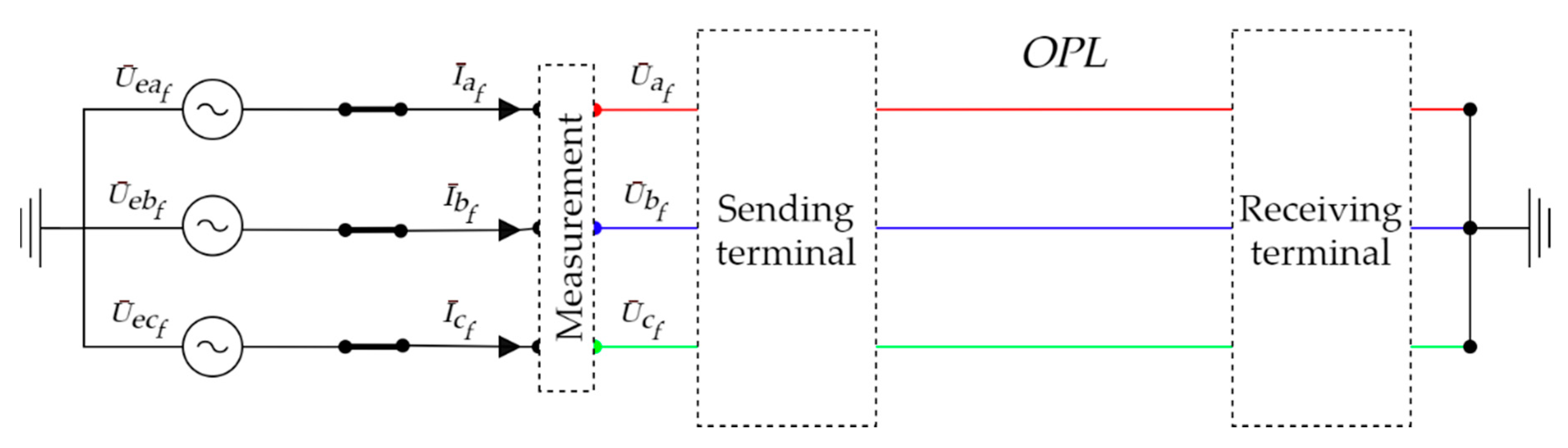
3.1.1. M1—Three-Phase Symmetrical Measurement of Positive Sequence Impedance

As shown in Figure 2, the receiving terminals of OPL are shorted and grounded. Three-phase power source is connected to sending terminals of each phase. OPL phase voltages ${\overline{U}}_{a_f},{\overline{U}}_{b_f},{\overline{U}}_{c_f}$ and currents ${\overline{I}}_{a_f},{\overline{I}}_{b_f},{\overline{I}}_{c_f}$ in each phase are measured for every $f$ from $f_{range}$.

Positive sequence impedance ${\overline{Z}}_{1f}$ measured at frequency $f$ is calculated as follows:

$${\overline{Z}}_{1_f}=\frac{1}{3}\left[\frac{{\overline{U}}_{a_f}}{{\overline{I}}_{a_f}}+\frac{{\overline{U}}_{b_f}}{{\overline{I}}_{b_f}}+\frac{{\overline{U}}_{c_f}}{{\overline{I}}_{c_f}}\right]=\frac{1}{3}\left[{\overline{Z}}_{1-A_f}+{\overline{Z}}_{1-B_f}+{\overline{Z}}_{1-C_f}\right]$$

(25)

Reactance is then recalculated to power frequency 50 Hz as follows:

$${\overline{Z}}_{1_{f50}}= {ℛ}_e\left\{{\overline{Z}}_{1_f}\right\}+j{ℐ}_m\left\{{\overline{Z}}_{1_f}\right\}\frac{50}{f}$$

(26)

Final ${\overline{Z}}_1$ is then calculated as an average value of ${\overline{Z}}_{1_{f50}}$:

$${\overline{Z}}_1=\frac{1}{n} {{\displaystyle \sum }}^{ }{\overline{Z}}_{1_{f50}}$$

(27)

where $n$ equals number of measured frequencies.

As can be seen in Equation (25), the measurement M1 gives us values of positive sequence impedances per phase which can be calculated by EMTP methodology, Equation (16), from impedance matrix. These values are further compared with other measurements and calculations.

The major disadvantage of this method is that the results are correct only with fully transposed line. In addition, this approach requires a more expensive three-phase source and other equipment. It will be shown in Section 4.4 that the result has slightly larger error compared to other measurement methods.

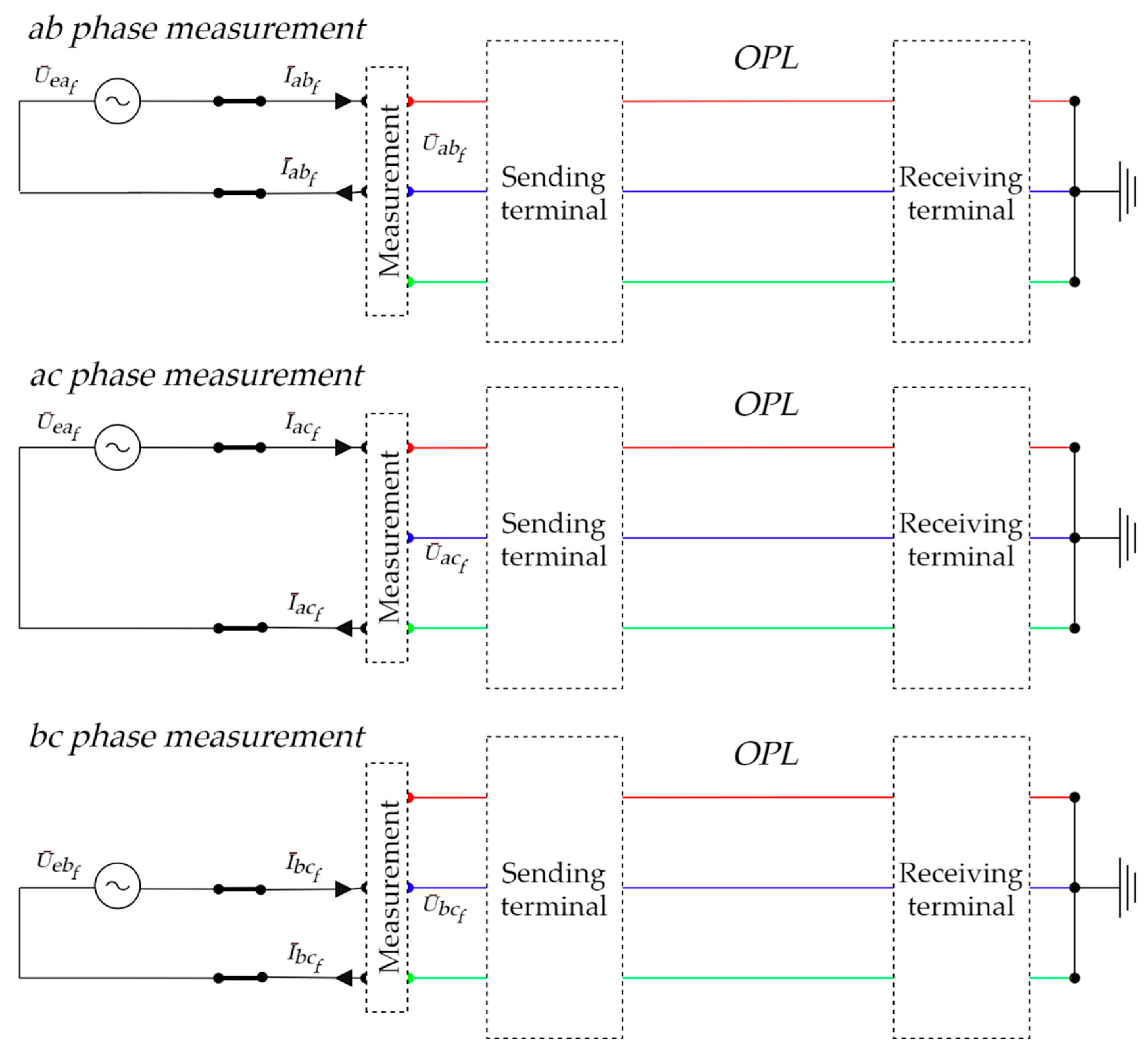
3.1.2. M2—Single-Phase Measurement of Positive Sequence Impedance by Phase-Phase Loops

As shown in Figure 3, the receiving terminals of OPL are shorted and grounded. Single-phase power source is ungrounded and connected to sending terminals between two measured phases $AB,AC,BC$ at a time Figure 3. OPL line-line voltages for every loop ${\overline{U}}_{a{b}_f},{\overline{U}}_{a{c}_f},{\overline{U}}_{b{c}_f}$ and currents ${\overline{I}}_{a{b}_f},{\overline{I}}_{a{c}_f},{\overline{I}}_{b{c}_f}$ in each phase are measured for every value of $f$ from $f_{range}$.

Positive sequence impedance ${\overline{Z}}_{A{B}_f}$ measured at frequency $f$ is calculated as follows:

$${\overline{Z}}_{A{B}_f}=\left[\frac{{\overline{U}}_{a{b}_f}}{{\overline{I}}_{a{b}_f}}\right]$$

(28)

${\overline{Z}}_{A{B}_{f50}}$ is calculated by recalculation reactance of ${\overline{Z}}_{A{B}_f}$ to power frequency by Equation (26). Similiary ${\overline{Z}}_{A{C}_{f50}}$ and ${\overline{Z}}_{B{C}_{f50}}$ is calculated. Positive sequency impedance ${\overline{Z}}_{1_{f50}}$ measured at frequency $f$ is then calculated as follows:

$${\overline{Z}}_{1_{f50}}=\frac{1}{6} \left[{\overline{Z}}_{A{B}_{f50}}+{\overline{Z}}_{A{C}_{f50}}+{\overline{Z}}_{B{C}_{f50}}\right]$$

(29)

Final ${\overline{Z}}_1$ is then calculated as an average value of ${\overline{Z}}_{1_{f50}}$, Equation (27).

Positive sequence impedances pre phase ${\overline{Z}}_{1-A_{f50}}^P$, ${\overline{Z}}_{1-B_{f50}}^P$, ${\overline{Z}}_{1-C_{f50}}^P$ measured at frequency $f$ are calculated from Equation (18). ${\overline{Z}}_{1-A}^P$, ${\overline{Z}}_{1-B}^P$, ${\overline{Z}}_{1-C}^P$ are calculated as an average value from $f_{range}$.

3.1.3. M3—Single Phase Measurement of Positive and Zero Sequence Impedance by Phase-Ground Loops

As shown in Figure 4, the receiving terminals of OPL are shorted and grounded. Measurement consists of three separate measurements (1,2,3) during which a single-phase power source is connected individually to terminal of phases $a, b, c$.

Measurement consists of following steps for every frequency $f$:

• Power source is connected to first phase. OPL phase voltages ${\overline{U}}_{a{a}_f},{\overline{U}}_{a{b}_f},{\overline{U}}_{a{c}_f}$ (the first index value of voltage indicates the phase which induced voltage on the phase of the second index value) and current conductor ${\overline{I}}_{a_f}$ are measured.
• Power source is connected to second phase. OPL voltages ${\overline{U}}_{b{a}_f},{\overline{U}}_{b{b}_f},{\overline{U}}_{b{c}_f}$ and current conductor ${\overline{I}}_{b_f}$ are measured.
• Power source is connected to third phase. OPL voltages ${\overline{U}}_{c{a}_f},{\overline{U}}_{c{b}_f},{\overline{U}}_{c{c}_f}$ and current conductor ${\overline{I}}_{c_f}$ are measured.

Impedance matrix ${\left[\overline{Z}\right]}_f$ is then constructed from the measured values as follows:

$${\left[\overline{Z}\right]}_f=\left[\begin{array}{ccc}\frac{{\overline{U}}_{a{a}_f}}{{\overline{I}}_{a_f}}& \frac{{\overline{U}}_{b{a}_f}}{{\overline{I}}_{b_f}}& \frac{{\overline{U}}_{c{a}_f}}{{\overline{I}}_{c_f}}\\ \frac{{\overline{U}}_{a{b}_f}}{{\overline{I}}_{a_f}}& \frac{{\overline{U}}_{b{b}_f}}{{\overline{I}}_{b_f}}& \frac{{\overline{U}}_{c{b}_f}}{{\overline{I}}_{c_f}}\\ \frac{{\overline{U}}_{a{c}_f}}{{\overline{I}}_{a_f}}& \frac{{\overline{U}}_{b{c}_f}}{{\overline{I}}_{b_f}}& \frac{{\overline{U}}_{c{c}_f}}{{\overline{I}}_{c_f}}\end{array}\right]=\left[\begin{array}{ccc}{\overline{Z}}_{a{a}_f}& {\overline{Z}}_{b{a}_f}& {\overline{Z}}_{c{a}_f}\\ {\overline{Z}}_{a{b}_f}& {\overline{Z}}_{b{b}_f}& {\overline{Z}}_{c{b}_f}\\ {\overline{Z}}_{a{c}_f}& {\overline{Z}}_{b{c}_f}& {\overline{Z}}_{c{c}_f}\end{array}\right]$$

(30)

${\left[\overline{Z}\right]}_{f50}$ is then calculated by recalculation reactance of ${\left[\overline{Z}\right]}_f$ to power frequency as follows:

$${\left[\overline{Z}\right]}_{f50}= {ℛ}_e\left\{{\left[\overline{Z}\right]}_f\right\}+j{ℐ}_m\left\{{\left[\overline{Z}\right]}_f\right\}\frac{50}{f}$$

(31)

Matrix ${\left[\overline{Z}\right]}_{f50}$ should by diagonally symmetrical. However, due to measurement, some error may occur. Therefore, the mean value of ${\left[\overline{Z}\right]}_{f50}$ is calculated as follows.

$${\left[\overline{Z}\right]}_{f50\_sym}= \frac{1}{2}({\left[\overline{Z}\right]}_{f50}+{\left[\overline{Z}\right]}_{f50}{}^T)$$

(32)

where ${\left[\overline{Z}\right]}_{f50}{}^T$ is transposed matrix ${\left[\overline{Z}\right]}_{f50}$. Using Equation (13), a matrix of symmetrical components is calculated from which ${\overline{Z}}_{1f50}$ and ${\overline{Z}}_{0f50}$ are extracted, Equation (14). Measurement is repeated for all frequencies in $f_{range}$. ${\overline{Z}}_1$ and ${\overline{Z}}_0$ is then calculated as average over the frequencies, Equation (27).

Positive sequency impedances pre phase ${\overline{Z}}_{1-A_{f50}}$, ${\overline{Z}}_{1-B_{f50}}$, ${\overline{Z}}_{1-C_{f50}}$ measured at frequency $f$ are calculated from ${\left[\overline{Z}\right]}_{f50\_sym}$ by Equation (16). ${\overline{Z}}_{1-A}$, ${\overline{Z}}_{1-B}$, ${\overline{Z}}_{1-C}$ are calculated as an average value from $f_{range}$.

Positive sequence impedances pre phase ${\overline{Z}}_{1-A_{f50}}^P$, ${\overline{Z}}_{1-B_{f50}}^P$, ${\overline{Z}}_{1-C_{f50}}^P$ measured at frequency $f$ are calculated from ${\left[\overline{Z}\right]}_{f50\_sym}$ by Equations (17) and (18). ${\overline{Z}}_{1-A}^P$, ${\overline{Z}}_{1-B}^P$, ${\overline{Z}}_{1-C}^P$ are calculated as an average value from $f_{range}$.

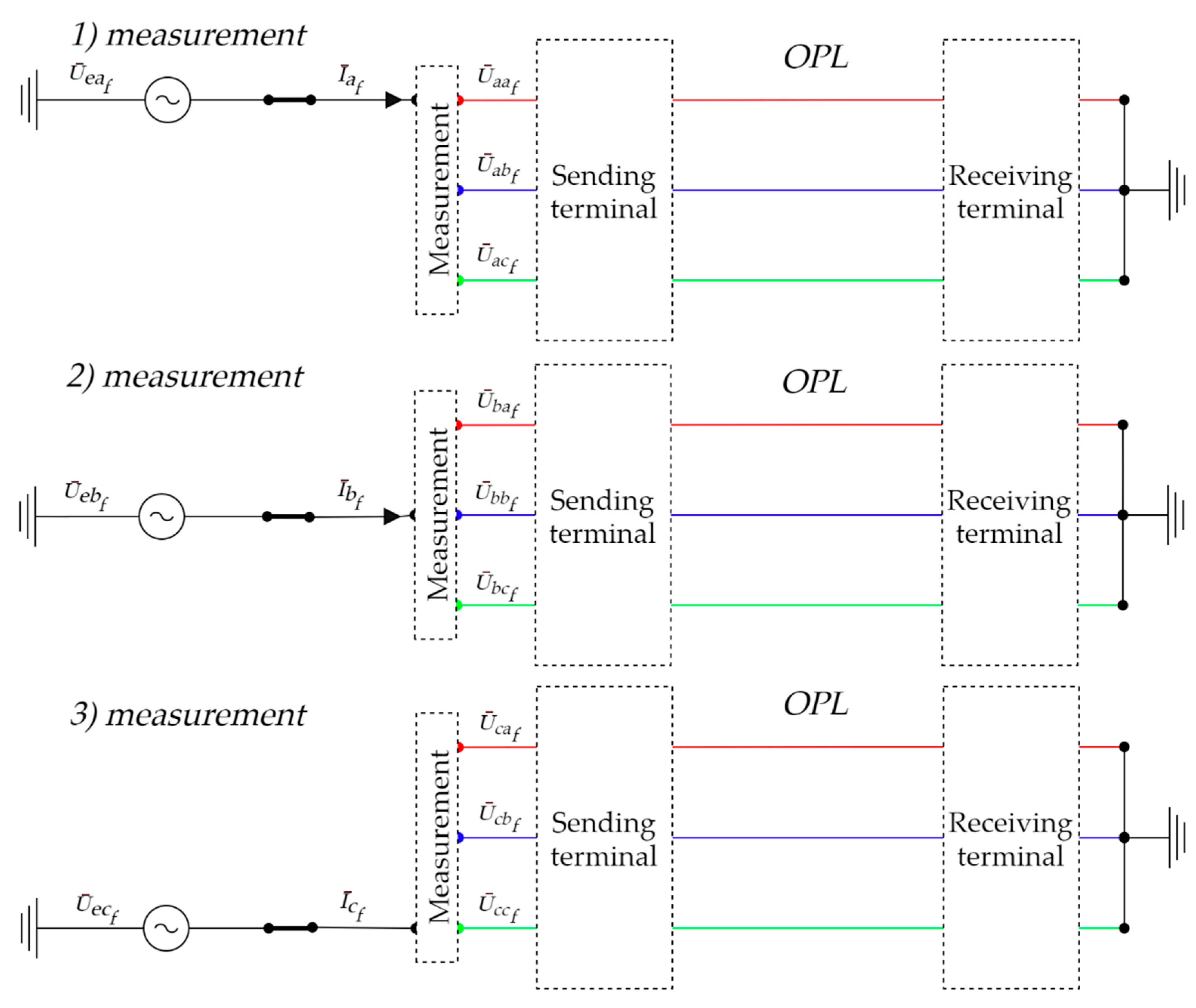
3.1.4. M3b—Alternative Way of Calculating Zero Sequence Impedance by Phase-Ground Loops Measurement

The following evaluation of ${\overline{Z}}_0$ is based on measurement of ${\overline{Z}}_1$ by M2 and phase loop measurement specified in Section 3.1.2. Advantage of this approach are simple mathematical calculation and need of only single-phase power analyzer for measurement. Voltages of not connected phases to source are irrelevant. Only ${\overline{U}}_{a{a}_f}$ at ${\overline{I}}_{a_f}$, ${\overline{U}}_{b{b}_f}$ at ${\overline{I}}_{b_f}$ and ${\overline{U}}_{c{c}_f}$ at ${\overline{I}}_{c_f}$ are measured from measurement at Figure 4. From the following measurement line ground impedance (earth impedance + impedance of ground wire) ${\overline{Z}}_{L{g}_f}$ is calculated as follows:

$${\overline{Z}}_{L{g}_f}=\left[\frac{{\overline{U}}_{a{a}_f}}{{\overline{I}}_{a_f}}+\frac{{\overline{U}}_{b{b}_f}}{{\overline{I}}_{b_f}}+\frac{{\overline{U}}_{c{c}_f}}{{\overline{I}}_{c_f}}\right]\frac{1}{3}$$

(33)

${\overline{Z}}_{L{g}_{f50}}$ is calculated by recalculation reactance of ${\overline{Z}}_{L{g}_f}$ to power frequebncy by Equation (26). Impedance ${\overline{Z}}_{L{g}_{f50}}$ can be writenn also as:

$${\overline{Z}}_{L{g}_{f50}}={\overline{Z}}_1+{\overline{Z}}_{g_{f50}}$$

(34)

where ${\overline{Z}}_{g_{f50}}$ is ground impedance and ${\overline{Z}}_1$ is positive sequence impedance measured by M2 measurement from phase-phase loops. Equation (34) can be rewritten as:

$${\overline{Z}}_{g_{f50}}={\overline{Z}}_{L{g}_{f50}}-{\overline{Z}}_1$$

(35)

Zero sequence impedance ${\overline{Z}}_{0_{f50}}$ can be generally expressed as:

$${\overline{Z}}_{0_{f50}}={\overline{Z}}_1+3{\overline{Z}}_{g_{f50}}$$

(36)

Combining Equations (35) and (36) we get:

$${\overline{Z}}_{0_{f50}}={3\overline{Z}}_{L{g}_{f50}}-2{\overline{Z}}_1$$

(37)

${\overline{Z}}_0$ is then calculated as an average value of ${\overline{Z}}_{0_{f50}}$ Equation (26).

3.1.5. M4—Three-Phase Measurement of Zero Sequence Impedance Using Single Phase Source

As shown in Figure 5, the receiving terminals of OPL are shorted and grounded. Sending terminal are shorted. Measurement consists of single measurements during which a single-phase power source is to OPL.

From the following measurement zero sequence impedance ${\overline{Z}}_{0_f}$ for every frequency $f$ is calculated as follows:

$${\overline{Z}}_{0_f}=3\left[\frac{{\overline{U}}_{a_f}}{{\overline{I}}_{a_f}}\right]$$

(38)

${\overline{Z}}_{0_{f50}}$ is calculated by recalculation reactance of ${\overline{Z}}_{0_f}$ to power frequency by Equation (26). ${\overline{Z}}_0$ is then calculated as an average value of ${\overline{Z}}_{0_{f50}}$, Equation (27).

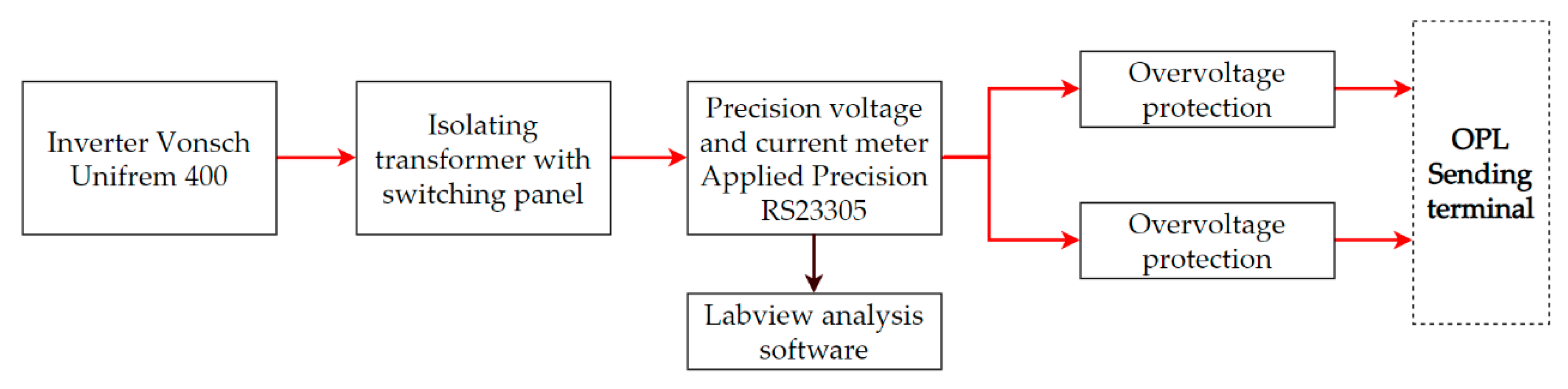
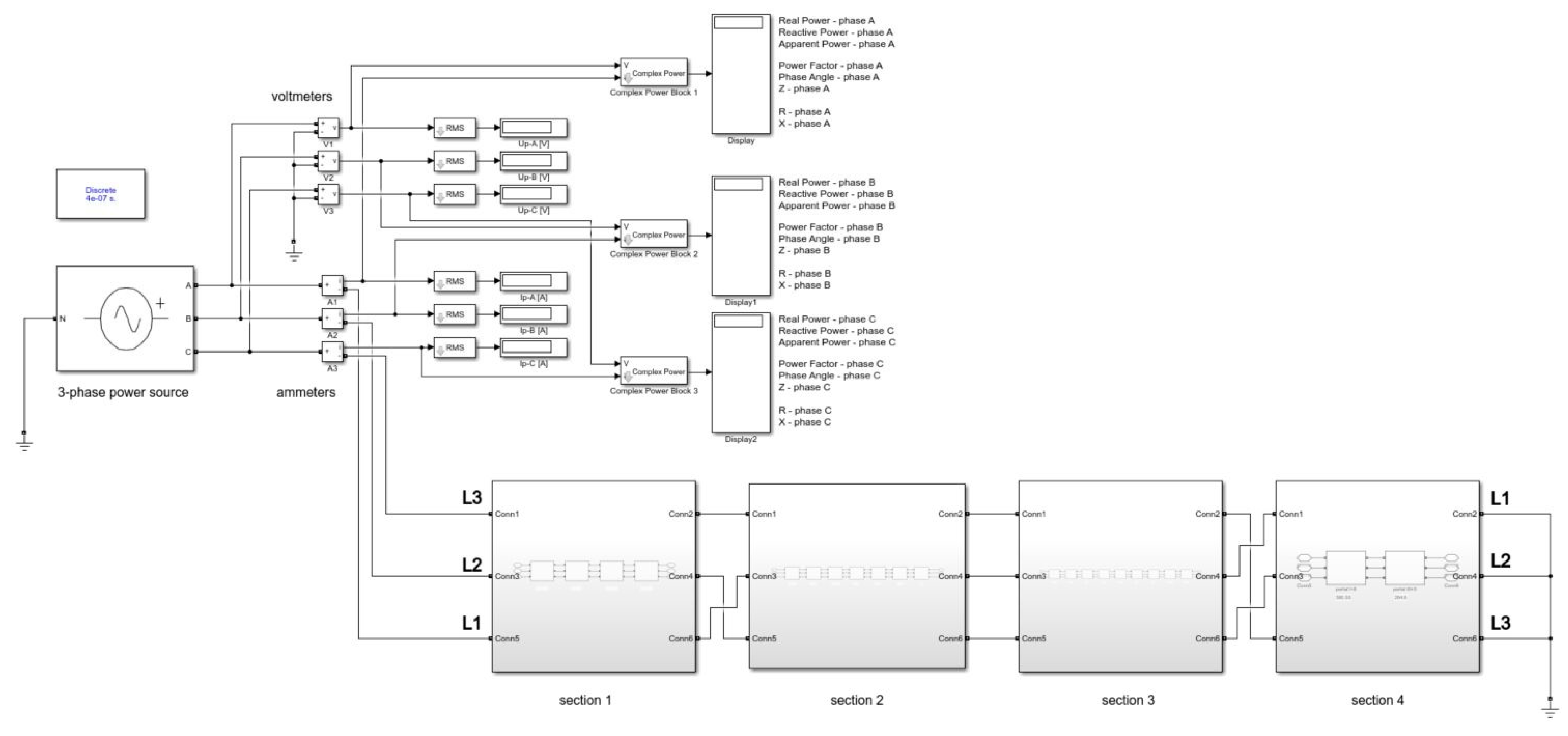
3.2. Measuring Apparatus and Data Analysis

For measuring purposes, our own apparatus was created, the design of which was based on commonly available elements with an emphasis on measurement accuracy and plausibility of single-phase and three-phase measurement. In order to evaluate the measured values, the measuring apparatus is unique in the use of software harmonic filters, where the block scheme is shown in Figure 6.

A standard inverter with an apparent power of 20 kVA is used as a measurement source for supplying a measured power line. This measurement source is connected to an isolating transformer with a switching panel, which is used to change the configuration of the power supply with the possibility of connection to the power line conductors and create the possibility of connection to ground. As a block of voltage and current measurement is used precision voltage and current meter—Applied Precision RS2330E.

During the measurement, this device is used in oscilloscopic mode, while the measured values are real-time sampled waveform (RMS values are not measured). The measuring device has separated voltage and current circuits to eliminate the error caused by voltage drops. For this reason, the connection to the power line is realized by two separate branches, i.e., the voltage as well as the current branch have overvoltage protections.

3.3. Specification of Measuring Apparatus Components

Precision voltage and current meter Applied precision RS2330E:

• Highest accuracy 0.01% (optionally up to 0.005%);
• Wide measuring range 0.1 mA to 120 A and 0.1 V to 600 V;
• Bandwidth 10 kHz and sampling rate 24-bit 125,000 samples/second.

Inverter Vonsch Unifrem 400:

• Output voltage range 3 × 0 ÷ 400 V;
• Output frequency 0 ÷ 500 Hz;
• Electronic protection against overcurrent, overvoltage, undervoltage, short circuit protection and ground fault protection.

Isolating transformer:

• Connection Dyn1;
• Voltage 360/550 V;
• Nominal power 20 kVA;
• Frequency 40 ÷ 100 Hz.

3.4. Measurement Safety

Measurement on OPL requires specific safety procedures as follows:

• Measurement planning:

  ○

  Possible inductive coupling from parallel or in the close vicinity power line to the measured power line is necessary to verify by simulation in order to assess the measurement possibility, i.e., the risk of high values of open circuit voltage and short-circuit current on power source terminals is represented by the loading of the parallel power line.

  ○

  Based on the voltage and current conditions, it is necessary to decide on the possibility of measuring the power line during operation of the parallel line or on it shutting off.

• Measurement performing:

  ○

  Measured power line is grounded on both terminals and before the measurement, it is necessary to verify the open circuit voltage and short-circuit current values in all phases on receiving terminal.

  ○

  Based on the open circuit voltage and short-circuit current conditions, it is necessary to decide on the possibility of measuring the power line, i.e., if the voltage and current exceed maximum power, then the power source will not be able to supply measured power line and measurement is not possible to perform.

  ○

  The required connection of power source to OPLs, according to specific measurements (m1–m4) by switching panel.

  ○

  Measurement is performed for whole $f_{range}$. The minimum source voltage is set when the power supply is first connected to the receiving terminal. Voltage is then slowly increased and the OPLs currents are monitored to not exceed the maximum current of the apparatus.

3.5. Sampled Waveform Processing

Measurement data are sampled waveforms for every frequency from $f_{range}$, as defined in Equation (23). The selected measurement frequencies are close to the grid frequency, which means that the resulting signal is repeated with a frequency $f_{signal}$ as follows:

$$f_{signal}=\left|f_{grid}-f_{source}\right|$$

(39)

where:

• $f_{signal}$—frequency of measured signal
• $f_{grid}$—frequency of power grid
• $f_{source}$—frequency of power supply apparatus

Above equation shows that the sampled signal length of the oscilloscope recording must be more than $1/f_{signal}$. Our measured signal length from varies from 40 to 60 s. The longer time decrease Type A evaluation of uncertainty. Signal processing is done using LabVIEW custom software. Core of program is frequency filter function Extract Sine Tone. It finds the single tone with the highest amplitude or searches a specified frequency range, and returns the single tone frequency, amplitude, and its phase [42]. The difference between the measured frequency and the grid frequency is from 1 Hz to 7 Hz and in this case, it is not possible to build a reliable hardware filter. By this approach coupled signals are reliably filtered out. MATLAB software filters were also tested in the analysis and the results were equally accurate.

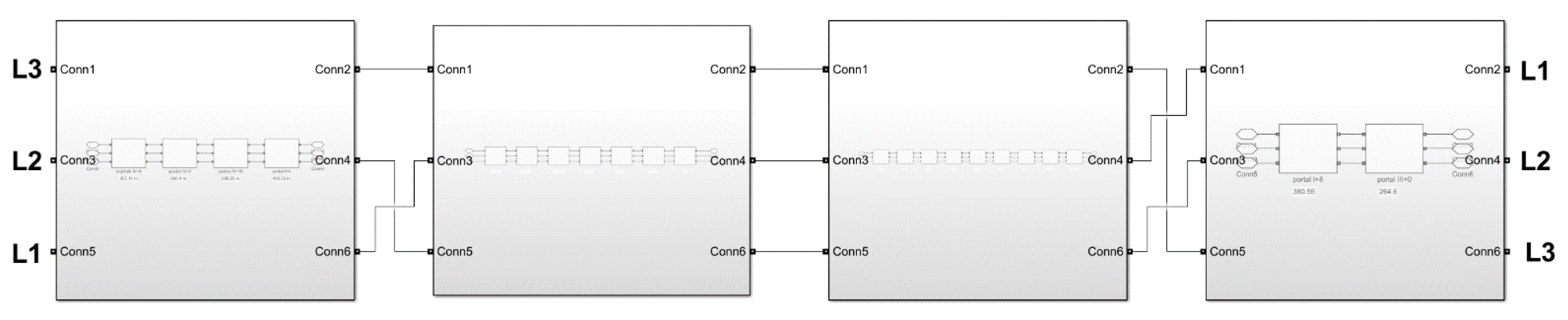
4. Comparison of Calculation, Simulation and Measurement Results

In the following part, overview information and results are provided for particular approaches of determining the impedance for a selected transmission line at 400 kV voltage level. These results are reciprocally compared in order to identify their accuracy, suitability for use and potential shortcomings of stated approaches.

4.1. Positive and Zero Sequence Impedance—Calculation

The investigated power line is defined by following parameters:

(a)

Towers’ geometry and height standardization

○

“Y” type, Portal, Cat, “V” type

○

+0/+4/+6/+8/+12/+14/+18

(b)

Phase arrangement

○

As shown in Figure 2

(c)

Conductor/ground wires types

○

Phase conductor:

▪

350AlFe4 (similar to 362-AL1/59-ST1A)

○

Ground wires:

▪

185AlFe3 (similar to 184-AL3/72-A20SA)

▪

Alcatel 24 Fo OPGW 147/59

▪

70Fe (steel wire)

▪

AL4/A20SA 147/30-17.7

(d)

Span lengths

○

Defined between every tower, total length 85.7863 km

(e)

Minimum clearing distance

○

Usually from 8–12 m for the lowest conductor

(f)

Ground resistivity

○

Usually from 50–200 Ωm

For the actual impedance computation, the MATLAB routine “power_lineparam” was used, which is utilizing the traditional Carson’s calculation methodology [43]. The complete power line is based on the line schedule, and it was divided on separate sections (as pictured in Figure 7), where every section has the same parameters (a), (b) and (c). The ground resistivity and minimum clearing distances of the lowest conductor are estimated through the calculation as constants. Span length is then divided and assigned to respective towers on its ends to ensure optimal distribution of the conductors’ height over the ground. Thanks to the span directly connected to the individual towers, it is possible to create the detailed model of the transmission line and therefore obtain the serial impedance matrix and also the symmetrical components of the impedance.

For the whole model, uniform ground resistivity of 100 Ωm was estimated, and the minimum clearing distance of the lowest conductor for each tower design was 8m. Final impedance matrix $\left[\overline{Z}\right]$ of calculated electrical parameters is then as follows:

$$\left[\overline{Z}\right]=\left[\begin{array}{ccc}7.501+j38.265& 4.806+j13.702& 4.789+j14.759\\ 4.806+j13.702& 7.292+j38.624& 4.634+j11.726\\ 4.789+j14.759& 4.634+j11.726& 7.266+j40.528\end{array}\right]$$

(40)

Positive and zero sequence impedances, ${\overline{Z}}_1, {\overline{ Z}}_0,$ are then calculated from $\left[\overline{Z}\right]$ by Equation (14). Both types of positive sequence impedances per phase are evaluated, EMTP methodology Equation (16), and phase-phase loop calculation Equations (17) and (18). Following

Table 2. Calculation results of symmetrical components (per phase as well).

		$\mathit{R} \left(\Omega \right)$	X (Ω)
Matrix calculation	${\overline{Z}}_1$	2.609	25.743
	${\overline{Z}}_0$	16.842	65.930
EMTP	${\overline{Z}}_{1-A}$	1.787	24.017
	${\overline{Z}}_{1-B}$	0.860	26.063
	${\overline{Z}}_{1-C}$	5.180	27.151
Phase-phase loop	${\overline{Z}}_{1-A}^P$	2.536	21.530
	${\overline{Z}}_{1-B}^P$	2.638	27.955
	${\overline{Z}}_{1-C}^P$	2.652	27.745

shows calculated results. As it can be seen, stated values are not equal because the power line is not perfectly transposed (Section 2.4).

4.2. Positive and Zero Sequence Impedance—Simulation

As stated above, based on power line schedule, a detailed model of the transmission line was created. This model was complemented by the necessary elements of measurement and configuration in terms of the corresponding methodology (Section 3).

Positive and zero sequence impedances, ${\overline{Z}}_1, {\overline{Z}}_0,$ are calculated based on measurement results in MATLAB Simulink (Figure 8). Positive sequence impedances per phase are evaluated, 1st from the 3-phase measurement directly, 2nd from the phase-phase loop measurement (needed also calculation Equation (18)) and 3rd from the phase-ground loop (needed also calculation Equation (30)). Zero sequence impedance is evaluated from the 3-phase measurement directly.

Table 3. Simulation results of symmetrical components (per phase).

		$\mathit{R} \left(\Omega \right)$	$\mathit{X} \left(\Omega \right)$
3-phase measurement (per phase)	${\overline{Z}}_{1-A}$	2.440	23.889
	${\overline{Z}}_{1-B}$	0.688	26.145
	${\overline{Z}}_{1-C}$	5.054	26.655
Phase-phase loop	${\overline{Z}}_{1-A}^P$	2.537	21.569
	${\overline{Z}}_{1-B}^P$	2.633	27.851
	${\overline{Z}}_{1-C}^P$	2.630	27.973
Phase-ground loop	${\overline{Z}}_{1-A}^G$	2.602	21.568
	${\overline{Z}}_{1-B}^G$	2.703	27.849
	${\overline{Z}}_{1-C}^G$	2.695	27.975
Zero sequence	${\overline{Z}}_0$	16.876	66.265

shows calculated results. As in previous results, it is possible to see that stated values are not equal because the power line is not perfectly transposed (Section 2.4).

4.3. Positive and Zero Sequence Impedance—Measurement

The power line impedance measurement was performed for 400 kV transmission line geographically located in the north part of Slovakia according to detailed parameters (see Section 4.1) where a simplified line schedule can be seen in Figure 9. This power line is characterized by an individual corridor with no crossings with other transmission power lines with the exception of perhaps 15 crossings with power lines at a 110 kV voltage level. There is only one exception of a parallel power line in close vicinity at the beginning from the measurement side location, which is particularly important regarding to safety precautions of the measurement.

Positive and zero sequence impedances, ${\overline{Z}}_1, {\overline{Z}}_0,$ are calculated based on measurement results according to the stated methodology above (Section 3). Positive sequence impedances per phase are evaluated: 1st—directly by the 3-phase measurement, 2nd—the 1-phase measurement (phase-phase loop) (needed also calculation Equation (18)) and 3rd—the 1-phase measurement (phase-ground loop) (needed also calculation Equation (30)). Zero sequence impedance is evaluated by means of two approaches: (a) determination by the 1-phase measurement (phase-ground loop); (b) directly by the 3-phase measurement using single phase source. In addition, the measurement took place during an environmental temperature of 26 °C. That means that the measured and evaluated resistance values of conductor must be converted into the resistance at 20 °C by Equation (24), where linear temperature coefficient α = 0.00403 K⁻¹ and quadratic linear coefficient β = 8 × 10⁻⁷ K⁻¹. In

Table 4. Measurement results of symmetrical components (per phase).

		$\mathit{R} \left(\Omega \right)$	$\mathit{R} \left(\Omega \right) *$	$\mathit{X} \left(\Omega \right)$
3-phase measurement (per phase)	${\overline{Z}}_{1-A}$	2.371	2.312	23.924
	${\overline{Z}}_{1-B}$	0.648	0.632	26.282
	${\overline{Z}}_{1-C}$	4.989	4.863	26.783
Phase-phase loop	${\overline{Z}}_{1-A}^P$	2.519	2.456	21.593
	${\overline{Z}}_{1-B}^P$	2.645	2.579	27.956
	${\overline{Z}}_{1-C}^P$	2.653	2.586	28.087
Phase-ground loop	${\overline{Z}}_{1-A}^G$	2.517	2.454	21.606
	${\overline{Z}}_{1-B}^G$	2.643	2.577	27.954
	${\overline{Z}}_{1-C}^G$	2.639	2.573	28.069
Zero sequence (determination from phase-ground loop)	${\overline{Z}}_0$	16.001	-	63.422
Zero sequence	${\overline{Z}}_0$	16.080	-	63.421

* converted resistance values into the resistance at 20 °C.

, the calculated results are shown.

4.4. Results Comparison

In the field of electrical parameters of power lines, research and analyses of modelling and measurement have been published in a relatively number scale of studies. Some studies were aimed at evaluating of calculation and simulation manners and some at measurement approaches.

In order to compare the calculation, simulation results and measurement results with each other, the calculated value of positive and zero sequence impedance is considered a reference value where the deviation is related precisely to these values. A comparison of the results of symmetrical components for the investigated 400kV transmission power line is shown in

Table 5. Comparison of simulation results of investigated power line.

		${\mathit{R}}_1 \left(\Omega \right) *$	${\mathit{X}}_1 \left(\Omega \right)$	${\mathit{R}}_0 \left(\Omega \right)$	${\mathit{X}}_0 \left(\Omega \right)$
Measurement	Calculation	2.609	25.743	16.842	65.930
M1	simulation	2.727	25.563	-	-
error (%)		4.54	0.70	-	-
M2	simulation	2.600	25.798	-	-
error (%)		0.35	0.21	-	-
M3	simulation	2.667	25.797	16.906	66.310
error (%)		2.22	0.21	0.38	0.58
M3b	simulation	-	-	16.906	66.309
error (%)		-	-	0.38	0.58
M4	simulation	-	-	16.876	66.265
error (%)		-	-	0.20	0.51

* converted resistance values into the resistance at 20 °C.

and

Table 6. Comparison of measurement results of investigated power line.

		${\mathit{R}}_1 \left(\Omega \right) *$	${\mathit{X}}_1 \left(\Omega \right)$	${\mathit{R}}_0 \left(\Omega \right)$	${\mathit{X}}_0 \left(\Omega \right)$
Measurement	Calculation	2.609	25.743	16.842	65.930
M1	measurement	2.602	25.663	-	-
error (%)		0.27	0.31	-	-
M2	measurement	2.540	25.878	-	-
error (%)		2.63	0.53	-	-
M3	measurement	2.539	25.876	16.013	63.427
error (%)		2.68	0.52	4.92	3.80
M3b	measurement	-	-	16.001	63.422
error (%)		-	-	4.99	3.80
M4	measurement	-	-	16.08	63.421
error (%)		-	-	4.52	3.81

* converted resistance values into the resistance at 20 °C.

, comparison results of positive sequence impedance per phase in

Table 7. Comparison results of positive sequence impedance per phase.

			${\mathit{R}}_1 \left(\Omega \right) *$	${\mathit{X}}_1 \left(\Omega \right)$
Measurement	Calculation		2.609	25.743
M1	measurement	${\overline{Z}}_{1-A}$	2.312	23.924
		${\overline{Z}}_{1-B}$	0.632	26.282
		${\overline{Z}}_{1-C}$	4.863	26.783
	simulation	${\overline{Z}}_{1-A}$	2.440	23.889
		${\overline{Z}}_{1-B}$	0.688	26.145
		${\overline{Z}}_{1-C}$	5.054	26.655
M2	measurement	${\overline{Z}}_{1-A}^P$	2.456	21.593
		${\overline{Z}}_{1-B}^P$	2.579	27.956
		${\overline{Z}}_{1-C}^P$	2.586	28.087
	simulation	${\overline{Z}}_{1-A}^P$	2.537	21.569
		${\overline{Z}}_{1-B}^P$	2.633	27.851
		${\overline{Z}}_{1-C}^P$	2.630	27.973
M3	measurement	${\overline{Z}}_{1-A}^G$	2.454	21.606
		${\overline{Z}}_{1-B}^G$	2.577	27.954
		${\overline{Z}}_{1-C}^G$	2.573	28.069
	simulation	${\overline{Z}}_{1-A}^G$	2.602	21.568
		${\overline{Z}}_{1-B}^G$	2.703	27.849
		${\overline{Z}}_{1-C}^G$	2.695	27.975

* converted resistance values into the resistance at 20 °C

.

By comparing the results of the calculation (according to the line schedule) and the simulation, the largest error is achieved in the case of evaluation using the 3-phase measurement, specifically for resistance R₁ 4.54% and X₁ reactance 0.70% compared to the calculation. This difference may be caused due to the evaluation methodology, as the measured power line is a real power line that is not fully transposed. Therefore, the asymmetry is proven to a considerable extent.

In the case of 1-phase measurement, specifically for approaches (a) phase-phase loop, and (b) phase-ground loop, the reactance results are almost equal, the error is at the level of 0.21% compared to the calculation. For R₁ resistance, the error is 0.35% (phase-phase loop approach) and 2.22% (phase-ground loop approach) compared to the calculation.

By comparing the zero-sequence impedance, the results obtained by the three different approaches are comparable. In the case of evaluation using the 1-phase measurement, concretely a phase-ground loop and an alternative method of determining the zero-sequence, they are equal. Specifically, the resistance R₀ error is 0.38% and the reactance X₀ 0.58% compared to the calculation. For 3-phase measurement using a single-phase source, the error for resistance R₀ is at the level of 0.20% and the reactance X₀ is 0.51% compared to the calculation.

On the other hand, by comparing the results of the calculation (according to line schedule) and the measurement, the smallest error is achieved in case of evaluation using the 3-phase measurement, specifically for resistance R₁ 0.27% and X₁ reactance 0.31% compared to the calculation. However, in this case, it is necessary to emphasize the discrepancy with the statistics of the results of measuring the power line impedance. The authors’ experience shows that the impedance results obtained using the 3-phase measurement are the least accurate. Statistical processing of the results of a larger number of measurements will be the subject of further publication. The results of the phase values of the impedance (Table 7) show a parametric asymmetry, where the average of these values is the resulting positive-sequence impedance. Proof of this finding is also described in Section 2.4. Subsequently, this fact is also confirmed by the results of two different approaches of the 1-phase measurement (phase-phase loop, and phase-ground loop), where the resistance R₁ error is at the level of 2.63% (2.68%) and reactance X₁ 0.52% (0.53%). The mentioned effect can be caused by, e.g., different boundary conditions in the power line schedule compared to the actual design and construction.

To compare the zero-sequence impedance, the results obtained by the three different approaches are comparable. In case of evaluation using a 1-phase measurement, concretely a phase-ground loop and an alternative method of determining the zero-sequence impedance, they are almost equal. Specifically, the resistance R₀ error is 4.92% (4.99%) and the reactance X₀ 3.80% compared to the calculation. For 3-phase measurement using a single-phase source, the error for resistance R₀ is 4.52% and reactance X₀ 3.81% compared to the calculation.

The results show that the calculation and measurement may differ, even though the calculation is performed according to a line schedule. For this reason, there is a need as well as a requirement to verify the line impedance by measurement in order to obtain accurate values.

Based on the achieved results, it can be stated for determination of the power line impedance, there is necessary interpretation divided into two frameworks:

• Positive-sequence and zero-sequence impedance (as average of phases values):

  ○

  Impedance value suitable in symmetrical models in power systems.

• Positive-sequence impedance (per phase):

  ○

  Impedance values per phase suitable in asymmetric models in power systems, as well as for correct setting of the distance protections.

5. Discussion on Measurement and Calculation Results, and On-Line Measurement

As already mentioned, the calculated impedance value is considered in this paper as the reference value. However, in the case of the calculation, it is necessary to point out the uncertainties as well. In particular, the calculation of power line impedance based on the line schedule may not be completely accurate for the following reasons:

-

Considered constant earth resistivity, i.e., the value of the ground resistivity influences the impedance of the phase-ground loop, that means it has an impact on the positive-sequence impedance of the untransposed power line and on the zero-sequence impedance;

-

Considered constant conductors sag and no considered terrain jaggedness under the power line, i.e., slightly affects the ground return current under the power line and thus the magnitude of the zero-sequence impedance;

-

No other power lines in the vicinity considered, in particular ground conductor, i.e., ground conductors in the vicinity of the measured power line can significantly affect the magnitude of the zero-sequence impedance;

-

The final length is based on the line schedule, i.e., the actual real length was not verified by measurement (based on our experience, we know that these lengths can often vary).

It can be stated that, with regard to all analyzed results, complexity and accuracy of evaluated methodologies, the 1-phase measurement methodology, specifically phase-ground loop, can be described as the most appropriate approach of determining power line impedance (resistance and reactance).

Currently, the trend in determining the power line parameters in many publications, e.g., [18,19,20,21,22,23], indicates the use of PMU, i.e., determination of power line parameters by on-line method from the measured voltage and current phasors. Regarding to our paper, we deal with the off-line measurement of power line parameters with no possibilities for on-line measurement, since the OPL needs to be powered off during the measurement. Furthermore, we want to point out the shortcomings and uncertainties of the on-line method using the PMU.

As a first problem of the online method, the roll-out of voltage and current phasor (PMU) measurements is missing in many power systems, especially in distribution networks. That means, the TSO’s (transmission system operator), but especially DSO’s (distribution system operator), would not avoid to determination of some power lines parameters by off-line measurement. In this case, it would probably weigh the argument of a uniform methodology of determining the power line parameters in the power system.

As a second and fundamental shortcoming, there are errors in synchronization of data acquisition and accuracy of voltage and current phasor measurement, as the accuracy of CT (current transformers) and VT (voltage transformers) also contributes to the measurement error. The accuracy of voltage and current phasor angle measurements can be limiting in determining power line parameters with the required accuracy. In particular, the parameters determination of short lines or lightly loaded power lines, i.e., when the transmission angles on the power line (the difference between the angles of the voltage phasors at the beginning and the end of the line) are very small, the accuracy of measuring of voltage phasors angles is very important for the accuracy of determining the parameters of a given power line. The mentioned problem is analyzed in [3,4].

Another shortcoming, (considering the IEEE methodology [6]), is the need to implement manipulations—switching off one phase of the power line to determine zero-sequence impedance, which, especially in transmission systems, may not be acceptable for the TSO.

In future research, we would like to focus our attention on comparing the results of determining power line parameters using off-line and on-line methods.

6. Conclusions

This paper describes calculation and measurements methods of the overhead power lines in order to evaluate electrical parameters. Mainly, attention is focused on the exact evaluation of the impedance of the investigated overhead power line by calculation, and subsequent comparison with evaluation obtained from the simulation results and different measurement approaches. Differences between calculation and experimental measurement are shown and discussed with a focus on the identification of potential uncertainties.

In general, the following two factors need to be considered when selecting an appropriate measurement methodology for determining power line impedance:

• Purpose of use;
• Accuracy.

In regard to a purpose of use, based on the analysis of off-line measurement results, the following applies to given measurement approaches:

• 3-phase measurement:

  ○

  Same measurement conditions for determining the zero-sequence impedance ${\overline{Z}}_0$, i.e., after manipulation on the measurement side (interconnection of phases behind the source), the measurement is performed for only one configuration;

  ○

  Not suitable for determining the phase values impedance of power line;

  ○

  To determine the positive-sequence impedance (as the average of phase values) is sufficient—with regard to the time management of measurement and the number of manipulations on the measuring apparatus during the measurement;

  ○

  Use of impedance value in symmetrical models in power systems;

  ○

  Disadvantage: 3-phase power source is required.

• 1-phase measurement:

  ○

  Different measurement conditions for determining the zero-sequence impedance ${\overline{Z}}_0$, i.e., it is necessary to perform measurements for at least three configurations, but to determine the zero-sequence impedance there are 2 ways to evaluate this value;

  ○

  Accurate results for determining the phase values impedance of the power line;

  ○

  Use of impedance values per phase also in asymmetric models in power systems, as well as for correct setting of the distance protections;

  ○

  Advantage: 1-phase power source is required.

In regard to an accuracy, it can be stated that 1-phase measurement (phase-phase loop, phase-ground loop) can be considered as exact methods of off-line measurement for determining the positive-sequence impedance. In addition, 1-phase measurement (phase-ground loop) as well as three-phase measurement using a single-phase source can be considered as an accurate measurement for determining the zero-sequence impedance.

Based on the above, it is clear that accurate electrical parameters (impedances) of overhead power lines used for example in simulation calculations, short-circuit calculations or correct setting of electrical relays are significant. In order to achieve stated requirements in practice, it is necessary to have the correct input data. These data may not be sufficient only from line schedule calculation, but also should be verified by measurement.

There are several areas where we see potential further research regarding the comprehensiveness of the electrical parameters’ measurement of overhead power lines (impedance, admittance):

• Statistical processing of the results of a larger number of measurements of power line impedances using 3-phase measurement;
• Calculation and measurement comparison of power line capacity (positive-sequence admittance, zero-sequence admittance);
• Identification and assessment of the influence of facts/phenomena/parameters influencing the size of power system admittance.

There are several areas where further research can lead, regarding on-line measurement:

• Analysis of measured data from PMU for selected power lines;
• Analysis and assessment of the influence of different measuring devices/equipment on measurement deviations;
• Quantification of deviations in the determination of power line parameters using the off-line method and the on-line method with regard to the different operating states of the power lines;
• Determine the conditions of usability of the calculated parameters from the on-line measurement;
• Comparing the results of determining power line parameters using off-line and on-line methods.