Energy Metering Integrated Circuit Behavior beyond Standards Requirements

Abstract

During the last few years, the accuracy of static electricity meters (SEM) has been questioned. Significant metering deviations with respect to a reference meter have been observed at customer premises, and laboratory experimental tests results support such findings. The root cause of such errors remains unknown, as there are multiple elements that could affect the accuracy of electricity meters. Furthermore, standard compliant meters exposed to distorted signals may produce negligible, positive or negative relative error depending on the instrument design. Distorted current signals with fast amplitude transitions have produced the highest error in SEMs reported in the literature. In this paper, the accuracy of an energy metering Integrated Circuit (IC) is evaluated beyond the limits of the standards requirements employing a selection of distorted signals from the standards, real-world captured signals and a set of waveforms designed to test the IC under fast changing currents conditions, which are representative of the waveforms resulting from power electronic devices. The experimental results reveal an accuracy boundary imposed by Gibb’s phenomenon for fast changing current signals and a strong relationship between the IC’s measurement error and two key parameters of the measured waveform: signal slope and phase angle. This paper therefore provides a methodology for the comprehensive analysis of SEMs in future power systems which are dominated with power electronic-controlled electrical demand and contributes to the search for the root cause of error in SEMs exposed to distorted waveforms.

1. Introduction

The accuracy of static electricity meters under non-sinusoidal situations is an important topic for both academic study and public interest [1]. It is not yet properly covered by the standards [2] but has been analyzed from different perspectives [3,4,5,6,7,8,9] during the last few years. However, addressing the problem of erroneous readings on SEMs when exposed to distorted signals is a complex task [10], where a large number of variables could affect the final measurement reported by the meter. The variables are often inter-related [11] and should be carefully assessed to understand the practical impact on meter accuracy.

One of the most important factors that affects the accuracy of electricity meters is the voltage or current signal profile itself, as distorted signals could have multiple different characteristics (i.e., amplitude, frequency, harmonic content, crest factor, etc.). Thus, the number of possible signals for evaluating the response of meters outside the standards requirements is virtually infinite [12]. In this regard, the present efforts in the literature to define methods and an appropriate set of test signals for non-sinusoidal conditions involves statistical/probabilistic harmonic predefined content [13], mathematically defined waveforms [14] or signals with random harmonic content [9,15]. Nevertheless, it has been observed that high peak currents with short transition duration produces the largest errors on SEMs [7,16,17,18,19,20,21] compared to the error produced by distorted signals without such fast transients.

The aforementioned proposals try to provide more realistic scenarios compared to those defined in the standards by means of including harmonic content on the voltage and current signals employing waveform generators, power amplifiers and controlled-current loads [10,11,14,22,23]. These methods, despite being useful to evaluate SEM measurements accuracy, treat the instrument as a black box and no strong conclusions can be made on how certain signals and its characteristics contributes to the error (and its propagation) on individual components inside the meter.

The design of the meter itself could vary significantly among manufacturers, employing different sensors or transducers, ADCs, filters and algorithms to calculate the relevant electrical quantities [2,24]. This broad flexibility for SEM design has led to a variety of measuring devices that meet accuracy requirements of applicable standards. However, the accuracy of a device is not guaranteed by the manufacturer beyond the limits prescribed by the standards, i.e., when applying a sinusoidal or quasi-sinusoidal waveform only. Moreover, applying the same distorted signal to different standard compliant SEMs leads to inconsistent measurements among the meters [18,21], where devices under test (DUT) could report a positive error, a negative error or an almost negligible error.

One of the most important components of SEM is the energy metering IC, which typically implement the metrology engine in an embedded digital signal processor (DSP). This kind of ICs has proved to be fairly accurate in the presence of harmonic content [25], but it is unknown how they perform under fast changing currents conditions.

In this paper, the focus is to evaluate the performance of one commercially available metering IC when exposed to signals with characteristics that are known to cause errors in SEMs, i.e., high signal slope and low power factor. The main objective is to identify weaknesses or limitations in the IC design which are not possible to find under standard test conditions and shed some light on the factors which cause errors in energy meters. Being a fundamental component of SEMs, detailed knowledge of metering IC technology and its behavior under certain non-sinusoidal conditions will allow useful conclusions to be drawn. In turn, this work will inform suitable tests for other ICs and future standards.

2. Experimental Tests Description

In this section, the experimental tests and test signals are described in detail. The first step to fully understand the root cause of misreadings (and variations in reading) in electricity meters is to split the measurement system into the different elements. For example, the system could be organized in three main groups: test signal, analog front-end and signal processing.

The voltage and current signals applied to the meter are intended to examine the behavior of one commercial energy metering IC beyond the requirements established by standards for SEM. In this regard, the proposed tests include sinusoidal waveforms, standard distorted signals, real-world captured distorted waveforms and synthesized signals sharing characteristics of different levels of crest factor and phase angle.

2.1. Sinusoidal Tests

The sinusoidal tests are mainly used to calibrate the system and verify the accuracy at different values of current and phase angle. In this paper, the term phase angle will always refer to the phase difference, in degrees, of the current waveform with respect to the voltage.

To calibrate the metering IC, the procedure described in [26] was followed using the “Accurate source method”. A full calibration of the IC should be performed including compensation for phase delay and gain and offset compensation for the following quantities:

• voltage r.m.s. $V_{rms}$;
• currernt r.m.s. $I_{rms}$;
• total active power P;
• total apparent power S;
• total reactive power Q;
• fundamental active power $E_1$; and
• fundamental reactive power $E_{Q_1}$.

After calibration, the phase angle between the voltage and current signal should be varied from 0${}^{\circ }$ to 360${}^{\circ }$ in steps of 15${}^{\circ }$, at nominal values $I_{ref}$ and $U_n$, in order to evaluate the accuracy of the measurements at different power factors.

2.2. Standard Distorted Tests

The standard distorted tests with waveforms presented in Figure 1 includes the test prescribed in EN 50470-3-2006 standard [27] for testing the accuracy of electric energy meters in the presence of harmonics (40% $I_{5th}$ and 10% $V_{5th}$, in phase), a variation of this test called “Harm Q” described in [25] ($I_{5th}$ and $V_{5th}$ 90${}^{\circ }$ shifted) and the “Quadriform” and “Peaked” tests described in the OIML-R46 document [28].

Through the standard distorted tests, the ability of the IC to accurately measure electrical quantities in the presence of different harmonic content and different harmonic power factor is evaluated.

2.3. Real-World Current Signal Tests

Three real-world distorted current waveforms representing household commonly used electronic equipment were selected for testing the IC. The signals corresponds to the current drawn by a compact fluorescent lamp (CFL), a switched-mode power supply and a modern entertainment system. The waveforms (Figure 2) were obtained from the equiPment hArmoNic DAtabase (PANDA) [29], the NPL power quality waveform library [30] and the EPRI library of harmonic spectrums [31], respectively.

The voltage signals where obtained by means of applying the distorted waveform and a sine waveform to a simulated pure resistive impedance of 0.1 $\Omega$, in order to include the effect of distorted currents in the voltage waveform. Different resistive values emulating the line impedance at the metering point were tested with negligible effects in the accuracy of the IC, compared to using a perfect sinusoidal signal for the voltage channel.

2.4. Crest Factor Tests

The waveforms applied to electricity meters in recent studies where significant errors have been reported [16,17,18,19,21] share some similarities: distorted current signals with high peak values and short transition duration. These kind of signals are typically produced by power electronics components used to control the power output of an electric appliance such as a water pump, a motor or a lamp. The crest factor is defined as the ratio of the signal peak value to the r.m.s. value. In this paper, the term crest factor (1) always refers to the current crest factor as follows:

$$CF=\frac{|i_{peak}|}{I_{rms}}$$

(1)

Depending on the power electronic design [32,33], the line impedance [20] and the type of load [8], different current waveforms may be produced, including signals with high CF values. In an effort to replicate the characteristics of such signals, for the crest factor tests, a perfect sine waveform is “chopped”, leaving only portions of the waveform. By this approach, the focus is moved from the harmonic (or subharmonic) signal content to the $I_{rms}$, $i_{peak}$ and transition duration values. A good reason to take this approach is that metering ICs have proved to be accurate in the presence of harmonic content [25], as seen below in Section 4, but it is unknown how the metering ICs cope with fast changing currents.

The proposed current waveforms retain only part of the original sinusoidal waveform, while the “removed” portion is kept to zero value, as can be seen in Figure 3. Two cases are considered: “leading” where the current is applied at the start of each half-cycle and “falling” where the current is applied at the end of each half-cycle. Figure 3 illustrates tests signals for 1/2, 1/4, 1/8 and 1/16 sub-cycle portions.

The characteristics of the signals were adjusted to reach similar $i_{peak}$ values, as shown in

Table 1. Tests waveforms parameters.

Signal	${\mathit{I}}_{\mathit{r}\mathit{m}\mathit{s}}$ (A)	${\mathit{i}}_{\mathit{p}\mathit{e}\mathit{a}\mathit{k}}$ (A)	CF	Transition Duration (ms)	Transition (A)	Slope (A/ms)	PF	THD${}_{\mathit{I}}$
Sine	20.00	28.28	1.41	3.32	22.63	6.98	1	0.00
CFL	10.07	28.28	2.81	0.26	25.00	96.16	0.609	0.94
Modern	12.55	28.20	2.25	3.99	25.12	6.29	0.936	0.36
Switched	10.56	28.31	2.68	1.31	25.60	19.47	0.667	1.07
1/2	14.14	28.28	2.00	3.24	22.63	6.98	0.688	0.62
1/4	8.44	28.00	3.32	1.97	22.40	11.37	0.281	1.26
1/8	5.80	28.11	4.84	0.99	22.51	22.57	0.097	2.02
1/16	4.00	27.55	6.91	0.49	22.03	44.13	0.029	3.02

. Parameters from sinusoidal and real-world tests waveforms were included for comparison. The transition duration, formerly known as “rising” or “falling” time, is defined as the time difference between 10% and 90% of the transition amplitude [34]. Appendix A provides illustrations and definitions of some terms presented in Table 1.

Crest Factor Firing Angle Test

A third test was performed, applying the “leading 1/8” signal to the metering IC, but this time changing the phase angle between the voltage and current signals to the following values: 0, 30, 45, 60, 90 and 120 degrees.

Similar to the real-world signal tests, a simulated pure resistive line impedance of 0.1 $\Omega$ was included to obtain the correspondent voltage signal, which is used to calculate the power factor shown in Table 1.

3. Measurement System Description

This section describes the measurement system setup used for the calibration and the accuracy tests for the metering IC, performed under sinusoidal and non-sinusoidal conditions. The experimental setup (Figure 4) is composed of a Rigol DG952 two-channel arbitrary waveform generator (AWG), EVAL-ADE7878AEBZ energy metering IC evaluation board, a Raspberry Pi (RPi) board and a personal computer (PC).

In this paper, the focus is to evaluate the performance and the accuracy of the energy metering IC itself. For this reason, voltage and current sensors are not included as they are known to be the most significant sources of uncertainty in digital measuring instruments [10]. Instead, ideal current transformer (CT) and voltage transformer (VT) output signals are emulated by the AWG. The “phantom-loading” technique (i.e., using independent signals for voltage and current, rather than an actual load) was implemented to avoid measuring errors introduced by transducers.

To inject the test system with data, the voltage and current signals are generated in a LabVIEW application, where the theoretical electrical quantities are calculated. The 16,384 points per cycle signals are exported as comma-separated values (csv) files and then uploaded to the AWG. The voltage and current signals are generated simultaneously and independently by the AWG with a sampling rate of 819.2 kSa/s and 16-bit of resolution [35].

Table 2. RIGOL DG952 AWG output characteristics [35].

Parameter	Specification
Accuracy	±1% of the setting value ±5 mV
Resolution	0.1 mVpp
THD	<0.075%
Frequency resolution	1 Hz
Frequency accuracy	±1 ppm of the setting value +10 pHz

present some output characteristics of the RIGOL DG952 AWG, used as the reference source in this study.

A Raspberry Pi board is used as the interface between the metering IC mounted on the EVAL-ADE7878AEBZ evaluation board and a LabVIEW application running on a personal computer. Through the RPi, it is possible to access any register inside the IC for read and write operations. This capability allows analysis of how calculations are performed by the different internal blocks of the IC instead of relying only on the final result (e.g., total active energy). The LabVIEW application displays and collects the data obtained during the tests, performs additional calculations and accumulates the energy measurements over a defined period of time.

3.1. Electricity Meter Design

The EVAL-ADE7878AEBZ board includes components required for a typical static electricity meter analog front-end (AFE) such as anti-aliasing (AA) filters, resistive voltage dividers (RVD), energy metering IC and digital isolators (Figure 5).

The EVAL-ADE7878AEBZ board was configured as follows:

• the resistive voltage divider (attenuation) was removed from the voltage input path;
• AA filter corner frequency = 7.2 kHz;
• high-pass filters (HPF) enabled (to remove d.c. signal components, see Figure 6); and
• external microcontroller managing the ADE7878A [36].

3.1.1. ADE7878A Energy Metering IC

The ADE7878A is a poly-phase energy metering IC with per phase total and fundamental active and reactive powers calculation capabilities. Although it is a three-phase metering IC, all the tests carried out use only a single-phase for simplicity. This does not affect results for evaluating the accuracy, as a three-phase meter is composed by three identical single-phase circuits [22,37]. The ADE7878A single-phase functional block diagram can be seen in Figure 6.

The ADE7878A has 24-bit differential second-order sigma-delta ($\mathsf{\Sigma }-\Delta$) ADCs with specifications given in

Table 3. ADE7878A 24-bit differential ADC’s specifications [37].

Parameter	Specification
Bandwidth	2 kHz
Sampling rate *	1.024 MHz
SNR	74 dB
Input range	±500 mV peak
Impedance (DC)	400 k$\Omega$ min
Offset error	±25 mV max
Gain error	±4%

* Oversampling rate. The ADC outputs at 8 kSps.

. Because the ADCs signal to noise ratio (SNR) = 74 dB [37], the effective number of bits (ENOB) is 12 and it produces a 0.02% error of full scale or 0.2 mV, which is 10 times better than the most stringent 0.2 S class allowed error for industrial SEMs.

For all tests carried out, the LabVIEW application accesses the IC internal registers through the RPi, using I${}^2$C communication protocol, to read the quantities listed in

Table 4. ADE7878A measurements.

Symbol	Description	Unit
$V_{rms}$	rms voltage	V
$I_{rms}$	rms current	A
f	line frequency	Hz
$\theta$	phase angle	Degrees
$i_{peak}$	peak current	A
$CF$	crest factor *
P	total active power	W
S	apparent power	VA
Q	total reactive power	var
$PF$	power factor *
E	total active energy	Whr
$E_S$	apparent energy	VAhr
$E_Q$	total reactive energy	varhr
$E_1$	fundamental active energy	Whr
$E_{Q_1}$	fundamental reactive energy	varhr

* Calculated from ADE7878A registers.

. Additionally, the IC include waveform sample registers which can be accessed through High Speed Data Capture (HSDC) communication protocol to acquire the waveforms directly as has been digitized by the ADC. Some quantities such as crest factor and power factor are not directly available from the IC registers, but they are calculated from $I_{rms}$, $i_{peak}$, P and S registers.

3.1.2. Electrical Current and Voltage Level Definitions

According to the IEC 62052-11:2003 [38] and EN 50470-1:2006 [39] standards, the voltage and current reference values in

Table 5. Definitions of meter quantities.

Name	Symbol	Value
Starting current	$I_{st}$	0.1 A
Minimum current	$I_{min}$	1 A
Transitional current	$I_{tr}$	2 A
Reference current	$I_{ref}$	20 A
Maximum current	$I_{max}$	100 A
Reference Voltage	$U_n$	230 V
Reference frequency	f	50 Hz

were defined. The voltage and current values defined in Table 5 are scaled to map to the range of the internal ADCs (i.e., ±500 mV peak, which represents $I_{max}$).

4. Experimental Results and Discussion

The results from the tests described in Section 2 are presented in this section. For the sake of simplicity, only the most relevant results are discussed. The full results are provided in Appendix B and Appendix C. Most of the results are reported as relative error as follows:

$$\delta x=\frac{x_0-x}{x}\times 100$$

(2)

where $x_0$ is the measured value and x is the reference value.

For measurements with reference value equal to zero, the absolute error is calculated as:

$$\Delta x=x_0-x$$

(3)

For both cases (absolute and relative error), the reference x value was theoretically calculated and generated by a calibrated AWG with a declared uncertainty of ±0.05 mV at $I_{ref}$ (see Table 2).

4.1. Sinusoidal Tests Results

After calibration, different emulated power inputs were applied to the IC, by means of changing the current signal value, whereas the voltage input signal was kept at nominal value $U_n$. The accuracy of the IC was evaluated, in sinusoidal conditions, over the IC’s ADC full scale. For a more detailed appreciation, the results are plotted in two graphs.

Figure 7 shows relative error for the measurements obtained when applying sinusoidal current signals from 0.2 to 1 A (i.e., below and at $I_{min}$), where more relaxed standard accuracy requirements are applied.

Figure 8 shows relative error energy for measurements in the range from 1 to 100 A ($I_{max}$). The IC can measure total active energy E, in sinusoidal conditions, with a relative error lower than $\pm 0.5\%$, corresponding to a “C” class meter. Fundamental energy $E_1$ results present an offset which could be corrected during calibration or compensated after calculations.

Sinusoidal Phase Swept Test Results

The phase angle has been highlighted as a possible parameter which significantly influences meter accuracy [13,14]. For this reason, a phase angle sweep as performed in sinusoidal conditions, from 0${}^{\circ }$ to 360${}^{\circ }$ in steps of 15${}^{\circ }$, at nominal values $I_{ref}$ and $U_n$.

Figure 9 illustrates that the total active power relative error varies depending on the phase angle between the voltage and current signals. Furthermore, there are both negative and positive relative errors. This is an interesting finding, as positive errors have been previously related with an over-estimation of the input signals, whereas a negative error is believed to be caused by a low sampling rate [19]. In this test, however, the signal amplitudes and the ADC sampling frequency remained constant while only phase angle was changed.

A well performed calibration and phase delay compensation will impact on the final power (and energy) measurement, particularly at lower power factors [37]. The grey bars in Figure 9 and Figure 10 corresponds to a typical 0.3${}^{\circ }$ phase angle absolute error, whereas the blue bars correspond to a better performed calibration (by means of using a more accurate reference) achieving 0.1${}^{\circ }$ absolute error. A careful phase delay compensation will prevent standard compliant meters to present large errors at low power factors.

Figure 10 shows the relative errors in the total reactive power measurements, with similar results as in Figure 9 for the total active power.

It is clear that the phase angle is a key parameter influencing the active and reactive power measurement error and its sign. Nonetheless, it is important to keep in mind that relative errors are larger when the reference (or ideal) value is close to zero. For this reason, the relative errors at 90${}^{\circ }$ and 270${}^{\circ }$ are omitted in Figure 9, while the relative errors at 0${}^{\circ }$ and 180${}^{\circ }$ are omitted in Figure 10.

4.2. Standard Distorted Tests and Real-World Current Waveform Tests Results

All the standard and real-world captured distorted test waveforms can be measured by the IC with a good accuracy. The results show total active energy relative errors up to +2%, only at and below $I_{tr}$ (i.e., 2% of the ADC full scale), proving that metering IC technology can effectively estimate electrical quantities in non-sinusoidal situations. The full results are given in Appendix B and Appendix C.

The total reactive power was not considered for distorted current signals, because there is no formal definition for total reactive power in non-sinusoidal conditions. Thus, only the fundamental reactive power was evaluated.

4.3. Crest Factor Tests Results

For all the crest factor tests, the voltage signal was a quasi-sinusoidal waveform, with a low level of distortion introduced only by the emulated 0.1 $\Omega$ resistive line impedance. Thus, the voltage r.m.s. measurements report a maximum relative error of 0.1%, regardless the current crest factor. The current signals, however, become more rapidly-changing as the signal slope increases with the crest factor (see Table 1), making the measurements more challenging for sampled-based measuring instruments.

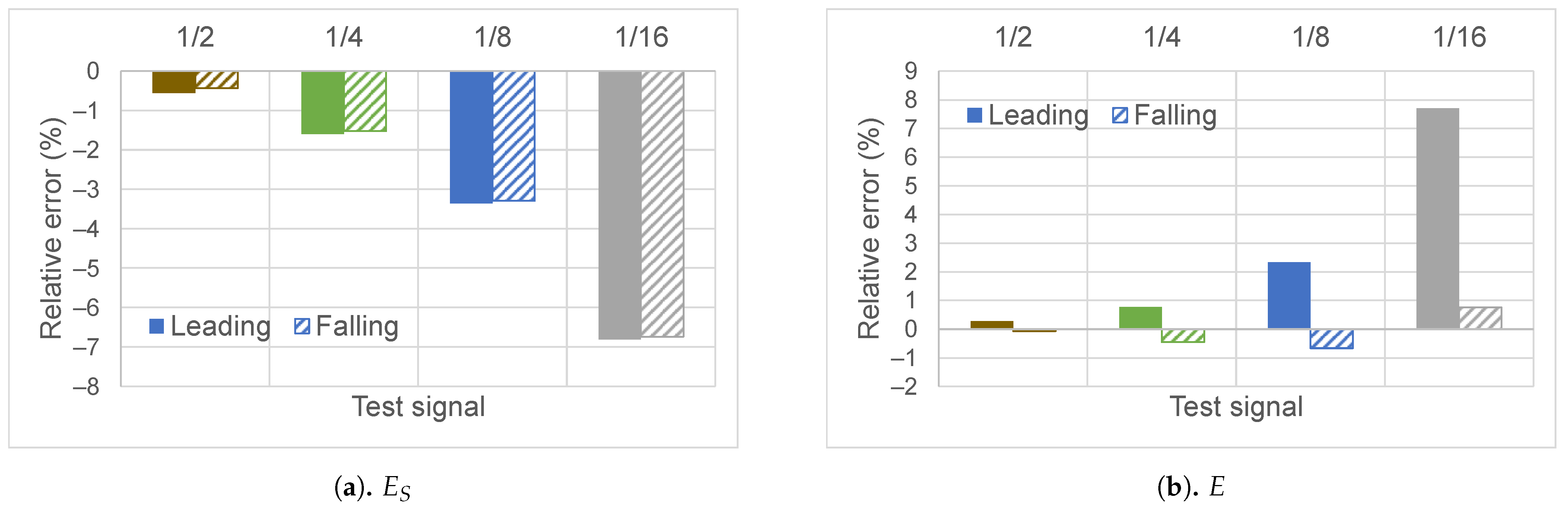
Figure 11 shows the $I_{rms}$ and $i_{peak}$ relative errors. $I_{rms}$ relative error is roughly the same for the revised “leading” and “falling” cases, increasing as the crest factor increases. The $i_{peak}$ measurement accuracy behavior, however, differs significantly and inconsistently depending on the crest factor. Large relative errors are present that can either significantly overestimate or underestimate the peak value of the signal (Figure 11b).

Figure 12a illustrates how the error in $I_{rms}$ (Figure 11a) is translated to the total apparent energy error. The magnitude of the error and its negative increase with respect to the crest factor are very similar in both graphs. This is expected, as the total apparent power calculation is based on r.m.s. measurements as per Formula (4).

$$S=V_{rms}\times I_{rms}$$

(4)

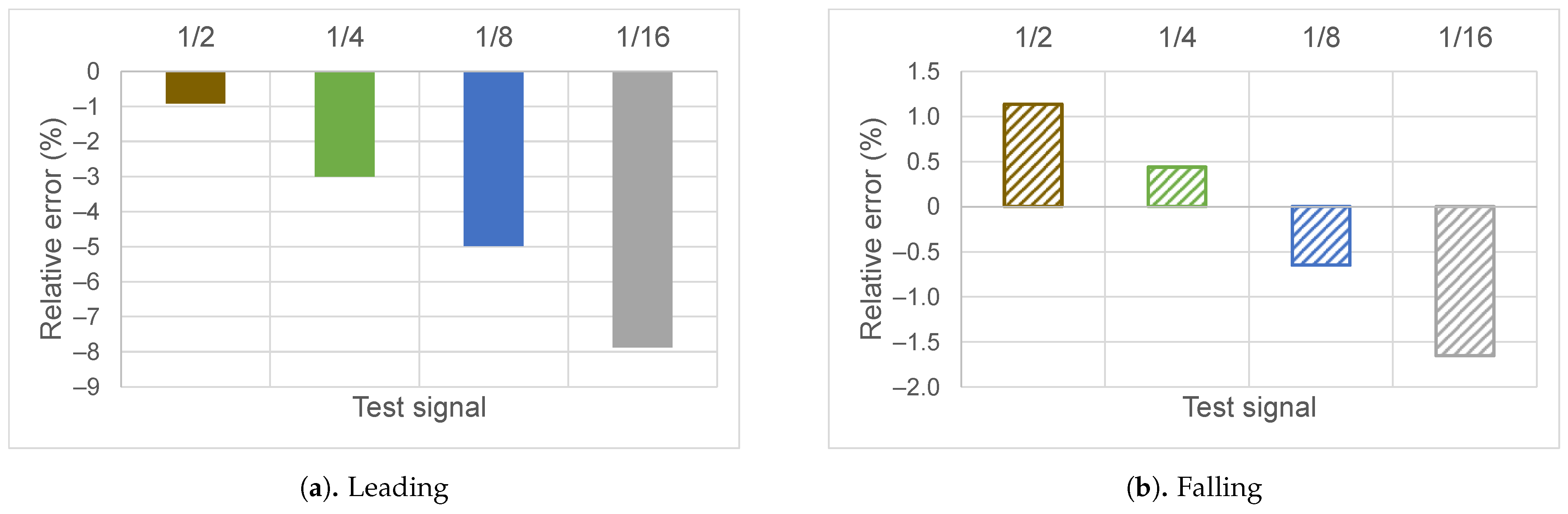
Figure 12b shows significantly larger errors in total active energy measurements for the “leading” test, compared to the “falling” test results. Since total active energy is the measurand used for billing purposes, particular attention was paid to the “leading” tests. To investigate this further, the test signal “leading 1/8” (Figure 3) was selected, due to its relatively large error in the total active energy calculations, to be shifted with respect to the voltage zero-crossing in order to approximate working conditions of power electronics devices operating at different phase firing angles.

Fundamental active energy $E_1$ relative error (Figure 13) shows a behavior clearly related to the $i_{peak}$ error displayed in Figure 11b. The graphs in Figure 13 are very similar in shape to the correspondent test in Figure 11b, although the magnitudes are smaller for the $E_1$ calculations. Again, the “leading” tests presents the larger relative errors.

4.3.1. ADE7878A Waveform Sampling

To further investigate the measurements error produced by the crest factor waveforms, the IC waveform sampling capabilities were used. Figure 14 shows how the crest factor current test signals were distorted during the analog to digital conversion process. This distortion is only present for the crest factor test signals and do not occur for any other test signal presented in this paper.

The sampled leading test signals in Figure 14a reveal that, effectively, the waveforms qwew attenuated and distorted by the ADC, causing the error observed in $i_{peak}$ (Figure 11b) and then translated to the fundamental active energy $E_1$ (Figure 13). The reference $i_{peak}$ value (red dotted line) is not reached by the leading waveforms and the sampled peak value decrease as the crest factor increase.

An undershoot effect is also noticeable during the transition from $i_{peak}$ to zero (Figure 14a and Figure 15a). This undershooting is related to the typical transient (or step) response of a FIR (finite impulse response) filter implemented inside the $\mathsf{\Sigma }-\Delta$ ADC for the decimation process. The undershooting (and/or overshooting) is known as Gibb’s phenomenon which is typical for Fourier series, orthogonal polynomials, splines, wavelets and some other approximation functions [40], and it is sometimes produced by applying specific window functions (e.g., Keiser–Bessel) to a digital filter in order to truncate the theoretically infinite number of Fourier series to a finite number of terms [41].

Falling test signals in Figure 14b exhibit a similar distortion and an overshooting effect following the transition from zero to $i_{peak}$, producing, as a result, sampled values above the reference (red dotted line) for the signals 1/2 and 1/4. Test signals 1/8 and 1/16 experience attenuation instead, despite the overshooting. These waveform distortions are reflected in the error plotted in Figure 11b and Figure 13.

The Gibb’s phenomenon is the limit reached by the FIR filter implemented in the $\mathsf{\Sigma }-\Delta$ ADC due to test signals approximating to a transient and thus, unavoidable. This effect is more noticeable for signals with transitions from peak value to zero (Figure 15a) compared to signals with transitions from zero to a peak value (Figure 15b).

Attenuation, on the other hand, is different for the leading and falling signals, but it consistently increase for signals with faster transitions (i.e., higher slope). The attenuation, produced during the analog to digital conversion are may be caused by the averaging performed inside the ADC’s $\mathsf{\Sigma }-\Delta$ modulator or, more likely, due to the decimation (down-sampling) process.

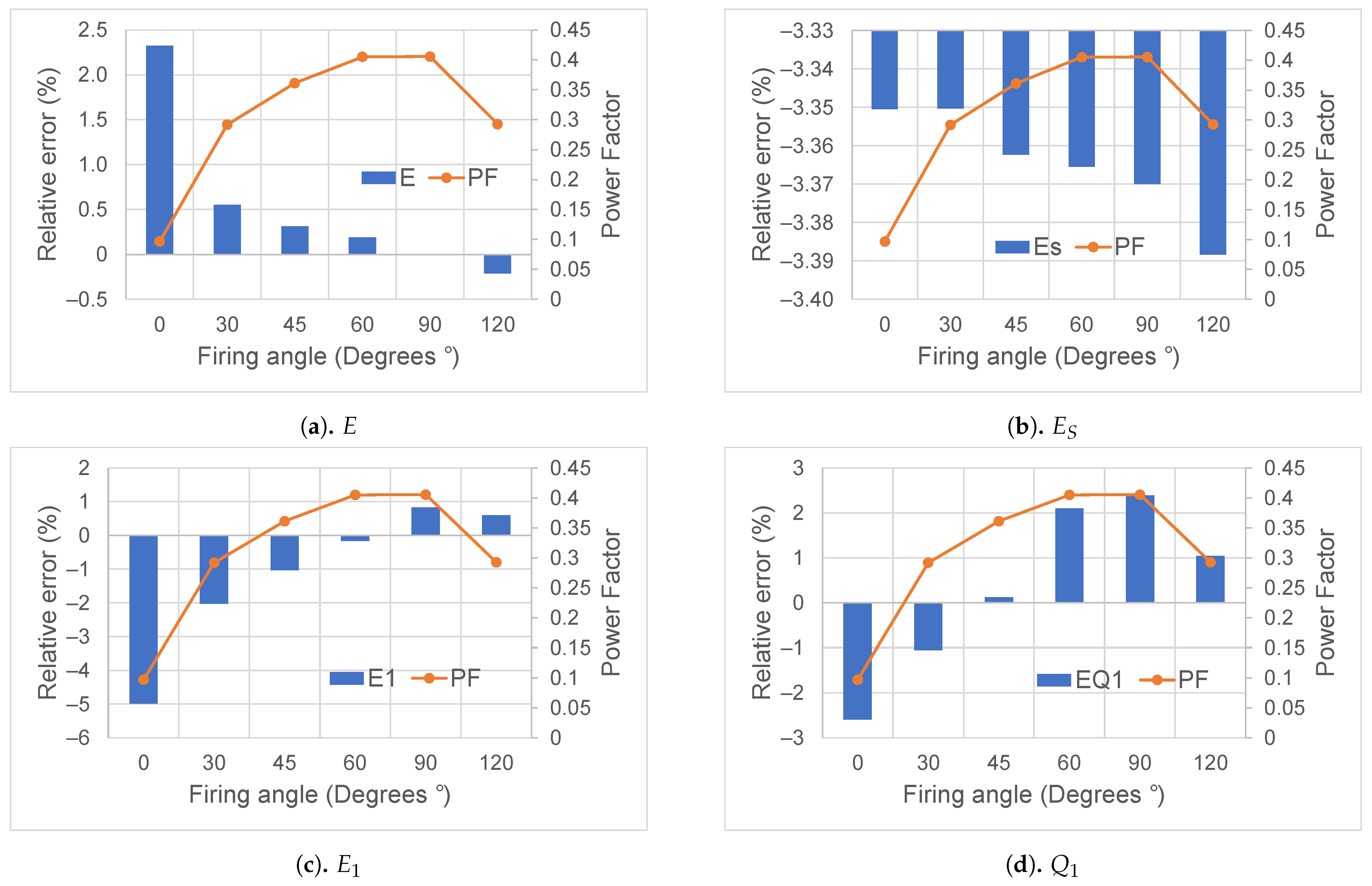
4.3.2. Crest Factor Firing Angle Test Results

The results from shifting the firing angle of the leading 1/8 current signal are shown in Figure 16. The applied waveform was selected because of its relatively significant error in the total active energy measurements (Figure 12b), compared to the signals from the “falling” tests. However, as can be observed in the graphs of Figure 16, the relative error amplitude and sign (bars) change according to the power factor magnitude (line). In general, the larger errors on E and $E_1$ are related to lower power factors; these errors could have either positive or negative magnitude.

Total apparent energy $E_S$ relative error remains almost constant (Figure 16b), regardless the power factor, as the calculation is based on r.m.s. measurements, as previously discussed.

Finally, the fundamental reactive energy in Figure 16d presents relative errors up to approximately ±2.5%, but the magnitudes are not clearly related to the power factor level.

5. Conclusions

This paper shows how typical electricity metering IC technology is capable of measuring electrical quantities from distorted signals with good accuracy. The limitations found in the results from the performed tests are mostly related to the Gibbs phenomenon, which produces overshooting and undershooting effects in the vicinity of a signal with fast amplitude changes such as the proposed crest factor test waveforms.

It is possible to find both positive and negative relative errors for any particular measured quantity, depending on a combination of factors such as the sign of power factor and the crest factor magnitude. This seemingly inconsistent result is caused by the waveform profile and has a strong relationship to the phase angle between the voltage and current signals.

For any particular transient occurring in a waveform, a negative-going transition produces larger relative error in the $\mathsf{\Sigma }-\Delta$ ADC compared to positive-going transitions.

The accuracy of the $I_{rms}$ measurements degrades as the signal slope increases, causing a similar magnitude of error in the apparent energy $E_S$. Relative errors in total active energy E and fundamental active energy $E_1$ calculations are related to the errors produced during the instantaneous current measurements such as $i_{peak}$. The phase angle between the voltage and current signal strongly affects the accuracy of the ADE7878A measurements, becoming, in general, less accurate at lower power factors.

An important contribution of this paper is the detailed investigation of the impact of crest factor and signal slope, including varying firing angle to mimic the plausible behavior of power electronic devices. The proposed crest factor tests push the metering IC capabilities to the limit and could be used as a starting point to define standard tests for evaluating the accuracy of SEMs and current transducers exposed to fast changing currents.