Evaluation of the Worldwide Wave Energy Distribution Based on ERA5 Data and Altimeter Measurements
Abstract
:1. Introduction
2. Materials and Methods
2.1. Datasets
2.2. Wave Power and Wave Energy Density Evaluation
3. Results
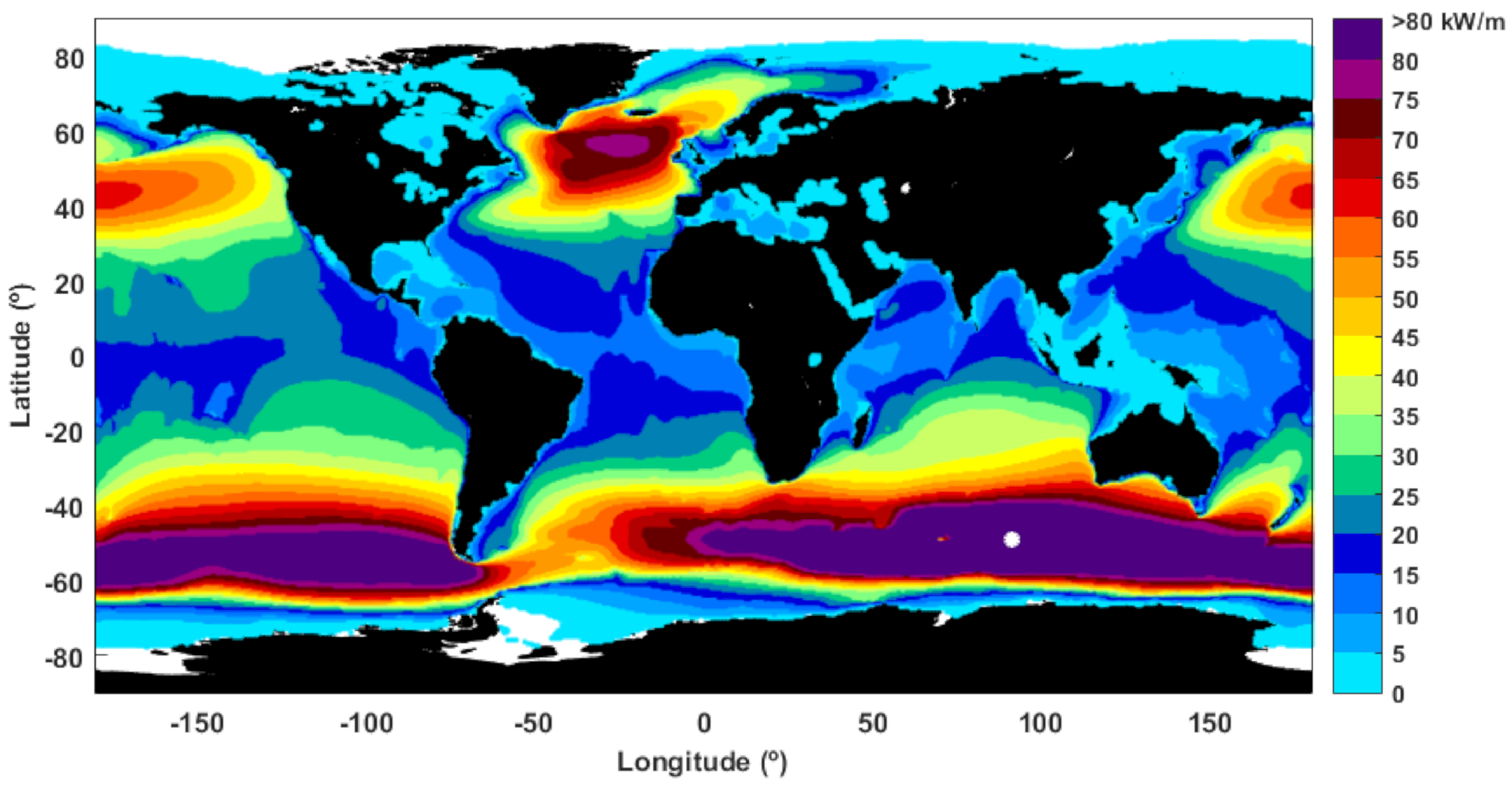
3.1. Global Wave Power According to ERA5 Database
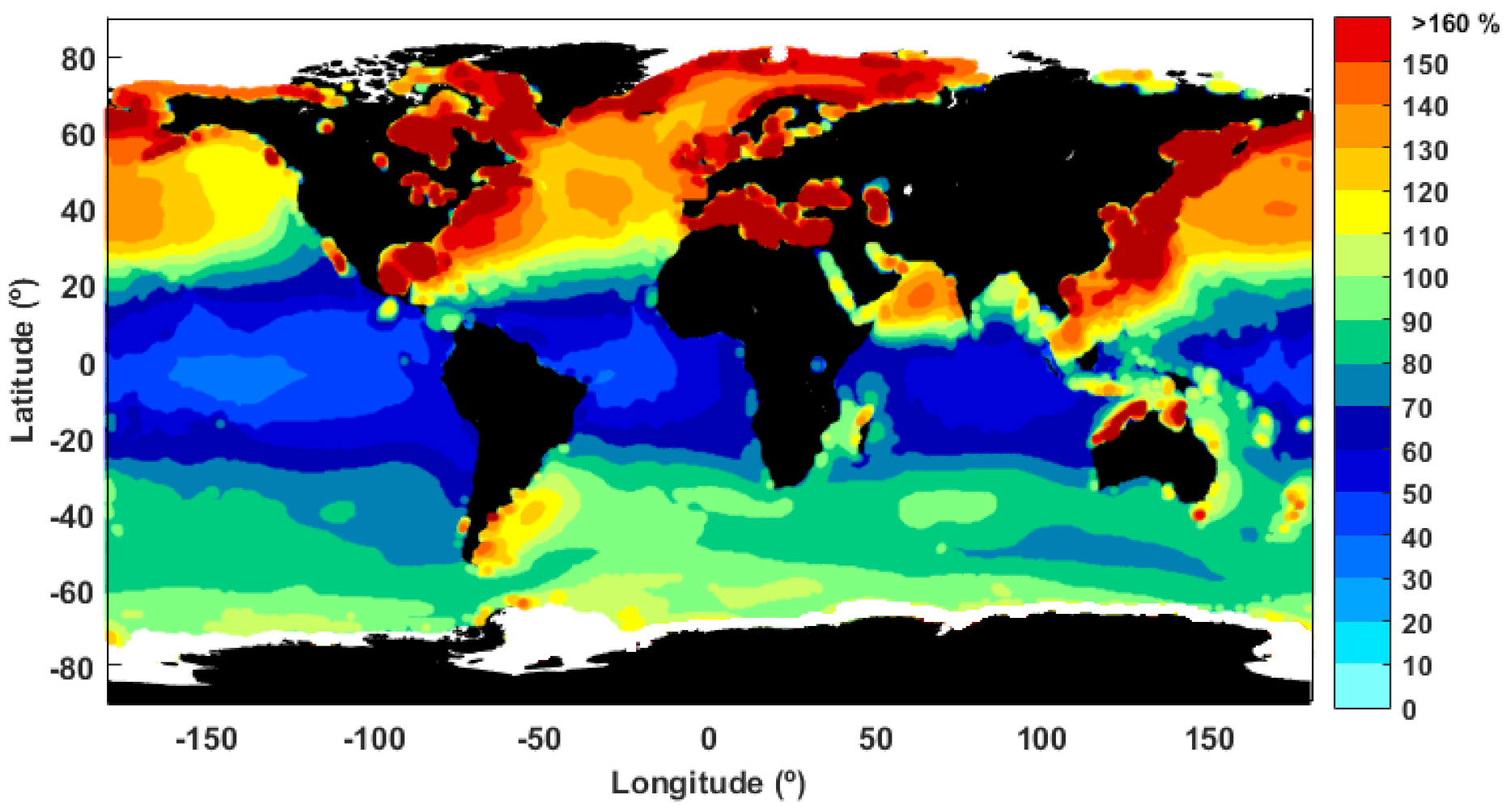
3.2. Wave Power Variability
3.3. Comparisons of the Wave Energy Density between CCI-SS and ERA5
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- United Nations Framework Convention on Climate Change, The Paris Agreement|UNFCCC. Available online: https://unfccc.int/process-and-meetings/the-paris-agreement/the-paris-agreement (accessed on 30 October 2020).
- IRENA Global Renewables Outlook: Energy Transformation 2050. Available online: https://www.irena.org/publications/2020/Apr/Global-Renewables-Outlook-2020/publications/2020/Apr/Global-Renewables-Outlook-2020 (accessed on 28 October 2020).
- IEA. World Energy Outlook. 2020. Available online: https://www.iea.org/reports/%0brenewable-energy-market-update (accessed on 28 October 2020).
- Kuzemko, C.; Bradshaw, M.; Bridge, G.; Goldthau, A.; Jewell, J.; Overland, I.; Scholten, D.; van de Graaf, T.; Westphal, K. Covid-19 and the Politics of Sustainable Energy Transitions. Energy Res. Soc. Sci. 2020, 68, 101685. [Google Scholar] [CrossRef] [PubMed]
- Hepburn, C.; O’Callaghan, B.; Stern, N.; Stiglitz, J.; Zenghelis, D. Will COVID-19 Fiscal Recovery Packages Accelerate or Retard Progress on Climate Change? Oxf. Rev. Econ. Policy 2020, 36, S359–S381. [Google Scholar] [CrossRef]
- Østergaard, P.A.; Duic, N.; Noorollahi, Y.; Kalogirou, S. Latest Progress in Sustainable Development Using Renewable Energy Technology. Renew. Energy 2020, 162, 1554–1562. [Google Scholar] [CrossRef]
- Soukissian, T.H.; Denaxa, D.; Karathanasi, F.; Prospathopoulos, A.; Sarantakos, K.; Iona, A.; Georgantas, K.; Mavrakos, S. Marine Renewable Energy in the Mediterranean Sea: Status and Perspectives. Energies 2017, 10, 1512. [Google Scholar] [CrossRef] [Green Version]
- Soukissian, T.; Karathanasi, F.; Belibassakis, K.; Kontoyiannis, H. Marine Renewable Energy in the Greek Seas. In The Handbook of Environmental Chemistry; Springer: Berlin/Heidelberg, Germany, 2020; pp. 1–22. [Google Scholar]
- Guanche, R.; de Andrés, A.D.; Simal, P.D.; Vidal, C.; Losada, I.J. Uncertainty Analysis of Wave Energy Farms Financial Indicators. Renew. Energy 2014, 68, 570–580. [Google Scholar] [CrossRef]
- Neill, S.P.; Hashemi, M.R. Wave Power Variability over the Northwest European Shelf Seas. Appl. Energy 2013, 106, 31–46. [Google Scholar] [CrossRef]
- Maria-Arenas, A.; Garrido, A.J.; Rusu, E.; Garrido, I. Control Strategies Applied to Wave Energy Converters: State of the Art. Energies 2019, 12, 3115. [Google Scholar] [CrossRef] [Green Version]
- Rusu, E.; Onea, F. A Review of the Technologies for Wave Energy Extraction. Clean Energy 2018, 2, 10–19. [Google Scholar] [CrossRef] [Green Version]
- Babarit, A. A Database of Capture Width Ratio of Wave Energy Converters. Renew. Energy 2015, 80, 610–628. [Google Scholar] [CrossRef]
- Rusu, L.; Onea, F. The Performance of Some State-of-the-Art Wave Energy Converters in Locations with the Worldwide Highest Wave Power. Renew. Sustain. Energy Rev. 2017, 75, 1348–1362. [Google Scholar] [CrossRef]
- Gunn, K.; Stock-Williams, C. Quantifying the Global Wave Power Resource. Renew. Energy 2012, 44, 296–304. [Google Scholar] [CrossRef]
- Lavidas, G.; Kamranzad, B. Assessment of Wave Power Stability and Classification with Two Global Datasets. Int. J. Sustain. Energy 2020. [Google Scholar] [CrossRef]
- Onea, F.; Rusu, E. Sustainability of the Reanalysis Databases in Predicting the Wind and Wave Power along the European Coasts. Sustainability 2018, 10, 193. [Google Scholar] [CrossRef] [Green Version]
- Martinez, A.; Iglesias, G. Wave Exploitability Index and Wave Resource Classification. Renew. Sustain. Energy Rev. 2020, 134, 110393. [Google Scholar] [CrossRef]
- Mo̸rk, G.; Barstow, S.; Kabuth, A.; Pontes, M.T. Assessing the Global Wave Energy Potential; American Society of Mechanical Engineers Digital Collection (OMAE2010): New York, NY, USA, 2010; pp. 447–454. [Google Scholar]
- Akpınar, A.; Jafali, H.; Rusu, E. Temporal Variation of the Wave Energy Flux in Hotspot Areas of the Black Sea. Sustainability 2019, 11, 562. [Google Scholar] [CrossRef] [Green Version]
- Belibassakis, K.; Bonovas, M.; Rusu, E. A Novel Method for Estimating Wave Energy Converter Performance in Variable Bathymetry Regions and Applications. Energies 2018, 11, 2092. [Google Scholar] [CrossRef] [Green Version]
- Kamranzad, B.; Etemad-Shahidi, A.; Chegini, V. Developing an Optimum Hotspot Identifier for Wave Energy Extracting in the Northern Persian Gulf. Renew. Energy 2017, 114, 59–71. [Google Scholar] [CrossRef]
- Kamranzad, B.; Takara, K. A Climate-Dependent Sustainability Index for Wave Energy Resources in Northeast Asia. Energy 2020, 209, 118466. [Google Scholar] [CrossRef]
- Triasdian, B.; Indartono, Y.S.; Ningsih, N.S. Energy Capture Potential of Existing Wave Energy Converters for Indonesian Sea. AIP Conf. Proc. 2018, 1984, 030002. [Google Scholar] [CrossRef]
- Rusu, L.; Onea, F. Assessment of the Performances of Various Wave Energy Converters along the European Continental Coasts. Energy 2015, 82, 889–904. [Google Scholar] [CrossRef]
- Gonçalves, M.; Martinho, P.; Guedes Soares, C. A 33-Year Hindcast on Wave Energy Assessment in the Western French Coast. Energy 2018, 165, 790–801. [Google Scholar] [CrossRef]
- Rusu, E.; Guedes Soares, C. Wave Energy Assessments in the Coastal Environment of Portugal Continental; American Society of Mechanical Engineers Digital Collection (OMAE2008): New York, NY, USA, 2008; pp. 761–772. [Google Scholar]
- Silva, D.; Rusu, E.; Guedes Soares, C. High-Resolution Wave Energy Assessment in Shallow Water Accounting for Tides. Energies 2016, 9, 761. [Google Scholar] [CrossRef] [Green Version]
- Gallagher, S.; Tiron, R.; Whelan, E.; Gleeson, E.; Dias, F.; McGrath, R. The Nearshore Wind and Wave Energy Potential of Ireland: A High Resolution Assessment of Availability and Accessibility. Renew. Energy 2016, 88, 494–516. [Google Scholar] [CrossRef]
- Rusu, L. The Wave and Wind Power Potential in the Western Black Sea. Renew. Energy 2019, 139, 1146–1158. [Google Scholar] [CrossRef]
- Lavidas, G.; Venugopal, V. A 35 Year High-Resolution Wave Atlas for Nearshore Energy Production and Economics at the Aegean Sea. Renew. Energy 2017, 103, 401–417. [Google Scholar] [CrossRef] [Green Version]
- Morim, J.; Cartwright, N.; Etemad-Shahidi, A.; Strauss, D.; Hemer, M. Wave Energy Resource Assessment along the Southeast Coast of Australia on the Basis of a 31-Year Hindcast. Appl. Energy 2016, 184, 276–297. [Google Scholar] [CrossRef]
- Cuttler, M.V.W.; Hansen, J.E.; Lowe, R.J. Seasonal and Interannual Variability of the Wave Climate at a Wave Energy Hotspot off the Southwestern Coast of Australia. Renew. Energy 2020, 146, 2337–2350. [Google Scholar] [CrossRef]
- Allahdadi, M.N.; Gunawan, B.; Lai, J.; He, R.; Neary, V.S. Development and Validation of a Regional-Scale High-Resolution Unstructured Model for Wave Energy Resource Characterization along the US East Coast. Renew. Energy 2019, 136, 500–511. [Google Scholar] [CrossRef]
- Guillou, N.; Chapalain, G. Assessment of Wave Power Variability and Exploitation with a Long-Term Hindcast Database. Renew. Energy 2020, 154, 1272–1282. [Google Scholar] [CrossRef]
- López, M.; Veigas, M.; Iglesias, G. On the Wave Energy Resource of Peru. Energy Convers. Manag. 2015, 90, 34–40. [Google Scholar] [CrossRef]
- Duić, N.; Krajačić, G.; da Graça Carvalho, M. RenewIslands Methodology for Sustainable Energy and Resource Planning for Islands. Renew. Sustain. Energy Rev. 2008, 12, 1032–1062. [Google Scholar] [CrossRef]
- Rusu, E.; Onea, F. An Assessment of the Wind and Wave Power Potential in the Island Environment. Energy 2019, 175, 830–846. [Google Scholar] [CrossRef]
- Sierra, J.P.; Casas-Prat, M.; Campins, E. Impact of Climate Change on Wave Energy Resource: The Case of Menorca (Spain). Renew. Energy 2017, 101, 275–285. [Google Scholar] [CrossRef]
- Bernardino, M.; Rusu, L.; Guedes Soares, C. Evaluation of the Wave Energy Resources in the Cape Verde Islands. Renew. Energy 2017, 101, 316–326. [Google Scholar] [CrossRef]
- Stopa, J.E.; Filipot, J.-F.; Li, N.; Cheung, K.F.; Chen, Y.-L.; Vega, L. Wave Energy Resources along the Hawaiian Island Chain. Renew. Energy 2013, 55, 305–321. [Google Scholar] [CrossRef]
- Morim, J.; Cartwright, N.; Hemer, M.; Etemad-Shahidi, A.; Strauss, D. Inter- and Intra-Annual Variability of Potential Power Production from Wave Energy Converters. Energy 2019, 169, 1224–1241. [Google Scholar] [CrossRef]
- Rusu, L.; Ganea, D.; Mereuta, E. A Joint Evaluation of Wave and Wind Energy Resources in the Black Sea Based on 20-Year Hindcast Information. Energy Explor. Exploit. 2017, 36, 335–351. [Google Scholar] [CrossRef]
- Morim, J.; Hemer, M.; Wang, X.L.; Cartwright, N.; Trenham, C.; Semedo, A.; Young, I.; Bricheno, L.; Camus, P.; Casas-Prat, M.; et al. Robustness and Uncertainties in Global Multivariate Wind-Wave Climate Projections. Nat. Clim. Chang. 2019, 9, 711–718. [Google Scholar] [CrossRef] [Green Version]
- Rusu, L. A Projection of the Expected Wave Power in the Black Sea until the End of the 21st Century. Renew. Energy 2020, 160, 136–147. [Google Scholar] [CrossRef]
- Ribeiro, A.S.; deCastro, M.; Rusu, L.; Bernardino, M.; Dias, J.M.; Gomez-Gesteira, M. Evaluating the Future Efficiency of Wave Energy Converters along the NW Coast of the Iberian Peninsula. Energies 2020, 13, 3563. [Google Scholar] [CrossRef]
- Rusu, L. Evaluation of the near Future Wave Energy Resources in the Black Sea under Two Climate Scenarios. Renew. Energy 2019, 142, 137–146. [Google Scholar] [CrossRef]
- ESA. European Space Agency Climate Change Initiative for Sea State: Project Website and Data Access. Available online: https://climate.esa.int/en/projects/sea-state/ (accessed on 4 June 2020).
- Hersbach, H.; Bell, B.; Berrisford, P.; Hirahara, S.; Horányi, A.; Muñoz-Sabater, J.; Nicolas, J.; Peubey, C.; Radu, R.; Schepers, D.; et al. The ERA5 Global Reanalysis. Q. J. R. Meteorol. Soc. 2020, 146, 1999–2049. [Google Scholar] [CrossRef]
- Dodet, G.; Piolle, J.-F.; Quilfen, Y.; Abdalla, S.; Accensi, M.; Ardhuin, F.; Ash, E.; Bidlot, J.-R.; Gommenginger, C.; Marechal, G.; et al. The Sea State CCI Dataset v1: Towards a Sea State Climate Data Record Based on Satellite Observations. Earth Syst. Sci. Data 2020, 12, 1929–1951. [Google Scholar] [CrossRef]
- Piollé, J.-F.; Dodet, G.; Quilfen, Y. ESA Sea State Climate Change Initiative (Sea_State_cci). Global Remote Sensing Merged Multi-Mission Monthly Gridded Significant Wave Height, L4 Product, Version 1.1. Available online: https://climate.esa.int/en/projects/sea-state/data/ (accessed on 3 September 2020).
- Timmermans, B.W.; Gommenginger, C.P.; Dodet, G.; Bidlot, J.-R. Global Wave Height Trends and Variability from New Multimission Satellite Altimeter Products, Reanalyses, and Wave Buoys. Geophys. Res. Lett. 2020, 47, e2019GL086880. [Google Scholar] [CrossRef]
- Quartly, G.D.; Kurekin, A.A. Sensitivity of Altimeter Wave Height Assessment to Data Selection. Remote Sens. 2020, 12, 2608. [Google Scholar] [CrossRef]
- Herbich, J.B. Handbook of Coastal Engineering; McGraw-Hill: New York, NY, USA, 2000; ISBN 978-0-07-134402-9. [Google Scholar]
- Holthuijsen, L.H. Waves in Oceanic and Coastal Waters, 1st ed.; Cambridge University Press: Cambridge, UK, 2010; ISBN 978-0-521-12995-4. [Google Scholar]
- Babanin, A.V.; Rogers, W.E.; de Camargo, R.; Doble, M.; Durrant, T.; Filchuk, K.; Ewans, K.; Hemer, M.; Janssen, T.; Kelly-Gerreyn, B.; et al. Waves and Swells in High Wind and Extreme Fetches, Measurements in the Southern Ocean. Front. Mar. Sci. 2019, 6. [Google Scholar] [CrossRef] [Green Version]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A Recent Increase in Global Wave Power as a Consequence of Oceanic Warming. Nat. Commun. 2019, 10. [Google Scholar] [CrossRef] [Green Version]
- Stopa, J.E.; Cheung, K.F.; Tolman, H.L.; Chawla, A. Patterns and Cycles in the Climate Forecast System Reanalysis Wind and Wave Data. Ocean. Model. 2013, 70, 207–220. [Google Scholar] [CrossRef]
- Semedo, A.; Sušelj, K.; Rutgersson, A.; Sterl, A. A Global View on the Wind Sea and Swell Climate and Variability from ERA-40. J. Clim. 2011, 24, 1461–1479. [Google Scholar] [CrossRef]
- Aguirre, C.; Rutllant, J.A.; Falvey, M. Wind Waves Climatology of the Southeast Pacific Ocean. Int. J. Climatol. 2017, 37, 4288–4301. [Google Scholar] [CrossRef]
- Young, I.R. Seasonal Variability of the Global Ocean Wind and Wave Climate. Int. J. Climatol. 1999, 19, 931–950. [Google Scholar] [CrossRef]
- Chaichitehrani, N.; Allahdadi, M.N. Overview of Wind Climatology for the Gulf of Oman and the Northern Arabian Sea. Am. J. Fluid Dyn. 2018, 8, 1–9. [Google Scholar]
- Stefanakos, C. Intercomparison of Wave Reanalysis Based on ERA5 and WW3 Databases. In Proceedings of the International Society of Offshore and Polar Engineers, Honolulu, HI, USA, 16–21 June 2019. [Google Scholar]
- Bruno, M.F.; Molfetta, M.G.; Totaro, V.; Mossa, M. Performance Assessment of ERA5 Wave Data in a Swell Dominated Region. J. Mar. Sci. Eng. 2020, 8, 214. [Google Scholar] [CrossRef] [Green Version]
- Allahdadi, M.N.; He, R.; Neary, V.S. Predicting Ocean Waves along the US East Coast during Energetic Winter Storms: Sensitivity to Whitecapping Parameterizations. Ocean. Sci. 2019, 15, 691–715. [Google Scholar] [CrossRef] [Green Version]
- Reguero, B.G.; Losada, I.J.; Méndez, F.J. A Global Wave Power Resource and Its Seasonal, Interannual and Long-Term Variability. Appl. Energy 2015, 148, 366–380. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, D.P.; et al. The ERA-Interim Reanalysis: Configuration and Performance of the Data Assimilation System. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Reguero, B.G.; Menéndez, M.; Méndez, F.J.; Mínguez, R.; Losada, I.J. A Global Ocean Wave (GOW) Calibrated Reanalysis from 1948 Onwards. Coast. Eng. 2012, 65, 38–55. [Google Scholar] [CrossRef]
- Onea, F.; Ciortan, S.; Rusu, E. Assessment of the Potential for Developing Combined Wind-Wave Projects in the European Nearshore. Energy Environ. 2017, 28, 580–597. [Google Scholar] [CrossRef]
- Onea, F.; Rusu, E. The Expected Efficiency and Coastal Impact of a Hybrid Energy Farm Operating in the Portuguese Nearshore. Energy 2016, 97, 411–423. [Google Scholar] [CrossRef]
- Ruiz, A.; Onea, F.; Rusu, E. Study Concerning the Expected Dynamics of the Wind Energy Resources in the Iberian Nearshore. Energies 2020, 13, 4832. [Google Scholar] [CrossRef]
- Ribeiro, A.; Costoya, X.; de Castro, M.; Carvalho, D.; Dias, J.M.; Rocha, A.; Gomez-Gesteira, M. Assessment of Hybrid Wind-Wave Energy Resource for the NW Coast of Iberian Peninsula in a Climate Change Context. Appl. Sci. 2020, 10, 7395. [Google Scholar] [CrossRef]
- Raileanu, A.; Onea, F.; Rusu, E. An Overview of the Expected Shoreline Impact of the Marine Energy Farms Operating in Different Coastal Environments. J. Mar. Sci. Eng. 2020, 8, 228. [Google Scholar] [CrossRef] [Green Version]
- Bento, A.R.; Rusu, E.; Martinho, P.; Guedes Soares, C. Assessment of the Changes Induced by a Wave Energy Farm in the Nearshore Wave Conditions. Comput. Geosci. 2014, 71, 50–61. [Google Scholar] [CrossRef]








| Mission | Covered Period | Repeat Period (Days) |
|---|---|---|
| ERS-1 | 1992−2000 | 35 |
| TOPEX | 1992−2006 | 10 |
| ERS-2 | 1995−2011 | 35 |
| GFO | 1998−2008 | 17 |
| JASON-1 | 2001−2013 | 10 |
| ENVISAT | 2002−2012 | 35 |
| JASON-2 | 2008−2018 | 10 |
| CRYOSAT-2 | 2010−2018 | 369 |
| SARAL | 2013−2018 | 35 |
| JASON-3 | 2016−2018 | 10 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rusu, L.; Rusu, E. Evaluation of the Worldwide Wave Energy Distribution Based on ERA5 Data and Altimeter Measurements. Energies 2021, 14, 394. https://doi.org/10.3390/en14020394
Rusu L, Rusu E. Evaluation of the Worldwide Wave Energy Distribution Based on ERA5 Data and Altimeter Measurements. Energies. 2021; 14(2):394. https://doi.org/10.3390/en14020394
Chicago/Turabian StyleRusu, Liliana, and Eugen Rusu. 2021. "Evaluation of the Worldwide Wave Energy Distribution Based on ERA5 Data and Altimeter Measurements" Energies 14, no. 2: 394. https://doi.org/10.3390/en14020394
APA StyleRusu, L., & Rusu, E. (2021). Evaluation of the Worldwide Wave Energy Distribution Based on ERA5 Data and Altimeter Measurements. Energies, 14(2), 394. https://doi.org/10.3390/en14020394






