Optimization Techniques for Mining Power Quality Data and Processing Unbalanced Datasets in Machine Learning Applications

Abstract

In recent years, machine learning applications have received increasing interest from power system researchers. The successful performance of these applications is dependent on the availability of extensive and diverse datasets for the training and validation of machine learning frameworks. However, power systems operate at quasi-steady-state conditions for most of the time, and the measurements corresponding to these states provide limited novel knowledge for the development of machine learning applications. In this paper, a data mining approach based on optimization techniques is proposed for filtering root-mean-square (RMS) voltage profiles and identifying unusual measurements within triggerless power quality datasets. Then, datasets with equal representation between event and non-event observations are created so that machine learning algorithms can extract useful insights from the rare but important event observations. The proposed framework is demonstrated and validated with both synthetic signals and field data measurements.

1. Introduction

The application of machine learning algorithms has expanded noticeably in many fields in the last few decades, especially due to the increased power and reduced expense of computation, the growth of field data collection and the advent of novel techniques to process and analyze large datasets. This trend has also been observed in power systems, where most machine learning applications are related to distributed energy resources (such as solar, wind, and storage) and smart grid control. Such examples include the following: load and demand forecasts [1,2], electricity production forecasts [2], solar radiation forecasts [1], wind speed/power forecasts [3], automated control of smart grids [2], management of electric vehicle fleets [1], predictive maintenance [4], fault detection and location [3,5,6] and power quality disturbance classification [3].

Data for machine learning applications in power systems can be acquired from multiple sources. A common source of field data measurements is power quality monitors (PQM), which record instantaneous voltage and current waveforms with a high time resolution (hundreds of samples per cycle). The latest version of these devices allows the addition of precise and synchronized time stamps to the measured data, expanding the suitability of the recorded data to more advanced applications [7]. Traditionally, PQMs employ a limited set of triggering features to detect disturbances within the dataset and, once they have been detected, store a few waveform cycles as individual events [8]. More recently, however, a triggerless data acquisition approach has emerged, where all waveform samples are stored for further analysis.

The main advantage of this approach is that even inconspicuous disturbances are successfully captured [9]; on the other hand, triggerless PQMs generate voluminous datasets and require large data storage capabilities [10,11]. Further, most of the data correspond to the steady-state operation of the power system, whereas only a small part of the recorded data shows disturbances. In other words, the dataset is highly unbalanced, with the steady-state observations heavily outnumbering the disturbance observations, which, as will be discussed later, can cause performance deterioration in most machine learning algorithms. Thus, one of the focuses of this paper is dataset rebalancing, such that the disturbance and non-disturbance classes are equally represented in the input dataset prior to its use by a machine learning algorithm.

1.1. Disturbance Detection in Power System Datasets

Multiple techniques have been proposed over the years for detecting disturbances in PQM data, and they are broadly classified into two categories: in the first category, the trigger mechanism is based on the magnitude of a time series (e.g., overvoltage, overcurrent, signal rate of rise and root-mean-square (RMS) voltage variations) [12] or employs time–frequency and time–scale transformations to decompose the signal into several subbands (e.g., short-time Fourier transform and wavelet transform) [13,14]; the second category is composed of methods based on prominent signal residuals, which are obtained through time-varying mathematical models (e.g., autoregressive (AR) models and Kalman filters) or direct data comparison (e.g., point-by-point or cycle-by-cycle comparison) [15].

It has been shown that these techniques are effective for detecting conspicuous disturbances (i.e., cases where the underlying system event causes transients in the voltage and/or current waveforms) [16]. On the other hand, they are unable to detect most inconspicuous disturbances [17,18], hindering their suitability for the processing of triggerless PQM datasets. Further, they might be sensitive to harmonics, sampling frequency and other user-selected parameters (such as a mother wavelet for the detector based on a wavelet transform). These drawbacks often result in disturbances being missed by the detector, especially those that are very short and/or subtle.

Although waveforms collected by PQMs are valuable assets for power system analysis, these raw measurements might not directly provide useful information for disturbance identification and classification [12]. In fact, various power system events might not cause conspicuous disturbances in the PQM waveforms; instead, they are characterized by an abrupt step change in the RMS voltage profile. Common examples of power system events that belong to this category include capacitor switching de-energizing [19], transformer tap-changing, voltage regulator operation and switching of large loads [13].

Thus, RMS voltage step changes have been proposed as an alternative triggering feature to detect events (both conspicuous and inconspicuous) within PQM datasets [8,12]. This task, however, is complicated by the fact that the magnitude of these RMS voltage step changes is often quite small (even less than 0.5% of the nominal voltage). Moreover, the presence of rapidly varying fluctuations in an RMS voltage profile hinders the detection of RMS voltage step changes. Therefore, prior to being used in the disturbance identification process, the RMS voltage profile must be processed to remove those rapid voltage fluctuations. The desired output of this process is an RMS voltage profile with a high signal-to-noise ratio and sharp edges during the step changes [8], which is another focus of this paper.

1.2. Contributions

This paper proposes a framework for the detection of RMS voltage step changes and rebalancing of highly unbalanced PQM datasets. Its main contributions are as follows: (a) the proposal of a strategy for filtering RMS voltage profiles such that rapidly varying noise is removed or significantly attenuated, whilst preserving the steep edges of the RMS voltage profile caused by switching events; (b) the automatic detection of RMS voltage step changes in the filtered RMS voltage profile, so that both conspicuous and inconspicuous events within a PQM dataset are identified; and (c) the proposal of a framework for rebalancing highly unbalanced PQM datasets.

All optimization problems presented in this paper are implemented and solved in Pyomo [20].

1.3. Article Organization

The remainder of this paper is organized as follows. Section 2 discusses the effects of highly unbalanced datasets in machine learning training and proposes a strategy for rebalancing highly unbalanced PQM datasets. Section 3 presents a literature review on the filtering of RMS voltage profiles and detection of RMS voltage step changes. Section 4 describes the proposed approaches for RMS voltage profile filtering and dataset rebalancing, as well as presenting the PQM datasets analyzed throughout this paper. Section 5 demonstrates the performance of the proposed framework through field data measurements and Section 6 addresses some final considerations.

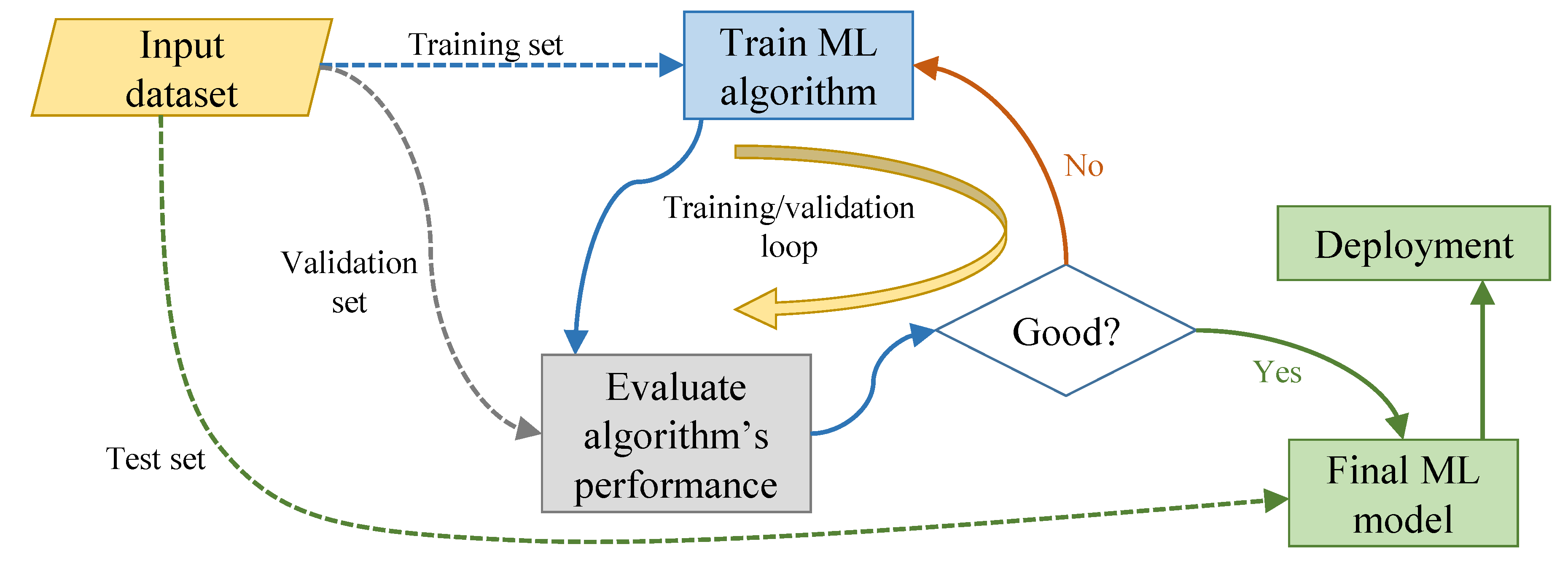
2. The Problem of Unbalanced Datasets in Machine Learning Training

The main goal of any machine learning algorithm is to learn patterns directly from the data through some computational methods, without relying on a predetermined physical model or some other strong assumptions about the data features. In general, the performance of these algorithms improves as the amount and variability of available samples increase [21,22]. The growth in popularity of machine learning applications is a direct consequence of the rise in big data, as most rule-based models are inadequate to extract insight from such large, complex and ever-changing datasets. Some real-world machine learning applications already in use include such diverse fields as the following [23]:

• Computational finance, for credit scoring and algorithmic trading;
• Image processing and computer vision, for face recognition, motion detection and object detection;
• Computational biology, for tumor detection, drug discovery and DNA sequencing;
• Energy production, for price and load forecasting;
• Automotive, aerospace and manufacturing, for predictive maintenance;
• Natural language processing.

Machine learning methods are broadly classified into two categories: supervised learning, where the algorithm tries to establish a mapping between input features and output targets so that it can be used to predict the output target for future input features; and unsupervised learning, where there is no output target and the goal is to group and interpret the data based only on its input features. As will become clear in the following discussion, the focus of this paper is on supervised learning—either in terms of classification (i.e., the output variable is categorical/discrete) or regression (i.e., the output variable is continuous).

A machine learning application is often divided into three stages—training, validation and testing—with the input dataset split into three corresponding subsets as well [21,22]. Figure 1 represents the general workflow of a typical machine learning application. First, the training set (which usually is the largest of the three subsets) is used to train a machine learning model. The performance of the resulting model is then evaluated using the validation set. If its performance is satisfactory with respect to some metric, the current model is considered as the final version of the machine learning model; otherwise, an iterative loop of successive training and validation stages is executed to incrementally improve the model’s predictive power until the desired performance is achieved. This training/validation loop consists of hyper-parameter tuning (if the selected algorithm has any hyper-parameters) or even the selection of an entirely different algorithm. Due to the large number of machine learning algorithms, this step involves some trial-and-error, as there is no one-size-fits-all approach in machine learning (i.e., there is no algorithm that outperforms all other counterpart algorithms for all types of application, datasets size and types of data or desired insights).

Once the final machine learning model has been selected, the test set is used to produce its performance metrics. It is important to emphasize that the test set should not overlap with the training and validation sets, as the goal in this evaluation step is to estimate the predictive power of the final model on samples that have not been used to fine-tune the model’s parameters.

In this paper, we focus on a pre-processing step to be employed prior to any of those three stages in an attempt to improve the performance of the machine learning algorithm. More specifically, our focus is on the handling and processing of highly unbalanced input datasets; i.e., cases in which the observations in the training dataset belonging to one class heavily outnumber the observations in the other class. A general overview of this pre-processing step is shown in Figure 2; the components of the dataset rebalancing block are detailed in Figure 5.

Highly unbalanced datasets in machine learning training might influence the model performance and often result in a phenomena called the accuracy paradox. This occurs when the accuracy measure simply reflects the underlying class distribution, rather than learning the actual patterns present in the dataset. Most standard machine learning algorithms are developed under the assumption that the class distributions are roughly balanced. When presented with unbalanced datasets, these algorithms fail to capture the effects of severe class distribution skewness [24], as well as experience difficulties learning the concepts related to the minority class [25].

For example, consider a binary classification problem where the training dataset is composed of 95% of observations for Class 1 and only 5% of observations for Class 2. Most of the machine learning algorithms tend to be biased toward the majority class. If an algorithm classifies a new observation based only on the majority class in the training set (Class 1 in this case), its accuracy would be 95%, which is an excellent value for most practical applications. This approach, however, does not take into account the features of each observation; i.e., there is no actual learning during the training stage, and the final machine learning model is likely to have low predictive accuracy on new observations.

The drawbacks caused by unbalanced datasets might be even worse than is apparent [26]. For example, consider the study presented in [27], where the goal is to predict voltages throughout a distribution network. Not surprisingly, most of the target values in the training dataset are around 1.0 pu, with only a few observations for which the target value is less than 0.95 pu or greater than 1.05 pu. However, prediction accuracy is more important for these scenarios with extreme voltage values (the minority class) than scenarios with voltages around 1.0 pu (the majority class). This difference in prediction accuracy importance is due to the fact that the scenarios with very low or very high voltages are those in which a voltage control device has to operate.

There are multiple practical examples in which class unbalance is quite common and even expected to occur. The minority class often represents rare but important events [25]. A well-known example is represented by the datasets of credit card transactions, where nearly all transactions were authorized by the card holder (not-fraud class), while only a few transactions belong to the fraud class. A similar situation is observed in power system measurements: most of the measurements correspond to steady-state conditions (non-event), while only a few of them are events.

Multiple strategies have been proposed for handling unbalanced datasets, including the following [24,28,29]:

• Collect more data;
• Explore alternative performance metrics, such as the confusion matrix, precision, recall, F-score, Cohen’s kappa and receiver operating characteristic (ROC) curves [30];
• Resample the dataset (either through under-sampling or over-sampling, depending on the dataset’s initial size);
• Generate synthetic observations;
• Investigate penalized models, where additional costs are imposed on the misclassification of the minority class during training and a higher cost of prediction is associated with rarity [31];
• Reconstruct the training dataset, where the minority observations are identified through anomaly or change detection.

This paper employs the resampling and change detection approaches to construct balanced training datasets. Given an RMS voltage profile, a training dataset is constructed as follows:

(1)

Partition the input profile into multiple equal-length segments and determine which contain significant changes in the RMS voltage levels; a significant change is defined as an RMS voltage step change greater than a pre-specified threshold, which will be introduced in later sections. Each one of these selected segments corresponds to one observation of the minority class (event) in the training dataset—let $n_{\mathrm{E}}$ denote the number of such observations;

(2)

Among the segments without a significant change in the RMS voltage level (non-event), randomly select $n_{\mathrm{E}}$ segments to form the majority class (non-event) in the training dataset.

Note that the minority and majority classes are used in the steps above only for consistency with the previous discussion. In fact, the newly created training dataset is evenly balanced between the two classes.

3. The State-of-the-Art

As mentioned in Section 1, this paper focuses on the detection of substantial changes in RMS voltage profiles, so that datasets with a more balanced ratio between events and non-events can be obtained for use in the training and validation stages of a machine learning application pipeline. The most straightforward method to detect such changes in an RMS voltage profile is based on RMS voltage gradients. There are also other alternative detectors proposed in the literature, and these are discussed below.

3.1. The RMS Voltage Gradient Profile Detection Approach

Let the vector $V\in {\mathbb{R}}^n$ represent an RMS voltage profile with a one-sample time resolution; then, the corresponding RMS voltage gradient profile is defined as

$$\Delta V_k=V_k-V_{k-pN},\mathrm{for}k=pN+1,\cdots ,n$$

(1)

where N is the number of waveform samples per cycle. The quantity $pN$ controls which RMS voltage values are compared to each other; it is recommended to adopt $p\ge 2$ [13] so that there is at least a one-cycle gap between the waveform samples used to compute $V_k$ and $V_{k-pN}$. Otherwise, the magnitude of the RMS voltage gradient might be smaller than the true magnitude of the step change when those sets of waveform samples contain a mix of both event and non-event data, possibly causing the event to be undetected [12]. On the other hand, adopting $p\ge 2$ guarantees that any waveform transients lasting less than one cycle will have dissipated and that at least one value in the $\Delta V$ profile captures the true magnitude of the step change. The computation of the RMS voltage gradient profile is illustrated in Figure 3 for $p=2$.

In the RMS voltage gradient approach, an event is detected whenever the following condition is satisfied:

$$\left|\Delta V_k\right|>{\delta }_{\mathrm{step}},\mathrm{for}k=pN+1,\cdots ,n$$

(2)

where ${\delta }_{\mathrm{step}}$ is a pre-specified threshold for the triggering criteria. The chosen value for this threshold has great impacts on the detector’s performance, as unsuitable values might cause multiple false positives (${\delta }_{\mathrm{step}}$ is too small) or false negatives (${\delta }_{\mathrm{step}}$ is too large).

In this paper, ${\delta }_{\mathrm{step}}$ is selected based on well-known characteristics of power systems; more specifically, we consider switching events that cause the most subtle change in RMS voltage profiles, as described below:

• Voltage regulators are devices that adjust the voltage level by changing the tap positions in an autotransformer. In general, they provide a −10% to +10% regulation range with 32 steps, where each step represents ±0.625% of the nominal voltage [32].
• Switched capacitor banks cause voltage variations, the magnitudes of which depend on the capacitor bank size and the short-circuit capacity at the bank location. For practical scenarios, the voltage variation falls between 0.36% and 4% of the nominal voltage [19,32,33,34].

Based on this discussion, we adopted ${\delta }_{\mathrm{step}}=0.0018$ pu, which follows the rule of thumb of setting the threshold as half of the minimum-expected step change [35]. This detection technique has been shown to achieve high accuracy, especially in cases where the signal-to-noise ratio of the RMS voltage profile is high (i.e., low noise levels) [12,36]. On the other hand, this detector fails if the RMS voltage profile has high noise levels or it has not been properly filtered.

3.2. Alternative Standard Detector

In the 2015 update, the International Electrotechnical Commission (IEC) added the concept of a rapid voltage change (RVC) to one of its standards [14]. An RVC is defined as an abrupt transition between two RMS voltage values, and its detection is performed as follows:

1

Compute the arithmetic mean of the immediately preceding RMS voltage values:

$${\overline{V}}_k=\frac{1}{2f}\sum _{p=k-2f+1}^k{V}_k$$

(3)

where f is the system frequency (either 50 or 60 Hz).

2

Flag a new RMS voltage value as part of an RVC if it deviates from ${\overline{V}}_k$ by more than a given threshold ${\delta }_{\mathrm{RVC}}$:

$$\left|V_k-{\overline{V}}_k\right|>{\delta }_{\mathrm{RVC}}⟹\mathrm{Flag}\mathrm{as}\mathrm{RVC}$$

(4)

The RVC threshold ${\delta }_{\mathrm{RVC}}$ is set by the user according to the desired application; the standard recommends considering values in the range of 0.01 pu to 0.06 pu. Due to the computation of arithmetic means, this detection approach behaves similarly to linear filtering, which, as discussed in the next section, has the drawback of blurring out the steep edges of the signal.

3.3. RMS Voltage Profile Filtering

The event detectors described previously can exhibit great performance degradation if the RMS voltage profiles are contaminated with noise. In the context of this paper, the following are factors that contribute to noise corruption:

• Noise introduced by the measurement device;
• Varying system frequency, which results in incorrect RMS voltage computations, as N waveform samples do not correspond to an integer number of cycles [36,37];
• Small load variations, which create intermittent variations in the RMS voltage profile and have the potential to hinder the detection of the events of interest.

Thus, a low-pass filtering technique must be applied to the RMS voltage profiles as a pre-processing step [35]. Linear filters, such as a moving average filter, have been shown to be effective in removing or attenuating rapidly varying noise while preserving the slowly varying signal. However, they blur out any steep edges of the signal [8,38,39], such as RMS voltage step changes, making this type of filter unfit for applications based on the detection of switching events [8].

On the other hand, median filters are well-known as suitable options for signals that contain sharp edges [39,40]. The performance of median filters can be further improved through an iterated and multiscale filtering approach, where multiple median filters are applied sequentially from a fine scale (narrow window) to a coarse scale (wide window). The goal of this process is to increase the signal-to-noise ratio at each stage such that the advantages of median filtering can be leveraged at increasingly low noise levels [12,39]. Previous work has compared the performance of single-stage and three-stage median filters applied to RMS voltage profiles around capacitor switching instants. It has been shown that both filters successfully attenuate the signal noise while preserving the RMS step changes in most cases; however, the three-stage median filter provided a faster transition between the steady-state levels prior and posterior to the switching instant [12]. This study also presented scenarios in which median filtering (both single- and three-stage) fails; for example, if the signal varies linearly (i.e., not a constant value) immediately before the step change, median filtering is not able to accurately track the signal.

4. Methodology

As mentioned in Section 1, techniques for properly filtering RMS voltage profiles are one of the main contributions of this paper. This section describes the proposed filtering approach, which is demonstrated through test signals.

4.1. Problem Setup

This subsection presents the data analyzed in the paper (both field measurements and synthetic signals), as well as definitions and formulations that are used in later sections.

4.1.1. Data

Field Measurements

The field measurements analyzed in this study consisted of 28-min continuous power quality data (voltage and current waveforms) collected at the feeder head of a 25 kV, 60 Hz radial distribution system with multiple parallel feeders. The power quality monitor was installed immediately downstream of the substation transformer, and its sampling frequency was 7.68 kHz (i.e., 128 waveform samples per cycle). The entire monitoring period contained eight major switching events: four capacitor energizing operations and four capacitor de-energizing operations. Further, some relatively large load switching events were also observed, although they had a smaller impact on the RMS voltage profile compared to capacitor switching events.

Synthetic Signals

Synthetic signals were also used in this study because they contained information about the true RMS voltage value without noise contamination at each time instant. The following signals are analyzed in later sections:

• Signal 1: The voltage level in a distribution system was in a quasi-stationary condition at 0.996 pu for 1 second. At that time instant, a capacitor bank was energized, instantaneously increasing the RMS voltage to 1.0 pu. After another 1 second had elapsed, the capacitor bank was de-energized and the RMS voltage level returned to 0.996 pu.
• Signal 2: The voltage level in a distribution system was in a quasi-stationary condition at 1.0 pu for 1 second. At that time instant, the load size connected to the system increased gradually over 1 second, causing the RMS voltage to drop linearly to 0.996 pu. This voltage drop triggered the energizing of a capacitor bank, instantaneously increasing the voltage level back to 1.0 pu. Note: this is the scenario in which median filtering was unable to track the original signal, as mentioned in Section 3.3.

These synthetic signals represented RMS voltage profiles with a half-cycle time resolution, so that each second contained 120 RMS voltage values (for a 60 Hz system). Further, each signal also contained additive noise originating from a normal distribution with zero-mean and standard deviation equal to 0.00025 pu. Figure 4 depicts both synthetic signals.

4.1.2. RMS Profile Computation

Let a sampled waveform signal be represented by a vector z; then, its RMS value at instant k, $Z_k$, is defined as

$$Z_k={\left(\frac{1}{N}\sum _{s=k-N+1}^k{z}_s^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(5)

where N is the number of samples per cycle in the waveform signal. Industrial standards recommend updating an RMS voltage profile every half-cycle ($N/2$ samples) [14,41]; profiles with this time resolution will be indicated as $Z^{(1/2)}$ in the rest of this paper.

On the other hand, computing a new RMS value once every waveform sample becomes available might result in hundreds or thousands of updates per second. The high computational burden involved in this approach is often pointed out as a drawback of having RMS profiles with such a high time resolution [13,14]. However, it has been shown that a recursive approach eliminates such issues [36]. In the recursive approach, the RMS value at instant k is computed as

$$Z_k={\left[Z_{k-1}^2+\frac{1}{N}\left(z_k^2-z_{k-N}^2\right)\right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(6)

This recursive approach will be employed throughout the paper wherever RMS profile computation with a high time resolution is necessary.

4.1.3. Vector Norms

For a given vector $z\in {\mathbb{R}}^n$, its $l_1$-norm (Manhattan norm) and $l_2$-norm (Euclidean norm) are defined according to Equations (7) and (8), respectively:

$${\parallel z\parallel }_1=\sum _{i=1}^n\left|z_i\right|$$

(7)

$${\parallel z\parallel }_2={\left(\sum _{i=1}^n{z}_i^2\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}$$

(8)

Note that in the following sections, the squared Euclidean norm ${\parallel z\parallel }_2^2$ is preferred over ${\parallel z\parallel }_2$ in order to avoid the square root operator.

4.2. Proposed Approach

Figure 5 depicts an overview of the PQM dataset rebalancing framework proposed in this paper. First, the input voltage waveforms were converted into the corresponding RMS voltage profiles (Section 4.1.2), which were filtered to remove/attenuate additive noise (Section 4.3). The filtered RMS voltage profiles were segmented into fixed-length, non-overlapping windows (in this study, we set each window length to 1 s). Each one of these segments was classified as an event or non-event, using the RMS voltage gradient profile approach that was introduced in Section 3.1. After all segments were classified into one of the two categories, dataset rebalancing was performed as described in Section 2. Finally, the resulting dataset could be used for the training/validation of machine learning algorithms.

4.3. Data Filtering

This section describes the filtering of time series through optimization techniques. Consider a signal represented by the vector $x\in {\mathbb{R}}^n$, where each coefficient $x_i$ represents the signal value sampled at the i-th time instant and the sampling interval is fixed. Without loss of generality, it is often assumed that the signal does not vary too rapidly for most of the time, as was the case for the signals analyzed in this study, so that $x_i\approx x_{i+1}$.

As commonly observed in field measurements, the signal x is corrupted by an additive noise $\nu$, i.e., $x_{\mathrm{cor}}=x+\nu$. Note that $x_{\mathrm{cor}}$ is observable by measurement devices, whereas the true underlying signal x is unknown. The additive noise $\nu$ can be modeled based on known characteristics of the process under study; however, for generality, it will be assumed that it follows an unknown distribution, has a small amplitude and varies much more rapidly than the signal x [42].

The objective of time series filtering is to produce an estimate $x^{*}$ of the original signal x, given the corrupted signal $x_{\mathrm{cor}}$; this process is also called signal reconstruction or de-noising. The reconstructed signal $x^{*}$ should be similar to the corrupted signal and smooth; i.e., the rapidly varying noise is removed or significantly attenuated. The closeness between the corrupted and reconstructed signals is often measured with respect to the $l_2$-norm, and a penalty function $\varphi$ is used to assess the non-smoothness of the reconstructed signal. Thus, this signal filtering problem can be formulated as a convex vector optimization problem [42], as follows:

$$x^{*}=\underset{\widehat{x}\in {\mathbb{R}}^n}{argmin}\mathbf{F}(\widehat{x},x_{\mathrm{cor}})$$

(9)

where the objective function

$$\mathbf{F}(\widehat{x},x_{\mathrm{cor}})=\left[\begin{array}{c}{∥\widehat{x}-x_{\mathrm{cor}}∥}_2\\ \varphi \left(\widehat{x}\right)\end{array}\right]$$

(10)

is a vector. Its first component, $F_1={∥\widehat{x}-x_{\mathrm{cor}}∥}_2$ represents a measure of fit or consistency between the corrupted and estimated signals, whereas the second component, $F_2=\varphi \left(\widehat{x}\right)$, measures the roughness or lack of smoothness of the estimate $\widehat{x}$. The function $\varphi :{\mathbb{R}}^n\to \mathbb{R}$ is convex and often given as some norm. Note, however, that $F_1$ and $F_2$ do not need to be measured with respect to the same norm, and this fact will be exploited later to produce better estimates for $x^{*}$. In problems involving $l_2$-norms, it is common practice to consider the corresponding squared norms [42], so that the nonlinearities caused by square roots are removed from the problem formulation; thus, we will adopt $F_1={∥\widehat{x}-x_{\mathrm{cor}}∥}_2^2$.

The formulation presented in Equation (9) corresponds to a multi-objective optimization problem, where each component can be interpreted as different scalar objectives. The goal is to minimize each one of these components; however, they represent competing objectives, and a decrease in $F_1$ is accompanied by an increase in $F_2$ and vice-versa.

A standard approach for solving such optimization problems is called scalarization or regularization, where the objective function in Equation (9) is reformulated as ${\lambda }^{\mathrm{T}}\mathbf{F}(\widehat{x},x_{\mathrm{cor}})={\lambda }_1{∥\widehat{x}-x_{\mathrm{cor}}∥}_2^2+{\lambda }_2\varphi \left(\widehat{x}\right)$ for any weight vector $\lambda >0$ [42]. Note that ${\lambda }^{\mathrm{T}}\mathbf{F}(\widehat{x},x_{\mathrm{cor}})$ is scalar-valued and convex, since it is a weighted sum of convex functions [43]. Therefore, the reformulated problem is an ordinary scalar convex optimization problem, which can be solved easily.

The weight vector $\lambda$ has a great influence on the filtering process as it controls the smoothness level of the output signal, and choosing a suitable value is critical to achieving the desired level of noise removal [44]. In general, each choice of $\lambda$ results in a different estimate $x^{*}$ [42]. Let $\lambda ={[1,\delta ]}^{\mathrm{T}}$, for some $\delta >0$; as $\delta$ varies over $[0,\infty )$, the solution of the equivalent scalar optimization problem traces out the optimal trade-off curve (or Pareto curve) between minimizing each component $F_1$ and $F_2$ separately. Figure 6 depicts a typical Pareto curve for a bi-criterion vector optimization problem, where values of components $F_1$ and $F_2$ are plotted on the horizontal and vertical axes, respectively.

For any $\delta$, the slope of the Pareto curve represents the local optimal trade-off between the two objectives: if the slope is steep, small changes in $F_1$ are accompanied by large changes in $F_2$, and vice-versa [42]. In other words, a Pareto curve allows us to determine how large one of the objectives must be in order to have the other one be small. Thus, the filtering of signals with a low signal-to-noise ratio (high noise levels) requires a larger $\delta$ [44].

In the extremes of a Pareto curve, we have the following interpretation:

• $\delta =0$: there is no penalty associated with the roughness of the output signal; thus, no smoothing is performed and $x^{*}=x_{\mathrm{cor}}$. This scenario corresponds to the endpoint at the left in the Pareto curve, and it represents the smallest possible value of $F_1$ without any consideration of $F_2$.
• $\delta \to \infty$: a stronger emphasis is placed on the smoothness of the output signal, at the expense of disregarding the similarity between the corrupted and estimated signals; for a sufficiently large $\delta$, $x^{*}$ becomes a constant signal. This scenario corresponds to the endpoint at the right in the Pareto curve, and it represents the smallest possible value of $F_2$ without any consideration of $F_1$.

Choosing a suitable $\delta$ is a compromise between $F_1$ and $F_2$. In practice, its value is chosen empirically by analyzing the Pareto curve and selecting a value such that a small decrease in one objective is accompanied by a small increase in the other objective [42]. The $\delta$ values that satisfy this requirement form the knee of the Pareto curve.

In the next sections, we present different strategies for quantifying the smoothness of the filtered signal; i.e., we present formulations for the component $F_2=\varphi \left(\widehat{x}\right)$ of the objective function.

4.3.1. Quadratic Smoothing

The most straightforward roughness measure of a signal is given in terms of the sum of squares of differences. The quadratic smoothing function is defined as

$$F_2={\varphi }_{\mathrm{quad}}\left(\widehat{x}\right)=\sum _{i=1}^{n-1}{({\widehat{x}}_{i+1}-{\widehat{x}}_i)}^2={∥D\widehat{x}∥}_2^2$$

(11)

where $D\in {\mathbb{R}}^{(n-1)\times n}$ is the bidiagonal matrix

$$D={\begin{array}{ccccccc}\hfill \left[r\right]-1& 1& 0\hfill & \cdots & 0& 0& 0\\ \hfill 0& -1& 1\hfill & \cdots & 0& 0& 0\\ \hfill ⋮& ⋮& ⋮\hfill & \ddots & ⋮& ⋮& ⋮\\ \hfill 0& 0& 0\hfill & \cdots & -1& 1& 0\\ \hfill 0& 0& 0\hfill & \cdots & 0& -1& 1\end{array}}_{(n-1)\times n}$$

(12)

and represents an approximation to the first-order differentiation operator. As ${\varphi }_{\mathrm{quad}}\left(\widehat{x}\right)$ is defined in terms of a $l_2$-norm, its squared value is used in the optimization problem, as discussed previously.

The estimate $x^{*}$ is the solution to the following unconstrained scalar optimization problem:

$$\underset{\widehat{x}\in {\mathbb{R}}^n}{minimize}{∥\widehat{x}-x_{\mathrm{cor}}∥}_2^2+\delta {∥D\widehat{x}∥}_2^2$$

(13)

where $\delta >0$ parametrizes the optimal trade-off curve between ${∥\widehat{x}-x_{\mathrm{cor}}∥}_2^2$ and ${∥D\widehat{x}∥}_2^2$. This formulation corresponds to a quadratic problem, which can be solved very efficiently [42].

Figure 7a shows the Pareto curve for $\delta \in [0,500]$ for the synthetic signal 1 defined in Section 4.1.1, where it can be observed that $\delta \approx 2$ is the optimal weight. Figure 7b depicts three smoothed signals on the optimal trade-off curve:

• $\delta =0.2$ (under-filtering): the weight associated with the output signal roughness is too small; although the steep edges in the signal are preserved, there is almost no reduction in the signal noise.
• $\delta =2$ (optimal): this scenario represents the optimal trade-off between corrupted and estimated signals similarity and noise reduction; however, the noise level in the filtered signal is still quite high.
• $\delta =100$ (over-filtering): an excessive weight is placed on the signal smoothness, resulting in over-filtering; the similarity between the corrupted and estimated signals is rather low.

Figure 8 shows the filtering results for the synthetic signal 2, and the discussion presented above is also valid for this test case.

This analysis shows that quadratic smoothing either removes the rapidly varying noise or preserves the steep signal edges, but not both; in fact, quadratic smoothing behaves as a low-pass filter. Thus, this technique is not suitable for the category of signals analyzed in this paper.

4.3.2. Total Variation Smoothing

Given the limitations of quadratic smoothing discussed previously, this section describes a smoothing function that is effective at removing/attenuating the signal noise, while still preserving the steep edges of the original signal [45,46]. In this case, the signal smoothness is measured according to the following function:

$$F_2={\varphi }_{\mathrm{tv}}\left(\widehat{x}\right)=\sum _{i=1}^{n-1}\left|{\widehat{x}}_{i+1}-{\widehat{x}}_i\right|={∥D\widehat{x}∥}_1$$

(14)

which is called the total variation of $\widehat{x}\in {\mathbb{R}}^n$. Note that, compared to ${\varphi }_{\mathrm{quad}}$ in Equation (11), ${\varphi }_{\mathrm{tv}}$ is not squared, as it is given in terms of a $l_1$-norm and there are no square root terms to be removed.

The estimate $x^{*}$ is the solution of the following unconstrained scalar optimization problem:

$$\underset{\widehat{x}\in {\mathbb{R}}^n}{minimize}{∥\widehat{x}-x_{\mathrm{cor}}∥}_2^2+\delta {∥D\widehat{x}∥}_1$$

(15)

The optimization problem in Equation (15) cannot be easily solved because the $l_1$-norm is non-differentiable [47]. The following problem reformulation is based on [43]. First, for simplicity, we introduce a new variable $y_i={\widehat{x}}_{i+1}-{\widehat{x}}_i,\forall i=1,\cdots ,n-1$, so that ${\varphi }_{\mathrm{tv}}\left(\widehat{x}\right)={\sum }_{i=1}^{n-1}\left|y_i\right|$.

Let $y_i=y_i^{+}-y_i^{-},\forall i=1,\cdots ,n-1$, where $y_i^{+}$ and $y_i^{-}$ are variables constrained to be nonnegative. It can be shown that these two variables cannot be simultaneously nonzero; i.e., at least one of the variables $y_i^{+}$ and $y_i^{-}$ is zero for each index i. Therefore,

$$y_i=\left\{\begin{array}{cc}{y}_i^{+},\hfill & \mathrm{if}{y}_i\ge 0(y_i^{+}\ge 0,y_i^{-}=0)\hfill \\ -y_i^{-},\hfill & \mathrm{if}{y}_i<0(y_i^{+}=0,y_i^{-}>0)\hfill \end{array}\right.⟹\left|y_i\right|=y_i^{+}+y_i^{-}$$

(16)

By replacing $\left|y_i\right|$ in Equation (15), the following alternative formulation is obtained:

$$\begin{array}{c}\underset{\widehat{x},y,y^{+},y^{-}\in {\mathbb{R}}^n}{minimize}{∥\widehat{x}-x_{\mathrm{cor}}∥}_2^2+\delta \sum _{i=1}^{n-1}\left(y_i^{+}+y_i^{-}\right)\\ \begin{array}{ccc}\hfill \mathrm{subject}\mathrm{to}& y_i={\widehat{x}}_{i+1}-{\widehat{x}}_i,\hfill & \hfill i=1,\cdots ,n-1\\ \hfill & y_i=y_i^{+}-y_i^{-},\hfill & \hfill i=1,\cdots ,n-1\\ \hfill & y_i^{+}\ge 0,\hfill & \hfill i=1,\cdots ,n-1\\ \hfill & y_i^{-}\ge 0,\hfill & \hfill i=1,\cdots ,n-1\end{array}\end{array}$$

(17)

which is a constrained, convex and differentiable optimization problem.

Figure 9 demonstrates the filtering of synthetic signal 1 through total variation smoothing. Figure 9a shows the Pareto curve for $\delta \in [0,5]$, where it can be observed that $\delta \approx 0.004$ is the optimal weight. Figure 9b depicts three smoothed signals on the optimal trade-off curve:

• $\delta =0.0002$ (under-filtering): the weight associated with the output signal roughness is too small, meaning that there is almost no reduction in the signal noise.
• $\delta =0.004$ (optimal): this scenario represents the optimal trade-off between corrupted and estimated signal similarity and noise reduction.
• $\delta =0.2$ (over-filtering): an excessive weight is placed on the signal smoothness, resulting in over-filtering; due to the large penalty associated with variations in the signal, the magnitude of the step change in the filtered signal is much smaller than the magnitude of the true step change.

Figure 10 shows the filtering results for the synthetic signal 2, and the discussion presented above is also valid for this test case. Further, unlike median filtering, total variation smoothing was able to track this piecewise linear signal.

This analysis shows that total variation smoothing exhibits great performance in noise reduction without blurring the sharp transitions of the original signal, as long as the weight $\delta$ has been properly selected.

4.3.3. Quadratic vs. Total Variation Smoothing

As discussed in the previous sections, total variation smoothing shows better performance in the filtering of RMS voltage profiles when compared to quadratic smoothing. In this section, we explore and compare the characteristics of these two smoothing operators in order to justify the superiority achieved by total variation smoothing.

Both ${\varphi }_{\mathrm{quad}}$ and ${\varphi }_{\mathrm{tv}}$, which were defined in Equations (11) and (14), respectively, assign large penalty costs to rapidly varying $\widehat{x}$. However, the quadratic smoothness function assigns a relatively small penalty to small values of $\left|{\widehat{x}}_{i+1}-{\widehat{x}}_i\right|$ [48]. For example, if $\left|{\widehat{x}}_{i+1}-{\widehat{x}}_i\right|=0.001$, then the penalties assigned by the quadratic and total variation smoothness functions are ${10}^{-6}$ and ${10}^{-3}$, respectively. In other words, the quadratic smoothing operator tolerates some variation in the filtered signal, whereas the total variation smoothing operator is subject to a much larger penalty if such signal variations exist, meaning that it enforces $\left|{\widehat{x}}_{i+1}-{\widehat{x}}_i\right|\approx 0$ for almost all i’s.

In general, the following characteristics are observed in the solutions of optimization problems with penalty functions [42]:

• $l_2$-norm penalty: ${∥D\widehat{x}∥}_2$ has many non-zero small entries and relatively few larger ones;
• $l_1$-norm penalty: ${∥D\widehat{x}∥}_1$ has many zero or very small entries and more larger ones.

The optimization problem scalarized with an $l_1$-norm is a heuristic for finding a solution in which ${∥D\widehat{x}∥}_1$ is sparse. As D represents an approximation to the first-order differentiation operator, total variation smoothing is biased toward solutions in which the filtered signal is linear or piecewise linear.

This behavior can be observed in Figure 11, which depicts the histogram of $\left|x_{i+1}-x_i\right|$ for the filtered signals computed in Section 4.3.1 (Figure 7b, quadratic smoothing with $\delta =2$) and Section 4.3.2 (Figure 9b, total variation smoothing with $\delta =0.004$), respectively. As expected, quadratic smoothing allows some $\left|{\widehat{x}}_{i+1}-{\widehat{x}}_i\right|$ to be greater than zero, which correspond to the smooth transition around the steep edges of the original signal. On the other hand, almost all $\left|{\widehat{x}}_{i+1}-{\widehat{x}}_i\right|$ in Figure 11b are approximately zero, except for two values that correspond to the two step changes present in the original signal.

5. Results

This section demonstrates the application of the proposed framework (i.e., total variation smoothing) using field data collected at the feeder head of a 25 kV radial distribution system, which is described in Section 4.1.1. Based on the results in Section 4.3.2, we adopted $\delta =0.0035$. Figure 12a shows the unfiltered and filtered RMS voltage profiles for the entire 28-min measurement interval, whereas Figure 12b shows the corresponding RMS voltage gradient profiles. Using the triggering threshold ${\delta }_{\mathrm{step}}=0.0018$ pu (Section 3.1), all RMS voltage step changes were successfully detected without any false positives. The root causes of the detected RMS voltage step changes were capacitor de-energizing (events 1, 2, 5 and 6) and capacitor energizing (events 3, 4, 7 and 8). Further, the unfiltered RMS voltage gradient profile did not create any false positives either; however, the gradient values were much larger compared to the filtered cases (as large as 0.0015 pu), indicating that the unfiltered profile might create false positives for some datasets.

Detailed views of the unfiltered and filtered RMS voltage profiles are shown in Figure 13 for four scenarios: capacitor de-energizing, capacitor energizing, load energizing and steady-state. Note that the filtered profile did not contain rapidly varying noise and its step changes were not affected, as initially desired. The unfiltered RMS voltage profile in Figure 13b contained a spike immediately after the RMS voltage step change, which was due to high-frequency transients in the voltage waveform caused by a capacitor energizing operation. On the other hand, total variation smoothing successfully removed this spike. This is an important advantage of using the filtered profile, as the magnitude of the step change might be one of the features employed by the machine learning algorithm (the magnitude given by the unfiltered profile is about 50% larger than the correct value).

Both unfiltered and filtered RMS voltage profiles were segmented into non-overlapping 1 s windows and classified as an event or non-event, as described in Section 4.2.

Table 1. Class distribution for the PQM dataset before and after rebalancing.

	Before Rebalancing	After Rebalancing
Majority class (Event)	1672 (99.52%)	8 (50%)
Minority class (Non-Event)	8 (0.48%)	8 (50%)

shows the distribution of classes before and after the rebalancing of the PQM dataset.

Before dataset rebalancing, less than 0.5% of the observations in the input dataset corresponded to power system disturbances; in this case, machine learning algorithms are very unlikely to be able to extract any useful information about the minority class. On the hand, the dataset was perfectly balanced using the framework proposed in this paper. It should be noted, however, that the rebalanced dataset contained only 16 observations, which is often considered too small for successfully training machine learning algorithms. One solution would be to select more observations for the majority class, as long as the resulting dataset does not become highly unbalanced. Another solution consists of collecting more PQM data; the field data considered in this paper represent only 28 minutes of measurement, whereas utilities have access to much longer measurement intervals (days, weeks or even months).

6. Conclusions

The RMS voltage profile filtering proposed in this paper was shown to be robust for removing/attenuating rapidly varying signal noise without blurring out the RMS voltage step changes due to switching events. By combining filtering and step change detection techniques, both conspicuous and inconspicuous events present in a PQM dataset can be successfully identified. Detecting such events is the basis for rebalancing highly unbalanced PQM datasets, consequently improving the performance of machine learning algorithms that use these datasets in their training and validations stages.

As observed in Figure 7b, Figure 8b, Figure 9b and Figure 10b, the parameter $\delta$ has a great effect on the RMS voltage profile filtering process. Further, the optimal value for $\delta$ depends on the noise level present in the signal; i.e., scenarios with a higher signal-to-noise ratio (low noise level) require a lower $\delta$ value. Therefore, the optimal $\delta$ value adopted in this paper might not be the most suitable choice for field measurements collected at other locations, as the signal-to-noise ratio might be different.

Future research directions include the development of techniques for automatically determining the optimal $\delta$ for each dataset. For example, for a given RMS voltage profile, such techniques would first analyze only a short segment of the profile for multiple $\delta$ values in order to construct the Pareto curve. Then, the optimal $\delta$ would be the value corresponding to the knee of the Pareto curve, as shown in Figure 6. Once this optimal value has been determined, the whole RMS voltage profile would be filtered through total variation smoothing. It is important to emphasize that optimization applications based on the Pareto curve in all fields—and not only power systems—empirically determine the optimal $\delta$ by visually inspecting the Pareto curve. Thus, a technique for automatically determining this value would represent a meaningful contribution.