Analysis of Safety Requirements for Securing the Semi-Trailer Truck on the Intermodal Railway Wagon
Abstract
:1. Introduction
2. Analysis of Cargo Securing Requirements
- Only a road vehicle which condition meets the requirements of the Road Transport Regulation may be approved for loading, e.g., in terms of dimensions, total weight, and permissible axial loads.
- Ensure that the tarpaulin mounts are correctly closed, the side mirrors are folded in, and the outer equipment is correctly fitted or secured (spoilers, snow chains, ladders, bridges, handrails, tank covers, closing flaps, buckets, shovels, etc.).
- Radio antennas must be fully retracted or removed if the truck’s height exceeds 4 m. Radio receiving and transmitting devices (including alarm systems) must be turned off to prevent automatic height changes of the antennas.
- After loading, gear must be engaged, the parking or hydraulic brake applied, and the engine turned off, which will remain off while the train is running.
- Secure the car with wheel wedges and, if necessary, depressurize the air suspension and lock the door.
- Critical wind velocities of overturning vary with natural wind directions and train speeds. For a fixed cross-wind speed, the rollover moment increases with vehicle speed. A critical wind speed is the gust speed (a few second gust) with a certain annual probability of exceedance [22,23,24,25,26,27].
- Several strategies can be used to successfully reduce the vehicle overturning moment in cross-wind successfully. Changing the shape of the trailer can mitigate the overturning risk (e.g., it is possible to reduce the overturning moment by 25% with a rounded corner [32]). Other schemes include meteorological warnings (roadside anemometry or the local weather station), vehicle restrictions, and roadside wind barriers [32,33,34,35].
3. Analysis of Aerodynamic and Inertia Effects
4. Discussion
Funding
Institutional Review Board Statement
Informed Consent Statement
Conflicts of Interest
References
- The European Commission. European Strategies, the White Paper. Available online: https://ec.europa.eu/transport/themes/strategies/2011_white_paper_en (accessed on 11 October 2021).
- Cempírek, V.; Vrbová, P.; Zákorová, E. The Possibility of Transferring the Transport Performance on Railway Transport. MATEC Web Conf. 2017, 134, 00006. [Google Scholar] [CrossRef]
- DNV GL AS, Container securing, DNVGL-CG-0060. 2016. Available online: https://rules.dnv.com/docs/pdf/DNV/CG/2016-02/DNVGL-CG-0060.pdf (accessed on 11 October 2021).
- Lew, H.S.; Sadek, F.; Anderson, E.D. Strength Evaluation of Connectors for Intermodal Containers; NISTIR 6557; NIST, United States Department of Commerce, Technology Administration: Washington, DC, USA, 2000. [Google Scholar]
- Krasoń, W.; Niezgoda, T.; Stankiewicz, M. Innovative Project of Prototype Railway Wagon and Intermodal Transport System. Transp. Res. Procedia 2016, 14, 615–624. [Google Scholar] [CrossRef] [Green Version]
- Nader, M.; Sala, M.; Korzeb, J.; Kostrzewski, A. Kolejowy wagon transportowy jako nowatorskie, innowacyjne rozwiązanie konstrukcyjne do przewozu naczep siodłowych i zestawów drogowych dla transportu intermodalnego (Railroad transport wagon as a novel, innovative construction solution for transporting semi-trailers and road sets for intermodal transport). Logistyka 2014, 4, 2272–2279. [Google Scholar]
- Nader, M.; Opala, M.; Korzeb, J. Wybrane zagadnienia badania dynamiki wagonu typu platforma do przewozu zestawów drogowych (Selected issues of testing the dynamics of a platform wagon for carrying road sets). Pr. Nauk. Politech. Warsz. Transp. 2019, 125, 101–111. [Google Scholar]
- Accident Investigation Board (AIB Denmark), Safety Alert. January 2021. Available online: https://en.havarikommissionen.dk/media/12715/j_2021_haendelse_2021-24_andet_storebaelt_safety-alert.pdf (accessed on 11 October 2021).
- UIC Freight Department, Report on Combined Transport in Europe. November 2020. Available online: https://uic.org/IMG/pdf/2020_combined_transport_report_press_conference_202010230.pdf (accessed on 11 October 2021).
- Mikusova, M.; Gnap, J. Experiences with the implementation of measures and tools for road safety improvement. In Proceedings of the CIT2016—XII Congreso de Ingeniería del Transporte, València, Spain, 7–9 June 2016; Universitat Politècnica de València: València, Spain, 2016. [Google Scholar] [CrossRef] [Green Version]
- Nader, M.; Sala, M. Rail Transport Wagon, Rail Transport Unit and Rail Transport System Incorporating Such a Wagon, Invention. Patent/right number: PL 214797; Application date (in the first country of application): 14 December 2009, Grant date: 17 December 2012,
- UIC. Loading Guidelines Code of Practice for the Loading and Securing of Goods on Railway Wagons, Volume 1, Principles, 3rd ed. 2019. Available online: https://uic.org/freight/wagon-issues/loading-rules (accessed on 11 October 2021).
- UIC. Loading Guidelines Code of Practice for the Loading and Securing of Goods on Railway Wagons, Volume 2, Goods, 3rd ed. 2019. Available online: https://uic.org/freight/wagon-issues/loading-rules (accessed on 11 October 2021).
- UIC 571-4 Standard wagons—Wagons for combined transport—Characteristics. 2011.
- UIC 596-6 Transport of road vehicles on wagons—Technical Organisation—Conveyance of semi-trailers with P coding or N coding on recess wagons. 2008.
- Rail Cargo Group/ROLA, Loading Instructions. 2021. Available online: https://rola.railcargo.com (accessed on 11 October 2021).
- Ralpin, General Conditions of Carriage. 2021. Available online: https://ralpin.com (accessed on 11 October 2021).
- Day, A. Breaking of Road Vehicle, 1st ed.; Elsevier: Amsterdam, The Netherlands, 2014; ISBN 978-0-12-397314-6. [Google Scholar]
- PN-EN 13452-1:2003—Kolejnictwo—Hamowanie—Systemy hamowania w transporcie publicznym—Część 1: Wymagania eksploatacyjne (Railroad applications—Braking—Braking systems in public transport—Part 1: Performance requirements).
- Obwieszczenie Ministra Infrastruktury i Budownictwa z dnia 27 Października 2016 r. W Sprawie Ogłoszenia Jednolitego Tekstu Rozporządzenia Ministra Infrastruktury w Sprawie Warunków Technicznych Pojazdów oraz Zakresu ich Niezbędnego Wyposażenia (Announcement by the Minister on the Consolidated Text of the Regulation of the Minister of Infrastructure on Technical Conditions of Vehicles and the Scope of Their Necessary Equipment). 2016. Available online: http://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20160002022 (accessed on 11 October 2021).
- Rozporządzenie Ministra Infrastruktury z dnia 24 Grudnia 2019 r. Zmieniające Rozporządzenie w Sprawie Warunków Technicznych Pojazdów oraz Zakresu ich Niezbędnego Wyposażenia (Regulation of the Minister of Infrastructure on Technical Conditions of Vehicles and the Scope of Their Necessary Equipment). 2019. Available online: http://isap.sejm.gov.pl/isap.nsf/DocDetails.xsp?id=WDU20190002560 (accessed on 11 October 2021).
- Cheli, F.; Corradi, R.; Tomasini, G. Crosswind action on rail vehicles: A methodology for the estimation of the characteristic wind curves. J. Wind Eng. Ind. Aerodyn. 2012, 104–106, 248–255. [Google Scholar] [CrossRef]
- Bettle, J.; Holloway, A.G.L.; Venart, J.E.S. A computational study of the aerodynamic forces acting on a tractor-trailer vehicle on a bridge in cross-wind. J. Wind Eng. Ind. Aerodyn. 2003, 91, 573–592. [Google Scholar] [CrossRef]
- Fujii, T.; Maeda, T.; Ishida, H.; Imai, T.; Tanemoto, K.; Suzuki, M. Wind-Induced Accidents of Train/Vehicles and Their Measures in Japan. Q. Rep. RTRI 1999, 40, 50–55. [Google Scholar] [CrossRef] [Green Version]
- Proppe, C.; Wetzel, C. Overturning Probability of Railway Vehicles under Wind Gust Loads. In Iutam Symposium on Dynamics and Control of Nonlinear Systems with Uncertainty; Hu, H.Y., Kreuzer, E., Eds.; IUTAM Book Series; Springer: Dordrecht, The Netherlands, 2007; Volume 2. [Google Scholar] [CrossRef]
- Li, A.; Xiong, X. Research on the Influence of Strong Crosswind on Aerodynamic Characteristics and Operation Safety of EMUs. In DEStech Transactions on Engineering and Technology Research; 2017; pp. 443–451. ISBN 978-1-60595-481-3. [Google Scholar] [CrossRef] [Green Version]
- Baker, C.; Johnson, T.; Flynn, D.; Hemida, H.; Quinn, A.; Soper, D.; Sterling, M. Train Aerodynamics; Butterworth-Heinemann: Oxford, UK, 2019; ISBN 978-0-12-813310-1. [Google Scholar]
- Baker, C.; Cheli, F.; Orellano, A.; Paradot, N.; Proppe, C.; Rocchi, D. Cross-wind effects on road and rail vehicles. Veh. Syst. Dyn. 2009, 47, 983–1022. [Google Scholar] [CrossRef]
- Charuvisit, S.; Kimurab, K.; Fujinoc, Y. Experimental and semi-analytical studies on the aerodynamic forces acting on a vehicle passing through the wake of a bridge tower in cross wind. J. Wind Eng. Ind. Aerodyn. 2004, 92, 749–780. [Google Scholar] [CrossRef]
- Diedrichs, B.; Sima, M.; Orellano, A.; Tengstrand, H. Crosswind stability of a high-speed train on a high embankment. Proc. Inst. Mech. Eng. Part F-J. Rail Rapid Transit 2007, 221, 205–225. [Google Scholar] [CrossRef]
- Abdulwahab, A.; Mishra, R. Estimation of LTR rollover index for a high-sided tractor semitrailer vehicle under extreme crosswind conditions through dynamic simulation. In Proceedings of the 2017 23rd International Conference on Automation and Computing (ICAC), Huddersfield, UK, 7–8 September 2017. [Google Scholar] [CrossRef]
- Salati, L.; Schito, P.; Cheli, F. Strategies to reduce the risk of side wind induced accident on heavy truck. J. Fluids Struct. 2019, 88, 331–351. [Google Scholar] [CrossRef]
- Chen, N.; Li, Y.; Wang, B.; Su, Y.; Xiang, H. Effects of wind barrier on the safety of vehicles driven on bridges. J. Wind Eng. Ind. Aerodyn. 2015, 143, 113–127. [Google Scholar] [CrossRef]
- Deng, E.; Yang, W.; He, X.; Zhu, Z.; Wang, H.; Wang, Y.; Wang, A.; Zhou, L. Aerodynamic response of high-speed trains under crosswind in a bridge-tunnel section with or without a wind barrier. J. Wind Eng. Ind. Aerodyn. 2021, 210, 104502. [Google Scholar] [CrossRef]
- Guo, X.; Tang, J. Effects of Wind Barrier Porosity on the Coupled Vibration of a Train-Bridge System in a Crosswind. Struct. Eng. Int. 2019, 29, 268–275. [Google Scholar] [CrossRef]


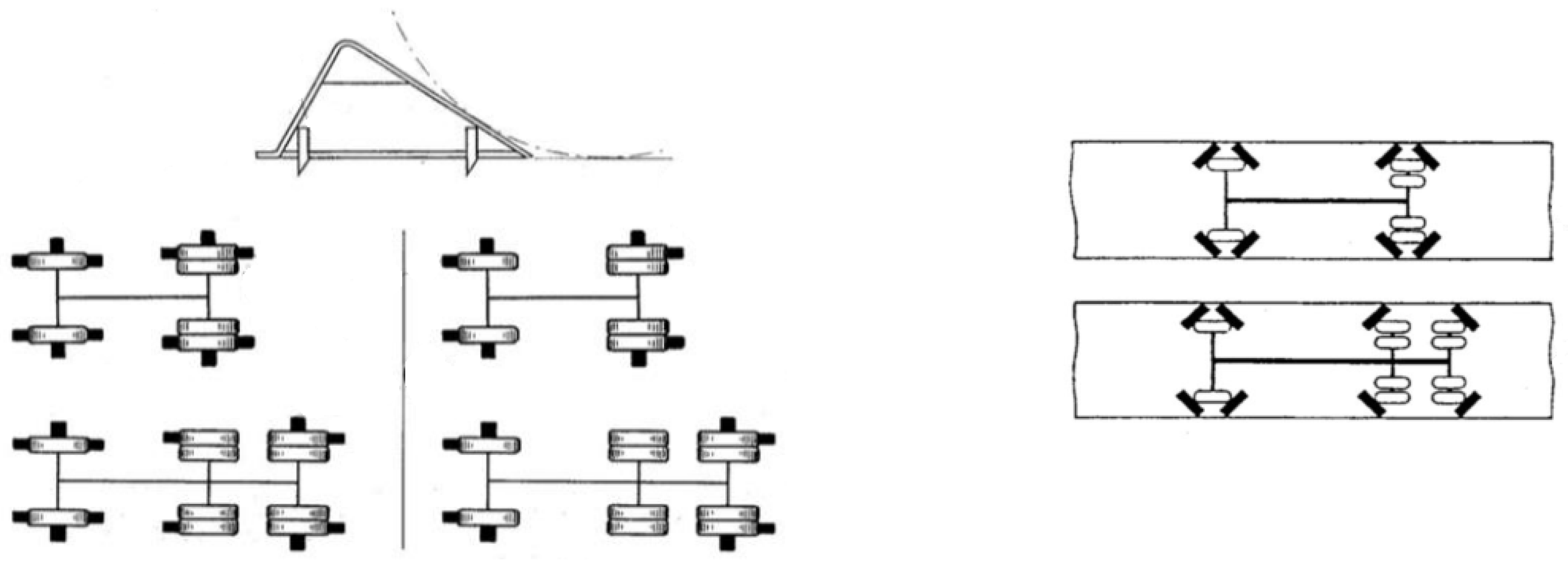
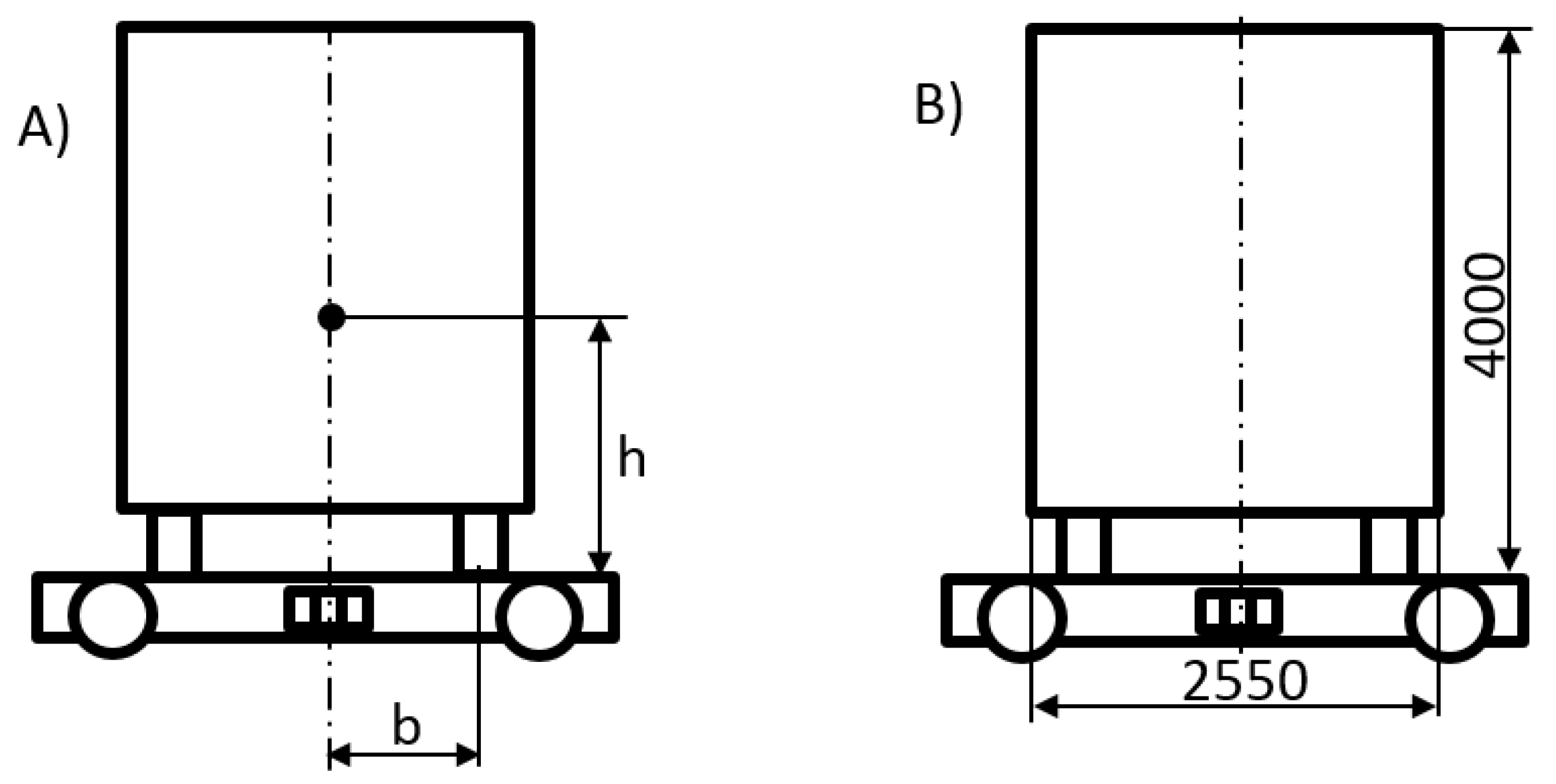
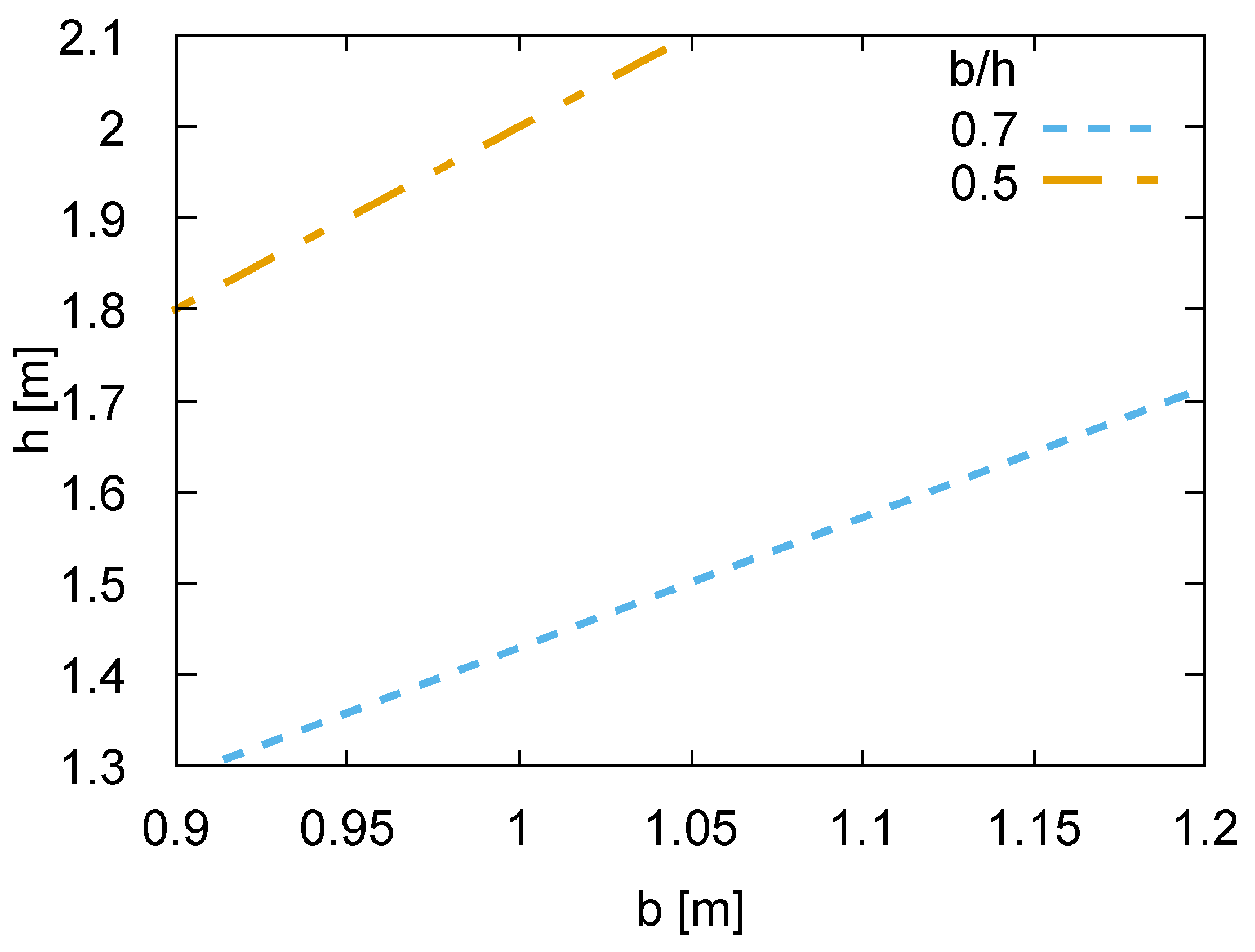
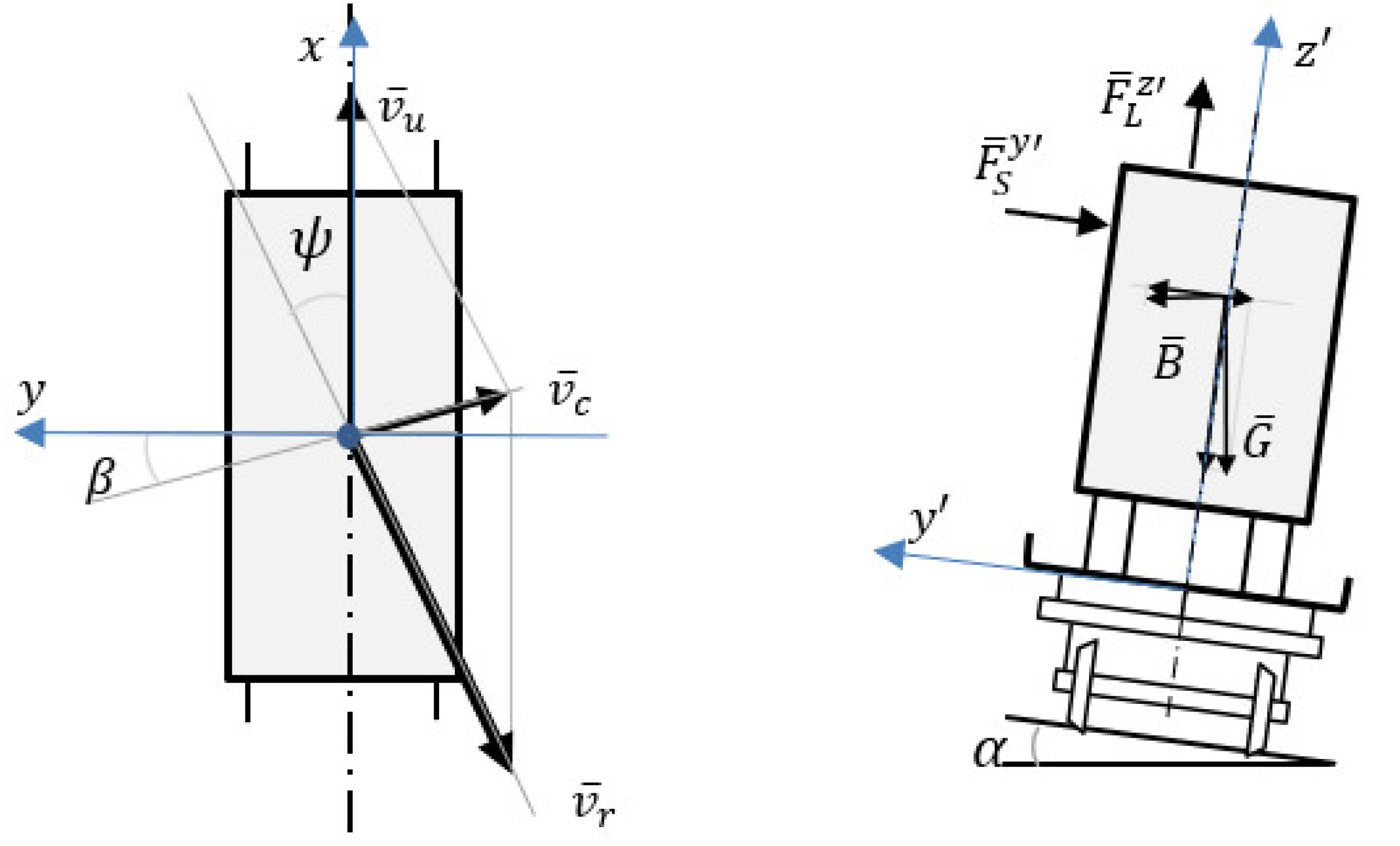
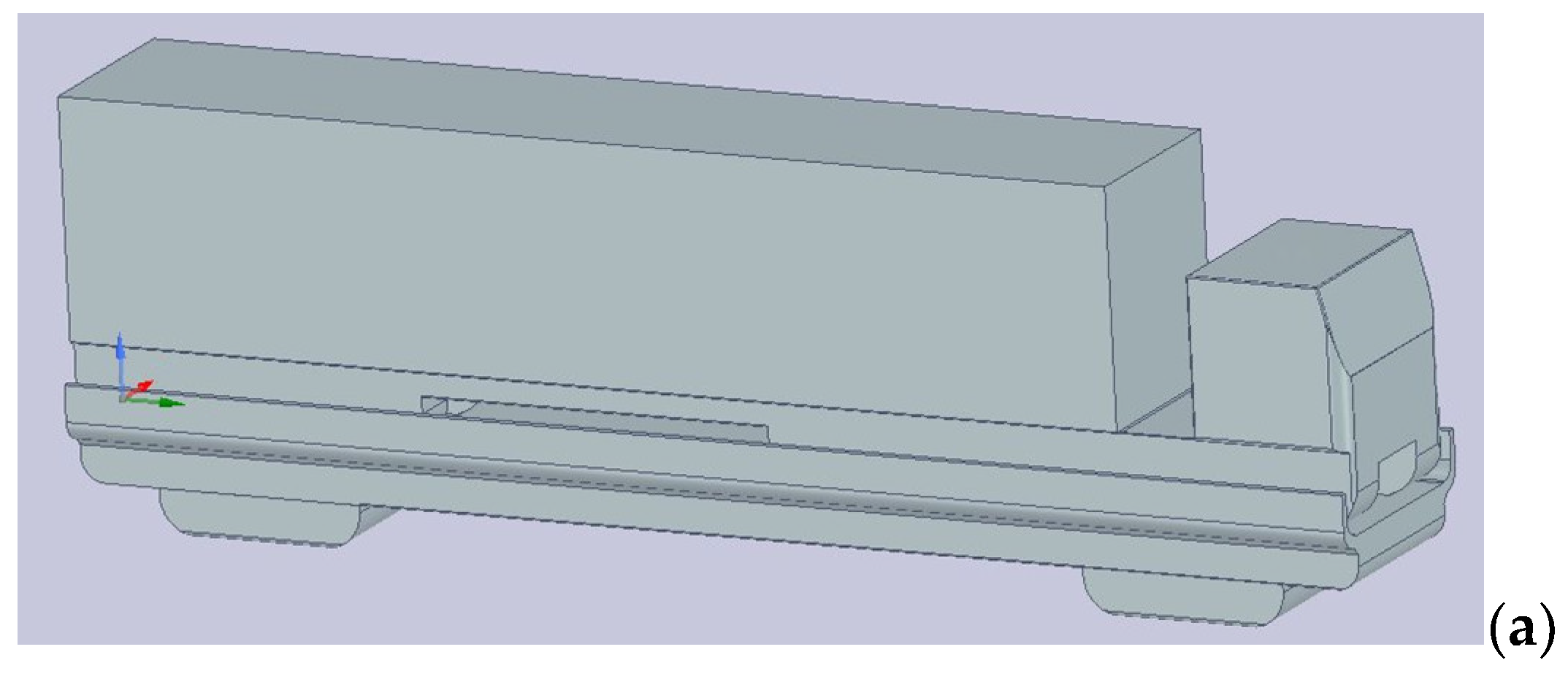
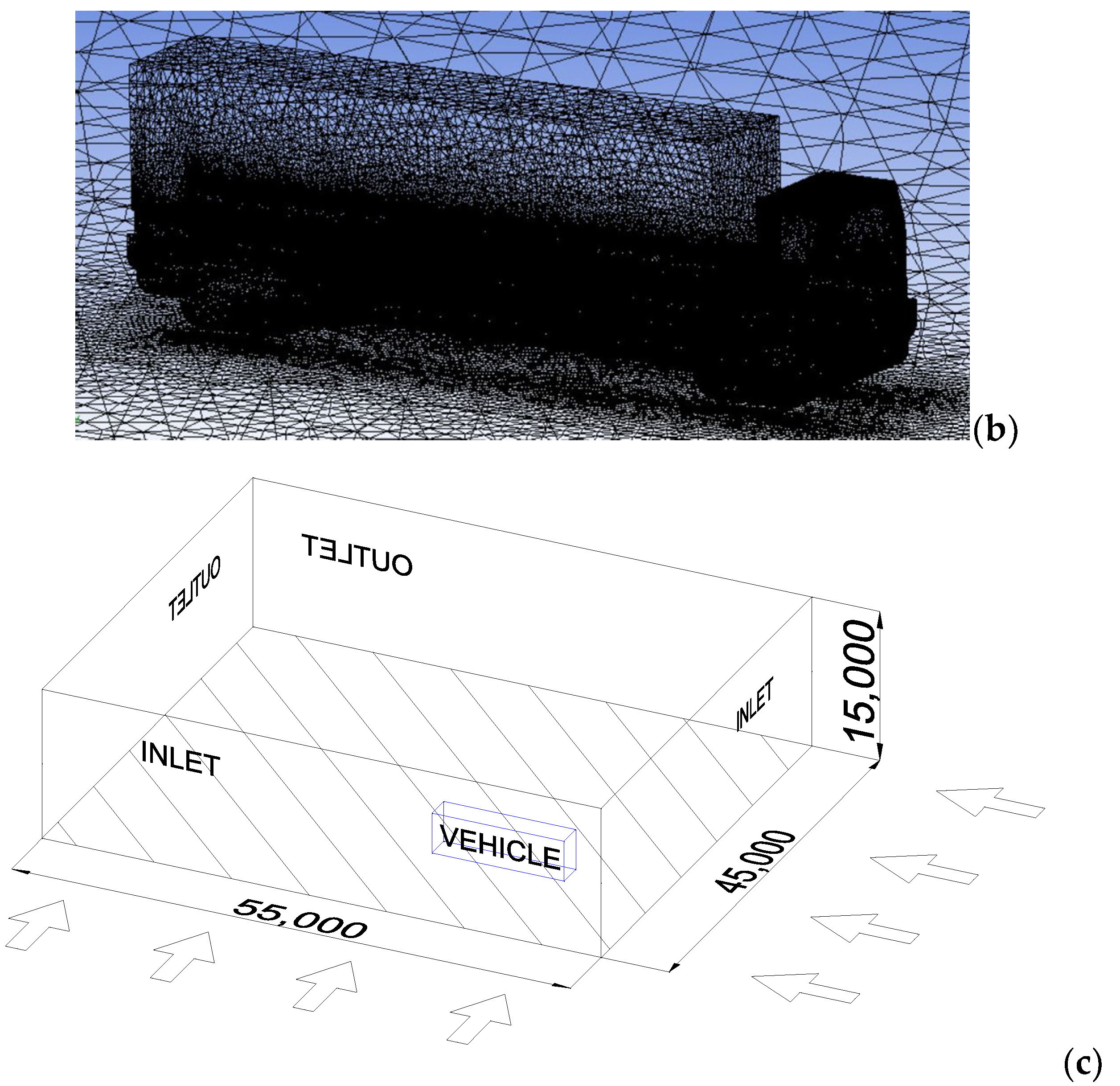
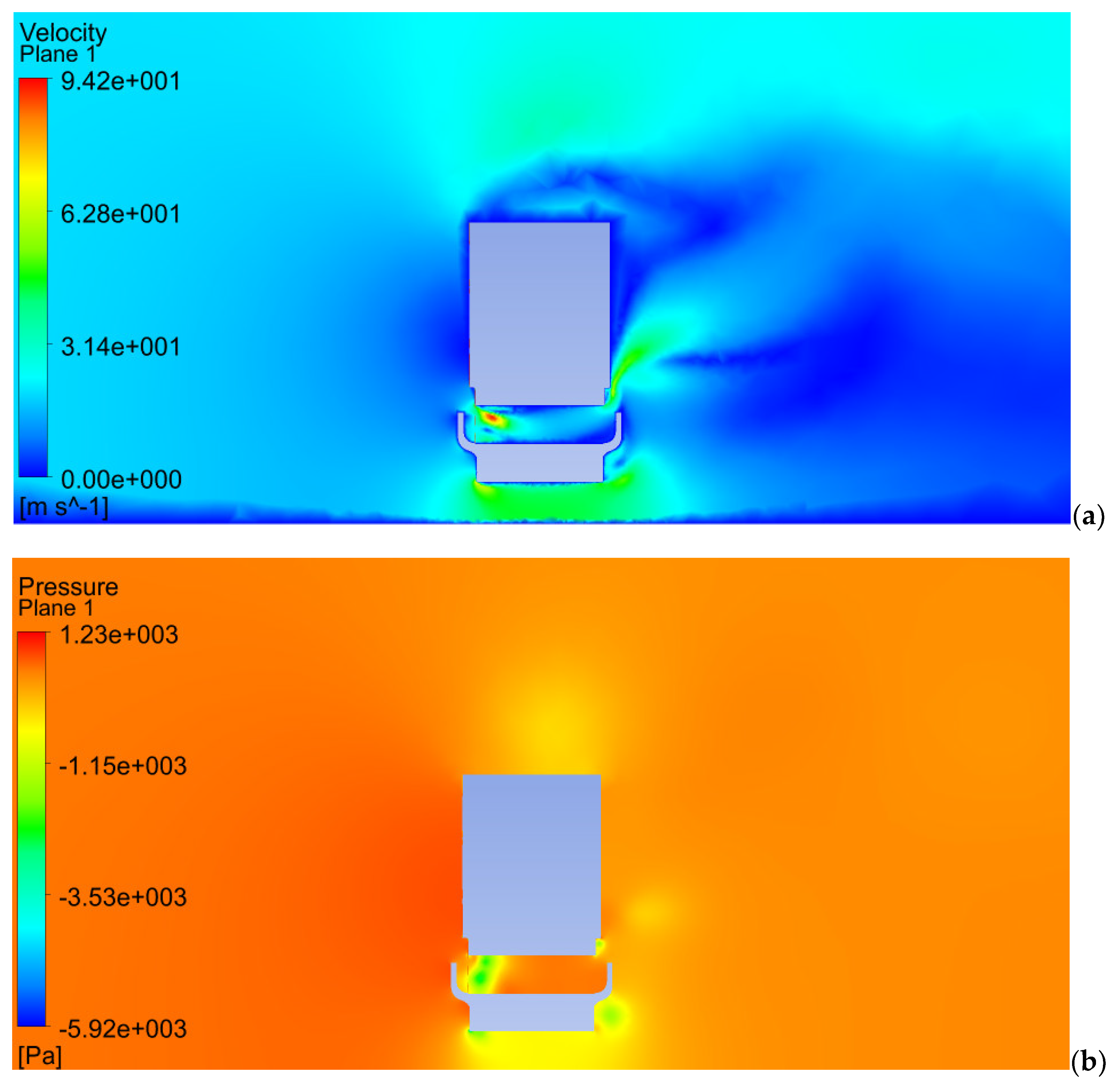
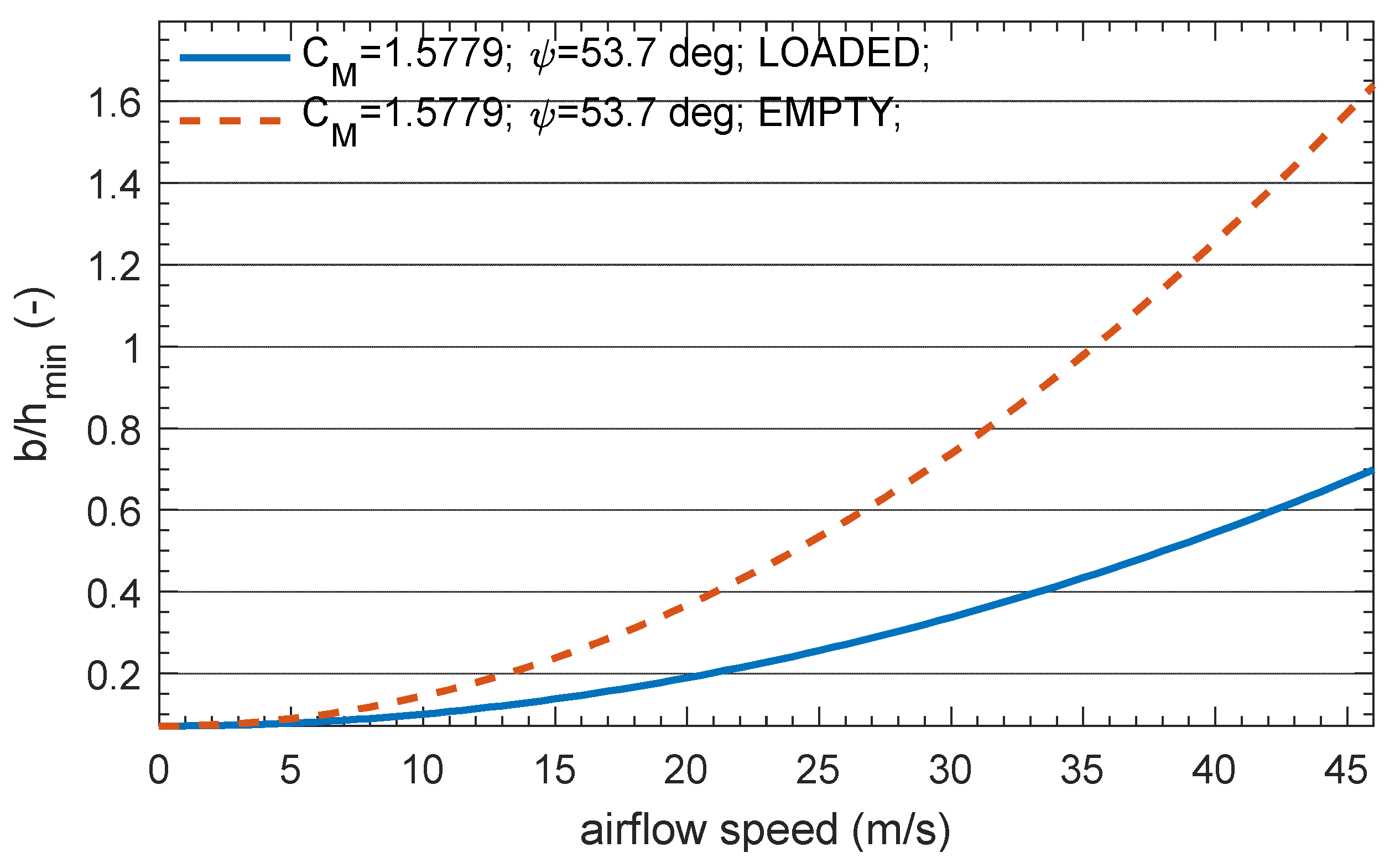
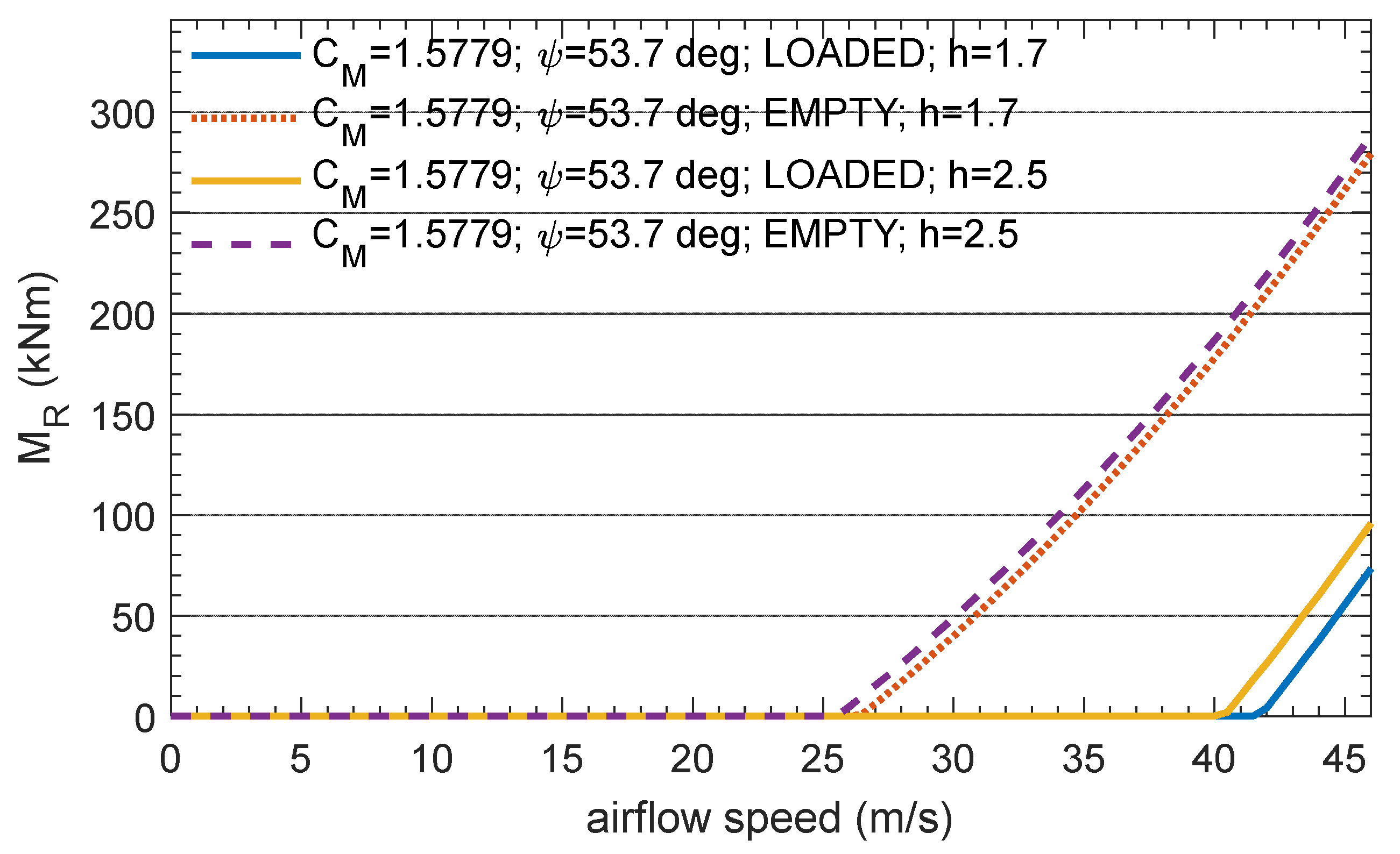
| Loading Case | N1 [kN] | N2 [kN] | N3 [kN] | N4 [kN] | N1 + N2 + N3 [kN] |
|---|---|---|---|---|---|
| Empty | 38.8 | 59.6 | 58.6 | 19.9 | 157 |
| Loaded | 44.6 | 108.3 | 219.8 | 74.5 | 372.7 |
| Values during emergency braking of the train (a = 1.5 m/s2) | N1 [kN] | N2 [kN] | N3 [kN] | N4 [kN] | N1 + N2 + N3 [kN] |
| Empty | 43.2 | 57.6 | 56.2 | 22.2 | 157 |
| Loaded | 52.2 | 109.5 | 211 | 83.3 | 372.7 |
| Load | T1 [kN] | T2 [kN] | T3 [kN] | T4 [kN] | T1 + T2 + T3 [kN] |
|---|---|---|---|---|---|
| Empty | 6.6 | 8.8 | 8.6 | 3.4 | 24 |
| Loaded | 8 | 16.7 | 32.3 | 12.7 | 57 |
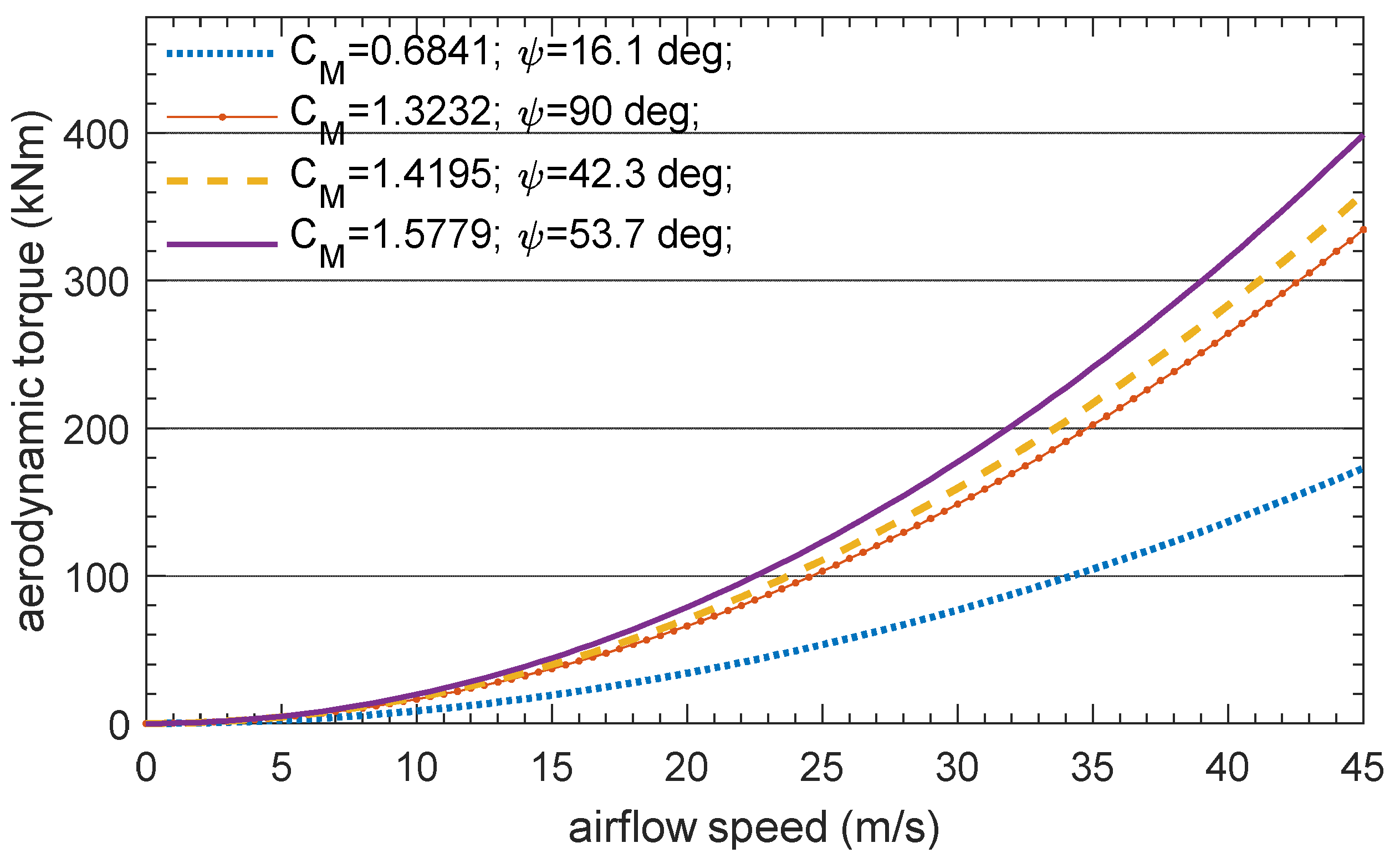
| No. | |vx| (m/s) | |vy| (m/s) | CM (−) | (kN) | (kN) | (kNm) | (kNm) | (kNm) |
|---|---|---|---|---|---|---|---|---|
| 1 | 33 | 30 | 1.419 | 154.1 | 51.2 | 352.4 | 215 | 9 |
| 2 | 33 | 20 | 1.171 | 95.8 | 29.2 | 217.8 | 80.4 | 0 |
| 3 | 33 | 10 | 0.684 | 45.3 | 12.7 | 101.5 | 0 | 0 |
| 4 | 22 | 30 | 1.5779 | 119 | 41.1 | 272.5 | 135.1 | 0 |
| 5 | 22 | 20 | 1.4190 | 68.4 | 22.9 | 156.5 | 19.2 | 0 |
| 6 | 0 | 30 | 1.323 | 64.6 | 25.9 | 148.6 | 11.3 | 0 |
| 7 | 0 | 20 | 1.322 | 28.6 | 11.6 | 66 | 0 | 0 |
| 8 | 0 | 10 | 1.316 | 71 | 3 | 16.4 | − | − |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Opala, M. Analysis of Safety Requirements for Securing the Semi-Trailer Truck on the Intermodal Railway Wagon. Energies 2021, 14, 6539. https://doi.org/10.3390/en14206539
Opala M. Analysis of Safety Requirements for Securing the Semi-Trailer Truck on the Intermodal Railway Wagon. Energies. 2021; 14(20):6539. https://doi.org/10.3390/en14206539
Chicago/Turabian StyleOpala, Michał. 2021. "Analysis of Safety Requirements for Securing the Semi-Trailer Truck on the Intermodal Railway Wagon" Energies 14, no. 20: 6539. https://doi.org/10.3390/en14206539
APA StyleOpala, M. (2021). Analysis of Safety Requirements for Securing the Semi-Trailer Truck on the Intermodal Railway Wagon. Energies, 14(20), 6539. https://doi.org/10.3390/en14206539






