Optimal Experimental Design for Inverse Identification of Conductive and Radiative Properties of Participating Medium
Abstract
:1. Introduction
2. Theory and Methods
2.1. Combined Conductive and Radiative Heat Transfer in Participating Medium
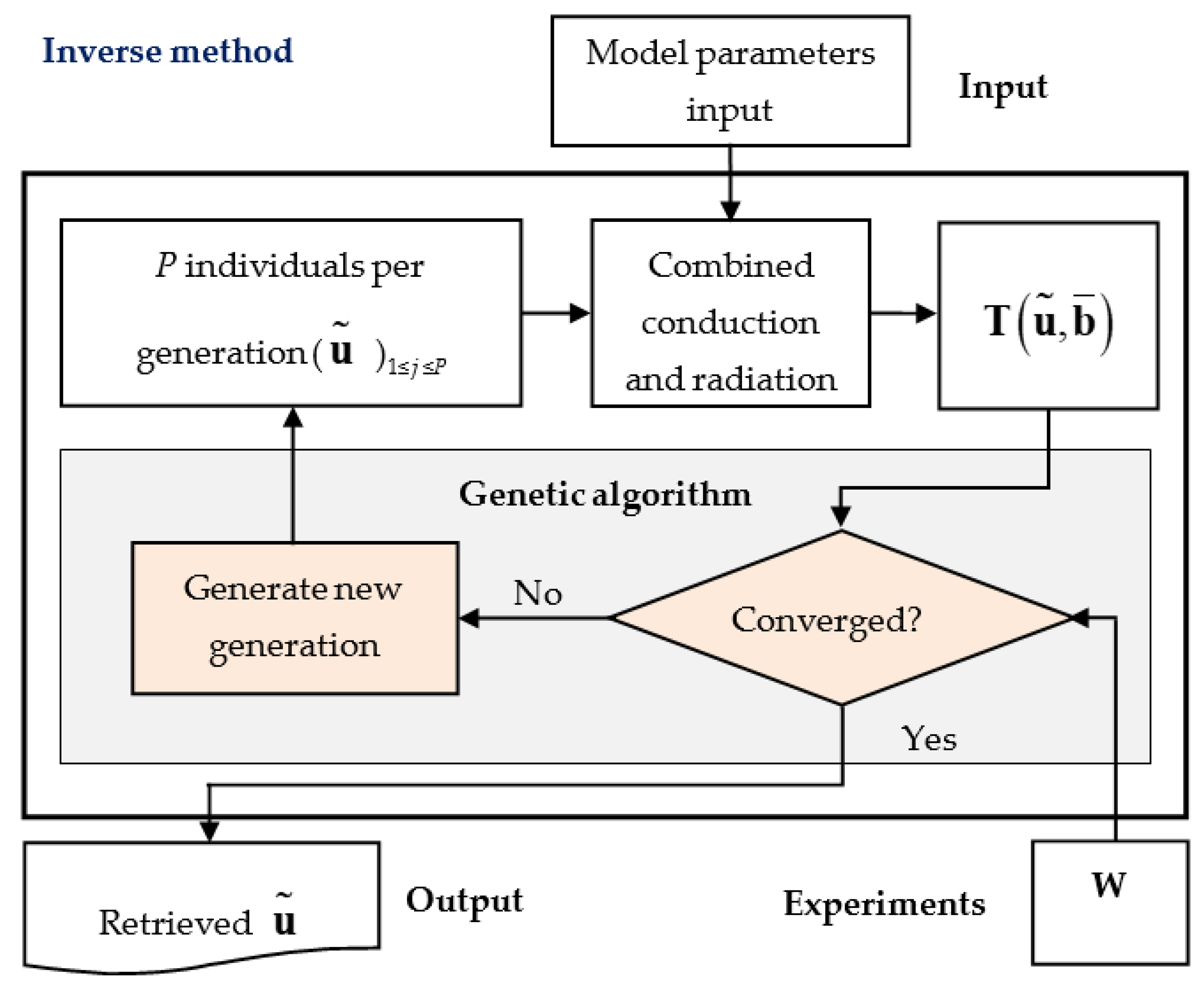
2.2. Inverse Method
2.3. Uncertainty Estimation and Design of Experiment
3. Results and Discussion
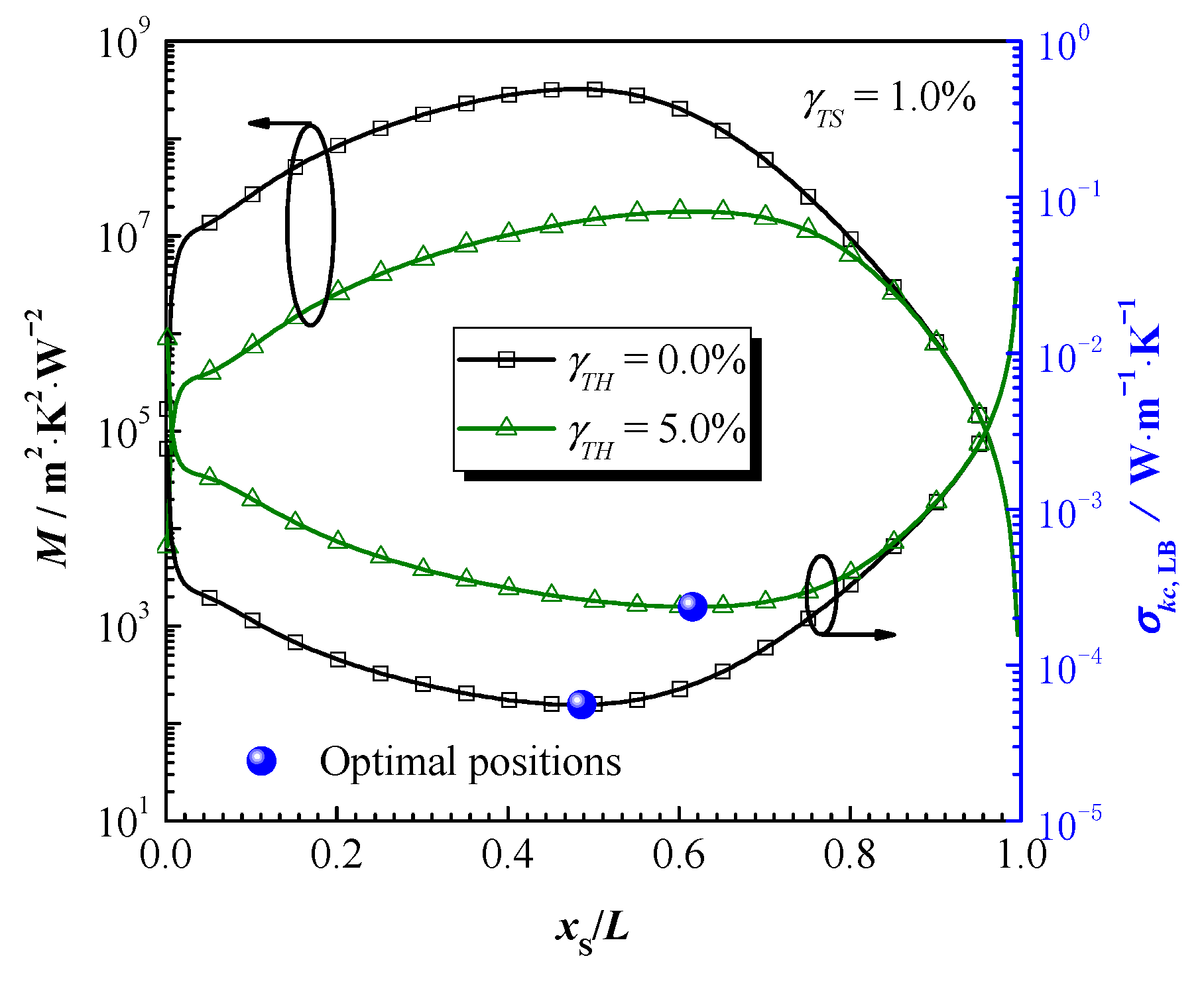
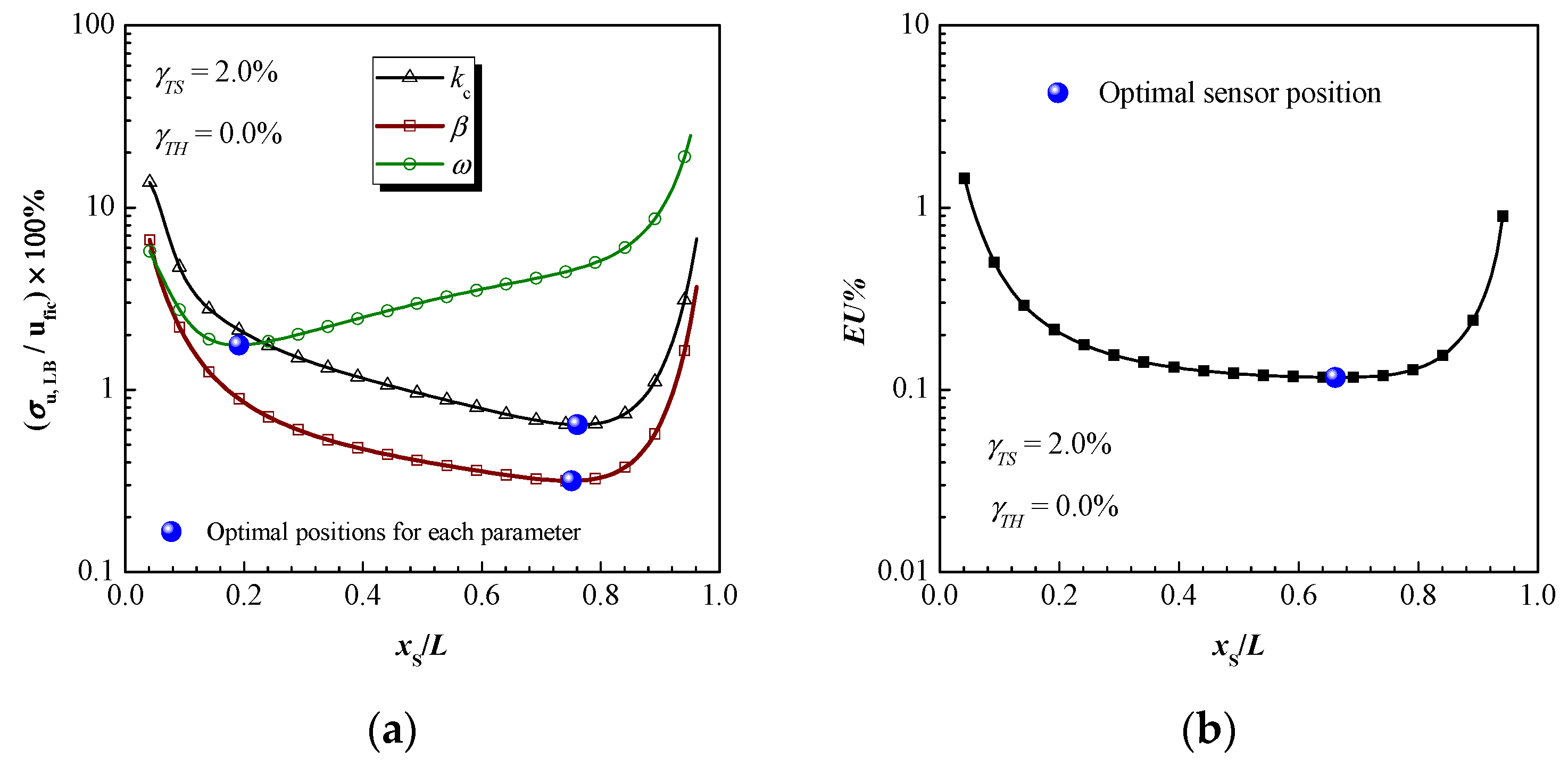
3.1. Identification of Conductive Thermal Conductivity: The Optimal Experimental Design
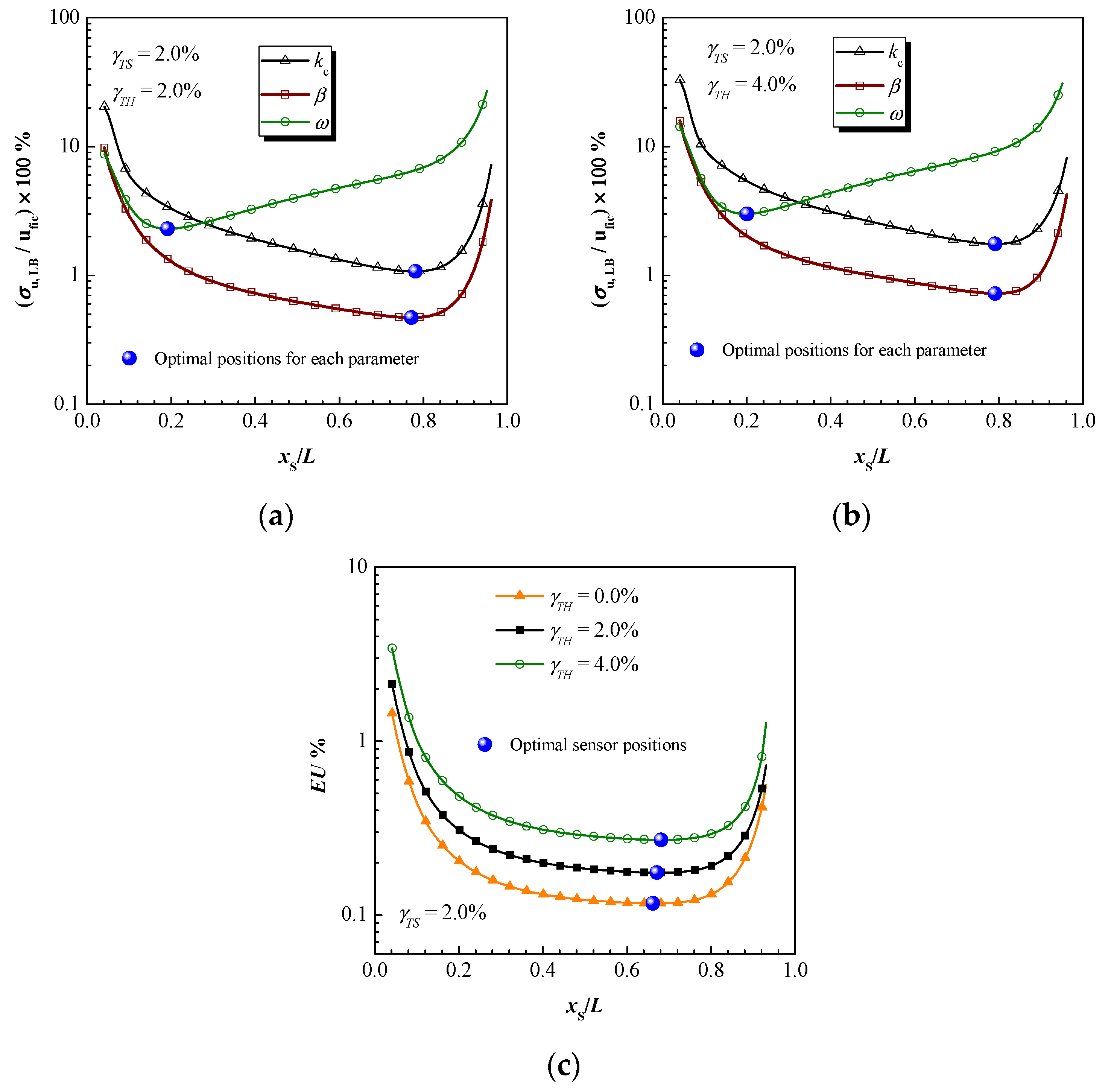
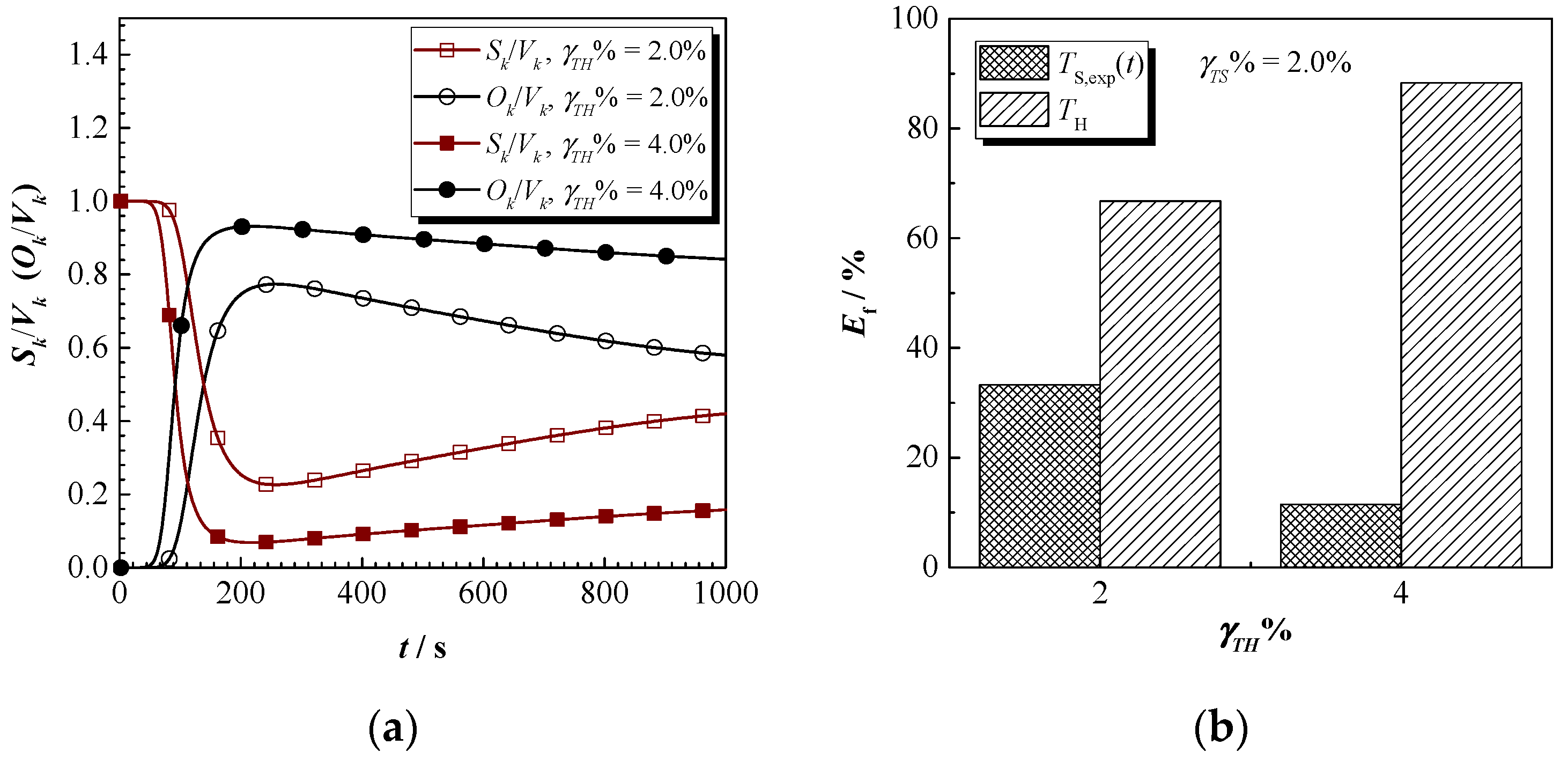
3.2. Identification of Conductive and Radiative Properties: The Optimal Experimental Design
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Coquard, R.; Rochais, D.; Baillis, D. Experimental investigations of the coupled conductive and radiative heat transfer in metallic/ceramic foams. Int. J. Heat Mass Transf. 2009, 52, 4907–4918. [Google Scholar] [CrossRef]
- Das, R.; Mishra, S.C.; Uppaluri, R. Inverse analysis applied to retrieval of parameters and reconstruction of temperature field in a transient conduction-radiation heat transfer problem involving mixed boundary conditions. Int. Commun. Heat Mass Transf. 2010, 37, 52–57. [Google Scholar] [CrossRef]
- Li, H.Y. Estimation of thermal properties in combined conduction and radiation. Int. J. Heat Mass Transf. 1999, 42, 565–572. [Google Scholar] [CrossRef]
- Zmywaczyk, J.; Koniorczyk, P. Numerical solution of inverse radiative-conductive transient heat transfer problem in a grey participating medium. Int. J. Thermophys. 2009, 30, 1438–1451. [Google Scholar] [CrossRef]
- Qi, H.; Niu, C.Y.; Gong, S.; Ren, Y.T.; Ruan, L.M. Application of the hybrid particle swarm optimization algorithms for simultaneous estimation of multi-parameters in a transient conduction-radiation problem. Int. J. Heat Mass Transf. 2015, 83, 428–440. [Google Scholar] [CrossRef]
- Braiek, A.; Adili, A.; Albouchi, F.; Karkri, M.; Nasrallah, S.B. Estimation of radiative and conductive properties of a semitransparent medium using genetic algorithms. Meas. Sci. Technol. 2016, 27, 65601. [Google Scholar] [CrossRef]
- Liu, Y.; Billaud, Y.; Saury, D.; Lemonnier, D. Simultaneous identification of thermal conductivity and absorption coefficient of a homogeneous medium. Int. Heat Transf. Conf. 2018, 8834–8841. [Google Scholar] [CrossRef]
- Lazard, M.; Andre, S.; Maillet, D.; Baillis, D.; Degiovanni, A. Flash experiment on a semitransparent material: Interest of a reduced model. Inverse Probl. Eng. 2001, 9, 413–429. [Google Scholar] [CrossRef] [Green Version]
- Zhao, S.Y.; Zhang, B.M.; Du, S.Y.; He, X.D. Inverse identification of thermal properties of fibrous insulation from transient temperature measurements. Int. J. Thermophys. 2009, 30, 2021–2035. [Google Scholar] [CrossRef]
- Zhao, S.; Sun, X.; Li, Z.; Xie, W.; Meng, S.; Wang, C.; Zhang, W. Simultaneous retrieval of high temperature thermal conductivities, anisotropic radiative properties, and thermal contact resistance for ceramic foams. Appl. Therm. Eng. 2019, 146, 569–576. [Google Scholar] [CrossRef]
- Sun, K.K.; Jung, B.S.; Kim, H.J.; Lee, W.I. Inverse estimation of thermophysical properties for anisotropic composite. Exp. Therm. Fluid Sci. 2003, 27, 697–704. [Google Scholar]
- Sawaf, B.; Ozisik, M.N.; Jarny, Y. An inverse analysis to estimate linearly temperature dependent thermal conductivity components and heat capacity of an orthotropic medium. Int. J. Heat Mass Transf. 1995, 38, 3005–3010. [Google Scholar] [CrossRef]
- Neto, A.J.S.; Özişik, M.N. An inverse problem of simultaneous estimation of radiation phase function, albedo and optical thickness. J. Quant. Spectrosc. Radiat. Transf. 1995, 53, 397–409. [Google Scholar] [CrossRef]
- Lazard, M.; André, S.; Maillet, D.; Degiovanni, A. Radiative and conductive heat transfer: A coupled model for parameter estimation. High Temp.-High Press. 2000, 32, 9–17. [Google Scholar] [CrossRef]
- Fadale, T.D.; Nenarokomov, A.V.; Emery, A.F. Uncertainties in parameter estimation: The inverse problem. Int. J. Heat Mass Transf. 1995, 38, 511–518. [Google Scholar] [CrossRef]
- Fadale, T.D.; Nenarokomov, A.V.; Emery, A.F. Two approaches to optimal sensor locations. J. Heat Transf. 1995, 117, 373–379. [Google Scholar] [CrossRef]
- Emery, A.F.; Nenarokomov, A.V.; Fadale, T.D. Uncertainties in parameter Estimation: The optimal experiment design. Int. J. Heat Mass Transf. 2000, 43, 3331–3339. [Google Scholar] [CrossRef]
- Skog, I.; Nilsson, J.O.; Händel, P.; Nehorai, A. Inertial sensor arrays, Maximum Likelihood, and Cramér-Rao bound. IEEE Trans. Signal Process. 2016, 64, 4218–4227. [Google Scholar] [CrossRef] [Green Version]
- Radich, B.M.; Buckley, K.M. EEG dipole localization bounds and MAP algorithms for head models with parameter uncertainties. IEEE Trans. BioMed. Eng. 1995, 42, 233–241. [Google Scholar] [CrossRef]
- Abdallh, A.A.; Crevecoeur, G.; Dupré, L. Optimal needle placement for the accurate magnetic material quantification based on uncertainty analysis in the inverse approach. Meas. Sci. Technol. 2010, 21, 115703. [Google Scholar] [CrossRef]
- Abdallh, A.A.; Crevecoeur, G.; Dupré, L. A priori experimental design for inverse identification of magnetic material properties of an electromagnetic device using uncertainty analysis. Compel-Int. J. Comput. Math. Electr. Electron. Eng. 2012, 31, 972–984. [Google Scholar] [CrossRef] [Green Version]
- Abdallh, A.A.; Crevecoeur, G.; Dupré, L. Selection of measurement modality for magnetic material characterization of an electromagnetic device using stochastic uncertainty analysis. IEEE Trans. Magn. 2011, 47, 4564–4573. [Google Scholar] [CrossRef]
- Modest, M.F. Radiative Heat Transfer; Academic Press: San Diego, CA, USA, 2003. [Google Scholar]
- Howell, J.R.; Siegel, R.; Mengüç, M.P. Thermal Radiation Heat Transfer; Taylor and Francis: New York, NY, USA, 2011. [Google Scholar]
- Czél, B.; Gróf, G. Genetic algorithm-based method for determination of temperature-dependent thermophysical properties. Int. J. Thermophys. 2009, 30, 1975–1991. [Google Scholar] [CrossRef]
- Czél, B.; Gróf, G. Inverse identification of temperature-dependent thermal conductivity via genetic algorithm with cost function-based rearrangement of genes. Int. J. Heat Mass Transf. 2012, 55, 4254–4263. [Google Scholar] [CrossRef]
- Czél, B.; Gróf, G. Simultaneous identification of temperature-dependent thermal properties via enhanced genetic algorithm. Int. J. Thermophys. 2012, 33, 1023–1041. [Google Scholar] [CrossRef]




| Sensor Position | Standard Deviation of Thermal Conductivity, W/(m∙K) | |||
|---|---|---|---|---|
| = 0% and = 1% | ||||
| CRB | MC | CRB | MC | |
| xs/L = 0.5 | 0.55 × 10−4 | 1.0 × 10−4 | 2.6 × 10−4 | 5.2 × 10−4 |
| xs/L = 0.6 | 0.70 × 10−4 | 1.3 × 10−4 | 2.4 × 10−4 | 4.1 × 10−4 |
| xs/L = 0.9 | 11.1 × 10−4 | 18.7 × 10−4 | 11.2 × 10−4 | 19.3 × 10−4 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Chen, X.; Chen, Z.; Wei, C.; Chen, Z.; Wang, J.; Duan, Y.; Ren, N.; Li, J.; Zhang, X. Optimal Experimental Design for Inverse Identification of Conductive and Radiative Properties of Participating Medium. Energies 2021, 14, 6593. https://doi.org/10.3390/en14206593
Liu H, Chen X, Chen Z, Wei C, Chen Z, Wang J, Duan Y, Ren N, Li J, Zhang X. Optimal Experimental Design for Inverse Identification of Conductive and Radiative Properties of Participating Medium. Energies. 2021; 14(20):6593. https://doi.org/10.3390/en14206593
Chicago/Turabian StyleLiu, Hua, Xue Chen, Zhongcan Chen, Caobing Wei, Zuo Chen, Jiang Wang, Yanjun Duan, Nan Ren, Jian Li, and Xingzhou Zhang. 2021. "Optimal Experimental Design for Inverse Identification of Conductive and Radiative Properties of Participating Medium" Energies 14, no. 20: 6593. https://doi.org/10.3390/en14206593





