The Effect of Crankshaft Phasing and Port Timing Asymmetry on Opposed-Piston Engine Thermal Efficiency
Abstract
:1. Introduction
1.1. Context
1.2. Review of Range Extender Engines
1.3. Scavenging in OP2S Engines
1.4. Research Aim
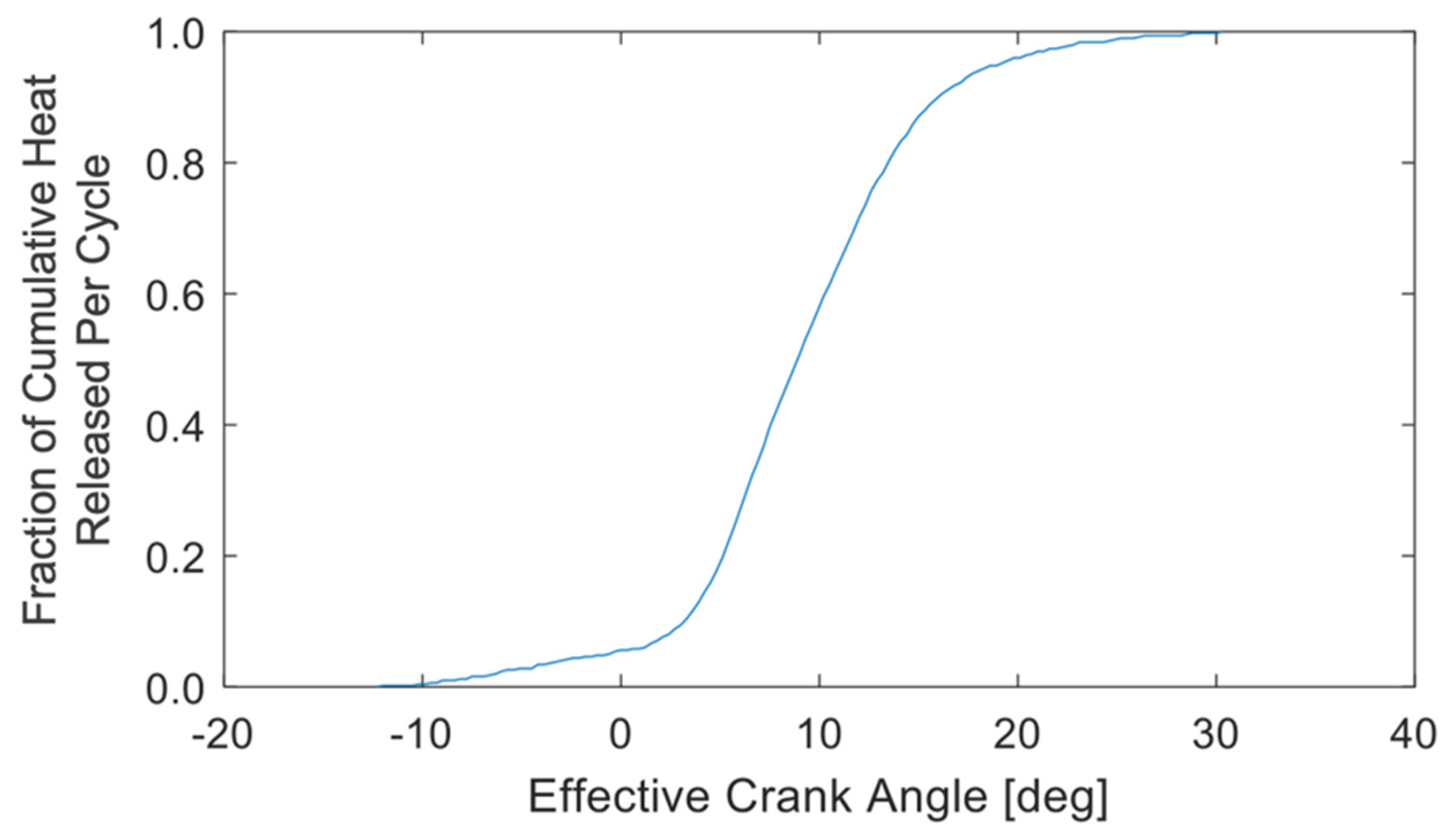
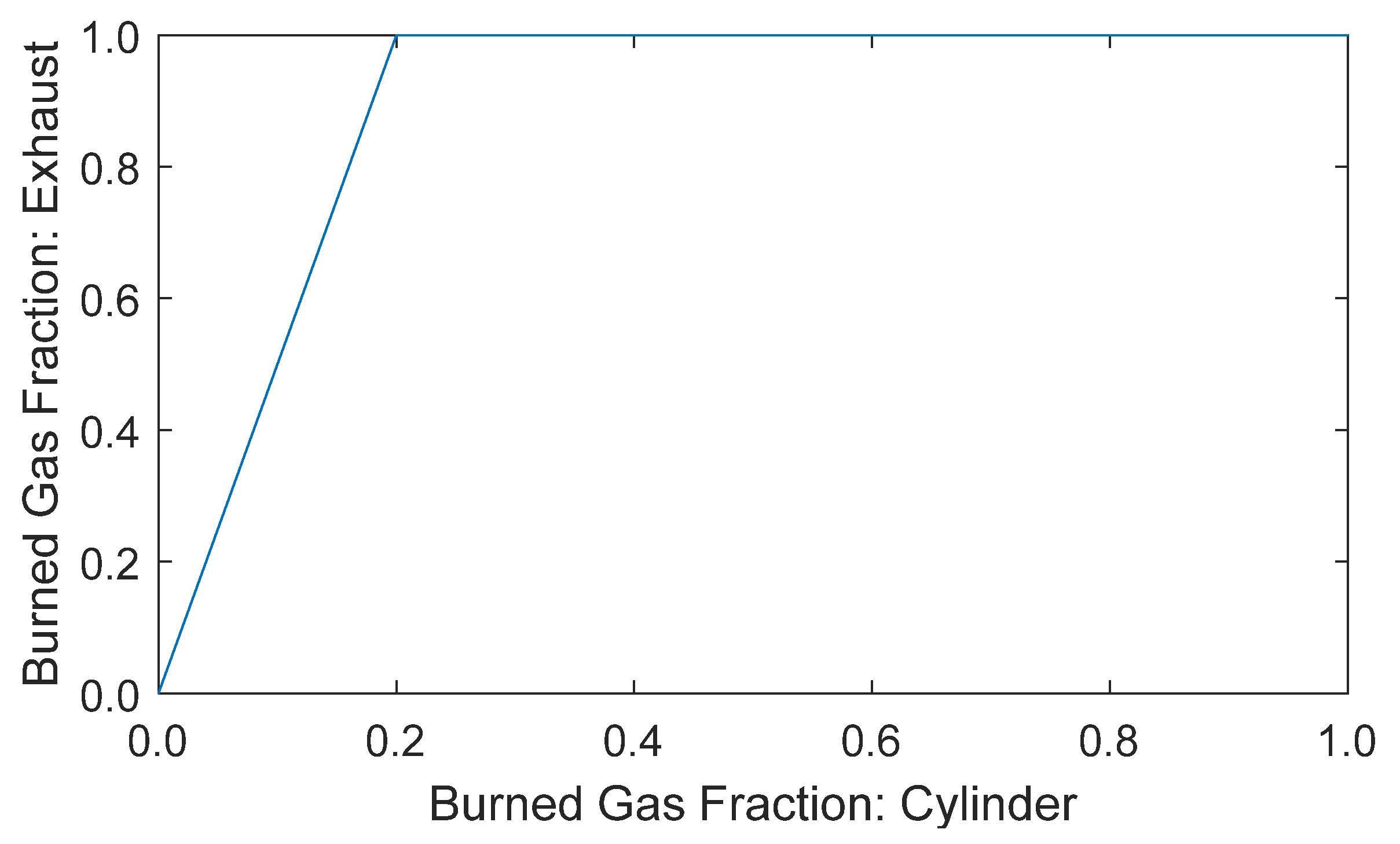
2. Method
2.1. OP2S Engine Model
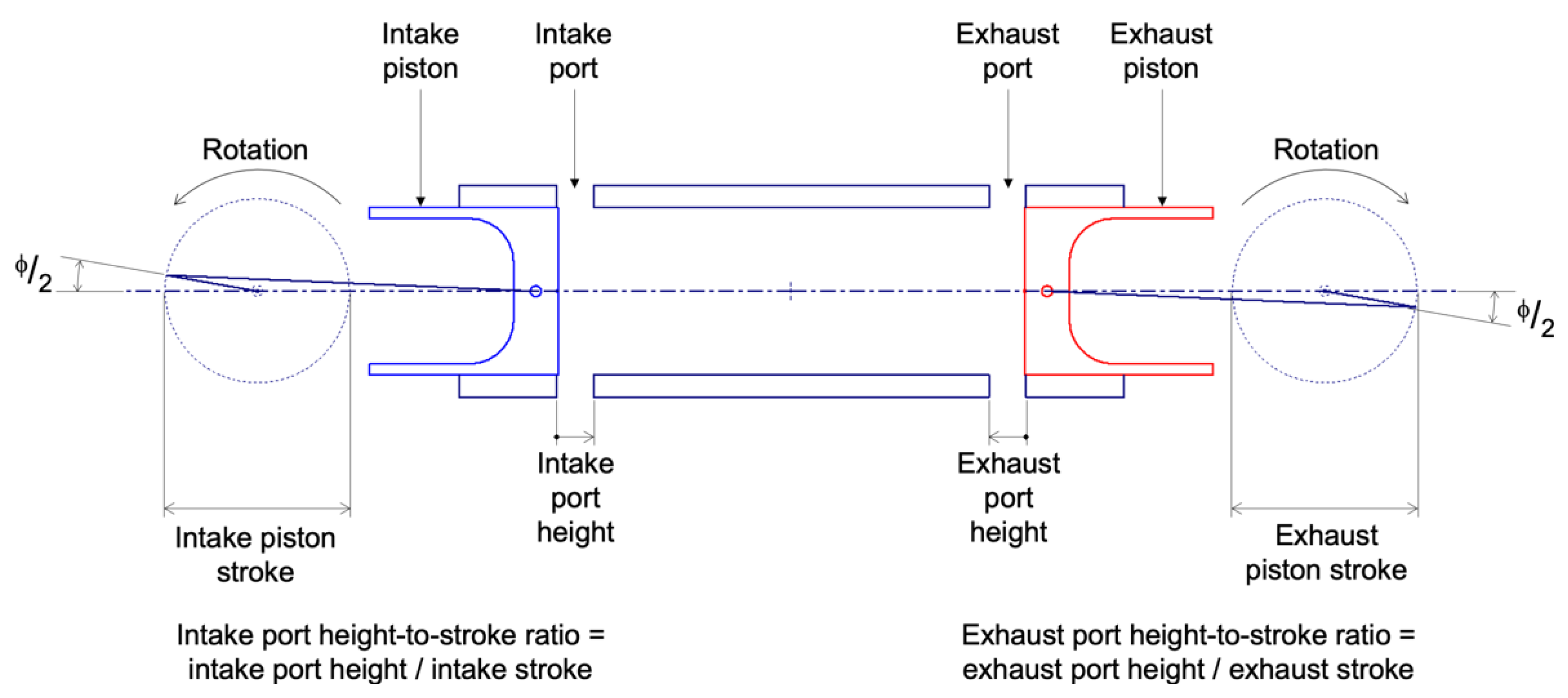
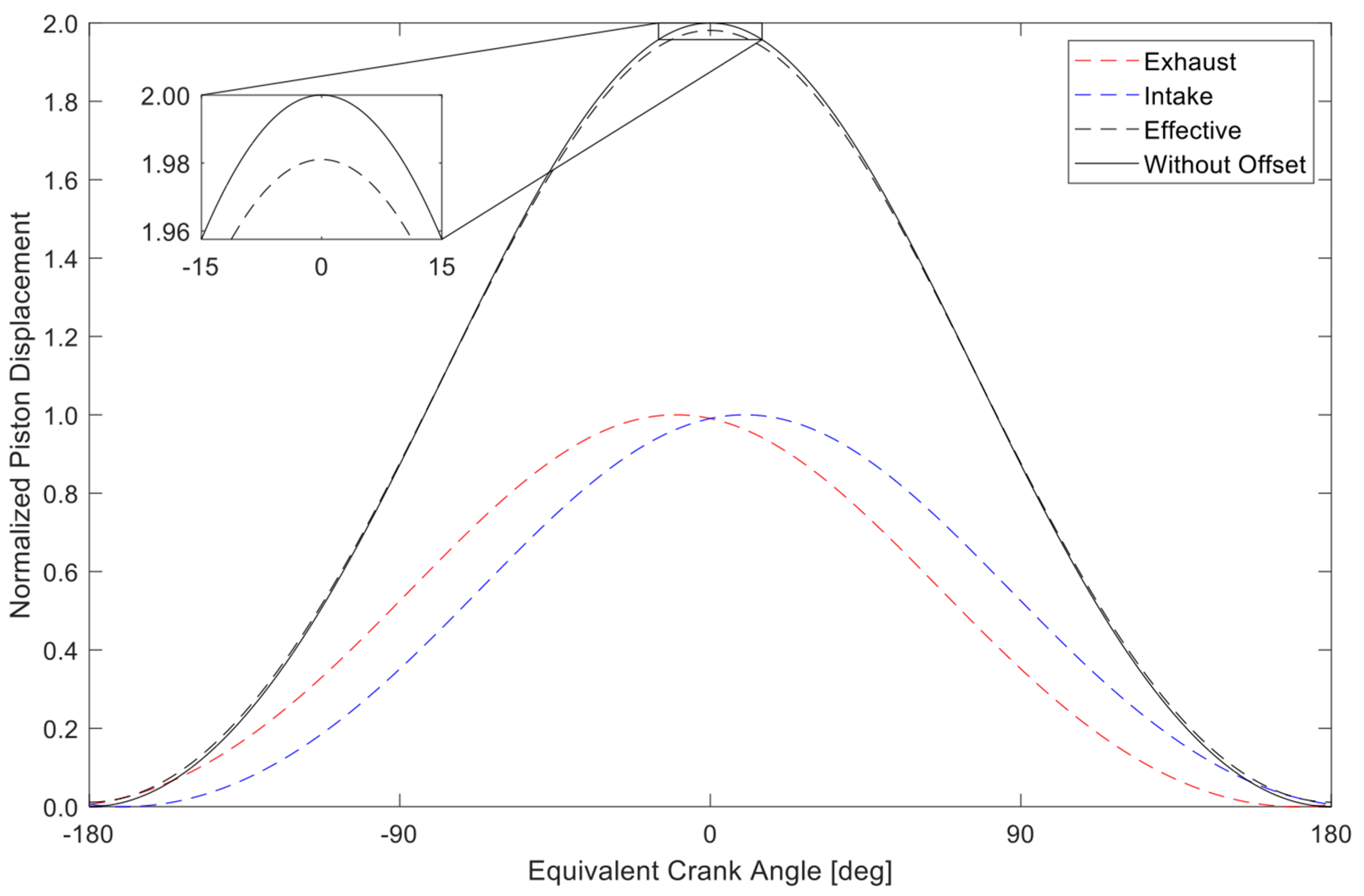
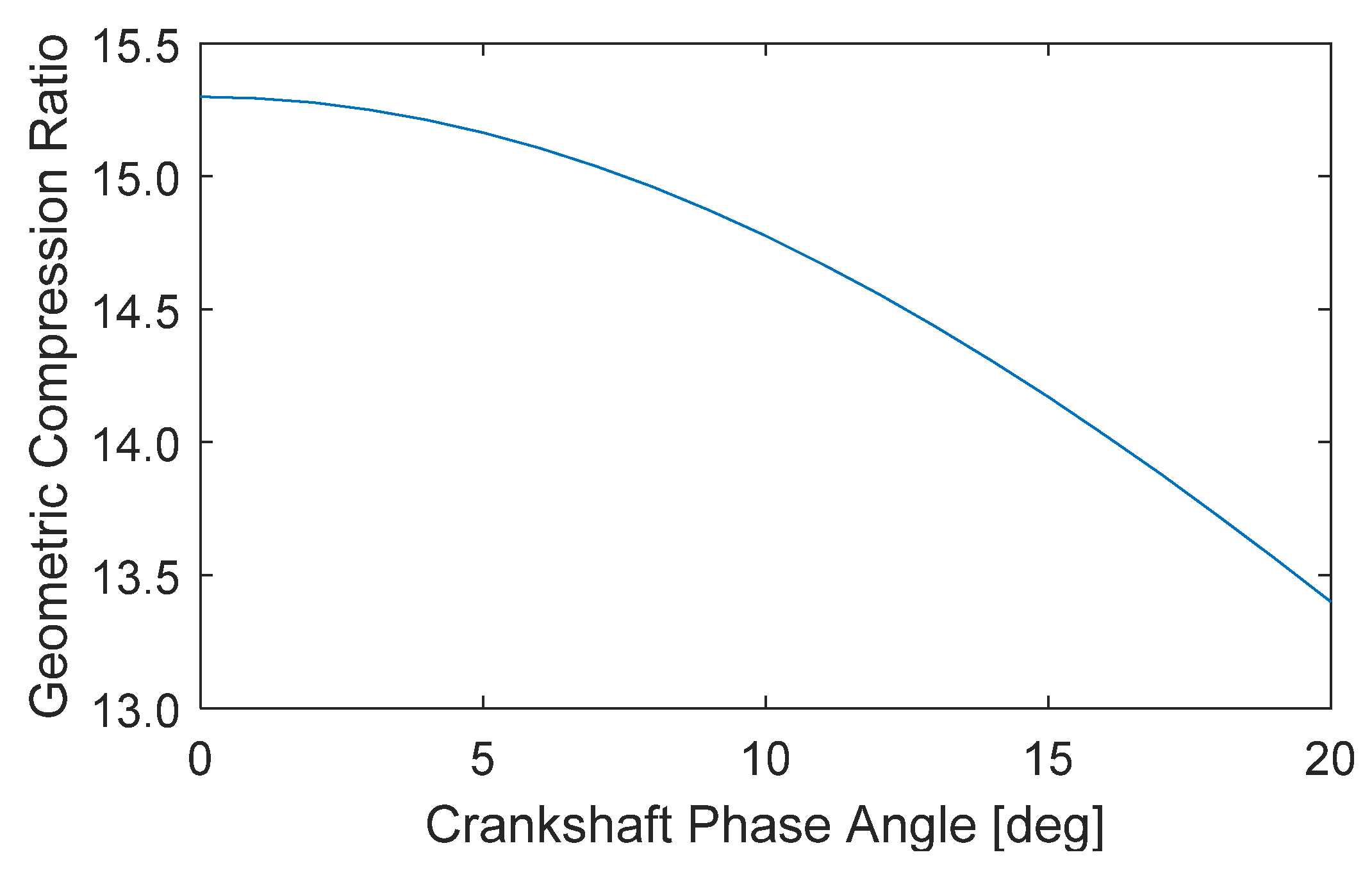
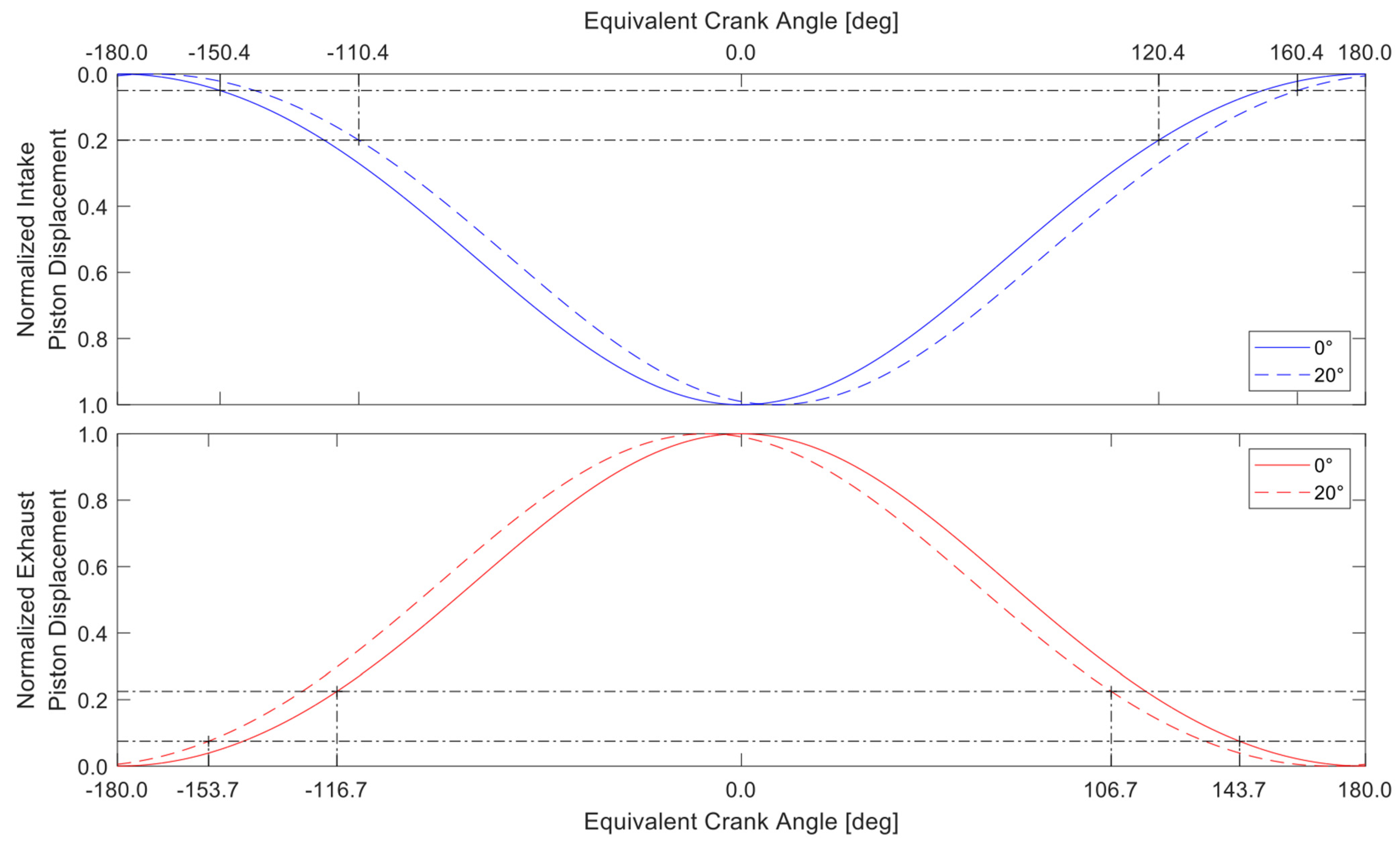
2.2. OP2S Geometry
2.3. Design of Experiment
3. Results and Discussion
3.1. Medium-Duty Application
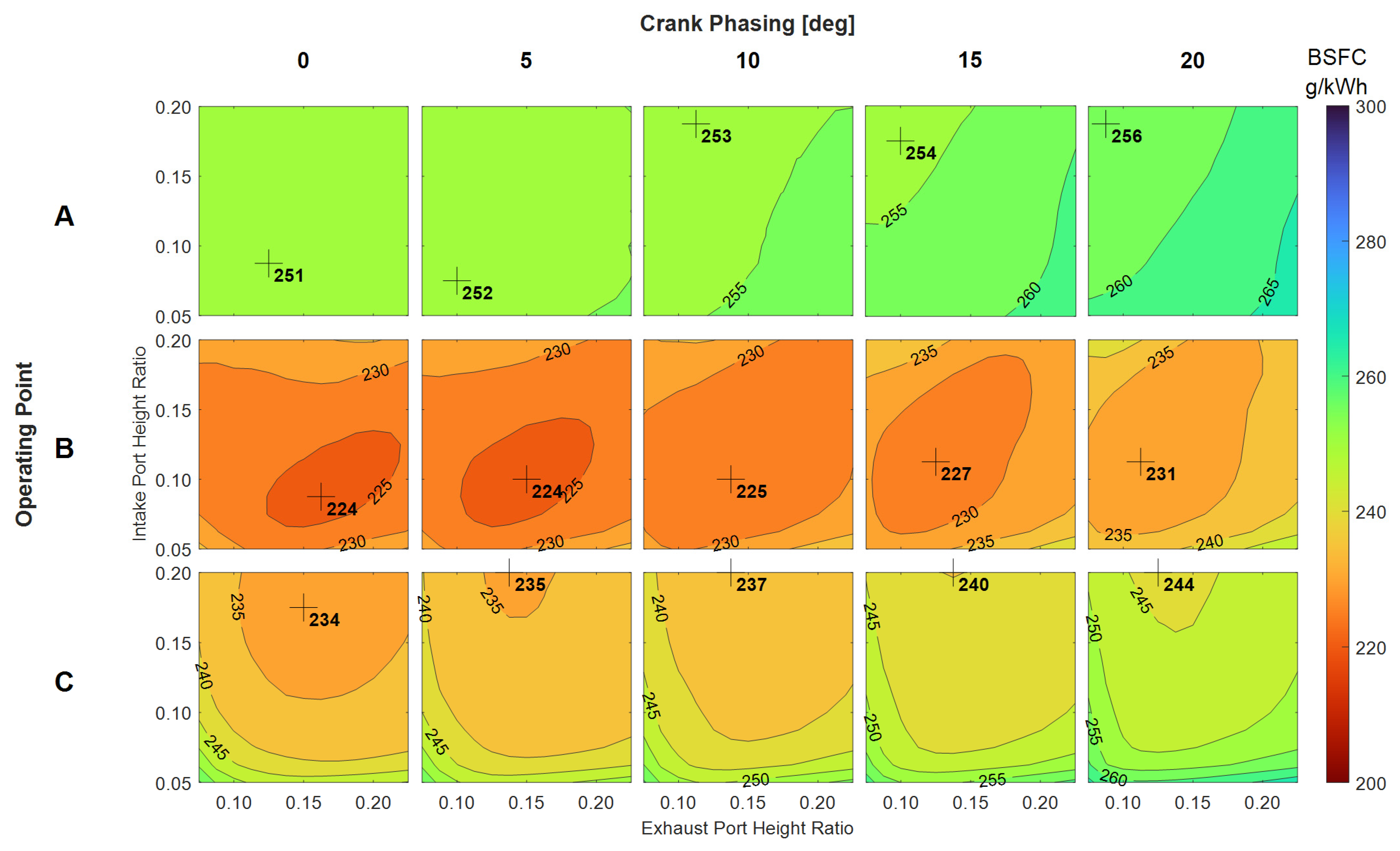
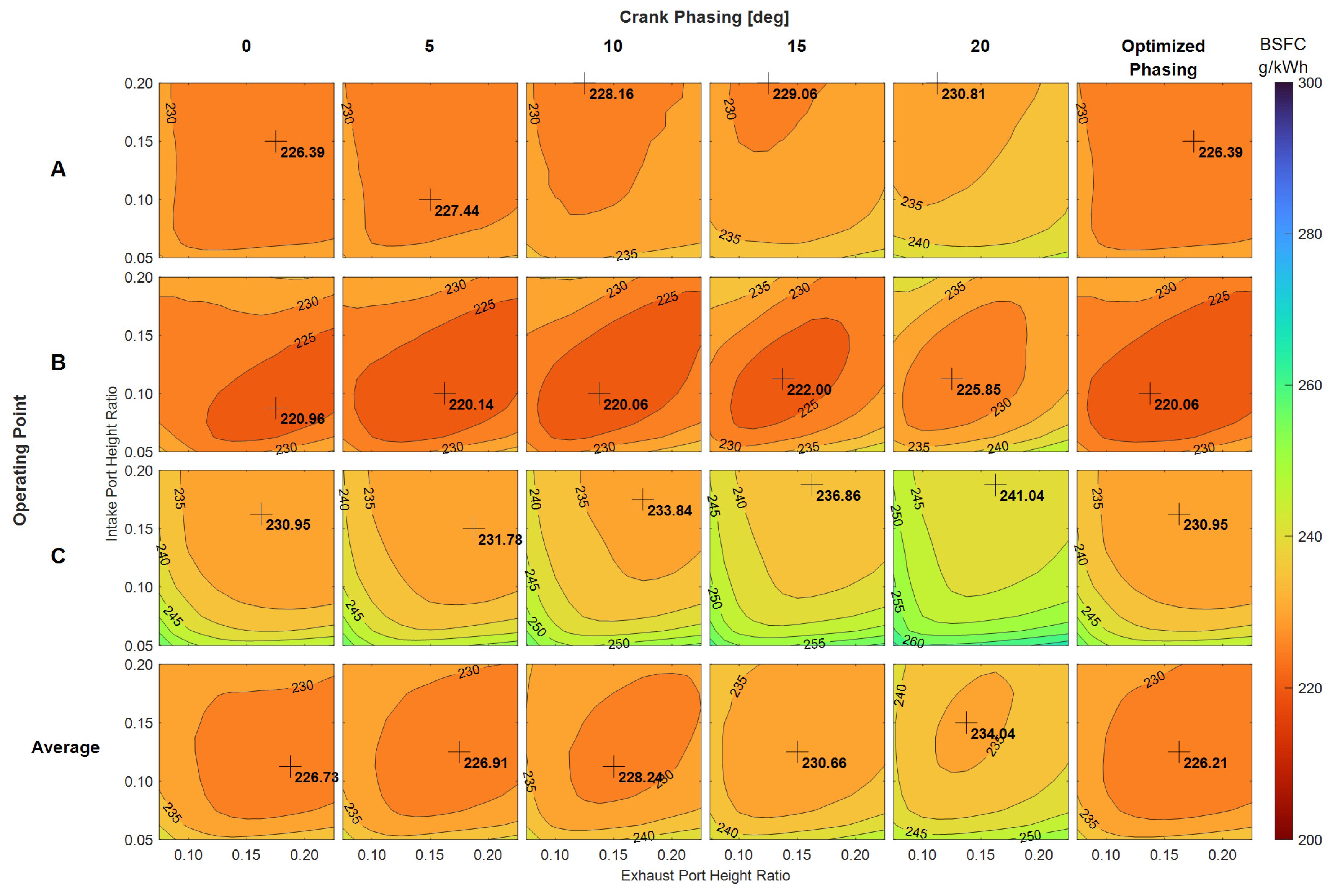
3.1.1. Effect of Crankshaft Phasing and Port Height on BSFC for Stoichiometric Operation
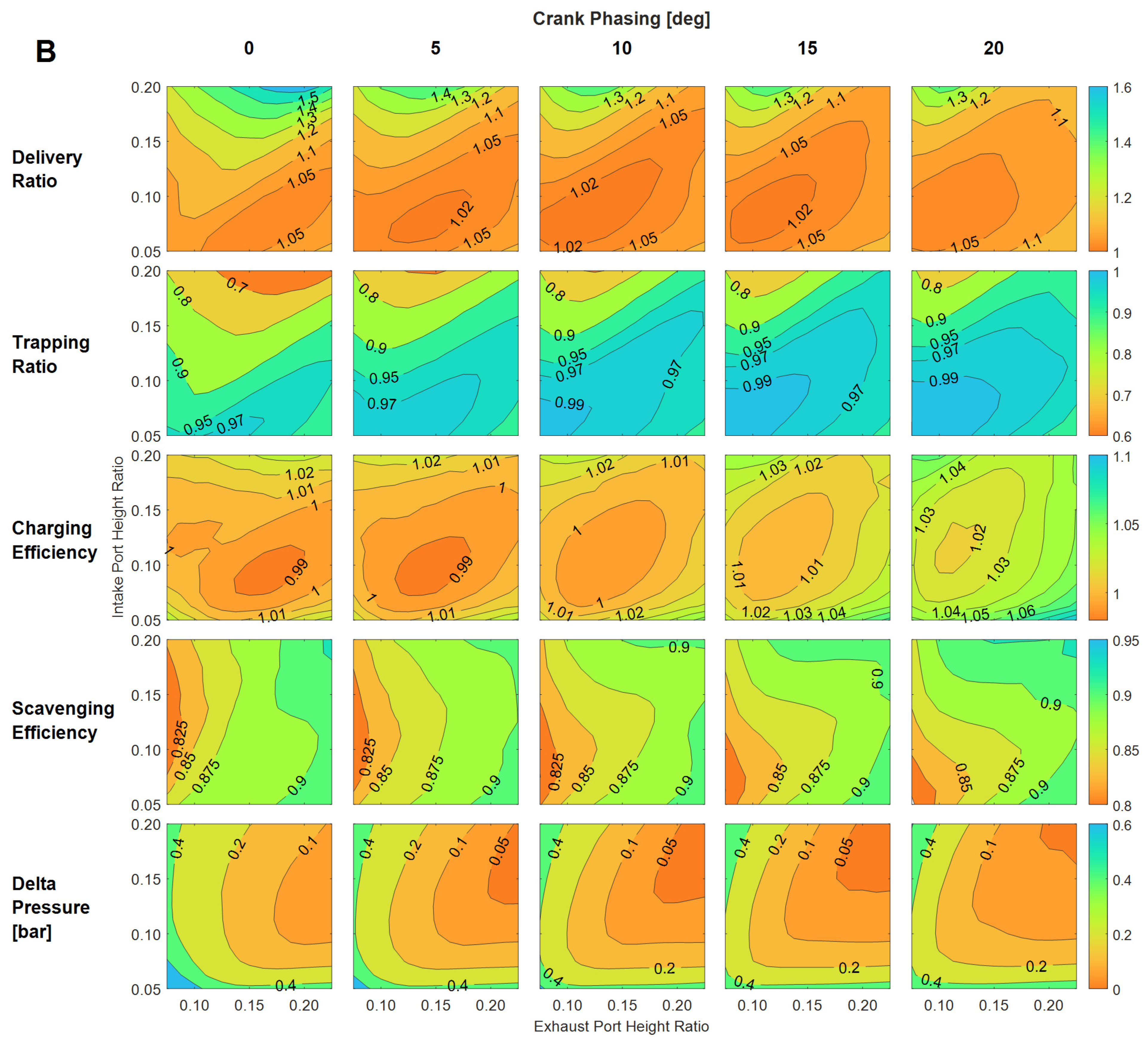
3.1.2. Examining the Effect of Crankshaft Phasing and Port Height on Gas Exchange
3.1.3. Effect of Crankshaft Phasing and Port Height on BSFC under Lean Conditions
3.1.4. Effect of Crankshaft Phasing and Port Height on BSFC for Optimal λ Conditions
3.1.5. Optimal Port Height-To-Stroke Ratios for Medium-Duty Truck Applications
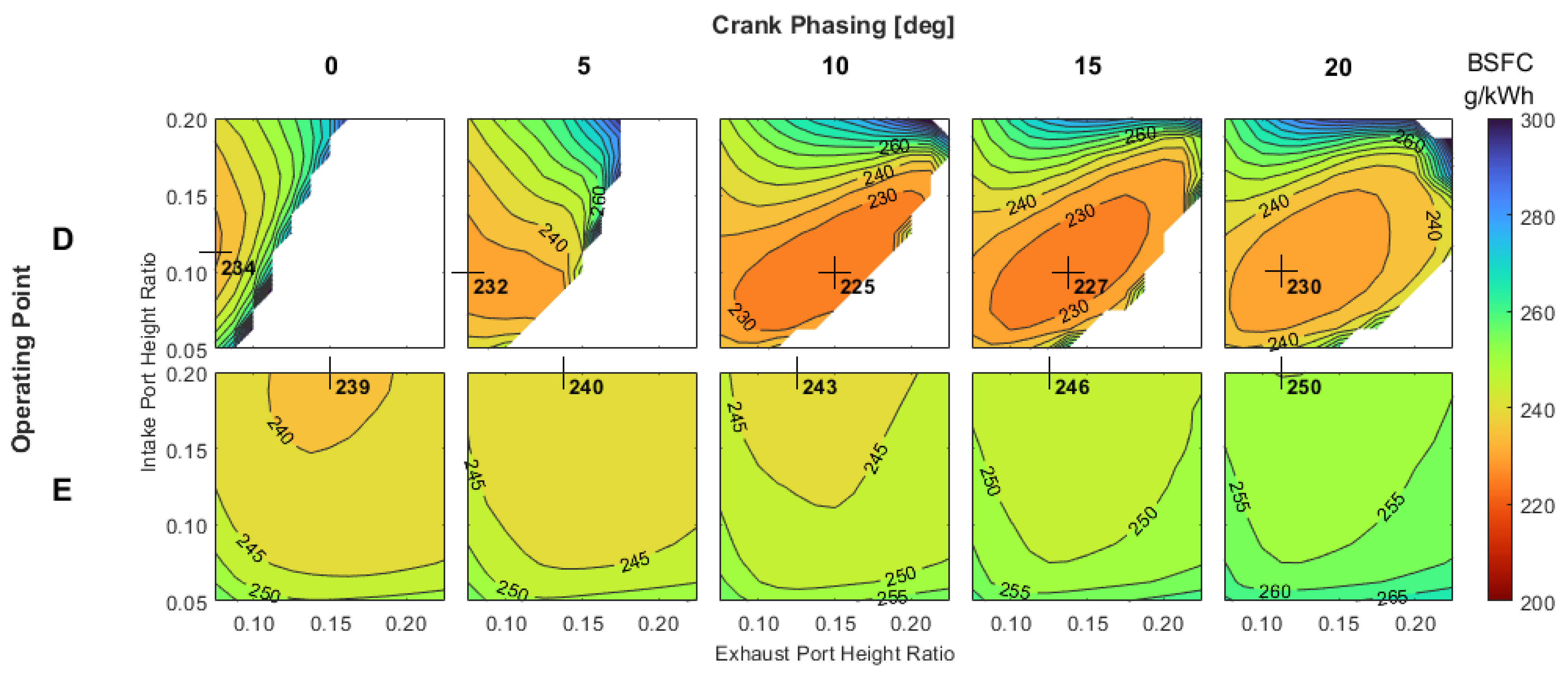
3.2. Range Extender Application
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Nomenclature
| Greek symbols | |
| ϕ | Crankshaft phase angle |
| λ | Air-to-fuel equivalence ratio |
Abbreviations
| 2S-ROPE | Two-Stroke Rodless Opposed Piston Engine |
| BMEP | Brake Mean Effective Pressure |
| BSFC | Brake Specific Fuel Consumption |
| C | Compressor |
| CAC | Charge Air Cooler |
| CFD | Computational Fluid Dynamics |
| EAT | Exhaust Aftertreatment |
| EM | Electric Machine |
| EU | European Union |
| EV | Electric Vehicle |
| FMEP | Friction Mean Effective Pressure |
| FPEG | Free Piston Engine Generator |
| GCI | Gasoline Compression Ignition |
| GDP | Gross Domestic Product |
| GHG | Greenhouse Gas |
| HCCI | Homogeneous Charge Compression Ignition |
| ICE | Internal Combustion Engine |
| NA | Naturally Aspirated |
| NVH | Noise, Vibration, Harshness |
| OP2S | Opposed-Piston Two-Stroke |
| REEV | Range-Extended Electric Vehicle |
References
- Sims, R.; Schaeffer, R.; Creutzig, F.; Cruz-Núñez, X.; D’Agosto, M.; Dimitriu, D.; Figueroa Meza, M.J.; Fulton, L.; Kobayashi, S.; Lah, O.; et al. Transport. In Climate Change 2014: Mitigation of Climate Change. Contribution of Working Group III to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- Advanced Propulsion Centre. Light Duty Vehicle <3.5 t—Propulsion Technologies Roadmap; Automotive Council UK and Advanced Propulsion Centre UK 2020 Product Roadmaps. Available online: https://www.apcuk.co.uk/product-roadmaps (accessed on 5 July 2021).
- Mock, P.; Diaz, S. European Vehicle Market. Statistics—Pocketbook 2020/21; International Council on Clean Transportation Europe: Berlin, Germany, 2020; Available online: http://eupocketbook.theicct.org/ (accessed on 5 July 2021).
- Weymar, E.; Finkbeiner, M. Statistical analysis of empirical lifetime mileage data for automotive LCA. Int. J. Life Cycle Assess. 2016, 21, 215–223. [Google Scholar] [CrossRef]
- Turner, J.; Blake, D.; Moore, J.; Burke, P.; Pearson, R.; Patel, R.; Blundell, D.; Chandrashekar, R.; Matteucci, L.; Barker, P.; et al. The Lotus Range Extender Engine; SAE Technical Paper 2010-01-2208; SAE International: Detroit, MI, USA, 2010. [Google Scholar] [CrossRef]
- Bassett, M.; Hall, J.; OudeNijeweme, D.; Darkes, D.; Bisordi, A.; Warth, M. The Development of a Dedicated Range Extender Engine; SAE Technical Paper 2012-01-1002; SAE International: Detroit, MI, USA, 2012. [Google Scholar] [CrossRef] [Green Version]
- Bassett, M.; Hall, J.; Warth, M. Development of a Dedicated Range Extender Unit and Demonstration Vehicle. In Proceedings of the EVS27 International Battery, Hybrid and Fuel Cell Electric Vehicle Symposium, Barcelona, Spain, 17–20 November 2013. [Google Scholar]
- MAHLE Compact Range Extender Engine; MAHLE Product Information. 2021. Available online: https://www.mahle-powertrain.com/en/experience/mahle-compact-range-extender-engine/ (accessed on 28 August 2021).
- ENGIRO 40 kW Range Extender Prototype for Light and Heavy Duty Vehicles: Preliminary Datasheet; Engiro GmbH Datasheet. 2016. Available online: https://www.engiro.de/en/products/drive-systems/range-extender/all-range-extenders/re-40 (accessed on 28 August 2021).
- Kemper, H. Plug-in e-vehicle with and without range extender. FEV Spectr. 2008, 39, 1–3. [Google Scholar]
- Fischer, R.; Fraidl, G.K.; Hubmann, C.; Kapus, P.E.; Kunzemann, R.; Sifferlinger, B.; Beste, F. Range extender module—Enabler for electric mobility. ATZ Autotechnol. 2009, 9, 40–46. [Google Scholar] [CrossRef]
- Sams, T.; Sifferlinger, B. AVL Rotary Range Extender—A Rotary Engine Based Range Extender Concept. In Proceedings of the E-Mobility Conference 2013, Graz, Austria, 30 January 2013. [Google Scholar]
- Reducing Vehicle Carbon Emissions through Development of a Compact, Efficient, and Intelligent Powertrain. Available online: https://gtr.ukri.org/projects?ref=113127#/tabOverview (accessed on 28 August 2021).
- Vorraro, G.; Islam, R.; Turner, M.; Turner, J.W.G. Application of a Rotary Expander as an Energy Recovery System for a Modern Wankel Engine. In Proceedings of the IMechE Internal Combustion Engines and Powertrain Systems for Future Transport Conference, Birmingham, UK, 11–12 December 2019. [Google Scholar]
- Turner, J.; Turner, M.; Islam, R.; Shen, X.; Costall, A. Further Investigations into the Benefits and Challenges of Eliminating Port Overlap in Wankel Rotary Engines; SAE Technical Paper 2021-01-0638; SAE International: Detroit, MI, USA, 2021. [Google Scholar] [CrossRef]
- MicroTurbine Range Extender (MiTRE). Available online: https://gtr.ukri.org/projects?ref=101309 (accessed on 28 August 2021).
- HIPERCAR—High Performance Carbon Reduction Sports Car. Available online: https://gtr.ukri.org/projects?ref=101808 (accessed on 28 August 2021).
- HIPERCARII—Enhancing Manufacturability of a High Performance REEV with Microturbine Range Extender. Available online: https://gtr.ukri.org/projects?ref=113154 (accessed on 28 August 2021).
- Catalytic Generator—Cosworth. Available online: https://www.cosworth.com/capabilities/electrification/hybrid-solutions/catalytic-generator/ (accessed on 28 August 2021).
- Mitsubishi Turbocharger and Engine Europe Introduces RANGE+. Available online: https://www.mhi.com/news/grp170912.html (accessed on 28 August 2021).
- Mitsubishi Heavy Industries: Mitsubishi Turbocharger and Engine Europe Introduces RANGE+. Available online: http://www.publicnow.com/view/35C3A9B710EBD4E59CD7DEE8718E41959CC4F440 (accessed on 28 August 2021).
- Van Blarigan, P.; Paradiso, N.; Goldsborough, S. Homogeneous Charge Compression Ignition with A Free Piston: A New Approach to Ideal Otto Cycle Performance; SAE Technical Paper 982484; SAE International: Detroit, MI, USA, 1998. [Google Scholar] [CrossRef] [Green Version]
- Mikalsen, R.; Roskilly, A.P. Free-Piston Internal Combustion Engine. U.S. Patent 20,130,118,453, 19 May 2015. [Google Scholar]
- Andrew Smallbone, A.; Hanipah, M.R.; Jia, B.; Scott, T.; Heslop, J.; Towell, B.; Lawrence, C.; Roy, S.; Shivaprasad, K.V.; Roskilly, A.P. Realization of a novel free-piston engine generator for hybrid-electric vehicle applications. Energy Fuels 2020, 34, 12926–12939. [Google Scholar] [CrossRef] [PubMed]
- Regner, G.; Johnson, D.; Koszewnik, J.; Dion, E.; Redon, F.; Fromm, L. Modernizing the Opposed Piston, Two Stroke Engine for Clean, Efficient Transportation; SAE Technical Paper 2013-26-0114; SAE International: Detroit, MI, USA, 2013. [Google Scholar] [CrossRef] [Green Version]
- McGough, M.; Fanick, E. Experimental Investigation of the Scavenging Performance of a Two-Stroke Opposed-Piston Diesel Tank Engine; SAE Technical Paper 2004-01-1591; SAE International: Detroit, MI, USA, 2004. [Google Scholar] [CrossRef]
- Hofbauer, P. Opposed Piston Opposed Cylinder (Opoc) Engine for Military Ground Vehicles; SAE Technical Paper 2005-01-1548; SAE International: Detroit, MI, USA, 2005. [Google Scholar] [CrossRef]
- Serrano, J.R.; García, A.; Monsalve-Serrano, J.; Martínez-Boggio, S. High efficiency two stroke opposed piston engine for plug-in hybrid electric vehicle applications: Evaluation under homologation and real driving conditions. Appl. Energy 2020, 282 Pt A, 116078. [Google Scholar] [CrossRef]
- Goldsborough, S.S.; Van Blarigan, P. Optimizing the Scavenging System for a Two-Stroke Cycle, Free Piston Engine for High Efficiency and Low Emissions: A Computational Approach; SAE Technical Paper 2003-01-0001; SAE International: Detroit, MI, USA, 2013. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.-K.; Zhao, C.; Zhang, F.; Zhao, Z.; Zhang, S. Effects of scavenging system configuration on in-cylinder air flow organization of an opposed-piston two-stroke engine. Energies 2015, 8, 5866–5884. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.-K.; Wang, J.; Feng, Y.-N.; Zhang, Y.-G.; Su, T.-X.; Zhang, Y.; Liu, Y.-H. Parameter optimization on the uniflow scavenging system of an OP2S-GDI engine based on indicated mean effective pressure (IMEP). Energies 2017, 10, 368. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.; Zhao, Z.; Zhang, Y.; Wang, J.; Feng, Y.; Su, T.; Zhang, Y.; Liu, Y. Simulation modeling method and experimental investigation on the uniflow scavenging system of an opposed-piston folded-cranktrain diesel engine. Energies 2017, 10, 727. [Google Scholar] [CrossRef] [Green Version]
- Ma, F.; Zhang, L.; Su, T. Simulation modeling and optimization of uniflow scavenging system parameters on opposed-piston two-stroke engines. Energies 2018, 11, 940. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Li, X.-R.; Kang, Y.-N.; Zuo, H.; Liu, F.-S. Evaluating the scavenging process by the scavenging curve of an opposed- piston, two-stroke (OP2S) diesel engine. Appl. Therm. Eng. 2019, 147, 336–346. [Google Scholar] [CrossRef]
- Mattarelli, E.; Rinaldini, C.; Savioli, T.; Cantore, G.; Warey, A.; Potter, M.; Gopalakrishnan, V.; Balestrino, S. Scavenge Ports Optimization of a 2-Stroke Opposed Piston Diesel Engine; SAE Technical Paper 2017-24-0167; SAE International: Detroit, MI, USA, 2017. [Google Scholar] [CrossRef]
- Turner, J.W.G.; Head, R.A.; Chang, J.; Engineer, N.; Wijetunge, R.; Blundell, D.W.; Burke, P. 2-Stroke Engine Options for automotive Use: A Fundamental Comparison of Different Potential Scavenging Arrangements for Medium-Duty Truck Applications; SAE Technical Paper 2019-01-0071; SAE International: Detroit, MI, USA, 2019. [Google Scholar] [CrossRef]
- Young, A.; Turner, J.; Head, R. Turbocompounding the Opposed-Piston 2-Stroke Engine; SAE Technical Paper 2021-01-0636; SAE International: Detroit, MI, USA, 2021. [Google Scholar] [CrossRef]
- GT-SUITE Overview. Available online: https://www.gtisoft.com/gt-suite/gt-suite-overview/ (accessed on 30 August 2021).
- Badra, J.A.; Sim, J.; Elwardany, A.; Jaasim, M.; Viollet, Y.; Chang, J.; Amer, A.; Im, H.G. Numerical simulations of hollow-cone injection and gasoline compression ignition combustion with naphtha fuels. J. Energy Resour. Technol. 2016, 138, 052202. [Google Scholar] [CrossRef]
- Hanson, R.; Salvi, A.; Redon, F.; Regner, G. Experimental comparison of gasoline compression ignition and diesel combustion in a medium-duty opposed-piston engine. J. Energy Resour. Technol. 2019, 141, 122201. [Google Scholar] [CrossRef]
- Marseglia, G.; Medaglia, C.M. Energy efficiency in gasoline direct injection engines. WIT Trans. Built. Environ. 2019, 182, 85–91. [Google Scholar] [CrossRef] [Green Version]
- Salvi, A.; Hanson, R.; Zermeno, R.; Regner, G.; Sellnau, M.; Redon, F. Initial Results on a New Light-Duty 2.7L Opposed-Piston Gasoline Compression Ignition Multi-Cylinder Engine. In Proceedings of the ASME 2018 Internal Combustion Engine Division Fall Technical Conference, San Diego, CA, USA, 4–7 November 2018. [Google Scholar] [CrossRef]
- Herold, R.; Wahl, M.; Regner, G.; Lemke, J. Thermodynamic Benefits of Opposed-Piston Two-Stroke Engines; SAE Technical Paper 2011-01-2216; SAE International: Detroit, MI, USA, 2011. [Google Scholar] [CrossRef] [Green Version]
- Development of Post-Euro 6/VI Emission Standards for Cars, Vans, Lorries and Buses. Available online: https://eur-lex.europa.eu/legal-content/EN/ALL/?uri=cellar:d2216ca0-704d-11ea-a07e-01aa75ed71a1 (accessed on 31 August 2021).
- European Vehicle Emissions Standards—Euro 7 for Cars, Vans, Lorries and Buses. Available online: https://ec.europa.eu/info/law/better-regulation/have-your-say/initiatives/12313-European-vehicle-emissions-standards-Euro-7-for-cars-vans-lorries-and-buses_en (accessed on 31 August 2021).




| Organization | Project/Product | Timeframe | Specifications | Target Power | Ref. |
|---|---|---|---|---|---|
| Lotus Engineering | Lotus Range Extender Engine | 2010 |
| 38 kW | [5] |
| MAHLE Powertrain | Compact Range Extender Engine (‘REx’) | 2012 |
| 30 kW (40 kW) (50 kW supercharged) | [6,7,8] |
| Engiro GmbH | Range Extender RE 40 | 2016 |
| 40 kW (45 kW max.) | [9] |
| FEV | Range Extender Module | 2008 |
| 20 kW | [10] |
| AVL | FUEREX | 2009 |
| 15 kWe | [11,12] |
| Advanced Innovative Engineering (UK) Ltd. | ADAPT/AIE 225CS Gen 2 | 2017–2021 |
| 30 kW | [13,14,15] |
| Delta Motorsport Limited | MiTRE | 2012–2016 |
| 17 kW | [16] |
| HiPERCAR | 2015–2017 | 35 kW | [17] | ||
| HiPERCAR 2 | 2017–2021 | [18] | |||
| Delta-Cosworth | CatalyticGenerator | Current | [19] | ||
| Mitsubishi | Range+ | 2017– |
| 35 kWe | [20,21] |
| Sandia National Lab. | Free piston linear alternator | 1998– |
| 30 kWe | [22] |
| Durham University | FPEG (Free Piston Engine Generator | 2013– |
| 24 kWe | [23,24] |
| INNengine company &CMT, Universitat Politècnica de València | 2S-ROPE (2-stroke rodless opposed piston engine) | 2020– |
| 33 kW | [28] |
| Parameter | Units | Value |
|---|---|---|
| Bore | mm | 75.75 |
| Total stroke | mm | 166.65 |
| Bore-to-stroke ratio | - | 0.455 |
| Cylinder swept volume | L | 0.75104 |
| Compression ratio at 0° phase | - | 15.3:1 |
| Con-rod length | mm | 166.65 |
| Scavenging system | - | Uniflow |
| Parameter | Units | Value |
|---|---|---|
| Average ratio of H:C atoms | - | 2.009 |
| Lower Heating Value | MJ/kg | 42.1 |
| Density | kg/m3 | 721 |
| Parameter | Units | Operating Point | ||||
|---|---|---|---|---|---|---|
| Medium-Duty Truck | Range Extender | |||||
| A | B | C | D | E | ||
| Engine speed | min−1 | 1500 | 1500 | 3000 | 1500 | 3000 |
| BMEP | bar | 3 | 12 | 10 | 16 | 8 |
| Power (per cylinder) | kW | 5.63 | 22.5 | 37.6 | 30.0 | 30.0 |
| Power density | kW/l | 7.50 | 30.0 | 50.0 | 40.0 | 40.0 |
| Exhaust pressure | bar | 1.05 | 1.50 | 2.00 | 1.50 | 2.00 |
| Operating Point | Units | Minimum | Maximum |
|---|---|---|---|
| Crankshaft phase angle (exhaust leads intake) | °CA | 0 | 20 |
| Intake port height-to-stroke ratio | - | 0.050 | 0.200 |
| Exhaust port height-to-stroke ratio | - | 0.075 | 0.225 |
| Air-to-fuel equivalence ratio, λ (N.B. max. value varies by op. point) | - | 1.0 | 2.0 (A), 1.5 (B, C) 1.0 (D, E) |
| Phasing | Parameter | Units | Stoichiometric Operation (λ = 1) | Variable Stoichiometry (λ = 1–2) |
|---|---|---|---|---|
| Fixed | Intake port height-to-stroke ratio | - | 0.1125 | 0.1125 |
| Exhaust port height-to-stroke ratio | - | 0.1625 | 0.1875 | |
| Average BSFC | g/kWh | 236.98 | 226.73 | |
| Variable | Intake port height-to-stroke ratio | - | 0.1125 | 0.1250 |
| Exhaust port height-to-stroke ratio | - | 0.1500 | 0.1625 | |
| Average BSFC | g/kWh | 236.75 | 226.21 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Young, A.G.; Costall, A.W.; Coren, D.; Turner, J.W.G. The Effect of Crankshaft Phasing and Port Timing Asymmetry on Opposed-Piston Engine Thermal Efficiency. Energies 2021, 14, 6696. https://doi.org/10.3390/en14206696
Young AG, Costall AW, Coren D, Turner JWG. The Effect of Crankshaft Phasing and Port Timing Asymmetry on Opposed-Piston Engine Thermal Efficiency. Energies. 2021; 14(20):6696. https://doi.org/10.3390/en14206696
Chicago/Turabian StyleYoung, Alex G., Aaron W. Costall, Daniel Coren, and James W. G. Turner. 2021. "The Effect of Crankshaft Phasing and Port Timing Asymmetry on Opposed-Piston Engine Thermal Efficiency" Energies 14, no. 20: 6696. https://doi.org/10.3390/en14206696
APA StyleYoung, A. G., Costall, A. W., Coren, D., & Turner, J. W. G. (2021). The Effect of Crankshaft Phasing and Port Timing Asymmetry on Opposed-Piston Engine Thermal Efficiency. Energies, 14(20), 6696. https://doi.org/10.3390/en14206696







