Contaminant Source Identification from Finite Sensor Data: Perron–Frobenius Operator and Bayesian Inference
Abstract
:1. Introduction
2. Methodology
2.1. Problem Definition
2.2. Construction of Transfer PF Operator for Contaminant Transport
2.3. Bayesian Formulation
3. Results
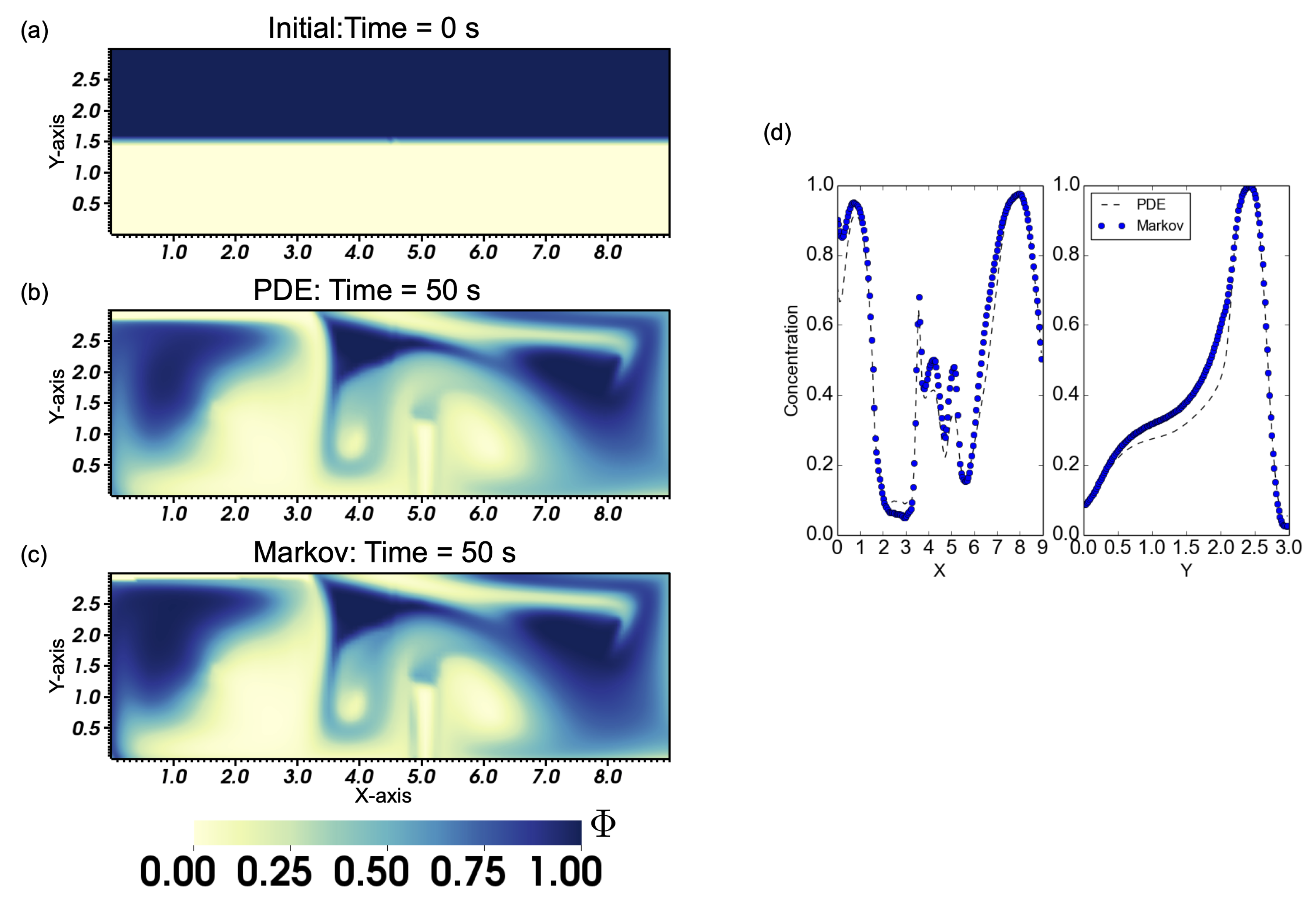
3.1. Validation of Contaminant Transport from PF Operator
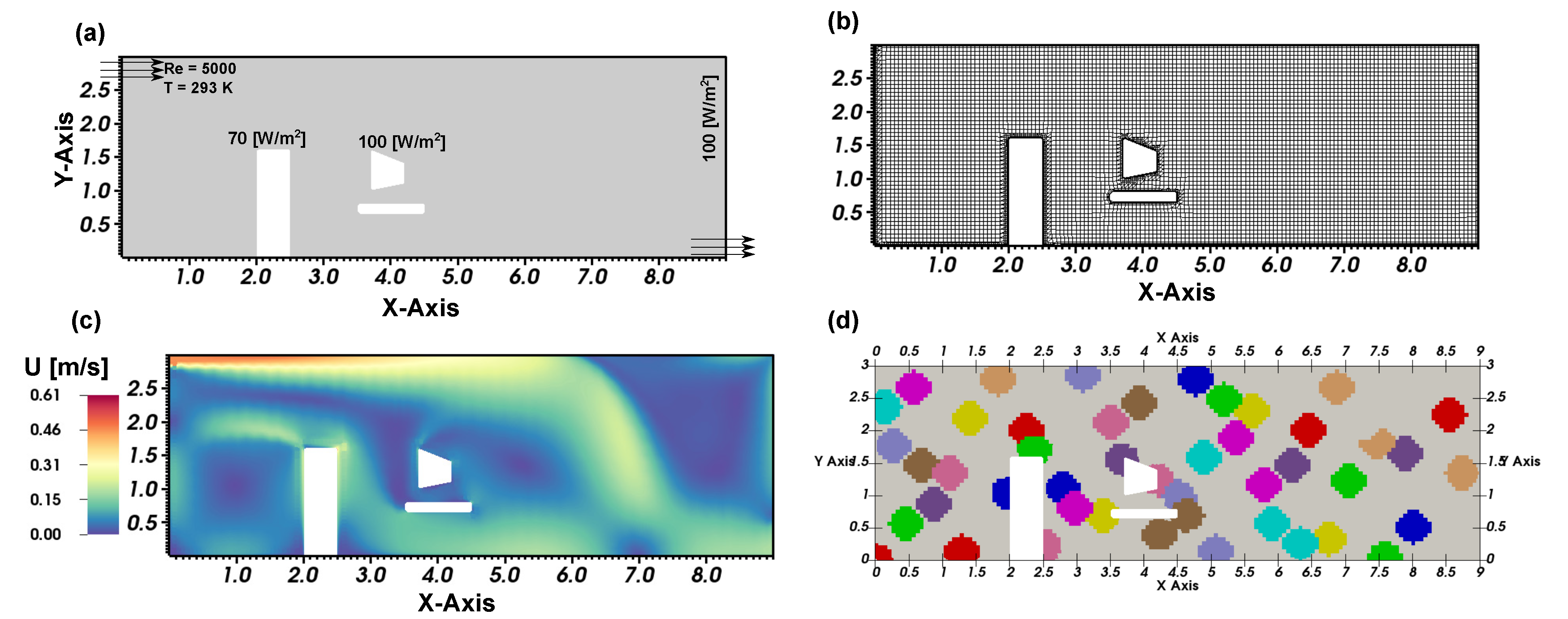
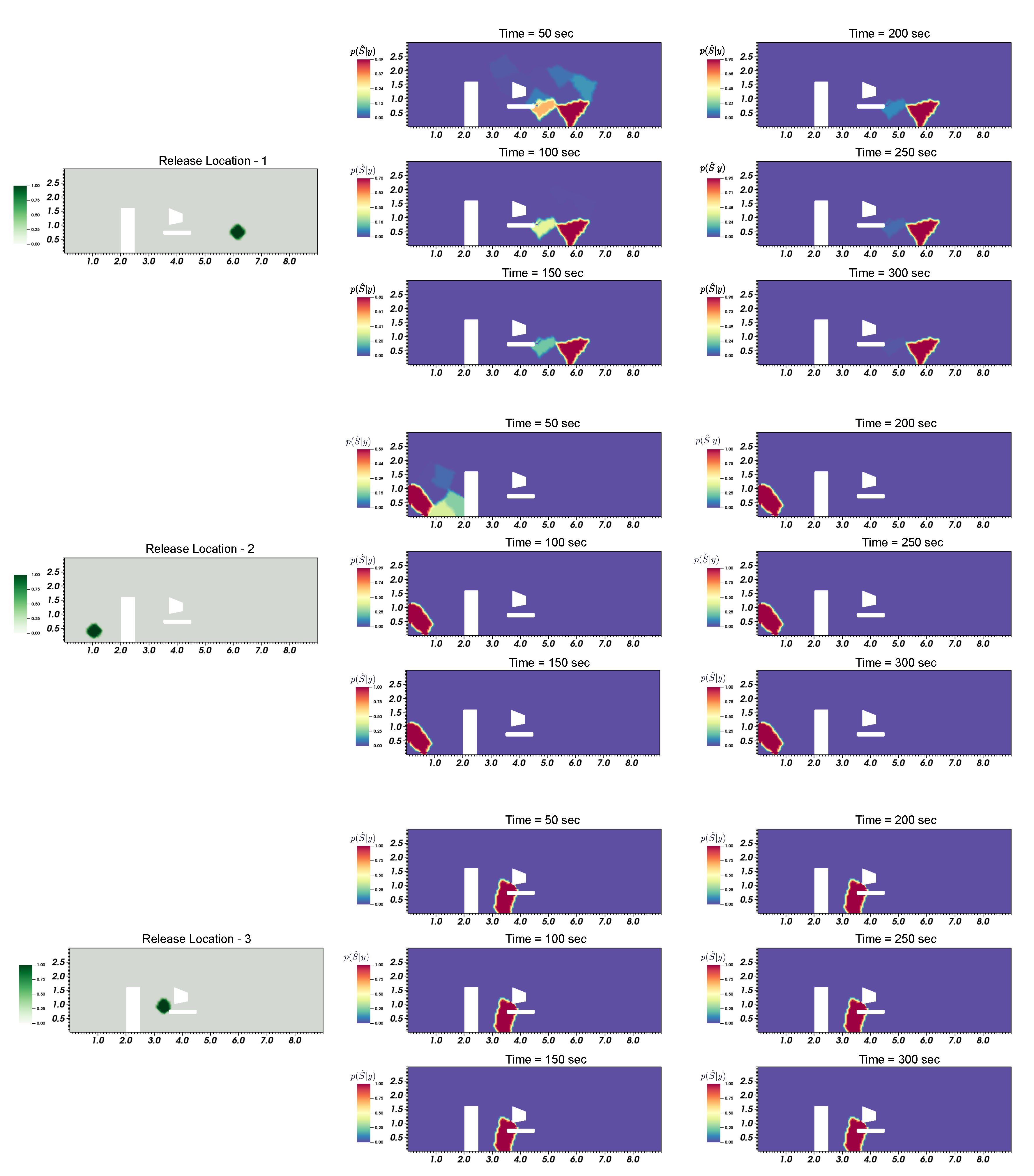
3.2. Contaminant Source Identification in 2D Office Space
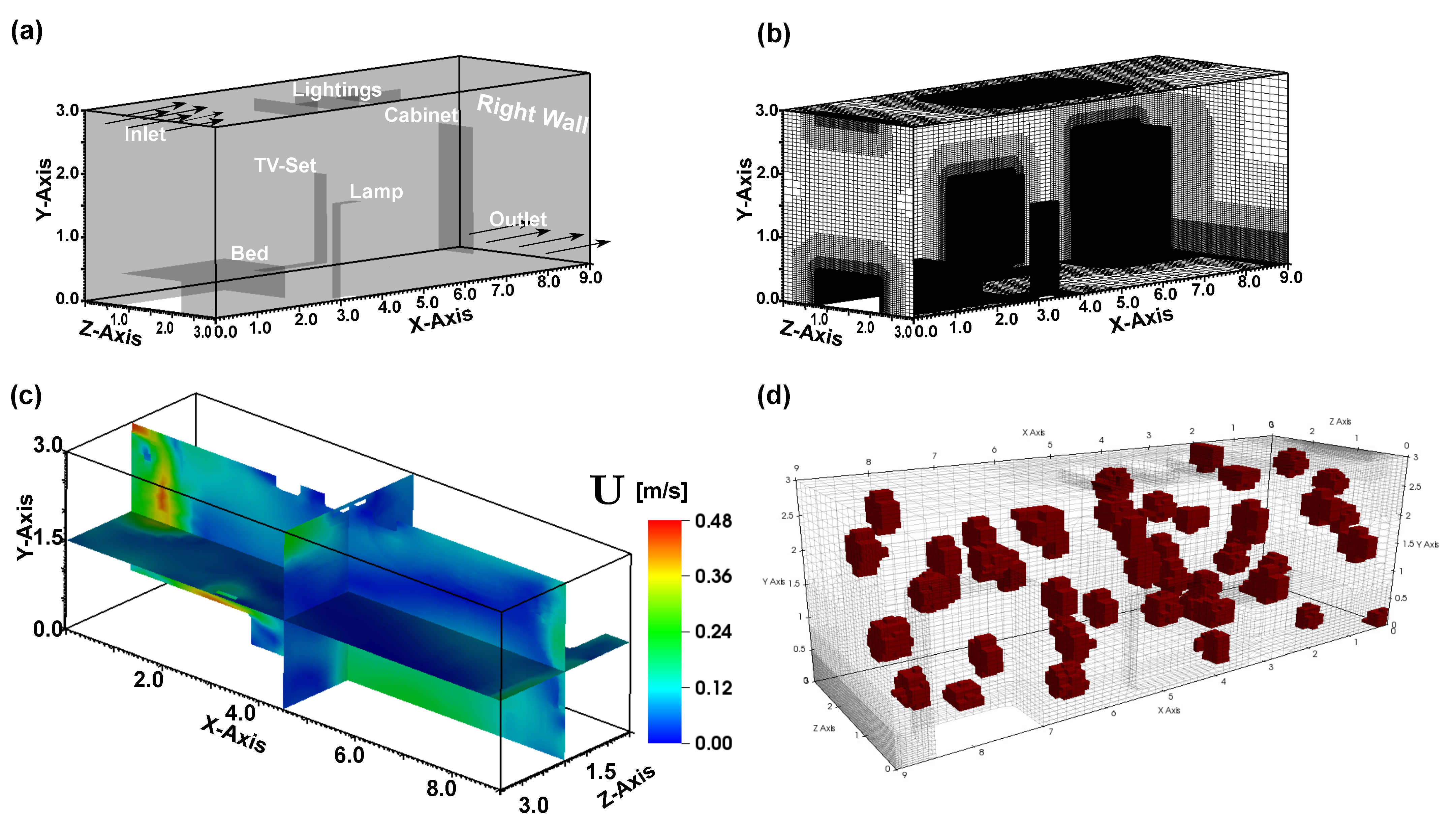
3.3. Contaminant Source Identification in 3D Furnished Room
4. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
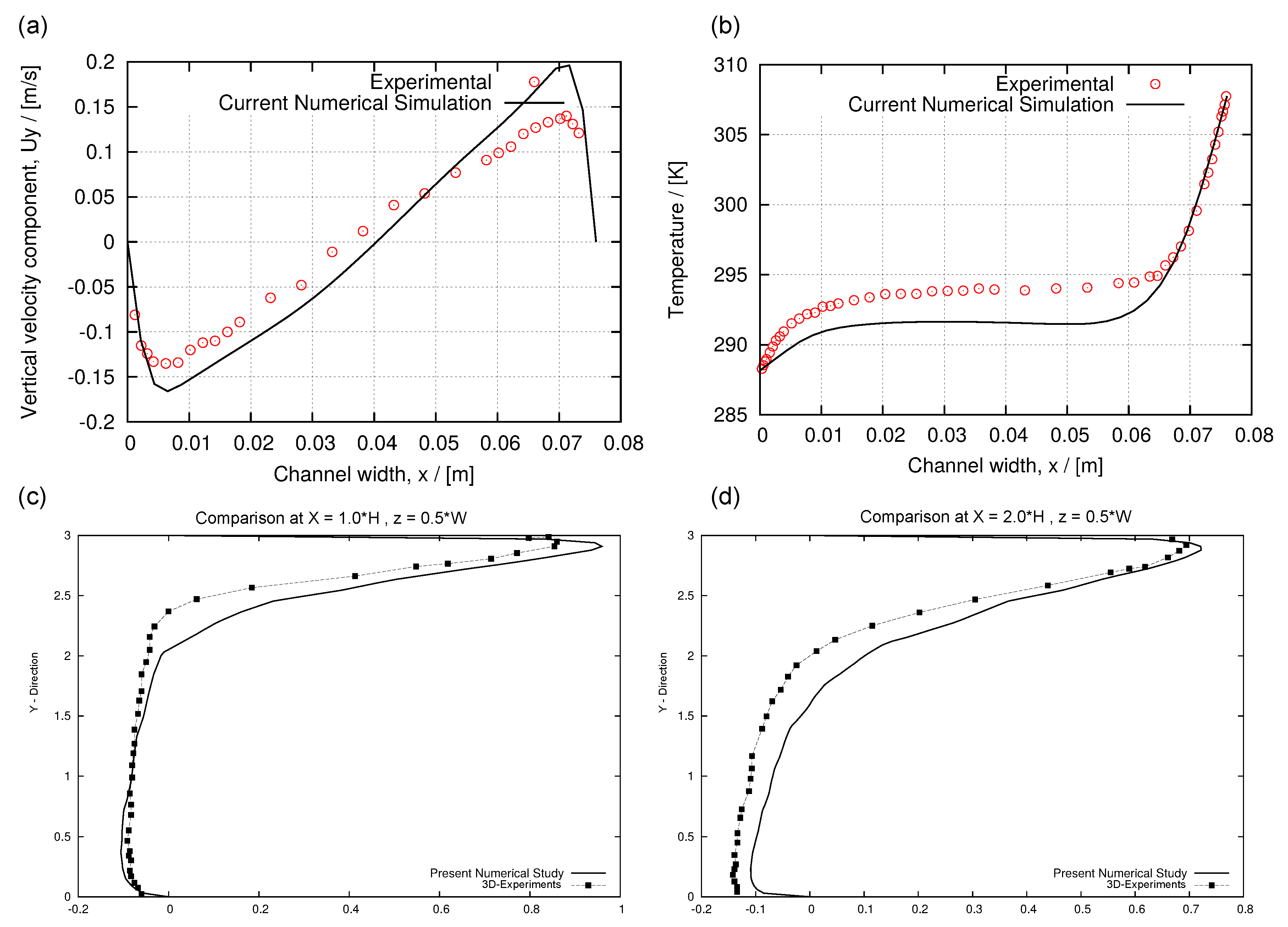
Appendix A. Validation of CFD Solvers
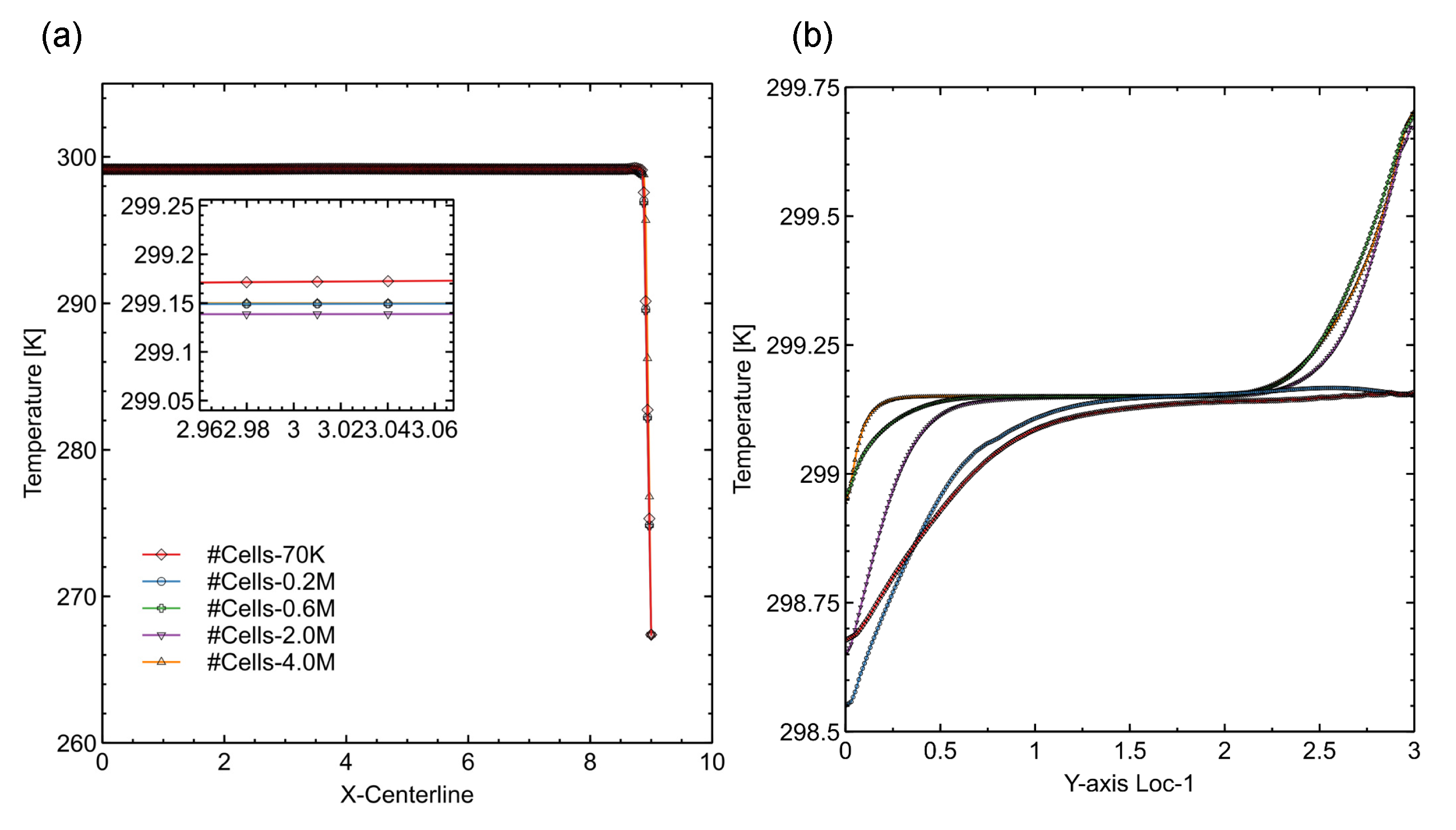
Appendix B. Grid Convergence
References
- EPA/Office of Radiation and Indoor Air. The Inside Story: A Guide to Indoor Air Quality. 2012. Available online: https://www.epa.gov/indoor-air-quality-iaq/inside-story-guide-indoor-air-quality (accessed on 15 September 2021).
- Inglesby, T.V.; O’toole, T.; Henderson, D.A.; Bartlett, J.G.; Ascher, M.S.; Eitzen, E.; Friedlander, A.M.; Gerberding, J.; Hauer, J.; Hughes, J.; et al. Anthrax as a biological weapon, 2002: Updated recommendations for management. JAMA 2002, 287, 2236–2252. [Google Scholar] [CrossRef] [PubMed]
- Pangi, R. Consequence management in the 1995 sarin attacks on the Japanese subway system. Stud. Confl. Terror. 2002, 25, 421–448. [Google Scholar] [CrossRef]
- Moser, M.R.; Bender, T.R.; Margolis, H.S.; Noble, G.R.; Kendal, A.P.; Ritter, D.G. An outbreak of influenza aboard a commercial airliner. Am. J. Epidemiol. 1979, 110, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Olsen, S.J.; Chang, H.L.; Cheung, T.Y.Y.; Tang, A.F.Y.; Fisk, T.L.; Ooi, S.P.L.; Kuo, H.W.; Jiang, D.D.S.; Chen, K.T.; Lando, J.; et al. Transmission of the Severe Acute Respiratory Syndrome on Aircraft. N. Engl. J. Med. 2003, 349, 2416–2422. [Google Scholar] [CrossRef]
- Morawska, L.; Tang, J.W.; Bahnfleth, W.; Bluyssen, P.M.; Boerstra, A.; Buonanno, G.; Cao, J.; Dancer, S.; Floto, A.; Franchimon, F.; et al. How can airborne transmission of COVID-19 indoors be minimised? Environ. Int. 2020, 142, 105832. [Google Scholar] [CrossRef]
- Zhang, R.; Li, Y.; Zhang, A.L.; Wang, Y.; Molina, M.J. Identifying airborne transmission as the dominant route for the spread of COVID-19. Proc. Natl. Acad. Sci. USA 2020, 117, 14857–14863. [Google Scholar] [CrossRef]
- Bloch, A.B.; Orenstein, W.A.; Ewing, W.M.; Spain, W.H.; Mallison, G.F.; Herrmann, K.L.; Hinman, A.R. Measles outbreak in a pediatric practice: Airborne transmission in an office setting. Pediatrics 1985, 75, 676–683. [Google Scholar]
- Menzies, D.; Fanning, A.; Yuan, L.; FitzGerald, J.M. Hospital ventilation and risk for tuberculous infection in Canadian health care workers. Ann. Intern. Med. 2000, 133, 779–789. [Google Scholar] [CrossRef]
- Sharma, H.; Vaidya, U.; Ganapathysubramanian, B. Estimating contaminant distribution from finite sensor data: Perron Frobenious operator and ensemble Kalman Filtering. Build. Environ. 2019, 159, 106148. [Google Scholar] [CrossRef]
- Rao, K.S. Source estimation methods for atmospheric dispersion. Atmos. Environ. 2007, 41, 6964–6973. [Google Scholar]
- Neupauer, R.M.; Wilson, J.L. Adjoint method for obtaining backward-in-time location and travel time probabilities of a conservative groundwater contaminant. Water Resour. Res. 1999, 35, 3389–3398. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Q. Identification of contaminant sources in enclosed spaces by a single sensor. Indoor Air 2007, 17, 439–449. [Google Scholar] [CrossRef]
- Zhang, T.; Chen, Q. Identification of contaminant sources in enclosed environments by inverse CFD modeling. Indoor Air 2007, 17, 167–177. [Google Scholar] [CrossRef]
- Zhang, T.; Yin, S.; Wang, S. An inverse method based on CFD to quantify the temporal release rate of a continuously released pollutant source. Atmos. Environ. 2013, 77, 62–77. [Google Scholar] [CrossRef]
- Zhang, T.; Zhou, H.; Wang, S. Inverse identification of the release location, temporal rates, and sensor alarming time of an airborne pollutant source. Indoor Air 2015, 25, 415–427. [Google Scholar] [CrossRef]
- Wei, Y.; Zhou, H.; Zhang, T.T.; Wang, S. Inverse identification of multiple temporal sources releasing the same tracer gaseous pollutant. Build. Environ. 2017, 118, 184–195. [Google Scholar] [CrossRef]
- Matsuo, T.; Kondo, A.; Shimadera, H.; Kyuno, T.; Inoue, Y. Estimation of indoor contamination source location by using variational continuous assimilation method. In Building Simulation; Springer: Berlin, Germany, 2015; Volume 8, pp. 443–452. [Google Scholar]
- Matsuo, T.; Shimadera, H.; Kondo, A. Identification of multiple contamination sources using variational continuous assimilation. Build. Environ. 2019, 147, 422–433. [Google Scholar] [CrossRef]
- Vukovic, V.; Tabares-Velasco, P.C.; Srebric, J. Real-time identification of indoor pollutant source positions based on neural network locator of contaminant sources and optimized sensor networks. J. Air Waste Manag. Assoc. 2010, 60, 1034–1048. [Google Scholar] [CrossRef] [Green Version]
- Bastani, A.; Haghighat, F.; Kozinski, J.A. Contaminant source identification within a building: Toward design of immune buildings. Build. Environ. 2012, 51, 320–329. [Google Scholar] [CrossRef] [PubMed]
- Park, Y.J.; Tagade, P.M.; Choi, H.L. Deep gaussian process-based Bayesian inference for contaminant source localization. IEEE Access 2018, 6, 49432–49449. [Google Scholar] [CrossRef]
- Tagade, P.M.; Jeong, B.M.; Choi, H.L. A Gaussian process emulator approach for rapid contaminant characterization with an integrated multizone-CFD model. Build. Environ. 2013, 70, 232–244. [Google Scholar] [CrossRef] [Green Version]
- Sohn, M.D.; Reynolds, P.; Singh, N.; Gadgil, A.J. Rapidly locating and characterizing pollutant releases in buildings. J. Air Waste Manag. Assoc. 2002, 52, 1422–1432. [Google Scholar] [CrossRef]
- Sreedharan, P.; Sohn, M.D.; Nazaroff, W.W.; Gadgil, A.J. Influence of indoor transport and mixing time scales on the performance of sensor systems for characterizing contaminant releases. Atmos. Environ. 2007, 41, 9530–9542. [Google Scholar] [CrossRef] [Green Version]
- Sohn, M.D.; Lorenzetti, D.M. Siting Bio-Samplers in Buildings. Risk Analysis 2007, 27, 877–886. [Google Scholar] [CrossRef] [PubMed]
- Walter, T.; Lorenzetti, D.M.; Sohn, M.D. Siting samplers to minimize expected time to detection. Risk Anal. Int. J. 2012, 32, 2032–2042. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sreedharan, P.; Sohn, M.D.; Nazaroff, W.W.; Gadgil, A.J. Towards improved characterization of high-risk releases using heterogeneous indoor sensor systems. Build. Environ. 2011, 46, 438–447. [Google Scholar] [CrossRef] [Green Version]
- Neupauer, R.M. Adjoint sensitivity analysis of contaminant concentrations in water distribution systems. J. Eng. Mech. 2010, 137, 31–39. [Google Scholar] [CrossRef]
- Liu, X.; Zhai, Z.J. Prompt tracking of indoor airborne contaminant source location with probability-based inverse multi-zone modeling. Build. Environ. 2009, 44, 1135–1143. [Google Scholar] [CrossRef]
- Liu, X.; Zhai, Z. Location identification for indoor instantaneous point contaminant source by probability-based inverse Computational Fluid Dynamics modeling. Indoor Air 2007, 18, 2–11. [Google Scholar] [CrossRef] [PubMed]
- Zhai, Z.; Liu, X.; Wang, H.; Li, Y.; Liu, J. Experimental verification of tracking algorithm for dynamically-releasing single indoor contaminant. Build. Simul. 2012, 5, 5–14. [Google Scholar] [CrossRef] [PubMed]
- Wang, H.; Lu, S.; Cheng, J.; Zhai, Z. Inverse modeling of indoor instantaneous airborne contaminant source location with adjoint probability-based method under dynamic airflow field. Build. Environ. 2017, 117, 178–190. [Google Scholar] [CrossRef] [Green Version]
- Fontanini, A.D.; Vaidya, U.; Ganapathysubramanian, B. A methodology for optimal placement of sensors in enclosed environments: A dynamical systems approach. Build. Environ. 2016, 100, 145–161. [Google Scholar] [CrossRef] [Green Version]
- Fontanini, A.D.; Vaidya, U.; Ganapathysubramanian, B. Constructing Markov matrices for real-time transient contaminant transport analysis for indoor environments. Build. Environ. 2015, 94, 68–81. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sinha, S.; Vaidya, U.; Rajaram, R. Operator theoretic framework for optimal placement of sensors and actuators for control of nonequilibrium dynamics. J. Math. Anal. Appl. J. Math. Anal. Appl. 2016, 440, 750–772. [Google Scholar] [CrossRef] [Green Version]
- Vaidya, U.; Rajaram, R.; Dasgupta, S. Actuator and sensor placement in linear advection PDE with building system application. J. Math. Anal. Appl. 2012, 394, 213–224. [Google Scholar] [CrossRef] [Green Version]
- Brand, K.P.; Small, M.J. Updating uncertainty in an integrated risk assessment: Conceptual framework and methods. Risk Analysis 1995, 15, 719–729. [Google Scholar] [CrossRef]
- Dilks, D.W.; Canale, R.P.; Meier, P.G. Development of Bayesian Monte Carlo techniques for water quality model uncertainty. Ecol. Model. 1992, 62, 149–162. [Google Scholar] [CrossRef] [Green Version]
- Schmid, P.J. Dynamic mode decomposition of numerical and experimental data. J. Fluid Mech. 2010, 656, 5–28. [Google Scholar] [CrossRef] [Green Version]
- Rowley, C.W.; Mezić, I.; Bagheri, S.; Schlatter, P.; Henningson, D.S. Spectral analysis of nonlinear flows. J. Fluid Mech. 2009, 641, 115–127. [Google Scholar] [CrossRef] [Green Version]
- Mezić, I. Spectral properties of dynamical systems, model reduction and decompositions. Nonlinear Dyn. 2005, 41, 309–325. [Google Scholar] [CrossRef]
- Fontanini, A.; Vaidya, U.; Passalacqua, A.; Ganapathysubramanian, B. Contaminant transport at large Courant numbers using Markov matrices. Build. Environ. 2017, 112, 1–16. [Google Scholar] [CrossRef]
- Sinha, S.; Huang, B.; Vaidya, U. Robust Approximation of Koopman Operator and Prediction in Random Dynamical Systems. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 5491–5496. [Google Scholar]
- Williams, M.O.; Kevrekidis, I.G.; Rowley, C.W. A data–driven approximation of the koopman operator: Extending dynamic mode decomposition. J. Nonlinear Sci. 2015, 25, 1307–1346. [Google Scholar] [CrossRef] [Green Version]
- Gelman, A.; Stern, H.S.; Carlin, J.B.; Dunson, D.B.; Vehtari, A.; Rubin, D.B. Bayesian Data Analysis; Chapman and Hall/CRC: London, UK, 2013. [Google Scholar]
- Michael Sohn, B.D.; Member, A.; Small, M.J.; Pantazidou, M. Reducing uncertainty in site characterization using Bayes Monte Carlo methods. J. Environ. Eng. 2000, 126, 893. [Google Scholar] [CrossRef]
- Nielsen, P.V. Specification of Two Dimensional Test Case; Technical Report; Aalborg University: Aalborg, Denmark, 1990. [Google Scholar]
- Jasak, H.; Jemcov, A.; Tukovi, Z. OpenFOAM: A C++ Library for Complex Physics Simulations. In International Workshop on Coupled Methods in Numerical Dynamics IUC; IUC Dubrovnik Croatia: Dubrovnik, Croatia, 2007. [Google Scholar]
- Zeng, L.; Gao, J.; Du, B.; Zhang, R.; Zhang, X. Probability-based inverse characterization of the instantaneous pollutant source within a ventilation system. Build. Environ. 2018, 143, 378–389. [Google Scholar] [CrossRef]
- Sharma, H.; Fontanini, A.D.; Vaidya, U.; Ganapathysubramanian, B. Transfer Operator Theoretic Framework for Monitoring Building Indoor Environment in Uncertain Operating Conditions. In Proceedings of the 2018 Annual American Control Conference (ACC), Milwaukee, WI, USA, 27–29 June 2018; pp. 6790–6797. [Google Scholar]
- Sharma, H.; Vaidya, U.; Ganapathysubramanian, B. A transfer operator methodology for optimal sensor placement accounting for uncertainty. Build. Environ. 2019, 155, 334–349. [Google Scholar] [CrossRef] [Green Version]
- Bucolo, M.; Buscarino, A.; Famoso, C.; Fortuna, L.; Frasca, M. Control of imperfect dynamical systems. Nonlinear Dyn. 2019, 98, 2989–2999. [Google Scholar] [CrossRef]
- Betts, P.; Bokhari, I. Experiments on turbulent natural convection in an enclosed tall cavity. Int. J. Heat Fluid Flow 2000, 21, 675–683. [Google Scholar] [CrossRef]
- Nielsen, P.V.; Restivo, A.; Whitelaw, J.H. The Velocity Characteristics of Ventilated Rooms. J. Fluids Eng. 1978, 100, 291–298. [Google Scholar] [CrossRef]
- Nielsen, P.V.; Murakami, S.; Kato, S.; Topp, C.; Yang, J.H. Benchmark tests for a computer simulated person. In Indoor Environmental Engineering; Aalborg University: Aalbrog, Denmark, 2003. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sharma, H.; Vaidya, U.; Ganapathysubramanian, B. Contaminant Source Identification from Finite Sensor Data: Perron–Frobenius Operator and Bayesian Inference. Energies 2021, 14, 6729. https://doi.org/10.3390/en14206729
Sharma H, Vaidya U, Ganapathysubramanian B. Contaminant Source Identification from Finite Sensor Data: Perron–Frobenius Operator and Bayesian Inference. Energies. 2021; 14(20):6729. https://doi.org/10.3390/en14206729
Chicago/Turabian StyleSharma, Himanshu, Umesh Vaidya, and Baskar Ganapathysubramanian. 2021. "Contaminant Source Identification from Finite Sensor Data: Perron–Frobenius Operator and Bayesian Inference" Energies 14, no. 20: 6729. https://doi.org/10.3390/en14206729
APA StyleSharma, H., Vaidya, U., & Ganapathysubramanian, B. (2021). Contaminant Source Identification from Finite Sensor Data: Perron–Frobenius Operator and Bayesian Inference. Energies, 14(20), 6729. https://doi.org/10.3390/en14206729




