SCADA Data-Based Working Condition Classification for Condition Assessment of Wind Turbine Main Transmission System
Abstract
:1. Introduction
- A transmission system working condition classification based on wind turbine operating characteristics and a k-means clustering algorithm is proposed. It can solve the problems of traditional classification systems, such as classes being insufficient in clarity or number and high false-alarm rates in the main drivetrain vibration detection process.
- A method for selecting the status parameters of the main transmission system based on correlation analysis is proposed. It avoids the influence of feature parameter omissions in the process of selecting feature parameters and improves the validity of SCADA data.
- During vibration monitoring, the false-alarm rate is used as an index to verify the validity of the transmission system’s working condition classification.
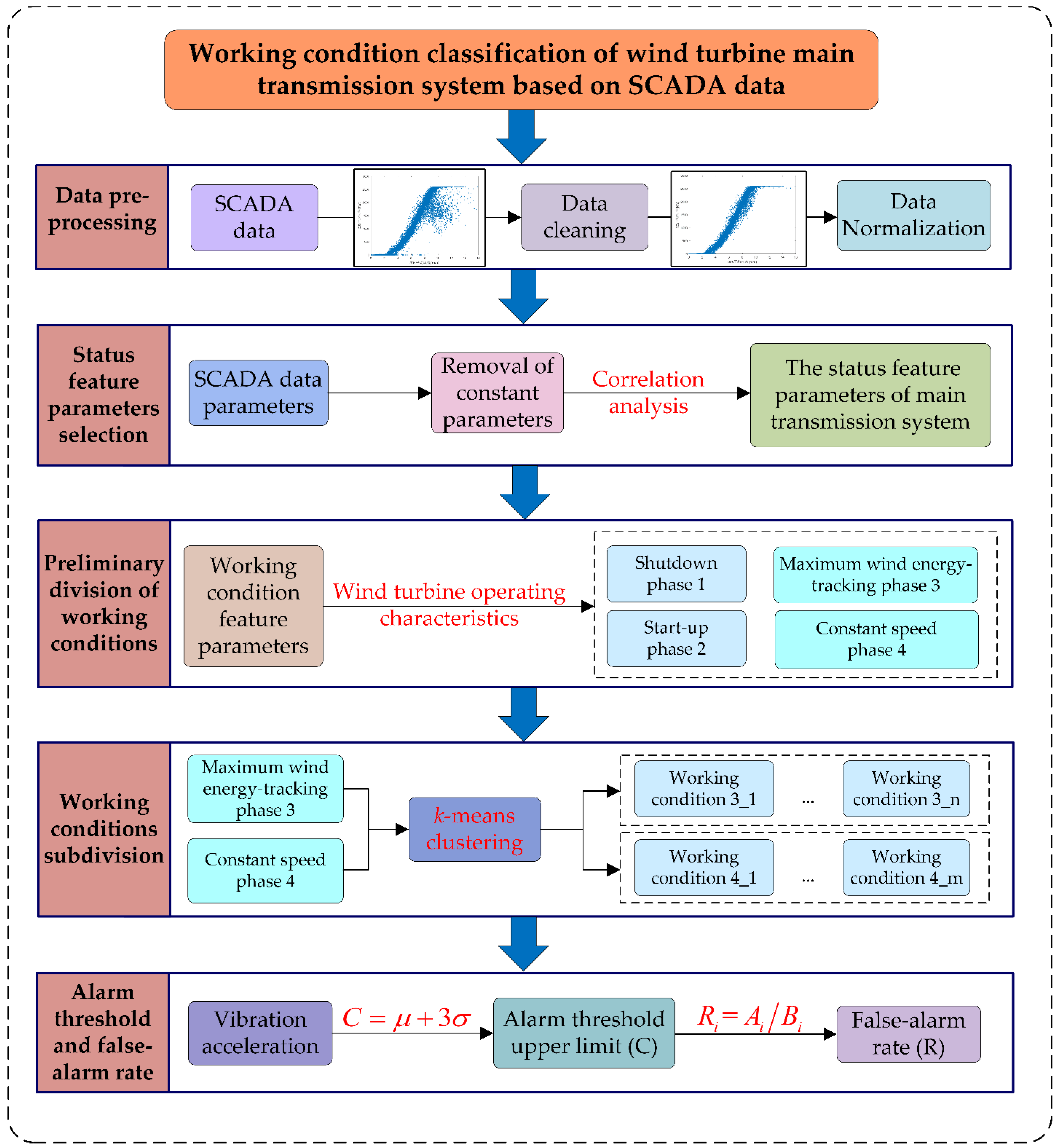
2. Selection of the Main Transmission System’s Status Feature Parameters
3. Classification of the Working Conditions of the Main Transmission System
3.1. Introduction to the Principles of the k-Means Clustering Algorithm
3.1.1. The k-Means Clustering Algorithm Process
- Generate k initial centre-of-mass points using the k-means++ algorithm: .
- Calculate the distance between each sample point and the centre-of-mass points.
- Assign sample points to the class nearest to them.
- Calculate the centre of mass of each class using the sample points that have just been grouped: calculate the mean value of each cluster coordinate as the centre of mass.
- Repeat steps 3–5 until its centre of mass no longer changes, or the maximum number of iteration steps is reached.
- Output the cluster division .
3.1.2. The k-Means++ Algorithm Process
- Create an empty set for storing the k prime points of the cluster.
- Select a random instance from the sample set called , and add it to the first cluster as the centre of mass.
- For each instance in the dataset , calculate the square of the distance to the centre of mass of each cluster within dataset , the smallest of which is the square of the distance to :
- The probability of each sample being selected as the next cluster centre is calculated as follows. The next cluster centre point is selected by the roulette wheel method and added to .
- Repeat steps 3–4 until k clusters of centre-of-mass points have been selected.
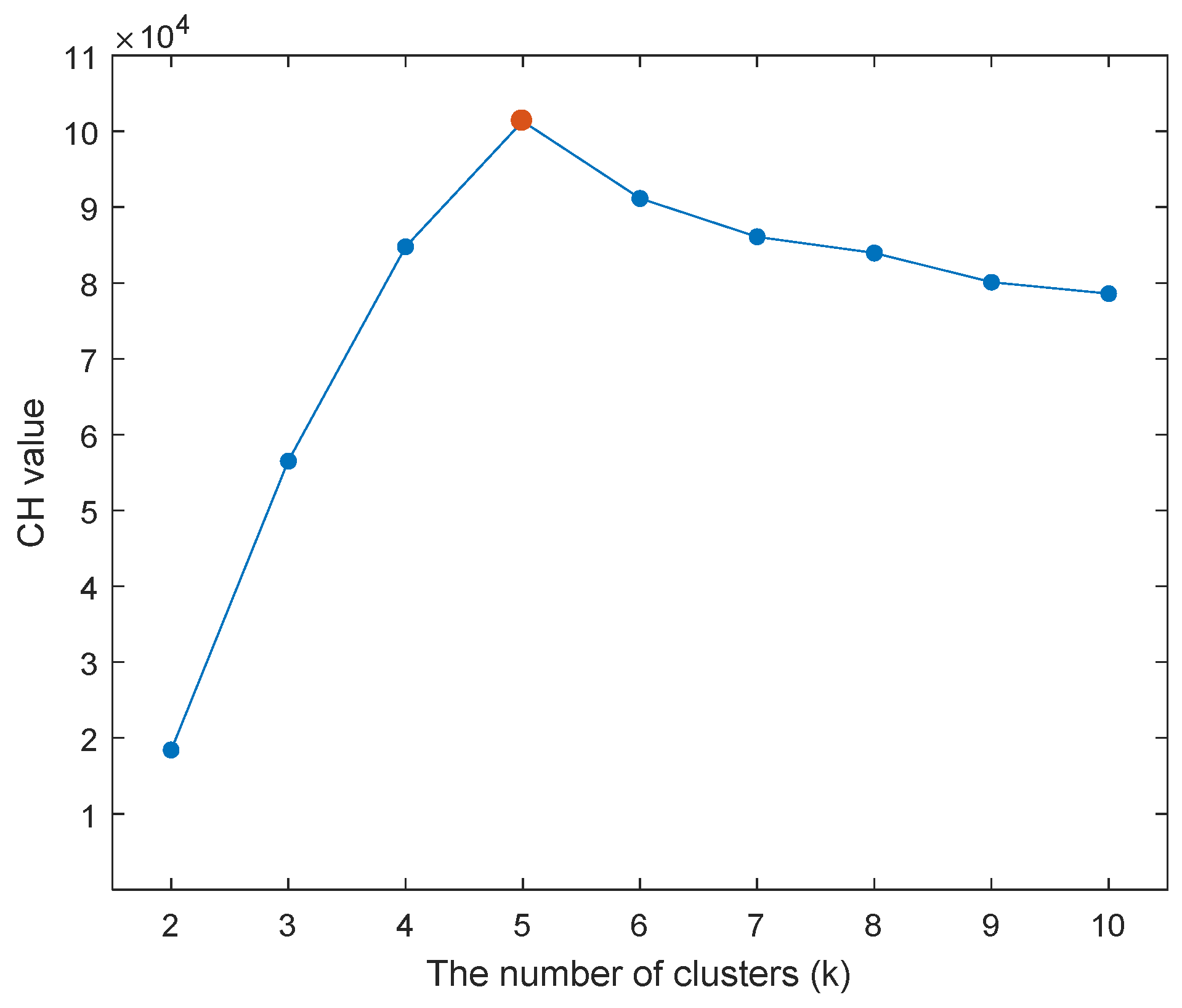
3.1.3. Determination of the Number of Clusters k
3.2. Main Transmission System Working Conditions Classification Based on the k-Means Clustering Algorithm
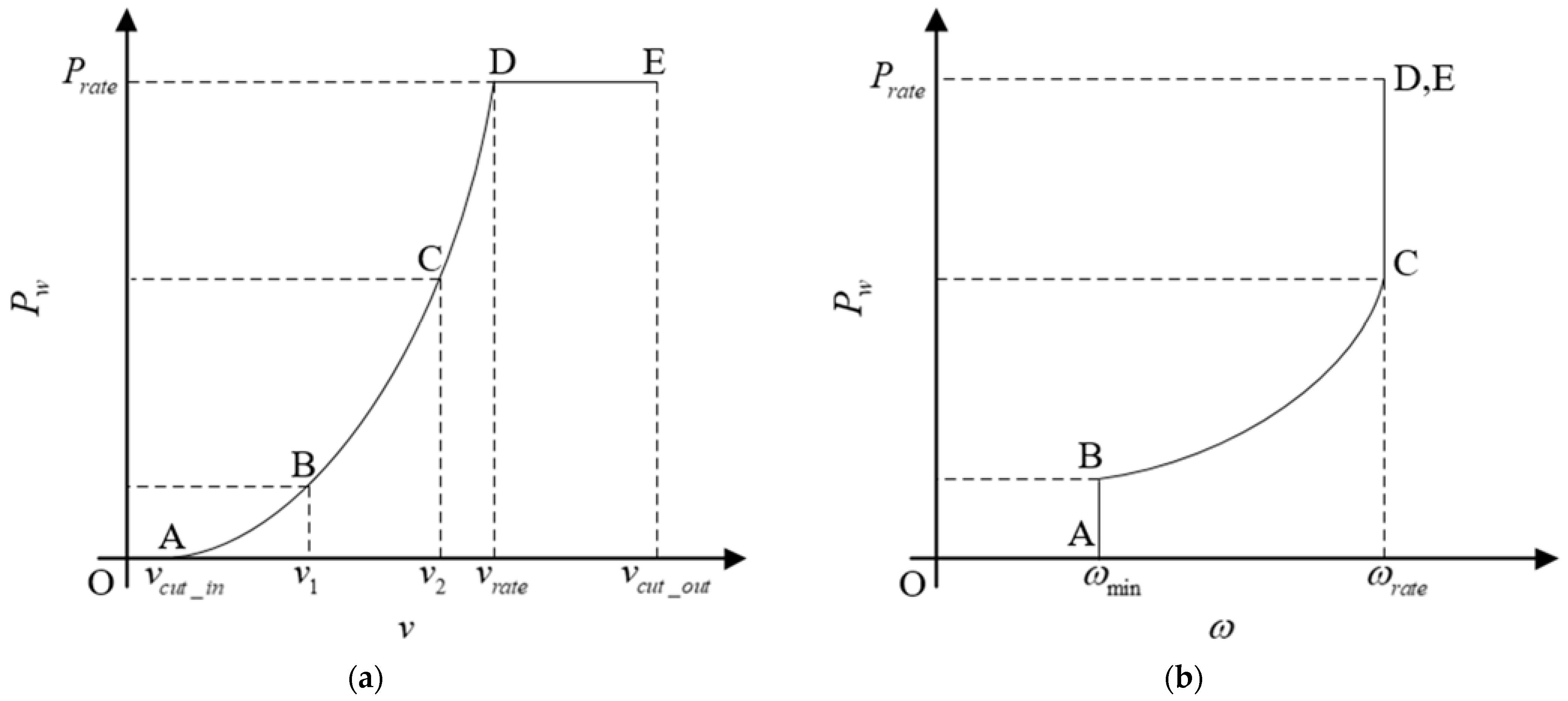
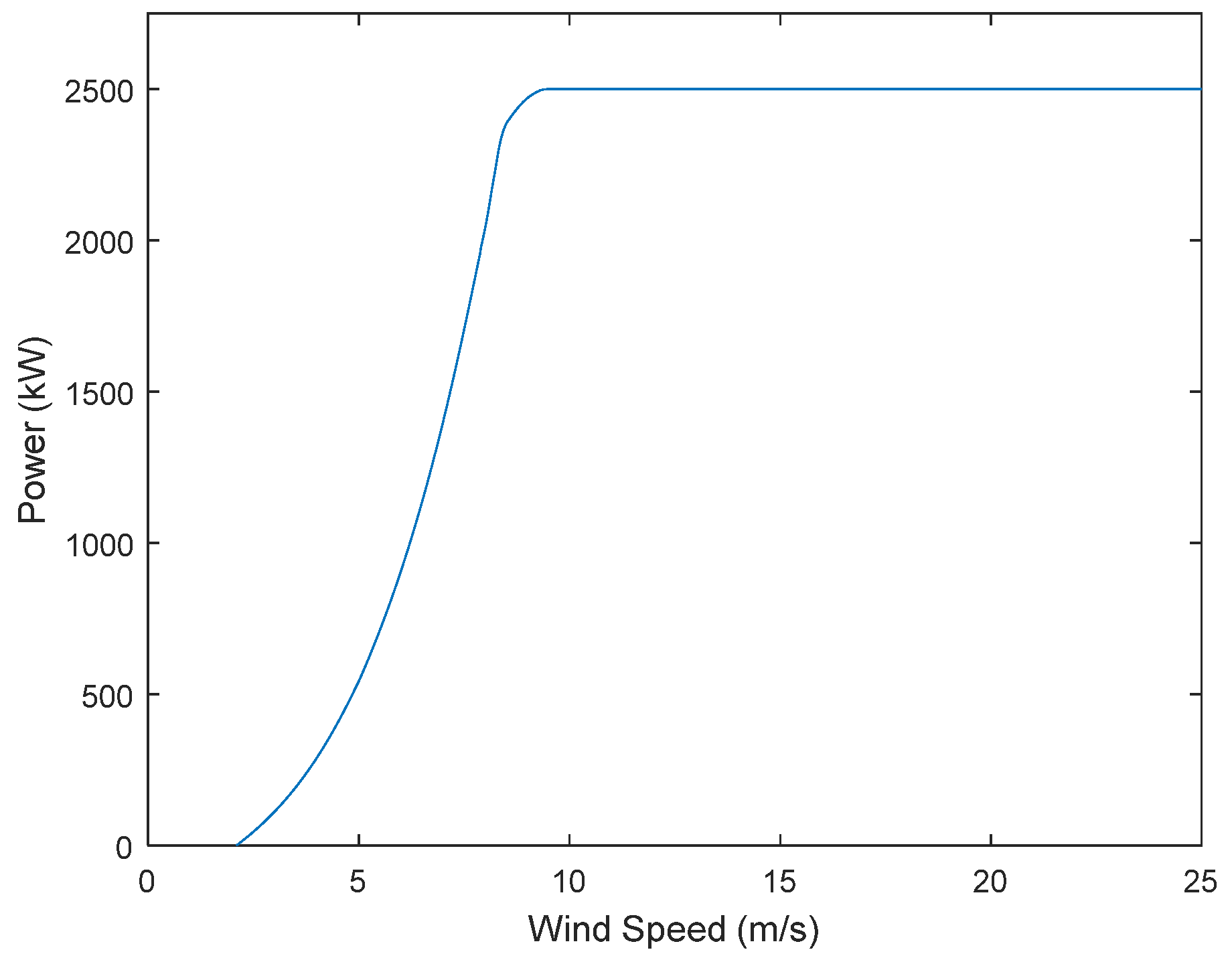
- Shutdown phase (OA and E+): Wind speeds are less than the cut-in wind speed or greater than the cut-out wind speed ;
- Start-up phase (AB): Wind speeds are greater than the cut-in wind speed and less than the wind speed . The wind turbine speed is limited to the minimum speed ;
- Maximum wind-energy tracking phase (BC): Wind speed is between and , the wind turbine speed is between the minimum speed and the rated speed , the wind turbine tip speed ratio remains optimal, and the wind energy utilization coefficient remains at the maximum;
- Constant speed phase (CD): Wind speeds are between and the rated wind speed , and the wind turbine speed remains at the rated speed ;
- Constant power phase (DE): Wind speeds are between the rated wind speed and cut-out wind speed , the wind turbine speed is at the rated speed , and the wind power utilization coefficient is adjusted by adjusting the pitch angle so that the wind power output is kept at the rated power .
4. Determination of Alarm Thresholds
5. A Case Study
5.1. Wind Turbine Overview and SCADA Monitoring Parameters
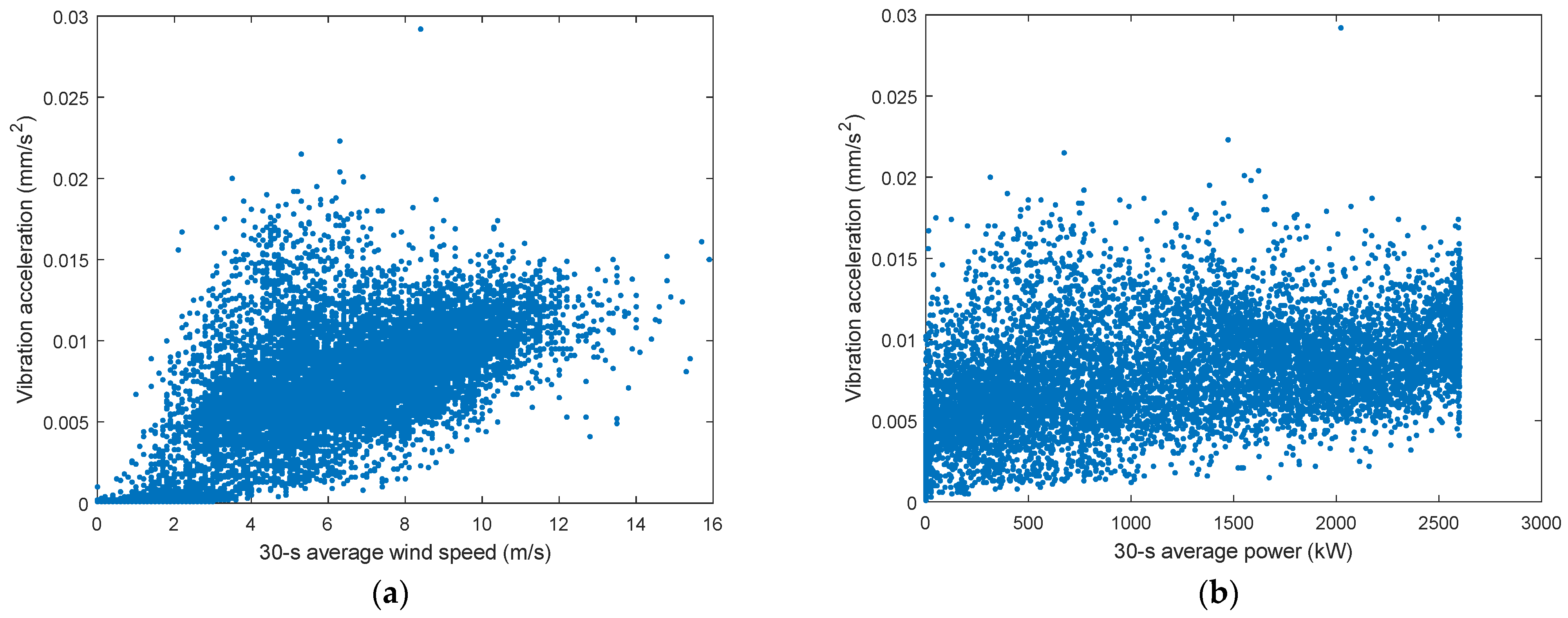
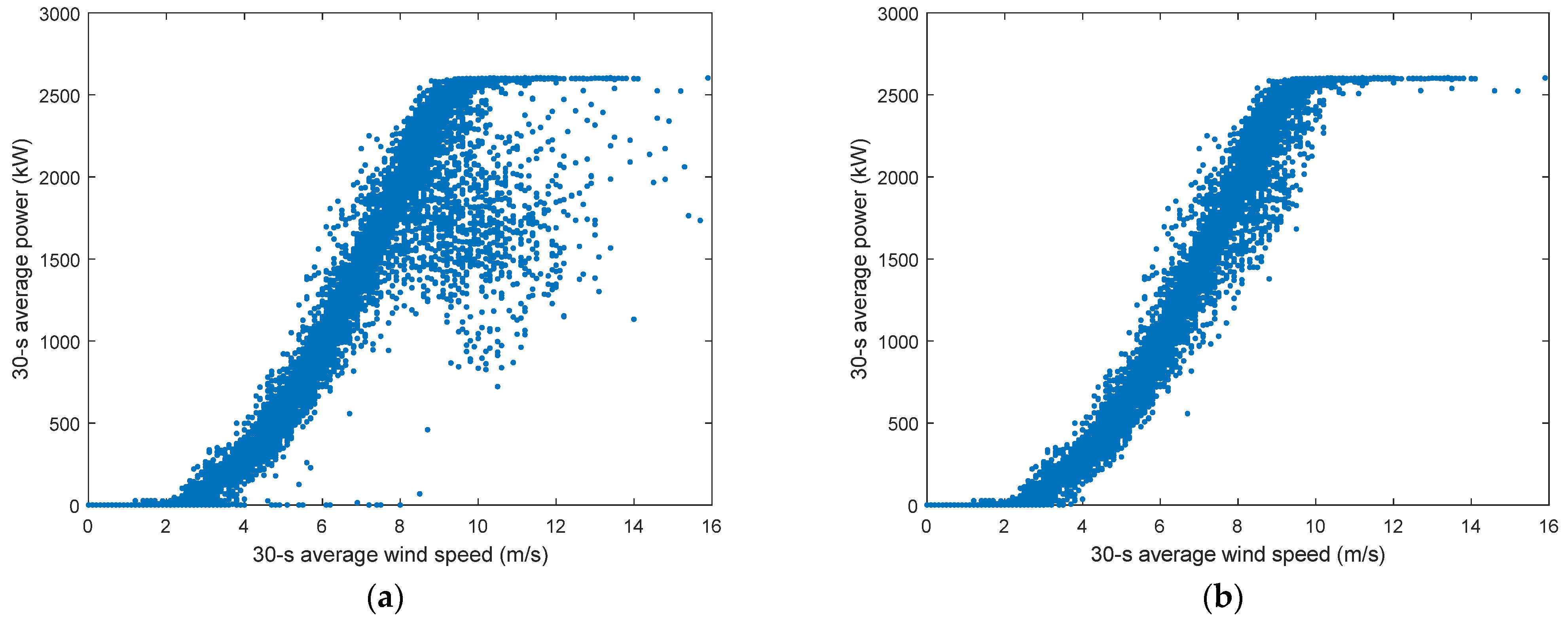
5.2. Data Pre-Processing
5.2.1. Data Cleaning
- Removal of records with status variable values that are missing or recorded as “0”.
- Referral to maintenance records to remove data recorded when the wind turbine was down for maintenance.
- Referring to the method described in [36]: the DBSCAN-based density clustering method is used to eliminate outlier anomalies, and the truncation method is used to eliminate points where the wind speed is greater than the cut-in wind speed, but the power is still 0.
5.2.2. Data Normalization
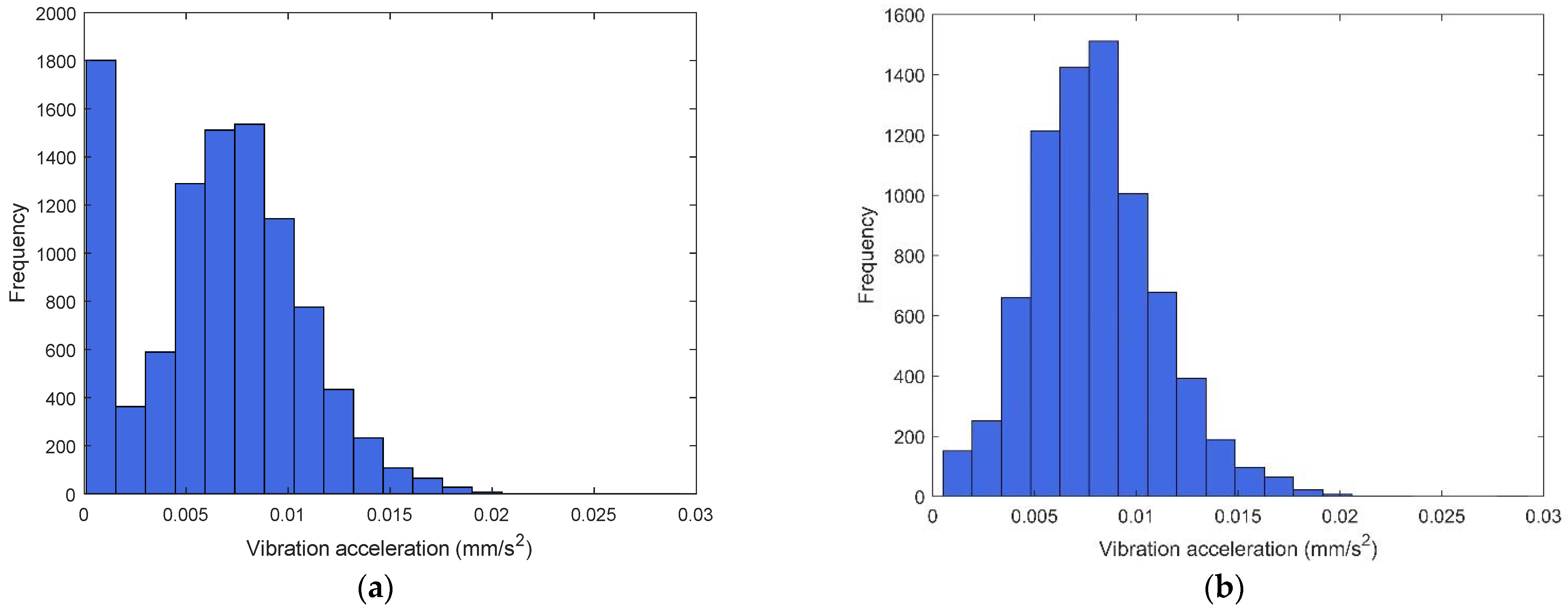
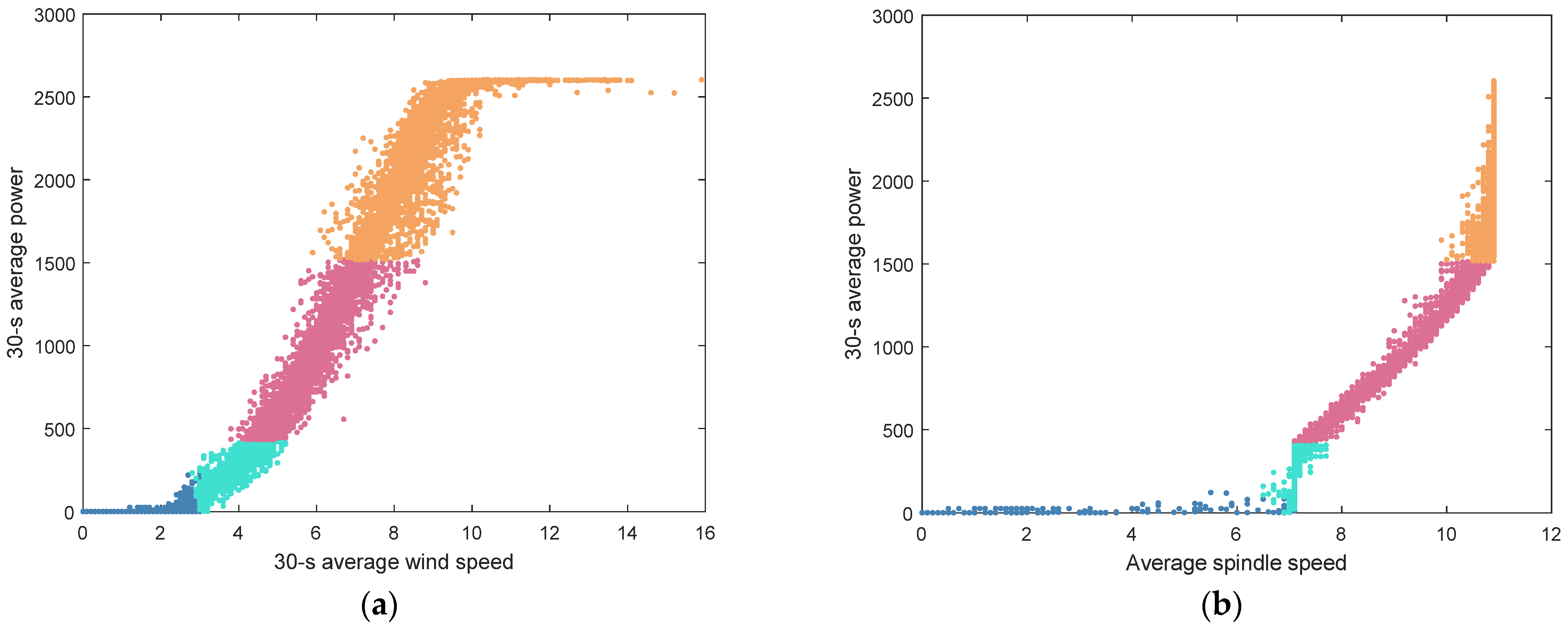
5.3. Clustering of Main Transmission System Working Conditions
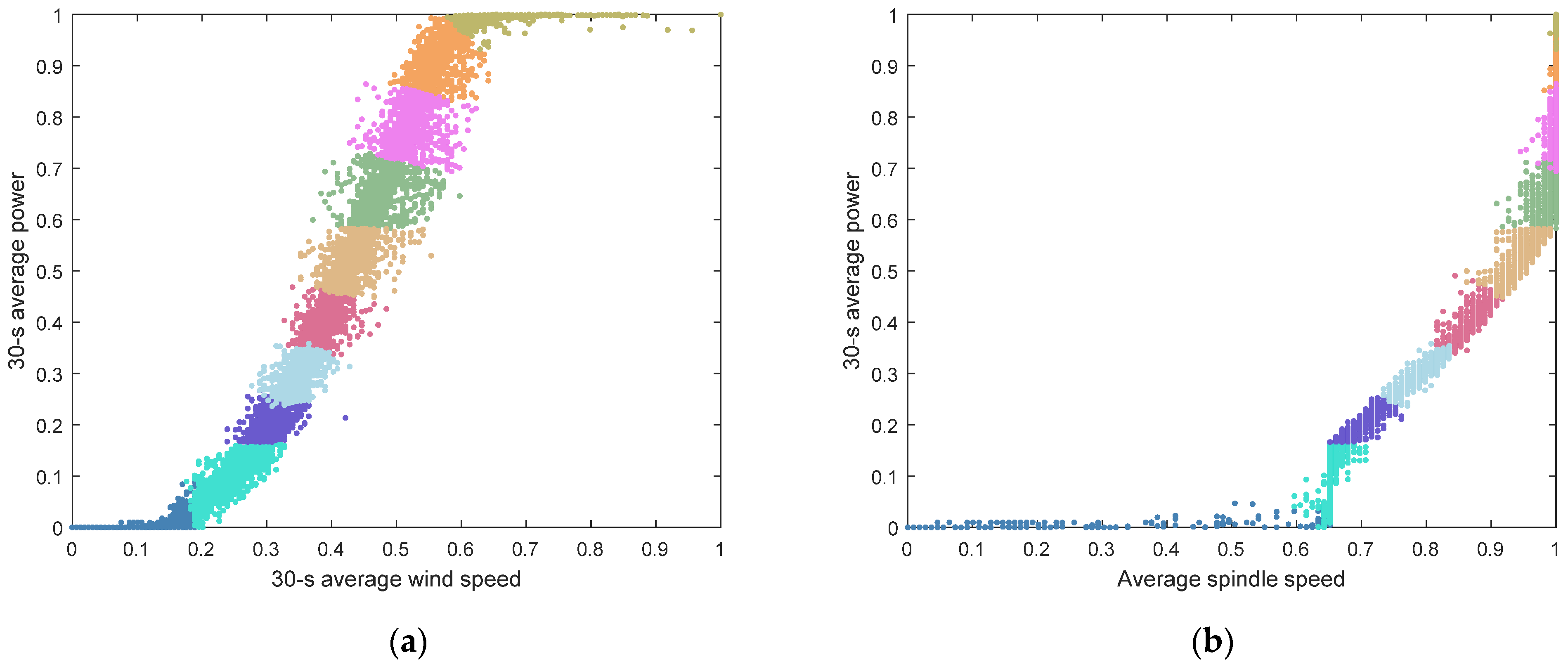
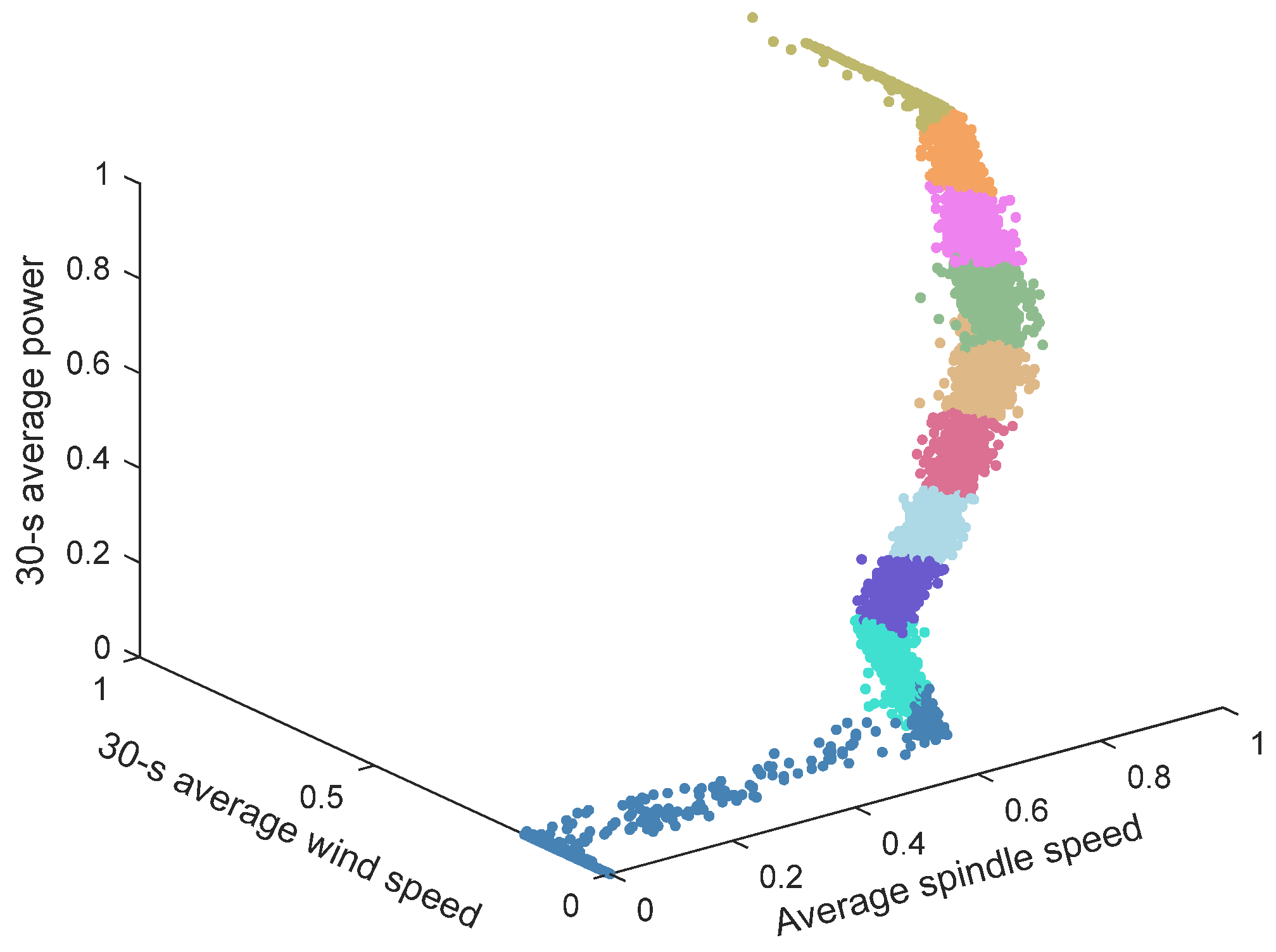
5.3.1. Direct Clustering of Working Conditions
5.3.2. Improved Working Condition Classification Method
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, H.; Li, X.L.; Wang, G.; Xiang, D.; Rong, Y.M. Research on failure of wind turbine gearbox and recent development of its design and manufacturing technologies. China Mech. Eng. 2013, 24, 1542–1549. [Google Scholar]
- Dai, J.C.; Tan, Y.; Shen, X.B. Investigation of energy output in mountain wind farm using multiple-units SCADA data. Appl. Energy 2019, 239, 225–238. [Google Scholar] [CrossRef]
- Yan, X. Research on Fault Early Warning Method for Wind Turbine Based on Condition Identification. Master’s Thesis, North China Electric Power University, Baoding, China, March 2017. [Google Scholar]
- Mei, Y.; Li, X.; Hu, Z.C.; Yao, H.; Liu, D. Identification and cleaning of wind power data methods based on control principle of wind turbine generator system. Chin. J. Power Eng. 2021, 41, 316–322. [Google Scholar]
- Dai, J.C.; Yang, W.X.; Cao, J.W.; Liu, D.S.; Long, X. Ageing assessment of a wind turbine over time by interpreting wind farm SCADA data. Renew. Energy 2018, 116, 199–208. [Google Scholar] [CrossRef] [Green Version]
- Yang, T.Y.; Zhao, L.J.; Xu, J.; Li, W.; Zhang, G.J. Abnormal identification method of wind power turbine based on Copula function. Electr. Switchg. 2021, 59, 26–31. [Google Scholar]
- Cheng, H.F.; Zhang, Q.Y. Multi-dimensional wind turbine operating state identification based on operating data. In Proceedings of the 6th China Wind Power After-Market Communication and Cooperation Conference, Tianjin, China, 13 June 2019. [Google Scholar]
- Ling, Y.Z. Research on Main Bearing Health Condition Assessment Method Based on Wind Turbine SCADA Data. Master’s Thesis, Changsha University of Technology, Changsha, China, April 2018. [Google Scholar]
- Gu, Y.J.; Su, L.W.; Zhong, Y.; Xu, T. An online fault early warning method for wind turbine gearbox based on operational condition division. Electr. Power Sci. Eng. 2014, 30, 1–5. [Google Scholar]
- Dong, H.Y.; Xu, K.L.; Yang, L.X.; Gu, Y.Q.; Chen, N.N. Operational Conditions Division of Wind Turbines. In Proceedings of the 29th China Control and Decision Making Conference, Chongqing, China, 28 May 2017. [Google Scholar]
- Xing, Y.S.; Zhuang, S.X.; Hou, Z.G.; Liao, Z.C.; Yan, W. Evaluation of wind turbine health trend based on the PCA-NAR neural network. Electr. Autom. 2020, 42, 64–66. [Google Scholar]
- Zhang, J.; Jiang, N.; Li, H.K.; Li, N. Online health assessment of wind turbine based on operational condition recognition. Trans. Inst. Meas. Control 2019, 41, 2970–2981. [Google Scholar] [CrossRef]
- Wang, H.; Wang, H.B.; Jiang, G.Q.; Li, J.M.; Wang, Y.L. Early Fault Detection of Wind Turbines Based on Operational Condition Clustering and Optimized Deep Belief Network Modeling. Energies 2019, 12, 984. [Google Scholar] [CrossRef] [Green Version]
- Liu, W.J.; Zhao, P.F.; Zhang, W.X.; Wang, J.G. Fault diagnosis method of wind turbine based on manifold semi-supervised k-means algorithm. Mach. Tool Hydraul. 2020, 48, 191–194. [Google Scholar]
- Jin, H.F. Research on Health Condition Monitoring of Wind Turbine Based on Data Mining. Master’s Thesis, North China Electric Power University, Baoding, China, March 2018. [Google Scholar]
- Liu, C.L.; Yan, X. Monitoring of the state of the gear box of a wind power generator unit based on the operating condition identification. J. Eng. Therm. Energy Power 2016, 31, 41–46. [Google Scholar]
- Yin, S.; Hou, G.L.; Chi, Y.; Gong, L.J.; Hu, X.D. Prediction method for health degree of front bearing of wind turbine generator and implementation. J. Syst. Simul. 2021, 33, 1323–1333. [Google Scholar]
- Chen, H.S.; Ma, H.Z.; Chu, X.N.; Xue, D.Y. Anomaly detection and critical attributes identification for products with multiple operating conditions based on isolation forest. Adv. Eng. Inform. 2020, 46, 101139. [Google Scholar] [CrossRef]
- Ma, R.; Li, W.Y.; Qi, R.S. Performance degradation prognostic and health assessment using wind power data for wind turbine generation unit. Renew. Energy Resour. 2019, 37, 1252–1259. [Google Scholar]
- Wang, D.L.; Lü, L.X.; Wang, Z.Q.; Chen, Y.; Li, X.N. Condition monitoring of wind turbine gearbox based on GMM operational condition identification and DAE. China Meas. Test 2021, 47, 89–95. [Google Scholar]
- Han, D.P. Health Status Evaluation of Wind Turbines Based on Scada Operation Data. Master’s Thesis, North China Electric Power University, Baoding, China, March 2019. [Google Scholar]
- Han, P.P.; Xia, Y.; Ding, M.; Zhang, Y.; Lin, Z.H.; Zhu, Q.L. Equivalent modeling of wind farm based on PCA and CA-ST methods. Acta Energ. Sol. Sin. 2020, 41, 267–277. [Google Scholar]
- Zheng, X.X.; Li, M.N.; Wang, J.; Ren, H.H.; Fu, Y. Operational conditions classification of offshore wind turbines based on kernel principal analysis optimized by PSO. Power Syst. Prot. Control. 2016, 44, 28–35. [Google Scholar]
- Wang, F. Research on Operation Condition Classification Method for Vibration Monitoring of Wind Turbine. Master’s Thesis, North China Electric Power University, Beijing, China, March 2010. [Google Scholar]
- Ma, H.Y.; Yang, B.Y.; Peng, R.J. Research on clustering data partition algorithm based on machine learning. Comput. Knowl. Technol. 2021, 17, 9–10. [Google Scholar]
- Putri, D.C.G.; Leu, J.-S.; Seda, P. Design of an Unsupervised Machine Learning-Based Movie Recommender System. Symmetry 2020, 12, 185. [Google Scholar] [CrossRef] [Green Version]
- Zhu, X.; Zhang, S.; Jin, X.Q.; Du, Z.M. Deep learning based reference model for operational risk evaluation of screw chillers for energy efficiency. Energy 2020, 213, 118833. [Google Scholar] [CrossRef]
- Cao, H.R.; Hou, X.G.; Feng, Y.; Bi, M. An environment modeling method in automatic layout of submarine piping. Ship Sci. Technol. 2020, 42, 103–107. [Google Scholar]
- Bastianoni, A.; Guastaldi, E.; Barbagli, A.; Bernardinetti, S.; Zirulia, A.; Brancale, M.; Colonna, T. Multivariate Analysis Applied to Aquifer Hydrogeochemical Evaluation: A Case Study in the Coastal Significant Subterranean Water Body between “Cecina River and San Vincenzo”, Tuscany (Italy). Appl. Sci. 2021, 11, 7595. [Google Scholar] [CrossRef]
- Wang, J.H.; Jiang, J.M. Unsupervised deep clustering via adaptive GMM modeling and optimization. Neurocomputing 2021, 433, 199–211. [Google Scholar] [CrossRef]
- Miao, K.H.; Wang, J.L.; Gao, Y.L.; Cao, C.; Xie, Y.W.; Gao, P. Robust fuzzy clustering algorithm based on adaptive neighbors. J. Phys. Conf. Ser. 2021, 2025, 012046. [Google Scholar] [CrossRef]
- Park, J.; Jeong, J.; Park, Y. Ship Trajectory Prediction Based on Bi-LSTM Using Spectral-Clustered AIS Data. J. Mar. Sci. Eng. 2021, 9, 1037. [Google Scholar] [CrossRef]
- Zhang, J. Data-Based Health Assessment and Fault Prediction of Wind Turbine Generator. Master’s Thesis, Shanghai Jiao Tong University, Shanghai, China, February 2019. [Google Scholar]
- Li, C.; Ye, Z.; Gao, W.; Jiang, Z. Modern Large-Scale Wind Turbine Design Principle, 1st ed.; Shanghai Scientific & Technical Publishers: Shanghai, China, 2013; pp. 333–341. [Google Scholar]
- Liu, Y.Q.; Wang, F.; Shi, W.G.; Zhuo, Y. Operation condition classification method for wind turbine based on support vector machine. Acta Energ. Sol. Sin. 2010, 31, 1191–1197. [Google Scholar]
- Wang, Y.M.; Liu, H.; Song, P.; Hu, Z.C.; Deng, X.Y.; Wu, L.L. An approach for the cleaning of abnormal wind turbine operation data based on multi-phase progressive recognition. Renew. Energy Resour. 2020, 38, 1470–1476. [Google Scholar]

| Category | Representative Algorithms | Advantages | Disadvantages |
|---|---|---|---|
| Partition-based clustering | k-means [25] | Simple and fast. Scalable and efficient for handling large data sets. | k-values are difficult to estimate. The choice of initial centroids can affect the clustering results to a large extent. |
| Hierarchy-based clustering | Balanced Iterative Reducing and Clustering Using Hierarchies (BIRCH) [26] | No need to enter the number of categories K. Memory saving and fast clustering. Noise points can be identified, and the dataset can be pre-processed for initial classification. | Not suitable for clustering data with high-dimensional features. Complex adjustment of key parameters has a large impact on the final result. |
| Density-based clustering | Density-Based Spatial Clustering of Applications with Noise (DBSCAN) [27] | No need to determine k-values in advance. Arbitrarily shaped clusters can be found. Outliers can be identified. Initial centroids do not affect clustering results. | Not suitable for clustering high-dimensional data. Not suitable for clustering data with changing density. Difficult to determine optimal values for parameters. |
| Network-based clustering | Statistical Information Grid (STING) [28] | Fast clustering | Parameter-sensitive, unable to handle irregularly distributed data. Low accuracy of clustering results. |
| Model-based clustering | Self-Organized Maps (SOM) [29], (Gaussian Mixture Model) GMM [30] | The classification of “classes” is expressed in probabilistic form and the characteristics of each class can be expressed in terms of parameters. | Inefficient execution, especially when the number of distributions is large, and the amount of data is small. |
| Fuzzy-based clustering | Fuzzy c-means (FCM) [31] | Classification according to the principle of maximum subordination in fuzzy sets. Better for clustering normally distributed data. | Dependent on initial clustering centres. Longer clustering time for larger data volumes. No guarantee of convergence to an optimal solution. |
| Graph-based clustering | Spectral clustering [32] | Spectral clustering works well when there are few clustering categories. Suitable for high-dimensional clustering. Has the ability to cluster on an arbitrarily shaped sample space and converge to a globally optimal solution. | Very sensitive to the choice of clustering parameters. Only applicable to balanced classification problems. |
| Status Parameter | Pearson Correlation Coefficient | Status Parameter | Pearson Correlation Coefficient |
|---|---|---|---|
| Average spindle speed | 0.8072 | Average wind speed | 0.9256 |
| Average torque | 0.9953 | 30-s average wind speed | 0.9263 |
| Average wind direction | 0.0396 | 600-s average wind speed | 0.9171 |
| Average outdoor temperature | −0.1739 | 600-s average power | 0.9822 |
| Average 30-s wind direction | 0.0403 | Average cabin temperature | −0.2198 |
| Average gearbox oil temperature | 0.4117 | Average cabin cabinet temperature | −0.1544 |
| Average gearbox high-speed end-bearing temperature | 0.7873 | Average main bearing temperature | 0.6464 |
| Average gearbox oil distributor outlet pressure | 0.7491 | Average gearbox low-speed end bearing temperature | 0.6206 |
| Average gearbox oil filter inlet pressure | 0.8267 | Average spindle vibration acceleration | 0.8133 |
| Time | Average Spindle Speed (rpm) | Average Wind Direction (°) | Average Wind Speed (m/s) | Average Power (kW) | ⋯ | Cumulative Power Generation (kW·h) |
|---|---|---|---|---|---|---|
| 1 September 2020 0:00 | 7.1 | 12.9 | 4 | 317 | ⋯ | 4,994,446 |
| 1 September 2020 0:05 | 7.7 | 14.1 | 5.1 | 523.5 | ⋯ | 4,994,491 |
| 1 September 2020 0:10 | 8.5 | 8 | 5.8 | 781.5 | ⋯ | 4,994,552 |
| 1 September 2020 0:15 | 7.1 | 6 | 4.7 | 397.6 | ⋯ | 4,994,584 |
| 1 September 2020 0:20 | 7.1 | −10 | 4.1 | 323.6 | ⋯ | 4,994,609 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Time | Average Spindle Speed | 30-s Average Wind Speed | 30-s Average Power | Average Main Bearing Temperature | ⋯ | Average Spindle Vibration Acceleration |
|---|---|---|---|---|---|---|
| 1 September 2020 0:00 | 0.6514 | 0.2516 | 0.1217 | 0.7977 | ⋯ | 0.2165 |
| 1 September 2020 0:05 | 0.7064 | 0.3082 | 0.2010 | 0.8006 | ⋯ | 0.2921 |
| 1 September 2020 0:10 | 0.7798 | 0.3711 | 0.3 | 0.8064 | ⋯ | 0.1890 |
| 1 September 2020 0:15 | 0.6514 | 0.2956 | 0.1526 | 0.8064 | ⋯ | 0.2027 |
| 1 September 2020 0:20 | 0.6514 | 0.2642 | 0.1242 | 0.8064 | ⋯ | 0.2405 |
| ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ | ⋮ |
| Working Condition Category (i) | Threshold (Ci) | Number of Samples Exceeding the Alarm Threshold (Ai) | Total Number of Samples (Bi) | False-Alarm Rate (Ri) |
|---|---|---|---|---|
| 2 | 0.0127 | 27 | 512 | 5.27% |
| 3 | 0.0144 | 21 | 419 | 5.01% |
| 4 | 0.0142 | 11 | 327 | 3.36% |
| 5 | 0.0136 | 15 | 373 | 4.02% |
| 6 | 0.0142 | 6 | 369 | 1.63% |
| Total | 80 | 2000 | 4.00% |
| Working Condition Category (i) | Threshold (Ci) | Number of Samples Exceeding the Alarm Threshold (Ai) | Total Number of Samples (Bi) | False-Alarm Rate (Ri) |
|---|---|---|---|---|
| 2 | 0.0147 | 7 | 420 | 1.67% |
| 3 | 0.0182 | 3 | 219 | 1.37% |
| 4 | 0.0182 | 0 | 220 | 0 |
| 5 | 0.0169 | 5 | 177 | 2.82% |
| 6 | 0.0172 | 1 | 196 | 0.51% |
| 7 | 0.0164 | 4 | 209 | 1.91% |
| 8 | 0.0161 | 0 | 200 | 0 |
| 9 | 0.0159 | 0 | 200 | 0 |
| 10 | 0.0166 | 3 | 159 | 1.89% |
| Total | 23 | 2000 | 1.15% |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, H.; Xie, C.; Dai, J.; Cen, E.; Li, J. SCADA Data-Based Working Condition Classification for Condition Assessment of Wind Turbine Main Transmission System. Energies 2021, 14, 7043. https://doi.org/10.3390/en14217043
Chen H, Xie C, Dai J, Cen E, Li J. SCADA Data-Based Working Condition Classification for Condition Assessment of Wind Turbine Main Transmission System. Energies. 2021; 14(21):7043. https://doi.org/10.3390/en14217043
Chicago/Turabian StyleChen, Huanguo, Chao Xie, Juchuan Dai, Enjie Cen, and Jianmin Li. 2021. "SCADA Data-Based Working Condition Classification for Condition Assessment of Wind Turbine Main Transmission System" Energies 14, no. 21: 7043. https://doi.org/10.3390/en14217043
APA StyleChen, H., Xie, C., Dai, J., Cen, E., & Li, J. (2021). SCADA Data-Based Working Condition Classification for Condition Assessment of Wind Turbine Main Transmission System. Energies, 14(21), 7043. https://doi.org/10.3390/en14217043






