An Experimental Performance Evaluation for a Swirl-Vane Separator Using an Air-Water Test Facility
Abstract
:1. Introduction
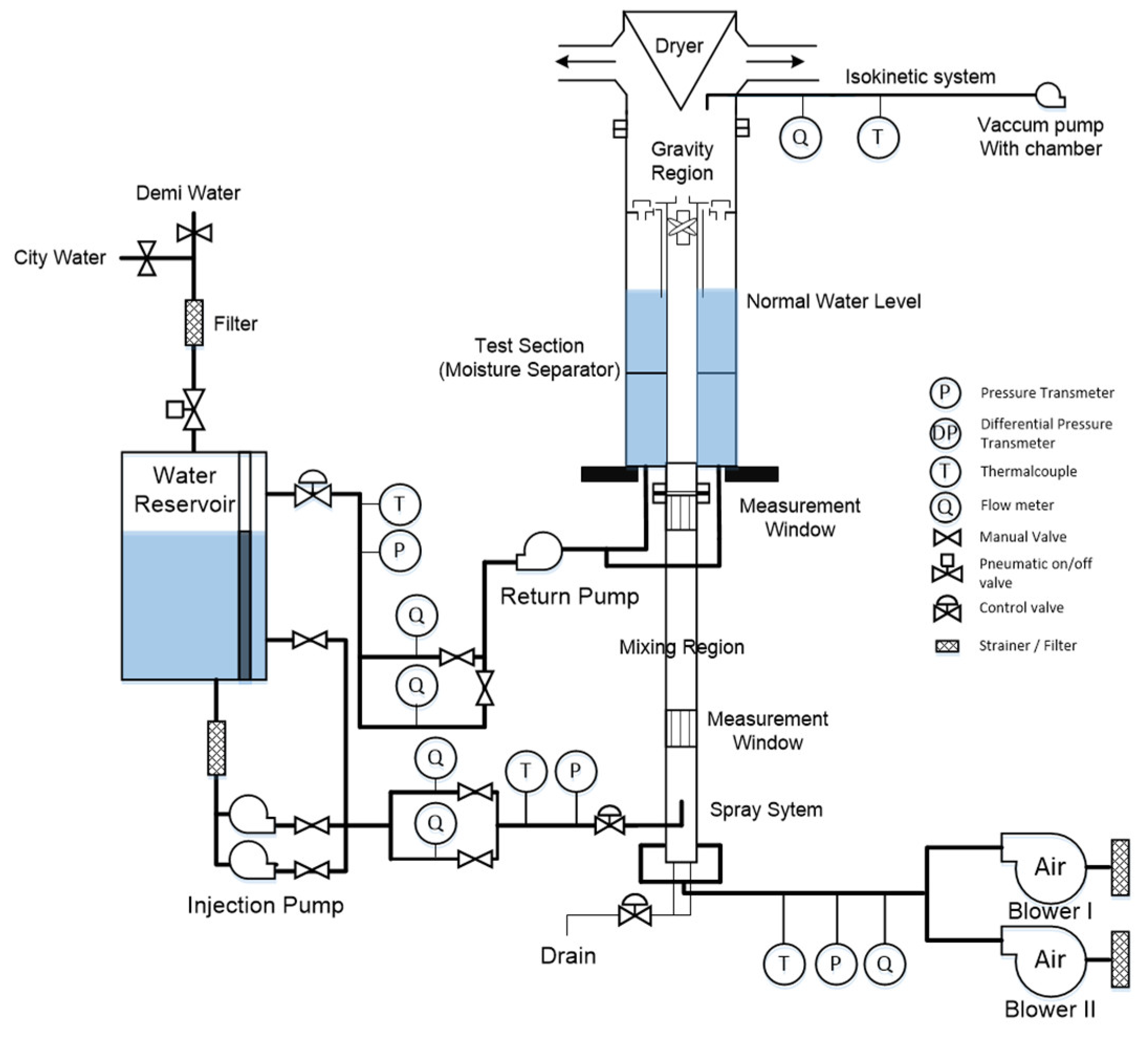
2. Experimental Test Facility and Methods
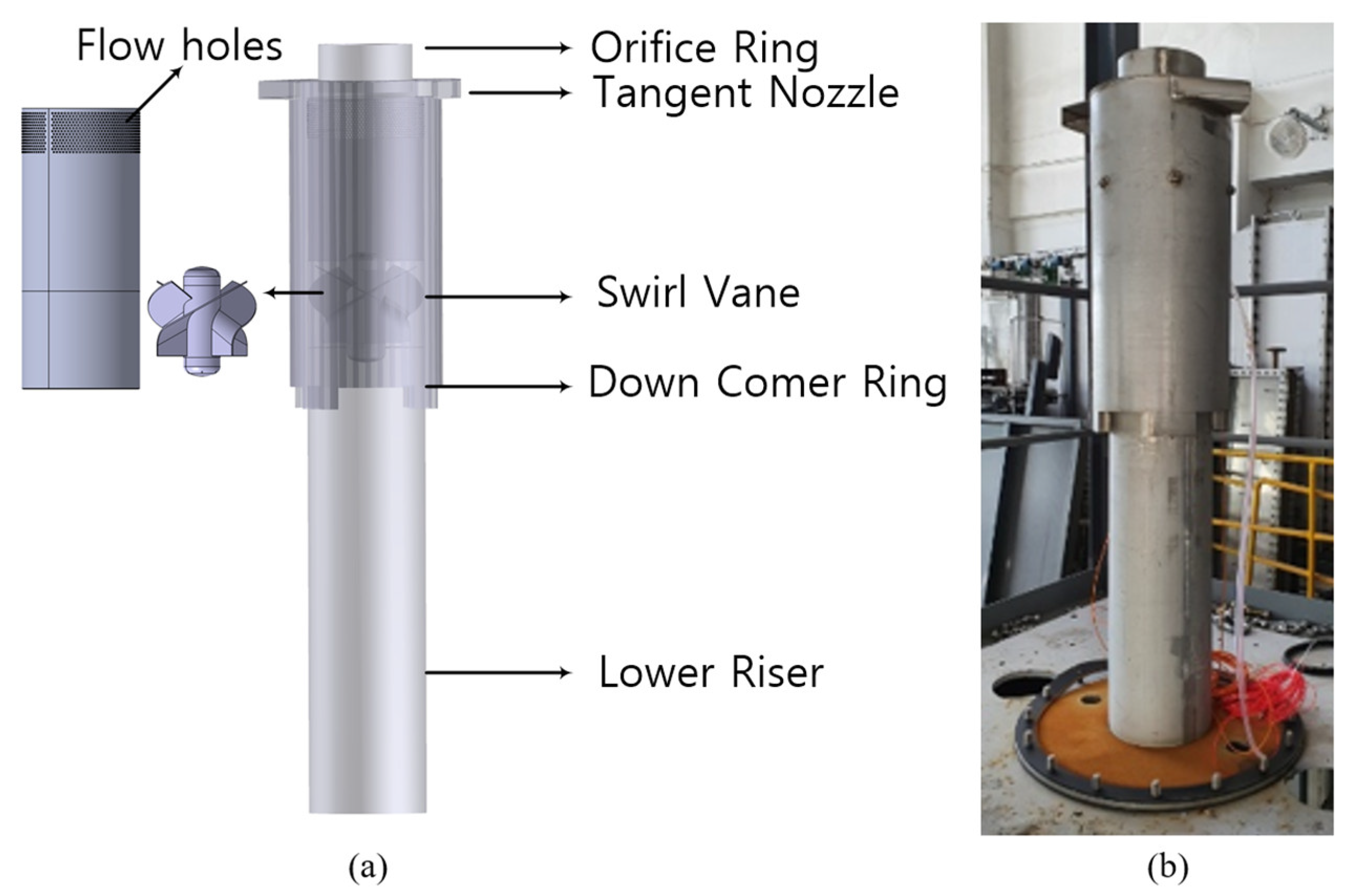
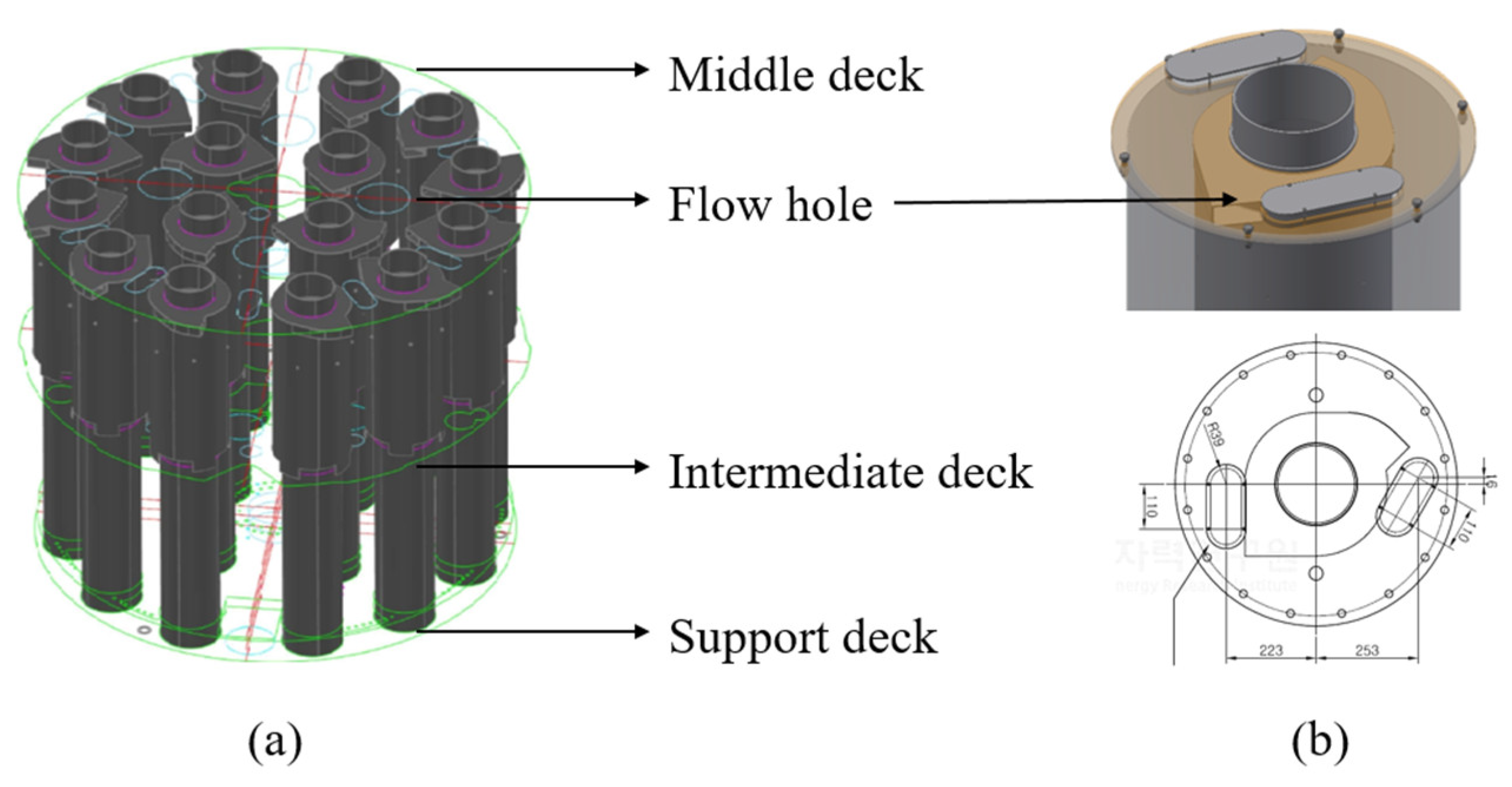
2.1. Half-Sclae Swirl-Vane Separator
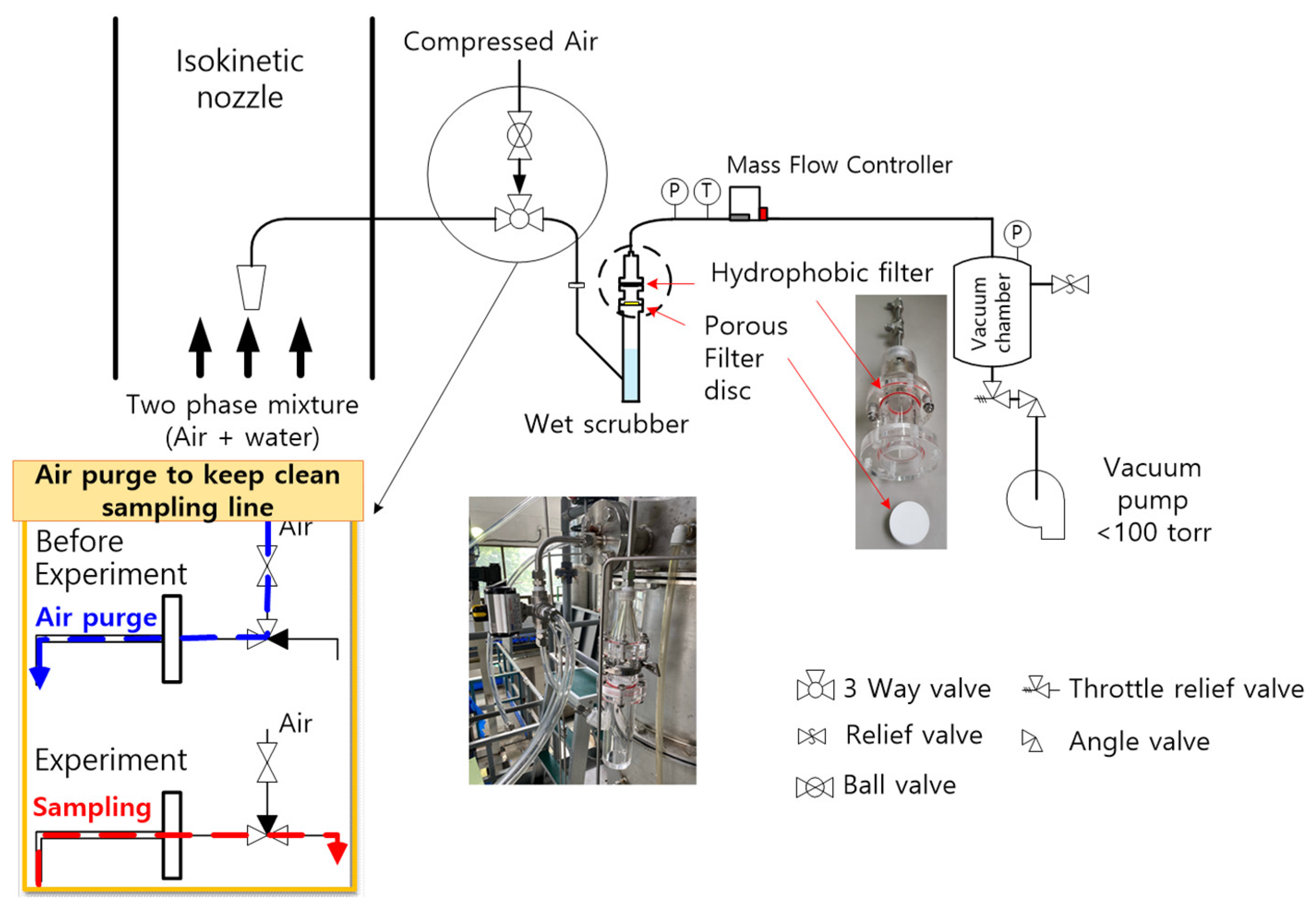
2.2. Experimental Method for MCO
2.3. Prediction Model for the Two-Phase Pressure Drop
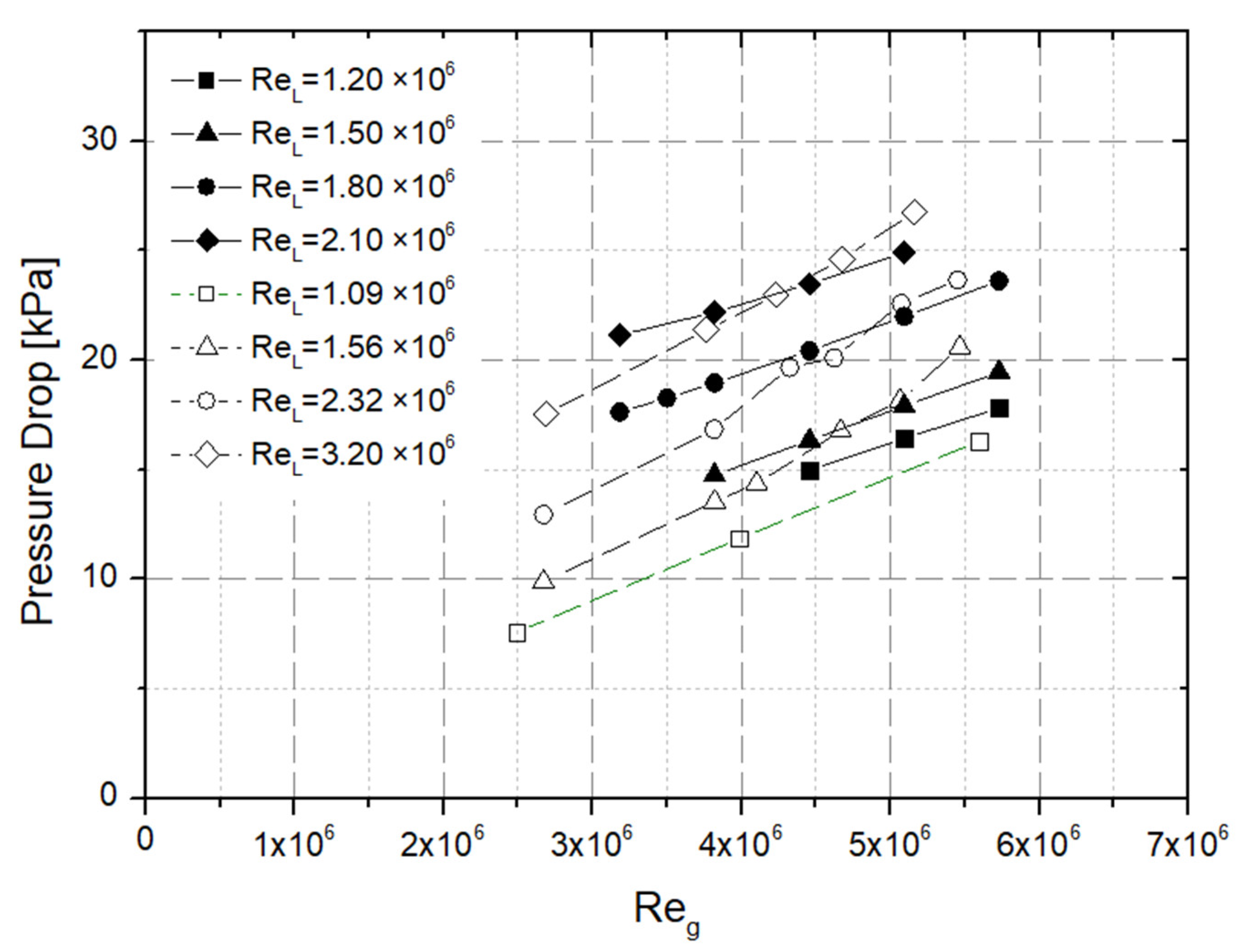
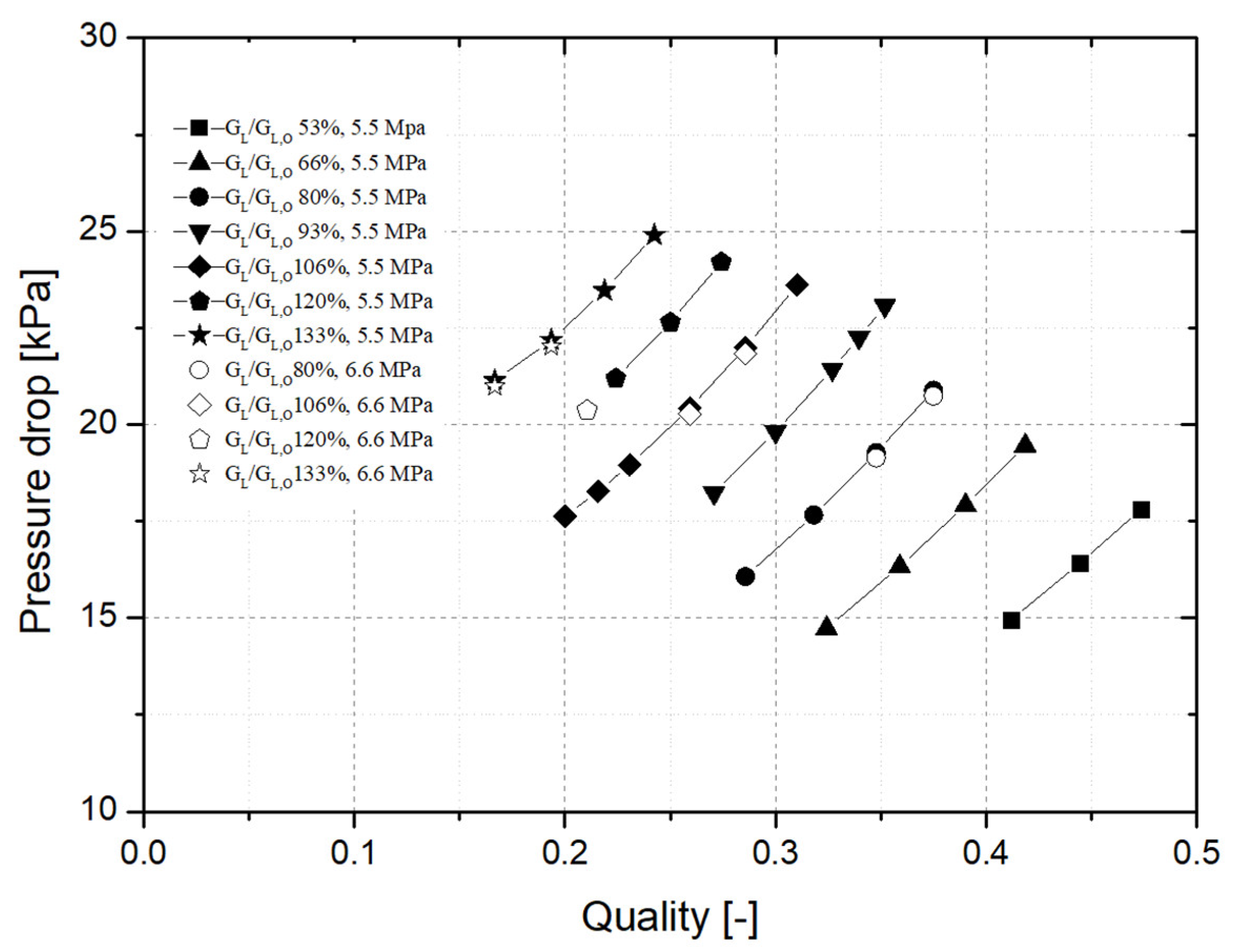
3. Experimental Results
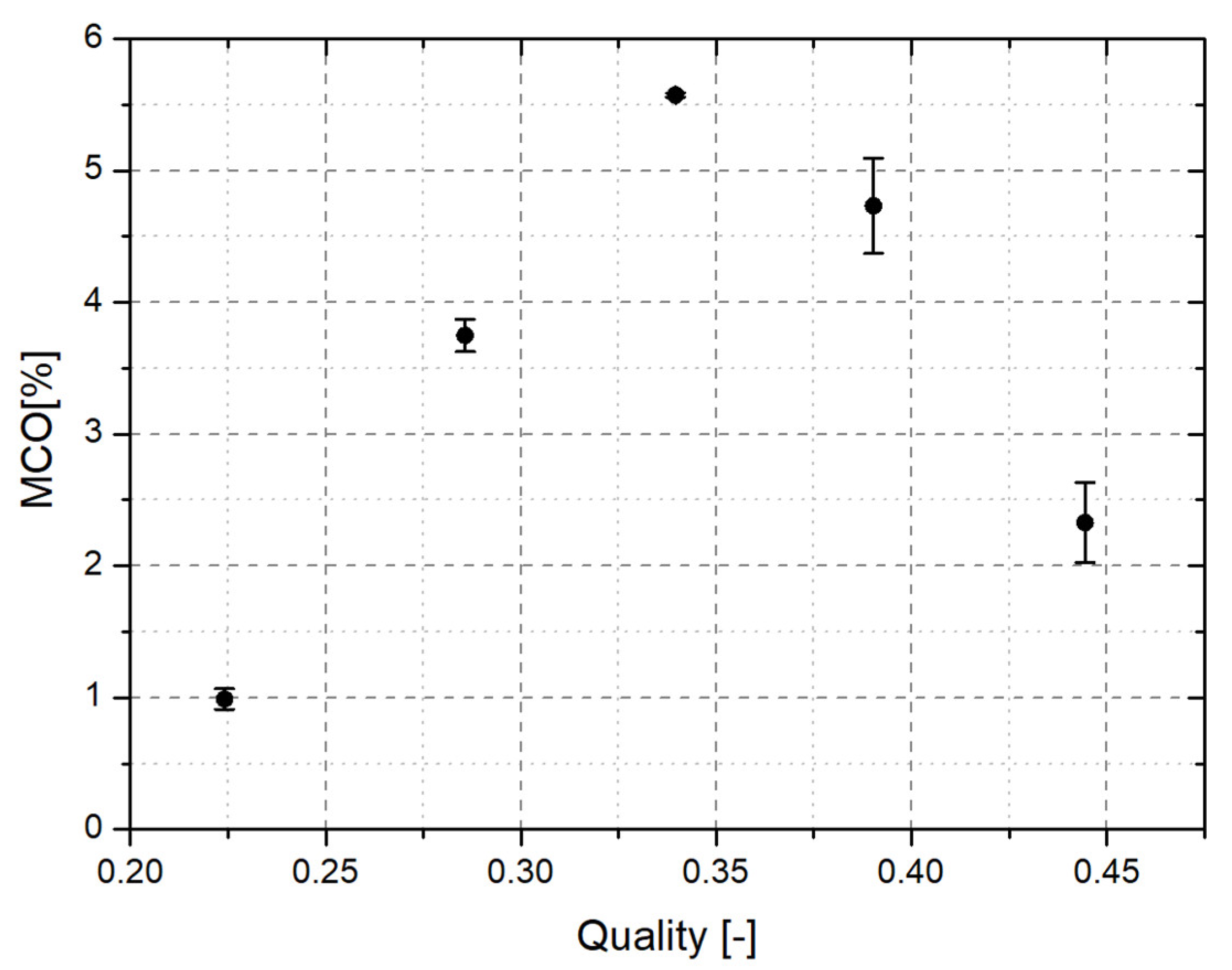
3.1. MCO Test Condtions and Results
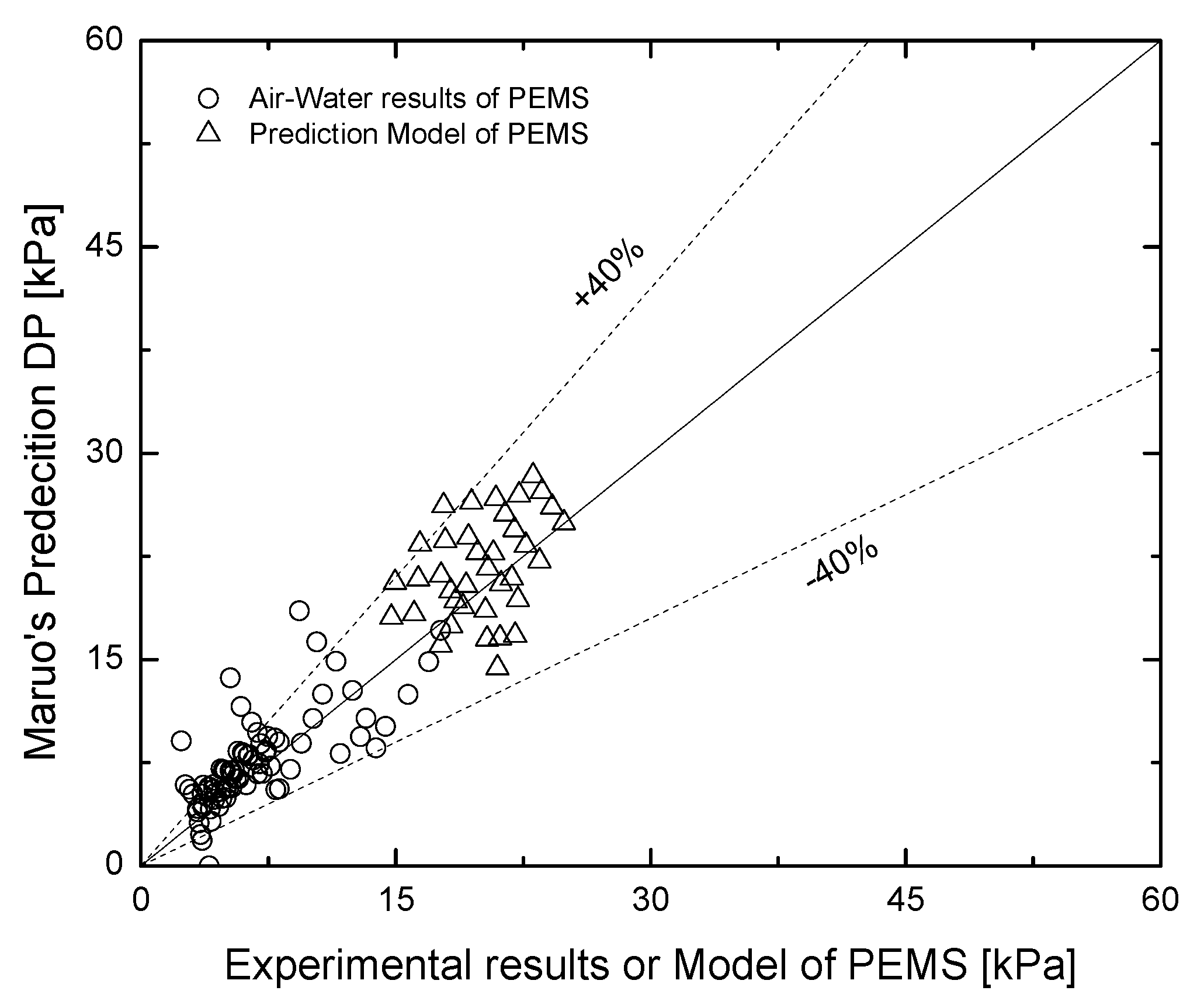
3.2. Improvement of the Emprical Correlation for Two-Phase Pressure Drop
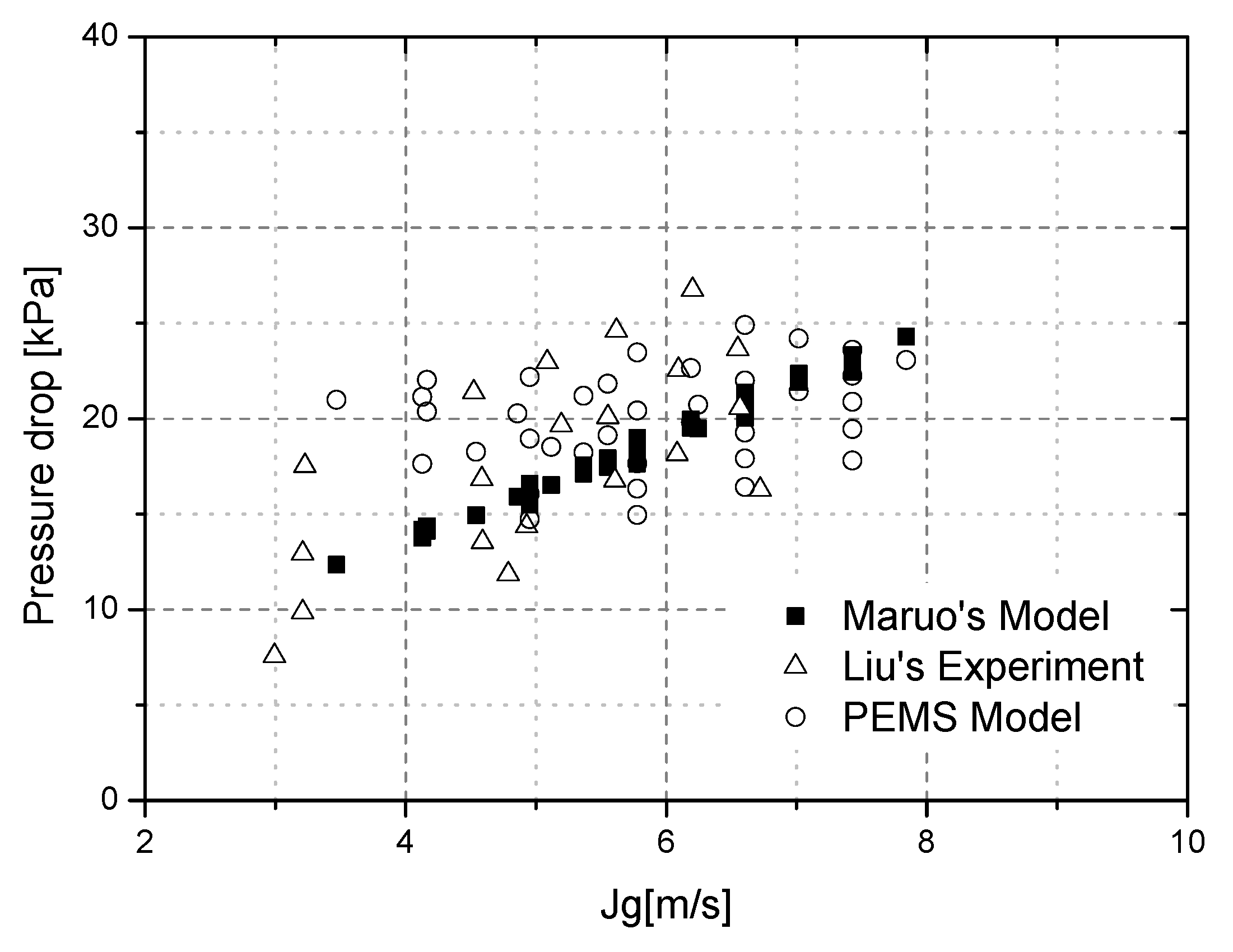
3.3. Discusssion of the Empricial Correlation Model
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Nomenclature
| C.V | coefficient of variation |
| hydraulic diameter of a moisture separator (m) | |
| Eu | Euler number |
| g | acceleration due to gravity (m/s2) |
| Fc | centrifugal force per unit volume (N/m3) |
| G | mass flux (kg/m2 s) |
| j | superficial velocity (m/s) |
| j* | non-dimensional superficial velocity |
| K | loss coefficient |
| average mass flow rate (kg/s) | |
| P | pressure (kPa) |
| Reynolds number | |
| swril-shape factor | |
| t | sampling time (sec) |
| Time (sec) | |
| x | vapor quality |
| averaged value | |
| Greek symbols | |
| void fraction | |
| density (kg/m3) | |
| homogeneous density (kg/m3) | |
| standard deviation | |
| two-phase pressure drop multiplier | |
| Subscripts | |
| 1 | single-phase |
| 2 | two-phase |
| a | air |
| CE | combustion engineering type |
| f | liquid phase |
| g | gas phase |
| i | index of sampling time |
| LO | meaning of liquid only |
| m | air/water model |
| MFC | mass flow controller |
| p | prototype model |
| tot | total |
| T | measurement time (s) |
| w | water |
| WH | westinghouse type |
References
- Paik, C.Y.; Mullen, G.; Knoess, C.; Griffith, P. Steam separator modeling for various nuclear reactor transients. Nucl. Eng. Des. 1988, 108, 83–97. [Google Scholar] [CrossRef]
- Green, S.J.; Hestroni, G. PWR steam generators. Int. J. Multiph. 1995, 21, 1–97. [Google Scholar] [CrossRef]
- Xiong, Z.; Lu, M.; Wang, M.; Gu, H.; Chen, X. Study on flow pattern and separation performance for air-water swirl-van separator. Ann. Nucl. Energy 2014, 63, 138–145. [Google Scholar] [CrossRef]
- Funahashi, H.; Hayashi, K.; Hosokawa, S.; Tomiyama, A. Study on two-phase swirling flows in a gas-liquid separator with three pick-off rings. Nucl. Eng. Des. 2016, 308, 205–213. [Google Scholar] [CrossRef]
- Liu, S.; Yang, L.L.; Zhang, D.; Xu, J.Y. Separation characteristics of the gas and liquid phases in a vane-type swirling flow field. Int. J. Multiph. Flow 2018, 107, 131–145. [Google Scholar] [CrossRef] [Green Version]
- Hoffmann, A.C.; Stein, L.E. Gas Cyclones and Swirl Tubes, 2nd ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Sun, F.T.; Xiangbo, L.; Ming, X.; Zhongning, S. The investigation on performance of steam generator stationary vane separator. Chin. J. Nucl. Sci. Eng. 1994, 15, 213–219. [Google Scholar]
- Liu, L.; Bai, B. Scaling laws for gas–liquid flow in swirl vane separators. Nucl. Eng. Des. 2016, 298, 229–239. [Google Scholar] [CrossRef]
- Mauro, G.; Sala, M.; Hetsroni, G. Improved Italian moisture separators (IIMS). Nucl. Eng. Des. 1990, 118, 179–192. [Google Scholar] [CrossRef]
- Katono, K.; Ishida, N.; Sumikawa, T.; Yasuda, K. Air-water Downscaled Experiments and Three-dimensional Two-phase Flow Simulations of Improved Steam Separator for Boiling Water Reactor. Nucl. Eng. Des. 2014, 278, 465–471. [Google Scholar] [CrossRef]
- Kim, K.; Kim, W.; Lee, J.; Jeon, W. Development and experimental validation for quantifying the moisture carryover in a moisture separator using an air/water test facility. Sci. Technol. Nucl. Install. 2021, 2021, 5522439. [Google Scholar] [CrossRef]
- Kim, W.; Lee, J.; Kim, K. Development of empirical correlation of two-phase pressure drop in moisture separator based on separated flow model. Energies 2021, 14, 4448. [Google Scholar] [CrossRef]
- Liu, L.; Ying, B.; Gu, H.; Xu, D.; Huang, C.; Chen, S. Experimental study on the separation performance of a full-scale SG steam-water separator. Ann. Nucl. Energy 2020, 141, 1–12. [Google Scholar] [CrossRef]
- Kim, K.; Lee, J.; Kim, W.; Choi, H.; Kim, J.I. Development of a prediction model relating the two-phase pressure drop in a moisture separator using an air/water test facility. Nucl. Eng. Technol 2021, in press. [Google Scholar]
- Wallis, G.B. One-Dimensional Two-Phase Flow; McGraw-Hill Inc.: New York, NY, USA, 1969. [Google Scholar]
- Zeghloul, A.; Azzi, A.; Saidj, F.; Messilem, A.; Azzopardi, B.J. Pressure drop through orifices for single- and two-phase vertically upward flow–implication for metering. J. Fluids Eng. 2017, 139, 031302. [Google Scholar] [CrossRef]
- Funahashi, H.; Kirkland, V.; Hayashi, K.; Hosokwa, S.; Tomiyama, A. Interfacial and wall friction factors of swirling annular flow in a vertical pipe. Nucl. Eng. Des. 2018, 330, 97–205. [Google Scholar] [CrossRef]



| Parameter | Operating Range |
|---|---|
| Design Pressure | 0.5 MPa |
| Design Temperature | 60 |
| Separator Diameter | 0.14~0.5 m |
| Separator Height | 0.79~3.4 |
| Water mass flow rate | 0.6 m3/min (ref. 1 atm, head of 57 m) |
| Air mass flow rate | 110 m3/min (ref. 1 atm, head of 1.2 kgf/cm2) |
| Parameter | Prototype | PEMS |
|---|---|---|
| Operating pressure [MPa] | 5.6 or 6.6 | 0.1 to 0.2 |
| Operating temperature [] | 270.9~281.4 | 15~30 |
| Separator diameter ratio [-] | 1 | 1/2 |
| Aspect ratio [-] | 1 | 1/2 |
| Area ratio [-] | 1 | 1/4 |
| Quality [-] | 1 | 1 |
| Centrifugal force [N/m3] | 1 | 1 |
| Parameter/Pres. (Prototype) | 5.5 MPa | 6.5 MPa | ||
|---|---|---|---|---|
| Quality | 0.348 | 0.375 | 0.348 | 0.375 |
| Centrifugal force [N/m3] | 15,445.7 | 18,000.4 | 13,169.7 | 15,325.5 |
| [m/s] of PEMS | 0.053 | 0.053 | 0.049 | 0.049 |
| [m/s] of PEMS | 23.5 | 26.3 | 21.7 | 24.3 |
| No. | Inlet Pres. (kPa) | Inlet Temp. (°C) | ρg (kg/m3) | ΔPg (kPa) | jg (m/s) | Eu (-) |
|---|---|---|---|---|---|---|
| 1 | 103.3 | 11.5 | 1.265 | 1.677 | 14.2 | 6.574 |
| 2 | 103.9 | 17.8 | 1.243 | 2.207 | 16.2 | 6.728 |
| 3 | 105.1 | 18.0 | 1.257 | 3.510 | 20.4 | 6.722 |
| 4 | 106.7 | 19.0 | 1.273 | 5.146 | 24.5 | 6.749 |
| 5 | 108.6 | 20.6 | 1.288 | 7.019 | 28.4 | 6.745 |
| 6 | 110.9 | 23.9 | 1.300 | 9.302 | 32.1 | 6.929 |
| 7 | 113.5 | 26.2 | 1.321 | 11.861 | 36.0 | 6.943 |
| CE Separator | WH Separator | |||||
|---|---|---|---|---|---|---|
| Quality | jg (m/s) | ΔP (kPa) | Quality | jg (m/s) | ΔP (kPa) | |
| 0.314 | 23.3 | 16.78 | 0.315 | 23.4 | 6.47 | 2.60 |
| 0.364 | 24.0 | 15.58 | 0.365 | 24.0 | 6.37 | 2.45 |
| 0.440 | 25.0 | 14.30 | 0.441 | 24.9 | 6.38 | 2.24 |
| 0.419 | 23.4 | 12.32 | 0.422 | 23.5 | 5.60 | 2.20 |
| 0.346 | 22.7 | 13.48 | 0.346 | 22.8 | 5.67 | 2.38 |
| 0.297 | 21.9 | 14.55 | 0.296 | 21.8 | 5.57 | 2.61 |
| 0.288 | 21.2 | 13.43 | 0.287 | 21.3 | 5.27 | 2.55 |
| 0.335 | 21.9 | 12.50 | 0.336 | 22.0 | 5.25 | 2.38 |
| 0.410 | 22.8 | 11.39 | 0.411 | 22.8 | 5.18 | 2.20 |
| 0.375 | 20.2 | 9.05 | 0.376 | 20.2 | 4.15 | 2.18 |
| 0.305 | 19.5 | 9.95 | 0.303 | 19.6 | 4.29 | 2.32 |
| 0.260 | 18.9 | 10.72 | 0.260 | 19.0 | 4.37 | 2.45 |
| 0.217 | 15.4 | 7.06 | 0.216 | 15.4 | 3.09 | 2.29 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, K.; Kim, W.-S.; Lee, J.-B. An Experimental Performance Evaluation for a Swirl-Vane Separator Using an Air-Water Test Facility. Energies 2021, 14, 7072. https://doi.org/10.3390/en14217072
Kim K, Kim W-S, Lee J-B. An Experimental Performance Evaluation for a Swirl-Vane Separator Using an Air-Water Test Facility. Energies. 2021; 14(21):7072. https://doi.org/10.3390/en14217072
Chicago/Turabian StyleKim, Kihwan, Woo-Shik Kim, and Jae-Bong Lee. 2021. "An Experimental Performance Evaluation for a Swirl-Vane Separator Using an Air-Water Test Facility" Energies 14, no. 21: 7072. https://doi.org/10.3390/en14217072
APA StyleKim, K., Kim, W.-S., & Lee, J.-B. (2021). An Experimental Performance Evaluation for a Swirl-Vane Separator Using an Air-Water Test Facility. Energies, 14(21), 7072. https://doi.org/10.3390/en14217072






