Dimensioning Optimization of the Permanent Magnet Synchronous Generator for Direct Drive Wind Turbines

Abstract

In the present work, a methodology that allows optimizing the permanent magnet synchronous generator (PMSG) design by establishing limit values of magnet radius and length that maximize efficiency for the nominal parameters of the wind turbine is developed. The methodology consists of two fundamental models. One model calculates the generator parameters from the radius of the magnet base, and the other optimization model determines two optimum generators according to the optimization criteria of maximum efficiency and maximum efficiency with minimum weight starting from the axial length and the radius of the magnet base. For the optimization, the numerical method of the golden section was used. The model was validated from a 10 kW PMSG and the results of two optimum generators are presented according to the optimization criteria. In addition, when the obtained results are compared with the reference electric generator, an increase in efficiency of 1.15% and 0.81% and a reduction in weight of 30.79% and 39.15% of the optimized generators are obtained for maximum efficiency and minimum weight, respectively. Intermediate options between the maximum efficiency generator and the minimum weight generator allows for the selection of the optimum dimensioning for the electric generator as a function of the parameters from the wind turbine design.

1. Introduction

The permanent magnet synchronous generator (PMSG) used for wind systems should have low weight [1,2] and high efficiency [3,4]; therefore, the PMGS geometry has been modified to reduce the volume of the materials for its production [4,5,6,7,8].

For the PMSG optimization, the magnetic model and the equivalent circuit are generally used to obtain the parameters at their nominal operation point [5,7,8,9,10]. To solve these models the finite analysis methods, genetic algorithms, or analytical calculations are used [9,11,12]; however, the differences in the results from these methods are minimal. Some researchers also consider the properties of the materials for the PMGS construction and its geometry [6,13] and then their theory is validated with experimental prototypes [8,9,14,15].

The input parameters for the electric generator dimensioning are usually obtained from the output parameters of the wind turbine rotor design [15,16,17], which are also obtained from the statistical model of Weibull or Raleigh [11,15,18].

The statistical models are also used for the estimation of the annual energy production (AEP) [11,12,19] and then the energy produced by the wind turbine at each wind speed is obtained from the simulation of the wind turbine rotor coupled to the PMSG [16,17,19], including the data of the maintenance and the emplacement.

Obtaining the highest AEP from the emplacement is commonly a criterion for wind turbine optimization for the fastest economic recovery [11,12,18,19]; H. Li, z. Chen et al., 2009 [12] optimized a PMSG design using a genetic algorithm and compared it to a 500 kW generator to demonstrate the effectiveness of the optimization, the wind turbine rotor dimension, and the AEP.

Another criterion used for the PMSG optimization is the reduction of the cogging to use the low wind speeds [8,10,14,20]; Potgieter et al., 2012 [7] proposed a method to identify the low pair of the cogging region through the variation of the magnet geometry of the PMSG.

The reduction of the PMSG weight is also an optimization criterion for its application on wind turbines to minimize the fixed and variable losses and to maximize the PMSG efficiency [21,22,23,24]; Chen et al., 2021 [24] simulated a cross-flow PMSG to reduce the volume of the magnetic poles using the finite element method and the magnetic equivalent circuit. In this work, they reported the yield improvement of the machine with a low volume of the magnetic poles and high-power density.

The relation of the weight of the PMSG with the cost is another criterion used for the wind turbines design where the goal is to reduce the energy and the wind turbine cost [16,23,25,26]; as Machado et al., 2016 [16], reported a multi-disciplinary optimization (MDO) of 55 kW PMSG to reduce the cost. This work included the cost models and the power converter losses and they obtained three options which simplified to one when the phase angle was considered in the power converter [16].

Maximizing the PMSG efficiency is another criterion used for wind turbines optimization [10,16,22,27,28]; with this goal, Tapia et al. [27] modified the stator geometry and obtained the PMSG losses with the equivalent circuit which was validated with the construction of a 10 kW prototype.

Generally, the research works related to the PMSG optimization for wind turbines have obtained only a design as the result of the criteria used for the optimization [14,24,25,29,30]. This contribution aims to develop an optimization methodology for the PMSG dimensioning to be coupled to wind turbines regarding the wind resource, the turbine rotor, and the power converter; also the PMSG dimensioning involves two optimization criteria where for each radius of the magnet base (R_bi), the generator was optimized based on maximum efficiency and later the obtained optimal generator for maximum efficiency that had the minimum weight was searched but the optimization process based on minimum weight was not carried out. Finally, two designs of the electric generator were obtained and compared with a commercial prototype of 10 kW used as reference.

In contrast with the reviewed previous works, the present study establishes a procedure that allows one to obtain in a practical way dimension of an optimal PMSG for maximum efficiency with a method that defines the limits of maximum efficiency and minimum weight for maximum efficiency. This avoids PMSG solutions with greater weight and lower efficiencies and gives design options that guarantee the combination of both requirements depending on the design parameters of the wind turbine.

2. Materials and Methods

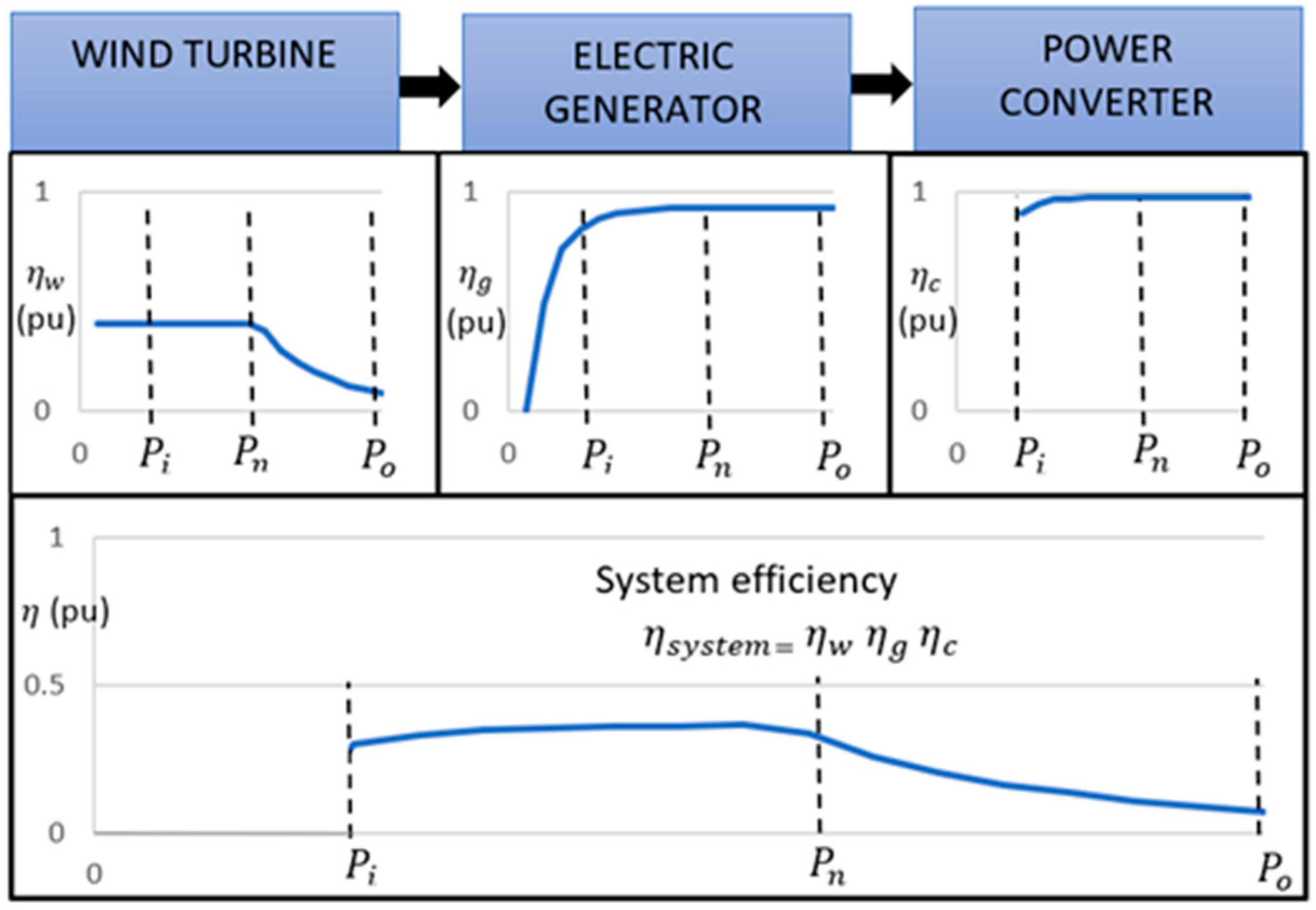
The output power of a wind turbine depends on the efficiency of each component (Figure 1). To maximize the efficiency of the system, the efficiency of the PMSG for wind turbines must be the maximum in the operation range which depends on initial power (pin) and the output power (pout).

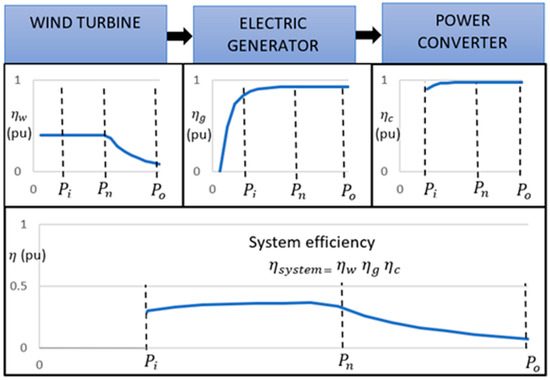
Figure 1. Efficiencies of the direct drive wind turbines components (obtained from own simulations).

2.1. Mechanical Power

The maximum mechanical power used by the turbine rotor from the available wind is given in Equation (1) [16].

$$P_{mec}=\frac{1}{2}\rho A{v}^3{C}_p=T_m{\omega }_m$$

(1)

where Cp is the power coefficient, ρ is the air density, A is the cross-section area of the turbine rotor, v is the wind speed, T_m is the mechanical torque from the turbine rotor to the PMSG shaft, and ω_m is the angular speed of the shaft.

2.2. Design Conditions

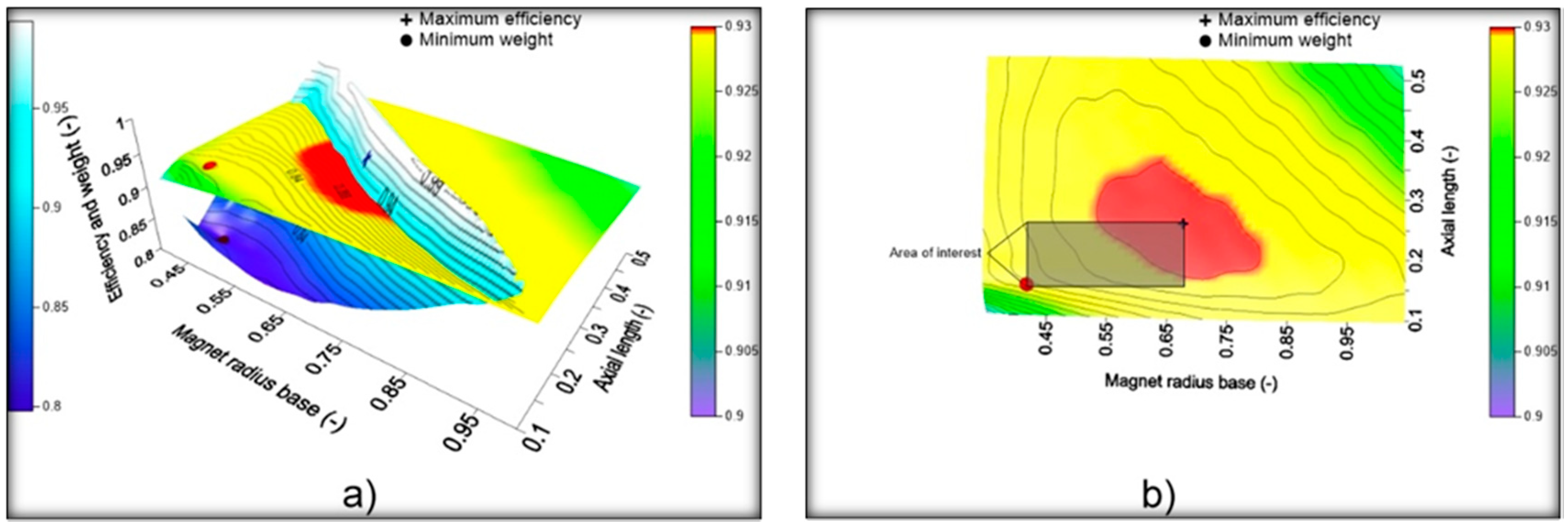
The maximum efficiency and the lowest weight of the PMGS are generally the criteria for the PMSG design for wind turbines applications. Figure 2a shows the typical behavior of the weight PMSG increases for lower values of R_bimin and L_min and similar efficiencies with lower weights can be obtained at lower values of de R_bimax y L_max to higher values, as Figure 2b shows. These limits also imply an area that represents the radio options and the possible lengths for the PMSG design for direct shaft wind turbines.

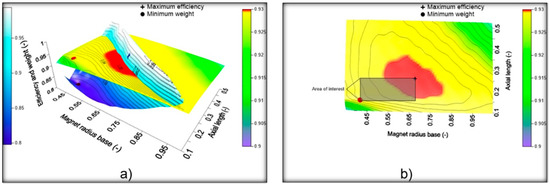
Figure 2. (a) Efficiencies behavior and weights of the electric generator with different dimensions. Area of the analysis delimited by the maximums and minimums points; (b) Interest area from the superior view (obtained from own simulations).

2.3. PMSG Design

The fundamental equations used for the PMSG design were obtained from the analytic analysis of the magnetic circuit of the permanent magnet synchronous motor [31]. These equations are resumed as follows:

2.4. PMGS Efficiency

The PMSG efficiency (η) depends on the process losses from the mechanical power conversion to electrical power as in Equation (2) [15,17,27,28,31].

$$\eta =\frac{P_{elec}}{P_{mec}}=\frac{P_{mec}-P_{Cu}-P_{Fe}-P_o}{P_{mec}}$$

(2)

where P_mec is the mechanical power from the turbine rotor and P_elec is the electrical power which depends on the copper losses P_cu, the iron core losses P_Fe, and other losses P_o.

2.5. Copper Losses

The copper losses depend on the ohmic resistance (R_ph) of a single-phase coil, the phase current (I_ph) through the conductor, and the number of phases of the PMSG (N_ph) [17,18,27,29,31] as in Equation (3).

$$P_{cu}=N_{ph}{I}_{ph}^2{R}_{ph}$$

(3)

2.6. Iron Core Losses

The iron losses depend on the electrical properties and the stator volume (Vol_est) [13,15,17,18,22,23,31], as in Equation (4).

$$P_{Fe}=\left(\left(K_h{f}_e{B}_m^2\right)+\left(k_e{f}_e^2{B}_m^2\right)+\left(K_c{f}_e^{1.5}{B}_m^{1.5}\right)\right)Vo{l}_{est}$$

(4)

where f_e is the electrical frequency, B_m is the maximum flux density of the iron; K_h, k_e, and K_c are the losses constants due to the properties of the iron alloy known as hysteresis loss, Eddy current loss, and coupling loss respectively [13,17,22,32]. The Vol_est of the radial flow PMSG was calculated with Equation (5)

$$Vo{l}_{est}=\left(\pi \left(R_{so}^2-R_{si}^2\right)-N_s{A}_s\right)L{K}_{st}$$

(5)

where R_so is the stator outer radius, R_si is the stator inner radius, N_s is the number of splines, A_s is the spline area, K_st is the stacking factor, and L is the PMSG axial length.

2.7. Other Losses

These losses involve the mechanical losses due to the bearing friction and the internal turbulence produced by the rotor of the electric generator. The Eddy currents losses in the rotor core are not considered because they are subjected to a continuous magnetic field [9,18,21].

2.8. Geometric Parameters of the PMSG

The rotor outer radius (R_er) is determined by R_bi and the magnet height (A_i) as Equation (6):

$$R_{er}=R_{bi}+A_{i }$$

(6)

The inner stator radius (R_si) is determined by R_er and the air gap (g) as Equation (7):

$$R_{si}=R_{er}+g$$

(7)

The outer stator radius (R_so) is calculated by R_si, the total spline depth (d_s), and the width of the stator back iron (w_bi) as Equation (8):

$$R_{so}=R_{si}+d_{s }+w_{bi }$$

(8)

2.9. Electrical Parameters

To determine the electrical parameters these were the considerations: a unity power factor, a parallel magnet surface to the inner stator surface, a square wave shape of the electrical sign which generates a pair of poles, and then the electromotive force (E_rms) is equal to the maximum (E_max) as Equation (9)

$$E_{max}=N_m{K}_d{K}_p{K}_s{B}_{g}L R_{ro}{N}_{spp }{n}_s{\omega }_m$$

(9)

where L is the axial length of the PMSG (which is the same for the rotor and the stator) R_ro is the rotor outer radius, B_g is the field density of the airgap, N_m is the number of magnetic poles, n_s is the number of turns per slot, N_spp is the number of slots per poles per phase, and K_d, K_p, K_s are the engine characteristic constants [31].

The PMSG current density (I_s) is determined from the mechanical torque (T_m) as Equation (10).

$$I_s=\frac{T_m}{N_m{K}_d{K}_p{K}_s{B}_{g}L R_{ro}{N}_{spp}}$$

(10)

The phase electric current (I_ph) is the relation between the I_s and the number of splines (N_s) and the number of the PMSG phases (N_ph) as in Equation (11).

$$I_{ph}=\frac{I_s}{N_{ph}{N}_s}$$

(11)

The phase voltage (V_ph) is the argument of the vector $\overrightarrow{V_{ph}}$ calculated from the equivalent circuit of the one-phase PMSG and its phasor diagram.

$$\overrightarrow{V_{ph}}=\overrightarrow{FEM}-j{X}_S\overrightarrow{I_{ph}}-R_{ph}\overrightarrow{I_{ph}}$$

(12)

Equation (13) shows the balance of the PMSG power.

$$P_{elec}=P_{mec}-P_{Cu}-P_{Fe}-P_o=3V_{ph}{I}_{ph}$$

(13)

2.10. Methodology Development

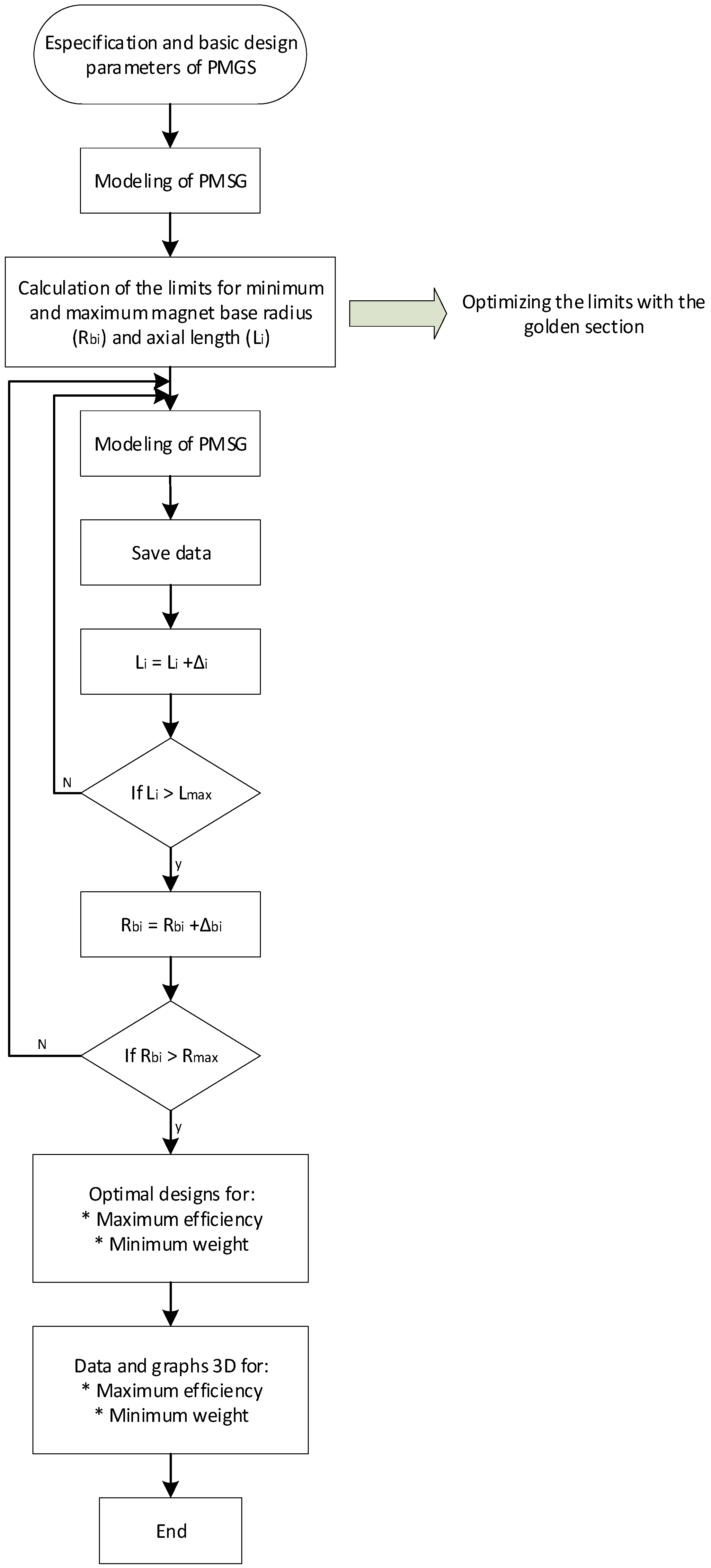
The methodology developed for the optimization is shown in the diagram of Figure 3 where the characteristics of the materials used are considered from the beginning as well as the design specifications for the PMSG (P_m, ω_m, R_bimax, R_bimin, and others) which were obtained from the nominal wind speed of the turbine rotor.

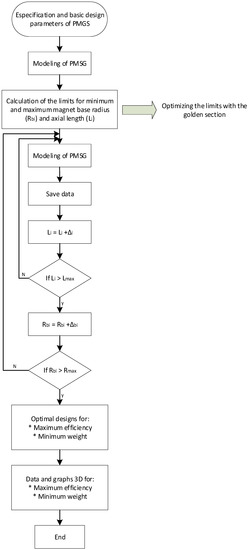
Figure 3. General flow diagram of the PMSG optimization.

First, the PMSG parameters for each optimization criterion are determined through a simulation process, in this way the R_bi and L values for each optimization criterion that define the limits used for the implementation of the methodology are obtained using the numerical method of the golden section (Steps 1–3).

Later, an analysis is carried out within the optimization limits to present alternatives of PMSG dimensioning to obtain a better option that couples to the components of the wind turbine. Two optimal dimensioning based on each criterium and the general mapping within the limits are obtained.

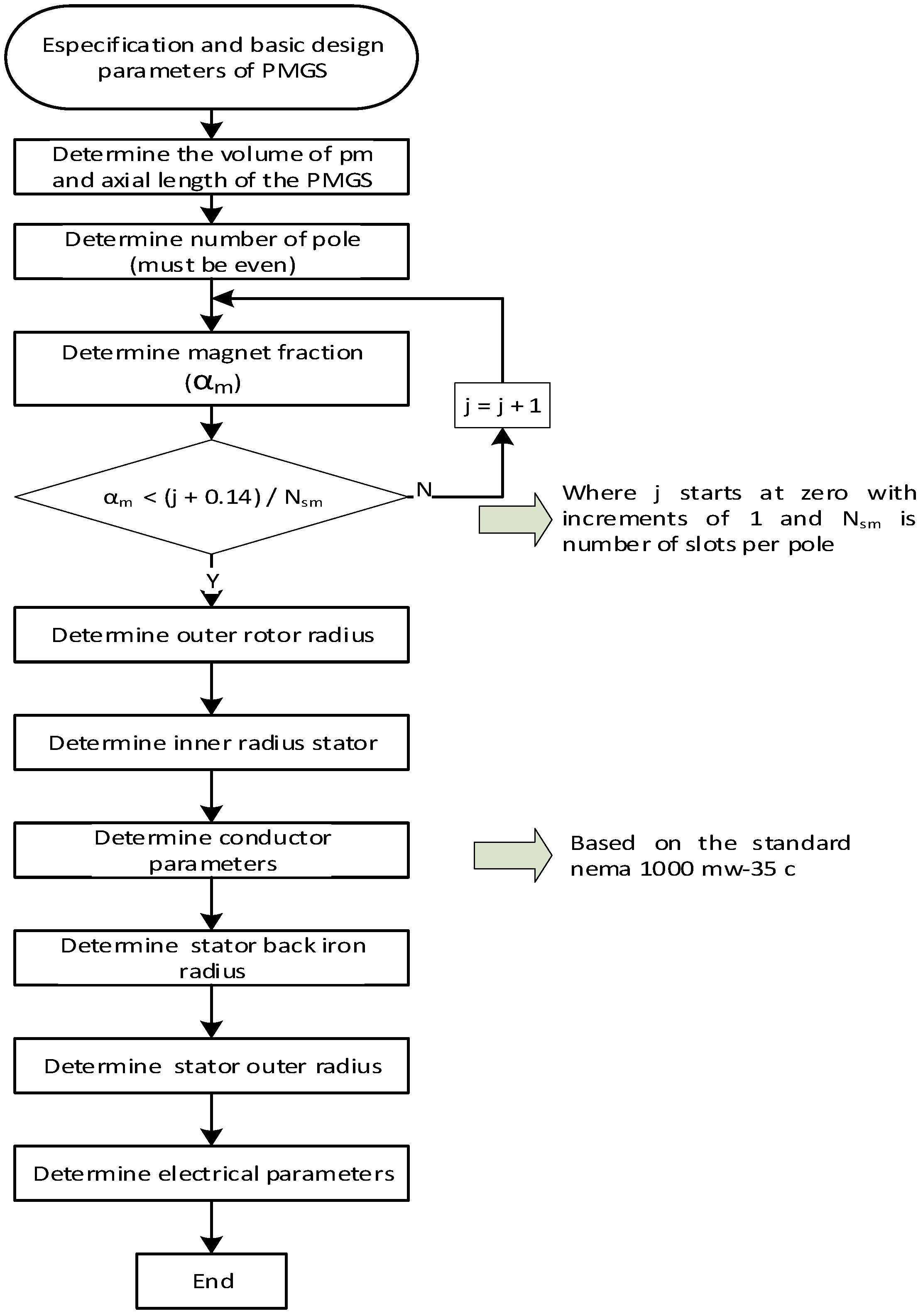
Figure 4 shows the PMSG sizing procedure where the input variable R_bi is related to fixed parameters such as volume of magnets, number of poles, number of slots, number of phases, and magnetic fraction. It then calculates the height and length of the magnet that maximizes efficiency to obtain the geometry of the PMSG and to determine the output parameters such as efficiency, current, voltages, power, phase resistance, copper losses, iron losses, power density, weight, and others.

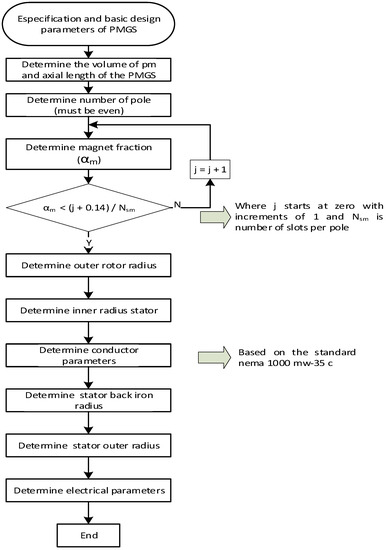
Figure 4. Flow diagram for the dimensions of the PMGS.

Finally, the simulations of the wind turbine are carried out to determine the power and efficiency curves using the method of the reference [17] and with these curves the energy produced from the Weibull distribution that characterizes the site is determined.

3. Results and Discussion

The methodology was validated using data from a PMGS prototype as a reference to calibrate the dimensioning software. This PMSG prototype of 10 kW was designed and fabricated by a specialized company. The material considered for the stator core was the JFE50JN400, Nd-Fe-B grade 35 for the permanent magnets and copper for the coils. These values are shown in Table 1.

Table 1. Calibration parameters for the PMSG dimensioning program.

Characteristic	Real Value	Reference	Error (%)
Mechanical angular speed	210 rpm	210.15 rpm	0.07
Line voltage	242.81 V	240 V	1.17
Output power	10 kVA	10.09 kVA	0.89
Current	24.002 A	24.0 A	0.01
Efficiency	92%	92.04%	0.04
Electrical frequency	56.04 Hz	56 Hz	0.07
Inner resistance	0.27 Ω	0.27 Ω	0.00
Total weight	82.0 kg	82.0 kg	0.00

The input fixed parameters used for the validation are shown in Table 2.

Table 2. Fixed parameters for the PMSG design.

Power	10 kW
FEM	260 V
Mechanical angular speed	210 rpm
Electrical frequency	56 Hz
Number of phases	3
Air gap	0.1 cm
Slot opening	0.3 cm
Shoe depth fraction	5
Number of slots per phase per pole	1

The proposed optimization methodology is applied and as a result, two optimal PMSG dimensioning is obtained in conformity with each optimization criterion; the fundamental parameters are compared with the reference PMSG as shown in Table 3.

Table 3. Comparison of the results for the different simulated optimization criteria.

Characteristics	Reference	Maximum Efficiency	Minimum Weight
Apparent power	10.09 kVA	10.21 kVA	10.18 kVA
Current	24.00 A	24.53 A	23.25 A
Line voltage	240 V	240.4 V	252.8 V
Efficiency	92.04%	93.1%	92.79%
Iron losses	411.27 W	408.95 W	369.93 W
Copper losses	466.64 W	348.23 W	421.18 W
Inner resistance	0.27 Ω	0.192 Ω	0.259 Ω
Total weight	82.00 kg	56.75 kg	49.89 kg
Axial length	19.70 cm	6.89 cm	5.91 cm
Output stator radius	18.85 cm	31.75 cm	27.98 cm
Magnet base radius	14.30 cm	26.5 cm	21.1 cm
Power density	123.12 W/kg	180.03 W/kg	204.11 W/kg

The optimal PMSG for maximum efficiency presented 1.06% more efficiency than that of the reference PMSG and the optimal PMSG for minimum weight showed a 0.75% increase of efficiency and a decrease of 32.1 kg of weight. For this study, the reference PMSG is out of the limits proposed by the methodology for the 3-D analysis, and therefore, it is not considered for the following analysis.

Machado et al., 2017 [16] optimized a PMSG and reported a maximum efficiency of 94.2% and a power density of 182.5 W/kg for a 50 kW commercial wind turbine; the generator efficiency increase was 2.9%.

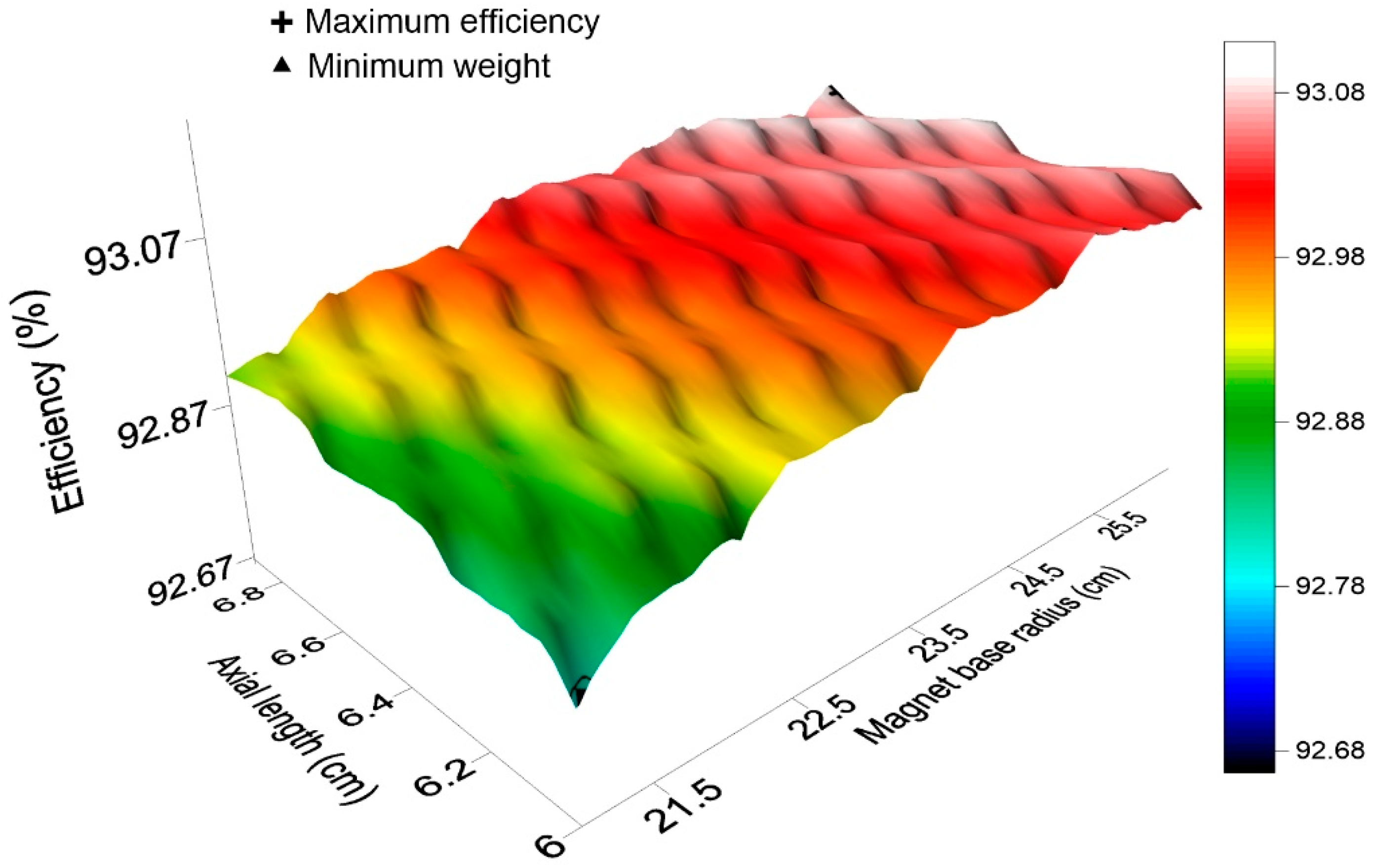
The general graphic of the efficiency behavior for the defined limits by the geometry dimensioning of the lower weight and major efficiency is shown in Figure 5. The radius of the magnet base varies from 21 to 26 cm and the axial length from 6 to 7 cm. Figure 5 shows the geometric limits with respect to the efficiency and there is a variation of 0.4% of the efficiency.

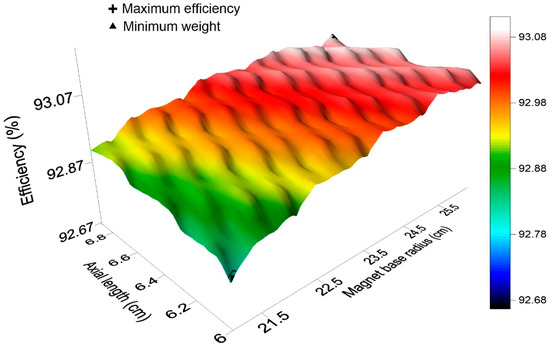
Figure 5. PMSG efficiency behavior as a function of the design limits (obtained from own simulations).

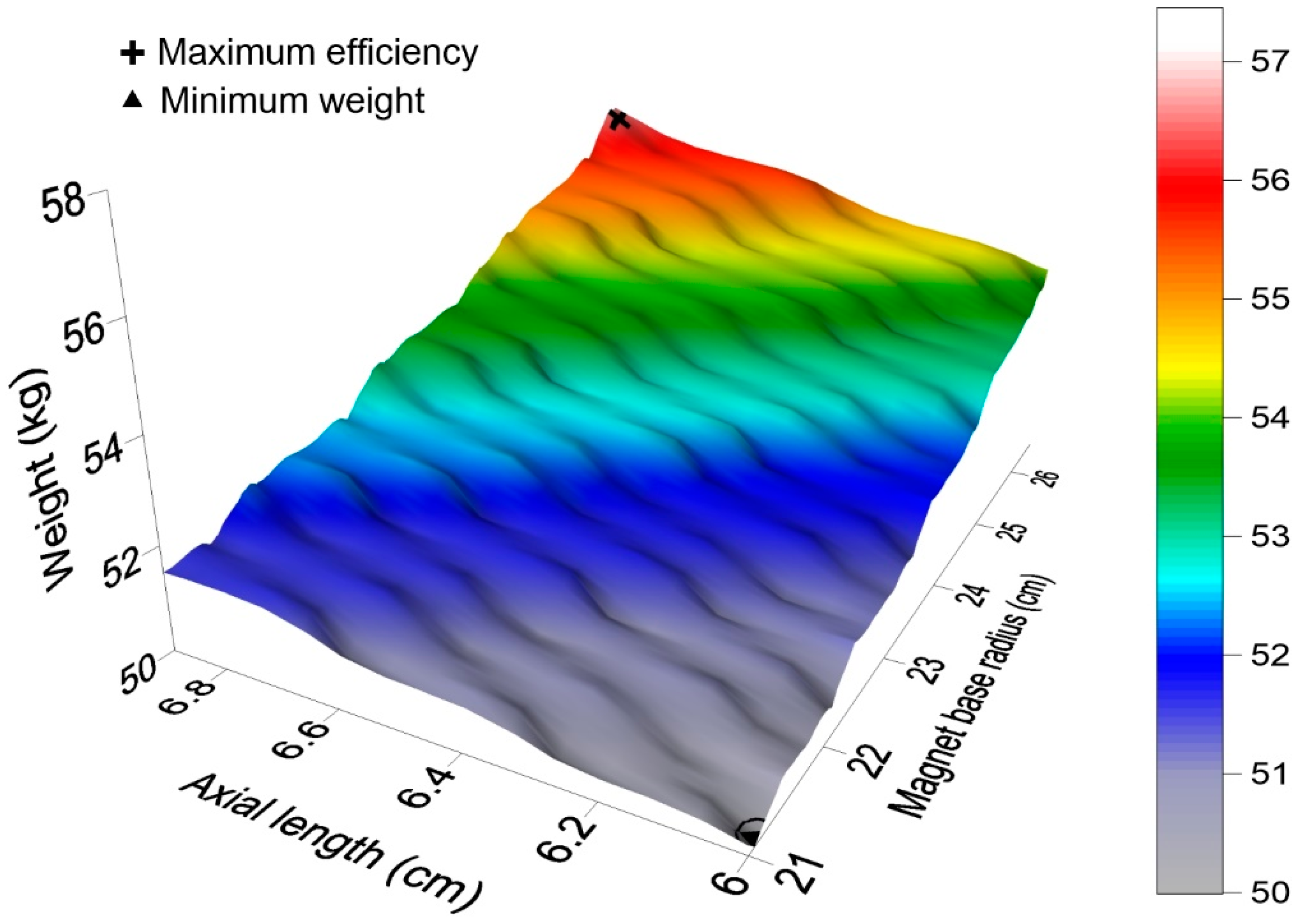
The general graphic of the weight behavior for the same limits established is shown in Figure 6. From this figure can be observed that the weight difference between the PMSG of the maximum efficiency and the PMSG of the minimum weight is 6.86 kg, which implies a difference of 12.16%.

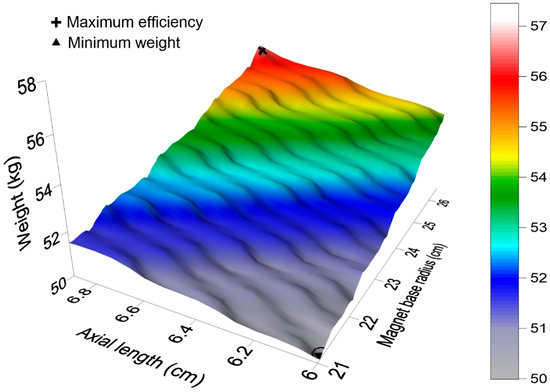
Figure 6. Behavior of the PMSG weight as a function of the design limits (obtained from own simulations).

The data for the coupling analysis of the optimum PMSG and the PMSG reference to the wind rotor for a specific emplacement are shown in Table 4.

Table 4. Emplacement parameters.

Shape factor	1.8
Scale factor	8.43 m/s
Air density	1.225 kg/m3

The parameters of the wind rotor for a 10 kW wind turbine are shown in Table 5.

Table 5. Wind rotor parameters.

Mechanical power	10,974 W
Input speed	3 m/s
Output velocity	18 m/s
Speed of the design	10.7 m/s
Power coefficient	0.4
Lambda of the design	7

Simulation of a Wind Turbine Using the Optimal PMSG Designs

For the coupling simulation, the power coefficient is considered constant since it is also considered that the wind rotor works with the constant specific speed, and it is the same for all simulations. It is considered that the order of variation of the voltages and powers between the PMSGS is very small compared to the order of variation of voltage and power of the converter efficiency curve and therefore its influence on the total efficiency of the system is minimal. In this way, the differences obtained are mainly caused by the PMSG.

The PMSG is simulated using the equations for the losses Equations (3) and (4), the equivalent electrical circuit model, and the power curve of a commercial inverter of the same power.

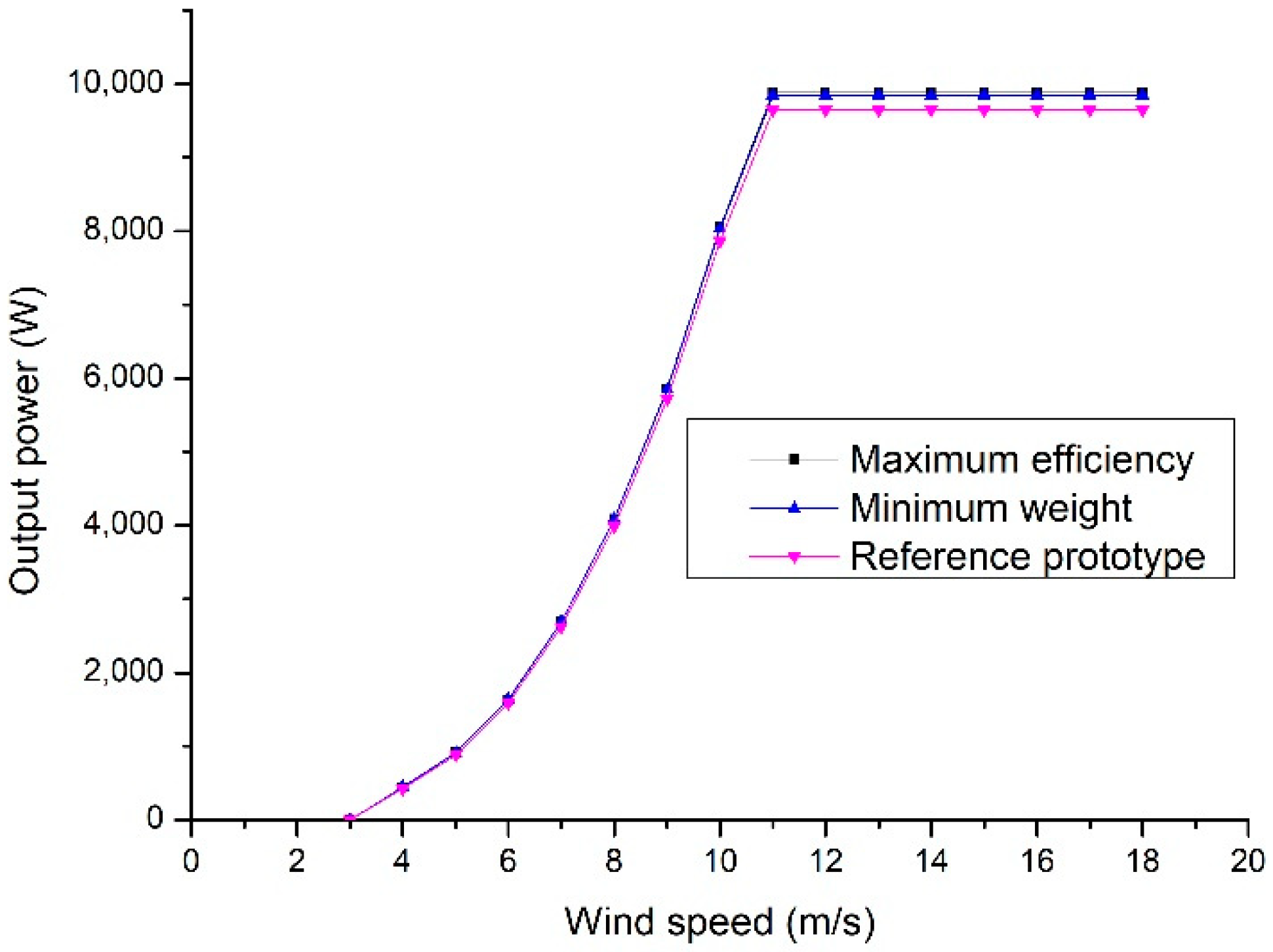
Figure 7 shows the power curves of the simulated PMSG. A nominal power increase of 2.03% for the optimum lower weight PMSG and 2.37% for the optimum maximum efficiency PMSG to the reference PMSG are observed.

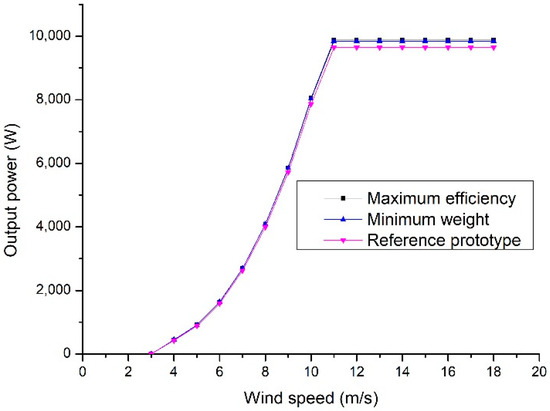
Figure 7. Power output of the analyzed PMSG.

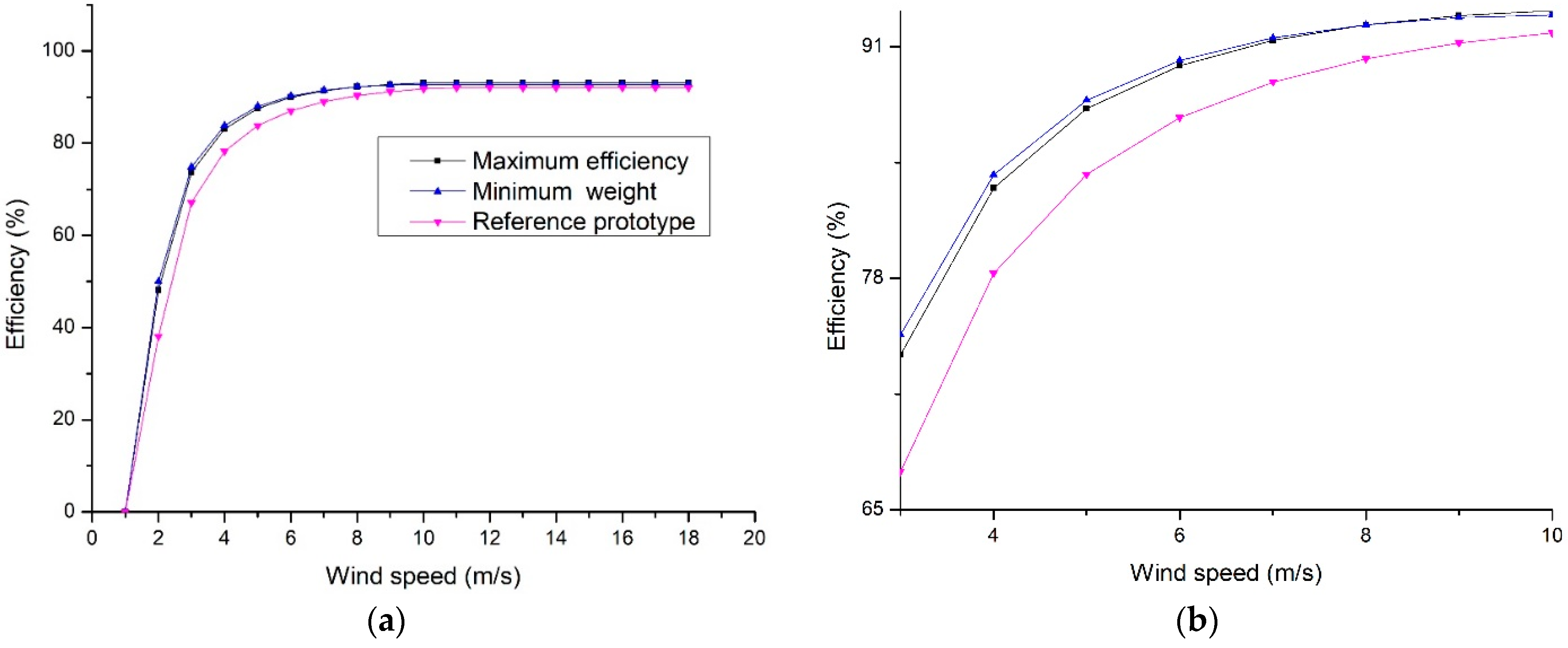
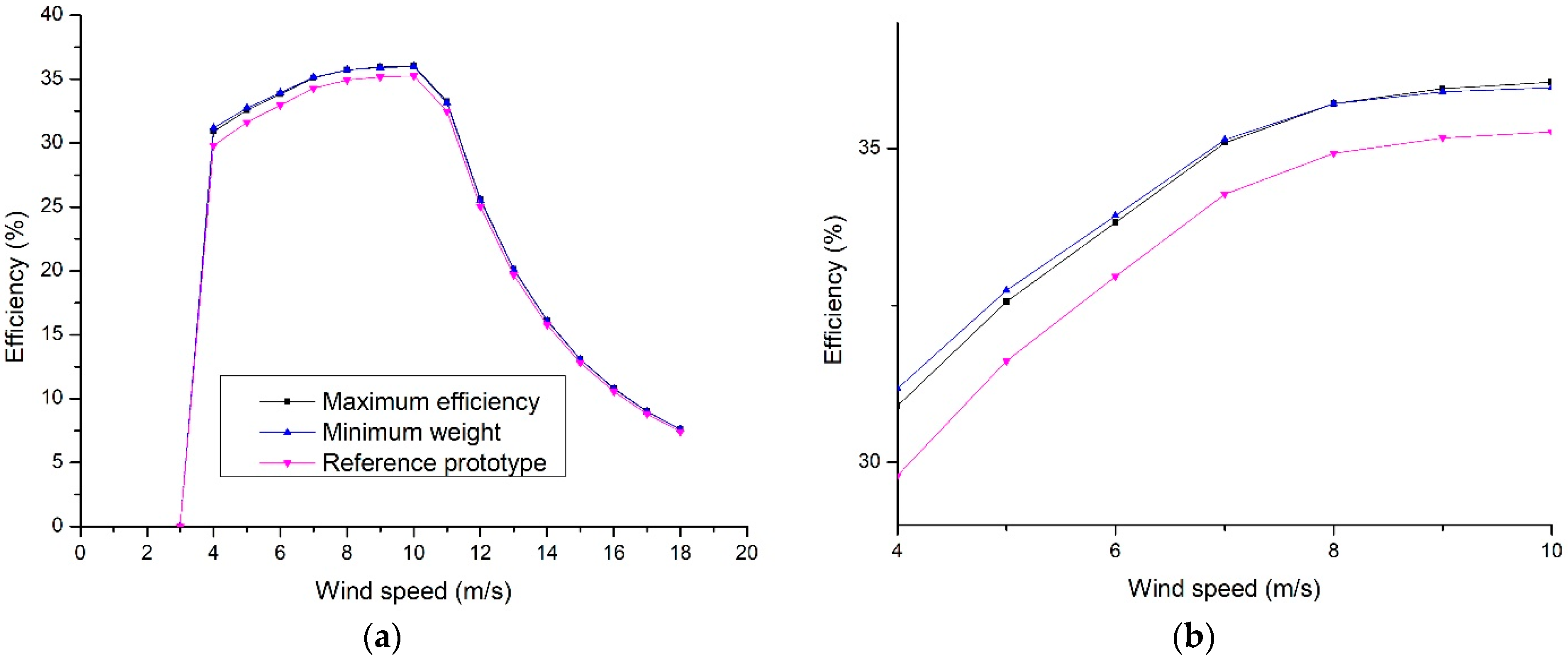
Figure 8a shows the performance of the efficiencies of each PMSG design, and Figure 8b shows the comparison of the reference generator with the optimized generators. It can be observed that from initial speed to nominal speed there is a difference of approximately 10% while at its nominal design speed this difference is 1%. This presumes an important improvement on the PMSG design for its application in wind turbines due to the improvement in the power extraction from the lower speeds as compared to the nominal wind speed.

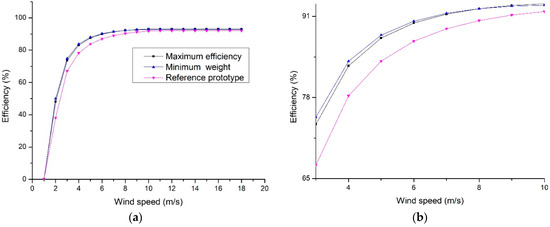
Figure 8. (a) PMSG efficiency as a function of the wind speed; (b) Approach to the variable operating zone.

The total efficiency behavior of the wind turbine is shown in Figure 9a. This is obtained from the multiplication of their component’s efficiencies, namely generator, wind rotor, and inverter. Figure 9b showed that the efficiencies of wind turbines with the optimized PMSGs are higher than that of the reference PMSG for the nominal speed. These efficiency differences are 0.75% and 0.64% higher for the maximum efficiency optimized PMSG and the minimum weight-optimized PMSG respectively and the difference between them is 0.11%. The PMSG of minimum weight has higher efficiency for low wind velocities and therefore the energy use is improving.

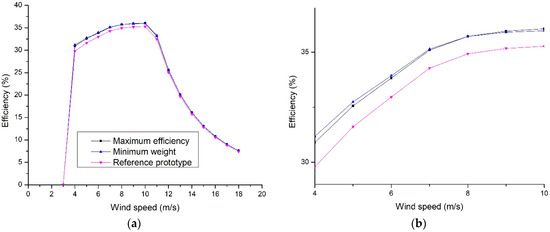
Figure 9. (a) Total efficiency of the system; (b) Approach to the variable operating zone.

To calculate the AEP the data of Table 1 and the PMSGs power curves were used. The results in Table 6 demonstrate the possibility of obtaining a design for higher AEP as compared to that obtained from the prototype. This difference is 794 kWh, and the difference between the minimum weight-optimized PMSG and the maximum efficiency optimized PMSG is 62 kWh.

Table 6. Annual energy production for each PMSG design.

PMGS	AEP (kWh)
Prototype	33,076
Maximum efficiency	33,870
Minimum weight	33,808

4. Conclusions

In the current work, a method that restricts the useful dimensioning options for direct axis wind turbines to a range of magnet radius and lengths (R_bi, L) is developed. This range of R_bi and L values is limited by the points of both maximum efficiency and maximum efficiency with minimum weight, neglecting the rest of the options that imply lower efficiencies and higher weights. In this way, it is established that all the options work with maximum efficiency.

The application of this methodology demonstrated the viability of maximizing the efficiency, reducing the PMSG weight, and improving the AEP and the wind turbines yield at all working speeds of their power curve.

The methodology was validated with a 10 kW wind turbine and two optimum generators were obtained. The results indicated that when they were compared with the reference electric generator results, an increase in efficiency of 1.15% and 0.81% and a reduction in weight of 30.79% and 39.15% of the optimized generators were obtained for maximum efficiency and for minimum weight, respectively. The AEP was estimated from simulation for each generator design and the generator designed for the minimum weight showed higher efficiency compared to the reference generator and the highest energy production was obtained with the design of the generator of maximum efficiency. It is important to highlight that a greater efficiency value was obtained in the region of low wind velocities of the system efficiency curve for the case of the PMSG with minimum weight.